Optimization of Irrigation of Wine Grapes with Brackish Water for Managing Soil Salinization
Abstract
:1. Introduction
2. Materials and Methods
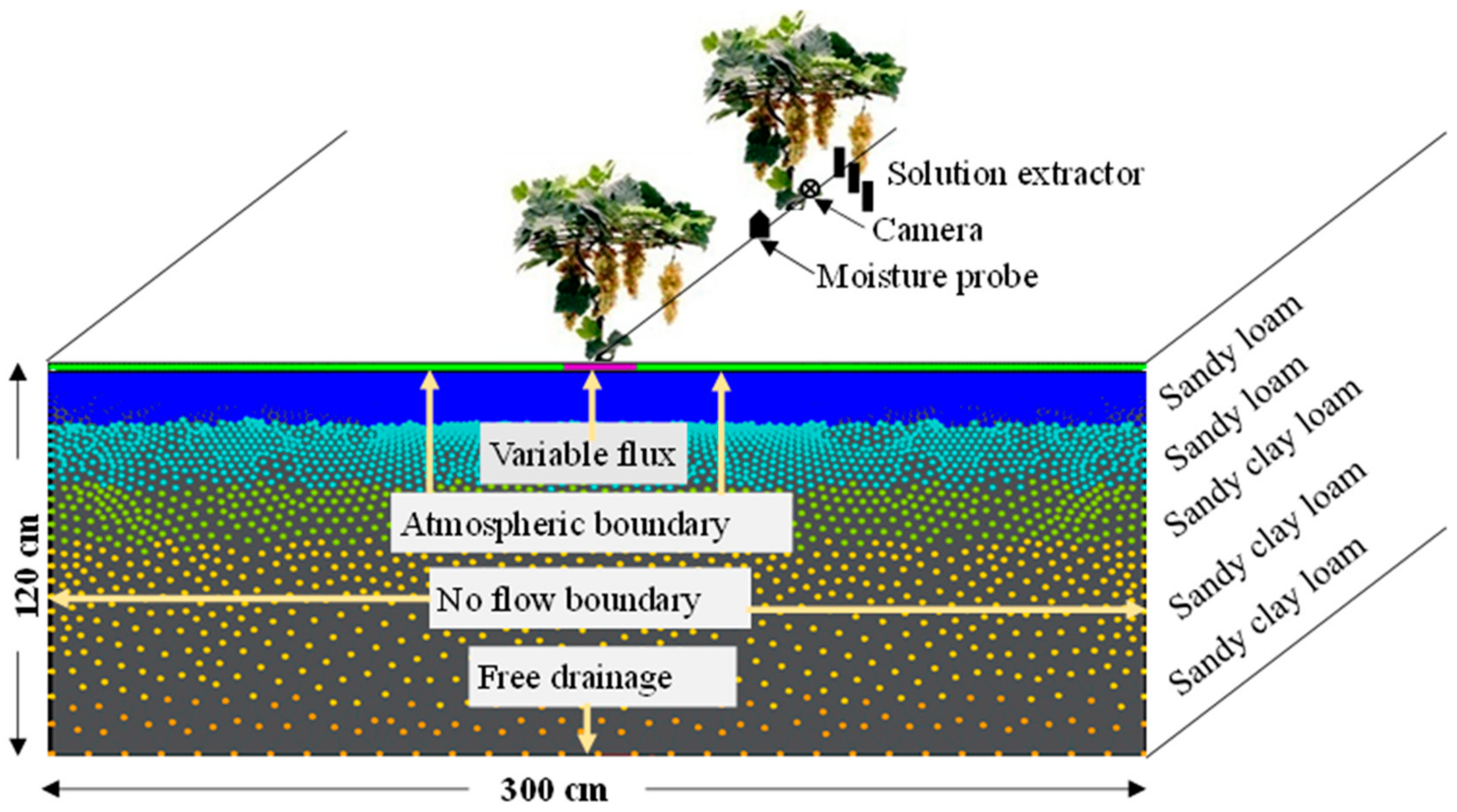
2.1. Description of the Experimental Site
2.2. Soil Water and Canopy Growth Measurements
2.3. Irrigation Application and Water Quality
2.4. Estimation of Soil Hydraulic Properties
2.5. Estimation of Potential Evaporation and Transpiration
2.6. Model Construction, and Initial and Boundary Conditions
2.7. Water Quality and Water Management Scenarios
2.8. Statistical Analysis
3. Results and Discussion
3.1. Model Calibration
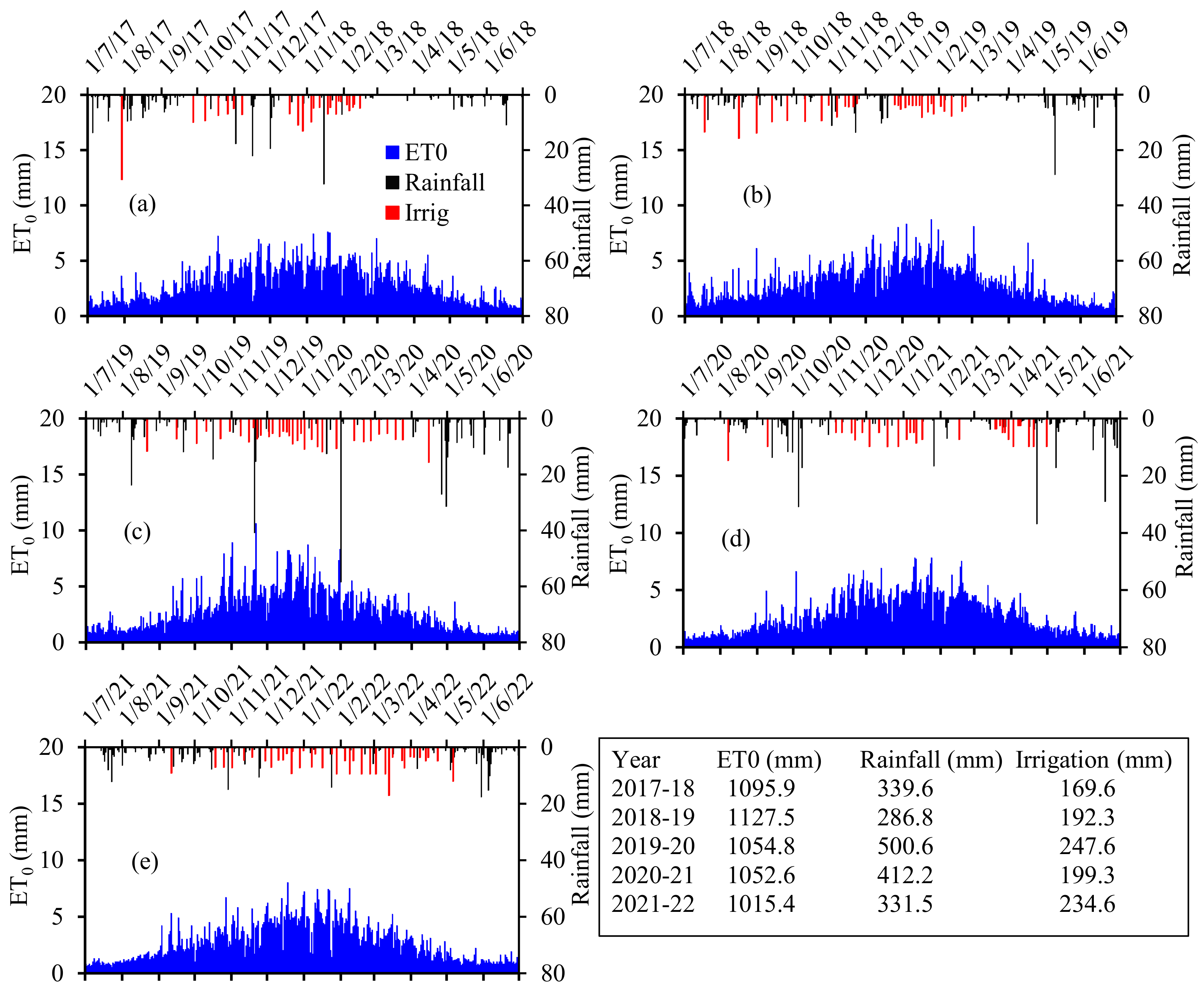
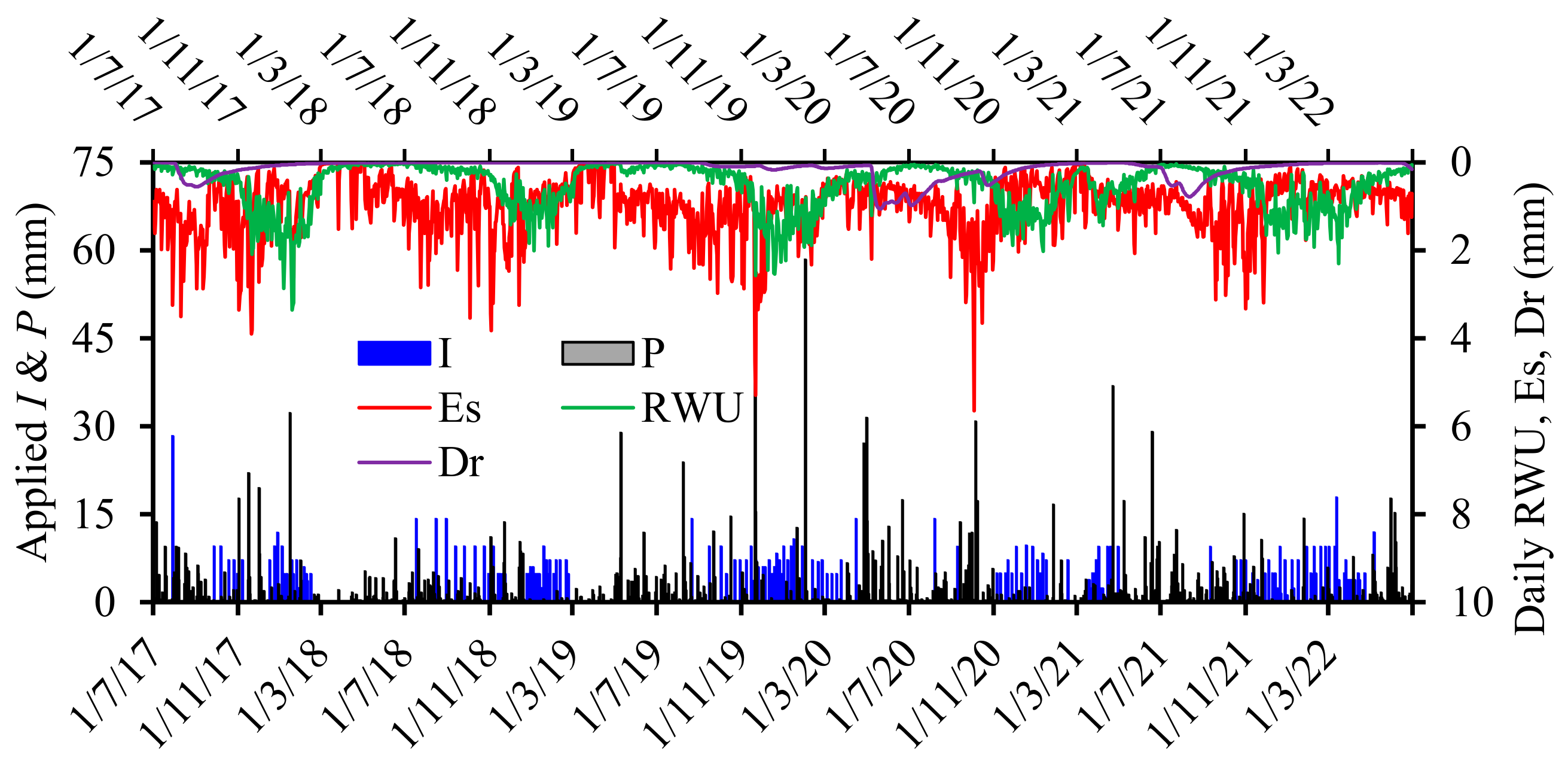
3.2. Soil Water Balance
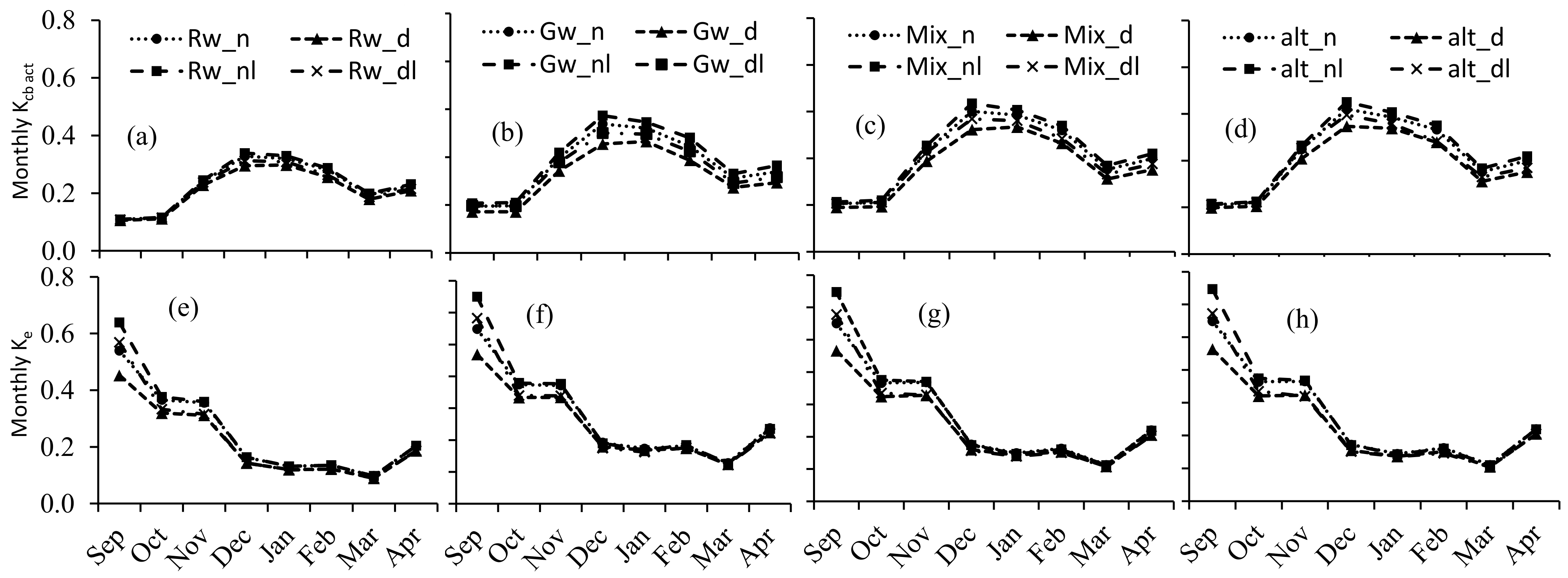
3.3. Crop Coefficients
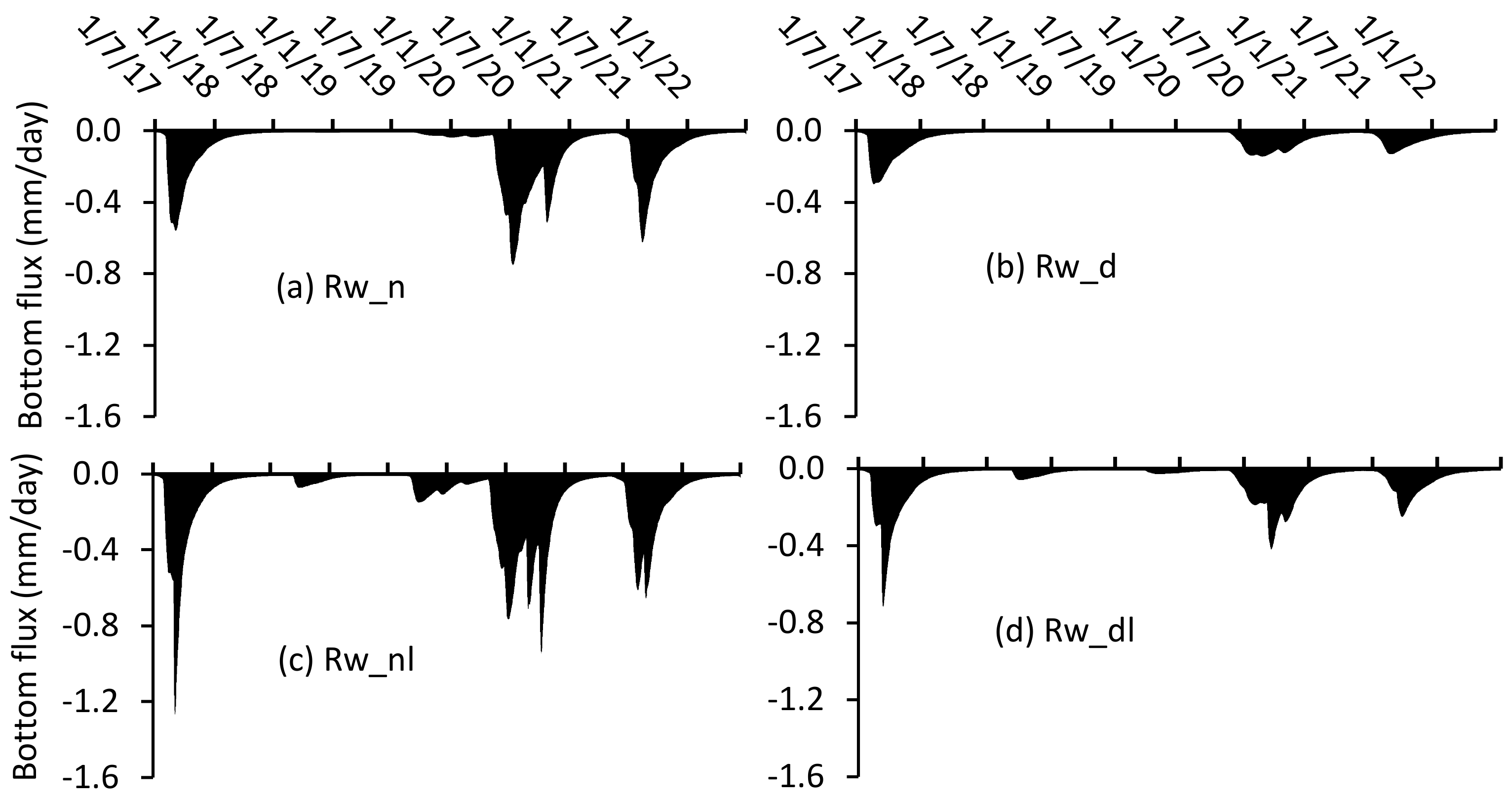
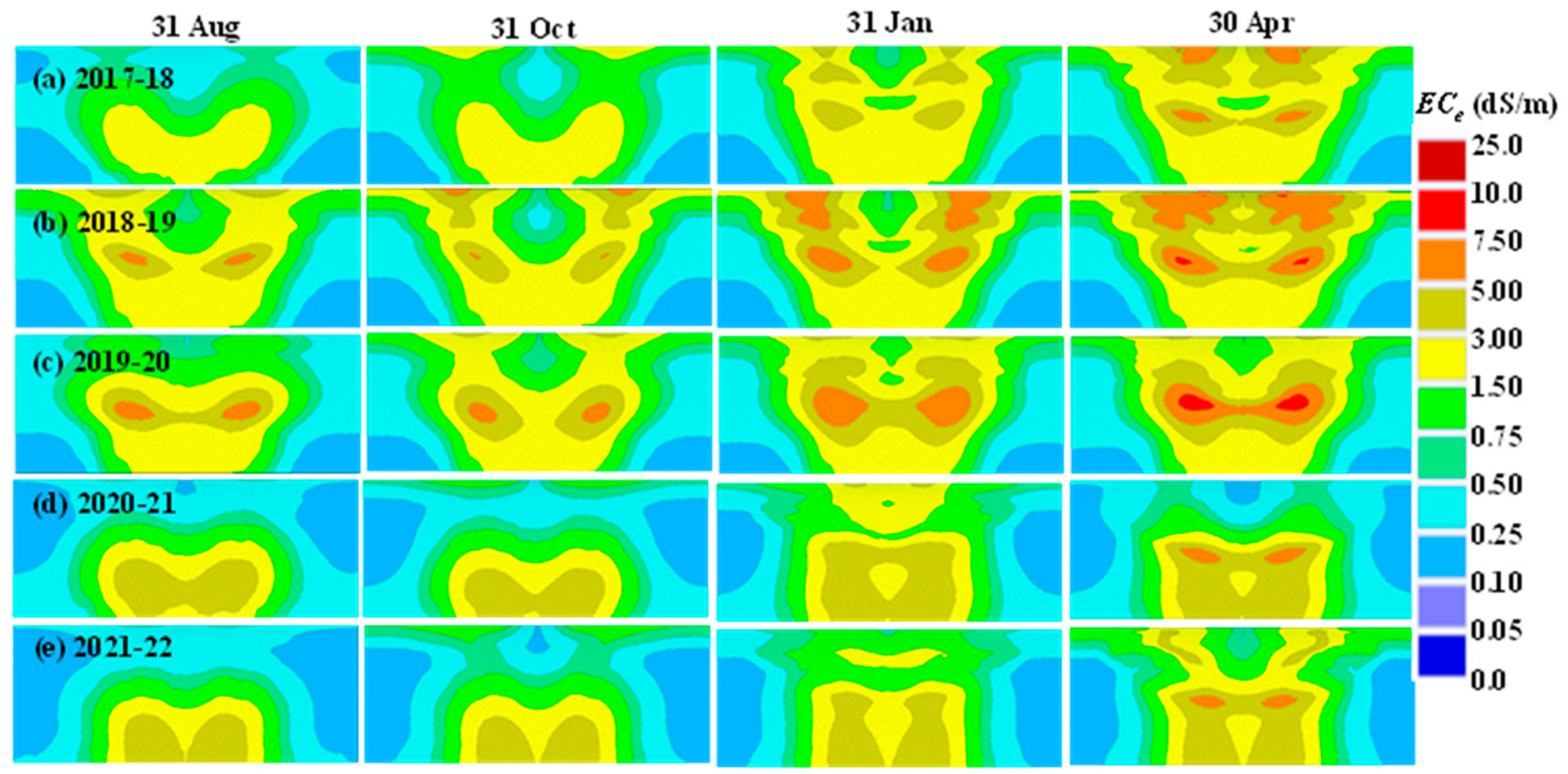
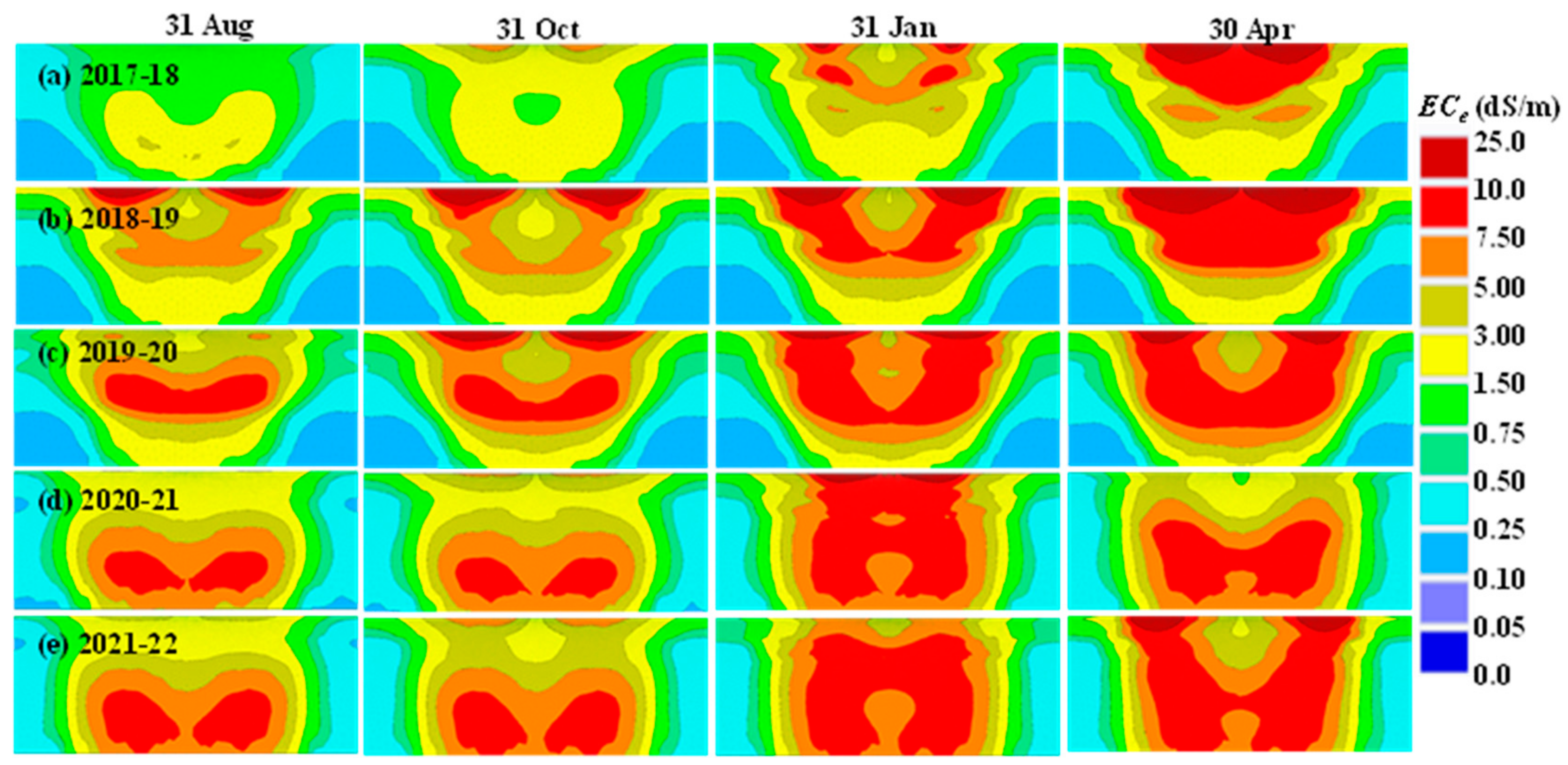
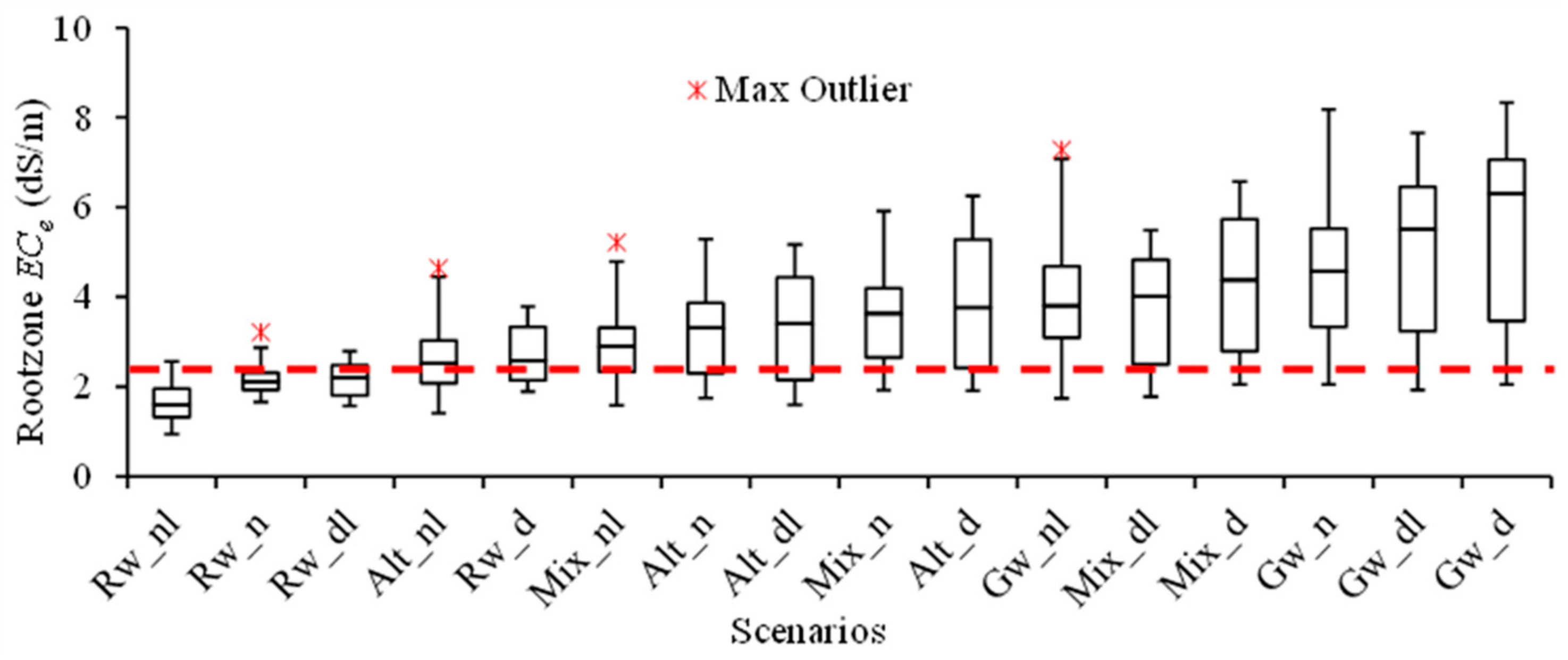
3.4. Salinity Dynamics in Soils
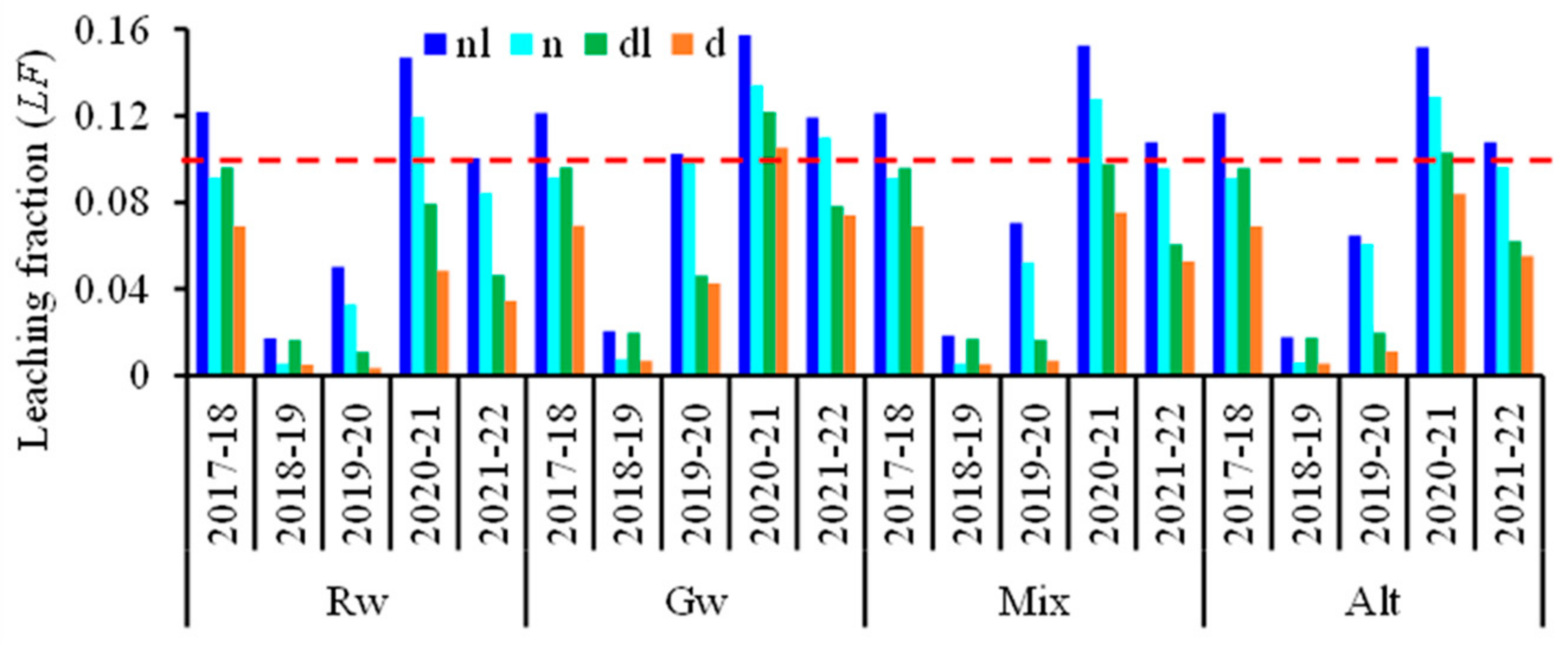
3.5. Leaching Fraction
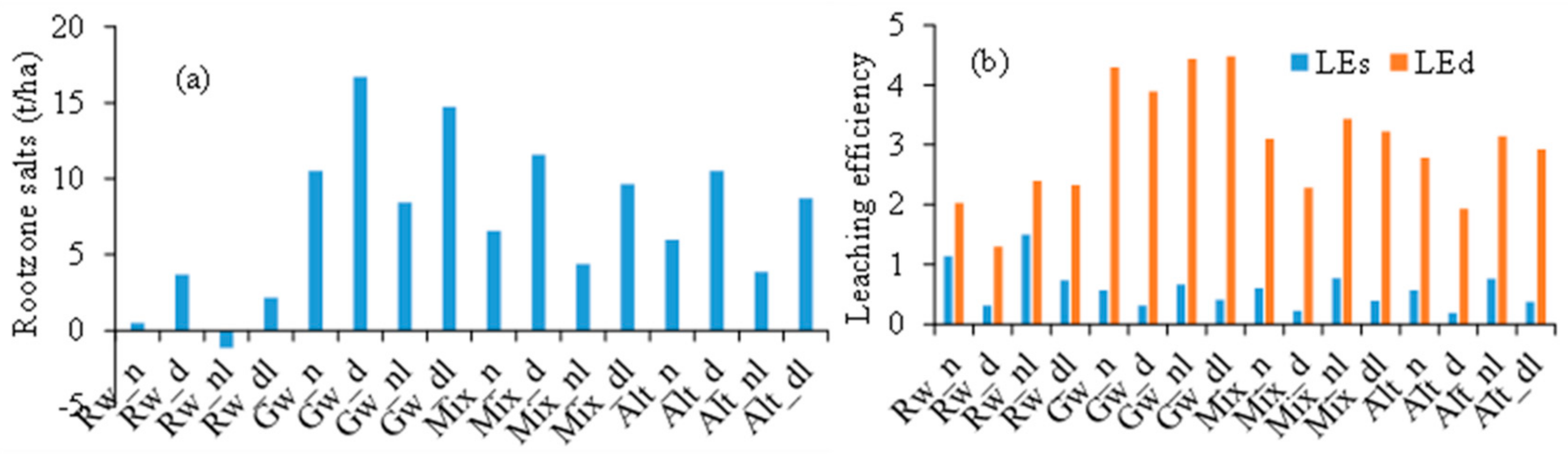
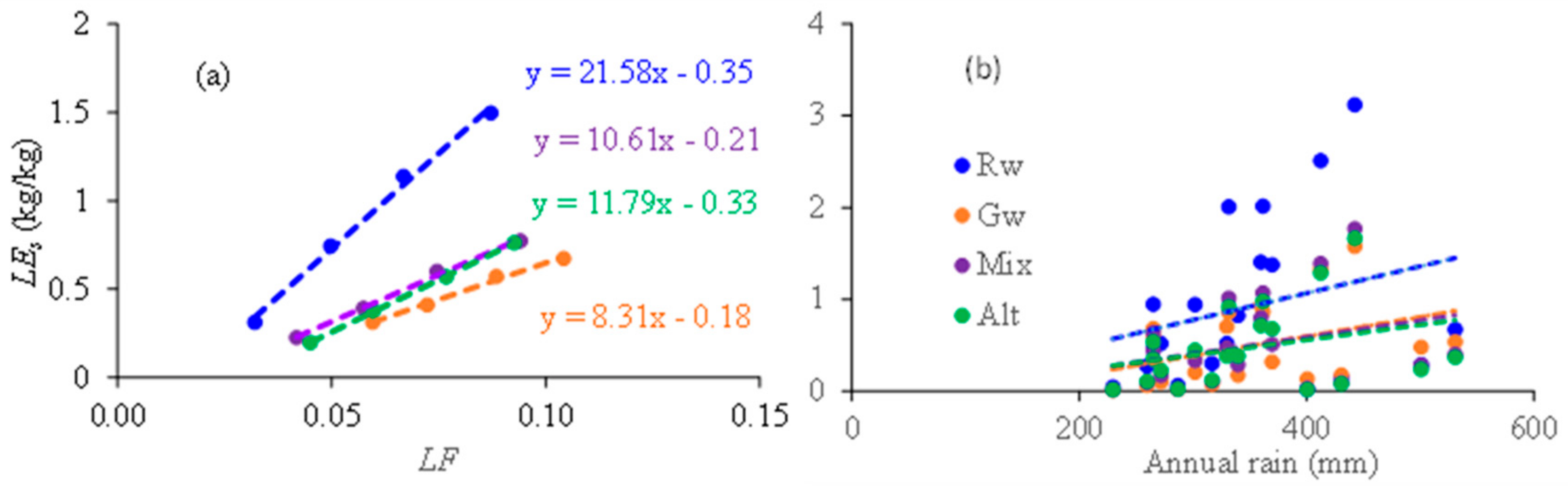
3.6. Leaching Efficiency
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
Appendix A.1. Brief Description of the Model
Appendix A.2. Solute Transport/Salinity Distribution in the Soil
| Parameter | Value | Parameter | Season | Value |
|---|---|---|---|---|
| Lini | 20 | Mid-season Min RH (%) | 2017–18 | 39.2 |
| Ldev | 40 | 2018–19 | 36.9 | |
| Lmid | 120 | 2019–20 | 33.7 | |
| Llate | 60 | 2020–21 | 36.9 | |
| θfc (0–15 cm) | 0.23 | 2021–22 | 41.0 | |
| θfc (15–30 cm) | 0.18 | Mid-season Av. Wind speed (m/s) | 2017–18 | 1.9 |
| θfc (30–60 cm) | 0.31 | 2018–19 | 2.1 | |
| θfc (60–100 cm) | 0.29 | 2019–20 | 2.2 | |
| fw | 0.3 | 2020–21 | 1.8 | |
| fw, Rain | 1 | 2021–22 | 1.8 | |
| RAW (mm) | 84 | Kcb mid adj | 2017–18 | 0.59 |
| TAW (mm) | 153 | 2018–19 | 0.61 | |
| TEW (mm) | 21 | 2019–20 | 0.62 | |
| REW (mm) | 7.4 | 2020–21 | 0.60 | |
| Plant height h (m) | 1.5 | 2021–22 | 0.59 | |
| Rooting depth Zr (m) | 1.0 | Kcb end adj | 2017–18 | 0.46 |
| Evaporable depth Ze (m) | 0.15 | 2018–19 | 0.48 | |
| Kcb ini (generic) 1 | 0.20 | 2019–20 | 0.49 | |
| Kcb mid (generic) 1 | 0.65 | 2020–21 | 0.47 | |
| Kcb end (generic) 1 | 0.50 | 2021–22 | 0.46 |
References
- Döll, P.; Fiedler, K.; Zhang, J. Global-scale analysis of river flow alterations due to water withdrawals and reservoirs. Hydrol. Earth Syst. Sci. 2009, 13, 2413–2432. [Google Scholar] [CrossRef]
- Huang, Z.; Yuan, X.; Liu, X. The key drivers for the changes in global water scarcity: Water withdrawal versus water availability. J. Hydrol. 2021, 601, 126658. [Google Scholar] [CrossRef]
- Wada, Y.; Bierkens, M.F.P. Sustainability of global water use: Past reconstruction and future projections. Environ. Res. Lett. 2014, 9, 104003. [Google Scholar] [CrossRef]
- IPCC. Climate Change 2022: Impacts, Adaptation and Vulnerability; IPCC: Cambridge, MA, USA, 2022; p. 3056. [Google Scholar]
- Riediger, J.; Breckling, B.; Nuske, R.S.; Schröder, W. Will climate change increase irrigation requirements in agriculture of Central Europe? A simulation study for Northern Germany. Environ. Sci. Eur. 2014, 26, 18. [Google Scholar] [CrossRef] [PubMed]
- Yang, H.; Luo, P.; Wang, J.; Mou, C.; Mo, L.; Wang, Z.; Fu, Y.; Lin, H.; Yang, Y.; Bhatta, L.D. Ecosystem Evapotranspiration as a Response to Climate and Vegetation Coverage Changes in Northwest Yunnan, China. PLoS ONE 2015, 10, e0134795. [Google Scholar] [CrossRef] [PubMed]
- Phogat, V.; Cox, J.W.; Šimůnek, J. Identifying the future water and salinity risks to irrigated viticulture in the Murray-Darling Basin, South Australia. Agric. Water Manag. 2018, 201, 107–117. [Google Scholar] [CrossRef]
- Phogat, V.; Cox, J.W.; Mallants, D.; Petrie, P.R.; Oliver, D.P.; Pitt, T.R. Historical and future trends in evapotranspiration components and irrigation requirement of winegrapes. Aust. J. Grape Wine Res. 2020, 26, 312–324. [Google Scholar] [CrossRef]
- Vogel, E.; Donat, M.G.; Alexander, L.V.; Meinshausen, M.; Ray, D.K.; Karoly, D.; Meinshausen, N.; Frieler, K. The effects of climate extremes on global agricultural yields. Environ. Res. Lett. 2019, 145, 054010. [Google Scholar] [CrossRef]
- Bindi, M.; Olesen, J.E. The responses of agriculture in Europe to climate change. Reg. Environ. Chang. 2011, 11, 151–158. [Google Scholar] [CrossRef]
- Iglesias, A.; Garrote, L.; Quiroga, S.; Moneo, M. A regional comparison of the effects of climate change on agricultural crops in Europe. Clim. Chang. 2012, 112, 29–46. [Google Scholar] [CrossRef]
- Fróna, D.; Szenderák, J.; Harangi-Rákos, M. Economic effects of climate change on global agricultural production. Nat. Conserv. 2021, 44, 117–139. [Google Scholar] [CrossRef]
- FAO. AQUASTAT—FAO’s Global Information System on Water and Agriculture; FAO: Rome, Italy, 2023. [Google Scholar]
- UN. The United Nations World Water Development Report 2022: Groundwater: Making the Invisible Visible; UNESCO: Paris, France, 2022. [Google Scholar]
- Assouline, S.; Narkis, K.; Gherabli, R.; Sposito, G. Combined Effect of Sodicity and Organic Matter on Soil Properties under Long-Term Irrigation with Treated Wastewater. Vadose Zone J. 2016, 15, 1–10. [Google Scholar] [CrossRef]
- Díaz, F.J.; Grattan, S.R.; Reyes, J.A.; de la Roza-Delgado, B.; Benes, S.E.; Jiménez, C.; Dorta, M.; Tejedor, M. Using saline soil and marginal quality water to produce alfalfa in arid climates. Agric. Water Manag. 2018, 199, 11–21. [Google Scholar] [CrossRef]
- Grattan, S.R.; Díaz, F.J.; Pedrero, F.; Vivaldi, G.A. Assessing the suitability of saline wastewaters for irrigation of Citrus spp.: Emphasis on boron and specific-ion interactions. Agric. Water Manag. 2015, 157, 48–58. [Google Scholar] [CrossRef]
- Minhas, P.S. Saline water management for irrigation in India. Agric. Water Manag. 1996, 30, 1–24. [Google Scholar] [CrossRef]
- Minhas, P.S.; Qadir, M.; Yadav, R.K. Groundwater irrigation induced soil sodification and response options. Agric. Water Manag. 2019, 215, 74–85. [Google Scholar] [CrossRef]
- Muyen, Z.; Moore, G.A.; Wrigley, R.J. Soil salinity and sodicity effects of wastewater irrigation in South East Australia. Agric. Water Manag. 2011, 99, 33–41. [Google Scholar] [CrossRef]
- Phogat, V.; Mallants, D.; Cox, J.W.; Šimůnek, J.; Oliver, D.P.; Pitt, T.; Petrie, P.R. Impact of long-term recycled water irrigation on crop yield and soil chemical properties. Agric. Water Manag. 2020, 237, 106167. [Google Scholar] [CrossRef]
- Singh, A. Soil salinization management for sustainable development: A review. J. Environ. Manag. 2021, 277, 111383. [Google Scholar] [CrossRef] [PubMed]
- DeGaris, K.A.; Walker, R.R.; Loveys, B.R.; Tyerman, S.D. Impact of deficit irrigation strategies in a saline environment on Shiraz yield, physiology, water use and tissue ion concentration. Aust. J. Grape Wine Res. 2015, 21, 468–478. [Google Scholar] [CrossRef]
- Pitt, T.; Cox, J.; Phogat, V.; Fleming, N.; Grant, C. Methods to Increase the Use of Recycled Wastewater in Irrigation by Overcoming the Constraint of Soil Salinity; Australian Water Recycling Centre of Excellence: Brisbane, Australia, 2015. [Google Scholar]
- Netzer, Y.; Shenker, M.; Schwartz, A. Effects of irrigation using treated wastewater on table grape vineyards: Dynamics of sodium accumulation in soil and plant. Irrig. Sci. 2014, 32, 283–294. [Google Scholar] [CrossRef]
- Stevens, R.M.; Harvey, G.; Partington, D.L. Irrigation of grapevines with saline water at different growth stages: Effects on leaf, wood and juice composition. Aust. J. Grape Wine Res. 2011, 17, 239–248. [Google Scholar] [CrossRef]
- Phogat, V.; Pitt, T.; Stevens, R.M.; Cox, J.W.; Šimůnek, J.; Petrie, P.R. Assessing the role of rainfall redirection techniques for arresting the land degradation under drip irrigated grapevines. J. Hydrol. 2020, 587, 125000. [Google Scholar] [CrossRef]
- Aragüés, R.; Medina, E.T.; Clavería, I.; Martínez-Cob, A.; Faci, J. Regulated deficit irrigation, soil salinization and soil sodification in a table grape vineyard drip-irrigated with moderately saline waters. Agric. Water Manag. 2014, 134, 84–93. [Google Scholar] [CrossRef]
- Stevens, R.M.; Pitt, T.R.; Dyson, C. Changes in vineyard floor management reduce the Na+ and Cl− concentrations in wine grapes grown with saline supplementary drip irrigation. Agric. Water Manag. 2013, 129, 130–137. [Google Scholar] [CrossRef]
- Aragüés, R.; Medina, E.T.; Zribi, W.; Clavería, I.; Álvaro-Fuentes, J.; Faci, J. Soil salinization as a threat to the sustainability of deficit irrigation under present and expected climate change scenarios. Irrig. Sci. 2014, 33, 67–79. [Google Scholar] [CrossRef]
- Phogat, V.; Cox, J.W.; Šimůnek, J.; Hayman, P. Modeling water and salinity risks to viticulture under prolonged sustained deficit and saline water irrigation. J. Water Clim. Chang. 2020, 11, 901–915. [Google Scholar] [CrossRef]
- Feng, D.; Zhang, J.; Cao, C.; Sun, J.; Shao, L.; Li, F.; Dang, H.; Sun, C. Soil Salt Accumulation and Crop Yield under Long-Term Irrigation with Saline Water. J. Irrig. Drain. Eng. 2015, 141, 04015025. [Google Scholar] [CrossRef]
- Murtaza, G.; Ghafoor, A.; Qadir, M. Irrigation and soil management strategies for using saline-sodic water in a cotton–wheat rotation. Agric. Water Manag. 2006, 81, 98–114. [Google Scholar] [CrossRef]
- Mohanavelu, A.; Naganna, S.R.; Al-Ansari, N. Irrigation Induced Salinity and Sodicity Hazards on Soil and Groundwater: An Overview of Its Causes, Impacts and Mitigation Strategies. Agriculture 2021, 11, 983. [Google Scholar] [CrossRef]
- Laurenson, S.; Bolan, N.S.; Smith, E.; McCarthy, M. Review: Use of recycled wastewater for irrigating grapevines. Aust. J. Grape Wine Res. 2012, 18, 1–10. [Google Scholar] [CrossRef]
- Shani, U.; Ben-Gal, A. Long-term Response of Grapevines to Salinity: Osmotic Effects and Ion Toxicity. Am. J. Enol. Vitic. 2005, 56, 148–154. [Google Scholar] [CrossRef]
- Suarez, D.L.; Celis, N.; Anderson, R.G.; Sandhu, D. Grape Rootstock Response to Salinity, Water and Combined Salinity and Water Stresses. Agronomy 2019, 9, 321. [Google Scholar] [CrossRef]
- Walker, R.R. Managing Salinity in the Vineyards; CSIRO Plant Industry: Adelaide, Australia, 2010.
- de Loryn, L.C.; Petrie, P.R.; Hasted, A.M.; Johnson, T.E.; Collins, C.; Bastian, S.E.P. Evaluation of Sensory Thresholds and Perception of Sodium Chloride in Grape Juice and Wine. Am. J. Enol. Vitic. 2014, 65, 124–133. [Google Scholar] [CrossRef]
- Martínez-Moreno, A.; Pérez-Álvarez, E.P.; Intrigliolo, D.S.; Mirás-Avalos, J.M.; López-Urrea, R.; Gil-Muñoz, R.; Lizama, V.; García-Esparza, M.J.; Álvarez, M.I.; Buesa, I. Effects of deficit irrigation with saline water on yield and grape composition of Vitis vinifera L. cv. Monastrell. Irrig. Sci. 2022, 41, 469–485. [Google Scholar] [CrossRef]
- Martínez-Moreno, A.; Pérez-Álvarez, E.; López-Urrea, R.; Intrigliolo, D.; González-Centeno, M.R.; Teissedre, P.-L.; Gil-Muñoz, R. Is deficit irrigation with saline waters a viable alternative for winegrowers in semiarid areas? OENO ONE 2022, 56, 101–116. [Google Scholar] [CrossRef]
- Ayers, R.S.; Westcot, D.W. Water Quality for Agriculture; Food and Agriculture Organisation: Rome, Italy, 1994. [Google Scholar]
- Dudley, L.M.; Ben-Gal, A.; Shani, U. Influence of Plant, Soil, and Water on the Leaching Fraction. Vadose Zone J. 2008, 7, 420–425. [Google Scholar] [CrossRef]
- Hanson, B.; Hopmans, J.W.; Simunek, J. Leaching with subsurface drip irrigation under saline, shallow groundwater conditions. Vadose Zone J. 2008, 7, 810–818. [Google Scholar] [CrossRef]
- Minhas, P.S.; Dubey, S.K.; Sharma, D.R. Comparative affects of blending, intera/inter-seasonal cyclic uses of alkali and good quality waters on soil properties and yields of paddy and wheat. Agric. Water Manag. 2007, 87, 83–90. [Google Scholar] [CrossRef]
- Phogat, V.; Mallants, D.; Šimůnek, J.; Cox, J.W.; Petrie, P.R.; Pitt, T. Modelling Salinity and Sodicity Risks of Long-Term Use of Recycled Water for Irrigation of Horticultural Crops. Soil Syst. 2021, 5, 49. [Google Scholar] [CrossRef]
- Ben-Gal, A.; Yermiyahu, U.; Cohen, S. Fertilization and blending alternatives for irrigation with desalinated water. J. Environ. Qual. 2009, 38, 529–536. [Google Scholar] [CrossRef] [PubMed]
- Naresh, R.K.; Minhas, P.S.; Goyal, A.K.; Chauhan, C.P.S.; Gupta, R.K. Conjunctive use of saline and non-saline waters. II. Field comparisions of cyclic uses and mixing for wheat. Agric. Water Manag. 1993, 23, 139–148. [Google Scholar] [CrossRef]
- Phogat, V.; Mallants, D.; Cox, J.W.; Šimůnek, J.; Oliver, D.P.; Awad, J. Management of soil salinity associated with irrigation of protected crops. Agric. Water Manag. 2020, 227, 105845. [Google Scholar] [CrossRef]
- Ben-Gal, A.; Ityel, E.; Dudley, L.; Cohen, S.; Yermiyahu, U.; Presnov, E.; Zigmond, L.; Shani, U. Effect of irrigation water salinity on transpiration and on leaching requirements: A case study for bell peppers. Agric. Water Manag. 2008, 95, 587–597. [Google Scholar] [CrossRef]
- Singh, A. Environmental problems of salinization and poor drainage in irrigated areas: Management through the mathematical models. J. Clean. Prod. 2019, 206, 572–579. [Google Scholar] [CrossRef]
- Wichelns, D.; Qadir, M. Achieving sustainable irrigation requires effective management of salts, soil salinity, and shallow groundwater. Agric. Water Manag. 2015, 157, 31–38. [Google Scholar] [CrossRef]
- Šimůnek, J.; van Genuchten, M.T.; Sejna, M. Recent developments and applications of the HYDRUS computer software packages. Vadose Zone J. 2016, 15, 1–25. [Google Scholar] [CrossRef]
- Chen, L.-J.; Feng, Q.; Li, F.-R.; Li, C.-S. Simulation of soil water and salt transfer under mulched furrow irrigation with saline water. Geoderma 2015, 241–242, 87–96. [Google Scholar] [CrossRef]
- Phogat, V.; Skewes, M.A.; Cox, J.W.; Sanderson, G.; Alam, J.; Šimůnek, J. Seasonal simulation of water, salinity and nitrate dynamics under drip irrigated mandarin (Citrus reticulata) and assessing management options for drainage and nitrate leaching. J. Hydrol. 2014, 513, 504–516. [Google Scholar] [CrossRef]
- Mallants, D.; Phogat, V.; Oliver, D.; Ouzman, J.; Beirgadhar, Y.; Cox, J.W. Sustainable Expansion of Irrigated Agriculture and Horticulture in Northern Adelaide Corridor; Technical Report Series No. 19/15; Goyder Institute for Water Research: Adelaide, SA, Australia, 2019. [Google Scholar]
- Ramos, T.B.; Šimůnek, J.; Gonçalves, M.C.; Martins, J.C.; Prazeres, A.; Pereira, L.S. Two-dimensional modeling of water and nitrogen fate from sweet sorghum irrigated with fresh and blended saline waters. Agric. Water Manag. 2012, 111, 87–104. [Google Scholar] [CrossRef]
- Selim, T.; Bouksila, F.; Berndtsson, R.; Persson, M. Soil Water and Salinity Distribution under Different Treatments of Drip Irrigation. Soil Sci. Soc. Am. J. 2013, 77, 1144–1156. [Google Scholar] [CrossRef]
- Cresswell, R.G.; Herczeg, A.L. Groundwater Recharge, Mixing and Salinity Across the Angas-Bremer Plains, South Australia: Geochemical and Isotopic Constraints; CSIRO Land and Water: Canberra, Australia, 2004.
- Allen, R.G.; Pereira, L.S.; Raes, D.; Smith, M. Crop Evapotranspiration: Guidelines for Computing Crop Water Requirements; 9251042195; FAO: Rome, Italy, 1998. [Google Scholar]
- De Bei, R.; Fuentes, S.; Gilliham, M.; Tyerman, S.; Edwards, E.; Bianchini, N.; Smith, J.; Collins, C. VitiCanopy: A Free Computer App to Estimate Canopy Vigor and Porosity for Grapevine. Sensors 2016, 16, 585. [Google Scholar] [CrossRef] [PubMed]
- Fuentes, S.; Bei, R.; Pozo, C.; Tyerman, S. Development of a smartphone application to characterise temporal and spatial canopy architecture and leaf area index for grapevines. Wine Vitic. J. 2012, 6, 56–60. [Google Scholar]
- Fuentes, S.; Poblete-Echeverría, C.; Ortega-Farias, S.; Tyerman, S.; De Bei, R. Automated estimation of leaf area index from grapevine canopies using cover photography, video and computational analysis methods. Aust. J. Grape Wine Res. 2014, 20, 465–473. [Google Scholar] [CrossRef]
- Macfarlane, C.; Hoffman, M.; Eamus, D.; Kerp, N.; Higginson, S.; McMurtrie, R.; Adams, M. Estimation of leaf area index in eucalypt forest using digital photography. Agric. For. Meteorol. 2007, 143, 176–188. [Google Scholar] [CrossRef]
- Ben-Asher, J.; Tsuyuki, I.; Bravdo, B.-A.; Sagih, M. Irrigation of grapevines with saline water. I. Leaf area index, stomatal conductance, transpiration, and photosynthesis. Agric. Water Manag. 2006, 83, 13–21. [Google Scholar] [CrossRef]
- Yunusa, I.A.M.; Walker, R.R.; Blackmore, D.H. Characterisation of water use by Sultana grapevines (Vitis vinifera L.) on their own roots or on Ramsey rootstock drip-irrigated with water of different salinities. Irrig. Sci. 1997, 17, 77–86. [Google Scholar] [CrossRef]
- Vélez, S.; Poblete-Echeverría, C.; Rubio, J.A.; Vacas, R.; Barajas, E. Estimation of Leaf Area Index in vineyards by analysing projected shadows using UAV imagery. OENO ONE 2021, 55, 159–180. [Google Scholar] [CrossRef]
- Allen, R.G.; Pereira, L.S. Estimating crop coefficients from fraction of ground cover and height. Irrig. Sci. 2009, 28, 17–34. [Google Scholar] [CrossRef]
- Anzecc, A. National Water Quality Management Strategy: Australian and New Zealand Guidelines for Fresh and Marine Water Quality: Volume 1: The Guidelines (Chapters 1–7); Australian and New Zealand Environment and Conservation Council and the Agriculture and Resource Management Council of Australia and New Zealand: Canberra, Austrilia, 2000.
- Youngs, E.G. Hydraulic conductivity of saturated soils. In Soil and Environmental Analysis: Physical Methods; Smith, K.A., Mullins, C.E., Eds.; Marcel Dekker, Inc.: New York, NY, USA, 2001; pp. 141–181. [Google Scholar]
- Van Genuchten, M.T. A Closed-form Equation for Predicting the Hydraulic Conductivity of Unsaturated Soils. Soil Sci. Soc. Am. J. 1980, 44, 892–898. [Google Scholar] [CrossRef]
- Phogat, V.; Skewes, M.A.; McCarthy, M.G.; Cox, J.W.; Šimůnek, J.; Petrie, P.R. Evaluation of crop coefficients, water productivity, and water balance components for wine grapes irrigated at different deficit levels by a sub-surface drip. Agric. Water Manag. 2017, 180, 22–34. [Google Scholar] [CrossRef]
- Skaggs, T.H.; Trout, T.J.; Šim Nek, J.; Shouse, P.J. Comparison of HYDRUS-2D Simulations of Drip Irrigation with Experimental Observations. J. Irrig. Drain. Eng. 2004, 130, 304–310. [Google Scholar] [CrossRef]
- Feddes, R.A.; Kowalik, P.J.; Zaradny, H. Simulation of Field Water Use and Crop Yield; Pudoc for the Centre for Agricultural Publishing and Documentation: Wageningen, The Netherlands, 1978.
- Zhang, X.; Walker, R.R.; Stevens, R.M.; Prior, L.D. Yield-salinity relationships of different grapevine (Vitis vinifera L.) scion-rootstock combinations. Aust. J. Grape Wine Res. 2002, 8, 150–156. [Google Scholar] [CrossRef]
- Wang, J.; Bai, Z.; Yang, P. Simulation and prediction of ion transport in the reclamation of sodic soils with gypsum based on the support vector machine. Sci. World J. 2014, 2014, 805342. [Google Scholar] [CrossRef] [PubMed]
- Cote, C.M.; Bristow, K.L.; Charlesworth, P.B.; Cook, F.J.; Thorburn, P.J. Analysis of soil wetting and solute transport in subsurface trickle irrigation. Irrig. Sci. 2003, 22, 143–156. [Google Scholar] [CrossRef]
- Charles, S.P.; Fu, G. Statistically Downscaled Projections for South Australia; Technical Report No. 15/1; Goyder Institute for Water Research: Adelaide, Australia, 2015. [Google Scholar]
- Stirzaker, R.; Thomson, T. Fullstop at Angas Bremer: A Report on the 2002–03 Data; CSIRO: Canberra, Australia, 2004.
- Willmott, C.J.; Matsuura, K. Advantages of the mean absolute error (MAE) over the root mean square error (RMSE) in assessing average model performance. Clim. Res. 2005, 30, 79–82. [Google Scholar] [CrossRef]
- Li, H.; Yi, J.; Zhang, J.; Zhao, Y.; Si, B.; Hill, R.; Cui, L.; Liu, X. Modeling of Soil Water and Salt Dynamics and Its Effects on Root Water Uptake in Heihe Arid Wetland, Gansu, China. Water 2015, 7, 2382–2401. [Google Scholar] [CrossRef]
- Ramos, T.B.; Liu, M.; Paredes, P.; Shi, H.; Feng, Z.; Lei, H.; Pereira, L.S. Salts dynamics in maize irrigation in the Hetao plateau using static water table lysimeters and HYDRUS-1D with focus on the autumn leaching irrigation. Agric. Water Manag. 2023, 283, 108306. [Google Scholar] [CrossRef]
- Evett, S.R.; Schwartz, R.C.; Casanova, J.J.; Heng, L.K. Soil water sensing for water balance, ET and WUE. Agric. Water Manag. 2012, 104, 1–9. [Google Scholar] [CrossRef]
- Phogat, V.; Pitt, T.; Cox, J.W.; Šimůnek, J.; Skewes, M.A. Soil water and salinity dynamics under sprinkler irrigated almond exposed to a varied salinity stress at different growth stages. Agric. Water Manag. 2018, 201, 70–82. [Google Scholar] [CrossRef]
- Phogat, V.; Mahalakshmi, M.; Skewes, M.; Cox, J.W. Modelling soil water and salt dynamics under pulsed and continuous surface drip irrigation of almond and implications of system design. Irrig. Sci. 2012, 30, 315–333. [Google Scholar] [CrossRef]
- López-Urrea, R.; Montoro, A.; Mañas, F.; López-Fuster, P.; Fereres, E. Evapotranspiration and crop coefficients from lysimeter measurements of mature ‘Tempranillo’ wine grapes. Agric. Water Manag. 2012, 112, 13–20. [Google Scholar] [CrossRef]
- Pereira, L.S.; Paredes, P.; Melton, F.; Johnson, L.; Wang, T.; López-Urrea, R.; Cancela, J.J.; Allen, R.G. Prediction of crop coefficients from fraction of ground cover and height. Background and validation using ground and remote sensing data. Agric. Water Manag. 2020, 241, 106197. [Google Scholar] [CrossRef]
- Williams, L.E.; Ayars, J.E. Grapevine water use and the crop coefficient are linear functions of the shaded area measured beneath the canopy. Agric. For. Meteorol. 2005, 132, 201–211. [Google Scholar] [CrossRef]
- Pereira, L.S.; Paredes, P.; Melton, F.; Johnson, L.; Mota, M.; Wang, T. Prediction of crop coefficients from fraction of ground cover and height: Practical application to vegetable, field and fruit crops with focus on parameterization. Agric. Water Manag. 2021, 252, 106663. [Google Scholar] [CrossRef]
- Rallo, G.; Paço, T.A.; Paredes, P.; Puig-Sirera, À.; Massai, R.; Provenzano, G.; Pereira, L.S. Updated single and dual crop coefficients for tree and vine fruit crops. Agric. Water Manag. 2021, 250, 106645. [Google Scholar] [CrossRef]
- Ben-Asher, J.; van Dam, J.; Feddes, R.A.; Jhorar, R.K. Irrigation of grapevines with saline water: II. Mathematical simulation of vine growth and yield. Agric. Water Manag. 2006, 83, 22–29. [Google Scholar] [CrossRef]
- Ben-Gal, A.; Karlberg, L.; Jansson, P.-E.; Shani, U. Temporal robustness of linear relationships between production and transpiration. Plant Soil 2003, 251, 211–218. [Google Scholar] [CrossRef]
- Shani, U.; Ben-Gal, A.; Tripler, E.; Dudley, L.M. Plant response to the soil environment: An analytical model integrating yield, water, soil type, and salinity. Water Resour. Res. 2007, 43. [Google Scholar] [CrossRef]
- Bhantana, P.; Lazarovitch, N. Evapotranspiration, crop coefficient and growth of two young pomegranate (Punica granatum L.) varieties under salt stress. Agric. Water Manag. 2010, 97, 715–722. [Google Scholar] [CrossRef]
- Skaggs, T.H.; Shouse, P.J.; Poss, J.A. Irrigating Forage Crops with Saline Waters: 2. Modeling Root Uptake and Drainage. Vadose Zone J. 2006, 5, 824–837. [Google Scholar] [CrossRef]
- Keller, M. Chapter 3—Water Relations and Nutrient Uptake. In The Science of Grapevines, 2nd ed.; Keller, M., Ed.; Academic Press: San Diego, CA, USA, 2015; pp. 101–124. [Google Scholar]
- Yunusa, I.A.M.; Walker, R.R.; Guy, J.R. Partitioning of seasonal evapotranspiration from a commercial furrow-irrigated Sultana vineyard. Irrig. Sci. 1997, 18, 45–54. [Google Scholar] [CrossRef]
- Fandiño, M.; Cancela, J.J.; Rey, B.J.; Martínez, E.M.; Rosa, R.G.; Pereira, L.S. Using the dual-Kc approach to model evapotranspiration of Albariño vineyards (Vitis vinifera L. cv. Albariño) with consideration of active ground cover. Agric. Water Manag. 2012, 112, 75–87. [Google Scholar] [CrossRef]
- Kool, D.; Agam, N.; Lazarovitch, N.; Heitman, J.L.; Sauer, T.J.; Ben-Gal, A. A review of approaches for evapotranspiration partitioning. Agric. For. Meteorol. 2014, 184, 56–70. [Google Scholar] [CrossRef]
- Aquaterra. Angas-Bremer and Currency Creek Flow and Solute Transport Model- AB2010; Aquaterra: Adelaide, Australia, 2010. [Google Scholar]
- Silva, S.P.; Valín, M.I.; Mendes, S.; Araujo-Paredes, C.; Cancela, J.J. Dual Crop Coefficient Approach in Vitis vinifera L. cv. Loureiro. Agronomy 2021, 11, 2062. [Google Scholar] [CrossRef]
- Williams, L.E.; Phene, C.J.; Grimes, D.W.; Trout, T.J. Water use of mature Thompson Seedless grapevines in California. Irrig. Sci. 2003, 22, 11–18. [Google Scholar] [CrossRef]
- Cancela, J.J.; Fandiño, M.; Rey, B.J.; Martínez, E.M. Automatic irrigation system based on dual crop coefficient, soil and plant water status for Vitis vinifera (cv Godello and cv Mencía). Agric. Water Manag. 2015, 151, 52–63. [Google Scholar] [CrossRef]
- Rosa, R.D.; Ramos, T.B.; Pereira, L.S. The dual Kc approach to assess maize and sweet sorghum transpiration and soil evaporation under saline conditions: Application of the SIMDualKc model. Agric. Water Manag. 2016, 177, 77–94. [Google Scholar] [CrossRef]
- Morgani, M.B.; Peña, J.E.P.; Fanzone, M.; Prieto, J.A. Pruning after budburst delays phenology and affects yield components, crop coefficient and total evapotranspiration in Vitis vinífera L. cv. ‘Malbec’ in Mendoza, Argentina. Sci. Hortic. 2022, 296, 110886. [Google Scholar] [CrossRef]
- Poblete-Echeverría, C.; Sepúlveda-Reyes, D.; Zúñiga, M.; Ortega-Farías, S. Grapevine crop coefficient (Kc) determined by surface renewal method at different phenological periods. Acta Hortic. 2017, 1150, 61–66. [Google Scholar] [CrossRef]
- Darouich, H.; Ramos, T.B.; Pereira, L.S.; Rabino, D.; Bagagiolo, G.; Capello, G.; Simionesei, L.; Cavallo, E.; Biddoccu, M. Water Use and Soil Water Balance of Mediterranean Vineyards under Rainfed and Drip Irrigation Management: Evapotranspiration Partition and Soil Management Modelling for Resource Conservation. Water 2022, 14, 554. [Google Scholar] [CrossRef]
- Munitz, S.; Schwartz, A.; Netzer, Y. Water consumption, crop coefficient and leaf area relations of a Vitis vinifera cv. ‘Cabernet Sauvignon’ vineyard. Agric. Water Manag. 2019, 219, 86–94. [Google Scholar] [CrossRef]
- Wang, S.; Zhu, G.; Xia, D.; Ma, J.; Han, T.; Ma, T.; Zhang, K.; Shang, S. The characteristics of evapotranspiration and crop coefficients of an irrigated vineyard in arid Northwest China. Agric. Water Manag. 2019, 212, 388–398. [Google Scholar] [CrossRef]
- Williams, L.E.; Levin, A.D.; Fidelibus, M.W. Crop coefficients (Kc) developed from canopy shaded area in California vineyards. Agric. Water Manag. 2022, 271, 107771. [Google Scholar] [CrossRef]
- Pôças, I.; Paço, T.A.; Paredes, P.; Cunha, M.; Pereira, L.S. Estimation of Actual Crop Coefficients Using Remotely Sensed Vegetation Indices and Soil Water Balance Modelled Data. Remote Sens. 2015, 7, 2373–2400. [Google Scholar] [CrossRef]
- Phogat, V.; Šimůnek, J.; Skewes, M.A.; Cox, J.W.; McCarthy, M.G. Improving the estimation of evaporation by the FAO-56 dual crop coefficient approach under subsurface drip irrigation. Agric. Water Manag. 2016, 178, 189–200. [Google Scholar] [CrossRef]
- Chalmers, Y.M.; Downey, M.O.; Krstic, M.P.; Loveys, B.R.; Dry, P.R. Influence of sustained deficit irrigation on colour parameters of Cabernet Sauvignon and Shiraz microscale wine fermentations. Aust. J. Grape Wine Res. 2010, 16, 301–313. [Google Scholar] [CrossRef]
- Edwards, E.J.; Clingeleffer, P.R. Interseasonal effects of regulated deficit irrigation on growth, yield, water use, berry composition and wine attributes of Cabernet Sauvignon grapevines. Aust. J. Grape Wine Res. 2013, 19, 261–276. [Google Scholar] [CrossRef]
- Helalia, S.A.; Anderson, R.G.; Skaggs, T.H.; Jenerette, G.D.; Wang, D.; Šimůnek, J. Impact of Drought and Changing Water Sources on Water Use and Soil Salinity of Almond and Pistachio Orchards: 1. Observations. Soil Syst. 2021, 5, 50. [Google Scholar] [CrossRef]
- Yang, T.; Šimůnek, J.; Mo, M.; McCullough-Sanden, B.; Shahrokhnia, H.; Cherchian, S.; Wu, L. Assessing salinity leaching efficiency in three soils by the HYDRUS-1D and -2D simulations. Soil Tillage Res. 2019, 194, 104342. [Google Scholar] [CrossRef]
- Oster, J.D. Irrigation with poor quality water. Agric. Water Manag. 1994, 25, 271–297. [Google Scholar] [CrossRef]
- Corwin, D.L.; Grattan, S.R. Are Existing Irrigation Salinity Leaching Requirement Guidelines Overly Conservative or Obsolete? J. Irrig. Drain. Eng. 2018, 144, 02518001. [Google Scholar] [CrossRef]
- Letey, J.; Hoffman, G.J.; Hopmans, J.W.; Grattan, S.R.; Suarez, D.; Corwin, D.L.; Oster, J.D.; Wu, L.; Amrhein, C. Evaluation of soil salinity leaching requirement guidelines. Agric. Water Manag. 2011, 98, 502–506. [Google Scholar] [CrossRef]
- Isidoro, D.; Grattan, S.R. Predicting soil salinity in response to different irrigation practices, soil types and rainfall scenarios. Irrig. Sci. 2011, 29, 197–211. [Google Scholar] [CrossRef]
- Läuchli, A.; Epstein, E. Plant response to saline and sodic conditions. In Agricultural Salinity Assessment and Management; Tanji, K.K., Ed.; Manuals and Reports on Engineering Practice; ASCE: New York, NY, USA, 1990; pp. 113–137. [Google Scholar]
- Cucci, G.; Lacolla, G.; Mastro, A.M.; Caranfa, G. Leaching effect of rainfall on soil under four-year saline water irrigation. Soil Water Res. 2016, 11, 181–189. [Google Scholar] [CrossRef]
- Vrugt, J.A.; Hopmans, J.W.; Šimunek, J. Calibration of a Two-Dimensional Root Water Uptake Model. Soil Sci. Soc. Am. J. 2001, 65, 1027–1037. [Google Scholar] [CrossRef]



| Soil Depth | Texture | θr | θs | A | η | Ks | l |
|---|---|---|---|---|---|---|---|
| (cm) | cm3cm−3 | cm−1 | cm day−1 | ||||
| 0–15 | Sandy Loam | 0.041 | 0.4259 | 0.0353 | 1.743 | 141.238 | 0.5 |
| 15–30 | Sandy Loam | 0.053 | 0.347 | 0.058 | 1.774 | 98.61 | 0.5 |
| 30–50 | Sandy Clay Loam | 0.1527 | 0.3942 | 0.0339 | 1.495 | 10.93 | 0.5 |
| 50–100 | Sandy Loam | 0.1044 | 0.3413 | 0.0226 | 1.795 | 7.75 | 0.5 |
| 100–120 | Sandy Clay Loam | 0.1908 | 0.3731 | 0.0403 | 1.363 | 6.93 | 0.5 |
| Water Quality | Normal Rainfall (n) | Drought Season (d) | ||
|---|---|---|---|---|
| No Leaching | Leaching Irrigation (l) | No Leaching | Leaching Irrigation (l) | |
| River water (Rw) | Rw_n | Rw_nl | Rw_d | Rw_dl |
| Brackish water (Gw) | Gw_n | Gw_nl | Gw_d | Gw_dl |
| Mixing Rw and Gw | Mix_n | Mix_nl | Mix_d | Mix_dl |
| Alternate use of Rw and Gw | Alt_n | Alt_nl | Alt_d | Alt_dl |
| Statistics | Water Content (cm3/cm3) | ECsw (dS/m) | |||||
|---|---|---|---|---|---|---|---|
| 20 cm | 40 cm | 60 cm | 80 cm | 100 cm | Average | ||
| RMSE | 0.05 | 0.05 | 0.03 | 0.02 | 0.04 | 0.04 | 0.61 |
| ME/MBE | 0.05 | 0.04 | 0.00 | 0.00 | 0.02 | 0.02 | −0.13 |
| MAE | 0.04 | 0.05 | 0.02 | 0.02 | 0.03 | 0.03 | 0.42 |
| Scenarios | P | I | ETC act | RWU | Es | Dr | LF | ECe |
|---|---|---|---|---|---|---|---|---|
| (mm) | (%) | (dS/m) | ||||||
| Rw_n | 373 | 209 | 424 | 218 | 206 | 39 | 0.07 | 2.2 |
| Rw_d | 299 * | 209 | 382 * | 201 | 181 * | 15 * | 0.03 * | 2.7 |
| Rw_nl | 373 | 237 * | 438 * | 223 | 216 * | 53 | 0.09 | 1.6 |
| Rw_dl | 299 * | 237 * | 401 * | 210 | 192 * | 26 | 0.05 | 2.2 |
| Gw_n | 374 | 209 | 409 * | 177 * | 232 * | 53 | 0.09 | 4.5 * |
| Gw_d | 299 * | 209 | 366 * | 154 * | 213 | 31 | 0.06 | 5.5 * |
| Gw_nl | 374 | 237 * | 426 | 188 * | 238 * | 65 * | 0.10 * | 3.9 * |
| Gw_dl | 299 * | 237 * | 387 * | 168 * | 219 * | 39 | 0.07 | 4.9 * |
| Mix_n | 374 | 209 * | 417 | 198 * | 219 * | 45 | 0.07 | 3.6 * |
| Mix_d | 299 * | 209 | 375 * | 177 * | 197 * | 22 | 0.04 | 4.3 * |
| Mix_nl | 374 | 237 * | 434 | 208 | 226 * | 58 | 0.09 | 2.9 |
| Mix_dl | 299 * | 237 * | 395 * | 190 * | 205 | 31 | 0.06 | 3.8 * |
| Alt_n | 374 | 209 | 418 | 202 * | 216 * | 44 | 0.08 | 3.2 |
| Alt_d | 299 * | 209 | 376 * | 183 * | 193 * | 21 | 0.05 | 3.9 * |
| Alt_nl | 374 | 237 * | 434 | 210 | 224 * | 57 | 0.09 | 2.6 |
| Alt_dl | 299 * | 237 * | 396 * | 194 * | 202 | 30 | 0.06 | 3.4 |
| CD (0.05) | 16.5 | 0.005 | 13.5 | 16.3 | 8.9 | 19 | 0.03 | 1.3 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Phogat, V.; Pitt, T.; Petrie, P.; Šimůnek, J.; Cutting, M. Optimization of Irrigation of Wine Grapes with Brackish Water for Managing Soil Salinization. Land 2023, 12, 1947. https://doi.org/10.3390/land12101947
Phogat V, Pitt T, Petrie P, Šimůnek J, Cutting M. Optimization of Irrigation of Wine Grapes with Brackish Water for Managing Soil Salinization. Land. 2023; 12(10):1947. https://doi.org/10.3390/land12101947
Chicago/Turabian StylePhogat, Vinod, Tim Pitt, Paul Petrie, Jirka Šimůnek, and Michael Cutting. 2023. "Optimization of Irrigation of Wine Grapes with Brackish Water for Managing Soil Salinization" Land 12, no. 10: 1947. https://doi.org/10.3390/land12101947
APA StylePhogat, V., Pitt, T., Petrie, P., Šimůnek, J., & Cutting, M. (2023). Optimization of Irrigation of Wine Grapes with Brackish Water for Managing Soil Salinization. Land, 12(10), 1947. https://doi.org/10.3390/land12101947








