Fractal Organization of Chilean Cities: Observations from a Developing Country
Abstract
:1. Introduction

1.1. Evolution of Chilean Cities: A Brief Historical Description

2. Methodology
2.1. Region of Study
2.2. Morphological Indices
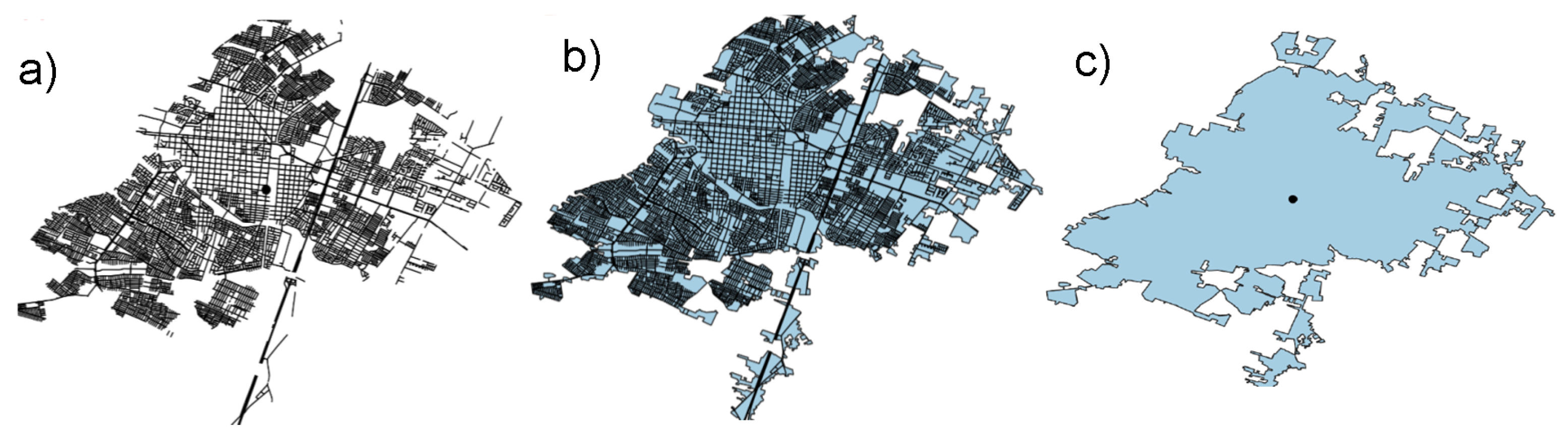
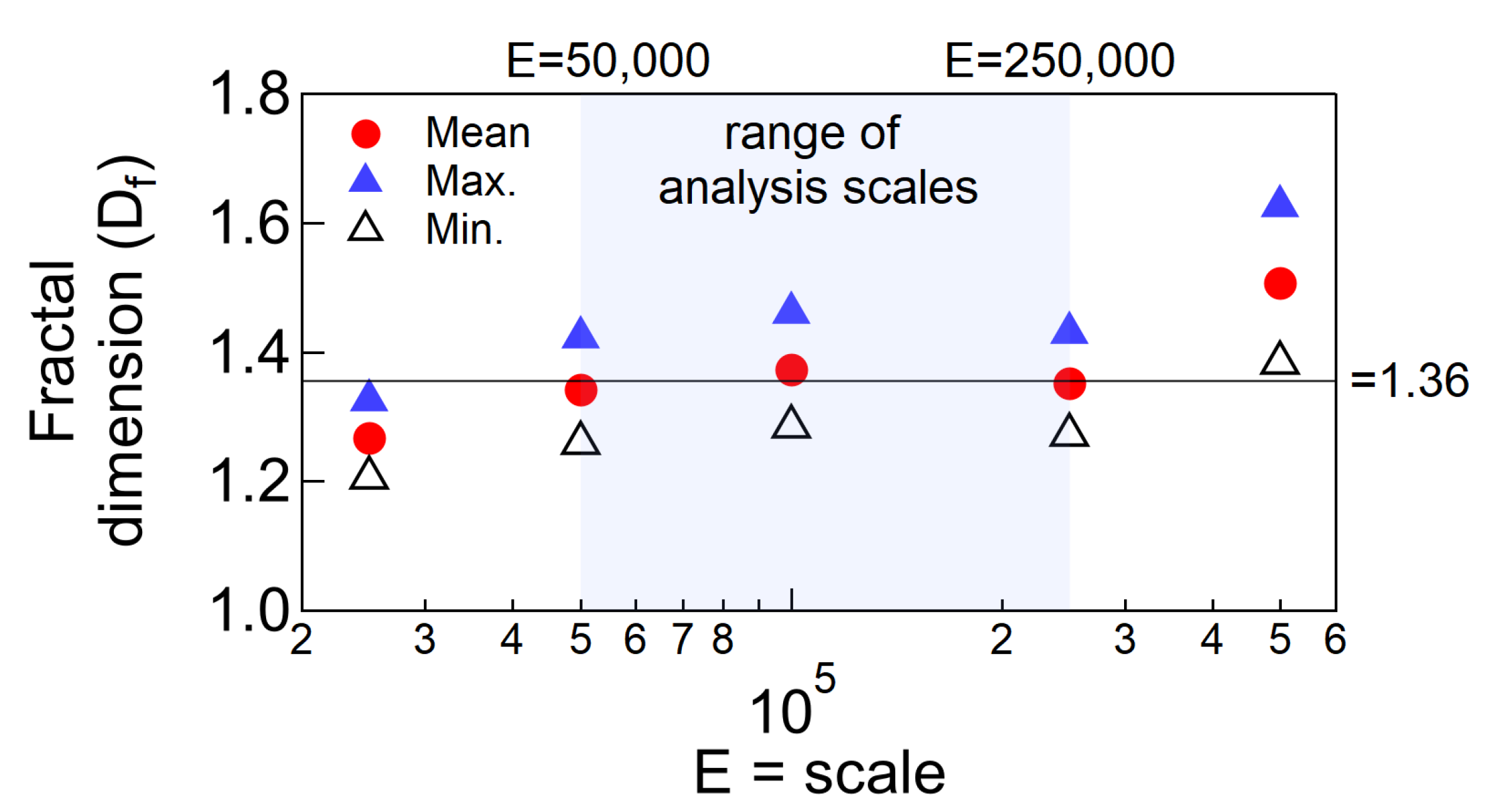
2.3. Fractal Dimension of Networks
3. Results
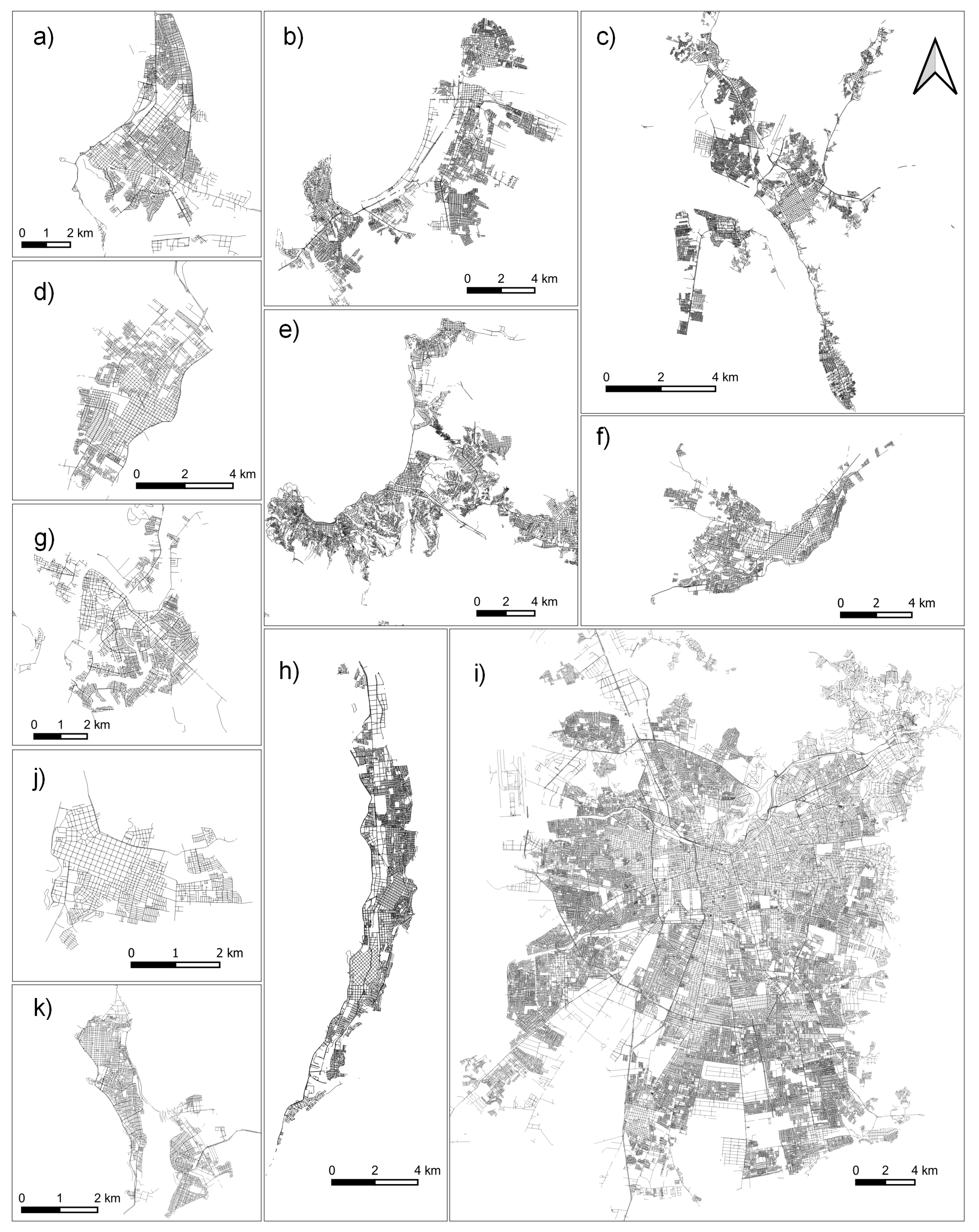
3.1. Morphometry and Patterns of Chilean Street Networks
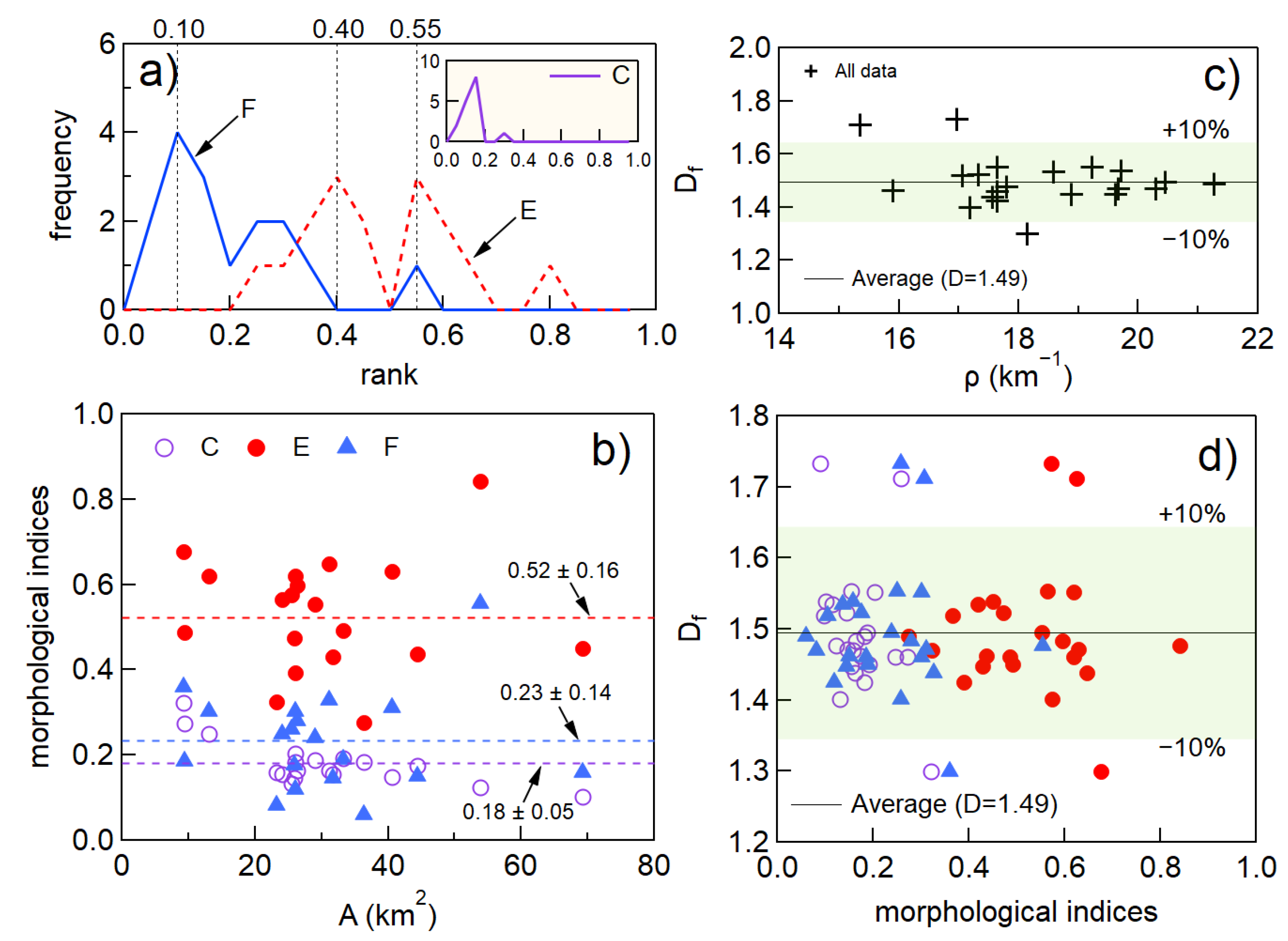
3.2. Fractality of Urban Networks
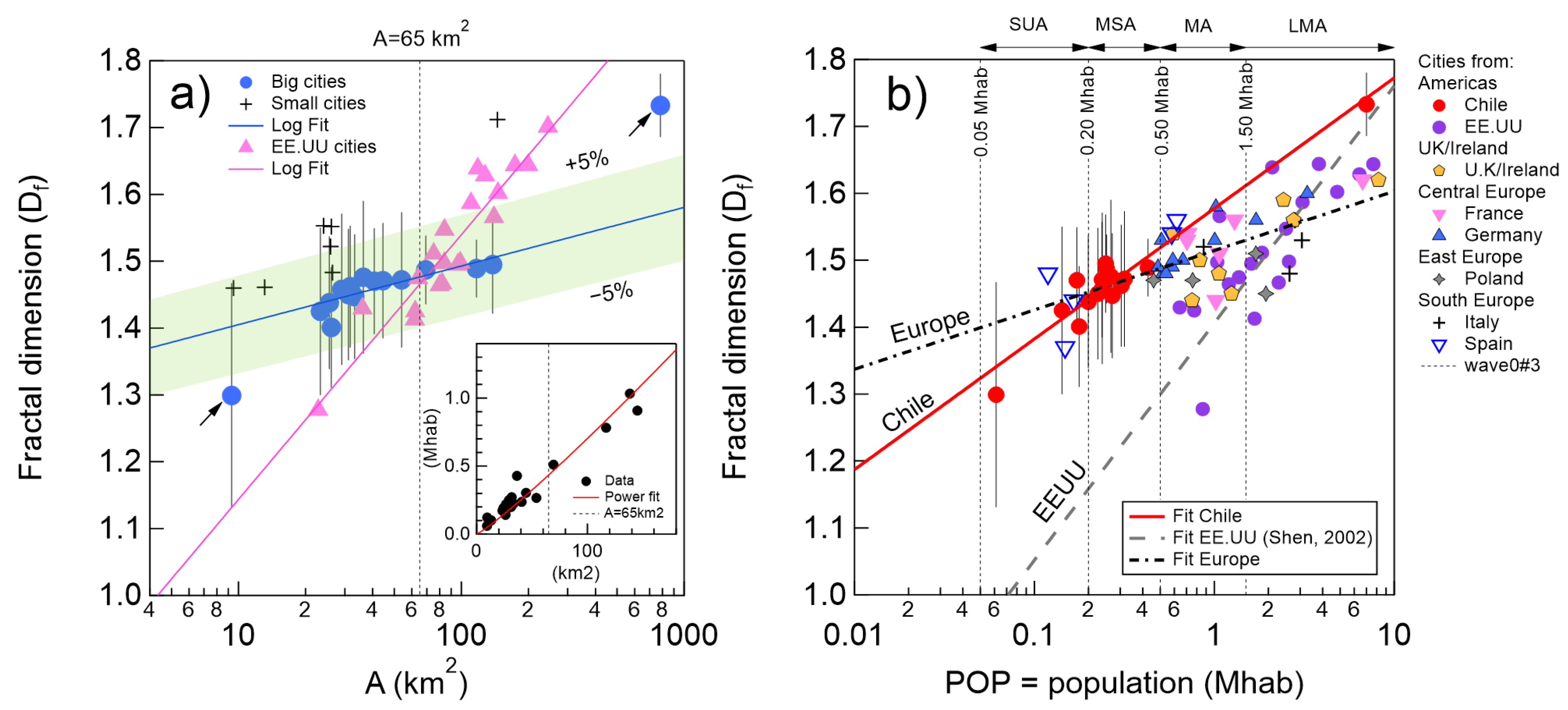
3.3. Allometric Laws for Chilean Cities
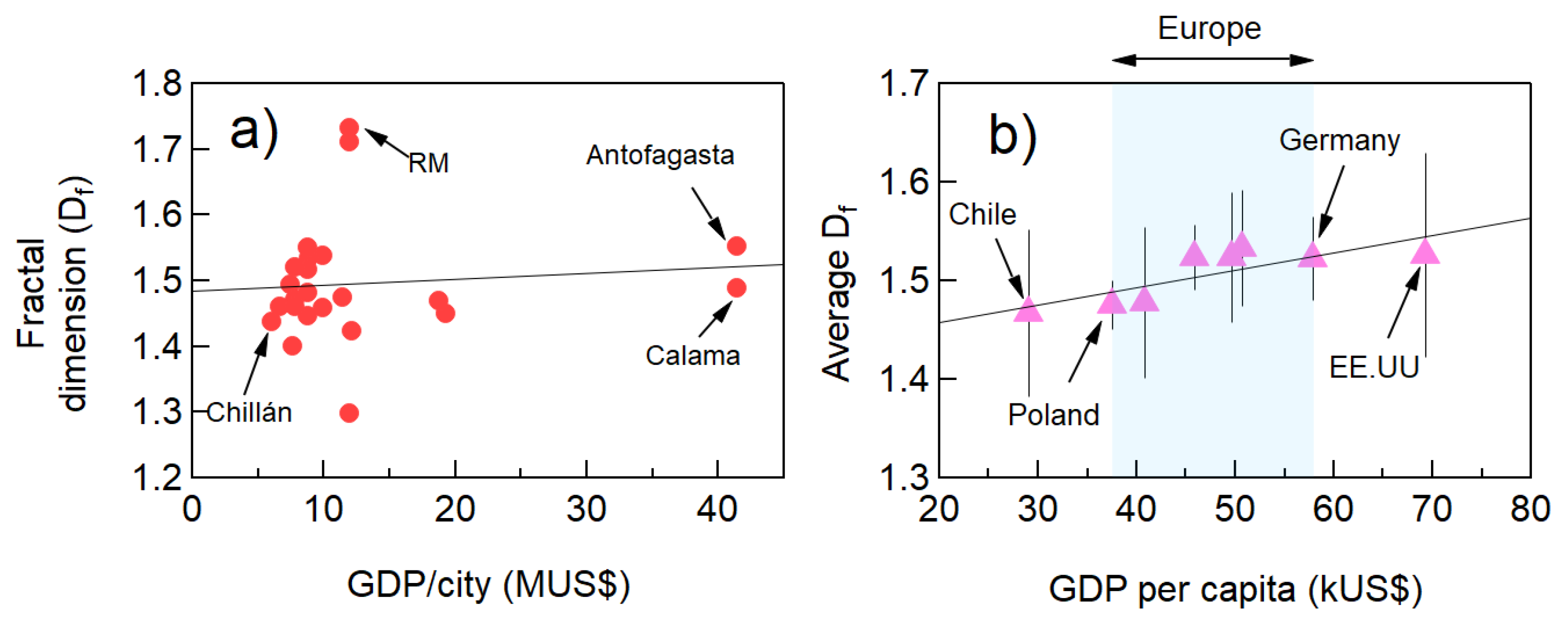
4. Discussion
5. Conclusions
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Feder, J. Fractals; Physics of Solids and Liquids, Plenum Press: New York, NY, USA, 1988. [Google Scholar]
- Bunde, A.; Havlin, S. Fractals and Disordered Systems; Springer Science & Business Media: Norwell, MA, USA, 2012. [Google Scholar]
- Bunde, A.; Havlin, S. Fractals in Science; Springer: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Mandelbrot, B. The Fractal Geometry of Nature; WH Freeman: New York, NY, USA, 1982. [Google Scholar]
- Gouyet, J.F. Physics and Fractal Structures; Elsevier Masson: Paris, France, 1996. [Google Scholar]
- Turcotte, D.L. Fractals in geology and geophysics. Pure Appl. Geophys. 1989, 131, 171–196. [Google Scholar] [CrossRef]
- Mandelbrot, B. How long is the coast of Britain? Statistical self-similarity and fractional dimension. Science 1967, 156, 636–638. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Scholz, C.H.; Mandelbrot, B.B. Fractals in Geophysics; Springer: Berlin/Heidelberg, Germany, 1989. [Google Scholar]
- Batty, M.; Longley, P.A. Fractal Cities: A Geometry of Form and Function; Academic Press: Cambridge, MA, USA, 1994. [Google Scholar]
- D’Acci, L.; Batty, M. The Mathematics of Urban Morphology; Springer: Berlin/Heidelberg, Germany, 2019. [Google Scholar]
- Chen, Y. Fractal Modeling and fractal dimension description of urban morphology. Entropy 2020, 22, 961. [Google Scholar] [CrossRef] [PubMed]
- Batty, M.; Longley, P.; Fotheringham, S. Urban growth and form: Scaling, fractal geometry, and diffusion-limited aggregation. Environ. Plan. A 1989, 21, 1447–1472. [Google Scholar] [CrossRef]
- Dupuy, G. Villes, Réseaux et Transport: Le Défi Fractal; Economica: Bonn, Germany, 2017. [Google Scholar]
- Batty, M.; Xie, Y. Preliminary evidence for a theory of the fractal city. Environ. Plan. A 1996, 28, 1745–1762. [Google Scholar] [CrossRef]
- Batty, M. Cities and Complexity: Understanding Cities with Cellular Automata, Agent-Based Models, and Fractals; The MIT Press: Cambridge, MA, USA, 2007. [Google Scholar]
- Frankhauser, P. Aspects fractals des structures urbaines. L’Espace GéOgraphique 1990, 45–69. [Google Scholar] [CrossRef]
- Frankhauser, P. La Fractalité des Structures Urbaines. Ph.D. Thesis, Anthropos, Paris, France, 1993. [Google Scholar]
- Frankhauser, P. Fractal geometry for measuring and modelling urban patterns. In The Dynamics of Complex Urban Systems; Springer: Berlin/Heidelberg, Germany, 2008; pp. 213–243. [Google Scholar]
- White, R.; Engelen, G. Urban systems dynamics and cellular automata: Fractal structures between order and chaos. Chaos Solitons Fractals 1994, 4, 563–583. [Google Scholar] [CrossRef]
- Thomas, I.; Frankhauser, P.; De Keersmaecker, M.L. Fractal dimension versus density of built-up surfaces in the periphery of Brussels. Pap. Reg. Sci. 2007, 86, 287–308. [Google Scholar] [CrossRef]
- Thomas, I.; Frankhauser, P.; Biernacki, C. The morphology of built-up landscapes in Wallonia (Belgium): A classification using fractal indices. Landsc. Urban Plan. 2008, 84, 99–115. [Google Scholar] [CrossRef]
- Thomas, I.; Frankhauser, P.; Badariotti, D. Comparing the fractality of European urban neighbourhoods: Do national contexts matter? J. Geogr. Syst. 2012, 14, 189–208. [Google Scholar] [CrossRef]
- Tannier, C. About Fractal Models in Urban Geography and Planning: Refuting the Aesthetics and The Universal Norm, 2018. Blog Post on ‘Cybergeo Conversation’. 13 March 2018. Available online: https://cybergeo.hypotheses.org/223 (accessed on 11 October 2022).
- Falconer, K. Fractal geometry: Mathematical Foundations and Applications; John Wiley & Sons: Hoboken, NJ, USA, 2004. [Google Scholar]
- Lagarias, A.; Prastacos, P. Fractal dimension of European Cities: A comparison of the patterns of built-up areas in the urban core and the peri-urban ring. Cybergeo Eur. J. Geogr. 2021, 987, 37243. [Google Scholar] [CrossRef]
- Shen, G. Fractal dimension and fractal growth of urbanized areas. Int. J. Geogr. Inf. Sci. 2002, 16, 419–437. [Google Scholar] [CrossRef]
- Rodin, V.; Rodina, E. The fractal dimension of Tokyo’s streets. Fractals 2000, 8, 413–418. [Google Scholar] [CrossRef]
- Feng, J.; Chen, Y. Spatiotemporal evolution of urban form and land-use structure in Hangzhou, China: Evidence from fractals. Environ. Plan. Plan. Des. 2010, 37, 838–856. [Google Scholar] [CrossRef]
- Jahanmiri, F.; Parker, D.C. An Overview of Fractal Geometry Applied to Urban Planning. Land 2022, 11, 475. [Google Scholar] [CrossRef]
- Marshall, S. Streets and Patterns; Routledge: London, UK, 2004. [Google Scholar]
- Oliveira, V. Urban Morphology: An Introduction to the Study of the Physical Form of Cities; Springer: Berlin/Heidelberg, Germany, 2016. [Google Scholar]
- Bettencourt, L.M. Introduction to Urban Science: Evidence and Theory of Cities as Complex Systems; MIT Press: Cambridge, MA, USA, 2021. [Google Scholar]
- International Monetary Fund. World Economic Outlook Database. 2022. Available online: https://www.imf.org/en/Publications/WEO/weo-database/2022/April/select-country-group (accessed on 11 October 2022).
- Nuñez, J.; Tartakowsky, A. Inequality of Outcomes vs. Inequality of Opportunities in a Developing Country. An exploratory analysis for Chile. Estud. Econ. 2007, 34, 185–202. [Google Scholar]
- Zhao, C.; Li, Y.; Weng, M. A Fractal Approach to Urban Boundary Delineation Based on Raster Land Use Maps: A Case of Shanghai, China. Land 2021, 10, 941. [Google Scholar] [CrossRef]
- Purevtseren, M.; Tsegmid, B.; Indra, M.; Sugar, M. The fractal geometry of urban land use: The case of Ulaanbaatar city, Mongolia. Land 2018, 7, 67. [Google Scholar] [CrossRef] [Green Version]
- Ma, D.; Guo, R.; Zheng, Y.; Zhao, Z.; He, F.; Zhu, W. Understanding Chinese urban form: The universal fractal pattern of street networks over 298 cities. ISPRS Int. J. Geo-Inf. 2020, 9, 192. [Google Scholar] [CrossRef] [Green Version]
- Karpinski, M.; Kuznichenko, S.; Kazakova, N.; Fraze-Frazenko, O.; Jancarczyk, D. Geospatial Assessment of the Territorial Road Network by Fractal Method. Future Internet 2020, 12, 201. [Google Scholar] [CrossRef]
- Bodini, H. Geografía Urbana de Chile; Instituto Geográfico Militar, Colección Geografía de Chile: Santiago, Chile, 1985; Volume 10. [Google Scholar]
- De Ramón, A. Suburbios y arrabales en un área metropolitana. El caso de Santiago de Chile, 1872–1932. In Ensayos Histórico-Sociales Sobre la Urbanización en América Latina; Hardoy, J.E., Morse, R.M., Schaedel, R.P., Eds.; Ediciones SIAP· CLACSO: Buenos Aires, Argentina, 1978. [Google Scholar]
- Cadaster of Camps in Chile, El Mercurio. Available online: https://www.emol.com/noticias/Economia/2018/12/26/932200/Gobierno-elabora-nuevo-catastro-de-campamentos-en-Chile.html (accessed on 24 October 2022).
- Fundación Ingeniería Sin Fronteras Chile, Proyecto “Escuela Dignidad, Etapa 4 Campamento Dignidad” (2021), La Florida, Región Metropolitana. Available online: https://isf-chile.org/portfolio/proyecto-escuela-dignidad-etapa-1/ (accessed on 24 October 2022).
- Vergara, L. Convivencia y conflictos en barrios de ingresos mixtos. BitáCora Urbano Territ. 2021, 31, 41–52. [Google Scholar] [CrossRef]
- Vista de Las Condes desde la Gran Torre Santiago. Available online: https://es.wikipedia.org/wiki/Sector_nororiente_de_Santiago (accessed on 24 October 2022).
- Manríquez, M.T.; Cáceres, D.F.; Jiménez, D.G. Reforma Agraria en Chile, ¿Palimpsesto de otra ruralidad? Reflexiones y propuestas. Polis. Rev. Latinoam. 2017, 47, 432. [Google Scholar] [CrossRef] [Green Version]
- La Reforma Agraria (1962–1973). Available online: https://www.memoriachilena.gob.cl/602/w3-article-3536.html#presentacion (accessed on 24 October 2022).
- Martínez Pizarro, J. Urbanización, Crecimiento Urbano y Dinámica de la población de las principales ciudades de Chile entre 1952 y 1992. Rev. Geogr. Norte Gd. 1997, 24, 23–30. [Google Scholar]
- Martínez Pizarro, J. Ciudades de Chile, migración interna y redistribución de la población: Algunas evidencias del período 1987–1992. Rev. Geogr. Norte Gd. 2002, 29, 21–38. [Google Scholar]
- Fuentes Arce, L. Competitividad urbana en el contexto latinoamericano: El caso de Santiago de Chile. Rev. Geogr. Norte Gd. 2011, 48, 81–106. [Google Scholar] [CrossRef]
- Ministerio de Bienes Nacionales de Chile, Infraestructura de Datos Geoespaciales (IDE). Red Vial Nacional. 2019. Available online: https://www.ide.cl/index.php/transporte/item/1708-red-vial-nacional (accessed on 5 October 2022).
- Ministerio de Bienes Nacionales de Chile, Infraestructura de Datos Geoespaciales (IDE). ¿Qué es el IDE Chile? 2022. Available online: https://www.ide.cl/ (accessed on 5 October 2022). (In Spanish).
- Ministerio de Bienes Nacionales de Chile, Infraestructura de Datos Geoespaciales (IDE). Área Urbana Consolidada. 2016. Available online: https://www.ide.cl/index.php/planificacion-y-catastro/item/1845-area-urbana-consolidada (accessed on 5 October 2022). (In Spanish).
- Observatorio Social—Ministerio de Desarrollo Social y Familia. Estimación de Tasa de Pobreza por Ingreso por Comuna. 2020. Available online: http://observatorio.ministeriodesarrollosocial.gob.cl/pobreza-comunal-2020 (accessed on 5 October 2022). (In Spanish).
- Observatorio del Sistema Nacional de Ciencia, Tecnología y Conocimiento e Innovación, Ministerio de Ciencias de Chile. PIB Total y per Cápita Regional. 2020. Available online: https://observa.minciencia.gob.cl/indicadores/contexto-socioeconomico/pib-per-capita-regional (accessed on 5 October 2022). (In Spanish).
- Ferreira, J.A.; Condessa, B.; e Almeida, J.C.; Pinto, P. Urban settlements delimitation in low-density areas—An application to the municipality of Tomar (Portugal). Landsc. Urban Plan. 2010, 97, 156–167. [Google Scholar] [CrossRef]
- Gregory, K.; Gregory, P.; Walling, D. Drainage Basin Form and Process: A Geomorphological Approach; Wiley: Hoboken, NJ, USA, 1973. [Google Scholar]
- Zavoianu, I. Morphometry of Drainage Basins; Elsevier: Amsterdam, The Netherlands, 2011. [Google Scholar]
- Rudin, W. Principles of Mathematical Analysis W. Rudin; McGraw-Hill: New York, NY, USA, 1953. [Google Scholar]
- Horton, R.E. Erosional development of streams and their drainage basins; hydrophysical approach to quantitative morphology. Geol. Soc. Am. Bull. 1945, 56, 275–370. [Google Scholar] [CrossRef] [Green Version]
- Schumm, S.A. Evolution of drainage systems and slopes in badlands at Perth Amboy, New Jersey. Geol. Soc. Am. Bull. 1956, 67, 597–646. [Google Scholar] [CrossRef]
- Strahler, A.N. Part II. Quantitative geomorphology of drainage basins and channel networks. In Handbook of Applied Hydrology; McGraw-Hill: New York, NY, USA, 1964; pp. 4–39. [Google Scholar]
- Beauvais, A.A.; Montgomery, D.R. Are channel networks statistically self-similar? Geology 1997, 25, 1063–1066. [Google Scholar] [CrossRef]
- Cheeseman, A.K.; Vrscay, E.R. Estimating the Fractal Dimensions of Vascular Networks and Other Branching Structures: Some Words of Caution. Mathematics 2022, 10, 839. [Google Scholar] [CrossRef]
- Kusák, M. Methods of fractal geometry used in the study of complex geomorphic networks. AUC Geogr. 2014, 49, 99–110. [Google Scholar] [CrossRef] [Green Version]
- Frankhauser, P. Comparing the morphology of urban patterns in Europe—A fractal approach. Eur.-Cities Insights Outskirts Rep. Cost Action 2004, 10, 79–105. [Google Scholar]
- Rodriguez-Iturbe, I.; Rinaldo, A. Fractal River Basins: Chance and Self-organization; Cambridge University Press: Cambridge, UK, 2001. [Google Scholar]
- Labini, F.S.; Gabrielli, A.; Montuori, M.; Pietronero, L. Finite size effects on the galaxy number counts: Evidence for fractal behavior up to the deepest scale. Phys. A Stat. Mech. Its Appl. 1996, 226, 195–242. [Google Scholar] [CrossRef] [Green Version]
- López, R.; Miller, S.J. Chile: The unbearable burden of inequality. World Dev. 2008, 36, 2679–2695. [Google Scholar] [CrossRef]
- Urban Population by City Size, OCDE 2020. Available online: https://data.oecd.org/popregion/urban-population-by-city-size.htm (accessed on 24 October 2022).
- Molinero, C.; Thurner, S. How the geometry of cities explains urban scaling laws and determines their exponents. arXiv 2019, arXiv:1908.07470. [Google Scholar]
- Castillo, M.J.; Forray, R. La vivienda, un problema de acceso al suelo. Arq (Santiago) 2014, 86, 48–57. [Google Scholar] [CrossRef] [Green Version]
- Hack, J.T. Studies of Longitudinal Stream Profiles in Virginia and Maryland; US Government Printing Office: Washington, DC, USA, 1957; Volume 294.
- Martinez, F.; Manriquez, H.; Ojeda, A.; Olea, G. Organization Patterns of Complex River Networks in Chile: A Fractal Morphology. Mathematics 2022, 10, 1806. [Google Scholar] [CrossRef]
- Leiva Gómez, S.; Parra Calderón, M. La voz de los pobres del Norte Grande de Chile: Estudio sobre la pobreza con participación de los afectados. Rev. Geogr. Norte Gd. 2011, 50, 87–104. [Google Scholar] [CrossRef]
- Dodds, P.S.; Rothman, D.H. Unified view of scaling laws for river networks. Phys. Rev. E 1999, 59, 4865. [Google Scholar] [CrossRef] [Green Version]
- Rosso, R.; Bacchi, B.; La Barbera, P. Fractal relation of mainstream length to catchment area in river networks. Water Resour. Res. 1991, 27, 381–387. [Google Scholar] [CrossRef]
- Phillips, J. Interpreting the fractal dimension of river networks. Fractals Geogr. 1993, 7, 142–157. [Google Scholar]
- Di Nardo, A.; Di Natale, M.; Giudicianni, C.; Greco, R.; Santonastaso, G.F. Complex network and fractal theory for the assessment of water distribution network resilience to pipe failures. Water Sci. Technol. Water Supply 2018, 18, 767–777. [Google Scholar] [CrossRef]
- Network Science. Available online: http://networksciencebook.com/ (accessed on 13 January 2023).
- Jiang, B. Head/tail breaks: A new classification scheme for data with a heavy-tailed distribution. Prof. Geogr. 2013, 65, 482–494. [Google Scholar] [CrossRef]
- Jiang, B.; Yin, J. Ht-index for quantifying the fractal or scaling structure of geographic features. Ann. Assoc. Am. Geogr. 2014, 104, 530–540. [Google Scholar] [CrossRef]



| Pop. | Poverty | GDP/Region | x | y | ||
|---|---|---|---|---|---|---|
| # | City | (khab) | (khab) | (MUS$) | (km) | (km) |
| 1 | Arica | 248.8 | 29.3 | 7.4 | 1661.9 | 0 |
| 2 | Iquique | 225.0 | 27.8 | 19.3 | 1467.4 | 0 |
| 3 | Antofagasta | 428.7 | 35.4 | 41.4 | 1092.4 | 0 |
| 4 | Copiapo | 172.4 | 14.9 | 18.7 | 676.5 | 61.1 |
| 5 | La Serena | 510.4 | 57.0 | 9.9 | 398.5 | 0 |
| 6 | Valparaiso | 1032.9 | 117.3 | 8.8 | 100.6 | 0 |
| 7 | R.M. | 7014.0 | 624.0 | 11.9 | 0 | 88.2 |
| 8 | Rancagua | 266.3 | 23.8 | 11.4 | −77.3 | 105.0 |
| 9 | Talca | 237.3 | 25.7 | 7.8 | −235.9 | 61.9 |
| 10 | Chillan | 199.2 | 27.4 | 6.0 | −372.2 | 72.1 |
| 11 | Concepción | 781.8 | 88.4 | 8.7 | −429.6 | 0 |
| 12 | Temuco | 303.6 | 44.9 | 6.6 | −609.3 | 68.1 |
| 13 | Valdivia | 177.3 | 17.4 | 7.6 | −741.8 | 11.7 |
| 14 | Puerto Montt | 270.6 | 28.3 | 8.7 | −910.2 | 0 |
| 15 | Coyhaique | 61.3 | 3.3 | 11.9 | −1349.4 | 59.8 |
| 16 | Punta Arenas | 142.5 | 8.3 | 12.1 | −2186.3 | 0 |
| Average | 754.5 | 73.3 | 12.4 | - | ||
| Min. | 61.3 | 3.3 | 6.0 | - | ||
| Max. | 7014.0 | 624.0 | 41.4 | - | ||
| 18 | Calama | 191.4 | 20.3 | 41.4 | 1232.7 | 135.6 |
| 19 | Ovalle | 121.6 | 13.5 | 9.9 | 322.8 | 48.1 |
| 20 | R.M. (east side) | 907.7 | 34.2 | 11.9 | 12.2 | 98.6 |
| 21 | Curicó | 164.4 | 16.6 | 7.8 | −175.1 | 85.0 |
| 22 | Linares | 101.4 | 11.1 | 7.8 | −276.9 | 87.7 |
| 23 | Osorno | 173.8 | 18.3 | 8.7 | −818.7 | 48.9 |
| 24 | Los Angeles | 219.1 | 29.5 | 8.7 | −468.9 | 81.7 |
| Average | 268.5 | 20.5 | 13.7 | - | ||
| Min. | 101.4 | 11.1 | 7.8 | - | ||
| Max. | 907.7 | 34.2 | 41.4 | - |
| A | P | Z | E | F | C | ||||
|---|---|---|---|---|---|---|---|---|---|
| # | City | (km2) | (km) | (km) | (km−1) | (-) | (-) | (-) | (-) |
| 1 | Arica | 29.1 | 101.7 | 594.4 | 20.5 | 0.55 | 0.24 | 0.19 | 1.495 |
| 2 | Iquique | 33.3 | 106.3 | 652.5 | 19.6 | 0.49 | 0.19 | 0.19 | 1.450 |
| 3 | Antofagasta | 36.4 | 117.4 | 773.3 | 21.3 | 0.28 | 0.06 | 0.18 | 1.489 |
| 4 | Copiapo | 23.3 | 108.5 | 472.6 | 20.3 | 0.32 | 0.08 | 0.16 | 1.470 |
| 5 | La Serena | 69.3 | 289.3 | 1365.6 | 19.7 | 0.45 | 0.16 | 0.10 | 1.538 |
| 6 | Valparaiso | 138.2 | 361.9 | 2566.9 | 18.6 | 0.42 | 0.14 | 0.12 | 1.535 |
| 7 | R.M. | 782.5 | 1092.0 | 13,274.9 | 17.0 | 0.57 | 0.26 | 0.09 | 1.733 |
| 8 | Rancagua | 53.9 | 209.2 | 959.5 | 17.8 | 0.84 | 0.56 | 0.12 | 1.476 |
| 9 | Talca | 40.6 | 152.7 | 799.1 | 19.7 | 0.63 | 0.31 | 0.15 | 1.471 |
| 10 | Chillán | 31.2 | 122.5 | 547.8 | 17.6 | 0.65 | 0.33 | 0.16 | 1.438 |
| 11 | Concepción | 116.9 | 385.4 | 1993.4 | 17.1 | 0.37 | 0.11 | 0.10 | 1.518 |
| 12 | Temuco | 44.5 | 135.4 | 707.4 | 15.9 | 0.44 | 0.15 | 0.18 | 1.462 |
| 13 | Valdivia | 25.5 | 135.4 | 438.6 | 17.2 | 0.57 | 0.26 | 0.13 | 1.401 |
| 14 | Puerto Montt | 31.7 | 129.7 | 598.2 | 18.9 | 0.43 | 0.15 | 0.15 | 1.447 |
| 15 | Coyhaique | 9.3 | 33.6 | 169.0 | 18.2 | 0.70 | 0.36 | 0.32 | 1.299 |
| 16 | Punta Arenas | 26.1 | 99.2 | 460.1 | 17.6 | 0.39 | 0.12 | 0.18 | 1.425 |
| Min. | 9.3 | 33.6 | 169.0 | 15.9 | 0.28 | 0.06 | 0.09 | 1.299 | |
| Max. | 782.5 | 1092.0 | 13,274.9 | 21.3 | 0.84 | 0.55 | 0.32 | 1.733 | |
| Average | 93.2 | 223.8 | 1648.3 | 18.5 | 0.50 | 0.22 | 0.16 | 1.478 | |
| 17 | Calama | 24.1 | 112.6 | 462.9 | 19.2 | 0.56 | 0.25 | 0.15 | 1.553 |
| 18 | Ovalle | 9.5 | 40.0 | 216.4 | 22.9 | 0.49 | 0.19 | 0.27 | 1.460 |
| 19 | RM (east side) | 145.0 | 164.7 | 2226.1 | 15.3 | 0.63 | 0.31 | 0.26 | 1.712 |
| 20 | Curicó | 25.9 | 124.7 | 448.9 | 17.3 | 0.47 | 0.18 | 0.14 | 1.522 |
| 21 | Linares | 13.1 | 51.7 | 230.1 | 17.6 | 0.62 | 0.30 | 0.25 | 1.461 |
| 22 | Osorno | 26.1 | 89.1 | 460.2 | 17.6 | 0.62 | 0.30 | 0.20 | 1.552 |
| 23 | Los Angeles | 26.4 | 111.1 | 359.6 | 13.6 | 0.60 | 0.28 | 0.16 | 1.483 |
| Min. | 9.5 | 40.0 | 216.4 | 13.6 | 0.47 | 0.18 | 0.14 | 1.460 | |
| Max. | 145.0 | 164.7 | 2226.1 | 22.9 | 0.63 | 0.31 | 0.27 | 1.712 | |
| Average | 38.6 | 99.1 | 629.2 | 17.7 | 0.57 | 0.26 | 0.21 | 1.535 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Martínez, F.; Sepúlveda, B.; Manríquez, H. Fractal Organization of Chilean Cities: Observations from a Developing Country. Land 2023, 12, 296. https://doi.org/10.3390/land12020296
Martínez F, Sepúlveda B, Manríquez H. Fractal Organization of Chilean Cities: Observations from a Developing Country. Land. 2023; 12(2):296. https://doi.org/10.3390/land12020296
Chicago/Turabian StyleMartínez, Francisco, Bastian Sepúlveda, and Hermann Manríquez. 2023. "Fractal Organization of Chilean Cities: Observations from a Developing Country" Land 12, no. 2: 296. https://doi.org/10.3390/land12020296
APA StyleMartínez, F., Sepúlveda, B., & Manríquez, H. (2023). Fractal Organization of Chilean Cities: Observations from a Developing Country. Land, 12(2), 296. https://doi.org/10.3390/land12020296










