The Impact of Land Cover Change on Surface Water Temperature of Small Lakes in Eastern Ontario from 1985 to 2020
Abstract
1. Introduction
2. Study Area and Datasets
2.1. Study Area
2.2. Datasets
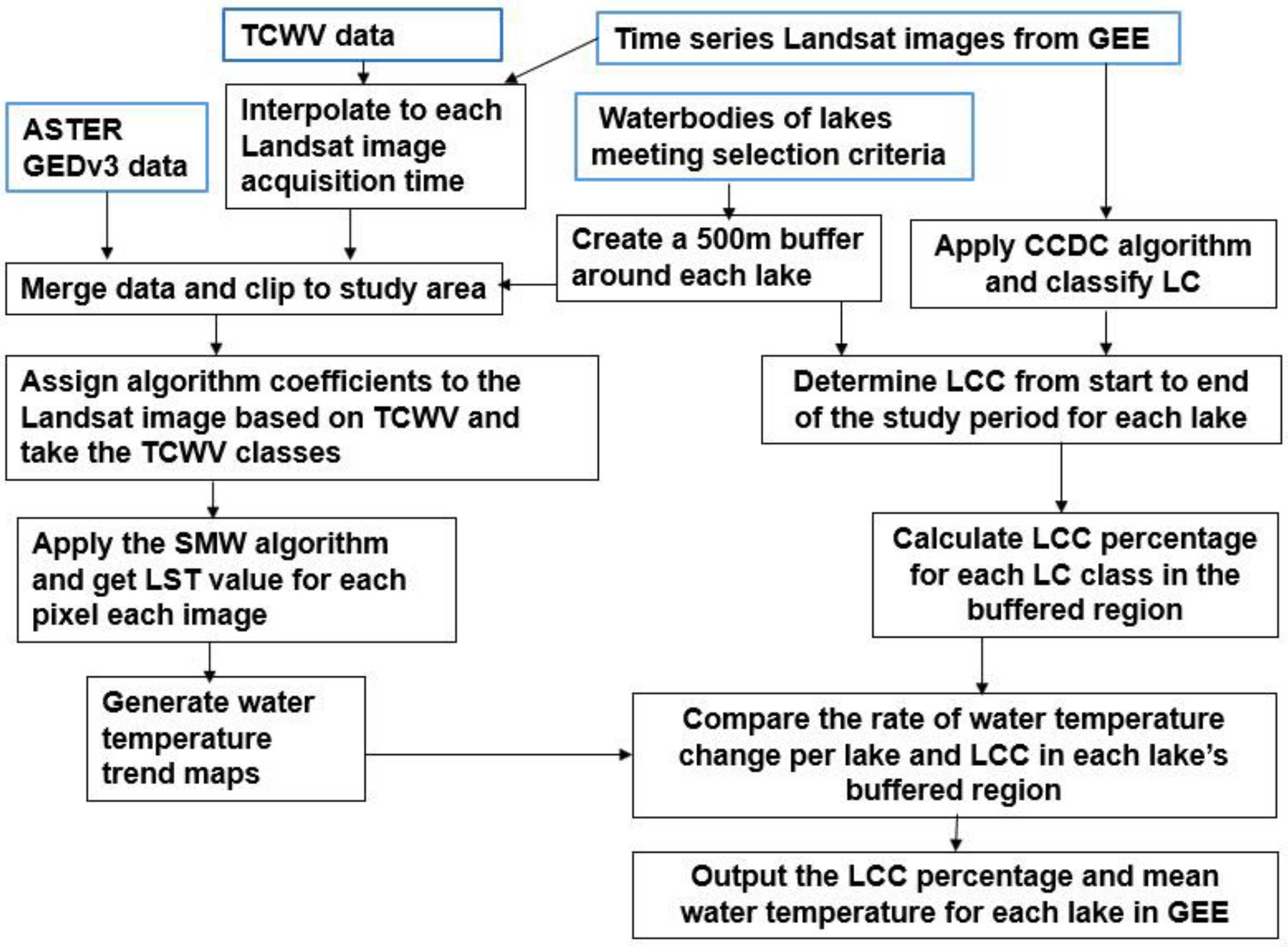
3. Methods
3.1. Continuous Change Detection Classification
3.2. Lake Surface Water Temperature (LSWT) Extraction
3.3. Trend Analysis
4. Results and Discussions
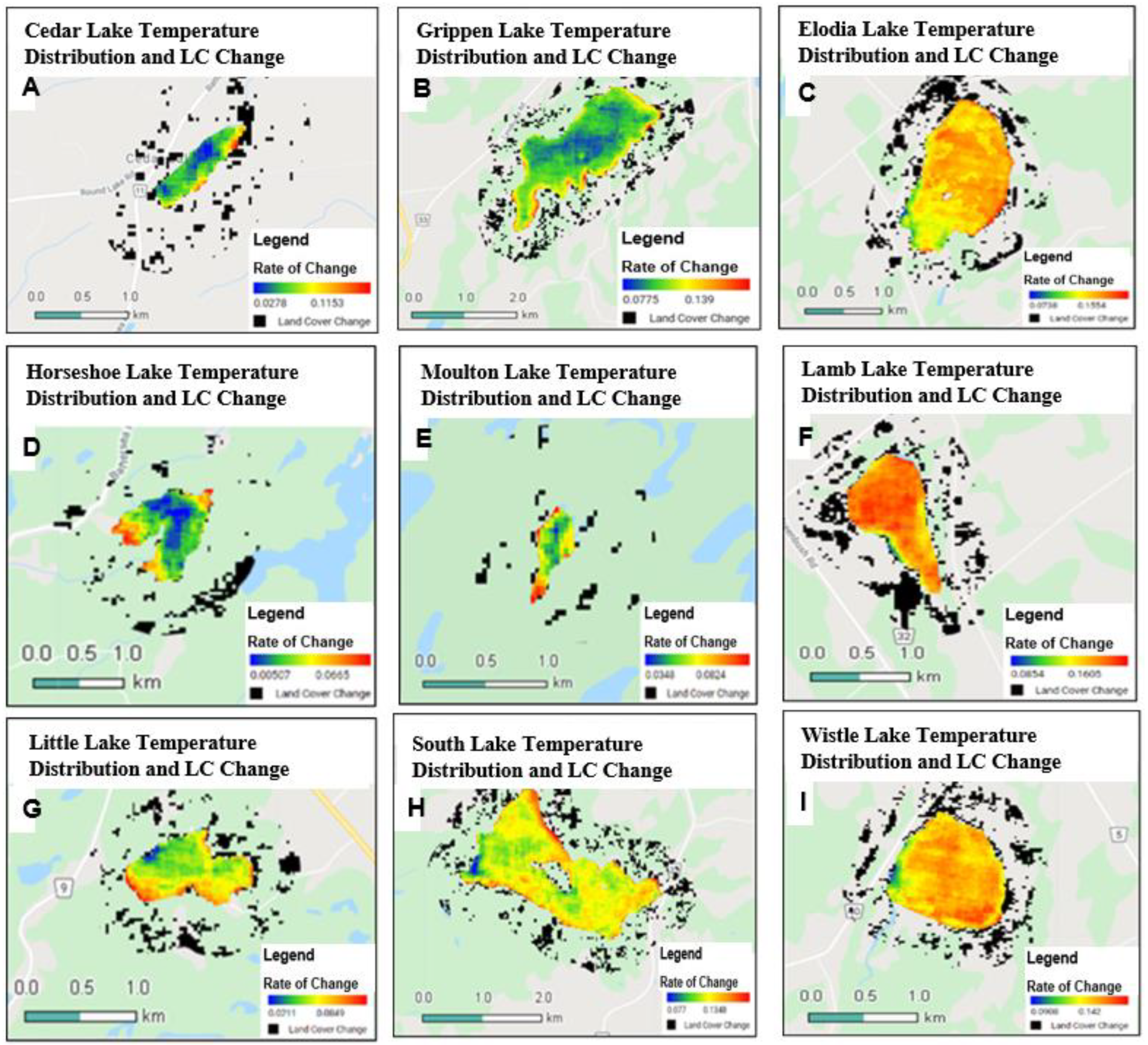
4.1. CCDC Classification Maps and LCC around Lakes
4.2. LCC and Lake Surface Water Temperature (LSWT) Change
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Ayanlade, A. Remote sensing approaches for land use and land surface temperature assessment: A review of methods. Int. J. Image Data Fusion 2017, 5, 188–210. [Google Scholar] [CrossRef]
- Tomlinson, C.J.; Chapman, L.; Thornes, J.E.; Baker, C. Remote sensing land surface temperature for meteorology and climatology: A review. Meteorol. Appl. 2011, 18, 296–306. [Google Scholar] [CrossRef]
- Gupta, N.; Mathew, A.; Khandelwal, S. Analysis of cooling effect of water bodies on land surface temperature in nearby region: A case study of Ahmedabad and Chandigarh cities in India. Egypt. J. Remote. Sens. Space Sci. 2018, 22, 81–93. [Google Scholar] [CrossRef]
- Chu, L.; Oloo, F.; Bergstedt, H.; Blaschke, T. Assessing the Link between Human Modification and Changes in Land Surface Temperature in Hainan, China Using Image Archives from Google Earth Engine. Remote. Sens. 2020, 12, 888. [Google Scholar] [CrossRef]
- Chang, C.-R.; Li, M.-H.; Chang, S.-D. A preliminary study on the local cool-island intensity of Taipei city parks. Landsc. Urban Plan. 2007, 80, 386–395. [Google Scholar] [CrossRef]
- Sun, R.; Chen, A.; Chen, L.; Lü, Y. Cooling effects of wetlands in an urban region: The case of Beijing. Ecol. Indic. 2012, 20, 57–64. [Google Scholar] [CrossRef]
- Sterling, S.M.; Ducharne, A.; Polcher, J. The impact of global land-cover change on the terrestrial water cycle. Nat. Clim. Chang. 2013, 3, 385–390. [Google Scholar] [CrossRef]
- Pitman, A.J. The evolution of, and revolution in, land surface schemes designed for climate models. Int. J. Clim. 2003, 23, 479–510. [Google Scholar] [CrossRef]
- Freitas, S.C.; Trigo, I.F.; Macedo, J.; Barroso, C.; Silva, R.; Perdigão, R.A.P. Land surface temperature from multiple geostationary satellites. Int. J. Remote. Sens. 2012, 34, 3051–3068. [Google Scholar] [CrossRef]
- Cao, X.; Onishi, A.; Chen, J.; Imura, H. Quantifying the cool island intensity of urban parks using ASTER and IKONOS data. Landsc. Urban Plan. 2010, 96, 224–231. [Google Scholar] [CrossRef]
- Wilson, J.S.; Clay, M.; Martin, E.; Stuckey, D.; Vedder-Risch, K. Evaluating environmental influences of zoning in urban ecosystems with remote sensing. Remote. Sens. Environ. 2003, 86, 303–321. [Google Scholar] [CrossRef]
- Spronken-Smith, R.A.; Oke, T.R.; Lowry, W.P. Advection and the surface energy balance across an irrigated urban park. Int. J. Climatol. 2000, 20, 1033–1047. [Google Scholar] [CrossRef]
- Findell, K.L.; Pitman, A.J.; England, M.H.; Pegion, P.J. Regional and Global Impacts of Land Cover Change and Sea Surface Temperature Anomalies. J. Clim. 2009, 22, 3248–3269. [Google Scholar] [CrossRef]
- Zhu, L.; Suomalainen, J.; Liu, J.; Hyyppä, J.; Kaartinen, H.; Haggren, H. A Review: Remote Sensing Sensors, Multi-Purposeful Application of Geospatial Data; IntechOpen: London, UK, 2018. [Google Scholar]
- Han, X.; Pan, J.; Devlin, A.T. Remote sensing study of wetlands in the Pearl River Delta during 1995–2015 with the support vector machine method. Front. Earth Sci. 2017, 12, 521–531. [Google Scholar] [CrossRef]
- Liu, C.; Zhang, Q.; Luo, H.; Qi, S.; Tao, S.; Xu, H.; Yao, Y. An efficient approach to capture continuous impervious surface dynamics using spatial-temporal rules and dense Landsat time series stacks. Remote. Sens. Environ. 2019, 229, 114–132. [Google Scholar] [CrossRef]
- Ma, L.; Li, M.; Ma, X.; Cheng, L.; Du, P.; Liu, Y. A review of supervised object-based land-cover image classification. ISPRS J. Photogramm. Remote. Sens. 2017, 130, 277–293. [Google Scholar] [CrossRef]
- Hansen, M.C.; Loveland, T.R. A review of large area monitoring of land cover change using Landsat data. Remote Sens. Environ. 2012, 122, 66–74. [Google Scholar] [CrossRef]
- Wulder, M.A.; Loveland, T.R.; Roy, D.P.; Crawford, C.J.; Masek, J.G.; Woodcock, C.E.; Allen, R.G.; Anderson, M.C.; Belward, A.S.; Cohen, W.B.; et al. Current status of Landsat program, science, and applications. Remote Sens. Environ. 2019, 225, 127–147. [Google Scholar] [CrossRef]
- Chen, T.; Sun, A.; Niu, R. Effect of Land Cover Fractions on Changes in Surface Urban Heat Islands Using Landsat Time-Series Images. Int. J. Environ. Res. Public Health 2019, 16, 971. [Google Scholar] [CrossRef]
- Ngie, A.; Abutaleb, K.; Ahmed, F.; Darwish, A.M.; Ahmed, M. Assessment of urban heat island using satellite remotely sensed imagery: A review. South Afr. Geogr. J. 2014, 96, 198–214. [Google Scholar] [CrossRef]
- Kennedy, R.E.; Andréfouët, S.; Cohen, W.B.; Gómez, C.; Griffiths, P.; Hais, M.; Healey, S.P.; Helmer, E.H.; Hostert, P.; Lyons, M.B.; et al. Bringing an ecological view of change to Landsat-based remote sensing. Front. Ecol. Environ. 2014, 12, 339–346. [Google Scholar] [CrossRef] [PubMed]
- Aldhshan, S.R.S.; Shafri, H.Z.M. Change detection on land use/land cover and land surface temperature using spatiotemporal data of Landsat: A case study of Gaza Strip. Arab. J. Geosci. 2019, 12, 443. [Google Scholar] [CrossRef]
- Du, H.; Song, X.; Jiang, H.; Kan, Z.; Wang, Z.; Cai, Y. Research on the cooling island effects of water body: A case study of Shanghai, China. Ecol. Indic. 2016, 67, 31–38. [Google Scholar] [CrossRef]
- Xue, Z.; Hou, G.; Zhang, Z.; Lyu, X.; Jiang, M.; Zou, Y.; Shen, X.; Wang, J.; Liu, X. Quantifying the cooling-effects of urban and peri-urban wetlands using remote sensing data: Case study of cities of Northeast China. Landsc. Urban Plan. 2018, 182, 92–100. [Google Scholar] [CrossRef]
- Jimenez-Munoz, J.C.; Sobrino, J.A. A Single-Channel Algorithm for Land-Surface Temperature Retrieval From ASTER Data. IEEE Geosci. Remote. Sens. Lett. 2009, 7, 176–179. [Google Scholar] [CrossRef]
- Li, Z.-L.; Tang, B.-H.; Wu, H.; Ren, H.; Yan, G.; Wan, Z.; Trigo, I.F.; Sobrino, J.A. Satellite-derived land surface temperature: Current status and perspectives. Remote Sens. Environ. 2013, 131, 14–37. [Google Scholar] [CrossRef]
- Peres, L.F.; DaCamara, C.C. Emissivity maps to retrieve land-surface temperature from MSG/SEVIRI. IEEE Trans. Geosci. Remote Sens. 2005, 43, 1834–1844. [Google Scholar] [CrossRef]
- Qin, Z.; Karnieli, A.; Berliner, P. A mono-window algorithm for retrieving land surface temperature from Landsat TM data and its application to the Israel-Egypt border region. Int. J. Remote. Sens. 2001, 22, 3719–3746. [Google Scholar] [CrossRef]
- Sattari, F.; Hashim, M. A Breif Review of Land Surface Temperature Retrieval Methods from Thermal Satellite Sensors. Middle-East J. Sci. Res. 2014, 22, 757–768. [Google Scholar]
- Cui, Y.; Li, L.; Chen, L.; Zhang, Y.; Cheng, L.; Zhou, X.; Yang, X. Land-Use Carbon Emissions Estimation for the Yangtze River Delta Urban Agglomeration Using 1994–2016 Landsat Image Data. Remote. Sens. 2018, 10, 1334. [Google Scholar] [CrossRef]
- Wu, J.; Li, C.; Zhang, X.; Zhao, Y.; Liang, J.; Wang, Z. Seasonal variations and main influencing factors of the water cooling islands effect in Shenzhen. Ecol. Indic. 2020, 117, 106699. [Google Scholar] [CrossRef]
- Lai, D.; Liu, W.; Gan, T.; Liu, K.; Chen, Q. A review of mitigating strategies to improve the thermal environment and thermal comfort in urban outdoor spaces. Sci. Total. Environ. 2019, 661, 337–353. [Google Scholar] [CrossRef]
- Yang, K.; Yu, Z.; Luo, Y. Analysis on driving factors of lake surface water temperature for major lakes in Yunnan-Guizhou Plateau. Water Res. 2020, 184, 116018. [Google Scholar] [CrossRef]
- Lamaro, A.A.; Mariñelarena, A.; Torrusio, S.E.; Sala, S.E. Water surface temperature estimation from Landsat 7 ETM+ thermal infrared data using the generalized single-channel method: Case study of Embalse del Río Tercero (Córdoba, Argentina). Adv. Space Res. 2012, 51, 492–500. [Google Scholar] [CrossRef]
- O’Reilly, C.M.; Sharma, S.; Gray, D.K.; Hampton, S.E.; Read, J.S.; Rowley, R.J.; Schneider, P.; Lenters, J.D.; McIntyre, P.B.; Kraemer, B.M.; et al. Rapid and highly variable warming of lake surface waters around the globe. Geophys. Res. Lett. 2015, 42, 10773–10781. [Google Scholar] [CrossRef]
- Schneider, P.; Hook, S.J. Space observations of inland water bodies show rapid surface warming since 1985. Geophys. Res. Lett. 2010, 37. [Google Scholar] [CrossRef]
- Niu, X.; Tang, J.; Wang, S.; Fu, C. Impact of future land use and land cover change on temperature projections over East Asia. Clim. Dyn. 2018, 52, 6475–6490. [Google Scholar] [CrossRef]
- Bharath, S.; Rajan, K.S.; Ramachandra, T.V. Land Surface Temperature Responses to Land Use Land Cover Dynamics. Geoinfor Geostat Overv. 2013, 54, 50–78. [Google Scholar] [CrossRef]
- Cataraqui Source Protection Area. Watershed Characterization Report; Cataraqui Region Conservation Authority: Kingston, ON, Canada, 2008; Volume 1, Available online: https://www.cleanwatercataraqui.ca/PDFs/Studies-and-Reports/WatershedCharacterizationReport/AppL-2WCRFullText.pdf (accessed on 7 January 2023).
- Cataraqui Region Conservation Authority. What are our region’s priority concerns? How can we enhance the watershed. In Cataraqui Region Watershed Report Card; Cataraqui Region Conservation Authority: Kingston, ON, Canada, 2018. [Google Scholar]
- Gorelick, N.; Hancher, M.; Dixon, M.; Ilyushchenko, S.; Thau, D.; Moore, R. Google Earth Engine: Planetary-scale geospatial analysis for everyone. Remote Sens. Environ. 2017, 202, 18–27. [Google Scholar] [CrossRef]
- Young, N.E.; Anderson, R.S.; Chignell, S.M.; Vorster, A.G.; Lawrence, R.; Evangelista, P.H. A survival guide to Landsat preprocessing. Ecology 2017, 98, 920–932. [Google Scholar] [CrossRef] [PubMed]
- Goodwin, N.R.; Collett, L.J.; Denham, R.J.; Flood, N.; Tindall, D. Cloud and cloud shadow screening across Queensland, Australia: An automated method for Landsat TM/ETM+ time series. Remote. Sens. Environ. 2013, 134, 50–65. [Google Scholar] [CrossRef]
- Government of Canada. 2010 Land Cover of Canada. 2017. Available online: https://open.canada.ca/data/en/dataset/c688b87f-e85f-4842-b0e1-a8f79ebf1133 (accessed on 6 May 2020).
- Hulley, G.C.; Hook, S.J.; Abbott, E.; Malakar, N.; Islam, T.; Abrams, M. The ASTER Global Emissivity Dataset ( ASTER GED ): Mapping Earth’s emissivity at 100 meter spatial scale. Geophys. Res. Lett. 2015, 42, 7966–7976. [Google Scholar] [CrossRef]
- Parastatidis, D.; Mitraka, Z.; Chrysoulakis, N.; Abrams, M. Online Global Land Surface Temperature Estimation from Landsat. Remote. Sens. 2017, 9, 1208. [Google Scholar] [CrossRef]
- Collins, W.; Deaven, D.; Gandin, L.; Iredell, M.; Jenne, R.; Joseph, D. The NCEP NCAR 40-Year Reanalysis Project. Bull. Am. Meteorol. Soc. 1996, 77, 437–472. [Google Scholar]
- Mieruch, S.; Schröder, M.; Noel, S.; Schulz, J. Comparison of monthly means of global total column water vapor retrieved from independent satellite observations. J. Geophys. Res. Atmos. 2010, 115. [Google Scholar] [CrossRef]
- Zhao, Y.; Zhou, T. Asian water tower evinced in total column water vapor: A comparison among multiple satellite and reanalysis data sets. Clim. Dyn. 2019, 54, 231–245. [Google Scholar] [CrossRef]
- Zhu, Z.; Woodcock, C.E. Continuous change detection and classification of land cover using all available Landsat data. Remote Sens. Environ. 2014, 144, 152–171. [Google Scholar] [CrossRef]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Congalton, R.G. Putting the map back in map accuracy assessment. In Remote Sensing and GIS Accuracy Assessment; Lunetta, R.S., Lyon, J.G., Eds.; CRC Press: Boca Raton, FL, USA; pp. 1–11.
- Chen, D.; Wei, H. The effect of spatial autocorrelation and class proportion on the accuracy measures from different sampling designs. ISPRS J. Photogramm. Remote. Sens. 2009, 64, 140–150. [Google Scholar] [CrossRef]
- Duguay-Tetzlaff, A.; Bento, V.A.; Göttsche, F.M.; Stöckli, R.; Martins, J.P.A.; Trigo, I.; Olesen, F.; Bojanowski, J.S.; Da Camara, C.; Kunz, H. Meteosat Land Surface Temperature Climate Data Record: Achievable Accuracy and Potential Uncertainties. Remote Sens. 2015, 7, 13139–13156. [Google Scholar] [CrossRef]
- Sun, D.; Pinker, R.T.; Basara, J.B. Land Surface Temperature Estimation from the Next Generation of Geostationary Operational Environmental Satellites: GOES M–Q. J. Appl. Meteorol. 2004, 43, 363–372. [Google Scholar] [CrossRef]
- Ermida, S.L.; Soares, P.; Mantas, V.; Göttsche, F.-M.; Trigo, I.F. Google Earth Engine Open-Source Code for Land Surface Temperature Estimation from the Landsat Series. Remote. Sens. 2020, 12, 1471. [Google Scholar] [CrossRef]
- Martins, J.P.A.; Trigo, I.F.; Bento, V.A.; Da Camara, C. A Physically Constrained Calibration Database for Land Surface Temperature Using Infrared Retrieval Algorithms. Remote. Sens. 2016, 8, 808. [Google Scholar] [CrossRef]
- Borbas, E.; Seemann, S.W.; Huang, H.-L.; Li, J.; Menzel, W.P. Global profile training database for satellite regression retrievals with estimates of skin temperature and emissivity. In Proceedings of the XIV. International ATOVS Study Conference, Beijing, China, 25–31 May 2005; University of Wisconsin-Madison, Space Science and Engineering Center, Cooperative Institute for Meteorological Satellite Studies (CIMSS): Madison, WI, USA, 2005; pp. 763–770. Available online: https://cimss.ssec.wisc.edu/training_data/data/itsc14_borbas_trainingData.pdf (accessed on 7 January 2023).
- Verbesselt, J.; Hyndman, R.; Newnham, G.; Culvenor, D. Detecting trend and seasonal changes in satellite image time series. Remote Sens. Environ. 2010, 114, 106–115. [Google Scholar] [CrossRef]
- Shumway, R.H.; Stoffer, D.S. Time Series Analysis and its Applications with R Examples; Springer: Berlin/Heidelberg, Germany, 2014; Volume 97. [Google Scholar] [CrossRef]
- Flaim, G.; Obertegger, U.; Anesi, A.; Guella, G. Temperature-induced changes in lipid biomarkers and mycosporine-like amino acids in the psychrophilic dinoflagellate Peridinium aciculiferum. Freshw. Biol. 2014, 59, 985–997. [Google Scholar] [CrossRef]
- Wu, D.; Wang, Y.; Fan, C.; Xia, B. Thermal environment effects and interactions of reservoirs and forests as urban blue-green infrastructures. Ecol. Indic. 2018, 91, 657–663. [Google Scholar] [CrossRef]
- Yang, K.; Yu, Z.; Luo, Y.; Zhou, X.; Shang, C. Spatial-Temporal Variation of Lake Surface Water Temperature and Its Driving Factors in Yunnan-Guizhou Plateau. Water Resour. Res. 2019, 55, 4688–4703. [Google Scholar] [CrossRef]
- Alofs, K.M.; A Jackson, D.; Lester, N.P. Ontario freshwater fishes demonstrate differing range-boundary shifts in a warming climate. Divers. Distrib. 2013, 20, 123–136. [Google Scholar] [CrossRef]
- Hudon, C.; Armellin, A.; Gagnon, P.; Patoine, A. Variations in water temperatures and levels in the St. Lawrence River (Québec, Canada) and potential implications for three common fish species. Hydrobiologia 2009, 647, 145–161. [Google Scholar] [CrossRef]
- Warren, D.R.; Robinson, J.M.; Josephson, D.C.; Sheldon, D.R.; Kraft, C.E. Elevated summer temperatures delay spawning and reduce redd construction for resident brook trout (Salvelinus fontinalis). Glob. Chang. Biol. 2012, 18, 1804–1811. [Google Scholar] [CrossRef]
- Woolway, I.R.; Merchant, C.J. Amplified surface temperature response of cold, deep lakes to inter-annual air temperature variability. Sci. Rep. 2017, 7, 1–8. [Google Scholar] [CrossRef] [PubMed]




| Land Cover | CCRS 2010 Land Cover | CCRS 2015 Land Cover |
|---|---|---|
| Impervious Surface | Settlement, Roads, Other land | Urban and built up, Barren land |
| Dense Vegetation | Forest (Treed area > 1 ha in size), Trees (Treed area < 1 ha in size) | Temperate or sub-polar needleleaf forest, sub-polar taiga needleleaf forest, Tropical or sub-tropical broadleaf evergreen forest, Tropical or sub-tropical broadleaf deciduous forest, Temperate or sub-polar broadleaf deciduous forest, Mixed forest |
| Sparse Vegetation | Cropland, Grassland managed, Grassland unmanaged | Tropical or sub-tropical shrubland, Temperate or sub-tropical shrubland |
| Wetland | Forest Wetland, Treed Wetland (wetland with tree cover), Wetland shrub, Wetland herb, Wetland | Wetland |
| Water | Water | Water |
| Impervious Surface (%) | Dense Vegetation (%) | Sparse Vegetation (%) | Water (%) | Wetland (%) | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 1985 | 2020 | 1985 | 2020 | 1985 | 2020 | 1985 | 2020 | 1985 | 2020 | |
| Grippen Lake | 2.30 | 1.71 | 57.15 | 58.64 | 24.35 | 25.92 | 12.68 | 9.22 | 3.51 | 4.51 |
| Wiltse Lake | 2.75 | 2.17 | 34.09 | 40.81 | 36.99 | 36.30 | 10.44 | 7.21 | 15.73 | 13.52 |
| Little Lake | 3.43 | 2.21 | 70.52 | 77.97 | 8.41 | 7.40 | 17.57 | 12.40 | 0.06 | 0.03 |
| South Lake | 2.55 | 1.77 | 65.59 | 70.22 | 17.47 | 17.10 | 11.81 | 8.23 | 2.58 | 2.68 |
| Cedar Lake | 11.74 | 11.96 | 49.34 | 49.11 | 14.47 | 15.89 | 24.45 | 23.04 | 0.00 | 0.00 |
| Horseshoe Lake | 2.85 | 3.26 | 61.06 | 64.38 | 8.21 | 8.94 | 22.62 | 17.96 | 5.26 | 5.46 |
| Moulton Lake | 0.00 | 0.00 | 90.63 | 91.59 | 0.34 | 0.30 | 9.03 | 8.11 | 0.00 | 0.00 |
| Lambs Lake | 11.31 | 8.30 | 40.44 | 40.63 | 23.86 | 26.82 | 12.52 | 10.43 | 11.86 | 13.83 |
| Elodia Lake | 6.26 | 5.91 | 34.00 | 36.08 | 29.61 | 32.40 | 10.84 | 8.23 | 19.30 | 17.38 |
| Lake | LCC% | Size of Lake and Buffer Size (km2) | Min Change Slope (×10−5) | Max Change Slope (×10−5) | Range (×10−6) | Average Slope (×10−5) | Overall Accuracy (%) |
|---|---|---|---|---|---|---|---|
| Horseshoe Lake | 5.20 | 0.37 (2.83) | 0.051 | 0.67 | 6.15 | 0.28 | 77.59 |
| Little Lake | 11.16 | 0.57 (2.53) | 0.21 | 0.85 | 6.37 | 0.52 | 88.76 |
| Cedar Lake | 7.30 | 0.13 (1.78) | 0.29 | 1.15 | 8.74 | 0.52 | 74.64 |
| Moulton Lake | 3.04 | 0.072 (1.25) | 0.35 | 0.82 | 4.75 | 0.55 | 96.91 |
| Grippen Lake | 14.67 | 2.056 (4.60) | 0.78 | 1.39 | 6.09 | 0.93 | 79.82 |
| South Lake | 14.7 | 2.38 (5.06) | 0.78 | 1.35 | 5.73 | 1.06 | 83.40 |
| Wiltse Lake | 15.84 | 1.38 (3.00) | 0.91 | 1.41 | 4.99 | 1.21 | 84.52 |
| Elodia Lake | 18.02 | 1.82 (2.44) | 0.74 | 1.57 | 8.31 | 1.23 | 87.45 |
| Lambs Lake | 17.26 | 0.06 (2.85) | 0.86 | 1.61 | 7.52 | 1.42 | 85.53 |
| Impervious Surface | Dense Vegetation | Sparse Vegetation | Wetland | Water | |
|---|---|---|---|---|---|
| Pearson Correlation (p value) | −0.09 (0.29) | −0.54 (0.01) | 0.57 (0.09) | 0.52 (0.02) | −0.04 (0.10) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Senyshen, M.D.; Chen, D. The Impact of Land Cover Change on Surface Water Temperature of Small Lakes in Eastern Ontario from 1985 to 2020. Land 2023, 12, 547. https://doi.org/10.3390/land12030547
Senyshen MD, Chen D. The Impact of Land Cover Change on Surface Water Temperature of Small Lakes in Eastern Ontario from 1985 to 2020. Land. 2023; 12(3):547. https://doi.org/10.3390/land12030547
Chicago/Turabian StyleSenyshen, Matthew D., and Dongmei Chen. 2023. "The Impact of Land Cover Change on Surface Water Temperature of Small Lakes in Eastern Ontario from 1985 to 2020" Land 12, no. 3: 547. https://doi.org/10.3390/land12030547
APA StyleSenyshen, M. D., & Chen, D. (2023). The Impact of Land Cover Change on Surface Water Temperature of Small Lakes in Eastern Ontario from 1985 to 2020. Land, 12(3), 547. https://doi.org/10.3390/land12030547







