Influence of Landscape Characteristics on Wind Dispersal Efficiency of Calotropis procera
Abstract
:1. Introduction
2. Materials and Methods
2.1. Study Sites and Species
2.2. Estimating Seed Dispersal Distance
2.3. Short Distance Seed Dispersal
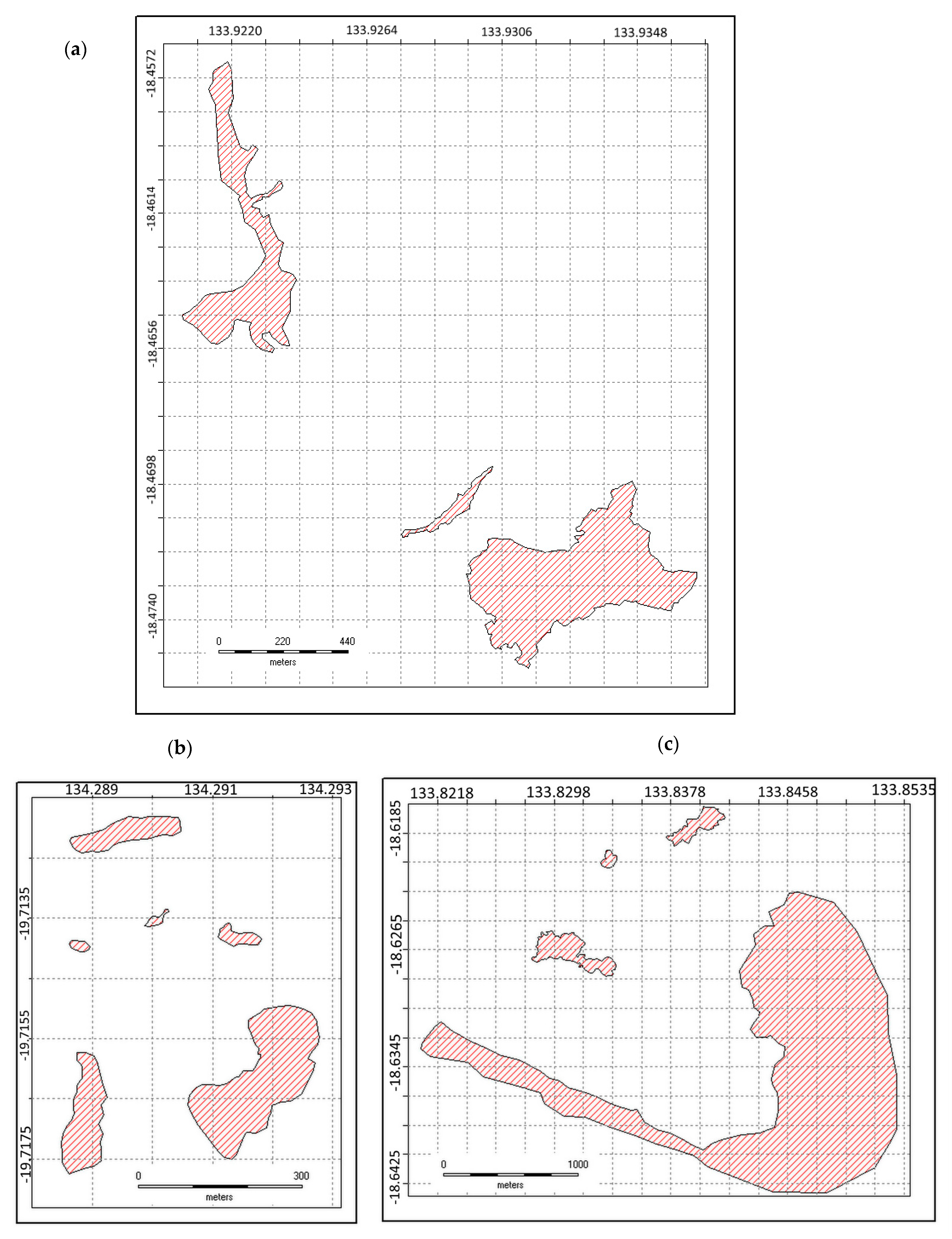
2.4. Spatial Configuration of All Adjacent Populations
2.5. Modelling the Seed Dispersal Kernel
- (1)
- Birnbaum–Saunders function
- (2)
- 2-parameter exponential function
- (3)
- 3-parameter log logistic probability density function
- (4)
- The 3-parameter Weibull probability density function
2.6. Estimation of Population Characteristics
- Exponential model
- Circular model
- Power model
2.7. Analyses
3. Results
3.1. Seed Dispersal Kernels
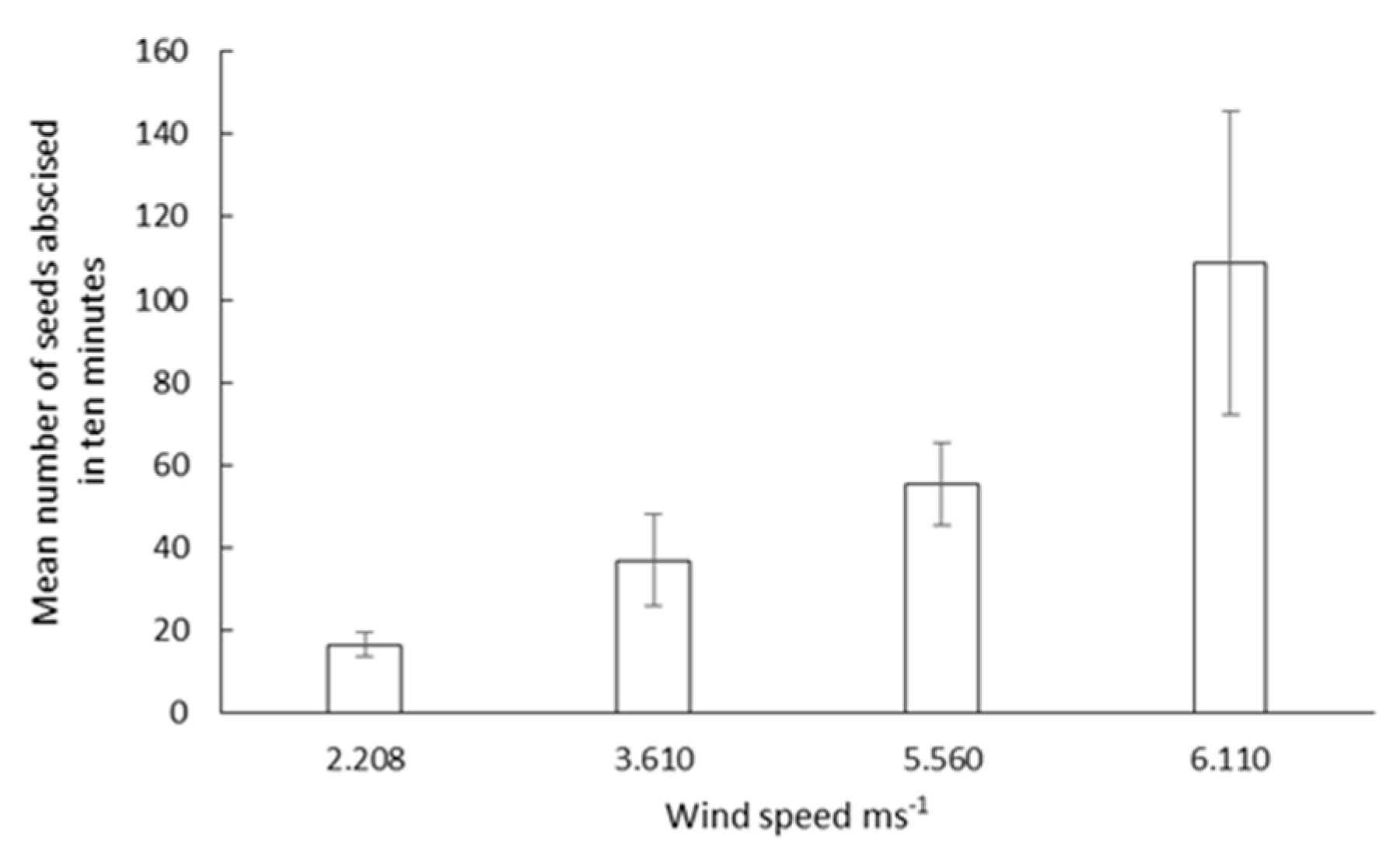
3.2. Seed Abscission
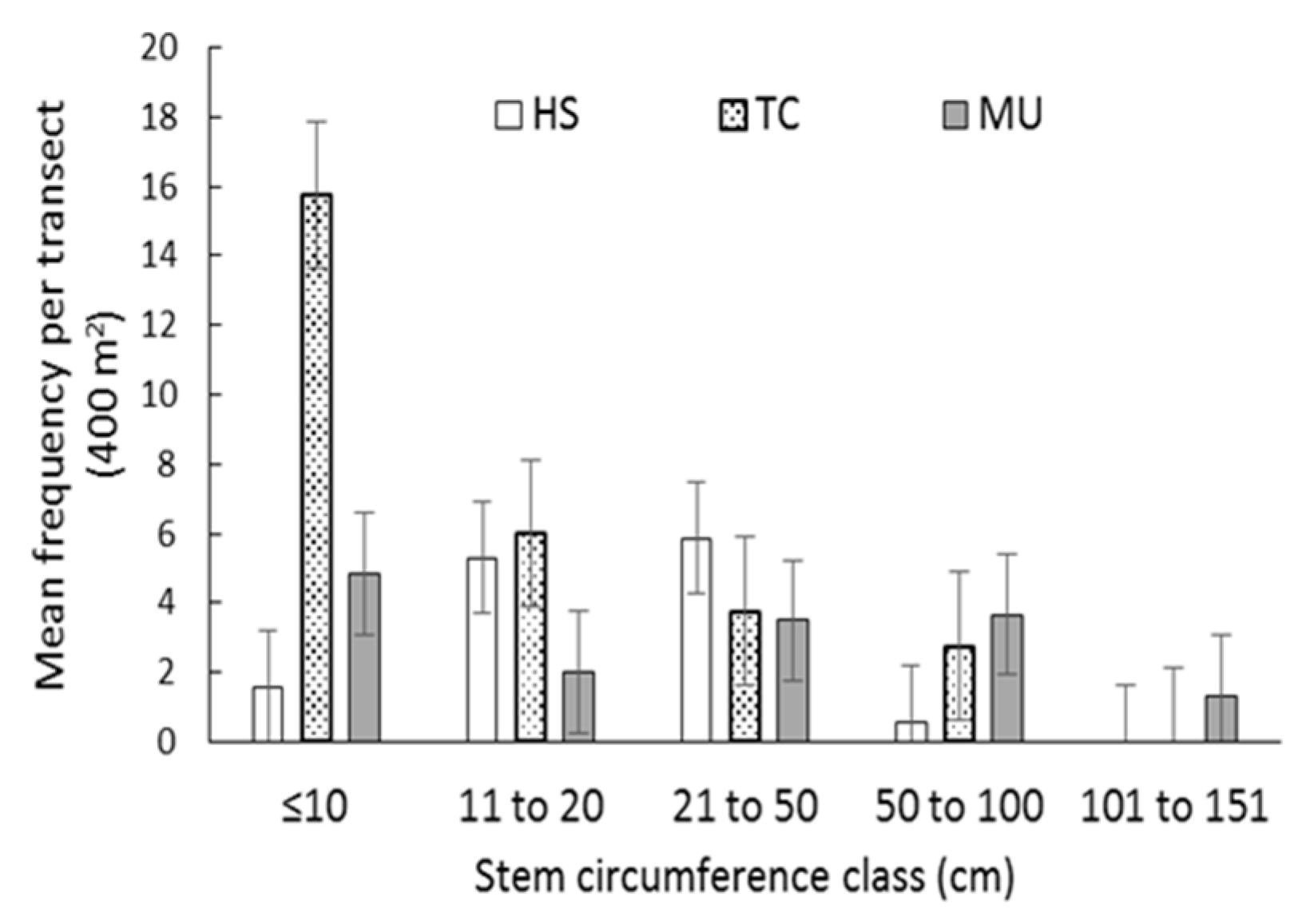
3.3. Stem Size and Spatial Characteristics of Existing Populations
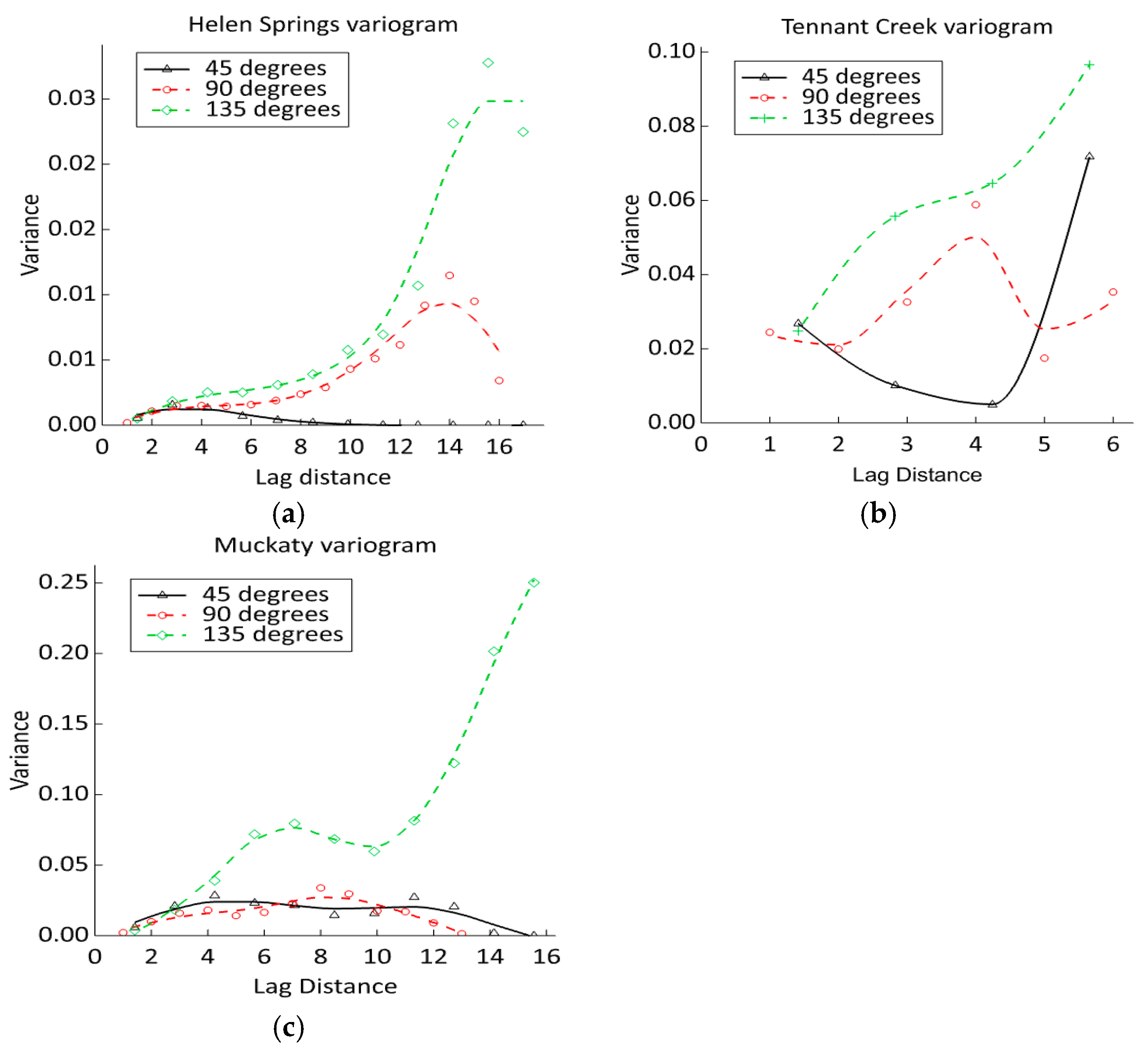
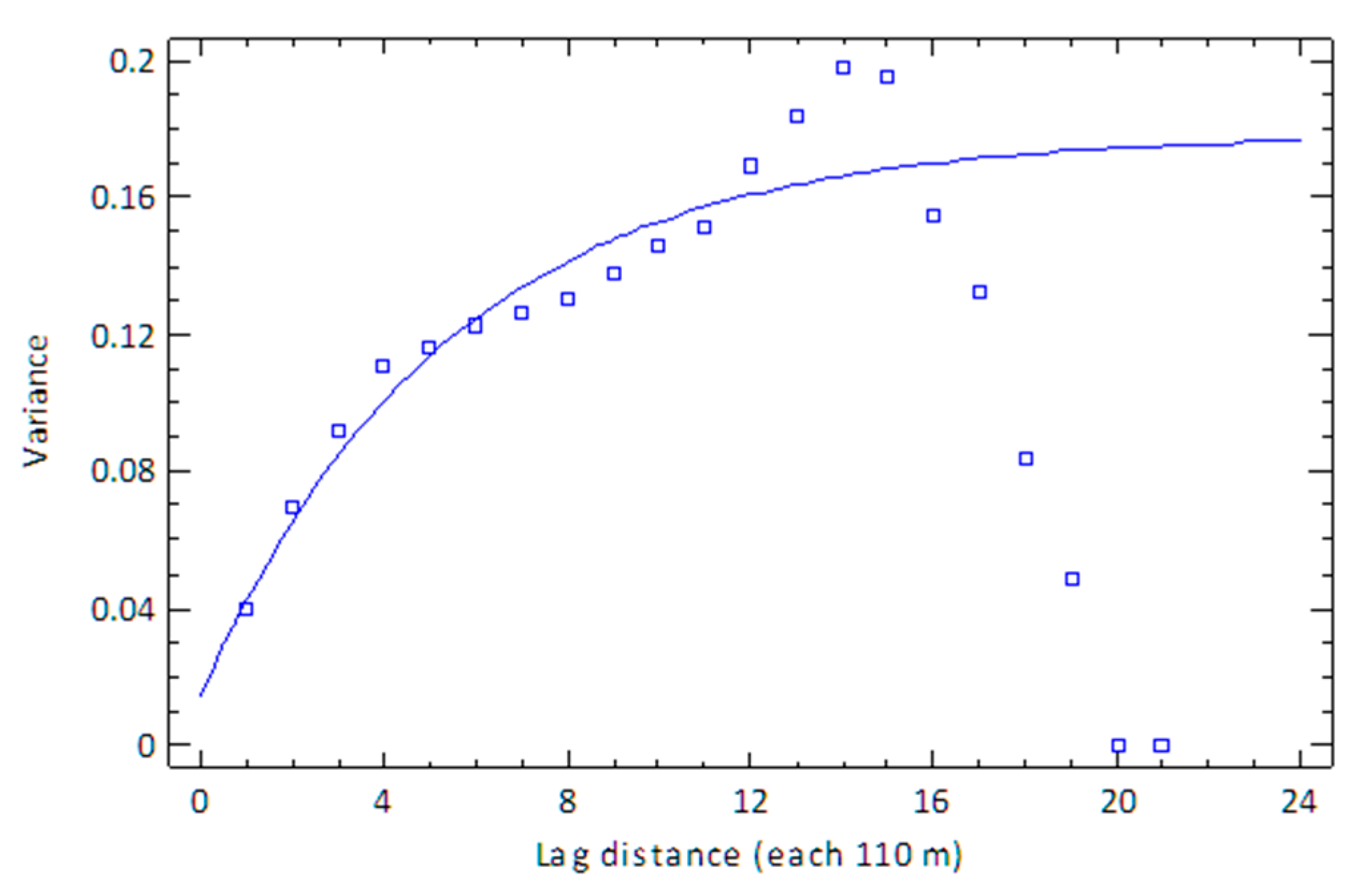
3.4. Kriging Variogram Models—The Spatial Likelihood of Invasion
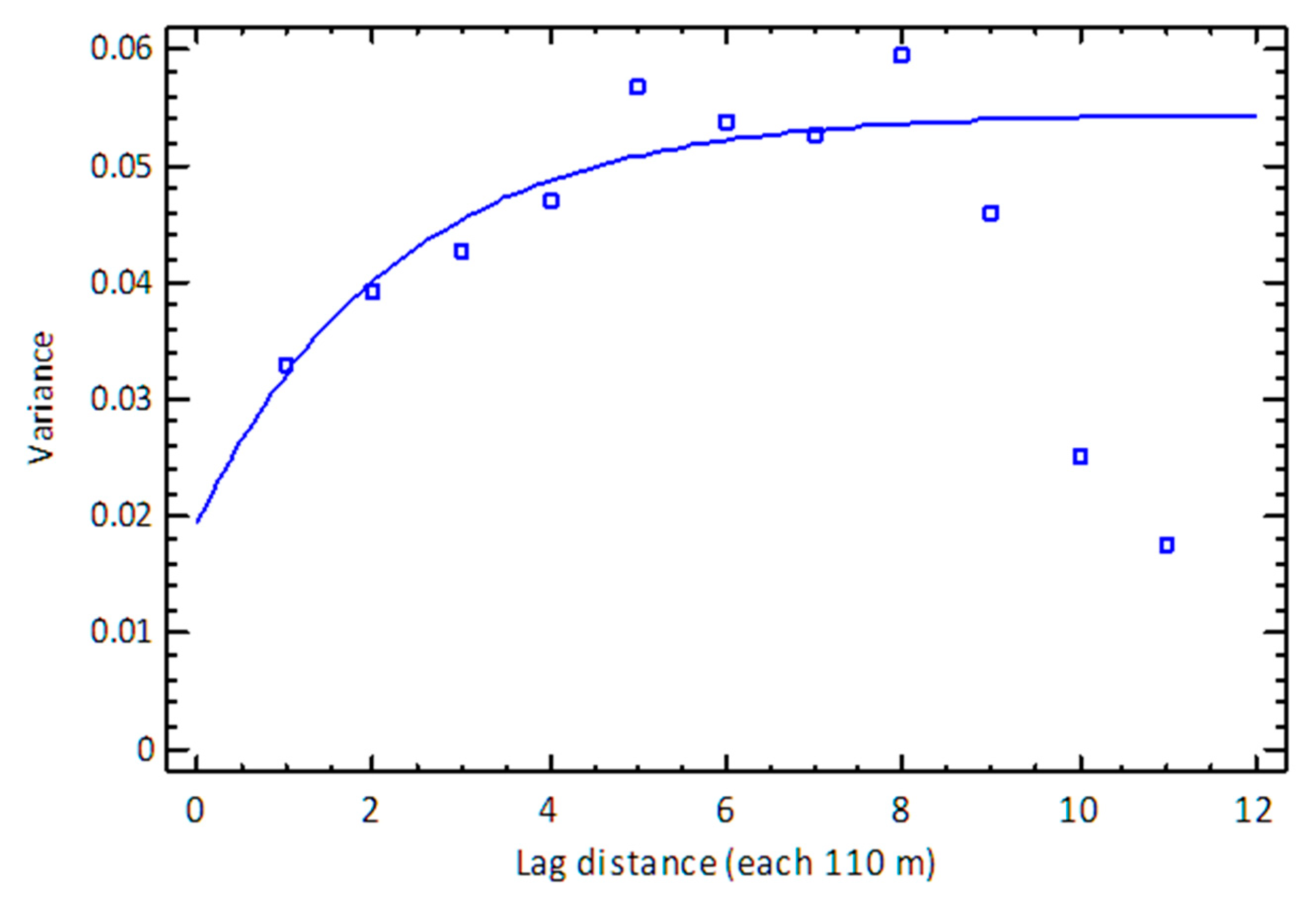
3.4.1. Tennant Creek
- Exponential model
3.4.2. Helen Springs
- Exponential model
3.4.3. Muckaty
- Exponential model
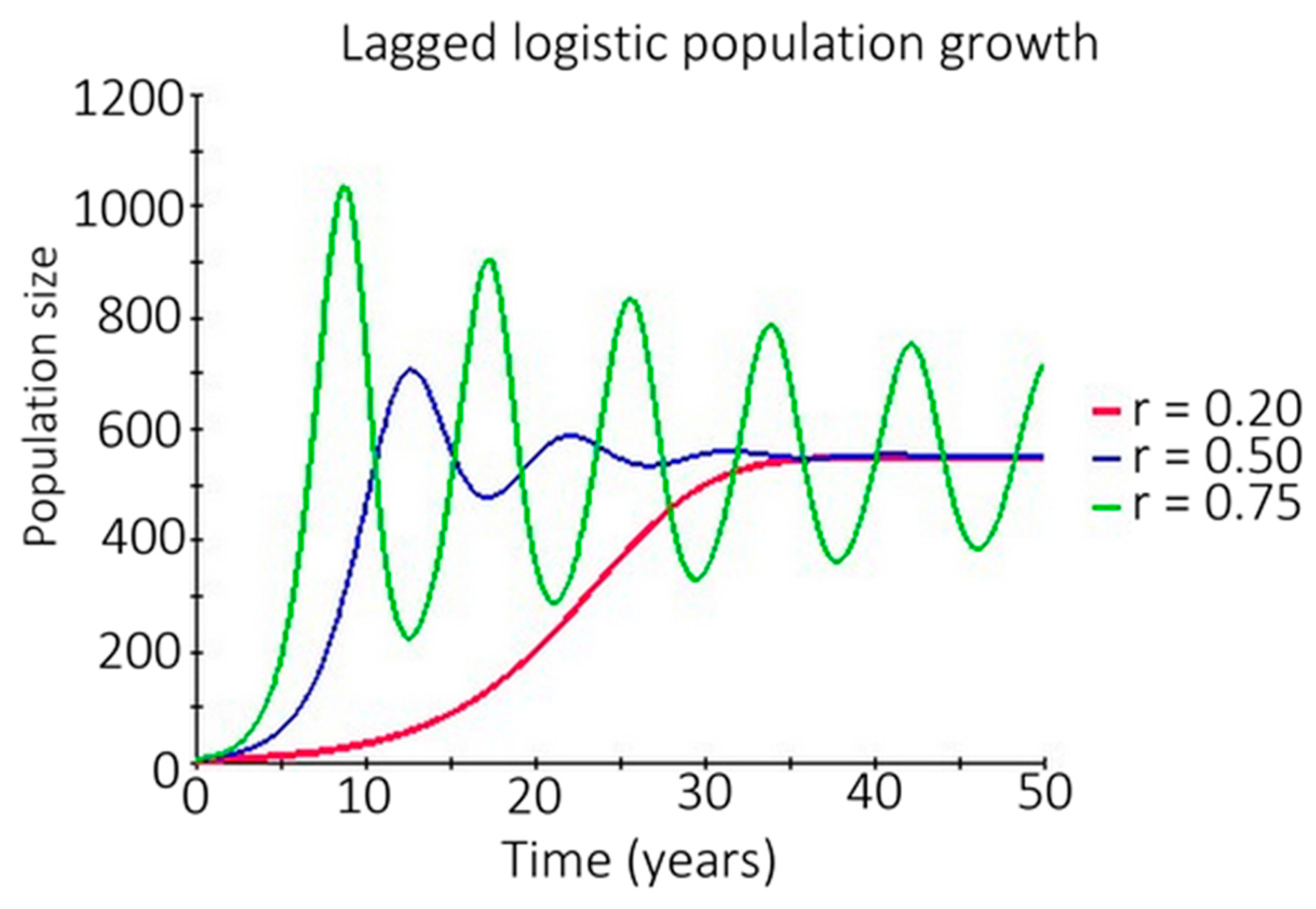
3.4.4. Density Dependent Lagged Logistic Population Growth
- (a)
- Seed shadow = fecundity × dispersal kernel [71];
- (b)
- Seedlings = Seed shadow × Ψ × 0.82
4. Findings
5. Discussion
6. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Nathan, R.; Katul, G.G.; Bohrer, G.; Kuparinen, A.; Soons, M.B.; Thompson, S.E.; Trakhtenbrot, A.; Horn, H.S. Mechanistic models of seed dispersal by wind. Theor. Ecol. 2011, 4, 113–132. [Google Scholar] [CrossRef]
- Soons, M.B.; Heil, G.W.; Nathan, R.; Katul, G. Determinants of long-distance seed dispersal by wind in grasslands. Ecology 2004, 85, 3056–3068. [Google Scholar] [CrossRef] [Green Version]
- Bullock, J.M.; Clarke, R.T. Long distance seed dispersal by wind: Measuring and modelling the tail of the curve. Oecologia 2000, 124, 506–521. [Google Scholar] [CrossRef]
- Moody, M.E.; Mack, R.N. Controlling the spread of plant invasions: The importance of nascent foci. J. Appl. Ecol. 1988, 25, 1009–1021. [Google Scholar] [CrossRef]
- Kot, M.; Lewis, M.A.; van den Driesshe, P. Dispersal data and the spread of invading organisms. Ecology 1996, 77, 2027–2042. [Google Scholar] [CrossRef]
- Neubert, M.G.; Caswell, H. Demography and dispersal: Calculation and sensitivity analysis of invasion spread for structured populations. Ecology 2000, 81, 1613–1628. [Google Scholar] [CrossRef]
- Higgins, S.I.; Richardson, D.M. A review of models of alien plant spread. Ecol. Model. 1996, 87, 249–265. [Google Scholar] [CrossRef]
- Satterthwaite, W.H. The importance of dispersal in determining seed versus safe site limitation of plant populations. Plant Ecol. 2007, 193, 113–130. [Google Scholar] [CrossRef]
- Terborgh, J.; Alvarez-Loayza, P.; Dexter, K.; Cornejo, F.; Carrasco, C. Decomposing dispersal limitation: Limits on fecundity or seed distribution? J. Ecol. 2011, 99, 935–944. [Google Scholar] [CrossRef]
- Nathan, R.; Katul, G.G.; Horn, H.S.; Thomas, S.M.; Oren, R.; Avissar, R.; Pacala, S.W.; Levin, S.A. Mechanisms of long-distance dispersal of seeds by wind. Nature 2002, 418, 409–413. [Google Scholar] [CrossRef] [PubMed]
- Greene, D.F.; Johnson, E.A. A model of wind dispersal of winged or plumed seeds. Ecology 1989, 70, 339–347. [Google Scholar] [CrossRef]
- Jongejans, E.; Schipper, P. Modeling seed dispersal by wind in herbacious species. Oikos 1999, 99, 362–372. [Google Scholar] [CrossRef]
- Liu, H.; Zhang, D.; Yang, X.; Huang, Z.; Duan, S.; Wang, X. Seed dispersal and germination traits of 70 plant species inhabiting the Gurbantunggut Desert in northwest China. Sci. World J. 2014, 2014, 346405. [Google Scholar] [CrossRef] [Green Version]
- Fort, K.P.; Richards, J.H. Does seed dispersal limit initiation of primary succession in desert playas? Am. J. Bot. 1998, 85, 1722–1731. [Google Scholar] [CrossRef] [PubMed]
- Horn, H.S.; Nathan, R.; Kaplan, S.R. Long-distance dispersal of tree seeds by wind. Ecol. Res. 2001, 16, 877–885. [Google Scholar] [CrossRef]
- Tackenberg, O. Modeling long-distance dispersal of plant diaspores by wind. Ecol. Monogr. 2003, 73, 173–189. [Google Scholar] [CrossRef]
- Davies, K.W.; Sheley, R.L. Influence of neighboring vegetation height on seed dispersal: Implications for invasive plant management. Weed Sci. 2007, 55, 626–630. [Google Scholar] [CrossRef]
- Thomson, F.J.; Moles, A.T.; Auld, T.D.; Kingsford, R.T. Seed dispersal distance is more strongly correlated with plant height than with seed mass. J. Ecol. 2011, 99, 1299–1307. [Google Scholar] [CrossRef]
- Menge, E.O.; Bellairs, S.M.; Lawes, M.J. Seed-germination responses of Calotropis procera (Asclepiadaceae) to temperature and water stress in northern Australia. Aust. J. Bot. 2016, 64, 441–450. [Google Scholar] [CrossRef]
- Menge, E.O.; Stobo-Wilson, A.; Oliveira, S.L.J.; Lawes, M.J. The potential distribution of the woody weed Calotropis procera (Aiton) W.T. Aiton (Asclepiadaceae) in Australia. Rangel. J. 2016, 38, 35–46. [Google Scholar] [CrossRef]
- Vitelli, J.; Madigan, B.; Wilkinson, P.; van Haaren, P. Calotrope (Calotropis procera) control. Rangel. J 2008, 30, 339–348. [Google Scholar] [CrossRef]
- Dhileepan, K. Prospects for the classical biological control of Calotropis procera (Apocynaceae) using co-evolved insects. Biocontrol Sci. Technol. 2014, 24, 977–998. [Google Scholar] [CrossRef]
- Campbell, S.; Roden, L.; Crowley, C. Calotrope (Calotropis procera): A weed on the move in northern Queensland. In Proceedings of the 12th Queensland Weed Symposium, Hervey Bay, QLD, Australia, 15–18 July 2013; Weed Society of Queensland: Brisbane, QLD, Australia, 2013. [Google Scholar]
- Menge, E.O.; Greenfield, M.L.; McConchie, C.A.; Bellairs, S.M.; Lawes, M.J. Density-dependent reproduction and pollen limitation in an invasive milkweed, Calotropis procera (Ait.) R.Br. Apocynaceae. Austral. Ecol. 2017, 42, 61–71. [Google Scholar] [CrossRef]
- Menge, E.O.; Bellairs, S.M.; Lawes, M.J. Disturbance-dependent invasion of the woody weed, Calotropis procera, in Australian rangelands. Rangel. J. 2017, 39, 201–211. [Google Scholar] [CrossRef]
- Menge, E.O.; McConchie, C.A.; Brown, G.; Lawes, M.J. Pollinators and mating system of Calotropis procera (Ait.) W.T. Aiton (Asclepiadaceae) in an invaded range. In Proceedings of the Ecological Society of Australia Annual Conference 2015, Hilton Hotel Adelaide, South Australia, 29 November–3 December 2015; Ecological Society of Australia: Windsor, QLD, Australia, 2015; p. 12. [Google Scholar]
- Richardson, D.M.; Rejmánek, M. Conifers as invasive aliens: A global survey and predictive framework. Divers. Distrib. 2004, 10, 321–331. [Google Scholar] [CrossRef]
- Finardi, S.; Morselli, M.G.; Jeannet, P.; Szepesi, D.J.; Vergeiner, I.; Deligiannis, P.; Lagouvardos, K.; Planinsek, A.; Borrel, L.; Fekete, K.; et al. Wind flow models over complex terrain for dispersion calculations. In Report of Working Group 4 Cost Action 710; Finardi, S., Morselli, M., Jeannet, P., Eds.; Aarhus University: Aarhus, Denmark, 1997. [Google Scholar]
- Fisher, A. Biogeography and conservation of Mitchell grasslands in northern Australia. In Faculty of Science, Information Technology and Education; Northern Territory University: Darwin, Australia, 2001; p. 557. [Google Scholar]
- Cousens, R.; Dytham, C.; Law, R. Dispersal in Plants: A Population Perspective; OUP: Oxford, UK, 2008; p. 220. [Google Scholar]
- Greene, D.F. The role of abscission in long-distance seed dispersal by the wind. Ecology 2005, 86, 3105–3110. [Google Scholar] [CrossRef]
- Pazos, G.E.; Greene, D.F.; Katul, G.; Bertiller, M.B.; Soons, M.B. Seed dispersal by wind: Towards a conceptual framework of seed abscission and its contribution to long-distance dispersal. J. Ecol. 2013, 101, 889–904. [Google Scholar] [CrossRef]
- Arim, M.; Abades, S.R.; Neill, P.E.; Lima, M.; Marquet, P.A. Spread dynamics of invasive species. Proc. Natl. Acad. Sci. USA 2006, 103, 374–378. [Google Scholar] [CrossRef] [Green Version]
- Shigesada, N.; Kawasaki, K. Biological Invasions: Theory and Practice; Oxford University Press: Oxford, UK, 1997; p. 224. [Google Scholar]
- Hanski, I.; Foley, P.; Hassell, M. Random walks in a metapopulation: How much density dependence is necessary for long-term persistence? J. Anim. Ecol. 1996, 65, 274–282. [Google Scholar] [CrossRef]
- Renshaw, E. Time-lag models of population growth. In Modelling Biological Populations in Space and Time; Cambridge University Press: Cambridge, UK, 1991; pp. 87–127. [Google Scholar] [CrossRef]
- Warren, I.; Robert, J.; Ursell, T.; Keiser, A.D.; Bradford, M.A. Habitat, dispersal and propagule pressure control exotic plant infilling within an invaded range. Ecosphere 2013, 4, 1–12. [Google Scholar] [CrossRef]
- Parker, I.M. Mating patterns and rates of biological invasion. Proc. Natl. Acad. Sci. USA 2004, 101, 13695–13696. [Google Scholar] [CrossRef] [Green Version]
- Allee, W.C. Animal Aggregations: A Study in General Sociology; University of Chicago Press: Chicago, IL, USA, 1931. [Google Scholar]
- Taylor, C.M.; Hastings, A. Allee effects in biological invasions. Ecol. Lett. 2005, 8, 895–908. [Google Scholar] [CrossRef]
- Bebawi, F.F.; Campbell, S.D.; Mayer, R.J. Seed bank longevity and age to reproductive maturity of Calotropis procera (Aiton) W.T. Aiton in the dry tropics of northern Queensland. Rangel. J. 2015, 37, 239–247. [Google Scholar] [CrossRef]
- Bastin, G.; Ludwig, J.; Eager, R.; Liedloff, A.; Andison, R.; Cobiac, M. Vegetation changes in a semiarid tropical savanna, northern Australia: 1973–2002. Rangel. J. 2003, 25, 3–19. [Google Scholar] [CrossRef]
- Foran, B.D.; Bastin, G.; Hill, B. The pasture dynamics and management of two rangeland communities in the Victoria River District of the Northern Territory. Aust. Rangel. J. 1985, 7, 107–113. [Google Scholar] [CrossRef]
- Vincke, C.; Diedhiou, I.; Grouzis, M. Long term dynamics and structure of woody vegetation in the Ferlo (Senegal). J. Arid Environ. 2010, 74, 268–276. [Google Scholar] [CrossRef]
- Bullock, J.M.; Shea, K.; Skarpaas, O. Measuring plant dispersal: An introduction to field methods and experimental design. Plant Ecol. 2006, 186, 217–234. [Google Scholar] [CrossRef]
- Willson, M.F. Dispersal mode, seed shadows, and colonization patterns. Vegetatio 1993, 107, 261–280. [Google Scholar] [CrossRef]
- Hijmans, R.J.; Guarino, L.; Mathur, P. DIVA-GIS, Version 7.5 Manual. 2012.
- Jongejans, E.; Telenius, A. Field experiments on seed dispersal by wind in ten umbelliferous species (Apiaceae). Plant Ecol. 2001, 152, 67–78. [Google Scholar] [CrossRef]
- Higgins, S.I.; Richardson, D.M. Predicting plant migration rates in a changing world: The role of long-distance dispersal. Am. Nat. 1999, 153, 464–475. [Google Scholar] [CrossRef]
- Nathan, R.; Perry, G.; Cronin, J.T.; Strand, A.E.; Cain, M.L. Methods for estimating long-distance dispersal. Oikos 2003, 103, 261–273. [Google Scholar] [CrossRef] [Green Version]
- Chesher, A. Testing the law of proportionate effect. J. Ind. Econ. 1979, 27, 403–411. [Google Scholar] [CrossRef]
- Schurr, F.M.; Steinitz, O.; Nathan, R. Plant fecundity and seed dispersal in spatially heterogeneous environments: Models, mechanisms and estimation. J. Ecol. 2008, 96, 628–641. [Google Scholar] [CrossRef]
- Cordeiro, G.M.; Lemonte, A.J. The β-Birnbaum-Saunders distribution: An improved distribution for fatigue life modeling. Comput. Stat. Data Anal. 2011, 55, 1445–1461. [Google Scholar] [CrossRef]
- StatPoint. Statgraphics Centurion XVII; Statpoint Technologies, Inc.: The Plains, VA, USA, 2017. [Google Scholar]
- Singh, V.P. Three-parameter log-logistic distribution. In Entropy-Based Parameter Estimation in Hydrology; Singh, V.P., Ed.; Springer: Dordrecht, The Netherlands, 1998; pp. 297–311. [Google Scholar] [CrossRef]
- Weibull, W. A statistical distribution function of wide applicability. ASME J. Appl. Mech. Trans. Am. Soc. Mech. Eng. 1951, 73, 293–297. [Google Scholar] [CrossRef]
- Wiegand, T.; Jeltsch, F.; Hanski, I.; Grimm, V. Using pattern-oriented modeling for revealing hidden information: A key to reconciling ecological theory and application. Oikos 2003, 100, 209–222. [Google Scholar] [CrossRef] [Green Version]
- Wiegand, T.; Kissling, W.D.; Cipriotti, P.A.; Aguiar, M.R. Extending point pattern analysis for objects of finite size and irregular shape. J. Ecol. 2006, 94, 825–837. [Google Scholar] [CrossRef]
- McIntire, E.J.B.; Fajardo, A. Beyond description: The active and effective way to infer processes from spatial patterns. Ecology 2009, 90, 46–56. [Google Scholar] [CrossRef]
- Fedriani, J.M.; Wiegand, T.; Delibes, M. Spatial pattern of adult trees and the mammal-generated seed rain in the Iberian pear. Ecography 2010, 33, 545–555. [Google Scholar] [CrossRef]
- Gotelli, H. A primer of Ecology, 3rd ed.; Sinauer Associates: Sunderland, MA, USA, 2001. [Google Scholar]
- Swannack, T.M. Growth Models. In Encyclopedia of Ecology, 2nd ed.; Fath, B., Ed.; Elsevier: Oxford, UK, 2019; pp. 388–394. [Google Scholar] [CrossRef]
- Alstad, D.N. Populus. In Simulations of Population Biology; College of Biological Sciences, University of Minnesota: Minneapolis, USA, 2015. [Google Scholar]
- Harsch, M.A.; Buxton, R.; Duncan, R.P.; Hulme, P.E.; Wardle, P.; Wilmshurst, J. Causes of tree line stability: Stem growth, recruitment and mortality rates over 15 years at New Zealand Nothofagus tree lines. J. Biogeogr. 2012, 39, 2061–2071. [Google Scholar] [CrossRef]
- Booth, B.D.; Murphy, S.D.; Swanton, C.J. Invasive Plant Ecology in Natural and Agricultural Systems, 2nd ed.; CAB International: Wallingford, UK, 2010; p. 211. [Google Scholar]
- Cousins, S.R.; Witkowski, E.T.F.; Pfab, M.F. Elucidating patterns in the population size structure and density of Aloe plicatilis, a tree aloe endemic to the Cape fynbos, South Africa. S. Afr. J. Bot. 2014, 90, 20–36. [Google Scholar] [CrossRef] [Green Version]
- Legendre, P.; Legendre, L. Chapter 13—Spatial analysis. In Developments in Environmental Modelling; Pierre, L., Louis, L., Eds.; Elsevier: Amsterdam, The Netherlands, 2012; pp. 785–858. [Google Scholar]
- Dormann, C.F.; McPherson, J.M.; Araújo, M.B.; Bivand, R.; Bolliger, J.; Carl, G.; Davies, R.G.; Hirzel, A.; Jetz, W.; Kissling, W.D.; et al. Methods to account for spatial autocorrelation in the analysis of species distributional data: A review. Ecography 2007, 30, 609–628. [Google Scholar] [CrossRef] [Green Version]
- Legendre, P.; Fortin, M.J. Spatial pattern and ecological analysis. Vegetatio 1989, 80, 107–138. [Google Scholar] [CrossRef]
- Rossi, R.E.; Mulla, D.J.; Journel, A.G.; Franz, E.H. Geostatistical tools for modeling and interpreting ecological spatial dependence. Ecol. Monogr. 1992, 62, 277–314. [Google Scholar] [CrossRef]
- Clark, J.S.; Silman, M.; Kern, R.; Macklin, E.; HilleRisLambers, J. Seed dispersal near and far: Patterns across temperate and tropical forests. Ecology 1999, 80, 1475–1494. [Google Scholar] [CrossRef]
- Legendre, P.; Legendre, L. Chapter 1—Complex ecological data sets. In Developments in Environmental Modelling; Pierre, L., Louis, L., Eds.; Elsevier: Amsterdam, The Netherlands, 2012; pp. 1–57. [Google Scholar]
- Clark, C.J.; Poulsen, J.R.; Levey, D.J.; Osenberg, C.W. Are plant populations seed limited? A critique and meta-analysis of seed addition experiments. Am. Nat. 2007, 170, 128–142. [Google Scholar] [CrossRef]
- Hall, N.H. Noxious Weeds: Rubber Bush; Pamphlet; Primary Industries Branch; no. 13: Darwin, Australia, 1967. [Google Scholar]
- Parsons, W.T.; Cuthbertson, E.G. Noxious Weeds of Australia; CSIRO Publishing: Melbourne, Australia, 2001. [Google Scholar]
- Accatino, F.; Ward, D.; Wiegand, K.; De Michele, C. Carrying capacity in arid rangelands during droughts: The role of temporal and spatial thresholds. Animal 2017, 11, 309–317. [Google Scholar] [CrossRef]
- Wilbur, H.M.; Rudolf, V.H.W. Life-history evolution in uncertain environments: Bet hedging in time. Am. Nat. 2006, 168, 398–411. [Google Scholar] [CrossRef]
- Catford, J.A.; Daehler, C.C.; Murphy, H.T.; Sheppard, A.W.; Hardesty, B.D.; Westcott, D.A.; Rejmánek, M.; Bellingham, P.J.; Pergl, J.; Horvitz, C.C.; et al. The intermediate disturbance hypothesis and plant invasions: Implications for species richness and management. Perspect. Plant Ecol. Evol. Syst. 2012, 14, 231–241. [Google Scholar] [CrossRef]
- Chambers, J.C.; Bradley, B.A.; Brown, C.S.; D’Antonio, C.; Germino, M.J.; Grace, J.B.; Hardegree, S.P.; Miller, R.F.; Pyke, D.A. Resilience to stress and disturbance, and resistance to Bromus tectorum L. invasion in cold desert shrublands of Western North America. Ecosystems 2013, 17, 360–375. [Google Scholar] [CrossRef]
- Hierro, J.L.; Villarreal, D.; Eren, Ö.; Graham, J.M.; Callaway, R.M. Disturbance facilitates invasion: The effects are stronger abroad than at home. Am. Nat. 2006, 168, 144–156. [Google Scholar] [CrossRef] [PubMed]
- Sorensen, A.E. Seed dispersal and the spread of weeds. In Proceedings of the VI International Symposium on Biological Control of Weeds, Vancouver, BC, Canada, 19–25 August 1984; pp. 121–126. [Google Scholar]
- Marushia, R.G.; Holt, J.S. The effects of habitat on dispersal patterns of an invasive thistle, Cynara Cardunculus. Biol. Invasions 2006, 8, 577–594. [Google Scholar] [CrossRef]
- Kowarik, I. Time lags in biological invasions with regard to the success and failure of alien species. In Plant Invasions: General Aspects and Special Problem; Pyšek, P., Prach, K., Rejmánek, M., Wade, M., Eds.; SPB Academic Publishing: Amsterdam, The Netherlands, 1995. [Google Scholar]
- Cousens, R.; Mortimer, M. Dynamics of Weed Populations; Cambridge University Press: Cambridge, UK, 1995. [Google Scholar]
- Crooks, J.A. Lag times and exotic species: The ecology and management of biological invasions in slow-motion. Ecoscience 2005, 12, 316–329. [Google Scholar] [CrossRef]
- Crooks, J.A.; Soulé, M.E. Lag times in population explosions of invasive species: Causes and implications. In Invasive Species and Biodiversity Management; Sandlund, O.T., Schei, P.J., Viken, A., Eds.; Kluwer Academic Press: Dordrecht, The Netherlands, 1999; pp. 103–125. [Google Scholar]
- Osunkoya, O.O.; Lock, C.B.; Dhileepan, K.; Buru, J.C. Lag times and invasion dynamics of established and emerging weeds: Insights from herbarium records of Queensland, Australia. Biol. Invasions 2021, 23, 3383–3408. [Google Scholar] [CrossRef]
- Payne, A.L.; Watson, I.W.; Novelly, P.E. Spectacular Recovery in the Ord River Catchment; Department of Agriculture and Food: Perth, WA, Australia, 2004; p. 47. [Google Scholar]
- DAF. Calotrope (Calotropis procera); The Government of Queensland: Brisbane, Australia, 2016; p. 3. [Google Scholar]
- van Putten, B.; Visser, M.D.; Muller-Landau, H.C.; Jansen, P.A. Distorted-distance models for directional dispersal: A general framework with application to a wind-dispersed tree. Methods Ecol. Evol. 2012, 3, 642–652. [Google Scholar] [CrossRef]
- Epperson, B.K. Estimating dispersal from short distance spatial autocorrelation. Heredity 2005, 95, 7–15. [Google Scholar] [CrossRef] [Green Version]
- Ansong, M.; Pickering, C. Are weeds hitchhiking a ride on your car? A systematic review of seed dispersal on cars. PLoS ONE 2013, 8, e80275. [Google Scholar] [CrossRef] [Green Version]
- Cain, M.L.; Milligan, B.G.; Strand, A.E. Long-distance seed dispersal in plant populations. Am. J. Bot. 2000, 87, 1217–1227. [Google Scholar] [CrossRef] [Green Version]
- Bass, D.A.; Crossman, N.D.; Lawrie, S.L.; Lethbridge, M.R. The importance of population growth, seed dispersal and habitat suitability in determining plant invasiveness. Euphytica 2006, 148, 97–109. [Google Scholar] [CrossRef]
- Kolb, A.; Dahlgren, J.P.; Ehrlén, J. Population size affects vital rates but not population growth rate of a perennial plant. Ecology 2010, 91, 3210–3217. [Google Scholar] [CrossRef]

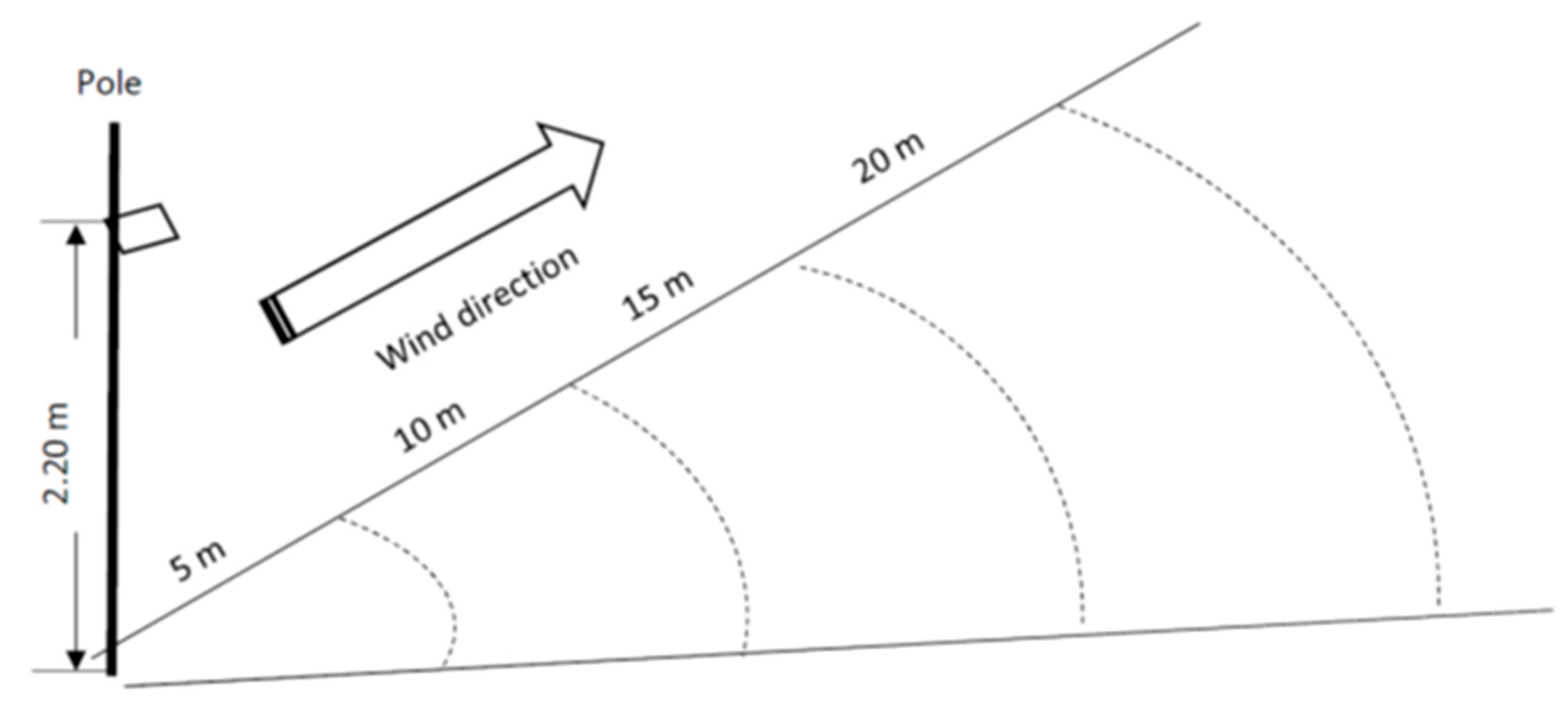
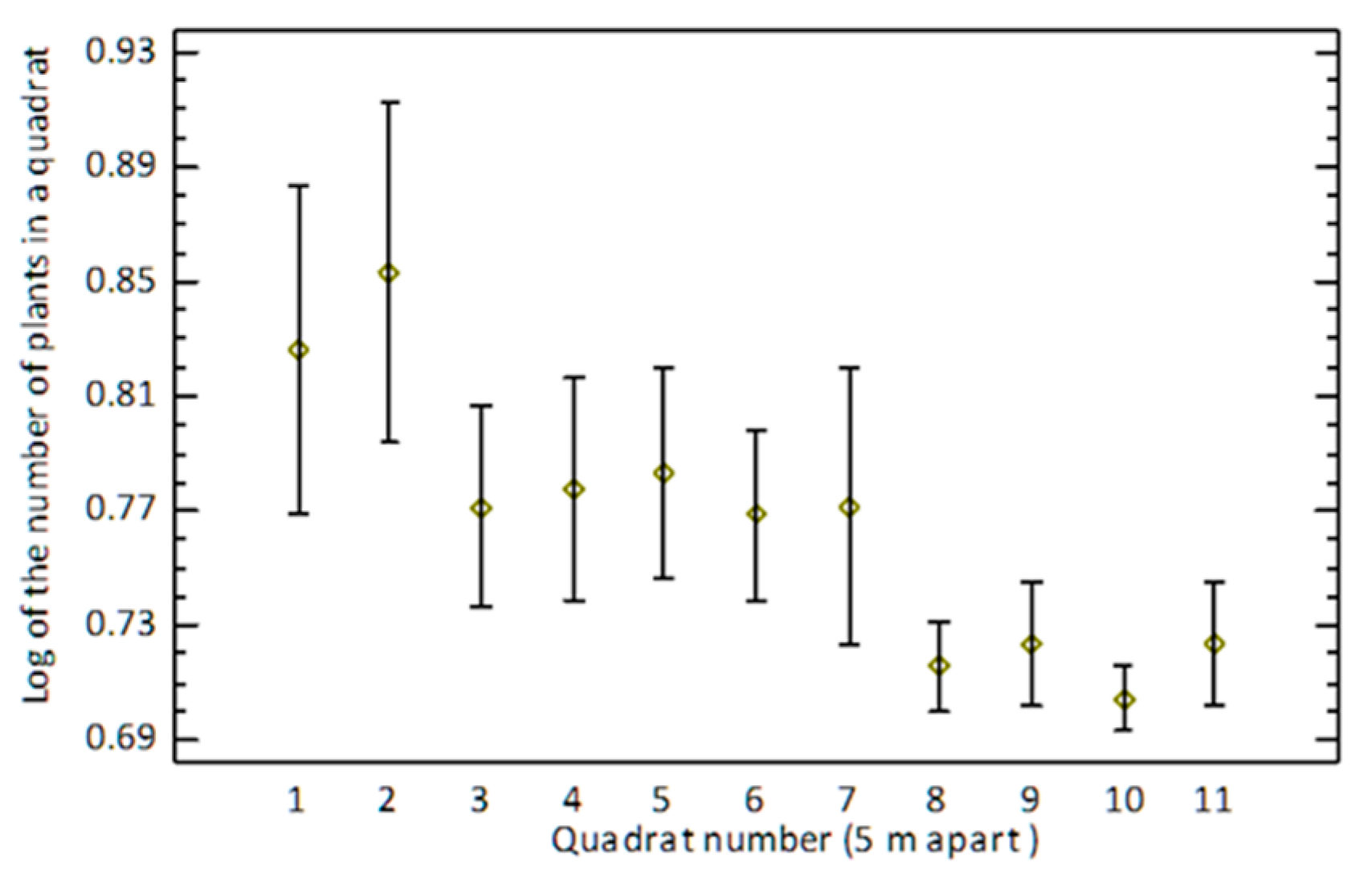
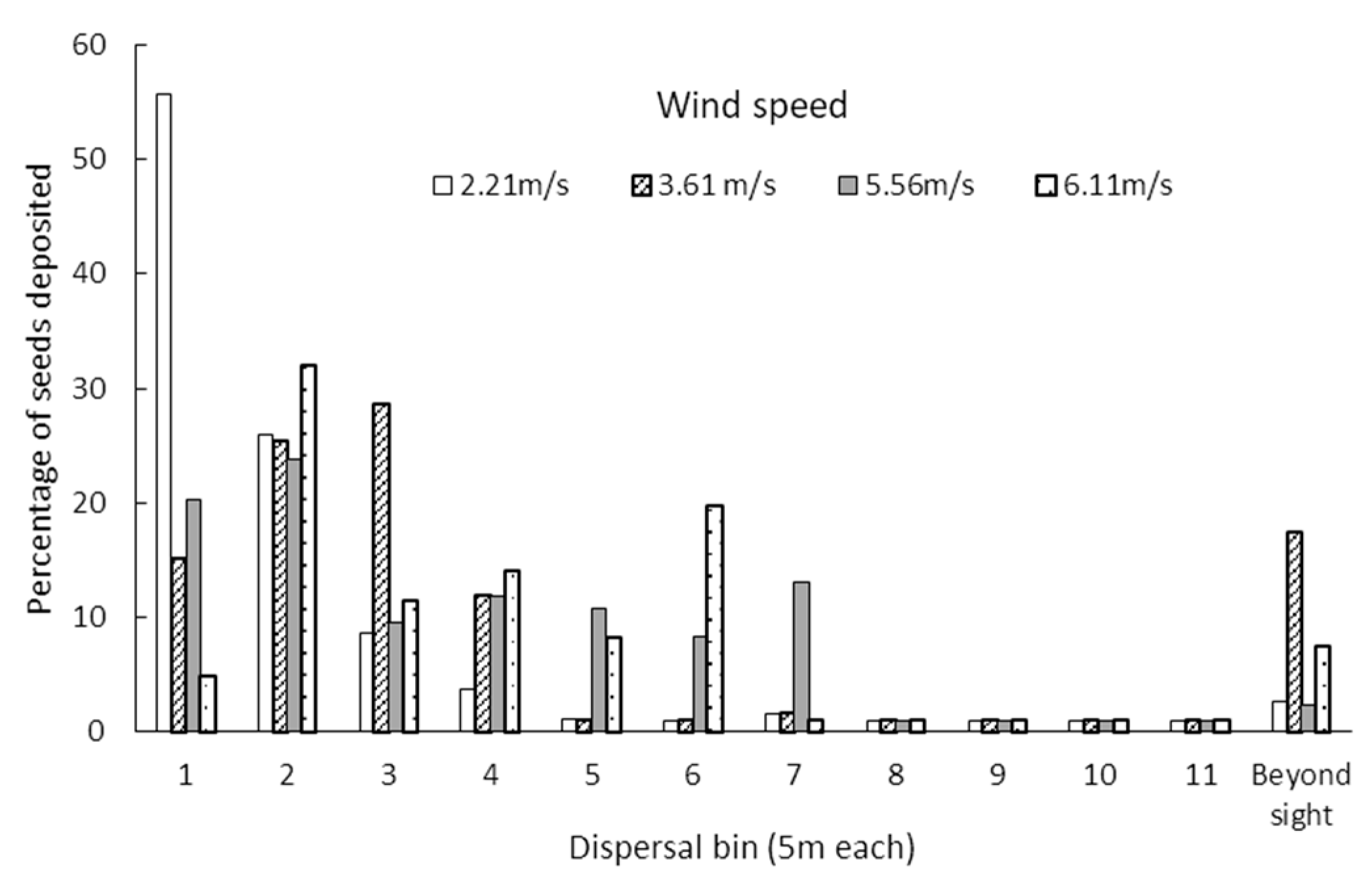



| Distance (m) | Mean Number of Seeds | SE | Percentage |
|---|---|---|---|
| 5 | 23.95 | 4.13 | 22.95 |
| 10 | 26.79 | 6.48 | 25.67 |
| 15 | 14.55 | 1.33 | 13.94 |
| 20 | 10.43 | 1.75 | 10.00 |
| 25 | 5.27 | 1.03 | 5.05 |
| 30 | 7.52 | 3.11 | 7.20 |
| 35 | 4.34 | 0.26 | 4.16 |
| 40 | 1 | 0.21 | 0.96 |
| 45 | 1 | 0.24 | 0.96 |
| 50 | 1 | 0.39 | 0.96 |
| 55 | 1 | 0.94 | 0.96 |
| Beyond 55 m | 7.5 | 3.52. | 7.19 |
| Birnbaum-Saunders | Exponential (2-Parameter) | Loglogistic (3-Parameter) | Weibull | Weibull (3-Parameter) | |
|---|---|---|---|---|---|
| shape = 0.977 | scale = 0.04 | median = 384.055 | shape = 1.683 | shape = 2.175 | |
| scale = 18.132 | shape = 0.025 | scale = 30.568 | scale = 36.546 | ||
| lower threshold = 2.5 | lower threshold = −356.699 | lower threshold = −4.829 | |||
| Dp-value | 0.6395 | 0.8363 | 0.9998 | 0.9956 | 0.9992 |
| Lag (m) | Sample Semivariance | Pairs | Model Semivariance | Residual |
|---|---|---|---|---|
| 110 | 0.0385 | 106 | 0.0385 | 0.000007 |
| 220 | 0.0464 | 122 | 0.0465 | −0.000069 |
| 330 | 0.0459 | 120 | 0.0468 | −0.000808 |
| 440 | 0.0499 | 146 | 0.0468 | 0.003089 |
| 550 | 0.0443 | 58 | 0.0468 | −0.002459 |
| 660 | 0.0442 | 37 | 0.0468 | −0.002620 |
| 770 | 0.0289 | 6 | 0.0468 | −0.017926 |
| Lag Distance (m) | Sample Semivariance | Pairs | Model Semivariance | Residual |
|---|---|---|---|---|
| 110 | 0.0330649 | 268 | 0.0320777 | 0.000987 |
| 220 | 0.0391773 | 344 | 0.0401866 | −0.001009 |
| 330 | 0.0427363 | 390 | 0.0453718 | −0.002636 |
| 440 | 0.0469197 | 614 | 0.0486874 | −0.001767 |
| 550 | 0.0568217 | 418 | 0.0508075 | 0.006014 |
| 660 | 0.0538615 | 440 | 0.0521632 | 0.001698 |
| 770 | 0.0527017 | 300 | 0.0530301 | −0.000328 |
| 880 | 0.0594065 | 208 | 0.0535845 | 0.005822 |
| 990 | 0.0460136 | 140 | 0.0539389 | −0.007925 |
| 1100 | 0.0251 | 28 | 0.0541656 | −0.029066 |
| 1210 | 0.01747 | 10 | 0.0543105 | −0.036841 |
| Lag Distance (m) | Sample Semivariance | Pairs | Model Semivariance | Residual |
|---|---|---|---|---|
| 110.0 | 0.0398248 | 861 | 0.0423905 | −0.002566 |
| 220.0 | 0.0698433 | 1188 | 0.0654273 | 0.0044166 |
| 330.0 | 0.092287 | 1459 | 0.0845653 | 0.007722 |
| 440.0 | 0.110667 | 2596 | 0.100465 | 0.010203 |
| 550.0 | 0.1163 | 2045 | 0.113673 | 0.002627 |
| 660.0 | 0.122065 | 2586 | 0.124646 | −0.002581 |
| 770.0 | 0.126083 | 2303 | 0.133762 | −0.007679 |
| 880.0 | 0.130734 | 2414 | 0.141335 | −0.010601 |
| 990.0 | 0.137636 | 2893 | 0.147627 | −0.009991 |
| 1100 | 0.145606 | 2000 | 0.152854 | −0.007247 |
| 1210 | 0.151494 | 2107 | 0.157196 | −0.005701 |
| 1320 | 0.169245 | 1586 | 0.160803 | 0.008442 |
| 1430 | 0.184004 | 1541 | 0.1638 | 0.020204 |
| 1540 | 0.198532 | 1042 | 0.16629 | 0.032243 |
| 1650 | 0.195169 | 648 | 0.168358 | 0.026811 |
| 1760 | 0.155208 | 552 | 0.170076 | −0.014869 |
| 1870 | 0.132717 | 230 | 0.171504 | −0.038786 |
| 1980 | 0.0833853 | 102 | 0.17269 | −0.089304 |
| 2090 | 0.0484263 | 40 | 0.173675 | −0.125248 |
| 2200 | 0.0000250625 | 8 | 0.174493 | −0.174468 |
| 2310 | 0.0 | 2 | 0.175173 | −0.175173 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Menge, E.O.; Lawes, M.J. Influence of Landscape Characteristics on Wind Dispersal Efficiency of Calotropis procera. Land 2023, 12, 549. https://doi.org/10.3390/land12030549
Menge EO, Lawes MJ. Influence of Landscape Characteristics on Wind Dispersal Efficiency of Calotropis procera. Land. 2023; 12(3):549. https://doi.org/10.3390/land12030549
Chicago/Turabian StyleMenge, Enock O., and Michael J. Lawes. 2023. "Influence of Landscape Characteristics on Wind Dispersal Efficiency of Calotropis procera" Land 12, no. 3: 549. https://doi.org/10.3390/land12030549
APA StyleMenge, E. O., & Lawes, M. J. (2023). Influence of Landscape Characteristics on Wind Dispersal Efficiency of Calotropis procera. Land, 12(3), 549. https://doi.org/10.3390/land12030549







