Combining Digital Covariates and Machine Learning Models to Predict the Spatial Variation of Soil Cation Exchange Capacity
Abstract
:1. Introduction
2. Materials and Methods
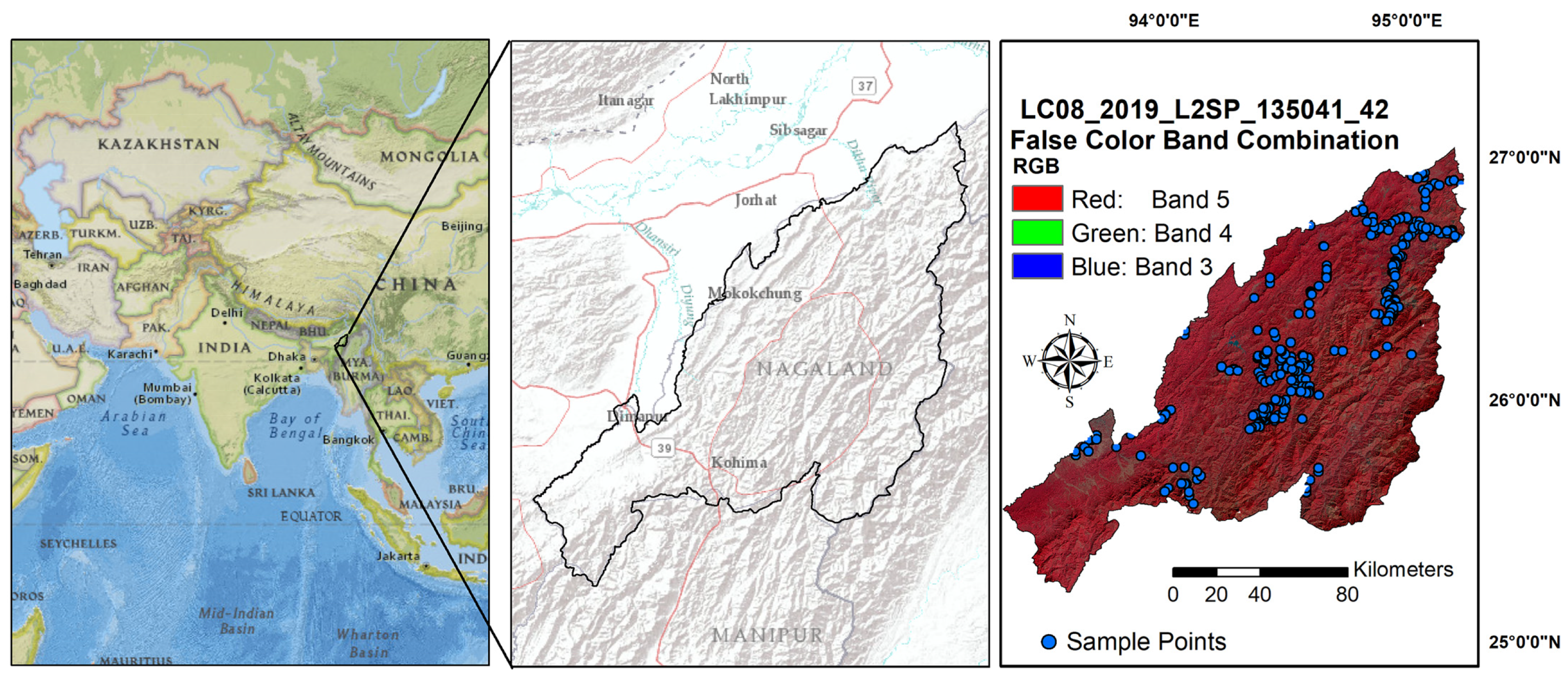
2.1. Study Area and Soil Data
2.2. Digital Covariates
2.3. Modelling Cation Exchange Capacity
| Algorithm | Digital Covariates | R Package | Tuning Hyperparameter |
|---|---|---|---|
| KNN | BIO-1, BIO-12, Elevation, TSR, TRI, NDVI-Mean, TPI, Slope, Pr-cur, Val-depth, Con-Ind | caret [63] | k: 9 |
| LR | BIO-1, BIO-12, Elevation | glmnet [52,64] | Lambda: 0.56 |
| RF | BIO-1, BIO-12, Elevation, TSR | randomForest [65] | mtry: 2 |
| GBM | BIO-1, BIO-12, Elevation | gbm [51] | shrinkage: 0.32, interaction.depth: 9, n.minobsinnode: 8, n.trees: 272 |
| SVR | BIO-1, BIO-12, Elevation, TSR | e1071 [66] | Sigma: 0.74, cost: 1 |
2.4. Model Performance Evaluation and Uncertainty Analysis
3. Results
3.1. Soil CEC Data Summary Statistics
3.2. Performance of Different Machine Learning Algorithms
3.3. Predictive Maps of CEC and Quantified Uncertainties
3.3.1. Mapping CEC Content and Its Uncertainty via RF
3.3.2. Mapping CEC Content and Its Uncertainty via SVR
3.3.3. Mapping CEC Content and Its Uncertainty via LR
3.3.4. Mapping CEC Content and Its Uncertainty via GBM
3.3.5. Mapping CEC Content and Its Uncertainty via KNN
3.4. Importance of Digital Covariates in Modelling Process
4. Discussion
4.1. Systematic Evaluation of the Five Machine-Learning Models
4.2. Physiography and Soil Cation Exchange Capacity
4.3. Factors Affecting Soil Cation Exchange Capacity
4.4. Limitations and Perspectives
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A

References
- Hou, D.; Bolan, N.S.; Tsang, D.C.W.; Kirkham, M.B.; O’Connor, D. Sustainable Soil Use and Management: An Interdisciplinary and Systematic Approach. Sci. Total Environ. 2020, 729, 138961. [Google Scholar] [CrossRef] [PubMed]
- Hou, D. Sustainable Soil Management for Food Security. Soil Use Manag. 2023, 39, 1–7. [Google Scholar] [CrossRef]
- Zhao, X.; Arshad, M.; Li, N.; Zare, E.; Triantafilis, J. Determination of the Optimal Mathematical Model, Sample Size, Digital Data and Transect Spacing to Map CEC (Cation Exchange Capacity) in a Sugarcane Field. Comput. Electron. Agric. 2020, 173, 105436. [Google Scholar] [CrossRef]
- Mishra, G.; Sulieman, M.M.; Kaya, F.; Francaviglia, R.; Keshavarzi, A.; Bakhshandeh, E.; Loum, M.; Jangir, A.; Ahmed, I.; Elmobarak, A.; et al. Machine Learning for Cation Exchange Capacity Prediction in Different Land Uses. Catena 2022, 216, 106404. [Google Scholar] [CrossRef]
- Moulatlet, G.M.; Zuquim, G.; Figueiredo, F.O.G.; Lehtonen, S.; Emilio, T.; Ruokolainen, K.; Tuomisto, H. Using Digital Soil Maps to Infer Edaphic Affinities of Plant Species in Amazonia: Problems and Prospects. Ecol. Evol. 2017, 7, 8463–8477. [Google Scholar] [CrossRef]
- Levis, C.; Costa, F.R.C.; Bongers, F.; Peña-Claros, M.; Clement, C.R.; Junqueira, A.B.; Neves, E.G.; Tamanaha, E.K.; Figueiredo, F.O.G.; Salomão, R.P.; et al. Persistent Effects of pre-Columbian Plant Domestication on Amazonian Forest Composition. Science 2017, 355, 925–931. [Google Scholar] [CrossRef]
- Cambule, A.H.; Rossiter, D.G.; Stoorvogel, J.J. A Methodology for Digital Soil Mapping in Poorly-Accessible Areas. Geoderma 2013, 192, 341–353. [Google Scholar] [CrossRef]
- Heuvelink, G.B.M.; Webster, R. Modelling Soil Variation: Past, Present, and Future. Geoderma 2001, 100, 269–301. [Google Scholar] [CrossRef]
- Iticha, B.; Takele, C. Soil–Landscape Variability: Mapping and Building Detail Information for Soil Management. Soil Use Manag. 2018, 34, 111–123. [Google Scholar] [CrossRef]
- Rossiter, D.G. Soil Mapping Today: Computer-Generated Predictive Soil Maps-Their Role in Soil Survey and Land Evaluation. Agric. Dev. 2021, 44, 5. [Google Scholar]
- Burke, M.; Lobell, D.B. Satellite-Based Assessment of Yield Variation and Its Determinants in Smallholder African Systems. Proc. Natl. Acad. Sci. USA 2017, 114, 2189–2194. [Google Scholar] [CrossRef] [Green Version]
- Huggett, R. Soil as Part of the Earth System. Prog. Phys. Geogr. 2023. [Google Scholar] [CrossRef]
- Huggett, R.J. Soil as a System. In Hydrogeology, Chemical Weathering, and Soil Formation; American Geophysical Union (AGU): Washington, DC, USA, 2021; pp. 1–20. ISBN 9781119563952. [Google Scholar]
- Minasny, B.; McBratney, A.B. Digital Soil Mapping: A Brief History and Some Lessons. Geoderma 2016, 264, 301–311. [Google Scholar] [CrossRef]
- Scull, P.; Franklin, J.; Chadwick, O.A.; McArthur, D. Predictive Soil Mapping: A Review. Prog. Phys. Geogr. Earth Environ. 2003, 27, 171–197. [Google Scholar] [CrossRef] [Green Version]
- Brevik, E.C.; Calzolari, C.; Miller, B.A.; Pereira, P.; Kabala, C.; Baumgarten, A.; Jordán, A. Soil Mapping, Classification, and Pedologic Modeling: History and Future Directions. Geoderma 2016, 264, 256–274. [Google Scholar] [CrossRef]
- Grunwald, S.; Böhner, J. Geographical Information Systems (GIS) and Soils. Ref. Modul. Earth Syst. Environ. Sci. 2022. [Google Scholar] [CrossRef]
- Sorenson, P.T.; Kiss, J.; Bedard-Haughn, A.K.; Shirtliffe, S. Multi-Horizon Predictive Soil Mapping of Historical Soil Properties Using Remote Sensing Imagery. Remote Sens. 2022, 14, 5803. [Google Scholar] [CrossRef]
- Reddy, N.N.; Das, B.S. Digital Soil Mapping of Key Secondary Soil Properties Using Pedotransfer Functions and Indian Legacy Soil Data. Geoderma 2023, 429, 116265. [Google Scholar] [CrossRef]
- Ballabio, C.; Lugato, E.; Fernández-Ugalde, O.; Orgiazzi, A.; Jones, A.; Borrelli, P.; Montanarella, L.; Panagos, P. Mapping LUCAS Topsoil Chemical Properties at European Scale Using Gaussian Process Regression. Geoderma 2019, 355, 113912. [Google Scholar] [CrossRef]
- Hengl, T.; Heuvelink, G.B.M.; Kempen, B.; Leenaars, J.G.B.; Walsh, M.G.; Shepherd, K.D.; Sila, A.; MacMillan, R.A.; de Jesus, J.M.; Tamene, L.; et al. Mapping Soil Properties of Africa at 250 m Resolution: Random Forests Significantly Improve Current Predictions. PLoS ONE 2015, 10, e0125814. [Google Scholar] [CrossRef]
- Akpa, S.I.C.; Ugbaje, S.U.; Bishop, T.F.A.; Odeh, I.O.A. Enhancing Pedotransfer Functions with Environmental Data for Estimating Bulk Density and Effective Cation Exchange Capacity in a Data-Sparse Situation. Soil Use Manag. 2016, 32, 644–658. [Google Scholar] [CrossRef]
- Liu, F.; Wu, H.; Zhao, Y.; Li, D.; Yang, J.L.; Song, X.; Shi, Z.; Zhu, A.X.; Zhang, G.L. Mapping High Resolution National Soil Information Grids of China. Sci. Bull. 2022, 67, 328–340. [Google Scholar] [CrossRef] [PubMed]
- Saidi, S.; Ayoubi, S.; Shirvani, M.; Azizi, K.; Zeraatpisheh, M. Comparison of Different Machine Learning Methods for Predicting Cation Exchange Capacity Using Environmental and Remote Sensing Data. Sensors 2022, 22, 6890. [Google Scholar] [CrossRef] [PubMed]
- Khanal, S.; Fulton, J.; Klopfenstein, A.; Douridas, N.; Shearer, S. Integration of High Resolution Remotely Sensed Data and Machine Learning Techniques for Spatial Prediction of Soil Properties and Corn Yield. Comput. Electron. Agric. 2018, 153, 213–225. [Google Scholar] [CrossRef]
- Forkuor, G.; Hounkpatin, O.K.L.; Welp, G.; Thiel, M. High Resolution Mapping of Soil Properties Using Remote Sensing Variables in South-Western Burkina Faso: A Comparison of Machine Learning and Multiple Linear Regression Models. PLoS ONE 2017, 12, e0170478. [Google Scholar] [CrossRef] [Green Version]
- Gray, J.M.; Bishop, T.F.A.; Wilford, J.R. Lithology and Soil Relationships for Soil Modelling and Mapping. Catena 2016, 147, 429–440. [Google Scholar] [CrossRef]
- Sawicka, K.; Heuvelink, G.B.M.; Walvoort, D.J.J. Spatial Uncertainty Propagation Analysis with the Spup R Package. R J. 2018, 10, 180–199. [Google Scholar] [CrossRef] [Green Version]
- Rossiter, D.G.; Poggio, L.; Beaudette, D.; Libohova, Z. How Well Does Digital Soil Mapping Represent Soil Geography? An Investigation from the USA. SOIL 2022, 8, 559–586. [Google Scholar] [CrossRef]
- Miller, B. Referee Comment on “How Well Does Digital Soil Mapping Represent Soil Geography? An Investigation from the USA” by David G. Rossiter et al. SOIL 2022, 8, 559–586. [Google Scholar] [CrossRef]
- GON Government of Nagaland. Available online: https://nagaland.gov.in/ (accessed on 4 August 2022).
- Mishra, G.; Francaviglia, R. Land Uses, Altitude and Texture Effects on Soil Parameters. A Comparative Study in Two Districts of Nagaland, Northeast India. Agriculture 2021, 11, 171. [Google Scholar] [CrossRef]
- Beck, H.E.; Zimmermann, N.E.; McVicar, T.R.; Vergopolan, N.; Berg, A.; Wood, E.F. Present and Future Köppen-Geiger Climate Classification Maps at 1-Km Resolution. Sci. Data 2018, 5, 180214. [Google Scholar] [CrossRef] [Green Version]
- STATE OF FOREST REPORT 2021. Forest Survey of India (Ministry of Environment Forest and Climate Change): Dehradun, IN. 2021. Available online: https://fsi.nic.in/forest-report-2021-details (accessed on 15 January 2023).
- Singh, A.K.; Bordoloi, L.J.; Kumar, M.; Hazarika, S.; Parmar, B. Land Use Impact on Soil Quality in Eastern Himalayan Region of India. Environ. Monit. Assess. 2014, 186, 2013–2024. [Google Scholar] [CrossRef]
- Mishra, G.; Das, J.; Sulieman, M. Modelling Soil Cation Exchange Capacity in Different Land-Use Systems Using Artificial Neural Networks and Multiple Regression Analysis. Curr. Sci. 2019, 116, 2020–2027. [Google Scholar] [CrossRef]
- Soil Survey Staff. Keys to Soil Taxonomy, 12th ed.; USDA-Natural Resources Conservation Service: Washington, DC, USA, 2014. [Google Scholar]
- Sumner, M.E.; Miller, W.P. Cation Exchange Capacity and Exchange Coefficients. In Methods of Soil Analysis, Part 3: Chemical Methods; Soil Science Society of America, Inc. and American Society of Agronomy, Inc.: Madison, WI, USA, 1996; pp. 1201–1229. ISBN 9780891188667. [Google Scholar]
- Conrad, O.; Bechtel, B.; Bock, M.; Dietrich, H.; Fischer, E.; Gerlitz, L.; Wehberg, J.; Wichmann, V.; Böhner, J. System for Automated Geoscientific Analyses (SAGA) v. 2.1.4. Geosci. Model Dev. 2015, 8, 1991–2007. [Google Scholar] [CrossRef] [Green Version]
- NASA Shuttle Radar Topography Mission (SRTM) Shuttle Radar Topography Mission (SRTM) Global. Distributed by OpenTopography; OpenTopography: La Jolla, CA, USA, 2013. [CrossRef]
- Sayler, K.; Glynn, T. Landsat 8 Collection 2 (C2) Level 2 Science Product (L2SP) Guide LSDS-1619 Version 2.0; EROS Sioux Falls: South Dakota, SD, USA, 2021. [Google Scholar]
- ESRI. ArcGIS User’s Guide. 2023. Available online: http://www.esri.com (accessed on 15 January 2023).
- Fick, S.E.; Hijmans, R.J. WorldClim 2: New 1-Km Spatial Resolution Climate Surfaces for Global Land Areas. Int. J. Climatol. 2017, 37, 4302–4315. [Google Scholar] [CrossRef]
- Gallant, J.C.; Dowling, T.I. A Multiresolution Index of Valley Bottom Flatness for Mapping Depositional Areas. Water Resour. Res. 2003, 39, 1347. [Google Scholar] [CrossRef]
- Moore, I.D.; Gessler, P.E.; Nielsen, G.A.; Peterson, G.A. Soil Attribute Prediction Using Terrain Analysis. Soil Sci. Soc. Am. J. 1993, 57, 443–452. [Google Scholar] [CrossRef]
- Brown, K.S.; Libohova, Z.; Boettinger, J. Digital Soil Mapping. In Soil Survey Manual; Ditzler, C., Scheffe, K., Monger, H.C., Eds.; USDA Handbook 18; Government Printing Office: Washington, DC, USA, 2017. [Google Scholar]
- Poggio, L.; de Sousa, L.M.; Batjes, N.H.; Heuvelink, G.B.M.; Kempen, B.; Ribeiro, E.; Rossiter, D. SoilGrids 2.0: Producing Soil Information for the Globe with Quantified Spatial Uncertainty. SOIL 2021, 7, 217–240. [Google Scholar] [CrossRef]
- Kuhn, M. caretFuncs: Backwards Feature Selection Helper Functions. In caret R Package Version 6.0-86. 2020. Available online: https://CRAN.R-project.org/package=caret (accessed on 15 January 2023).
- Hastie, T.; Tibshirani, R.; Friedman, J. Overview of Supervised Learning. In The Elements of Statistical Learning: Data Mining, Inference, and Prediction; Springer: New York, NY, USA, 2009; pp. 9–41. [Google Scholar] [CrossRef]
- Friedman, J.H. Stochastic Gradient Boosting. Comput. Stat. Data Anal. 2002, 38, 367–378. [Google Scholar] [CrossRef]
- Greenwell, B.; Boehmke, B.; Cunningham, J. gbm: Generalized Boosted Regression Models. 2020. Available online: https://cran.r-project.org/web/packages/gbm/gbm.pdf (accessed on 15 January 2023).
- Friedman, J.; Hastie, T.; Tibshirani, R. Regularization Paths for Generalized Linear Models via Coordinate Descent. J. Stat. Softw. 2010, 33, 1. [Google Scholar] [CrossRef] [Green Version]
- Breiman, L. Statistical Modeling: The Two Cultures. Stat. Sci. 2001, 16, 199–321. [Google Scholar] [CrossRef]
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef] [Green Version]
- Drucker, H.; Burges, C.J.; Kaufman, L.; Smola, A.; Vapnik, V. Support Vector Regression Machines. Adv. Neural Inf. Process. Syst. 1996, 9, 155–161. [Google Scholar]
- Chang, C.C.; Lin, C.J. LIBSVM: A library for support vector machines. ACM Trans. Intell. Syst. Technol. 2011, 2, 1–27. [Google Scholar] [CrossRef]
- Biau, G.; Scornet, E. A Random Forest Guided Tour. Test 2016, 25, 197–227. [Google Scholar] [CrossRef] [Green Version]
- Keshavarzi, A.; del Árbol, M.Á.S.; Kaya, F.; Gyasi-Agyei, Y.; Rodrigo-Comino, J. Digital Mapping of Soil Texture Classes for Efficient Land Management in the Piedmont Plain of Iran. Soil Use Manag. 2022, 38, 1705–1735. [Google Scholar] [CrossRef]
- Ferhatoglu, C.; Miller, B.A. Choosing Feature Selection Methods for Spatial Modeling of Soil Fertility Properties at the Field Scale. Agronomy 2022, 12, 1786. [Google Scholar] [CrossRef]
- Murphy, K.P. Sparse Linear Models. In Machine Learning: A Probabilistic Perspective; The MIT Press: London, UK, 2012; pp. 421–479. [Google Scholar]
- R Core Team. R: A Language and Environment for Statistical Computing. R Foundation for Statistical Computing. Available online: https://www.r-project.org/ (accessed on 15 January 2023).
- RStudio Team. RStudio: Integrated Development for R. RStudio, PBC, Boston, MA. Available online: http://www.rstudio.com/ (accessed on 15 January 2023).
- Kuhn, M. Caret: Classification and Regression Training. R Package Version 6.0-86. 2020. Available online: https://CRAN.R-project.org/package=caret (accessed on 15 January 2023).
- Simon, N.; Friedman, J.; Hastie, T.; Tibshirani, R. Regularization Paths for Cox’s Proportional Hazards Model via Coordinate Descent. J. Stat. Softw. 2011, 39, 1. [Google Scholar] [CrossRef]
- Liaw, A.; Wiener, M. Classification and Regression by RandomForest. R News 2002, 2, 18–22. [Google Scholar]
- Meyer, D.; Dimitriadou, E.; Hornik, K.; Weingessel, A.; Leisch, F. E1071: Misc Functions of the Department of Statistics, Probability Group (Formerly: E1071); TU Wien: Vienna, Austria, 2022. [Google Scholar]
- Rossiter, D.G. Maps and Models Are Never Valid, but They Can Be Evaluated. Pedometron 2017, 41, 19–21. [Google Scholar]
- Piikki, K.; Wetterlind, J.; Söderström, M.; Stenberg, B. Perspectives on Validation in Digital Soil Mapping of Continuous Attributes—A Review. Soil Use Manag. 2021, 37, 7–21. [Google Scholar] [CrossRef]
- Bian, Z.; Guo, X.; Wang, S.; Zhuang, Q.; Jin, X.; Wang, Q.; Jia, S. Applying statistical methods to map soil organic carbon of agricultural lands in northeastern coastal areas of China. Arch. Agron. Soil Sci. 2020, 66, 532–544. [Google Scholar] [CrossRef]
- Nalin, R.S.; Dalmolin, R.S.D.; de Araújo Pedron, F.; Moura-Bueno, J.M.; Horst, T.Z.; Schenato, R.B.; Soligo, M.F. Accounting for the Spatial Variation of Phosphorus Available Explained by Environmental Covariates. Geoderma Reg. 2023, 32, e00594. [Google Scholar] [CrossRef]
- Komsta, L. Outliers: Tests for Outliers, Version 0.15. Available online: https://cran.r-project.org/web/packages/outliers/outliers.pdf (accessed on 5 January 2023).
- Dharumarajan, S.; Kalaiselvi, B.; Suputhra, A.; Lalitha, M.; Hegde, R.; Singh, S.K.; Lagacherie, P. Digital Soil Mapping of Key GlobalSoilMap Properties in Northern Karnataka Plateau. Geoderma Reg. 2020, 20, e00250. [Google Scholar] [CrossRef]
- Chagas, C.D.S.; de Carvalho Júnior, W.; Pinheiro, H.S.K.; Xavier, P.A.M.; Bhering, S.B.; Pereira, N.R.; Filho, B.C. Mapping Soil Cation Exchange Capacity in a Semiarid Region through Predictive Models and Covariates from Remote Sensing Data. Rev. Bras. Ciênc. Solo 2018, 42, 170183. [Google Scholar] [CrossRef]
- Nascimento, C.M.; Demattê, J.A.M.; Mello, F.A.O.; Rosas, J.T.F.; Tayebi, M.; Bellinaso, H.; Greschuk, L.T.; Albarracín, H.S.R.; Ostovari, Y. Soil Degradation Detected by Temporal Satellite Image in São Paulo State, Brazil. J. S. Am. Earth Sci. 2022, 120, 104036. [Google Scholar] [CrossRef]
- Liu, Y.; Heuvelink, G.B.M.; Bai, Z.; He, P. Uncertainty quantification of nitrogen use efficiency prediction in China using Monte Carlo simulation and quantile regression forests. Comput. Electron. Agric. 2023, 204, 107533. [Google Scholar] [CrossRef]
- Fiorentini, M.; Schillaci, C.; Denora, M.; Zenobi, S.; Deligios, P.; Orsini, R.; Santilocchi, R.; Perniola, M.; Montanarella, L.; Ledda, L. A Machine Learning Modelling Framework for Triticum Turgidum Subsp. Durum Desf Yield Forecasting in Italy. Agron. J. 2022. [Google Scholar] [CrossRef]
- Blume, H.-P.; Brümmer, G.W.; Fleige, H.; Horn, R.; Kandeler, E.; Kögel-Knabner, I.; Kretzschmar, R.; Stahr, K.; Wilke, B.-M. (Eds.) Soil Development and Soil Classification. In Scheffer/Schachtschabel Soil Science; Springer: Berlin/Heidelberg, Germany, 2016; pp. 285–389. [Google Scholar]
- Mishra, G.; Marzaioli, R.; Giri, K.; Borah, R.; Dutta, A.; Jayaraj, R.S.C. Soil Quality Assessment under Shifting Cultivation and Forests in Northeastern Himalaya of India. Arch. Agron. Soil Sci. 2017, 63, 1355–1368. [Google Scholar] [CrossRef]
- Zarnetske, P.L.; Read, Q.D.; Record, S.; Gaddis, K.D.; Pau, S.; Hobi, M.L.; Malone, S.L.; Costanza, J.; Dahlin, K.M.; Latimer, A.M.; et al. Towards Connecting Biodiversity and Geodiversity across Scales with Satellite Remote Sensing. Glob. Ecol. Biogeogr. 2019, 28, 548–556. [Google Scholar] [CrossRef] [Green Version]
- Malone, B.; Arrouays, D.; Poggio, L.; Minasny, B.; McBratney, A. Digital Soil Mapping: Evolution, Current State and Future Directions of the Science. Ref. Modul. Earth Syst. Environ. Sci. 2022. [Google Scholar] [CrossRef]
- Brus, D.J. Spatial Sampling with R; Chapman and Hall/CRC: Boca Raton, FL, USA, 2022; ISBN 9781003258940. [Google Scholar]
- Broeg, T.; Blaschek, M.; Seitz, S.; Taghizadeh-Mehrjardi, R.; Zepp, S.; Scholten, T. Transferability of Covariates to Predict Soil Organic Carbon in Cropland Soils. Remote Sens. 2023, 15, 876. [Google Scholar] [CrossRef]
- Silva, B.P.C.; Silva, M.L.N.; Avalos, F.A.P.; de Menezes, M.D.; Curi, N. Digital Soil Mapping Including Additional Point Sampling in Posses Ecosystem Services Pilot Watershed, Southeastern Brazil. Sci. Rep. 2019, 9, 13763. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Camera, C.; Zomeni, Z.; Noller, J.S.; Zissimos, A.M.; Christoforou, I.C.; Bruggeman, A. A High Resolution Map of Soil Types and Physical Properties for Cyprus: A Digital Soil Mapping Optimization. Geoderma 2017, 285, 35–49. [Google Scholar] [CrossRef]
- Zhang, M.; Shi, W.; Xu, Z. Systematic Comparison of Five Machine-Learning Models in Classification and Interpolation of Soil Particle Size Fractions Using Different Transformed Data. Hydrol. Earth Syst. Sci. 2020, 24, 2505–2526. [Google Scholar] [CrossRef]
- Radočaj, D.; Jurišić, M.; Antonić, O.; Šiljeg, A.; Cukrov, N.; Rapčan, I.; Plaščak, I.; Gašparović, M. A Multiscale Cost-Benefit Analysis of Digital Soil Mapping Methods for Sustainable Land Management. Sustainability 2022, 14, 12170. [Google Scholar] [CrossRef]









| Covariate Name | Definition | Refs. | |
|---|---|---|---|
| Elevation | Elevation, measured as height above sea level | [40] | |
| Slope | Slope measures the elevation change and steepness of a line | [39] | |
| Pl-cur | Rate of change of aspect along a contour | [39] | |
| Pr-cur | Rate of change of slope down a slope line | [39] | |
| Con-Ind | Calculated using flow direction and neighboring cell aspects | [39] | |
| Flow-acc | Calculated accumulated flow | [39] | |
| Val-depth | The vertical height below the summit accumulation | [39] | |
| Flow-dir | Height differences between cells determine the flow direction. | [39] | |
| MRVBF | The measure of flatness and lowness depicting depositional areas | [44] | |
| MRRTF | The measure of flatness and upness depicting stable upland areas | [44] | |
| TWI | The measure of the propensity of an area to accumulate water | [39,45] | |
| TPI | Difference between a cell elevation value and the average elevation of the neighborhood around that cell | [39] | |
| TRI | Degree of roughness or irregularity of the landscape | [39] | |
| NDVI Stdv, Median, Mean | (1) | [46] | |
| Measures the amount and health of vegetation in a given area | |||
| RONR Stdv, Median, Mean | (2) | ||
| Landsat 8 OLI ProductIDs | LC08_L2SP_135041_20170204_20200905_02_T1, LC08_L2SP_135042_20170204_20200905_02_T1 | [41] | |
| LC08_L2SP_135041_20190125_20200829_02_T1, LC08_L2SP_135042_20190125_20200830_02_T1 | |||
| BIO-1 | The annual mean temperature in degrees Celsius. | [43] | |
| BIO-12 | Annual precipitation in millimeters. | ||
| TSR | Thirty-year mean solar radiation in 12 months in kJ m−2 year−1 | ||
| Criteria | Model | Mean | Standard Deviation | Median |
|---|---|---|---|---|
| RMSE | RF | 4.12 | 0.56 | 4.13 |
| SVR | 4.27 | 0.51 | 4.13 | |
| KNN | 4.45 | 0.66 | 4.46 | |
| LR | 4.67 | 0.75 | 4.55 | |
| GBM | 5.07 | 0.55 | 5.11 | |
| R2 | RF | 0.41 | 0.13 | 0.40 |
| SVR | 0.36 | 0.11 | 0.34 | |
| KNN | 0.30 | 0.12 | 0.31 | |
| LR | 0.25 | 0.16 | 0.26 | |
| GBM | 0.25 | 0.12 | 0.26 | |
| MAE | RF | 3.12 | 0.42 | 3.21 |
| SVR | 3.29 | 0.38 | 3.29 | |
| KNN | 3.44 | 0.49 | 3.38 | |
| LR | 3.56 | 0.55 | 3.44 | |
| GBM | 4.01 | 0.42 | 4.00 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kaya, F.; Mishra, G.; Francaviglia, R.; Keshavarzi, A. Combining Digital Covariates and Machine Learning Models to Predict the Spatial Variation of Soil Cation Exchange Capacity. Land 2023, 12, 819. https://doi.org/10.3390/land12040819
Kaya F, Mishra G, Francaviglia R, Keshavarzi A. Combining Digital Covariates and Machine Learning Models to Predict the Spatial Variation of Soil Cation Exchange Capacity. Land. 2023; 12(4):819. https://doi.org/10.3390/land12040819
Chicago/Turabian StyleKaya, Fuat, Gaurav Mishra, Rosa Francaviglia, and Ali Keshavarzi. 2023. "Combining Digital Covariates and Machine Learning Models to Predict the Spatial Variation of Soil Cation Exchange Capacity" Land 12, no. 4: 819. https://doi.org/10.3390/land12040819











