Common-Property Resource Exploitation: A Real Options Approach

Abstract

Agricultural land and forestlands can have multiple uses and generate multiple sources of utility. Although landowners benefit from most of them, society can benefit from others because of their intrinsic characteristics as common-property resources and customary practice. In many Italian territories, the picking of mushrooms is allowed on privately owned agricultural land and in forests. The management of these resources is challenging due to the emerging conflicts between landowners and users. In addition, the pressure exerted by users gives rise to issues on stock preservation, thus contributing to putting biodiversity at risk in contexts already heavily jeopardized by modern agriculture. Through the years, regulation established the primacy of the landowner’s right, introduced a permit fee for users, and set limits on the resource stock to be collected daily. Nonetheless, the relationship between public and private interests in common-property resource exploitation is still controversial. In this paper, we investigate and model a right holder’s decision whether to exploit a common-property resource according to their actual status of being an actual or potential user. The model is developed within the real options valuation framework. In detail, we investigate the entry/exit decision on the exploitation of the resource by considering the uncertainty that affects the resource stock, the entry/exist costs, and the number of rival users.

1. Introduction

The collective use of natural resources, first and foremost agricultural land and forests, has been an important factor in the social and economic development of many rural communities in Italy. Local historiography is scattered, in fact, with events directly or indirectly related to the exercise of collective rights over private land or the government of common-property land. The co-presence of public and private rights in the use of land has very ancient origins [1,2] and is probably linked to the impossibility of enforcing property rights over the wealth of benefits produced by land and/or the possibility of conditioning the benefit gained through the resource use to its specific characteristics (e.g., economies of scale, work organization, aversion to risk, etc.)¹.

In addition, the open access to wild products, such as mushrooms and wild herbs, and to the residuum of agricultural products lost in harvesting, guaranteed a minimum level of sustenance to the poor in times of famine. In some northern European countries, primarily Sweden and Finland, the right to pick berries and mushrooms is considered part of the Scandinavian lifestyle and is regulated under the Right of Public Access [3,4].

From their origins to the present day, collective uses in Italy have undergone significant changes that progressively diminished the importance of their role in favor of the primacy of private use [5]. There are various reasons for this trend: (a) the supremacy of a central national authority that took over the power of local communities; (b) the pressure exerted by large estate landownership on public lands²; (c) the opportunity of removing impediments hindering rational cultivation of land [7]³; (d) the progressive socio-economic development of rural areas that made the collective use of picking mushrooms and wild herbs irrelevant and marginal.

The historical evolution of common-property resources can also be investigated by analyzing the relationship between land productivity and socio-economic development:

• in areas where land productivity was subject to rapid improvements whose benefits could be easily taken possession of, a gradual privatization of common property occurred, as, for example, in the common-property lands of the northern plain of Italy;
• in areas where productivity was low (e.g., in forest land, marginal grazing land, etc.) and socio-economic development was good, common property was maintained and gave rise to institutions with primarily social and environmental objectives, such as the Communities of the Eastern Alps;
• in areas where productivity was low and socio-economic development lagged, commons were preserved for economic purposes, but did not promote institutions strong enough to face the challenges of an evolving role they would be called upon to play, as in the case of common lands in marginal areas.

Consequently, in rural areas where the tradition of local government was more firmly rooted, such as in alpine areas, or where the difficulties of private economic exploitation were greater, such as in marginal grazing lands, some forms of collective use of land survived. The reasons for this phenomenon are many and difficult to classify as various environmental, economic, and political factors are involved, the analysis of which goes beyond the scope of this paper. The contexts, in which some forms of collective land use have survived, however, appear united by the need to reorganize activities and establish use rights in accordance with emerging environmental objectives.

A topical issue, then, is the analysis of the best practices these communities have established to reconcile the rights of users and the conservation of the natural resources they govern. According to theoretical models of the use of the commons [8,9,10,11,12], there are significant examples of how some communities have succeeded in establishing a balance between the exploitation of the commons and the preservation of the surrounding environment while respecting the paradigm of sustainable resource use⁴. In addition, the success of these communities in governing common natural resources depends on the compromise solution they can find between private use and public interest. In fact, the pursuit of community goals in the governance of common properties is contingent on the adherence to the rules of community members. Social benefits, which arise from community governance of natural resources, are often closely related to productive uses by private actors: in this case, a positive externality is generated⁵.

The above condition is common for those ancillary resources/services generated by agricultural and forest land alongside the main agroforestry productions. These ancillary resources are mostly wild productions such as wild herbs and mushrooms, which grow in hill and mountain forests or in hedgerows surrounding cultivated fields. Wild productions, by necessity or tradition, were usually not the exclusive preserve of the landowner, but were accessible for common use by the entire local community. Solidarity among members of the local community thus enabled the poor to obtain food resources for subsistence. Nowadays, wild productions are no longer collected to satisfy sustenance need; nonetheless, they are valuable for recreational purposes and for keeping rural tradition and culture alive.

Picking of mushrooms and wild herbs is still possible but it is strongly opposed by landowners and generates growing conflicts between landowners and users. Landowners claim the right to exclusive use of both cultivated and wild products. By contrast, users consider the free picking of wild herbs and mushrooms as an established right. In addition, the pressure exerted by users on wild resources, such as mushrooms and wild herbs, gives rise to some issues on their preservation, thus contributing to putting biodiversity at risk in contexts already heavily jeopardized by modern agriculture. Over the years, regulation has established the primacy of landowners’ right by introducing a permit fee for users and setting limits on the stock that can be collected daily. Regulation has proved to be effective on forestlands, where some controls are present, whereas it is ineffective in agricultural areas where these controls are absent. Consequently, in these contexts, it is of paramount importance to investigate the user’s strategy on the optimal exploitation of common-property resources.

To address this issue, we start from and extend the seminal working paper by [18]. The primary objective of this paper is to model the entry/exit decision of a common-property resource user. In other words, we model firstly the right holder’s decision whether to start using, continue using, or abandon using the resource, depending on their current status (i.e., user or non-user) Secondly, we implement the model to investigate the optimal exploitation strategy in mushroom picking in rural areas in Italy.

The decision to exploit a common-property resource shares the characteristics of the majority of investment decisions, i.e., (a) it involves some irreversibility, (b) future payoffs are uncertain, and (c) it can be postponed. Consequently, it is reasonable to assume that the optimal user’s decision must satisfy slightly more restrictive assumptions on expected utility than those underpinning the net present value rule [19,20]. Due to the uncertainty on the evolution over time of the stock, a decision that is currently considered optimal may turn into a sub-optimal decision in the future. Finally, the option of waiting to decide allows the user to acquire more information on uncertain state variables, and thus it reduces the probability the user regrets the decision made. The (actual or potential) user’s decision to exploit the resource is analogous to the exercise of a real option (see, e.g., [21,22]). The user can decide at any point in time whether to use the resource and specifically to start using, continue using, or stop using the resource contingent on new information to come on uncertain decision variables. Whenever action entails a sunk cost, it is valuable to take action when an uncertain state variable reaches specific upper or lower thresholds and doing nothing otherwise. In detail, we investigate the entry/exit decision on the exploitation of the resource by considering the uncertainty that affects the resource stock, the entry/exit costs and the number of rival users.

The remainder of the paper is organized as follows. Section 2 provides a classification of economic goods based on their rivalry/non-rivalry and excludability/non-excludability; Section 3 presents and discusses the relevant literature on the exploitation of common-property and common-pool resources; Section 4 illustrates the real options model on the consumptive use of common-property resources, defines the value of the right to use the common-property resource, identifies the optimal right holders’ strategy and provide some comparative statistics; in Section 5, results from the model’s calibration are presented and discussed; finally, in Section 6 conclusions are drawn.

2. Common Goods, Common-Property and Common-Pool Resources

In this Section, we provide some considerations on what the economics of common-property resources are in order to properly introduce the model boundary conditions. Economic goods are usually classified according to their rivalry vs. non-rivalry and excludability vs. non-excludability in consumption.

Table 1. A taxonomy of economic goods based on rivalry, excludability, and control of harvesting.

Excludability	Harvest Control	Rivalry	Resource Topology
Difficult	Difficult	High	Common-pool
Difficult	Difficult	Low	Pure public
Easy	Difficult	Low	Club
Easy	Difficult	High	Common-property
Easy	Easy	High	Pure private

provides a synthetic characterization of economic goods that accounts for potential challenges in regulating stock consumption and harvesting⁶.

By considering excludability, harvest control, and rivalry, we can indeed distinguish goods into common-pool resources, pure public goods, club goods, common-property resources and pure private goods. When resources are excludable because of technical or economic reasons (i.e., efforts to exclude beneficiaries are costly) and harvesting is hard to monitor and control, resources are commonly identified as common-pool resources or “commons”, for which Hardin [8], in his famous article of 1968, predicted the “tragedy” (i.e., the complete depletion) in the absence of an external “coercive force” that imposed either government or private ownership of the resource [8]⁷.

By contrast, when rivalry is high, it is difficult to enforce some controls on the harvesting⁸, though some excludability of users can be set in place, resources are classified as common-property resources⁹.

Indeed, the rules relating to control and management of common-property resources, and the establishment of local institutions meant to develop, apply, and enforce these rules, are the core of common-property governance and management [9,12,23,26]. There are various forms of local institution, both informal and formal, which can take responsibility for common-property resource management. Some communities proved to be successful in the management of environmental resources mainly thanks to ethical norms, customary practice, and cultural factors¹⁰. In accordance with Refs. [23,24,26,30], the empirical evidence on the difficulties that have been encountered in re-establishing a community governance of common-pool and common-property resources reinforce the above findings [5,25,31,32].

The primary reason for the successful management of natural resources operated by local communities resides in the ability to create consensus on a set of rules for the use of common resources and their observance. The successful implementation and observance depends partly on the type of resource but mainly on the acknowledgment of its value by the users, who must engage in its conservation and sustainable use. An unambiguous classification of usage patterns for the foraging of minor productions of agricultural and forest lands, such as mushrooms and wild herbs, is quite problematic as foraging activities take place in very different social, economic, and institutional contexts. In some countries, such as in Scandinavia, mushrooms and wild herbs are free-access, common-pool resources [33,34]; whereas in others they are common-property resources reserved for local residents [35,36]. Nonetheless, due to regulating authorities’ different control capacity on the resource, its accessibility to individuals, and the quantities harvested, different excludability and rivalry conditions can arise starting from the above two polar cases [37,38,39,40,41]. The following Section provides a brief review of the most significant literature on the harvesting of common-property and common-pool resources.

3. Relevant Literature

Starting from the seminal contributions by Hardin and the noble-laureate Elinor Ostrom, significant efforts have been made in the literature to model the exploitation patterns of common-property and common-pool resources and design effective management policies. Most of this research has focused on water and fishing resources. Cox et al. and Gruber [42,43] provide a general overview of the principles on the grounds of management and governance of common-pool and common-property resources. More recently, papers on the recreational use and value of minor agricultural productions have appeared. As previously mentioned, these minor productions are spontaneous productions that grow on forest soils, marginal areas of agricultural land (e.g., hedges), or cultivated soils in autumn and winter when crops are not growing. Although these productions vary significantly depending on seasonality, altimetry, and latitude, their economic value can be significant (see, e.g., [36,44,45]). Various types of berries (e.g., Vaccinium myrtillus, Rubus idaeus, Ribes alpinum, etc.) and mushrooms (e.g., Boletus edulis, Armillaria mellea, Chantharellus cibarius, etc.) grow and are harvested in mountain forests and downland forests. By contrast, in the plains, people usually go picking honey mushrooms (Armillaria mellea) and harvest wild spring herbs, such as dandelion (Taraxacum officinalis), poppy sprouts (Papaver roeas), silene (Silene vulgaris), and hop sprouts (Humulus lupulus). Nonetheless, the existing literature does not report many contributions focusing on harvesting activities in rural areas. Without any claim to the exhaustiveness of the literature examined, the literature referred to in this contribution can be classified into three main strands. The first focuses on the motivations of these activities, the second on the value attributed to foraging by those who practice it, and the third on management issues, especially regarding the interaction with landowners. Some Scandinavian studies have proved via surveys that the foraging of mushrooms, wild herbs, and wild berries is a popular recreational activity, especially among older people, profoundly attached to a traditional lifestyle [3,46]. Wild products are generally harvested for self-consumption, and harvesting is considered a community right, never questioned by landowners [4]. On the contrary, the younger urban population is less attracted to harvesting activities, and prefers walking, trekking, and camping [33,47,48]. Other contributions have investigated preferences for wild productions in different geographical areas [46,49]. Comparative studies have shown that Asians (primarily Chinese) are attracted to forest areas for meditation and relaxation. By contrast, Europeans are more attracted to wild products, such as herbs and mushrooms, primarily for self-consumption rather than commercial sale. The latter is a marginal and sporadic option, usually adopted by low-income immigrants, often coming from Eastern Europe. Some research in Spain has shown that the hunting of wild mushrooms is also linked to emerging gastronomic tourism, which is grounded in local traditions [50].

A comprehensive analysis of common-property resources’ exploitation cannot be prescinded from the valuation of monetary values generated to users. To our knowledge, one of the first studies on this issue dates back to 1993. Mattsson and Li [47] implemented a contingent valuation study to assess the value of ‘non-wood’ services provided by Swedish forests and found that these services constituted a significant share of Swedish forests’ total economic value. Love et al. [51] explored the value of mushroom picking in a nature reserve in the State of Washington (USA). According to their analysis, foraging for commercial purposes is mainly conducted by Asians and Latinos and due to the market value of harvested resources, which induces commercial harvesters to overexploit the resource, potential conflicts between commercial harvesters and recreational pickers arise. Later works have focused mainly on the recreational value of wild herbs and mushroom picking: Starbuck et al. [52] adopted a travel coast approach to estimate the monetary value of mushroom picking in the Gifford Pinchot National Forest in Washington State (USA). Similarly, Martinez de Aragon et al. [53] implemented a travel cost study to assess the value of mushroom hunting in Catalonia (Spain). In addition, Marini Govigli et al. [54] implemented a travel cost approach and investigated the effect of interview methods on the value of mushroom hunting for recreational purposes in Catalonia (Spain).

Scientific contributions on wild herbs and mushroom hunting regulation usually address three main interrelated objectives. The first is to preserve the resources and avoid overexploitation. The second is resource valorization from a social (recreational) and economic (touristic) perspective. The third is to govern and monitor the relationships between the mushroom harvesters and landowners, which are not always friendly. Vail and Hultkrantz [55] point out that free-access regimes to land and resources do not match the objective of sustainable resource use, as it generates environmental degradation and discourages landowners from undertaking investments. Osés-Eraso and Viladrich-Grau [56] argue that social approval is crucial in encouraging responsible behaviors in exploiting common-property and common-pool resources. Chun [57] discusses the importance of coherence between the Common Law System, rooted in traditional knowledge, and the Status Legal System in governing common natural resources. Górriz-Mifsud et al. [38] investigate management issues of mushroom picking in Spain, where landowners’ property rights are not clearly defined. Optimal management policies depend on the perception of the damage caused by harvesters to the soils and the perception of property rights. Landowners that are more sensible about their property rights request stricter regulation on foraging, especially for non-residents. Pickers, in turn, are favorable towards regulatory measures that guarantee access rights to private lands [58,59]. Chavez et al. and Safarzynska [60,61] investigated the management of conflicts between landowners and illegal truffle harvesters and intra- and inter-group conflicts in the presence of uncertainty in resource availability. The latter demonstrated that uncertain resource availability favors resource conservation if there are no evident conflicts. In addition, de Frutos et al. [62] explored the possibility of controlling and managing mushroom picking by introducing different permit fees. Conversely, Abatayo and Lynham [63] emphasized the role of “social ostracism” in avoiding overexploitation. Finally, Gaglio et al. [64] illustrated the effects of the introduction of payments for ecosystem services in the governance of natural resources in the Po River Delta Park, and they found that the introduction of payment schemes for ecosystem services favors the protection and conservation of local common-property resources (game, fishery, truffles, mushrooms).

To conclude, it is worth mentioning the recent skyrocketing interest of scholars in common-property and common-pool resources management and governance. In line with the so-called institutional approach to the governance of common-property resources [65]. From the findings of the above literature, the prominent role of use rights on common-property resources and the sanctions users can incur, clearly emerges. Indeed, the institutional approach is well grounded in the definition of a benefit function, which will be discussed in the following Section.

4. The Model

In Section 2, the main characteristics of common-property resources have been described and their distinguishing elements with respect to open access goods have been discussed.

The focus now moves onto the analysis of an individual user’s behavior. The analysis is performed assuming that users cooperate and respect the norms for the use of common-property resources. Under this assumption, the modelling of the interactions between the competitors usually investigated through the theory of non-cooperative games [23] is not the main objective of the present contribution, which indeed focuses on the analysis of the net benefit gained by the individual user and of the main factors conditioning it¹¹.

The valuation of the opportunity to use a common-property resource is assessed by considering the relative costs and benefits trade-offs. Since the decision of exploiting the resource can be made at any point time and the utility flow generated by the resource is uncertain over time¹², we need to account for the value of the option (i.e., the right but not the obligation) to use the resource in the future.

To model the user’s decision on the exploitation of a common-property resource governed by a local community, we introduce the following simplifying assumptions:

(a)

by paying a permit fee, the user can acquire the right to use the resource at any time for a specific time;

(b)

the exercise of the right to use the resource involves a sunk cost;

(c)

the renunciation of the right to use the resource generates a sunk cost;

(d)

the decision to exercise the right to exploit, interrupt, or re-start exploiting the resource can be taken at any point in time.

Based on the previous assumptions and assuming that market prices as well as available production technology are known, the benefit function depends on the users’ expectation on the resource amount to be obtained. Therefore, the instantaneous expected net benefit is equal to:

$$B\left(x_t,n_t\right) \mathrm{with} B_{x_t}>0 \mathrm{and} B_{x_t{x}_t} \le 0$$

(1)

where x_t is the resource stock at time t and n_t represents the number of rival users exploiting the stock at the same time.

Since the number of individuals holding the right to use/exploit the resource n_t does not change significantly over time, without any loss in generality, in what follows, we consider it constant, i.e., n_t = n¹³.

The benefit function depends on n as we assume that the resource stock available to each user is negatively correlated with their number, due to a competition and congestion effect¹⁴. Therefore, an increase in the number of rival users reduces B, i.e., B_n < 0.

We assume the resource stock x_t evolves over time according to the following stochastic differential equation¹⁵:

$$d{x}_t=\mu \left(n\right)dt+\sigma x_{t}d{W}_t, \mathrm{with} x_0=x,\sigma >0.$$

(2)

where μ(x_t,n) is the variation of the stock between time t and time t + dt. It is worth noting that μ(x_t,n) is positively correlated to the stock amount x_t and negatively correlated to the number of users n [69].

The model accounts for some chance factors (e.g., meteorological conditions and climate change effects) to affect the stock and the stock growth rate. The instantaneous stock variability is σx_t, whereas dW_t is the differential of a Brownian motion with mean E(dW_t) = 0 and variance E[(dW_t)²] = dt¹⁶.

A simple reduced form for μ(x_t,n) is the following:

$$\mu \left(x_t,n\right)=\mu \left(n\right)x_t$$

(3)

where μ′(n) ≤ 0, to take into account that an increase in the number of rival users reduces the stock growth rate.

Consequently, the evolution over time of x_t can be described by a geometric Brownian motion:

$$d{x}_t=\mu \left(n\right)x_{t}dt+\sigma x_{t}d{W}_t, \mathrm{with} x_0=x,\sigma >0.$$

(4)

4.1. The Value of the Right to Use a Common-Property Resource

The right to use the resource allows the holder to draw on a common-property resource for a limited period, in a specific place and according to well-established community rules.

We assume that the right holder pays a sunk cost (i.e., entry cost) k > 0¹⁷ to exercise their right and a sunk cost (i.e., exit cost) l ≥ 0¹⁸ to stop using the resource [75]. In addition, the resource provides an instantaneous benefit B(x_t,n), which, as mentioned above, depends on x_t and n. We assume that B can be described as follows:

$$B\left(x_t,n\right)=B\left(n\right)x_t^{\xi }, \mathrm{with} 0<\xi \le 1$$

(5)

The net benefit obtained by the user at time t depends on whether or not the right holder is exercising it. If the right holder is using the resource at time t, the net instantaneous benefit is:

$$\pi \left(x_t,n\right)=B\left(n\right)x_t^{\xi }-c$$

(6)

where c is the operating cost.

By contrast, if the right holder does not exercise it, then π(x_t,n) = 0.

According to (2), the actual user is aware that the stock available can increase and diminish with a positive probability. Consequently, the user can continue using the resource regardless of the occurrence of adverse conditions in the hope of avoiding the exit cost l and/or any re-entry cost k. Analogously, the right holder will decide to use the resource whenever the expected benefit is significantly offsetting the entry cost k, to account for the possibility of receiving a reduced benefit because of a negative fluctuation of x_t.

As in [74,76], the right holder’s decision to use or stop using the resource (i.e., entry/exit decision) is contingent on the two thresholds x_L and x_K, where x_L < x_K. A current user will prolong the resource exploitation as long as the stock x_t remains above the minimum threshold x_L whereas they will suspend exploitation as soon as x_t drops below x_L On the contrary, a right holder who has to decide whether to exercise their right will start using the resource whenever the stock x_t exceeds the threshold x_K. As long as x_t does not exceed this threshold, the right holder’s optimal strategy is waiting to exercise the right (option) to use the resource.

Assuming that there is homogeneity among right holders and that each holder aims to maximize the present value of their future expected net benefits, it is possible to evaluate the right to use the common-property resource in two potential scenarios: actual vs. potential use.

The value of the right to use the resource for an individual who is actually using the resource W₁(x) is given by:

$$\begin{gathered} W_1\left(x\right)=E\left\{\underset{0}{\overset{T_L}{\int }} e^{-\rho t}\left[B\left(n\right)x_t^{\xi }-c\right]dt | x_0=x\right\} \\ +E\left\{e^{-\rho T_L}\left[W_0\left(x_L\right)-l\right] | x_0=x\right\}, \forall x\in \left(x_L,\infty \right) \end{gathered}$$

(7)

where ρ is the discount rate and W₀(x_L) represents the value of the right to use the resource for an individual who is not currently using it (i.e., a potential user), calculated at time T_L = inf(t ≥ 0|x_t < x_L). In other words, T_L is the time when the right holder will stop exercising their right.

By contrast, a potential user’s optimal decision is to start the resource whenever the stock reaches the threshold x_K. As the potential user does not receive any benefit from the resource use while waiting, then:

$$W_0\left(x\right)=E\left\{e^{-\rho T_H}\left[W_1\left(x_H\right)-k\right]| x_0=x\right\}, \forall x\in \left(0,x_H\right)$$

(8)

where T_H = inf(t ≥ 0|x_t ≥ x_H) is the time when the right holder will start exploiting the resource.

4.2. The Right Holders’ Optimal Use Strategy

We can now identify the (actual or potential) user’s optimal strategy for common-property resource exploitation (

Table 2. The options for the use of the common-property resource.

Initial Situation	Options	State of the Resource
The user currently uses	continues to use	xt ≥ xL
	stops using	$x_t<x_L$
The user currently does not use	continues not to use	$x_t\le x_K$
	begins using	$x_t>x_K$

).

The optimal strategy is obtained by solving a dynamic programming problem. Based on Equations (5) and (6), W₁ and W₀ must satisfy the following conditions [74,76]:

$$\Gamma W_1\left(x\right)=-\left[B\left(n\right)x^{\xi }-c\right] \forall x\in \left(x_L,\infty \right)$$

(9)

$$\Gamma W_0\left(x\right)=0 \forall x\in \left(0,x_H\right)$$

(10)

where Γ indicates the differential operator:

$$\Gamma =-\rho +\widehat{\mu }x\frac{\partial }{\partial x}+\frac{1}{2}{\widehat{\sigma }}^2{x}^2\frac{{\partial }^2}{\partial x^2} , \mathrm{where} \widehat{\mu }\equiv \xi \mu \left(n\right)-\frac{1}{2}\xi \left(\xi -1\right){\sigma }^2 \mathrm{and} \widehat{\sigma }\equiv \xi \sigma .$$

The value matching and smooth pasting conditions [74] are the following:

$$W_1\left(x_L\right)=W_0\left(x_L\right)-l$$

(11)

$$W_0\left(x_H\right)=W_1\left(x_H\right)-k$$

(12)

$$W_1^{\prime }\left(x_L\right)=W_0^{\prime }\left(x_L\right)$$

(13)

$$W_0^{\prime }\left(x_H\right)=W_1^{\prime }\left(x_H\right)$$

(14)

The value matching conditions (11) and (12) represent the right holder’s indifference at the time of switching from the status of actual user to that of potential user and vice versa. The smooth pasting conditions (13) and (14) identify the optimality conditions for the threshold x_L and x_K, respectively.

In addition to conditions (11)–(14), to solve the differential Equations (9) and (10), we need to impose the following boundary conditions:

$$\underset{x\to \infty }{\lim }\left\{W_1\left(x\right)-\left(\frac{B\left(n\right)x^{\xi }}{\rho -\widehat{\mu }}-\frac{c}{\rho }\right)\right\}=0$$

(15)

$$\underset{x\to 0}{\lim }{W}_0\left(x\right)=0$$

(16)

where the term $\frac{B\left(n\right)x^{\xi }}{\rho -\widehat{\mu }}-\frac{c}{\rho }$ is the present value of the future expected net benefits which the actual user expects to obtain from an indefinite use of the resource [68]. For this term to be positive, we need to assume $\varrho -\hat{\mu }>0$.

From the linearity of the differential Equations (9) and (10) and imposing the above boundary conditions, it is easy to show that the value of the right to use the resource for an actual user is given by:

$$W_1\left(x\right)=A_1{x}^{\alpha }+\left(\frac{B\left(n\right)x^{\xi }}{\rho -\widehat{\mu }}-\frac{c}{\rho }\right) \forall x\in \left(x_L,\infty \right)$$

(17)

whereas for a potential user it is:

$$W_0\left(x\right)=A_0{x}^{\beta } \forall x\in \left(0,x_H\right)$$

(18)

where α < 0 and β > 1, and specifically:

$$\beta =\frac{1}{2}-\frac{\rho -\mu \left(n\right)}{{\sigma }^2}+\sqrt{{(\frac{\rho -\mu \left(n\right)}{{\sigma }^2}-\frac{1}{2})}^2+\frac{2\rho }{{\sigma }^2}}>1$$

(19)

$$\alpha =\frac{1}{2}-\frac{\rho -\mu \left(n\right)}{{\sigma }^2}-\sqrt{{(\frac{\rho -\mu \left(n\right)}{{\sigma }^2}-\frac{1}{2})}^2+\frac{2\rho }{{\sigma }^2}}<0,$$

(20)

As $\frac{B\left(n\right)x^{\xi }}{\rho -\widehat{\mu }}-\frac{c}{\rho }$ represents the present value of the future expected net benefits, the additional terms A₁x^α and A₀x^β represent the value of the option to stop or start using the resource, respectively. Consequently, A₀ and A₁ must be positive. We can obtain these constants and the thresholds x_L and x_K by solving Equations (11)–(14).

Due to the non-linearity of the system of Equations (11)–(14), it is not possible to obtain a close-form solution for x_L and x_K, respectively. However, from Proposition 1, it is possible to derive some properties of x_L and x_K, which are the entry threshold of the potential user and exit threshold of the actual user, respectively.

Proposition 1 (see the Appendix A for the proof). 

If c > ρl,the threshold for stopping the resource exploitation satisfies the following inequality:

$$B\left(n\right)x_L^{\xi }\ge \frac{\alpha }{\alpha -1}\frac{\rho -\hat{\mu }}{\rho }\left(c-\rho l\right)$$

(21)

whereas the threshold for starting the resource exploitation satisfies the following inequality:

$$B\left(n\right)x_H^{\xi }\le \frac{\beta }{\beta -1}\frac{\rho -\hat{\mu }}{\rho }\left(c+\rho k\right)$$

(22)

Proposition 1 permits us to identify a lower and upper bound, within which the optimal thresholds fall. These lower and upper bounds are the Marshallian long-run average costs (c − ρl) and (c + ρk) multiplied by two factors, $\frac{\alpha }{\alpha -1}\frac{\rho -\widehat{\mu }}{\rho }<1$ and $\frac{\beta }{\beta -1}\frac{\rho -\widehat{\mu }}{\rho }>1$, respectively, which account for the irreversibility of the decision to abandon or start the exploitation of the resource.

According to the classic microeconomic approach, the potential user should start using the resource whenever the benefit exceeds the long-run average cost, whereby, long-run average cost means the cost c plus the annual interest on the entry cost k, i.e., ρk. Analogously, an actual user should abandon the resource exploitation whenever the benefit drops below the average costs c.

Nonetheless, if the cost of stopping the resource exploitation is non-null, i.e., l > 0, the actual user should account for the interest they would save by postponing the exit, therefore the long-run average cost turns out to be c − ρl.

According to Proposition 1, if the right holder has to make their decision under uncertainty, and such a decision involves both entry and exit sunk cost, the static Marshallian thresholds are no longer valid. The optimal thresholds can differ significantly: the potential user will wait for the benefit to rise well above the long-run average cost before starting the resource exploitation and the actual user will wait for the benefit to drop well below the long-run average exit cost before abandoning the resource exploitation.

Obviously if c ≤ ρl, as x_L cannot be negative, x_L is set equal to zero and the option value to abandon reduces, i.e., A₁ = 0 in (17). Consequently:

Corollary 1. 

If c ≤ ρl, x_L = 0 whereas the threshold x_L becomes:

$$B\left(n\right)x_H^{\xi }=\frac{\beta }{\beta -1}\frac{\rho -\widehat{\mu }}{\rho }\left(c+\rho k\right)$$

(23)

4.3. Analysis of Entry and Exit Thresholds

The relationship described in Proposition 1 can be used to assess the effect of changes in the boundary conditions relative to the resource use. The analysis is performed essentially for investigating the trends of the entry and exit thresholds and evaluating the effects of a specific action on the direction and stability of the resource exploitation decision over time.

Table 3. Dynamics of the common-property resource exploitation.

	Hysteresis (ΔKL)	Hysteresis (ΔKL)
Resource Situation	Low	High
$x_t<x_L$	Unstable abandonment	Stable abandonment
$x_L<x_t<x_K$	Unstable stagnation	Stable stagnation
$x_K<x_t$	Unstable use	Stable use

shows the resource exploitation scenarios that can be obtained by comparing the stock x_t to the thresholds x_L, x_K and to their difference Δ_KL = x_K − x_L, which can be defined as the hysteresis interval. This interval can be considered a proxy of the stability of the decision: the greater the hysteresis interval Δ_KL, the greater the fluctuations in the stock that do not affect the right holder’s decision.

The effects of the following factors are taken into consideration:

(1)

the sunk entry and exit costs, i.e., k and l;

(2)

the operating cost c;

(3)

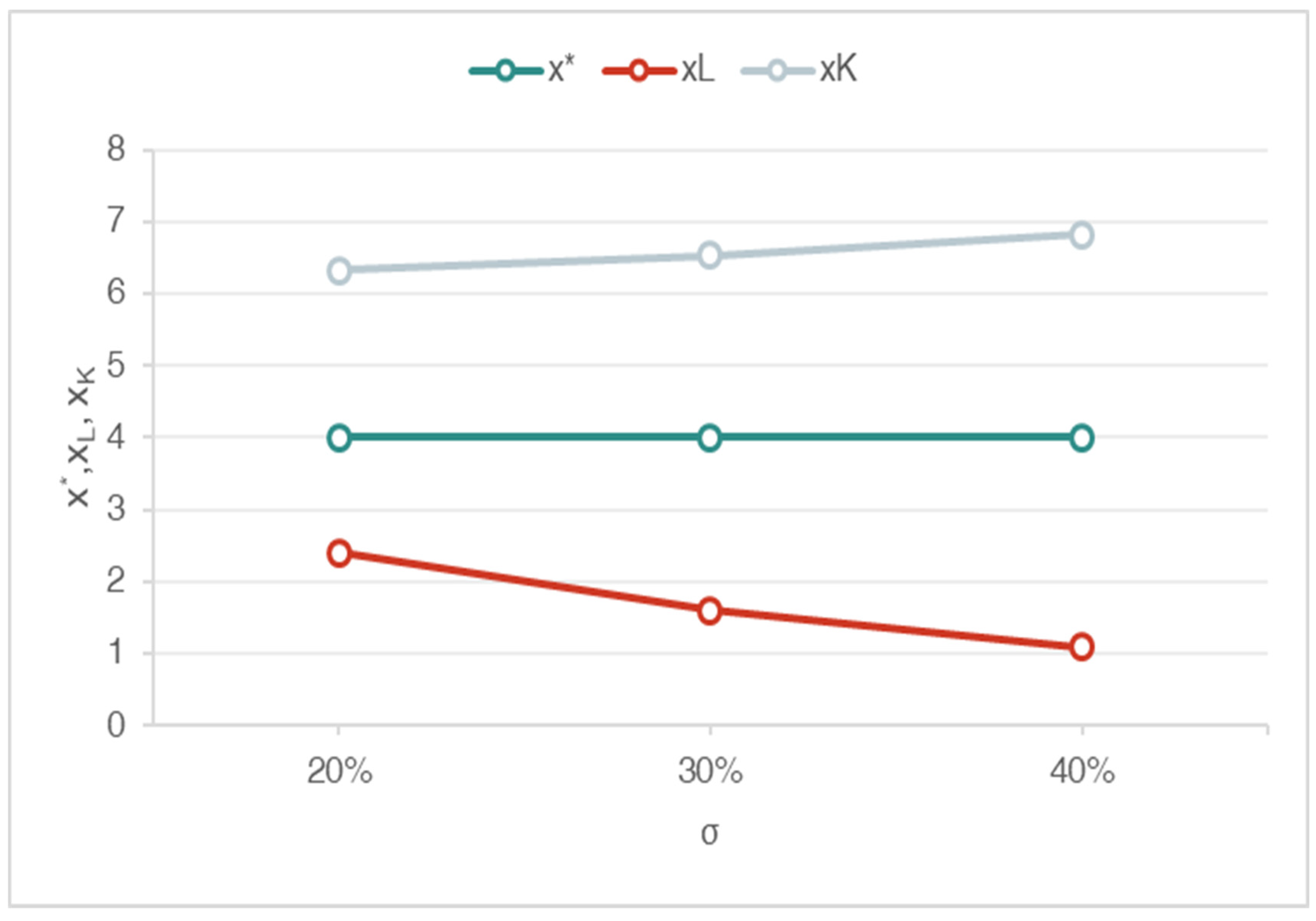
the uncertainty σ;

(4)

the number of rivals n.

As k increases, the hysteresis interval Δ_K expands. In other words, the thresholds diverge as the entry cost increases (i.e., $\frac{d{x}_K}{dk}>0 \mathrm{and} \frac{d{x}_L}{dk}<0$). The formal demonstration of this result can be found in Dixit and Pindyck [21]. Nonetheless, this result is also intuitively justified: the potential user postpones implementation of their decision as the cost increases and, consequently, x_K increases. It is also worth noting that as k increases, x_K decreases and, consequently, the probability of abandoning the resource exploitation once activated reduces. In fact, due to the stock uncertainty, there is the probability that the resource exploitation will turn out to be advantageous in the future. In this case, by continuing exploitation, the user can avoid incurring the increasing sunk cost k. By contrast, whenever k increases the value of the option to abandon resource exploitation increases and, consequently, the advantage of keeping it alive. The increase in the entry cost k results in a stabilization of the current situation: in fact, the threshold that make it advantageous to exercise any of the entry or exit options diverge.

The above result sheds light on the incentives to the entry of users of common-property resources. The incentive resides in a reduction in the sunk entry cost k, which makes the thresholds to converge and consequently increases flexibility, both at entry and exit.

Similar results can be obtained when the exit cost l increases. In fact, the thresholds diverge for increasing exit costs (i.e., $\frac{d{x}_K}{dl}>0 \mathrm{and} \frac{d{x}_L}{dl}<0$). The explanation, both formal and intuitive, is analogous to the previous one: if the exit cost increases, the advantage for the actual user of continuing exploitation and postponing re-entry costs increases. Similarly, when the exit cost increases, the potential user has no incentive to start using the resource, due to an increase in the cost to be paid if the stock reduces in the future, thus making resource exploitation no longer advantageous.

Because of entry and exit sunk costs, the entry and exit thresholds diverge. Obviously, if these costs are null, the right holder’s decision is perfectly flexible and the thresholds converge to the operating cost c (i.e., ${\lim }_{k,l\to 0}B\left(n\right)x_K^{\xi }, B\left(n\right)x_L^{\xi }=c)$ [18]. In this case, the threshold is unique and it increases as the operating cost c increases (i.e., $\frac{d{x}_{LK}}{dc}>0)$. A resource whose operating cost increases will be hardly exploited and easily abandoned.

Compared to traditional analysis, the model permits us to investigate the effect of uncertainty in more depth. It can be easily shown that an increase in the stock uncertainty σ generates an expansion in the hysteresis interval Δ_HL (i.e., $\frac{d{x}_K}{d\sigma }>0, \frac{d{x}_L}{d\sigma }<0$). In fact, as $\frac{\partial \beta }{\partial \sigma }<0,$ an increase in σ increases the multiplying coefficient $\frac{\beta }{\beta -1}$. Similarly, as $\frac{\partial \alpha }{\partial \sigma }>0,$ an increase in σ reduces the multiplying coefficient $\frac{\alpha }{\alpha -1}$. The overall effect of an increase in uncertainty is to increase the divergence between the optimal thresholds x_K and x_L. Consequently, uncertainty amplifies the entry and exit sunk costs and it can provide a lever to the governance of the common-property resource. The information to be circulated and the use policy to be implemented, by reducing uncertainty, can reduce the range of the hysteresis interval and increase flexibility of both entry and exit. It is worth noting, indeed, that uncertainty increases the user’s inertia, anchoring them to their present state.

Lastly, our simulations have highlighted that the effect of an increase in the number of users n has different effects depending on specific assumptions. For example, if the number of users does not alter the stock growth rate (i.e., μ′(n) = 0) and the individual user’s benefit decreases due to mutual disturbance regardless of rivalry (i.e., B′(n) < 0), an increase in the number of rivals generates an increase in both the thresholds (i.e., $\frac{d{x}_K}{dn}>0 \mathrm{and} \frac{d{x}_L}{dn}>0$). It is worth recalling that the marginal benefit is decreasing in the number of users. In the presence of a decreasing benefit, an increase in the number of rivals produces a disincentive to exercise the entry option. Similarly, the entry of new competitors can produce an incentive for the actual user to exercising the exit option.

If, on the other hand, the number of users does not alter the marginal benefit (i.e., B′(n) = 0) but it reduces the marginal productivity (i.e., μ′(n) < 0) an increase in the number of rivals reduces the thresholds (i.e., $\frac{d{x}_K}{dn}<0 \mathrm{and} \frac{d{x}_L}{dn}<0$). Indeed, an increase in n reduces μ′ which, in turn, causes β to increase, thus reducing the coefficient $\frac{\beta }{\beta -1}$. The opposite effect occurs for α. In short, if the right holder is aware that an increase in the number of users affects the stock growth rate, and there are no significant congestion effects, they will be stimulated to exploit the resource to avoid future competition over the decreasing stock.

Lastly, whenever an increase in the number of rivals simultaneously reduces the resource growth rate and a congestion effect affects the private benefit (i.e., μ′(n) < 0) and B′(n) < 0), it is not possible to define a priori the cumulative effect on the entry and exit thresholds.

5. A Numerical Example: Mushroom Picking

Mushroom picking is practiced in many areas of the world and is generally associated with local culture, social activities, and the interest in picking your food. Mushroom picking is a pastime that has recently grown in popularity. In this context, it is worth investigating how to forage in a way that does not overexploit the resource and respects animals who feed on fungi, the ecosystem, and others who pick.

To test the model’s theoretical results, we investigate a picker’s decision to harvest the Armillaria mellea mushroom in a rural area in the North of Italy. The Armillaria mellea is a basidiomycete fungus, commonly known as honey mushroom, which grows in temperate regions. It is a wild edible mushroom that generally grows on hardwoods but may be found around dead wood or hedges in open cultivated areas. Its picking is subject to a weak regulation by local regional authorities that guarantee the free harvesting to landowners and allows users different from landowners to pay an annual permit fee, which entitles them to pick a maximum amount per day over the year¹⁹.

5.1. Scenarios

To cover a wide range of situations, which can occur in real-world case studies, we considered two scenarios: Scenario 1 and Scenario 2. The former does not account for sunk entry or exist costs, whereas the latter does.

Scenario 1—The are no entry or exit costs (i.e., k = 0 and l = 0). In this scenario, the right holder decides whether to go picking mushrooms based on the trigger x*:

$$x^{*}=\frac{c}{B\left(n\right)}$$

Whenever x_t > x* the user goes picking mushrooms, whereas whenever x_t < x* the user suspends picking.

Scenario 2—Entry costs are positive, i.e., k > 0 and exit costs are null, i.e., l = 0. In this scenario, a proxy of the hysteresis interval is the following:

$$\left[x_H-x_L\right]=\frac{\frac{\beta }{\beta -1}\left(c+\rho k\right)-\frac{\alpha }{\alpha -1}c}{B\left(n\right)}$$

where:

$$x_K=\frac{\frac{\beta }{\beta -1}\left(c+\rho k\right)}{B\left(n\right)}$$

$$x_L=\frac{\frac{\alpha }{a-1}c}{B\left(n\right)}.$$

5.2. Calibration

To calibrate the model, we used data driven from the Italian context²⁰. In detail, we consider a 3000 ha rural area in the North East of Italy, approximately 3% of which is covered with hedges, i.e., 90 ha [77,78]. The local resident population is about 3000–4000 individuals [79]. Traditionally, potential mushroom pickers are locals, reside at the borders of the urban centers located in the rural area of interest, and represents about 20% of the active local population, for a total number of potential right holders of 600–700 individuals [79]. Due to the seasonality of honey mushroom picking, any mushroom picker goes picking usually 2–3 times per year and picks for 2–3 h at any time. On average, any picker devotes about 6 h to picking and thus collects annually 5–6 kilos of honey mushroom^21,22.

• Based on statistics performed on the time series of the annual production of Armillaria mellea, we assume the honey mushroom stock x_t evolves over time according to a geometric Brownian motion, where x₀ = 5.2 kg/year, μ(n) = 0²³, and σ = 30%²⁴.
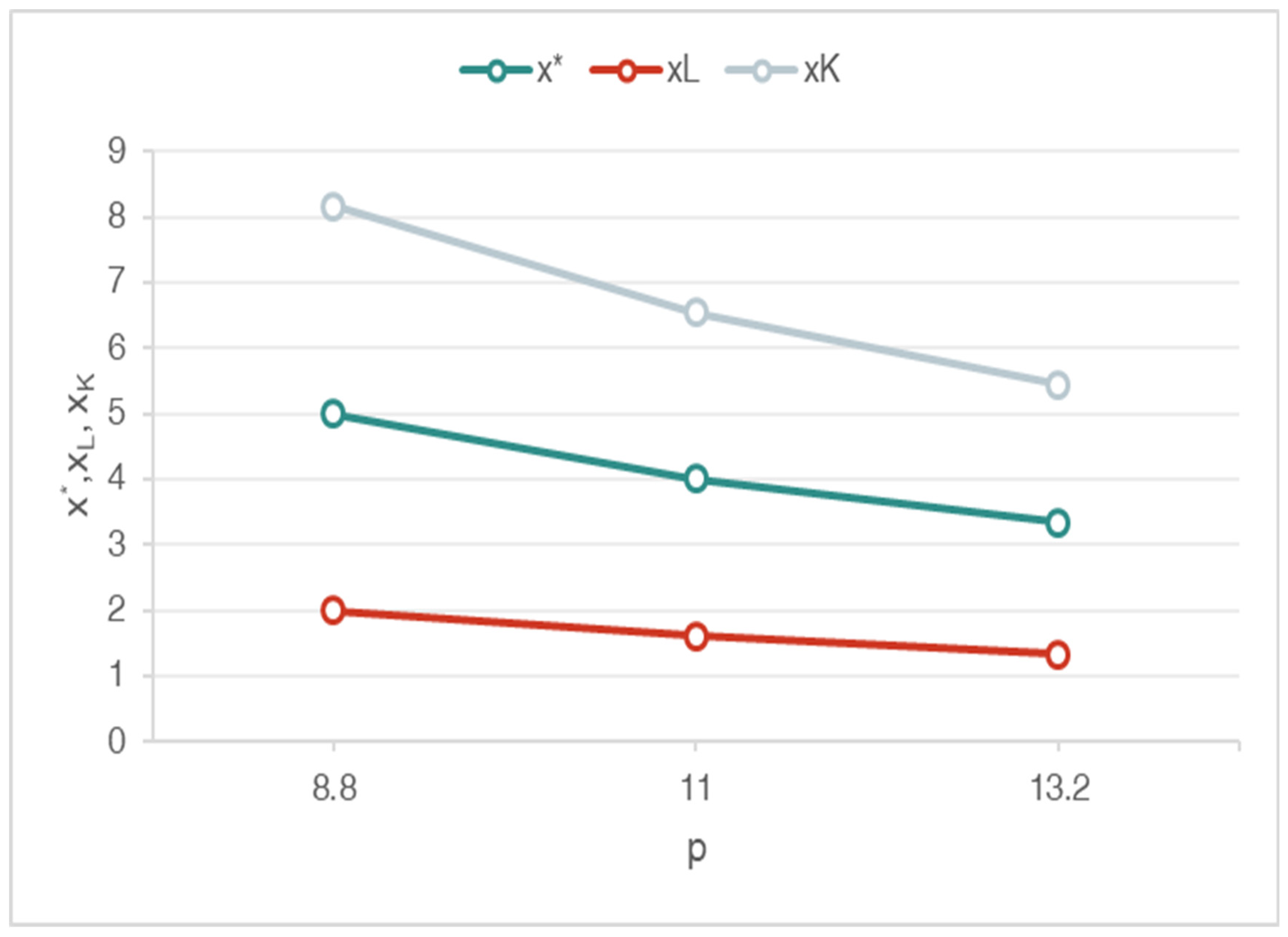
• The unit market price of honey mushrooms p is equal to p = 11 EUR/kg.
• We assume that B increases linearly with the stock x_t (i.e., ξ = 1). Consequently, Bx_t = p x_t.
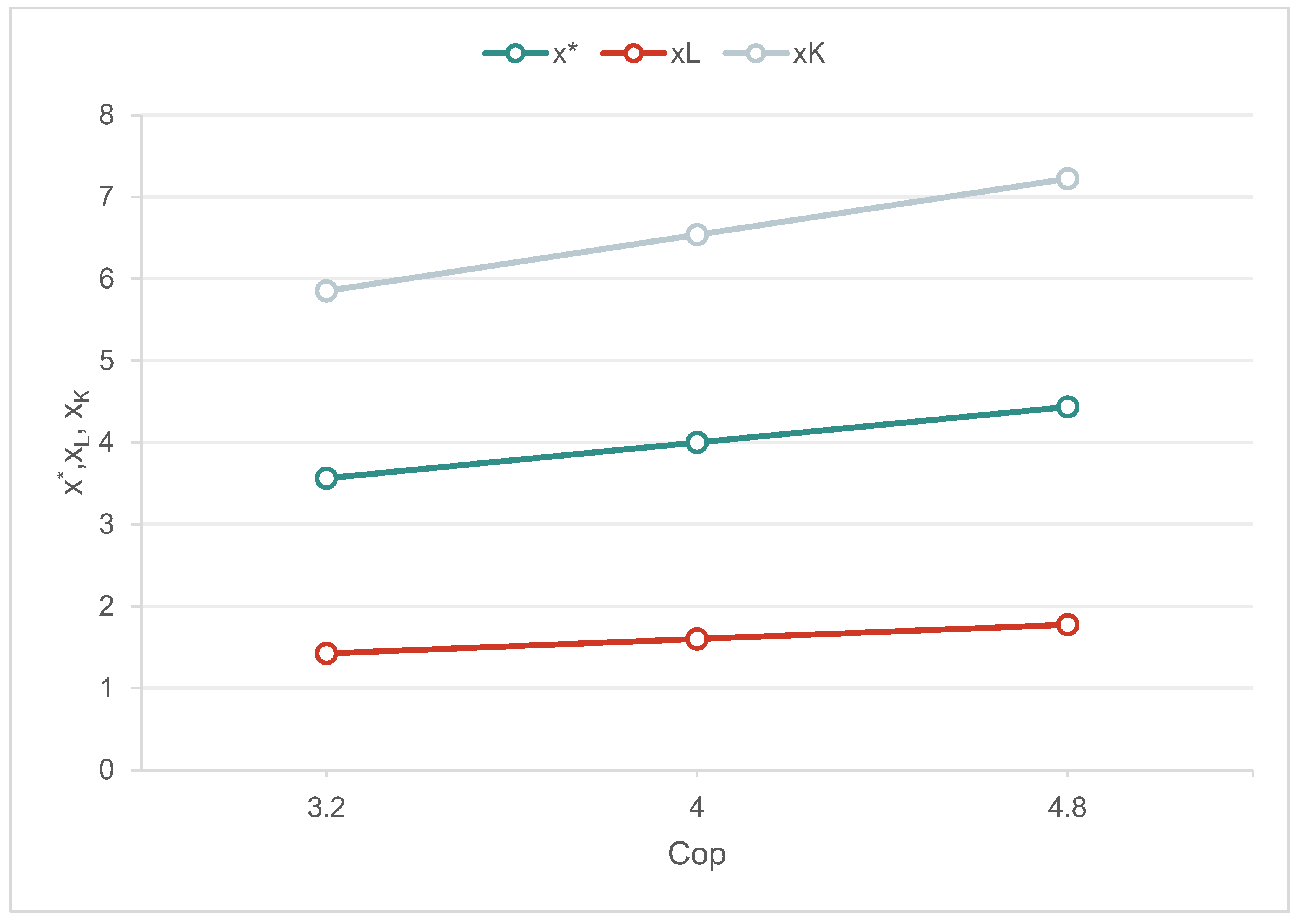
• Operating costs c account for the permit fee c_p (that represents a fix cost, independent of the area extension) and the opportunity cost of time of the user c_o. The cost paid by each user for the annual permit fee is c_p = 20 EUR/year, whereas we assume that the opportunity cost of the time spent in picking is about 30% [80] of the average hourly income per province, namely c_o = 4 EUR/h²⁵. Consequently, operating costs paid by each user are equal to c = c_p + t_p·c_o, where t_p = 6 h/year.
• To go picking mushrooms, the right holder must prove detailed knowledge of wild mushrooms and the ability to distinguish edible from non-edible mushrooms. Therefore, the right holder is requested to attend a specific one-off course. In other words, once the right holder has attended this course, they are not requested to take the course again if the picking takes place continuously for subsequent years. Nonetheless, if the right holder stops picking for one year, they must retake the course to start picking again²⁶. Consequently, entry costs are equal to k = 60 EUR.
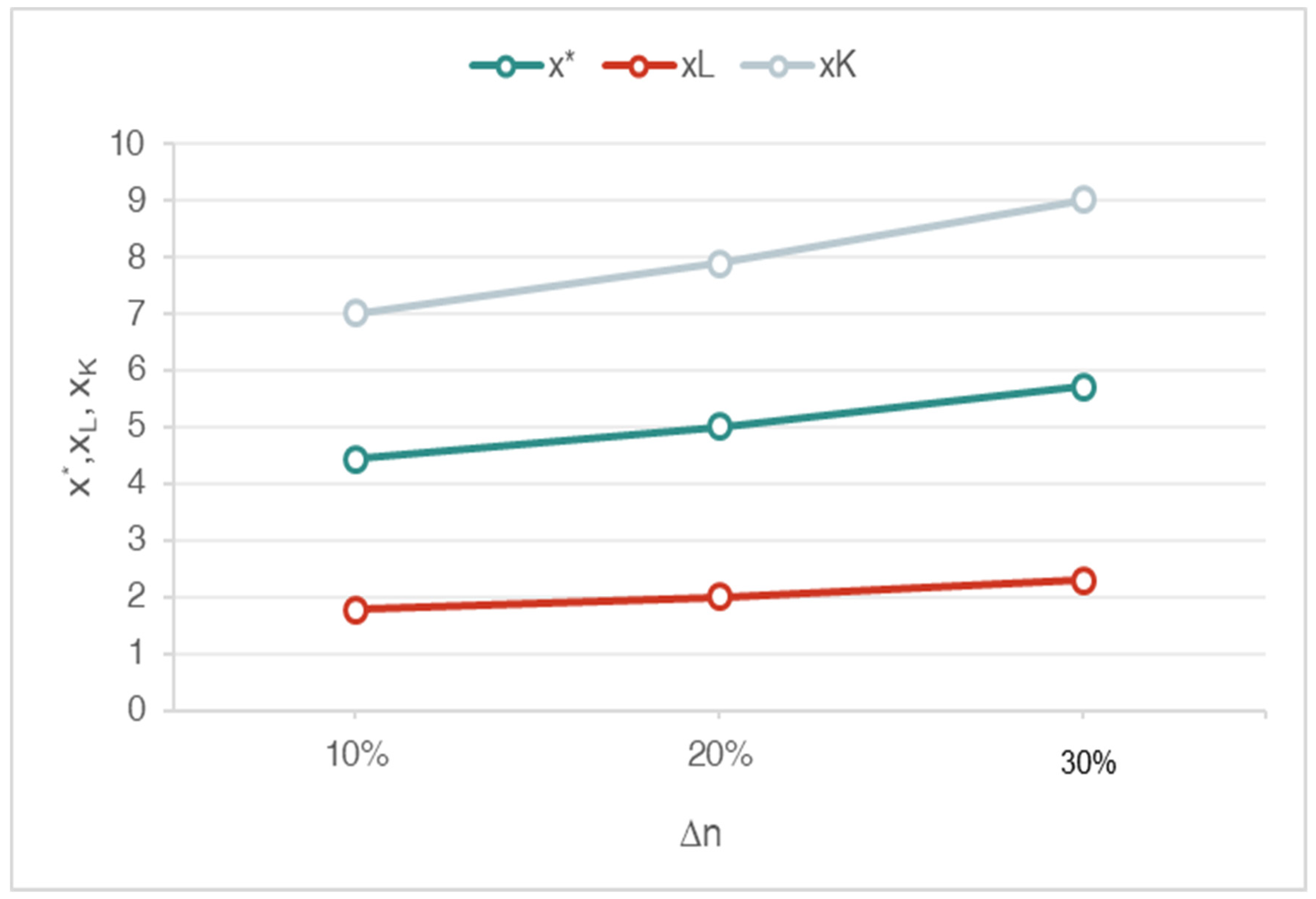
• The number of users per hectare is on average n = 7.2.
• The discount rate ρ is equal to ρ = 3% [82].

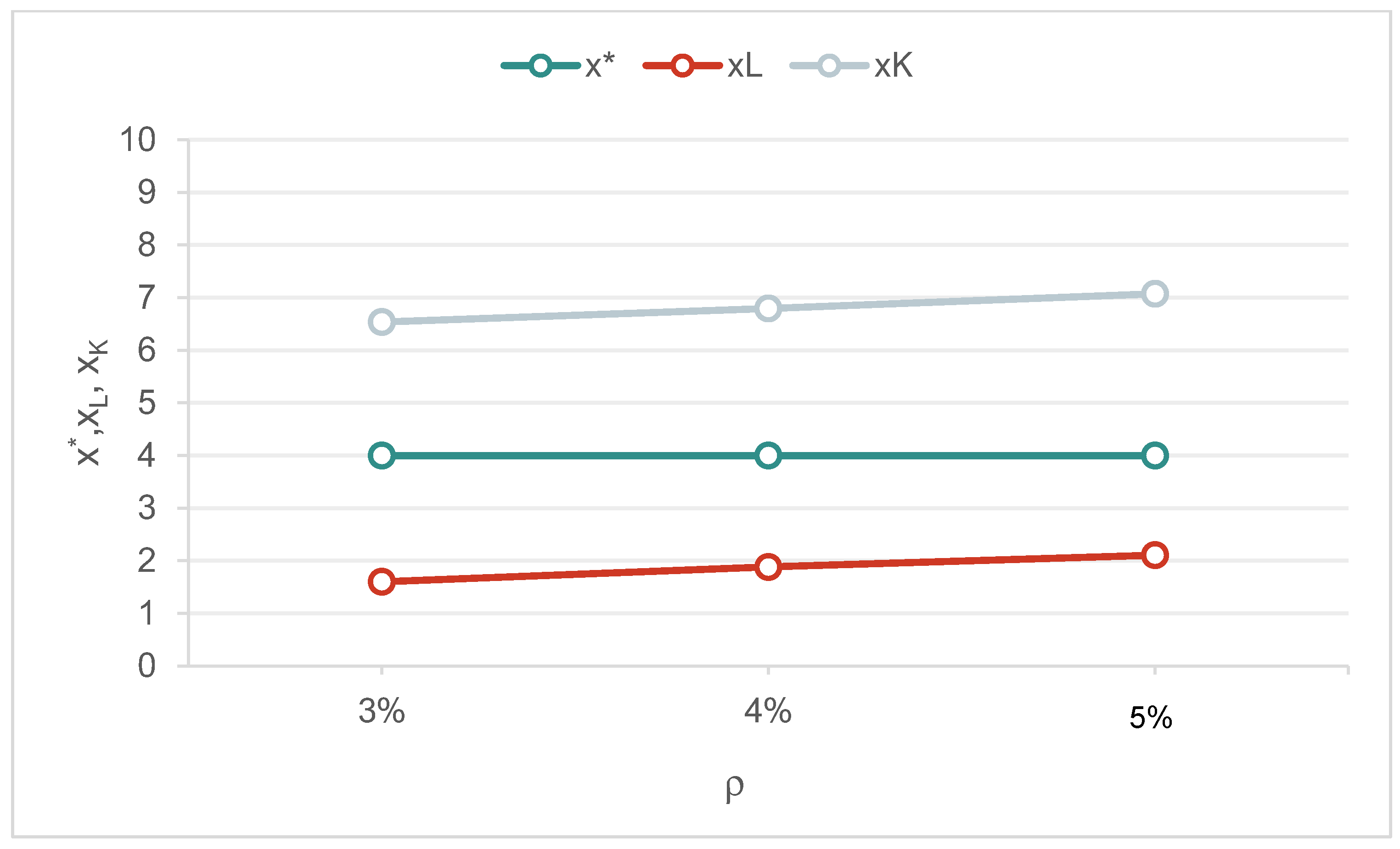
5.3. Results and Discussion

In what follows, the main results and comparative statistics are presented and discussed. We performed comparative statistics with respect to the volatility σ, the market price of honey mushrooms p, the opportunity cost c_o, the number of users per hectare n, and the discount rate ρ.

Table 4. Model parameters.

	Benchmark Case	Comparative Statics
σ	30%	20%	40%
p (EUR/kg)	11	8.8	13.2
cop (EUR/h)	4	3.2	4.8
n (ind/ha)	7.2	+10%	+20%	+30%
ρ	3%	4%	5%

summarizes input data for comparative statistics. In detail, the first column in Table 4 illustrates model input data for the benchmark case, whereas the second column ρ parative statistics.

Figure 1, Figure 2, Figure 3, Figure 4 and Figure 5 illustrate the main results obtained via simulations. From direct inspection of Figure 1 and Figure 5, it emerges that the threshold x* is independent of σ and ρ, whereas it increases linearly with the opportunity cost c_o (Figure 3), and decreases for increasing mushroom prices p (Figure 2). In line with the theoretical results discussed in Section 4.3, as σ, ρ, and c_op increase, the hysteresis interval enlarges (Figure 1, Figure 3 and Figure 5). In detail, for increasing σ, x_L decreases; nonetheless, x_K increases and x_L decreases. By contrast, for increasing c_op and increasing ρ both x_L and x_K increases, but at a different rate. Figure 3 shows that for increasing p, the hysteresis interval reduces. As an example, when k = 60 EUR, σ = 30%, p = 11 EUR/kg, and c_op = 4 EUR/h, at time t = 0 when the stock is x_o = 5.2 kg/year, the right holder is not picking (i.e., is in the status of a potential user) and will start picking honey mushroom when the stock will increase to x_K = 6.537 kg/year. By contrast, if the entry cost is null, i.e., k = 0, at time t = 0, the right holder is picking honey mushrooms and will not exit. Finally, Figure 4 displays the effect of an increase in the number of users. As long as the number of users increases by Δn = 10%, 20%, 30%, the hysteresis interval increases. In other words, the potential user will wait longer to start picking and the actual user will stop picking earlier compared to the benchmark case. Our findings show that there is a congestion effect that may significantly affect the individual’s net benefit. To our best knowledge, this is the first contribution implementing a real option approach to model a user’s decision whether to exploit a common-property resource according to their actual status of being an actual or potential user. Our results are substantially in line with the findings by Pacheco-Cobos et al. [83], who modelled a forager’s movement patter via efficient random walk search algorithms, and by Kaaronen [84], who analyzed how foragers make safe and efficient decisions under uncertainty.

Empirical evidence reveals that although long-term and systematic harvesting does not reduce the future yields of fruit bodies nor the species richness of wild forest fungi, forest floor trampling reduces fruit body numbers [85]. In Europe, the UK, and Asia, some mushroom species (e.g., Agarikon-Laricifomes officinalis, White Ferula Mushroom- Pleurotus nebrodensis) have become rare due to lack of sustainable mushroom foraging methods. Consequently, the congestion effect in mushroom harvesting is worth investigating as, recently, foraging has intensified in many countries worldwide. Foraging has, for example, skyrocketed in Victoria (Australia) through the extended lockdowns [86] and in the San Francisco Bay area [87]. In this respect, our results have interesting policy implications and can support policymakers in designing sustainable, non-depleting resource exploitation.

6. Conclusions

The government of common-property resources is a topical issue specifically in the domain of the valuation of ecosystem services. The analysis of institutions that in the past had proved the ability to operate a sustainable management of natural resources is essential to inform the governance and valorization of ecosystem services, which to some extent exhibit the characteristics of common-property resources, and mainly those ecosystem services which are related to cultural and supporting services. In many rural areas, where wild resources, such as mushrooms and wild herbs, are rival but little excludable, the pressure exerted by pickers generates some concerns on resource preservation, conflicts with landowners, and may put biodiversity at risk in contexts already heavily jeopardized by modern agriculture.

This study investigates an individual’s decision whether or not to exploit a common-property resource according to their status of actual or potential user. There is indeed a close analogy between the decisions to exercise a use right on the resource and the decision to exercise a real option, and specifically an entry/exist option.

Firstly, we assess the value of the right to use a common-property resource and, secondly, we determine the optimal right holder’s exploitation strategy. We then tested the model’s theoretical results by applying the model to the exploitation of honey mushrooms by recreational mushroom pickers in a rural area in the North East of Italy.

The right holders’ aim is to maximize their benefit net of costs. The right holders’ benefit depends on the mushroom stock and the number of individuals picking mushroom. Our simulations show that the right holder’s decision to exercise the entry or exit option is taken with respect to two different thresholds, which represent the stock lower and upper bounds (x_L and x_K), respectively, which induce the actual user to stop the resource exploitation and the potential user to start the resource exploitation. In line with the real options theory, the greater the uncertainty, the greater the hysteresis interval, i.e., the greater x_K − x_L. In addition, as the market prices of honey mushrooms p increases, the hysteresis interval decreases, whereas it increases for increasing users’ opportunity cost c_op. As the number of users increases, ceteris paribus, the right holder will wait longer to start picking and will stop picking earlier.

The stock thresholds diverge due to the sunk entry and exit costs and the uncertainty over future availability of honey mushrooms. The difference between thresholds, hysteresis, significantly influences the resource exploitation: a large hysteresis interval produces an increase in right holders’ hysteresis which is anchored to their initial condition, regardless of whether they are initially current or potential users.

These results provide useful insights on the design of both regulation mechanisms and management policy for common-property resource exploitation, when the stock is uncertain and future stock availability depends on the number of users and congestion effects.

Future research may involve the modelling of the mushroom pickers’ decision when competition and conflict between recreational pickers and landowners arise.