Terrain Analysis According to Multiscale Surface Roughness in the Taklimakan Desert †
Abstract
:1. Introduction
2. Materials and Methods
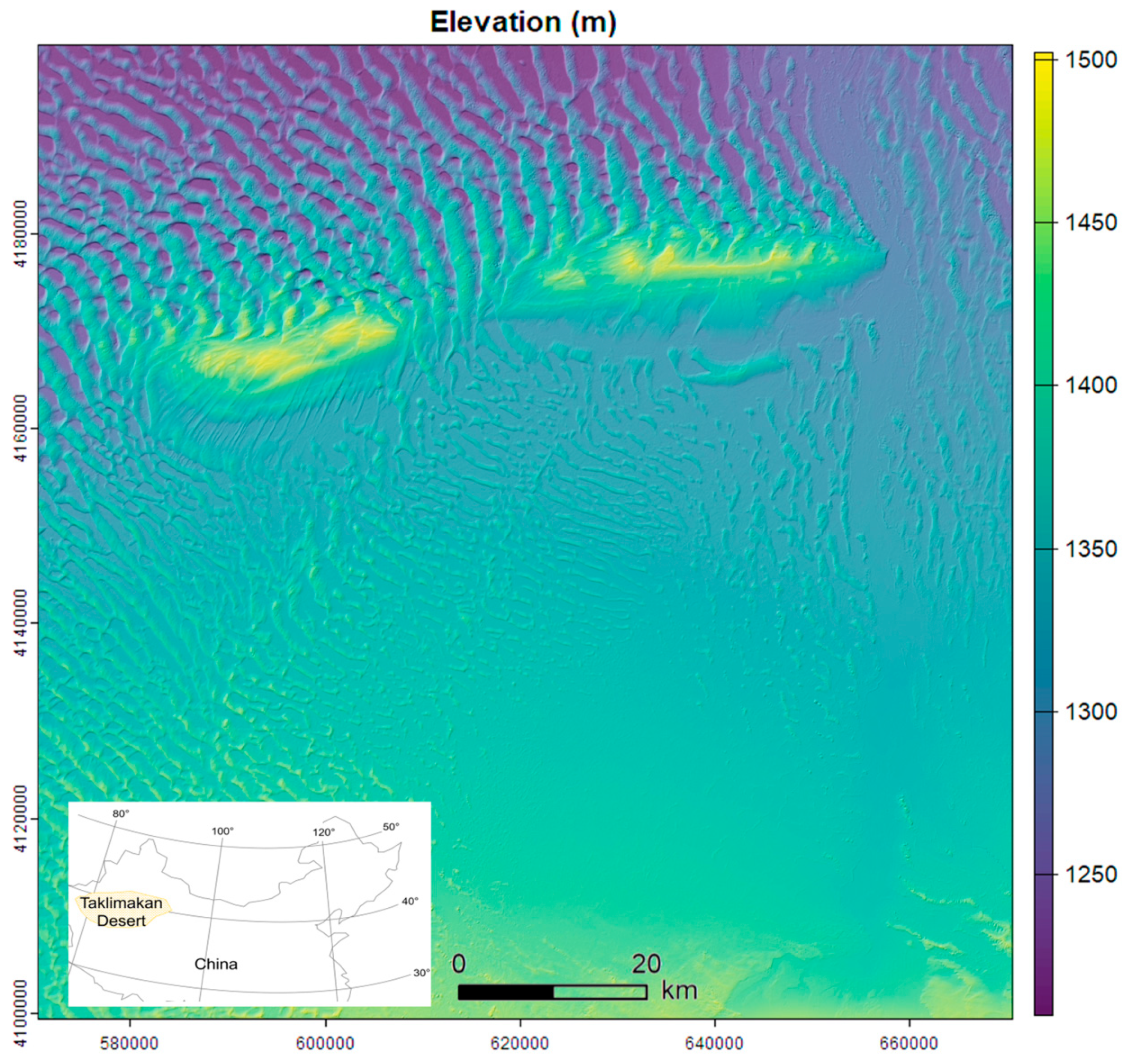
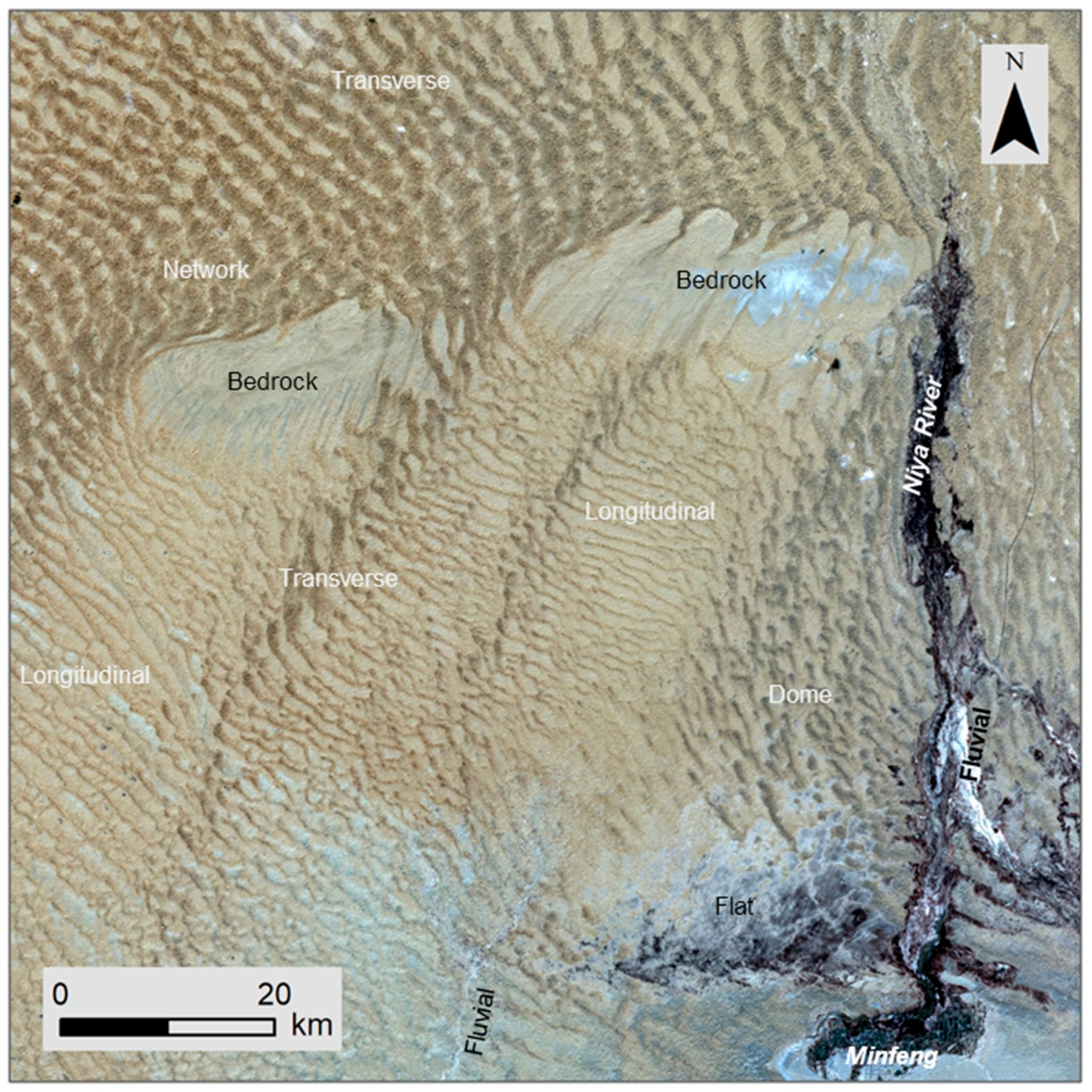
2.1. Study Area and Digital Elevation Model
2.2. Simplified Multiscale Geostatistical Approach
2.3. Unsupervised and Supervised Learning
3. Results and Discussion
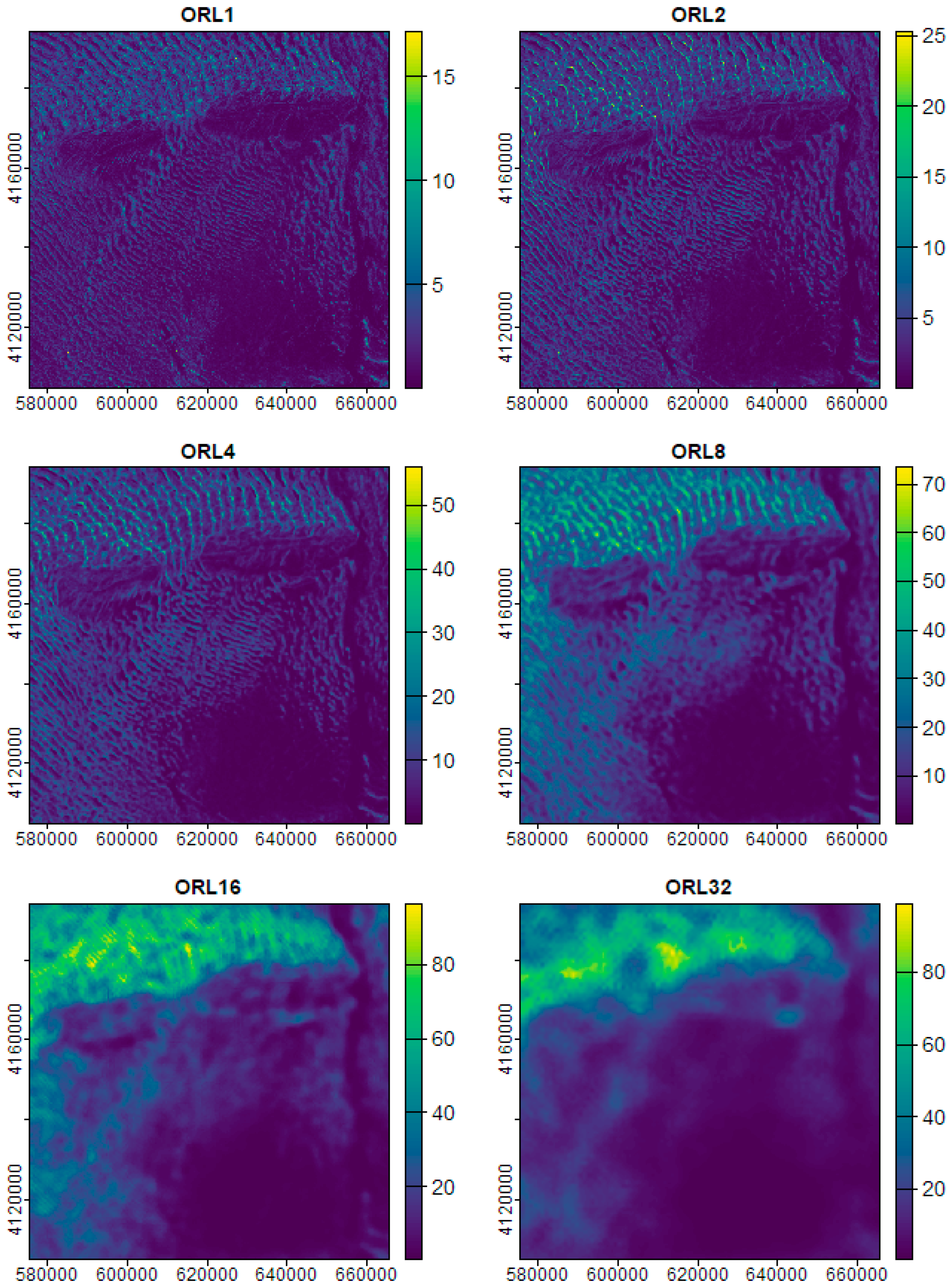
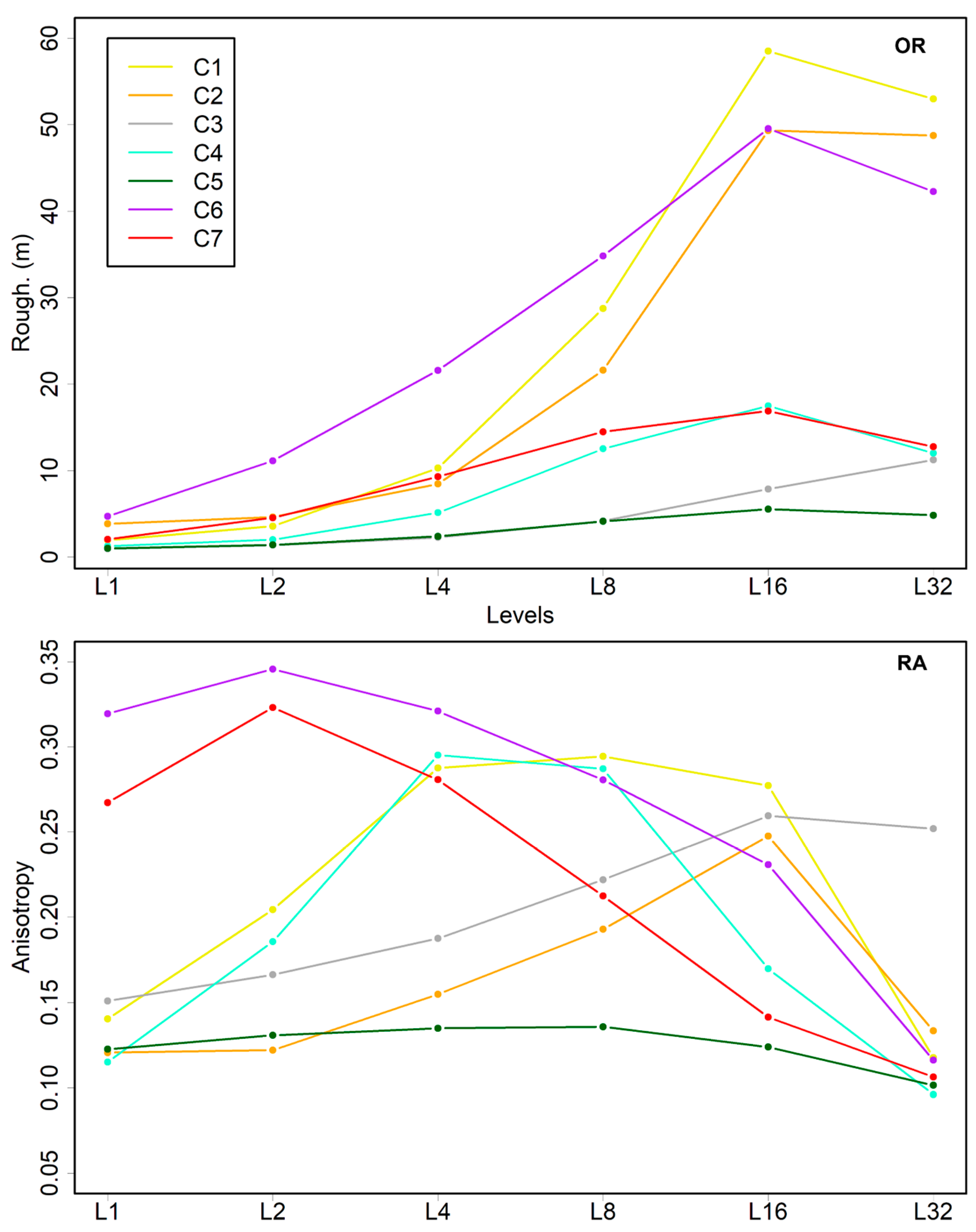
3.1. Multiscale Analysis of Surface Roughness
3.2. Unsupervised Learning
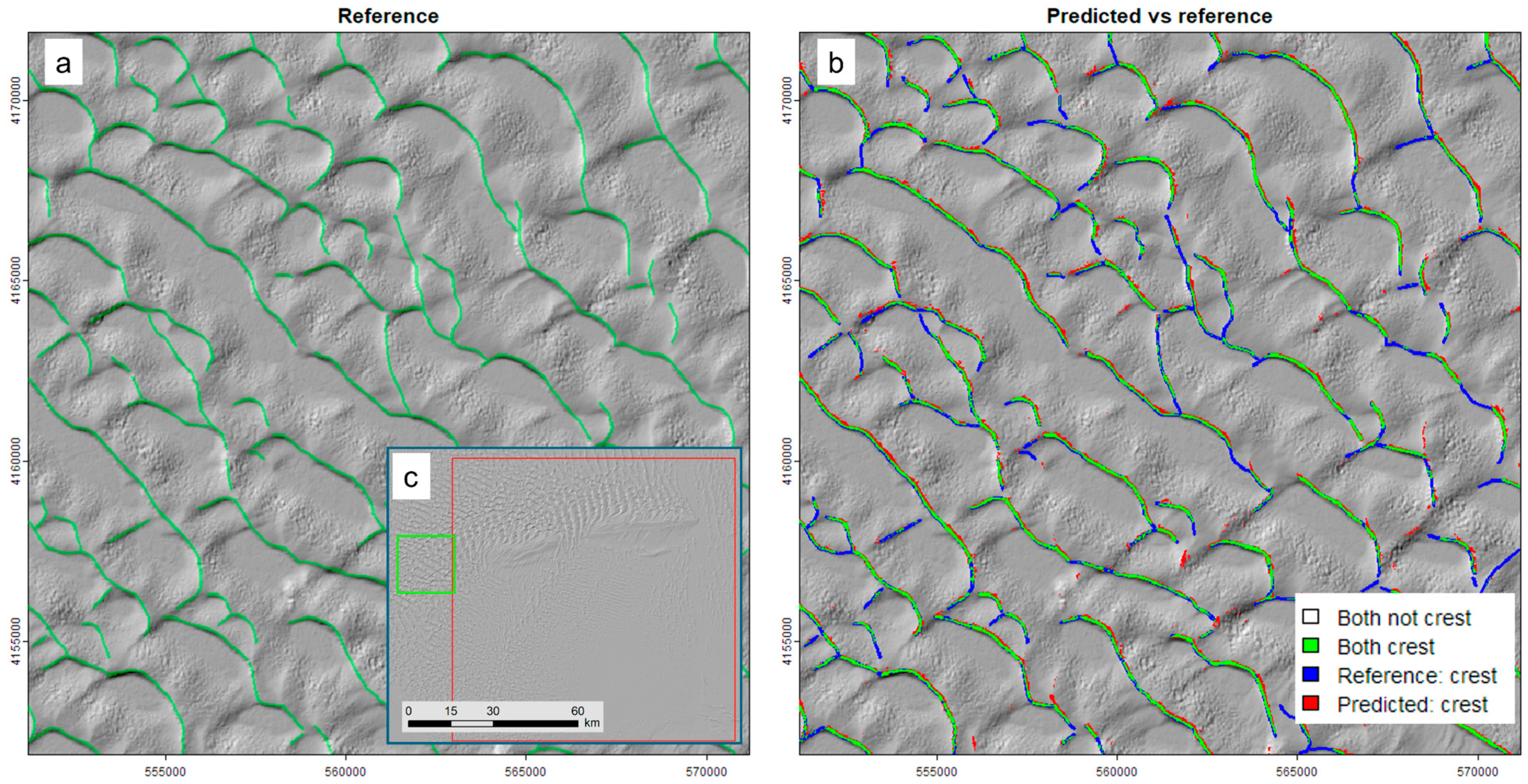
3.3. Supervised Learning: Predicting Crest Lines
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Guth, P.L. Quantifying Terrain Fabric in Digital Elevation Models. GSA Rev. Eng. Geol. 2001, 14, 13–25. [Google Scholar] [CrossRef]
- Shepard, M.K.; Campbell, B.A.; Bulmer, M.H.; Farr, T.G.; Gaddis, L.R.; Plaut, J.J. The Roughness of Natural Terrain: A Planetary and Remote Sensing Perspective. J. Geophys. Res. Planets 2001, 106, 32777–32795. [Google Scholar] [CrossRef]
- Lucieer, A.; Stein, A. Texture-Based Landform Segmentation of LiDAR Imagery. Int. J. Appl. Earth Obs. Geoinf. 2005, 6, 261–270. [Google Scholar] [CrossRef]
- Trevisani, S.; Cavalli, M.; Marchi, L. Variogram Maps from LiDAR Data as Fingerprints of Surface Morphology on Scree Slopes. Nat. Hazards Earth Syst. Sci. 2009, 9, 129–133. [Google Scholar] [CrossRef]
- Pollyea, R.M.; Fairley, J.P. Estimating Surface Roughness of Terrestrial Laser Scan Data Using Orthogonal Distance Regression. Geology 2011, 39, 623–626. [Google Scholar] [CrossRef]
- Grohmann, C.H.; Smith, M.J.; Riccomini, C. Multiscale Analysis of Topographic Surface Roughness in the Midland Valley, Scotland. IEEE Trans. Geosci. Remote Sens. 2011, 49, 1200–1213. [Google Scholar] [CrossRef]
- Smith, M.W. Roughness in the Earth Sciences. Earth-Sci. Rev. 2014, 136, 202–225. [Google Scholar] [CrossRef]
- Iwahashi, J.; Kamiya, I.; Matsuoka, M.; Yamazaki, D. Global Terrain Classification Using 280 m DEMs: Segmentation, Clustering, and Reclassification. Prog. Earth Planet. Sci. 2018, 5, 1. [Google Scholar] [CrossRef]
- Dusséaux, R.; Vannier, E. Soil Surface Roughness Modelling with the Bidirectional Autocorrelation Function. Biosyst. Eng. 2022, 220, 87–102. [Google Scholar] [CrossRef]
- Doane, T.H.; Gearon, J.H.; Martin, H.K.; Yanites, B.J.; Edmonds, D.A. Topographic Roughness as an Emergent Property of Geomorphic Processes and Events. AGU Adv. 2024, 5, 1–25. [Google Scholar] [CrossRef]
- Misiuk, B.; Lecours, V.; Prampolini, M.; Giona Bucci, M.; Araújo, T.C. Editorial: Frontiers in Marine Geomorphometry. Front. Mar. Sci. 2024, 11, 1419518. [Google Scholar] [CrossRef]
- Huang, G.; Yang, L.; Cai, Y.; Zhang, D. Terrain Classification-Based Rover Traverse Planner with Kinematic Constraints for Mars Exploration. Planet. Space Sci. 2021, 209, 105371. [Google Scholar] [CrossRef]
- Rowan, L.C.; McCauley, J.F.; Holm, E.A. Lunar Terrain Mapping and Relative-Roughness Analysis; US Geological Survey Professional Paper; US Government Printing Office: Washington, DC, USA, 1971. [Google Scholar]
- Trevisani, S.; Teza, G.; Guth, P. A Simplified Geostatistical Approach for Characterizing Key Aspects of Short-Range Roughness. CATENA 2023, 223, 106927. [Google Scholar] [CrossRef]
- Riley, S.J.; DeGloria, S.D.; Elliot, R. A Terrain Ruggedness Index That Quantifies Topographic Heterogeneity. Intermt. J. Sci. 1999, 5, 23–27. [Google Scholar]
- Trevisani, S.; Teza, G.; Guth, P.L. Hacking the Topographic Ruggedness Index. Geomorphology 2023, 439, 108838. [Google Scholar] [CrossRef]
- Ilich, A.R.; Misiuk, B.; Lecours, V.; Murawski, S.A. MultiscaleDTM: An Open-Source R Package for Multiscale Geomorphometric Analysis. Trans. GIS 2023, 27, 1164–1204. [Google Scholar] [CrossRef]
- Lindsay, J.B.; Newman, D.R.; Francioni, A. Scale-Optimized Surface Roughness for Topographic Analysis. Geosciences 2019, 9, 322. [Google Scholar] [CrossRef]
- Trevisani, S.; Cavalli, M. Topography-Based Flow-Directional Roughness: Potential and Challenges. Earth Surf. Dyn. 2016, 4, 343–358. [Google Scholar] [CrossRef]
- Trevisani, S.; Rocca, M. MAD: Robust Image Texture Analysis for Applications in High Resolution Geomorphometry. Comput. Geosci. 2015, 81, 78–92. [Google Scholar] [CrossRef]
- Herzfeld, U.C. Vario Functions of Higher Order—Definition and Application to Characterization of Snow Surface Roughness. Comput. Geosci. 2002, 28, 641–660. [Google Scholar] [CrossRef]
- Haralick, R.M.; Dinstein, I.; Shanmugam, K. Textural Features for Image Classification. IEEE Trans. Syst. Man Cybern. 1973, SMC-3, 610–621. [Google Scholar] [CrossRef]
- Atkinson, P.M.; Lewis, P. Geostatistical Classification for Remote Sensing: An Introduction. Comput. Geosci. 2000, 26, 361–371. [Google Scholar] [CrossRef]
- Xu, Y.; Zhang, S.; Li, J.; Liu, H.; Zhu, H. Extracting Terrain Texture Features for Landform Classification Using Wavelet Decomposition. ISPRS Int. J. Geo-Inf. 2021, 10, 658. [Google Scholar] [CrossRef]
- Booth, A.M.; Roering, J.J.; Perron, J.T. Automated Landslide Mapping Using Spectral Analysis and High-Resolution Topographic Data: Puget Sound Lowlands, Washington, and Portland Hills, Oregon. Geomorphology 2009, 109, 132–147. [Google Scholar] [CrossRef]
- Abedini, M.J.; Shaghaghian, M.R. Exploring Scaling Laws in Surface Topography. Chaos Solitons Fractals 2009, 42, 2373–2383. [Google Scholar] [CrossRef]
- Mariethoz, G.; Lefebvre, S. Bridges between Multiple-Point Geostatistics and Texture Synthesis: Review and Guidelines for Future Research. Comput. Geosci. 2014, 66, 66–80. [Google Scholar] [CrossRef]
- Trevisani, S. MADSurfaceTexture: V1.1 plus R Package. Available online: https://zenodo.org/records/7716927 (accessed on 2 November 2024).
- Guth, P.; Kane, M. Slope, Aspect, and Hillshade Algorithms for Non-Square Digital Elevation Models. Trans. GIS 2021, 25, 2309–2332. [Google Scholar] [CrossRef]
- Dong, Z.; Wang, X.; Chen, G. Monitoring Sand Dune Advance in the Taklimakan Desert. Geomorphology 2000, 35, 219–231. [Google Scholar] [CrossRef]
- Ma, F.; Lü, P.; Cao, M.; Yu, J.; Xia, Z. Morphological and Sedimentary Characteristics of Raked Linear Dunes in the Southeastern Taklimakan Desert, China. Aeolian Res. 2024, 67–69, 100923. [Google Scholar] [CrossRef]
- Sun, W.; Gao, X. Geomorphology of Sand Dunes in the Taklamakan Desert Based on ERA5 Reanalysis Data. J. Arid Environ. 2022, 207, 104848. [Google Scholar] [CrossRef]
- Wang, X.; Dong, Z.; Zhang, J.; Qu, J. Formation of the Complex Linear Dunes in the Central Taklimakan Sand Sea, China. Earth Surf. Process. Landf. 2004, 29, 677–686. [Google Scholar] [CrossRef]
- Wang, X.; Dong, Z.; Zhang, J.; Chen, G. Geomorphology of Sand Dunes in the Northeast Taklimakan Desert. Geomorphology 2002, 42, 183–195. [Google Scholar] [CrossRef]
- Trevisani, S.; Skrypitsyna, T.N.; Florinsky, I.V. Global Digital Elevation Models for Terrain Morphology Analysis in Mountain Environments: Insights on Copernicus GLO-30 and ALOS AW3D30 for a Large Alpine Area. Environ. Earth Sci. 2023, 82, 198. [Google Scholar] [CrossRef]
- Bielski, C.; Lopez-Vazquez, C.; Grohmann, C.H.; Guth, P.L.; Hawker, L.; Gesch, D.; Trevisani, S.; Herrera-Cruz, V.; Riazanoff, S.; Corseaux, A.; et al. Novel Approach for Ranking DEMs: Copernicus DEM Improves One Arc Second Open Global Topography. IEEE Trans. Geosci. Remote Sens. 2024, 62, 1–22. [Google Scholar] [CrossRef]
- Guth, P.L.; Trevisani, S.; Grohmann, C.H.; Lindsay, J.; Gesch, D.; Hawker, L.; Bielski, C. Ranking of 10 Global One-Arc-Second DEMs Reveals Limitations in Terrain Morphology Representation. Remote Sens. 2024, 16, 3273. [Google Scholar] [CrossRef]
- Tadono, T.; Nagai, H.; Ishida, H.; Oda, F.; Naito, S.; Minakawa, K.; Iwamoto, H. Generation of the 30 M-MESH Global Digital Surface Model by Alos Prism. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2016, 41, 157–162. [Google Scholar] [CrossRef]
- Shumack, S.; Hesse, P.; Farebrother, W. Deep Learning for Dune Pattern Mapping with the AW3D30 Global Surface Model. Earth Surf. Process. Landf. 2020, 45, 2417–2431. [Google Scholar] [CrossRef]
- White, K.; Bullard, J.; Livingstone, I.; Moran, L. A Morphometric Comparison of the Namib and Southwest Kalahari Dunefields Using ASTER GDEM Data. Aeolian Res. 2015, 19, 87–95. [Google Scholar] [CrossRef]
- Zheng, Z.; Du, S.; Taubenböck, H.; Zhang, X. Remote Sensing Techniques in the Investigation of Aeolian Sand Dunes: A Review of Recent Advances. Remote Sens. Environ. 2022, 271, 112913. [Google Scholar] [CrossRef]
- Guisan, A.; Weiss, S.B.; Weiss, A.D. GLM versus CCA Spatial Modeling of Plant Species Distribution. Plant Ecol. 1999, 143, 107–122. [Google Scholar] [CrossRef]
- Hiller, J.K.; Smith, M. Residual Relief Separation: Digital Elevation Model Enhancement for Geomorphological Mapping. Earth Surf. Process. Landf. 2008, 33, 2266–2276. [Google Scholar] [CrossRef]
- Wilson, M.F.J.; O’Connell, B.; Brown, C.; Guinan, J.C.; Grehan, A.J. Multiscale Terrain Analysis of Multibeam Bathymetry Data for Habitat Mapping on the Continental Slope. Mar. Geod. 2007, 30, 3–35. [Google Scholar] [CrossRef]
- Isaaks, E.H.; Srivastava, R.M. An Introduction to Applied Geostatistics; Oxford University Press: New York, NY, USA, 1989. [Google Scholar]
- Chilès, J.-P.; Delfiner, P. Geostatistics: Modeling Spatial Uncertainty, 2nd ed.; John Wiley & Sons: Hoboken, NJ, USA, 2012. [Google Scholar]
- Hani, A.F.M.; Sathyamoorthy, D.; Asirvadam, V.S. A Method for Computation of Surface Roughness of Digital Elevation Model Terrains via Multiscale Analysis. Comput. Geosci. 2011, 37, 177–192. [Google Scholar] [CrossRef]
- Fisher, P.; Wood, J.; Cheng, T. Where Is Helvellyn? Fuzziness of Multi-Scale Landscape Morphometry. Trans. Inst. Br. Geogr. 2004, 29, 106–128. [Google Scholar] [CrossRef]
- Kovesi, P. Fast Almost-Gaussian Filtering. In Proceedings of the 2010 Digital Image Computing: Techniques and Applications, DICTA 2010, Sydney, NSW, Australia, 1–3 December 2010; pp. 121–125. [Google Scholar]
- Newman, D.R.; Cockburn, J.M.H.; Drǎguţ, L.; Lindsay, J.B. Evaluating Scaling Frameworks for Multiscale Geomorphometric Analysis. Geomatics 2022, 2, 36–51. [Google Scholar] [CrossRef]
- Conrad, O.; Bechtel, B.; Bock, M.; Dietrich, H.; Fischer, E.; Gerlitz, L.; Wehberg, J.; Wichmann, V.; Böhner, J. System for Automated Geoscientific Analyses (SAGA) v. 2.1.4. Geosci. Model Dev. 2015, 8, 1991–2007. [Google Scholar] [CrossRef]
- Lindsay, J.B. Whitebox GAT: A Case Study in Geomorphometric Analysis. Comput. Geosci. 2016, 95, 75–84. [Google Scholar] [CrossRef]
- Wu, Q.; Brown, A. “Whitebox”: “WhiteboxTools” R Frontend; 2022. Available online: https://cran.r-project.org/package=whitebox (accessed on 2 November 2024).
- James, G.; Witten, D.; Hastie, T.; Tibshirani, R. An Introduction to Statistical Learning (with Applications in R); Springer Texts in Statistics; Springer: New York, NY, USA, 2021. [Google Scholar]
- Memarsadeghi, N.; Mount, D.M.; Netanyahu, N.S.; Le Moigne, J. A Fast Implementation of the Isodata Clustering Algorithm. Int. J. Comput. Geom. Appl. 2007, 17, 71–103. [Google Scholar] [CrossRef]
- Charrad, M.; Ghazzali, N.; Boiteau, V.; Niknafs, A. Nbclust: An R Package for Determining the Relevant Number of Clusters in a Data Set. J. Stat. Softw. 2014, 61, 1–36. [Google Scholar] [CrossRef]
- Daynac, J.; Bessin, P.; Pochat, S.; Mourgues, R.; Shumack, S. A New Workflow for Mapping Dune Features (Outline, Crestline and Defects) Combining Deep Learning and Skeletonization from DEM-Derived Data. Geomorphology 2024, 463, 109369. [Google Scholar] [CrossRef]
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Jiang, S.; Sweet, L.-B.; Blougouras, G.; Brenning, A.; Li, W.; Reichstein, M.; Denzler, J.; Shangguan, W.; Yu, G.; Huang, F.; et al. How Interpretable Machine Learning Can Benefit Process Understanding in the Geosciences. Earth’s Future 2024, 12, e2024EF004540. [Google Scholar] [CrossRef]
- Pike, R.J. The Geometric Signature: Quantifying Landslide-Terrain Types from Digital Elevation Models. Math. Geol. 1988, 20, 491–511. [Google Scholar] [CrossRef]
- Wang, Z.; Brenning, A. Unsupervised Active–Transfer Learning for Automated Landslide Mapping. Comput. Geosci. 2023, 181, 105457. [Google Scholar] [CrossRef]













| RF GDs | |||||
|---|---|---|---|---|---|
| Confusion Matrix (Training) | |||||
| Reference Data | Class Error | ||||
| OOB = 6.56% | Not Crest | Crest | |||
| AUC = 0.973 | Predicted | Not Crest | 605 | 31 | 0.049 |
| RMSEtest = 0.249 | Crest | 32 | 292 | 0.099 | |
| RF GDs + MRIs | |||||
| Confusion Matrix (Training) | |||||
| Reference Data | Class Error | ||||
| OOB = 5.31% | Not Crest | Crest | |||
| AUC = 0.995 | Predicted | Not Crest | 617 | 19 | 0.03 |
| RMSEtest = 0.153 | Crest | 32 | 292 | 0.099 | |
| Contingency Table | |||||
|---|---|---|---|---|---|
| Reference Data | Row Totals | ||||
| Not Crest | Crest | ||||
| Predicted | Not Crest | 412,434 | 9298 | 421,732 | |
| Crest | 6885 | 14,939 | 21,824 | ||
| Column Totals | 419,319 | 24,237 | 443,556 | ||
| Class Statistics | |||||
| Class | User’s Accuracy | Producer’s Accuracy | Overall Accuracy = 96.35% | ||
| Not Crest | 97.80% | 98.36% | Kappa2 = 0.629 | ||
| Crest | 68.45% | 61.64% | |||
| Average | 83.12% | 80.00% | |||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Trevisani, S.; Guth, P.L. Terrain Analysis According to Multiscale Surface Roughness in the Taklimakan Desert. Land 2024, 13, 1843. https://doi.org/10.3390/land13111843
Trevisani S, Guth PL. Terrain Analysis According to Multiscale Surface Roughness in the Taklimakan Desert. Land. 2024; 13(11):1843. https://doi.org/10.3390/land13111843
Chicago/Turabian StyleTrevisani, Sebastiano, and Peter L. Guth. 2024. "Terrain Analysis According to Multiscale Surface Roughness in the Taklimakan Desert" Land 13, no. 11: 1843. https://doi.org/10.3390/land13111843
APA StyleTrevisani, S., & Guth, P. L. (2024). Terrain Analysis According to Multiscale Surface Roughness in the Taklimakan Desert. Land, 13(11), 1843. https://doi.org/10.3390/land13111843








