Integrated PSInSAR and GNSS for 3D Displacement in the Wudongde Area
Abstract
:1. Introduction
2. Methodology
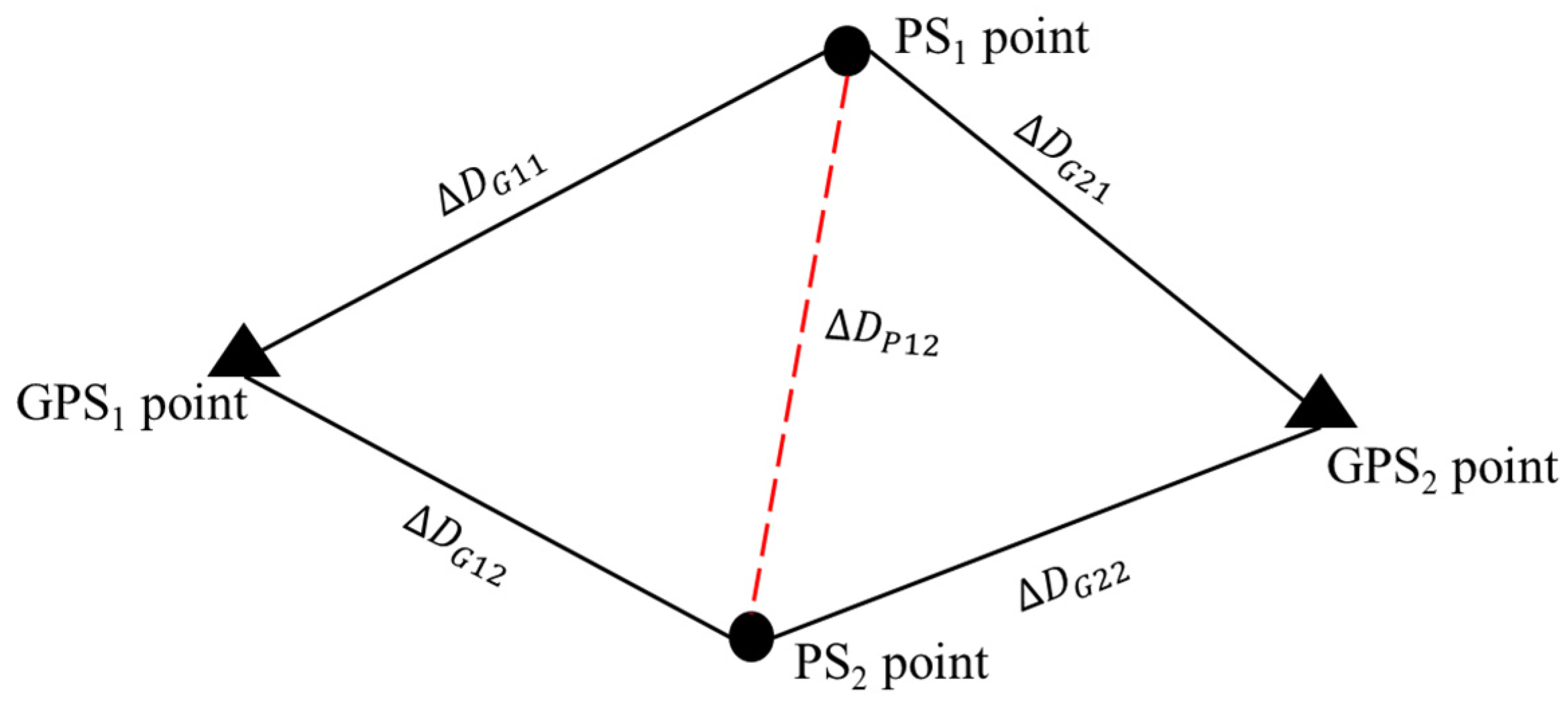
2.1. Algorithm for PSInSAR Technique Combined with GNSS Points
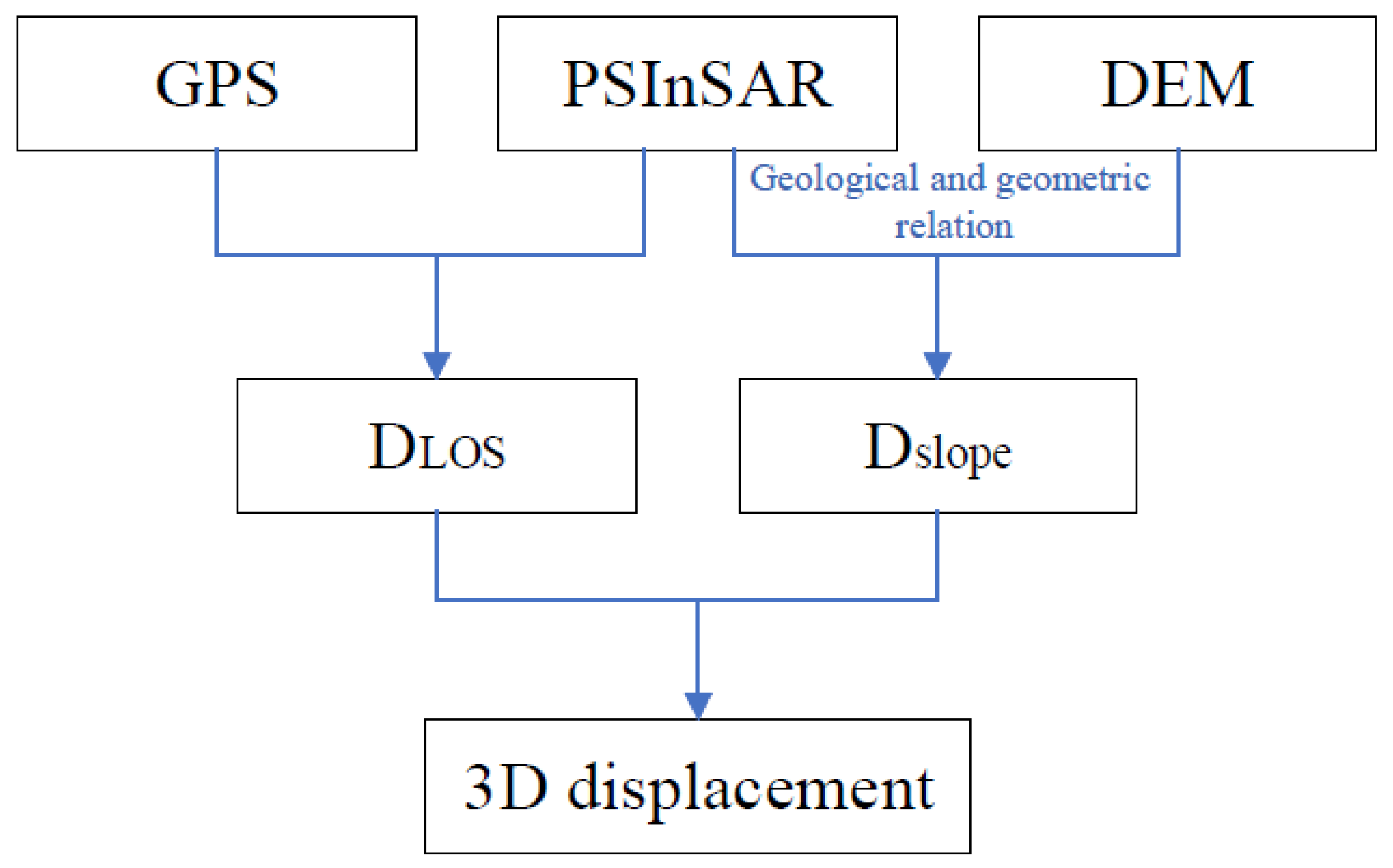
2.2. Algorithm for Calculating 3D Displacement
3. Experiment and Processing
3.1. Study Area
3.2. Dataset
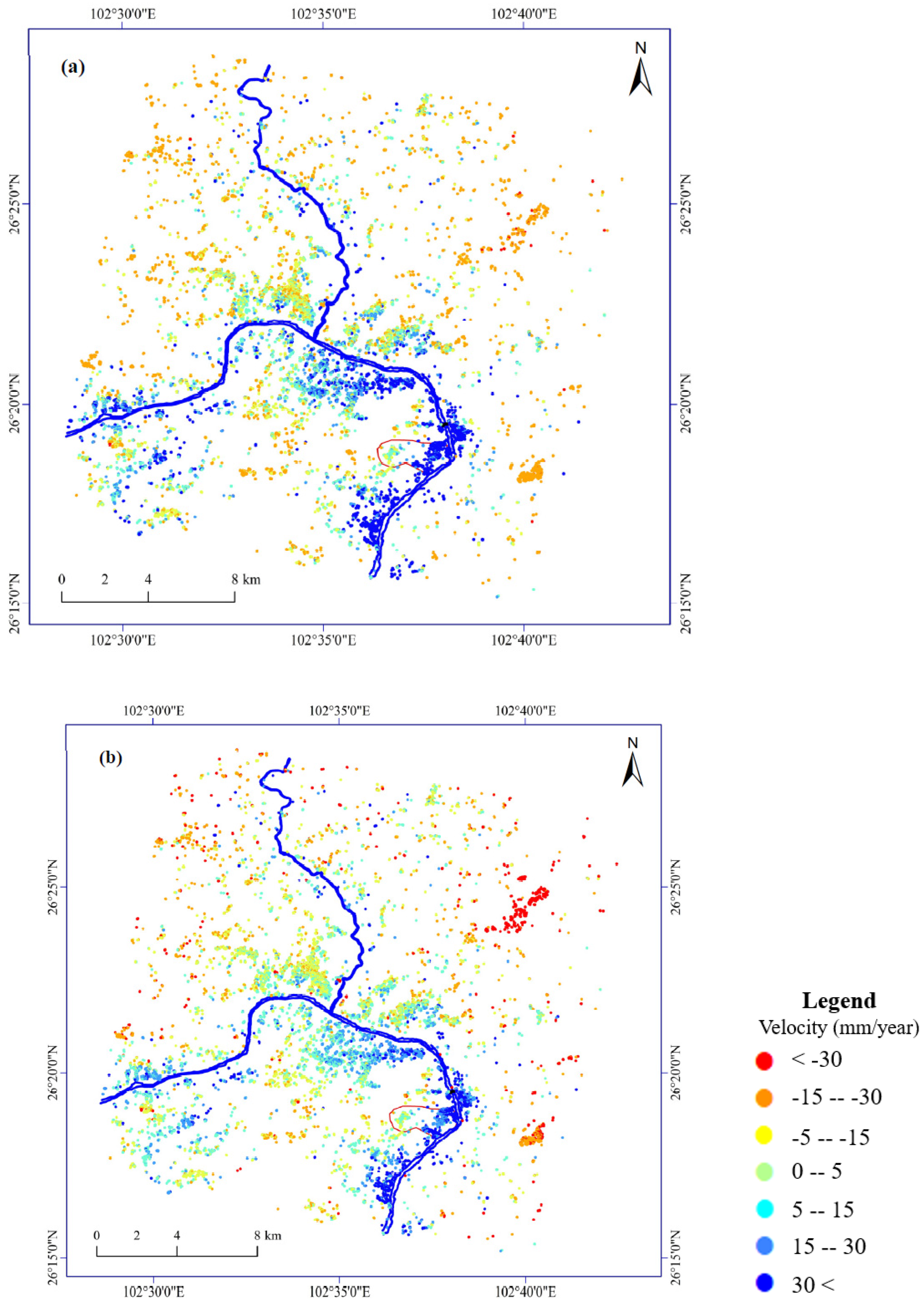
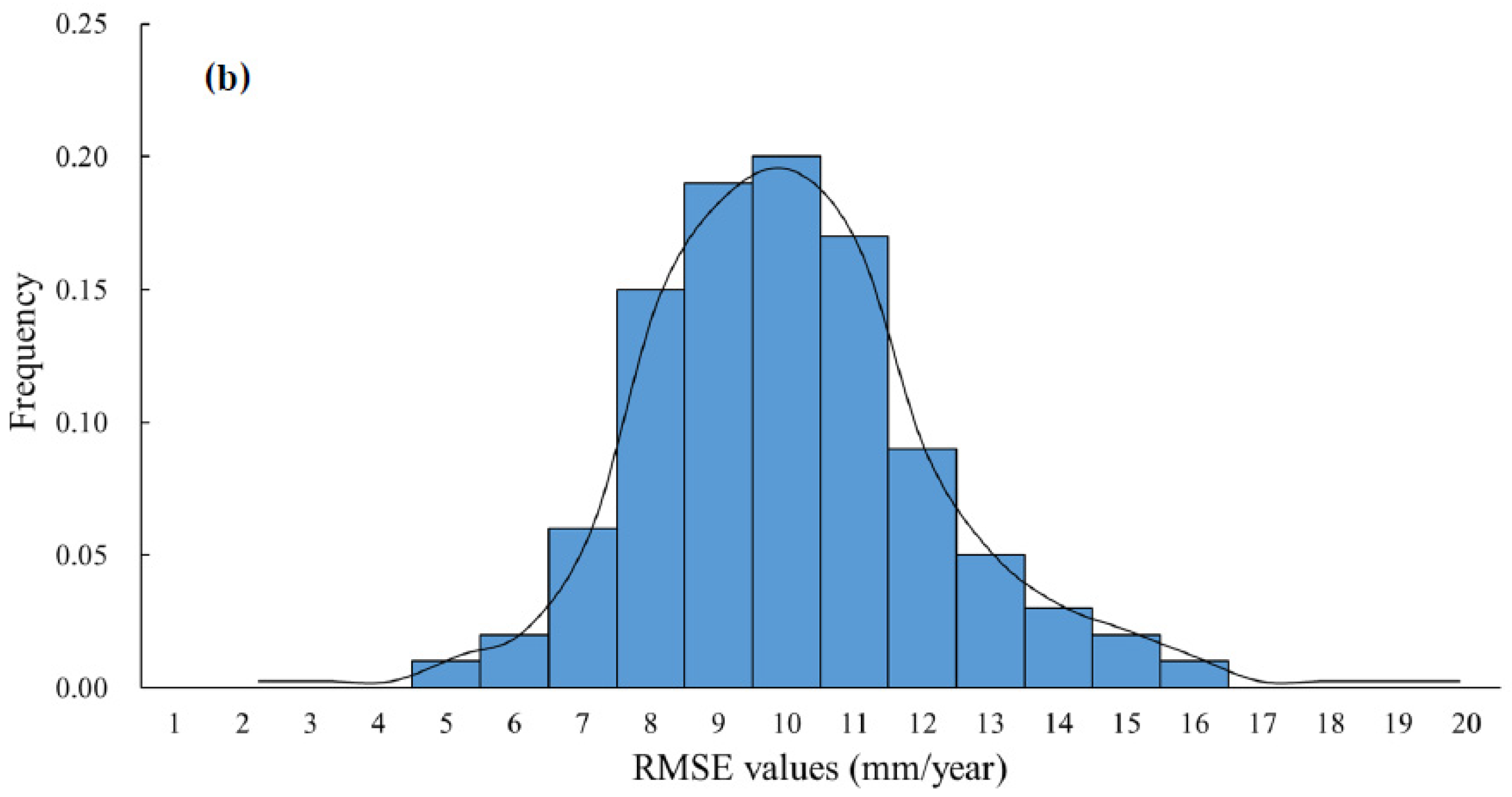
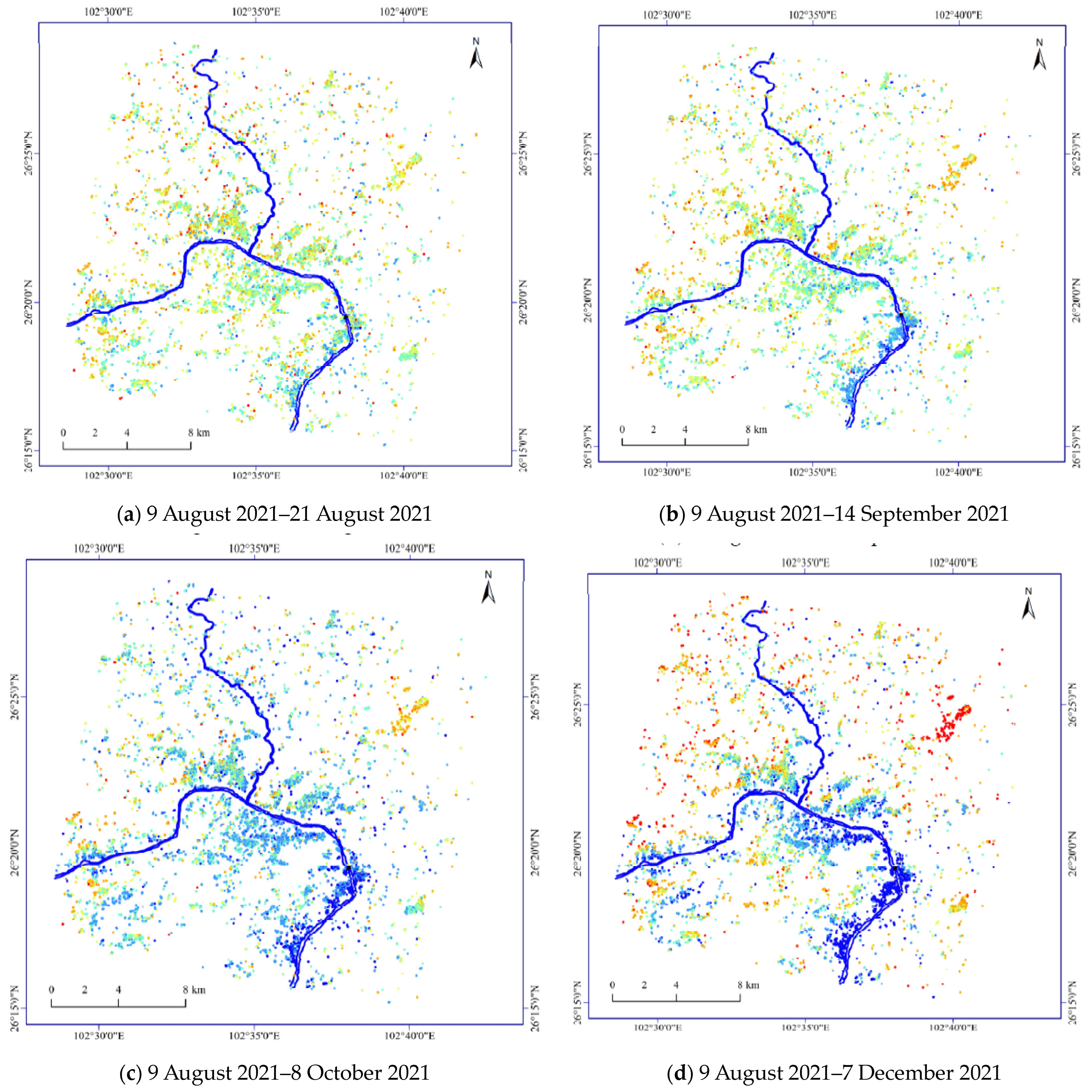
3.3. GNSS as Constraining Data in PSInSAR Processing
3.4. Three-Dimensional Displacement of Wudongde Area
3.5. Results
4. Discussion
5. Conclusions
- The accuracy of the deformation rate improved from 10 to 5 mm/year after incorporating PSInSAR with GNSS as the constraining data. The PS–GNSS network can help remove residual phase and height corrections in spatiotemporal unwrapping.
- Geological conditions were used to calculate the 3D displacement. Based on the relationship between InSAR geometric features and geological conditions, was proposed to calculate the 3D displacement using PSInSAR observations. The value was converted into vertical, east, and north displacements with maximum values of 11.5, 25.3, and 20.5 cm over the study period, respectively. The vertical direction was not the main sliding direction in the Wudongde area, and the north and east displacements were 2–3 times larger than that in the vertical direction.
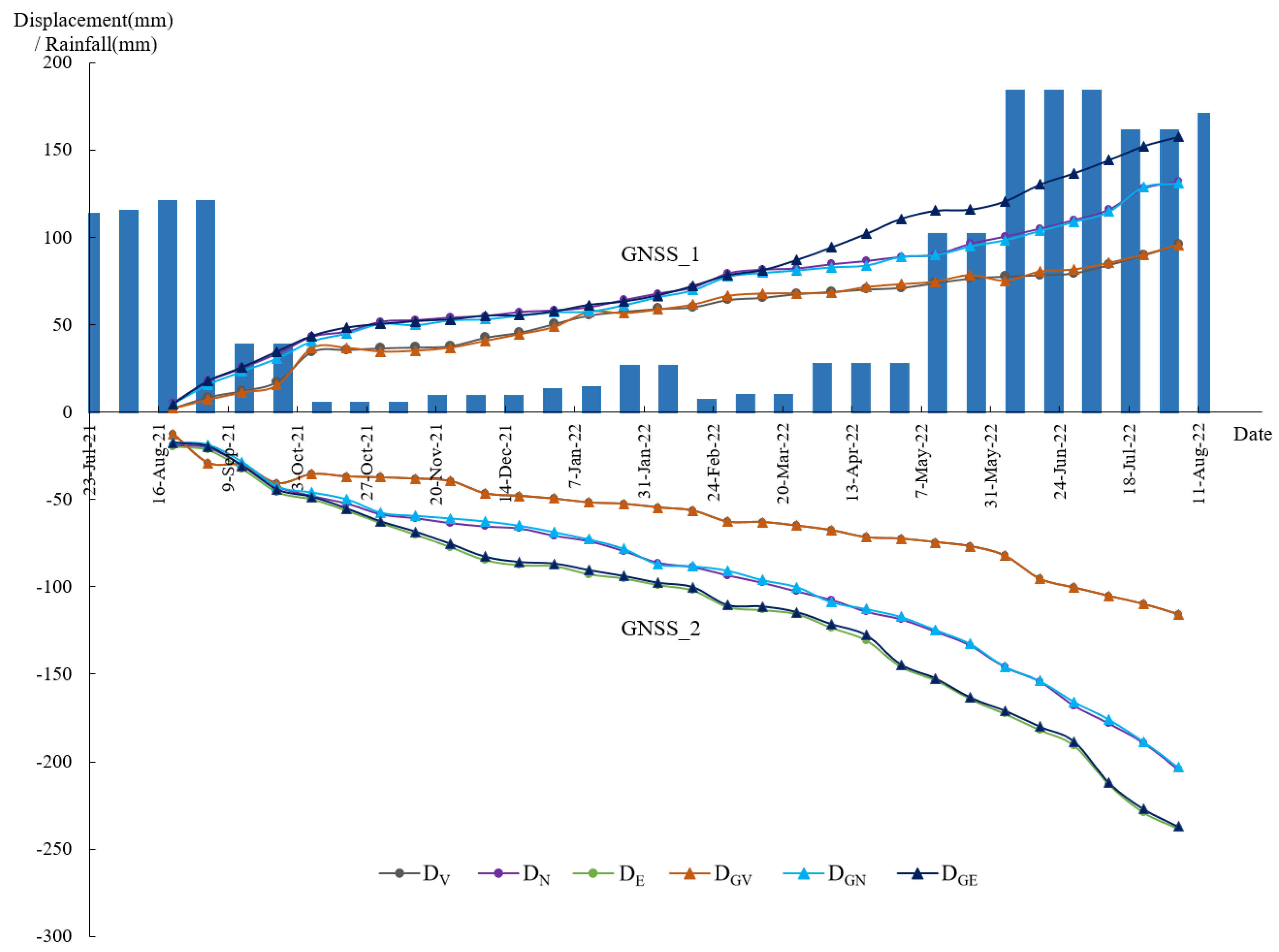
- The response time of the 3D displacement to rainfall exhibited hysteresis. Vertical displacement was the earliest response, occurring half a month after the rainfall season. The highest average deformation rate occurred in mid-October.
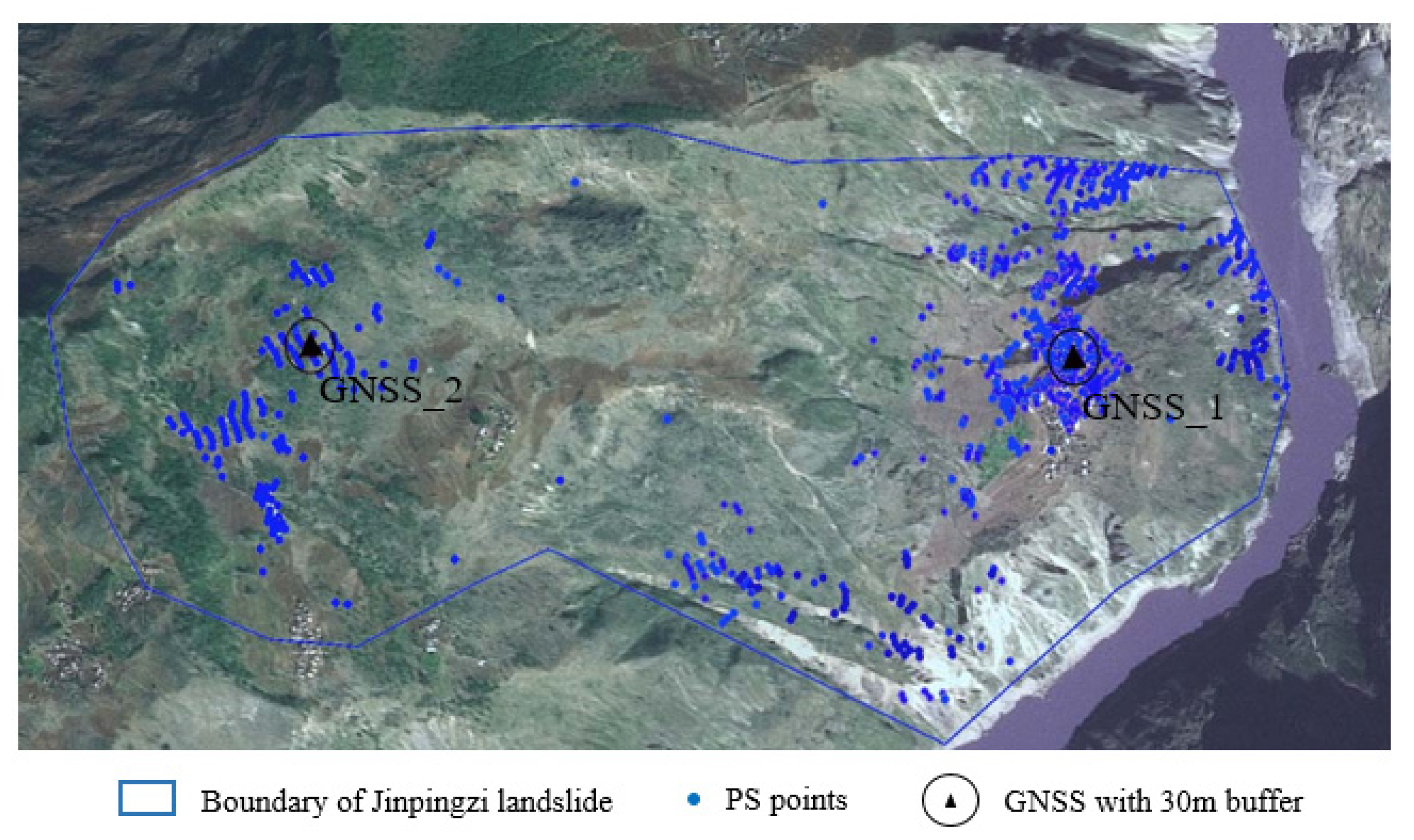
- When compared to the vertical displacement from the GNSS in the Jinpingzi landslide, the calculated 3D displacement from PSInSAR was proven to have high accuracy, and the deformation mechanism of the Jinpingzi landslide was analyzed. The sliding started at the toe of the slide and extended to the crown of the slide.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Refice, A.; Spalluto, L.; Bovenga, F.; Fiore, A.; Miccoli, M.N.; Muzzicato, P.; Nitti, D.O.; Nutricato, R.; Pasquariello, G. Integration of persistent scatterer interferometry and ground data for landslide monitoring: The Pianello landslide (Bovino, Southern Italy). Landslides 2019, 16, 447–468. [Google Scholar] [CrossRef]
- Jo, M.J.; Jung, H.S.; Won, J.S. Detecting the Source Location of Recent Summit Inflation via Three-Dimensional InSAR Observation of Kilauea Volcano. Remote Sens. 2015, 7, 14386–14402. [Google Scholar] [CrossRef]
- Hu, J.; Shi, J.W.; Liu, J.H.; Zheng, W.J.; Zhu, K. Calculating Co-Seismic Three-Dimensional Displacements from InSAR Observations with the Dislocation Model-Based Displacement Direction Constraint: Application to the 23 July 2020 Mw6.3 Nima Earthquake, China. Remote Sens. 2022, 14, 4481. [Google Scholar] [CrossRef]
- Hamdi, L.; Defaflia, N.; Merghadi, A.; Fehdi, C.; Yunus, A.P.; Dou, J.; Pham, Q.B.; Abdo, H.G.; Almohamad, H.; Al-Mutiry, M. Ground Surface Deformation Analysis Integrating InSAR and GNSS Data in the Karstic Terrain of Cheria Basin, Algeria. Remote Sens. 2023, 15, 1486. [Google Scholar] [CrossRef]
- Zhao, Y.; Wang, H.; Zhang, Q.; Zhang, D.; Xie, Y.; Yang, J. A study of landslide deformation fields with a digital correlation method. Nat. Hazards 2017, 89, 859–869. [Google Scholar] [CrossRef]
- Yin, Y.; Liu, X.; Zhao, C.; Tomás, R.; Zhang, Q.; Lu, Z.; Li, B. Multi-dimensional and long-term time series monitoring and early warning of landslide hazard with improved cross-platform SAR offset tracking method. Sci. China Technol. Sci. 2022, 65, 1891–1912. [Google Scholar] [CrossRef]
- Lei, K.C.; Ma, F.; Chen, B.; Luo, Y.; Cui, W.; Zhou, Y.; Liu, H.; Sha, T. Three-Dimensional Surface Deformation Characteristics Based on Time Series InSAR and GNSS Technologies in Beijing, China. Remote Sens. 2021, 13, 3964. [Google Scholar] [CrossRef]
- Liu, Y.H.; Wang, G.Q.; Yu, X.; Wang, K. Sentinel-1 InSAR and GNSS-Integrated Long-Term and Seasonal Subsidence Monitoring in Houston, Texas, USA. Remote Sens. 2022, 14, 6184. [Google Scholar] [CrossRef]
- Ma, Y.Y.; Li, F.; Wang, Z.M.; Zou, X.Q.; An, J.C.; Li, B. Landslide Assessment and Monitoring along the Jinsha River, Southwest China, by Combining InSAR and GNSS Techniques. J. Sens. 2022, 2022, 9572937. [Google Scholar] [CrossRef]
- Ferretti, A.; Prati, C.; Rocca, F. Permanent Scatterers in SAR Interferomerty. IEEE Trans. Geosci. Remote Sens. 2001, 39, 8–20. [Google Scholar] [CrossRef]
- Berardino, P.; Gianfranco, F.; Riccardo, L.; Eugenio, S. A new algorithm for surface deformation monitoring based on small baseline differential SAR interferograms. IEEE Trans. Geosci. Remote Sens. 2002, 40, 2375–2383. [Google Scholar] [CrossRef]
- Komac, M.; Holley, R.; Mahapatra, P.; van der Marel, H.; Bavec, M. Coupling of GNSS/GNSS and radar interferometric data for a 3D surface displacement monitoring of landslides. Landslides 2015, 12, 241–257. [Google Scholar] [CrossRef]
- Song, X.G.; Jiang, Y.; Shan, X.J.; Qu, C.Y. Deriving 3D coseismic deformation field by combining GNSS and InSAR data based on the elastic dislocation model. Int. J. Appl. Earth Obs. Geoinf. 2017, 57, 104–112. [Google Scholar] [CrossRef]
- Chen, M.K.; Xu, G.Y.; Zhang, T.X.; Xie, X.W.; Chen, Z.P. A novel method for inverting coseismic 3D surface deformation using InSAR considering the weight influence of the spatial distribution of GNSS points. Adv. Space Res. 2024, 73, 585–596. [Google Scholar] [CrossRef]
- Zhang, Z.W.; Wang, X.L.; Wu, Y.D.; Zhao, Z.P.; Yang, E. Applied Research on InSAR and GNSS Data Fusion in Deformation Monitoring. Sci. Program. 2021, 2021, 3888975. [Google Scholar]
- Chen, Q.A.; Liu, G.X.; Ding, X.L.; Hu, J.C.; Yuan, L.G.; Zhong, P.; Omura, M. Tight integration of GNSS observations and persistent scatterer InSAR for detecting vertical ground motion in Hong Kong. Int. J. Appl. Earth Obs. 2010, 12, 477–486. [Google Scholar]
- Shi, X.G.; Zhang, L.; Zhou, C.; Li, M.H.; Liao, M.S. Retrieval of time series three-dimensional landslide surface displacements from multi-angular SAR observations. Landslides 2018, 15, 1015–1027. [Google Scholar] [CrossRef]
- Xiong, L.Y.; Xu, C.J.; Liu, Y.; Wen, Y.M.; Fang, J. 3D Displacement Field of Wenchuan Earthquake Based on Iterative Least Squares for Virtual Observation and GNSS/InSAR Observations. Remote Sens. 2020, 12, 977. [Google Scholar] [CrossRef]
- Ren, K.Y.; Yao, X.; Li, R.J.; Zhou, Z.K.; Yao, C.C.; Jiang, S. 3D displacement and deformation mechanism of deep-seated gravitational slope deformation revealed by InSAR: A case study in Wudongde Reservoir, Jinsha River. Landslides 2022, 19, 2159–2175. [Google Scholar] [CrossRef]
- Hu, J.; Li, Z.W.; Ding, X.L.; Zhu, J.J.; Zhang, L.; Sun, Q. 3D coseismic Displacement of 2010 Darfield, New Zealand earthquake estimated from multi-aperture InSAR and D-InSAR measurements. J. Geod. 2012, 86, 1029–1041. [Google Scholar] [CrossRef]
- Dematteis, N.; Wrzesniak, A.; Allasia, P.; Bertolo, D.; Giordan, D. Integration of robotic total station and digital image correlation to assess the three-dimensional surface kinematics of a landslide. Eng. Geol. 2022, 303, 106655. [Google Scholar] [CrossRef]
- Rodriguez, J.; Deane, E.; Hendry, M.T.; Macciotta, R.; Evans, T.; Gräpel, C.; Skirrow, R. Practical evaluation of single-frequency dGNSS for monitoring slow-moving landslides. Landslides 2021, 18, 3671–3684. [Google Scholar]
- Corsini, A.; Bonacini, F.; Mulas, M.; Ronchetti, F.; Monni, A.; Pignone, S.; Primerano, S.; Bertolini, G.; Caputo, G.; Truffelli, G.; et al. A portable continuous GPS array used as rapid deployment monitoring system during landslide emergencies in Emilia Romagna. Rend. Online Soc. Geol. Ital. 2015, 35, 89–91. [Google Scholar] [CrossRef]
- Simons, W.; Broerse, T.; Shen, L.; Kleptsova, O.; Nijholt, N.; Hooper, A.; Pietrzak, J.; Morishita, Y.; Naeije, M.; Lhermitte, S.; et al. A Tsunami Generated by a Strike-Slip Event: Constraints From GPS and SAR Data on the 2018 Palu Earthquake. J. Geophys. Res. Solid Earth 2022, 127, e2022JB024191. [Google Scholar] [CrossRef]
- Zambanini, C.; Reinprecht, V.; Kieffer, D.S. InSARTrac Field Tests-Combining Computer Vision and Terrestrial InSAR for 3D Displacement Monitoring. Remote Sens. 2023, 15, 2031. [Google Scholar] [CrossRef]
- Hu, J.; Li, Z.W.; Ding, X.L.; Zhu, J.J.; Zhang, L.; Sun, Q. Resolving three-dimensional surface displacements from InSAR measurements: A review. Earth-Sci. Rev. 2014, 133, 1–17. [Google Scholar] [CrossRef]
- Bickel, V.T.; Manconi, A.; Amann, F. Quantitative Assessment of Digital Image Correlation Methods to Detect and Monitor Surface Displacements of Large Slope Instabilities. Remote Sens. 2018, 10, 865. [Google Scholar] [CrossRef]
- Xu, K.; Gan, W.; Wu, J.; Hou, Z. A robust method for 3D surface displacement fields combining GNSS and single-orbit InSAR measurements with directional constraint from elasticity model. GPS Solut. 2022, 26, 46. [Google Scholar] [CrossRef]
- Ciampalini, A.; Raspini, F.; Lagomarsino, D.; Catani, F.; Casagli, N. Landslide susceptibility map refinement using PSInSAR data. Remote Sens. Environ. 2016, 184, 302–315. [Google Scholar] [CrossRef]
- Yuan, M.Z.; Li, M.; Liu, H.; Lv, P.Y.; Li, B.; Zheng, W.B. Subsidence Monitoring Base on SBAS-InSAR and Slope Stability Analysis Method for Damage Analysis in Mountainous Mining Subsidence Regions. Remote Sens. 2021, 13, 3107. [Google Scholar] [CrossRef]
- Yin, Y.P.; Zheng, W.M.; Liu, Y.P.; Zhang, J.L.; Li, X.C. Integration of GPS with InSAR to monitoring of the Jiaju landslide in Sichuan, China. Landslides 2010, 7, 359–365. [Google Scholar] [CrossRef]
- Teshebaeva, K.; Roessner, S.; Echtler, H.; Motagh, M.; Wetzel, H.U.; Molodbekov, B. ALOS/PALSAR InSAR Time-Series Analysis for Detecting Very Slow-Moving Landslides in Southern Kyrgyzstan. Remote Sens. 2015, 7, 8973–8994. [Google Scholar] [CrossRef]
- Xing, X.M.; Zhu, J.J.; Wang, Y.Z.; Yang, Y.F. Time series ground subsidence inversion in mining area based on CRInSAR and PSInSAR integration. J. Cent. South Univ. 2013, 20, 2498–2509. [Google Scholar] [CrossRef]
- Dai, Z.L.; Huang, Y.; Cheng, H.L.; Xu, Q. 3D numerical modeling using smoothed particle hydrodynamics of flow-like landslide propagation triggered by the 2008 Wenchuan earthquake. Eng. Geol. 2014, 180, 21–33. [Google Scholar] [CrossRef]
- Franz, M.; Carrea, D.; Abellan, A.; Derron, M.H.; Jaboyedoff, M. Use of targets to track 3D displacements in highly vegetated areas affected by landslides. Landslides 2016, 13, 821–831. [Google Scholar] [CrossRef]
- Gojcic, Z.; Schmid, L.; Wieser, A. Dense 3D displacement vector fields for point cloud-based landslide monitoring. Landslides 2021, 18, 3821–3832. [Google Scholar] [CrossRef]
- Salih, W.H.M.; Soons, J.A.M.; Dirckx, J.J.J. 3D displacement of the middle ear ossicles in the quasi-static pressure regime using new X-ray stereoscopy technique. Hear. Res. 2016, 340, 60–68. [Google Scholar] [CrossRef]
- Donati, D.; Rabus, B.; Engelbrecht, J.; Stead, D.; Clague, J.; Francioni, M. A Robust SAR Speckle Tracking Workflow for Measuring and Interpreting the 3D Surface Displacement of Landslides. Remote Sens. 2021, 13, 3048. [Google Scholar] [CrossRef]
- Eriksen, H.O.; Bergh, S.G.; Larsen, Y.; Skrede, I.; Kristensen, L.; Lauknes, T.R.; Blikra, L.H.; Kierulf, H.P. Relating 3D surface displacement from satellite- and ground-based InSAR to structures and geomorphology of the Jettan rockslide, northern Norway. Nor. J. Geol. 2017, 97, 283–303. [Google Scholar] [CrossRef]
- Xiong, L.Y.; Xu, C.J.; Liu, Y.; Zhao, Y.W.; Geng, J.H.; Francisco, O.C. Three-dimensional displacement field of the 2010 Mw 8.8 Maule earthquake from GNSS and InSAR data with the improved ESISTEM-VCE method. Front. Earth Sci. 2022, 10, 970493. [Google Scholar] [CrossRef]
- Xie, M.W.; Huang, J.X.; Wang, L.W.; Huang, J.H.; Wang, Z.F. Early landslide detection based on D-InSAR technique at the Wudongde hydropower reservoir. Environ. Earth Sci. 2016, 75, 717. [Google Scholar] [CrossRef]
- Huang, J.X.; Xie, M.W.; Atkinson, P.M. Dynamic susceptibility mapping of slow-moving landslides using PSInSAR. Int. J. Remote Sens. 2020, 41, 7509–7529. [Google Scholar]
- Jiang, S.; Wang, Y.F.; Tang, C.; Pan, H.; Wang, K. Preliminary study of the creep mechanism of Jinpingzi zone II slow moving landslide in lower reaches of Jinsha River. J. Eng. Geol. 2017, 25, 1547–1556. [Google Scholar]
- Jiang, S.; Wang, Y.F.; Tang, C.; Liu, K. Long-term kinematics and mechanism of a deep-seated slow-moving debris slide near Wudongde hydropower station in Southwest China. J. Mt. Sci. 2018, 15, 364–379. [Google Scholar] [CrossRef]
- Ettazarini, S. GIS-based land suitability assessment for check dam site location, using topography and drainage information: A case study from Morocco. Environ. Earth Sci. 2021, 80, 567. [Google Scholar] [CrossRef]
- Highland, L.; Bobrowsky, P.T. The Landslide Handbook—A Guide to Understanding Landslides; US Geological Survey: Reston, VA, USA, 2008; pp. 1–47.
- Fey, C.; Rutzinger, M.; Wichmann, V.; Prager, C.; Bremer, M.; Zangerl, C. Deriving 3D displacement vectors from multi-temporal airborne laser scanning data for landslide activity analyses. GISci. Remote Sens. 2015, 52, 437–461. [Google Scholar] [CrossRef]
- Guglielmino, F.; Anzidei, M.; Briole, P.; Elias, P.; Puglisi, G. 3D displacement maps of the 2009 L’Aquila earthquake (Italy) by applying the SISTEM method to GNSS and DInSAR data. Terra Nova 2013, 25, 79–85. [Google Scholar] [CrossRef]
- Bovenga, F.; Pasquariello, G.; Pellicani, R.; Refice, A.; Spilotro, G. Landslide monitoring for risk mitigation by using corner reflector and satellite SAR interferometry: The large landslide of Carlantino (Italy). CATENA 2017, 151, 49–62. [Google Scholar] [CrossRef]
- Mazzanti, P.; Caporossi, P.; Muzi, R. Sliding Time Master Digital Image Correlation Analyses of CubeSat Images for landslide Monitoring: The Rattlesnake Hills Landslide (USA). Remote Sens. 2020, 12, 592. [Google Scholar] [CrossRef]
- Budimir, M.; Atkinson, P.M.; Lewis, H. A systematic review of landslide probability mapping using logistic regression. Landslides 2015, 12, 419–436. [Google Scholar] [CrossRef]
- Huang, Y.T.; Li, W.; Jiang, X. Co-seismic deformation field of the 2020 Nima Tibet Earthquake and fault slip distribution. Bull. Surv. Mapp. 2021, S1, 173–177. [Google Scholar] [CrossRef]
- Li, K.; Li, Y.; Tapponnier, P.; Xu, X.; Li, D.; He, Z. Joint InSAR and Field Constraints on Faulting During the Mw 6.4, July 23, 2020, Nima/Rongma Earthquake in Central Tibet. J. Geophys. Res. Solid Earth 2021, 126, e2021JB022212. [Google Scholar]
- Wu, Q.; Liu, Y.X.; Tang, H.M.; Kang, J.T.; Wang, L.Q.; Li, C.D.; Wang, D.; Liu, Z.Q. Experimental study of the influence of wetting and drying cycles on the strength of intact rock samples from a red stratum in the Three Gorges Reservoir area. Eng. Geol. 2023, 314, 107013. [Google Scholar] [CrossRef]
- Fang, K.; Tang, H.M.; Li, C.D.; Su, X.X.; An, P.J.; Sun, S.X. Centrifuge modelling of landslides and landslide hazard mitigation: A review. Geosci. Front. 2023, 14, 101493. [Google Scholar] [CrossRef]
- Wang, C.; Wang, H.; Qin, W.; Wei, S.; Tian, H.; Fang, K. Behaviour of pile-anchor reinforced landslides under varying water level, rainfall, and thrust load: Insight from physical modelling. Eng. Geol. 2023, 325, 107293. [Google Scholar] [CrossRef]










Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, J.; Du, W.; Jin, S.; Xie, M. Integrated PSInSAR and GNSS for 3D Displacement in the Wudongde Area. Land 2024, 13, 429. https://doi.org/10.3390/land13040429
Huang J, Du W, Jin S, Xie M. Integrated PSInSAR and GNSS for 3D Displacement in the Wudongde Area. Land. 2024; 13(4):429. https://doi.org/10.3390/land13040429
Chicago/Turabian StyleHuang, Jiaxuan, Weichao Du, Shaoxia Jin, and Mowen Xie. 2024. "Integrated PSInSAR and GNSS for 3D Displacement in the Wudongde Area" Land 13, no. 4: 429. https://doi.org/10.3390/land13040429
APA StyleHuang, J., Du, W., Jin, S., & Xie, M. (2024). Integrated PSInSAR and GNSS for 3D Displacement in the Wudongde Area. Land, 13(4), 429. https://doi.org/10.3390/land13040429







