Changes in Surface Runoff and Temporal Dispersion in a Restored Montane Watershed on the Qinghai–Tibetan Plateau
Abstract
:1. Introduction
2. Materials and Methods
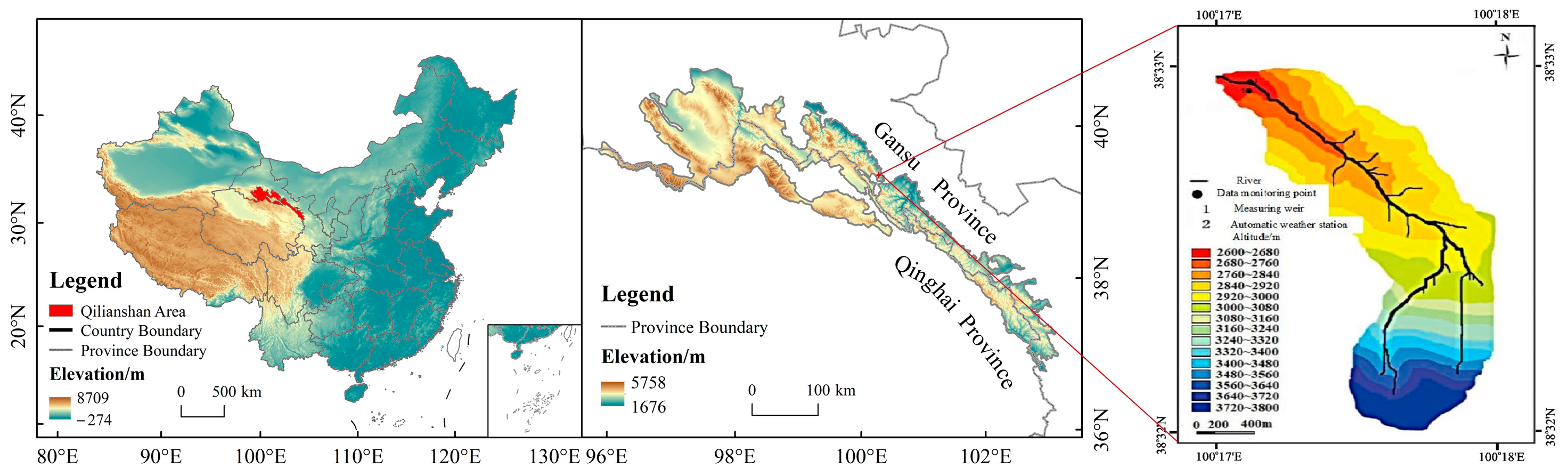
2.1. Study Area
2.2. Data
2.3. Research Methods
3. Results
3.1. Runoff Variation Characteristics of Pailugou Watershed
3.1.1. Statistical Characteristics of Runoff Series
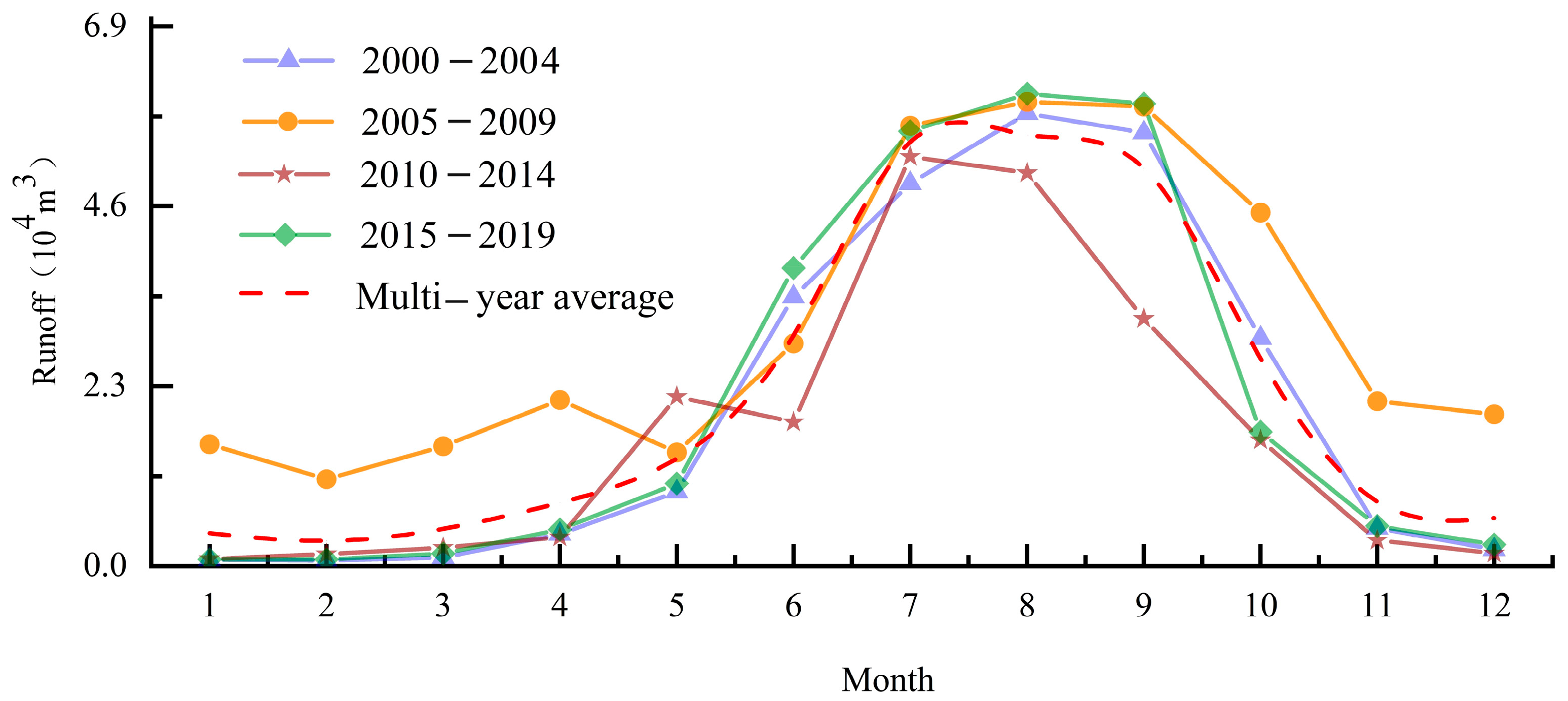
3.1.2. Variation Characteristics of Monthly Average Runoff
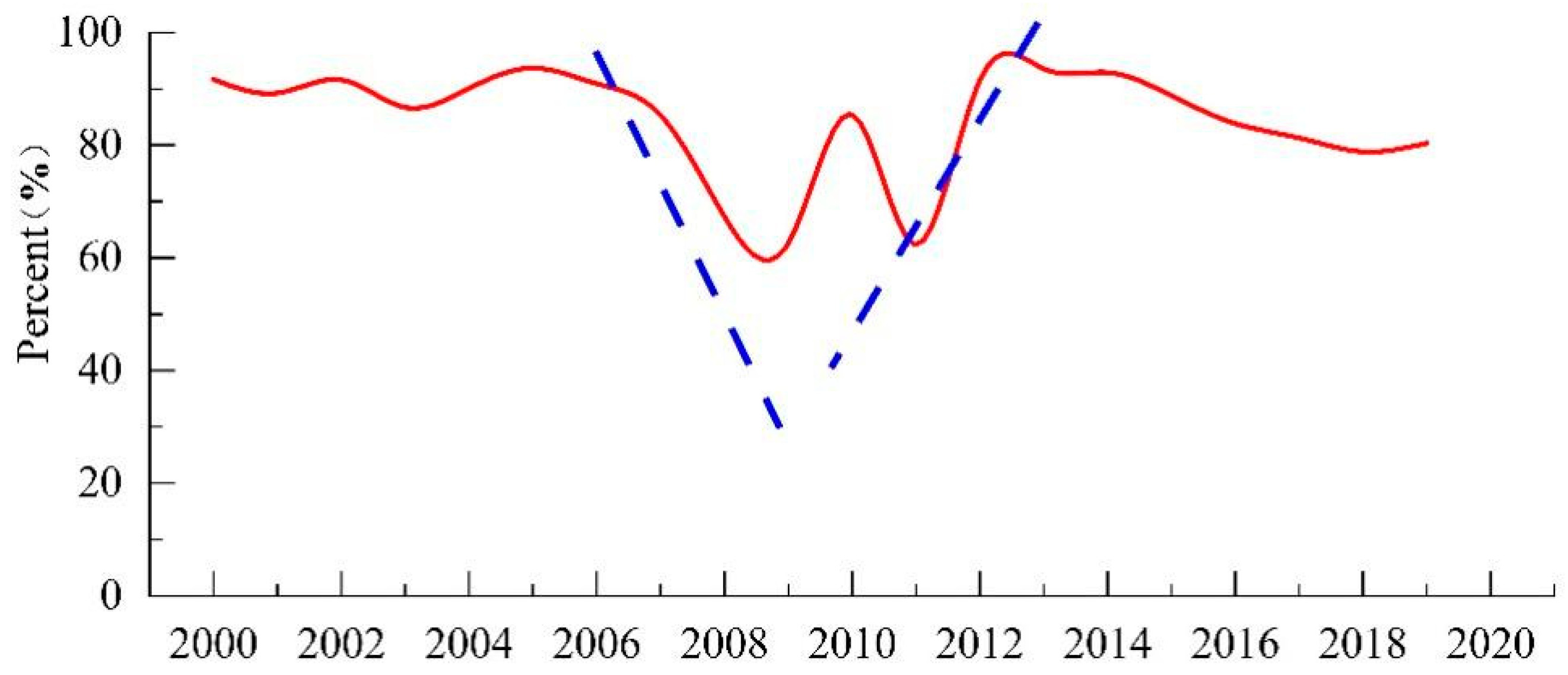
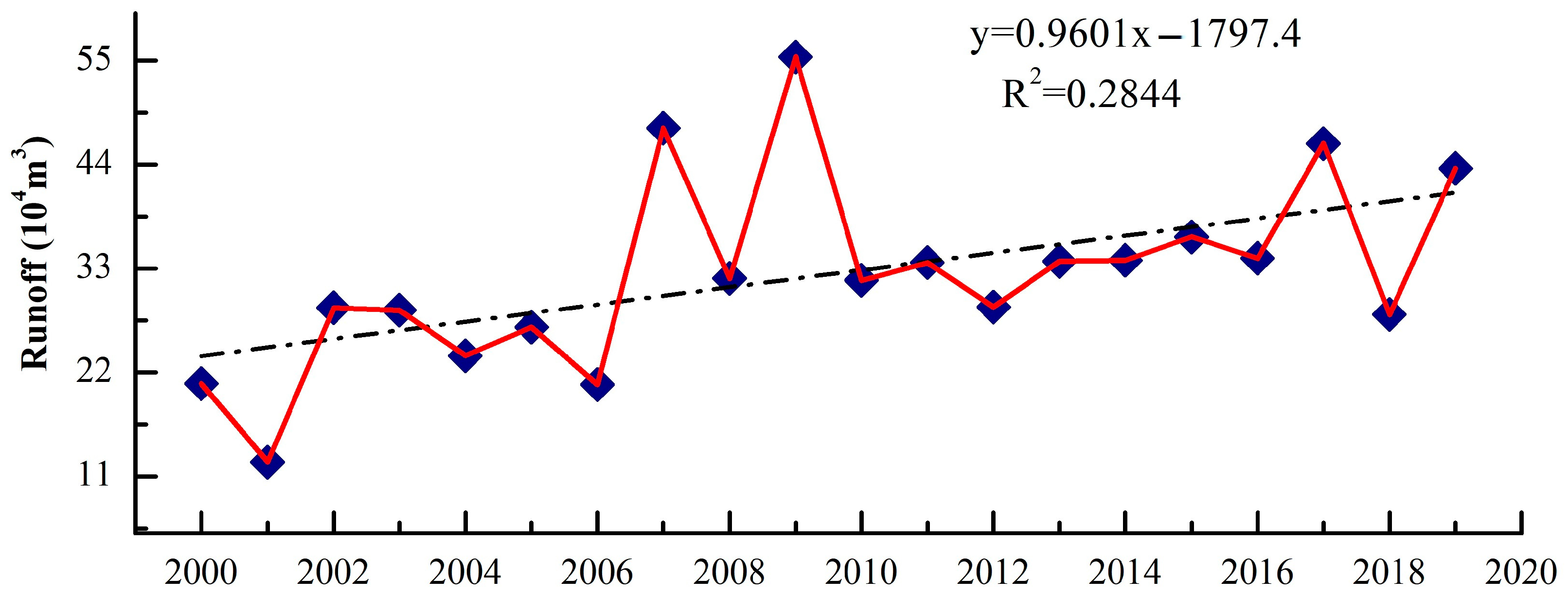
3.1.3. Annual Runoff Variation Characteristics
3.2. Climate Alteration in the Pailugou Basin
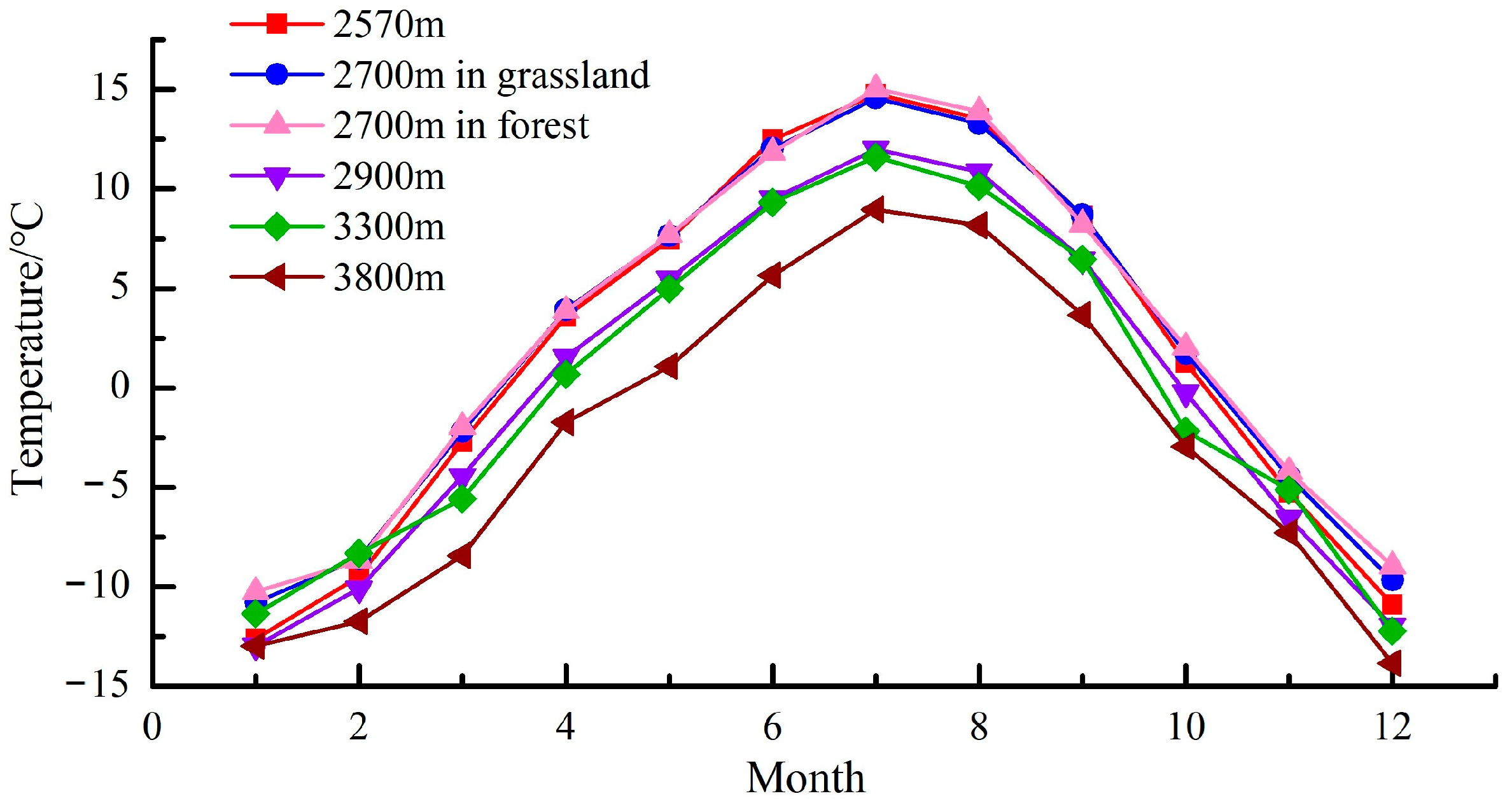
3.2.1. Air Temperature
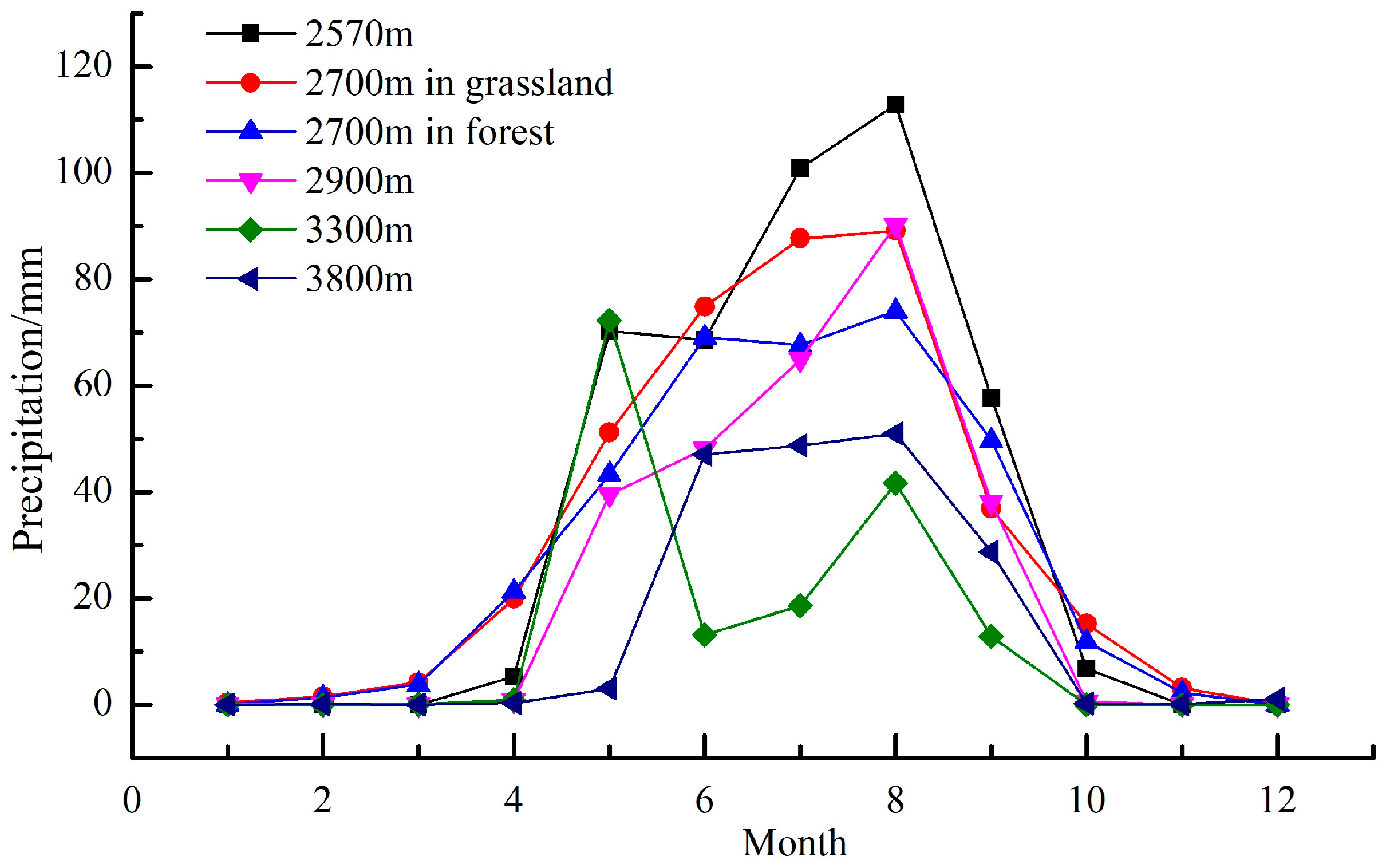
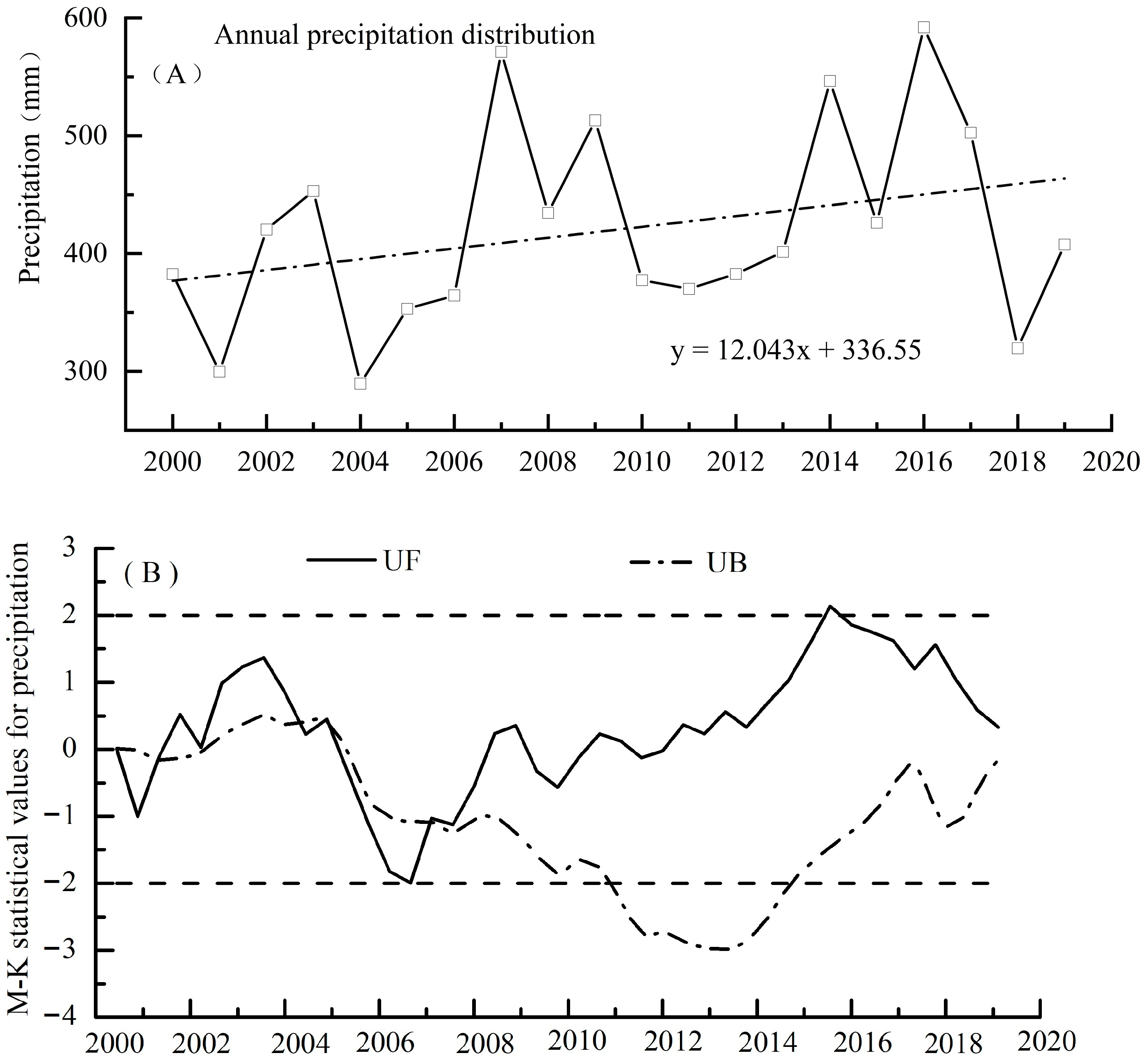
3.2.2. Atmospheric Precipitation
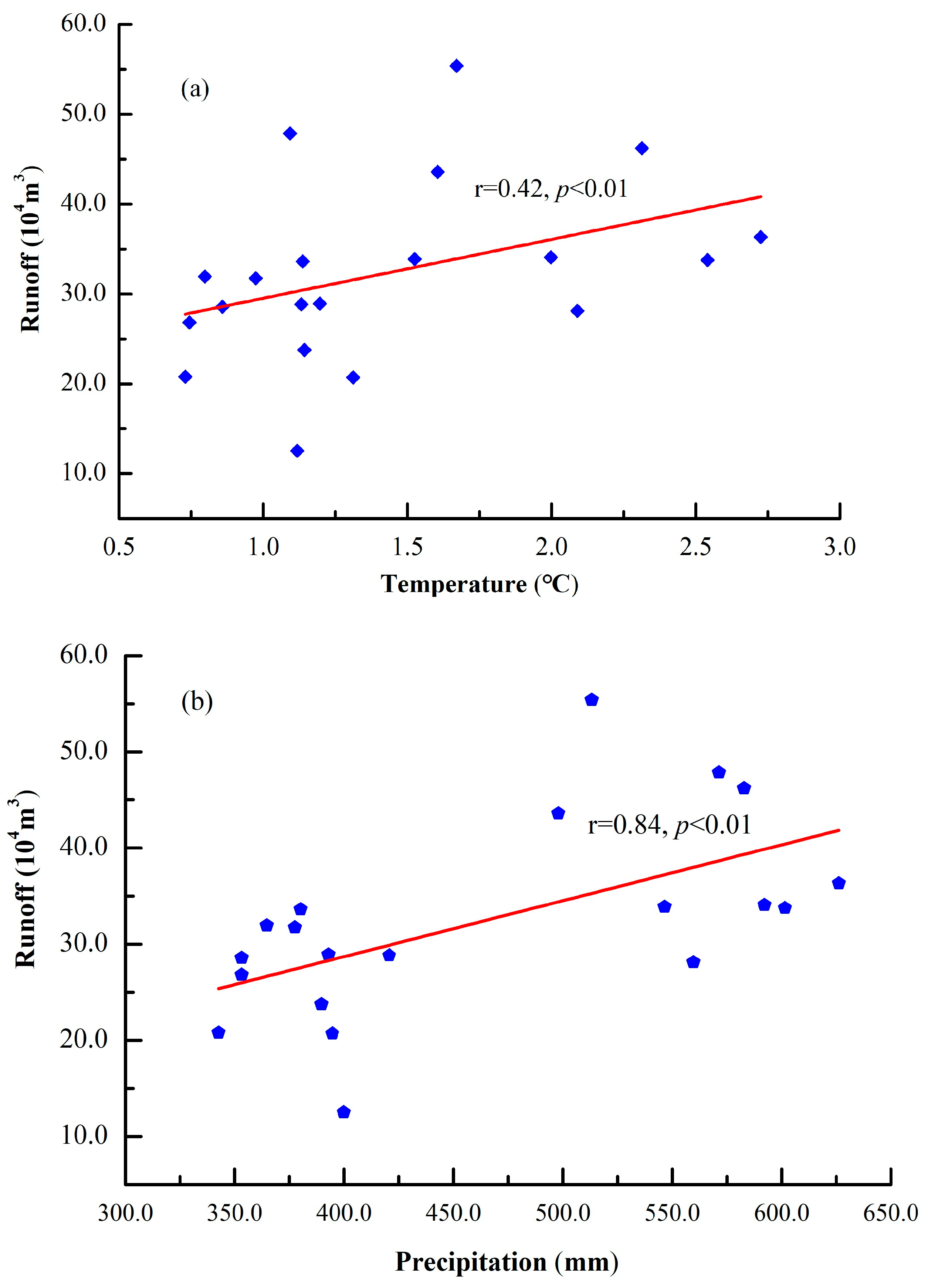
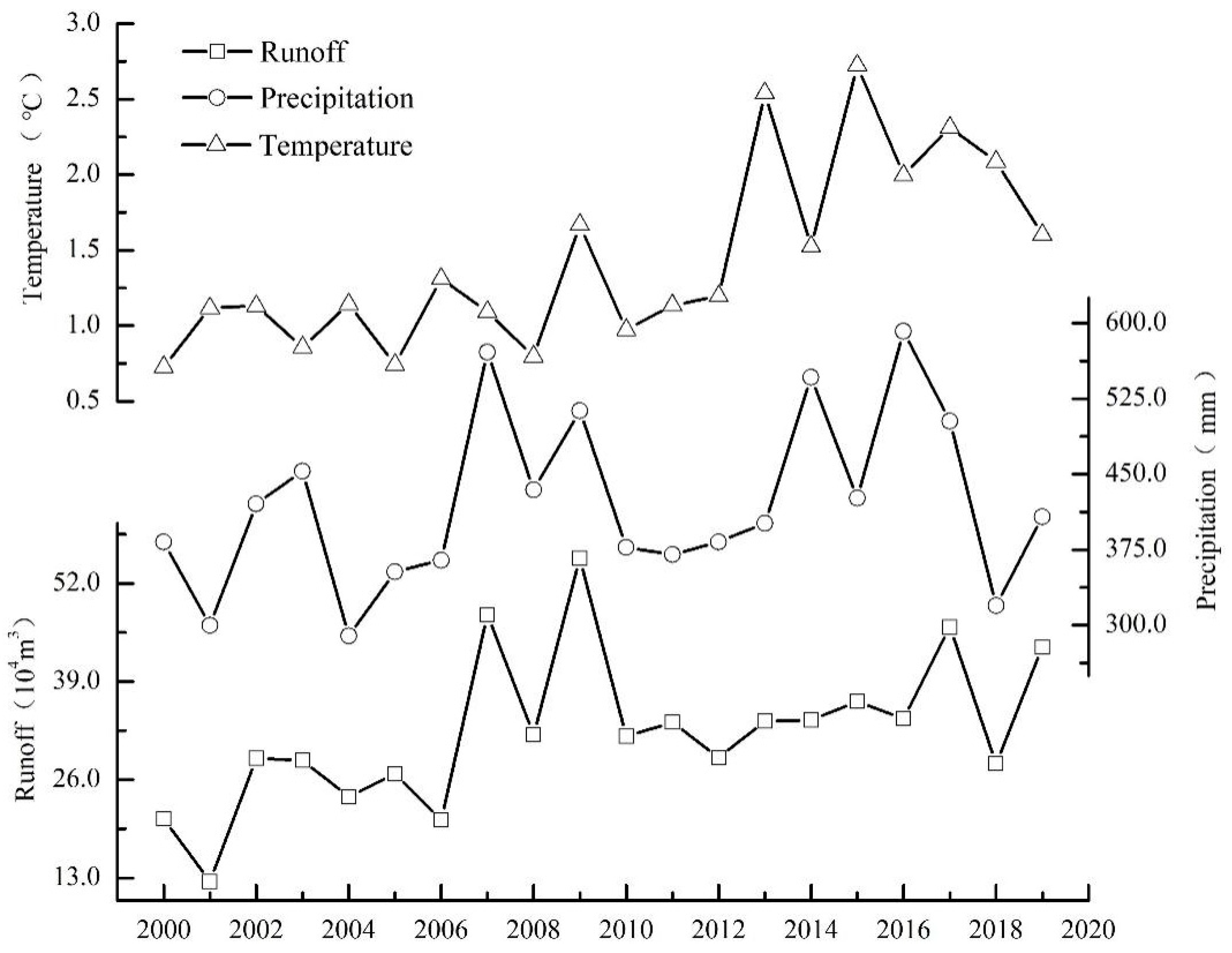
3.3. Relationships between Runoff, Temperature, and Precipitation
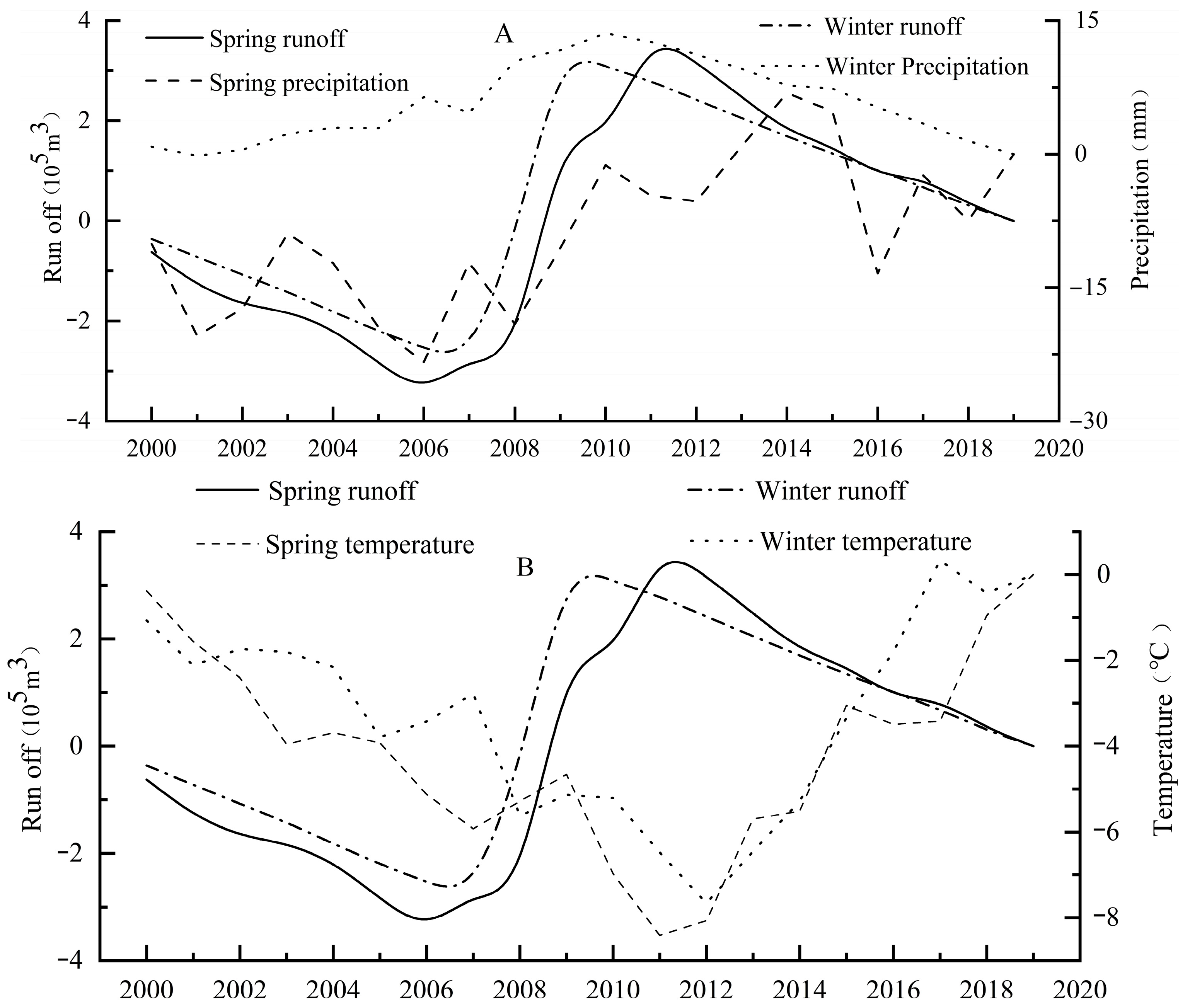
3.4. Response of Runoff to Climate
4. Discussion
5. Conclusions
- The annual surface runoff in the basin fluctuated over the 20-year period, but showed an overall upward trend, increasing by 3.94 × 105 m3, with an average increase rate of 0.42 × 105 m3/10a. The annual runoff series distribution of the Pailugou Basin in the Qilian Mountains was consistent with the basic characteristics of typical ice and snow basins, that is, the annual surface runoff distribution was relatively concentrated and positively biased, with a small dispersion degree, and the frequency of maximum and minimum values were relatively concentrated. Under the comprehensive influence of precipitation, temperature, and summer snowmelt (ice), the annual runoff distribution in the Pailugou Basin presents a unique “unimodal” curve and long runoff production time. The concentration of the runoff distribution was large, and the relative change amplitude exhibited a decreasing trend year by year.
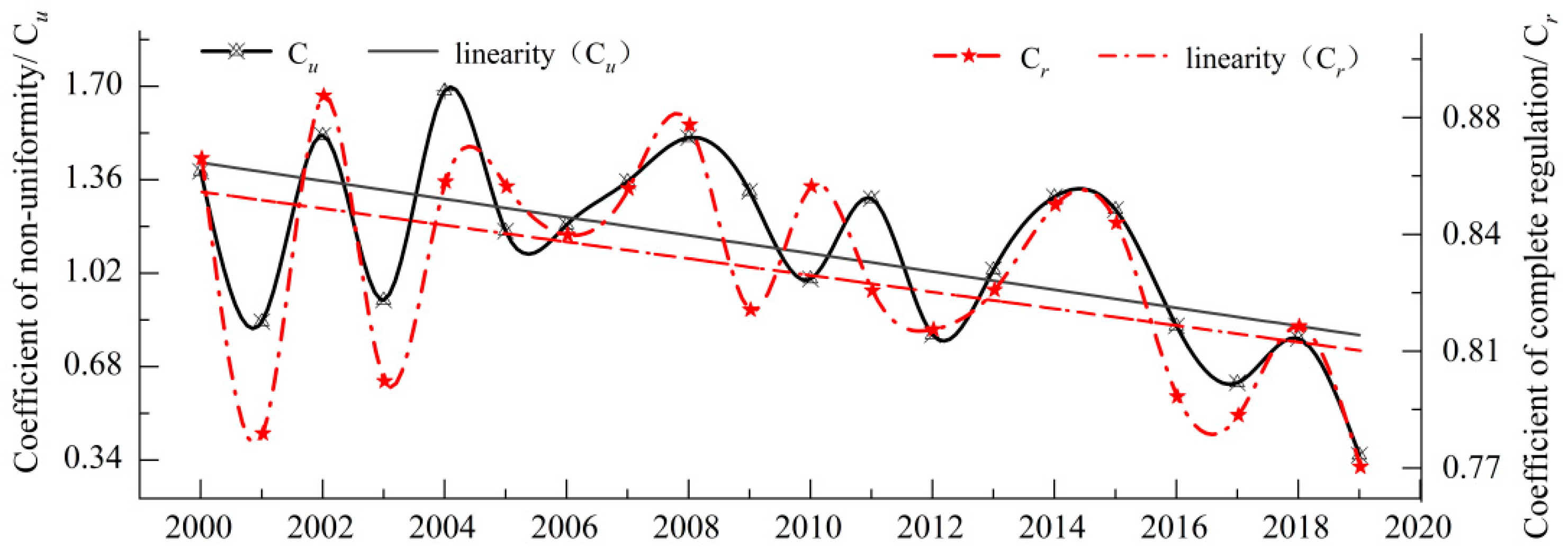
- The runoff from July to September accounted for 85.36% of the total. It was also found that the annual surface runoff in the basin fluctuated over the 20-year period but had an overall upward trend, increasing by 3.94 × 105 m3, with an average increase rate of 0.42 × 105 m3/10a. During 2006 to 2010, the annual runoff increased significantly and fluctuated greatly, forming an ‘M’-type change trend, with 2007 and 2009 as the peaks and 2008 as the valley. The maximum value of the annual distribution concentration Ci of runoff was 63.52%, corresponding to 231° in the vector direction, which appeared in 2000–2004, and the minimum value was 57.15%, corresponding to 227° in the vector direction, which appeared in 2015–2019, with an average value of 60.29%. The correlation between the runoff and precipitation was significantly high (r = 0.839, p < 0.05), whereas the correlation between air temperature and surface runoff was low (r = 0.421, p > 0.05), showing that the runoff was controlled mostly by precipitation.
- The annual runoff distribution in the Pailugou Basin gradually became smooth and uniform from the initial large fluctuation. Meanwhile, with the passage of time, the variation trend of the annual distribution uneven coefficient (Cu) of the runoff was highly consistent with the curve fluctuation of the complete regulation coefficient (Cr). The annual runoff of the Pailugou Basin exhibited an increasing trend during the fluctuation.
- There was a correlation between surface runoff, air temperature, and precipitation in the Pailugou Basin. Among them, a highly significant positive correlation was observed between the runoff and precipitation, while the correlation between the runoff and temperature was insignificant, so we concluded that the runoff was mainly controlled by the atmospheric precipitation in the region.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Brauman, K.A. Hydrologic ecosystem services: Linking ecohydrologic processes to human well-being in water research and watershed management. WIREs Water 2015, 2, 345–358. [Google Scholar] [CrossRef]
- Swift, D.A.; Nienow, P.W.; Hoey, T.B. Basal sediment evacuation by subglacial meltwater: Suspended sediment transport from Haut Glacier d’Arolla, Switzerland. Earth Surf. Process. Landf. 2005, 30, 867–883. [Google Scholar] [CrossRef]
- Zhu, L.; Xie, M.; Wu, Y. Quantitative analysis of lake area variations and the influence factors from 1971 to 2004 in the Nam Co basin of the Tibetan Plateau. Chin. Sci. Bull. 2010, 55, 1294–1303. [Google Scholar] [CrossRef]
- Ersi, K. Relationship between runoff and meteorological factors and its simulation in a Tianshan glacierized basin. In Proceedings of the 20th General Assembly of the International Union of Geodesy and Geophysics, Vienna, Austia, 11–24 August 1991; pp. 189–202. [Google Scholar]
- Stern, N.H. The Economics of Climate Change: The Stern Review; Cambridge University Press: Cambridge, UK, 2007; p. 662. [Google Scholar]
- Peterson, B.J.; Holmes, R.M.; McClelland, J.W.; Vorosmarty, C.J.; Lammers, R.B.; Shiklomanov, A.I.; Rahmstorf, S. Increasing river discharge to the Arctic Ocean. Science 2002, 298, 2171–2173. [Google Scholar] [CrossRef] [PubMed]
- Nie, W.; Yuan, Y.; Kepner, W.; Nash, M.S.; Jackson, M.; Erickson, C. Assessing impacts of landuse and landcover changes on hydrology for the upper San Pedro watershed. J. Hydrol. 2011, 407, 105–114. [Google Scholar] [CrossRef]
- Ahl, R.S.; Woods, S.W.; Zuuring, H.R. Hydrologic calibration and validation of swat in a snow-dominated rocky mountain watershed, Montana, USA. JAWRA 2008, 44, 1411–1430. [Google Scholar]
- Wang, Y.-J.; Qin, D.-H. Influence of climate change and human activity on water resources in arid region of Northwest China: An overview. Adv. Clim. Chang. Res. 2017, 8, 268–278. [Google Scholar] [CrossRef]
- Li, D.; Liu, H. Responding of Heihe River runoff to decadal climate change in Qilian Mountain Area. J. Desert Res. 2004, 24, 385–391. [Google Scholar]
- Zhang, Q.; Zhang, J.; Song, G.W.; Di, X.H. Research on atmospheric water-vapor distribution over Qilianshan Mountains. Acta Meteorol. Sin. 2007, 65, 633–643. [Google Scholar]
- Liu, S.; Li, X.; Xu, Z.; Che, T.; Xiao, Q.; Ma, M.; Liu, Q.; Jin, R.; Guo, J.; Wang, L.; et al. The Heihe Integrated Observatory Network: A basin-scale land surface processes observatory in China. VZJ 2018, 17, 1–21. [Google Scholar] [CrossRef]
- Zhou, T.; Akiyama, T.; Horita, M.; Kharrazi, A.; Kraines, S.; Li, J.; Yoshikawa, K. The impact of ecological restoration projects in dry lands: Data-based assessment and human perceptions in the lower reaches of Heihe River Basin, China. Sustainability 2018, 10, 1471. [Google Scholar] [CrossRef]
- Wang, Y.; Feng, Q.; Chien, L.; Yu, T. Significance and effect of ecological rehabilitation project in inland river basins in Northwest China. Environ. Manag. 2013, 52, 209–220. [Google Scholar] [CrossRef] [PubMed]
- Machiwal, D.; Jha, M.K. Time series analysis of hydrologic data for water resources planning and management: A review. J. Hydrol. Hydromech. 2006, 54, 237–257. [Google Scholar]
- Hanson, R.T.; Newhouse, M.W.; Dettinger, M.D. A methodology to asess relations between climatic variability and variations in hydrologic time series in the southwestern United States. J. Hydrol. 2004, 287, 252–269. [Google Scholar] [CrossRef]
- Singh, P.; Kumar, A.; Kumar, N. Hydro-meteorological correlations and relationships for estimating streamflow for Gangotri Glacier basin in western Himalayas. Int. J. Water Res. Environ. Eng. 2010, 3, 60–69. [Google Scholar]
- Srivastava, D.; Kumar, A.; Verma, A.; Swaroop, S. Analysis of climate and melt-runoff in Dunagiri glacier of Garhwal Himalaya (India). Water Resour. Manag. 2014, 28, 3035–3055. [Google Scholar] [CrossRef]
- Bao, Z.; Zhang, J.; Liu, J.; Wang, G.; Yan, X.; Wang, X.; Zhang, L. Sensitivity of hydrological variables to climate change in the Haihe River basin, China. Hydrol. Process. 2012, 26, 2294–2306. [Google Scholar] [CrossRef]
- Li, D.; Lu, X.; Overeem, I.; Walling, D.E.; Syvitski, J.; Kettner, A.J.; Bookhagen, B.; Zhou, Y.; Zhang, T. Exceptional increases in fluvial sediment fluxes in a warmer and wetter High Mountain Asia. Science 2021, 374, 599–603. [Google Scholar] [CrossRef] [PubMed]
- Meng, F.; Su, F.; Li, Y.; Tong, K. Changes in terrestrial water storage during 2003-2014 and possible causes in Tibetan Plateau. J. Geophys. Res. Atmos. 2019, 124, 2909–2931. [Google Scholar] [CrossRef]
- Lutz, A.F.; Immerzeel, W.W.; Shrestha, A.B.; Bierkens, M.F.P. Consistent increase in High Asia’s runoff due to increasing glacier melt and precipitation. Nat. Clim. Chang. 2014, 4, 587–592. [Google Scholar] [CrossRef]
- Zhao, Q.; Ding, Y.; Wang, J.; Gao, H.; Zhang, S.; Zhao, C.; Xu, J.; Han, H.; Shangguan, D. Projecting climate change impacts on hydrological processes on the Tibetan Plateau with model calibration against the glacier inventory data and observed streamflow. J. Hydrol. 2019, 573, 60–81. [Google Scholar] [CrossRef]
- Gu, H.; Yu, Z.; Yang, C.; Ju, Q. Projected changes in hydrological extremes in the Yangtze River Basin with an ensemble of regional climate simulations. Water 2018, 10, 1279. [Google Scholar] [CrossRef]
- Barnett, T.P.; Adam, J.C.; Lettenmaier, D.P. Potential impacts of a warming climate on water availability in snow-dominated regions. Nature 2005, 438, 303–309. [Google Scholar] [CrossRef] [PubMed]
- Jin, X. Ecohydrology in Water-Limited Environments using Quantitative Remote Sensing—The Heihe river Basin China (Case). Ph.D. Thesis, Wageningen Universiteit, Wageningen, The Netherlands, 2009; 121p. [Google Scholar]
- Baranova, A.N. Grazing Impacts on Vegetation Patterns in the Qilian Mountains, HeiHe River Basin, NW China. Ph.D. Thesis, Faculty of Mathematic, Informatics and Natural Sciences, Department of Earth Sciences, Universität Hamburg, Hamburg, Germany, 2018; 141p. [Google Scholar]
- Wang, G.; Zhou, G.; Yang, L.; Li, Z. Distribution, species diversity and life-form spectra of plant communities along an altitudinal gradient in the northern slopes of Qilianshan Mountains, Gansu, China. Plant Ecol. 2002, 165, 169–181. [Google Scholar] [CrossRef]
- Yin, Z.; Feng, Q.; Wen, X.; Deo, R.C.; Yang, L.; Si, J.; He, Z. Design and evaluation of SVR, MARS and M5Tree models for 1, 2 and 3-day lead time forecasting of river flow data in a semiarid mountainous catchment. Stoch. Environ. Res. Risk Assess. 2018, 32, 2457–2476. [Google Scholar] [CrossRef]
- Hou, X. Vegetation Atlas of China. In Chinese and in English; KexueChubanshe: Beijing, China, 2001. [Google Scholar]
- Kürschner, H.; Herzschuh, U.; Wagner, D. Phytosociological studies in the north-eastern Tibetan Plateau (NW China): A first contribution to the subalpine scrub and alpine meadow vegetation. Bot. Jahrb. Syst. 2005, 126, 273–315. [Google Scholar] [CrossRef]
- LY/T 1606-2003; Indicators System for Long-Term Observation of Forest Ecosystem. Standards Press of China: Beijing, China, 2003.
- LY/T 1721-2008; Specifications for Assessment of Forest Ecosystem Services in China. Standards Press of China: Beijing, China, 2008.
- Guo, Q.L.; Yang, Y.S.; Chang, X.Y. Annual variation of Heihe River runoff during 1957–2008. Prog. Geogr. 2011, 30, 550–556. [Google Scholar]
- Xue, J.; Li, L.H.; Li, X.M. Annual distribution of precipitation and runoff and the synchronicity of their variations in the Kaidu river basin. J. Arid Land Res. Environ. 2014, 28, 99–104. [Google Scholar]
- Tian, L.; Qi, S.; Ma, J.; Zhang, P.; Zhao, Y.; Ning, N. Changes of annual runoff distribution in Upper Bailongjiang River. J. Chin. Hydrol. 2012, 32, 82–87. [Google Scholar]
- Mann, H.B. Nonparametric tests against trend. Econometrica 1945, 13, 245–259. [Google Scholar] [CrossRef]
- Kendall, M.G. Rank Correlation Methods; Griffin: London, UK, 1955; p. 160. [Google Scholar]
- Hamed, K.H.; Rao, A.R. A modified Mann-Kendall trend test for auto correlated data. J. Hydrol. 1998, 204, 182–196. [Google Scholar] [CrossRef]
- Yang, Y.; Tian, F. Abrupt change of runoff and its major driving factors in Haihe River Catchment, China. J. Hydrol. 2009, 74, 373–383. [Google Scholar] [CrossRef]
- Xing, L.; Huang, L.; Chi, G.; Yang, L.; Li, C.; Hou, X. A dynamic study of karst spring based on wavelet analysis and the Mann-Kendall trend test. Water 2018, 10, 698. [Google Scholar] [CrossRef]
- Guna, A.; Zhang, J.; Tong, S.; Bao, Y.; Han, A.; Li, K. Effect of climate change on maize yield in the growing season: A case study of the Songliao Palin maize belt. Water 2019, 11, 2108. [Google Scholar] [CrossRef]
- Turney, S. Pearson Correlation Coefficient (r)|Guide & Examples. Scribbr. 2024. Available online: https://www.scribbr.com/statistics/pearson-correlation-coefficient/ (accessed on 22 April 2024).
- Liang, Z.; Qiang, Z.; Jianying, F.; Zhihu, B.; Jianhua, Z.; Xiaohua, X. A study of atmospheric water cycle over the Qilian Mountains (I): Variation of annual water vapor transport. J. Glaciol. Geocryol. 2014, 36, 1079–1091. [Google Scholar]
- Ma, Z.; Yao, R.; Sun, P.; Zhuang, Z.; Ge, C.; Zou, Y.; Lv, Y. Quantitative evaluation of runoff simulation and its driving forces based on hydrological model and multisource precipitation fusion. Land 2023, 12, 636. [Google Scholar] [CrossRef]
- Yue, S.; Ji, G.; Huang, J.; Cheng, M.; Guo, Y.; Chen, W. Quantitative assessment of the contribution of climate and underlying surface change to multiscale runoff variation in the Jinsha river basin, China. Land 2023, 12, 1564. [Google Scholar] [CrossRef]
- Huang, H.; Pan, Y.; Wang, C.; Wang, X. Nonlinear flood responses to tide level and land cover changes in small watersheds. Land 2023, 12, 1743. [Google Scholar] [CrossRef]
- Engelhardt, M.; Ramanathan, A.L.; Eidhammer, T.; Kumar, P.; Landgren, O.; Mandal, A.; Rasmussen, R.O.Y. Modelling 60 years of glacier mass balance and runoff for Chhota Shigri Glacier, Western Himalaya, Northern India. J. Glaciol. 2017, 63, 618–628. [Google Scholar] [CrossRef]
- Liu, G.; Wang, G. Insight into runoff decline due to climate change in China ’s Water Tower. Water Supply 2012, 12, 352–361. [Google Scholar] [CrossRef]
- Zhou, J.; Li, Q.; Wang, L.; Lei, L.; Huang, M.; Xiang, J.; Feng, W.; Zhao, Y.; Xue, D.; Liu, C.; et al. Impact of climate change and land-use on the propagation from meteorological drought to hydrological drought in the Eastern Qilian Mountains. Water 2019, 11, 1602. [Google Scholar] [CrossRef]
- Gao, B.; Qin, Y.; Wang, Y.; Yang, D.; Zheng, Y. Modeling ecohydrological processes and spatial patterns in the upper Heihe basin in China. Forests 2016, 7, 10. [Google Scholar] [CrossRef]
- Qin, X.; Liu, W.; Mao, R.; Song, J.; Chen, Y.; Ma, C.; Li, M. Quantitative assessment of driving factors affecting human appropriation of Net Primary Production (HANPP) in the Qilian Mountains, China. Ecol. Indic. 2021, 121, 106997. [Google Scholar] [CrossRef]
- Zou, C.B.; Lambert, L.H.; Everett, J.; Will, R.E. Response of surface runoff and sediment to the conversion of a marginal grassland to a switchgrass (Panicum virgatum) bioenergy feedstock system. Land 2022, 11, 540. [Google Scholar] [CrossRef]




| Basin | Length of Runoff Series (Years) | Mean Value (105 m3) | Mean Squared Error ((105 m3)2) | Coefficient of Variation | Skewness |
|---|---|---|---|---|---|
| Pailugou | 20 | 2.637 | 0.944 | 0.381 | 1.573 |
| Time (Years) | Spring | Summer | Autumn | Winter |
|---|---|---|---|---|
| 2000–2004 | 6.43 | 52.92 | 39.04 | 1.61 |
| 2005–2009 | 13.99 | 39.17 | 34.22 | 12.62 |
| 2011–2014 | 13.60 | 59.37 | 25.03 | 2.00 |
| 2015–2019 | 6.57 | 60.01 | 31.69 | 1.74 |
| Mean Value | 10.15 | 52.87 | 32.49 | 4.49 |
| Period | Concentration Ratio | Change Amplitude | ||
|---|---|---|---|---|
| Concentration Degree Ci (%) | Vector Direction (Degree, °) | Relative Change Amplitude ck (%) | Absolute Change Amplitude δr (%) | |
| 2000–2004 | 63.52 | 231 | 25.87 | 1.72 |
| 2005–2009 | 63.34 | 231 | 23.51 | 1.02 |
| 2011–2014 | 57.16 | 227 | 15.47 | 1.23 |
| 2015–2019 | 57.15 | 227 | 11.55 | 1.95 |
| Mean Value | 60.29 | 231 | 19.60 | 1.48 |
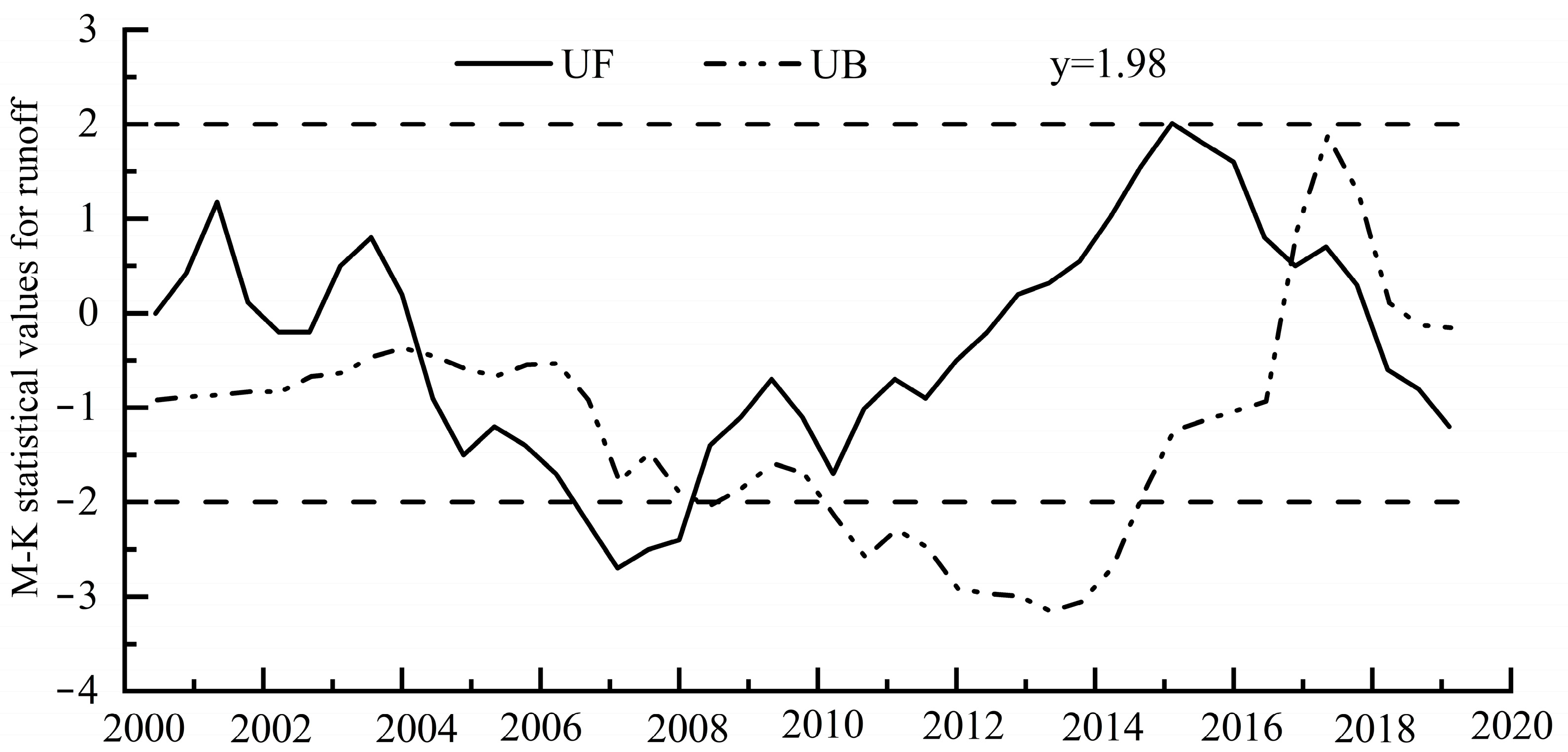
| M-K Test for Monotonicity | 2000–2019 | 2000–2007 | 2007–2015 | 2015–2019 |
|---|---|---|---|---|
| z | 1.74 | 1.03 | 1.44 | −0.64 |
| Runoff | Contemporaneous Precipitation | Average Temperature of the Same Period | Precedent Precipitation | Precedent Average Temperature |
|---|---|---|---|---|
| Spring | 0.685 ** | −0.166 | −0.224 | 0.033 |
| Summer | 0.875 ** | −0.332 | 0.599 ** | −0.236 |
| Autumn | 0.714 ** | −0.007 | 0.603 ** | 0.012 |
| Winter | −0.112 ns | −0.085 | 0.192 | −0.063 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ren, X.; Xu, E.; Smith, C.K.; Vrahnakis, M.; Jing, W.; Zhao, W.; Wang, R.; Jia, X.; Yan, C.; Liu, R. Changes in Surface Runoff and Temporal Dispersion in a Restored Montane Watershed on the Qinghai–Tibetan Plateau. Land 2024, 13, 583. https://doi.org/10.3390/land13050583
Ren X, Xu E, Smith CK, Vrahnakis M, Jing W, Zhao W, Wang R, Jia X, Yan C, Liu R. Changes in Surface Runoff and Temporal Dispersion in a Restored Montane Watershed on the Qinghai–Tibetan Plateau. Land. 2024; 13(5):583. https://doi.org/10.3390/land13050583
Chicago/Turabian StyleRen, Xiaofeng, Erwen Xu, C. Ken Smith, Michael Vrahnakis, Wenmao Jing, Weijun Zhao, Rongxin Wang, Xin Jia, Chunming Yan, and Ruiming Liu. 2024. "Changes in Surface Runoff and Temporal Dispersion in a Restored Montane Watershed on the Qinghai–Tibetan Plateau" Land 13, no. 5: 583. https://doi.org/10.3390/land13050583
APA StyleRen, X., Xu, E., Smith, C. K., Vrahnakis, M., Jing, W., Zhao, W., Wang, R., Jia, X., Yan, C., & Liu, R. (2024). Changes in Surface Runoff and Temporal Dispersion in a Restored Montane Watershed on the Qinghai–Tibetan Plateau. Land, 13(5), 583. https://doi.org/10.3390/land13050583







