Physical Parameterization Sensitivity of Noah-MP for Hydrothermal Simulation Within the Active Layer on the Qinghai–Tibet Plateau
Abstract
1. Introduction
2. Observation and Methods
2.1. Monitoring and In Situ Observation
2.2. Noah-MP Numerical Experiments
2.2.1. Model Description
2.2.2. Noah-MP Default Parameterization Scheme and Ensemble Numerical Experiment
| Physical Process | Parameterization Scheme |
|---|---|
| Soil moisture threshold for plant transpiration (BTR) | 1: Noah type [65] [Default] as a function of soil moisture 2: Community Land Model (CLM) type [82], matric potential related 3: Simplified Biosphere Model (SSiB) type [83], matric potential related |
| Surface-layer exchange coefficient (SFC) | 1: Monin–Obukhov (M-O) [84] [Default], M-O similarity theory 2: Noah type [64], neglecting the zero-displacement height |
| Supercooled liquid water in frozen soil (FRZ) | 1: NY06 [85] [Default], no iteration, general form of the freezing-point depression equation 2: Koren99 [86], Koren’s iteration, variant freezing point depression |
| Frozen soil permeability (INF) | 1: NY06 [85] [Default], linear effect, more permeable, as a function of soil moisture and ice 2: Koren99 [86], nonlinear effect, less permeable, function of liquid water |
| Radiation transfer (RAD) | 1: Modified two-stream [87], canopy gaps from 3D structure and solar zenith angle 2: Two-stream applied to a grid cell [87], no canopy gap 3: Two-stream applied to a vegetated fraction [87] [Default], gaps from the vegetated fraction (gap = 1−FVEG) |
| Snow surface albedo (ALB) | 1: BATS [88], computes snow surface albedo for direct and diffuse radiation over visible and near-infrared wave bands 2: CLASS [89] [Default], computes the overall snow surface albedo accounting for fresh snow albedo and snow age |
| Partitioning precipitation into rainfall and snowfall (PCP) | 1: Jordan [90] [Default], relatively complex functional form 2: BATS, assumes all precipitation as snowfall when air temperature below freezing temperature plus 2 °C 3: Assumes all precipitation as snowfall when air temperature below the freezing temperature 4: Wet-bulb temperature-based [91], a snow-rain partitioning scheme using the wet-bulb temperature (Tw), which is closer to the surface temperature of a falling hydrometeor than surface air temperature (Ta) and would lead to a larger fraction of snowfall |
| Lower boundary of soil temperature (TBOT) | 1: Zero-flux scheme, zero heat flux from the bottom soil layer 2: Noah [Default], TBOT at 8 m soil depth, read from a preset file |
| The first-layer snow or soil temperature time scheme (TEMP) | 1: Semi-implicit [Default], flux top boundary condition 2: Fully implicit, temperature top boundary condition |
| Surface resistance to evaporation (SRES) | 1: Sakaguchi and Zeng’s scheme [92] [Default] 2: Sellers’s scheme [93] |
| Runoff and groundwater (RUN) | 1: TOPMODEL with an equilibrium water table [94] 2: Original surface and subsurface runoff (free drainage) [95] [Default] 3: BATS surface and subsurface runoff (free drainage) [70,96,97] 4: Variable infiltration capacity model surface runoff scheme [98] 5: Dynamic VIC surface runoff scheme [99] with the Philip infiltration scheme |
| Experiment Name | Description of Experiment | Members |
|---|---|---|
| Def | In situ observation as the forcing data, default combination of parameterization schemes | 1 |
| Ens1 | Forcing data are the same as those used in Def, parameterization schemes for all 11 physical processes were combined | 23,040 |
| Ens2 | Forcing data are the same as those used in Def, INF = 1, parameterization schemes for the other 10 physical processes were combined | 11,520 |
| Ens3 | Forcing data are the same as those used in Def, INF = 2, parameterization schemes for the other 10 physical processes were combined | 11,520 |
| Opt1 | Forcing data are the same as those used in Def, INF = 1, configurations of optimal parameterization scheme for the other 10 physical processes were obtained based on the TOPSIS | 1 |
| Opt2 | Forcing data are the same as those used in Def, INF = 2, configurations of optimal parameterization scheme for the other 10 physical processes were obtained based on the TOPSIS | 1 |
2.3. Evaluation and Analysis Methods
2.3.1. Model Evaluation
2.3.2. Natural Selection
2.3.3. Tukey’s Test
2.3.4. TOPSIS
3. Results
3.1. Simulation of Hydrothermal Process Within the Active Layer
3.1.1. Validation of Soil Temperature
3.1.2. Validation of Soil Moisture
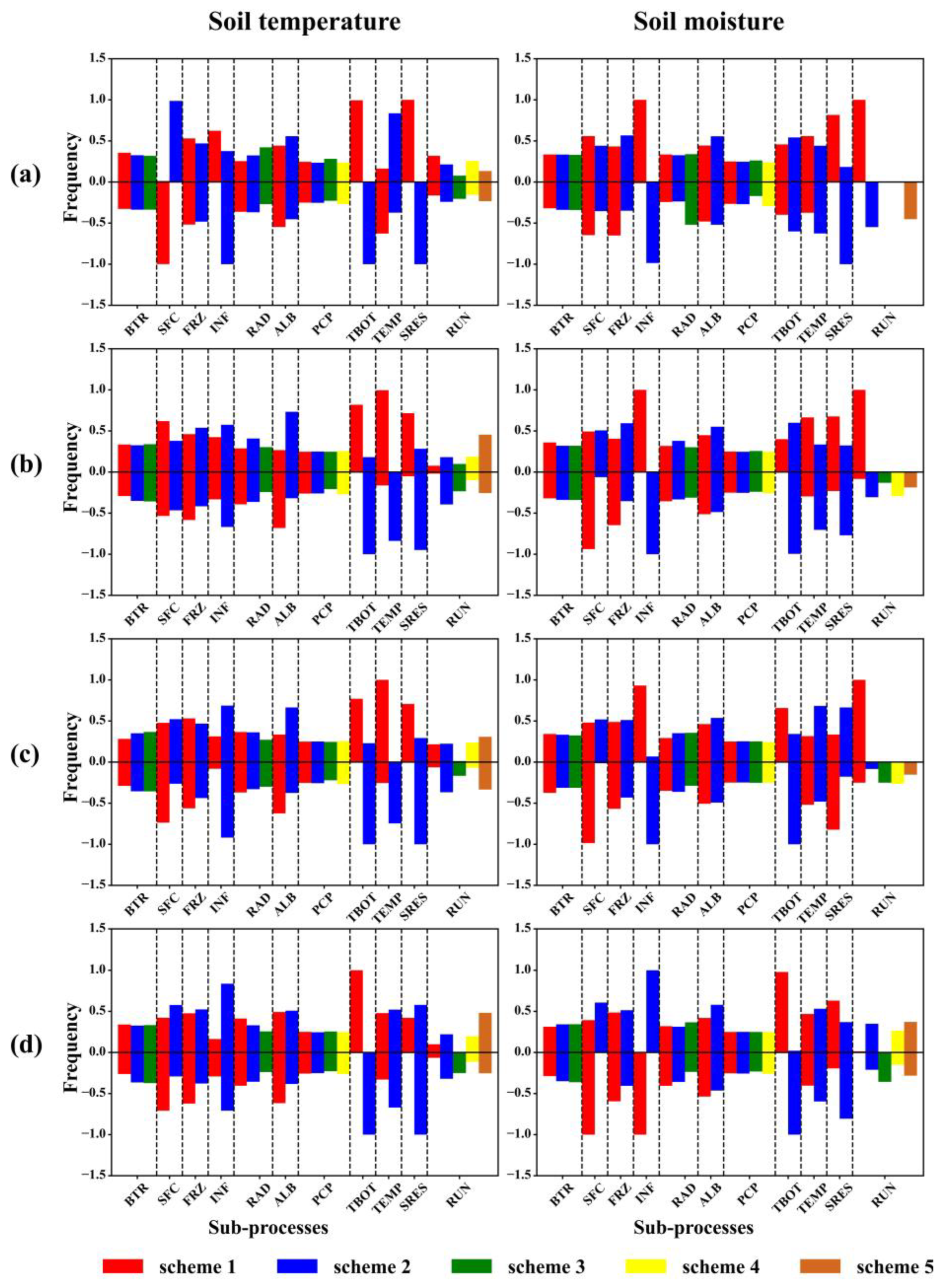
3.2. Results of Natural Selection
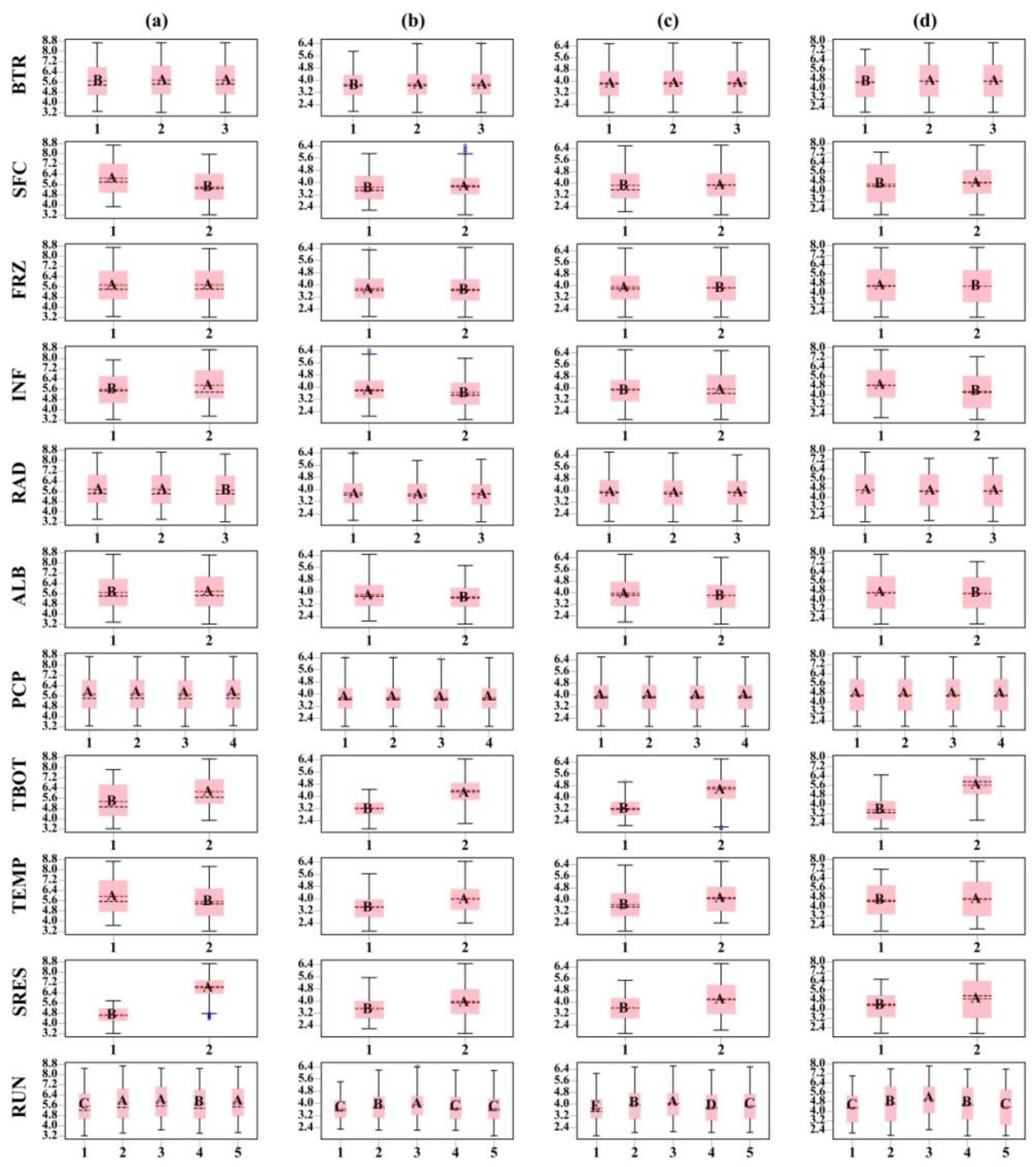
3.3. Results of Tukey’s Test
3.4. Ranking of Model Performance for Each Parameterization Scheme
4. Discussion
5. Conclusions
- Def could well reflect the seasonal pattern of hydrothermal dynamics within the active layer with a systematic underestimation. Compared with Def, Ens1 considerably improved the hydrothermal simulation during the frozen period, which was very limited or even negative for shallow soil during the thawed period. The large uncertainty of Ens1 in the soil temperature simulation during the frozen period and soil moisture simulation during the thawed period was mainly caused by their respective complex influencing factors.
- The results of Natural Selection revealed that for most soil layers, the selected frequency of parameterization schemes in SFC, ALB, TEMP, TBOT, and SRES was consistent in soil temperature simulation and that the selected frequency for FRZ, INF, and RUN was consistent for soil moisture. The results of Tukey’s test generally agreed with the results from Natural Selection, and Tukey’s test identified more parameterization schemes with similar model performance for both soil temperature and moisture. Moreover, the results of TOPSIS showed that the determination of the optimal scheme was consistent for the simulation of soil temperature and moisture in each physical process except for INF.
- Both parameterization schemes in INF considerably reduced the uncertainty in soil moisture simulation during the frozen period. The soil moisture simulated by Opt1 and Opt2 at shallow layers during the frozen period agreed better with the observations compared with that of Def, and Opt2 yielded better simulation results than Opt1. Influenced by the thawing process, Opt1 and Opt2 showed better performance than Def in the soil moisture simulation during the thawed period, and Opt2 showed the best performance.
- Controlled by the soil moisture simulation during the frozen period, the soil temperature simulated by Opt1 and Opt2 agreed better with observation than Def during the same period, and Opt2 yielded better simulation accuracy. Compared with Def, Opt1 and Opt2 showed better performance for RMSE and MBE at the top layer in the soil temperature simulation during the thawed period, and Opt2 showed an overwhelming better performance for R at four soil layers compared with Opt1. Neither Opt1 nor Opt2 could improve the soil temperature simulation for the deeper three layers during the thawed period and even led to a deterioration, which indicated that Def had an advantage in the soil temperature simulation during the thawed period.
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Qiu, J. China: The third pole. Nature 2008, 454, 393–396. [Google Scholar] [CrossRef]
- Yao, T.; Bolch, T.; Chen, D.; Gao, J.; Immerzeel, W.; Piao, S.; Su, F.; Thompson, L.; Wada, Y.; Wang, L.; et al. The imbalance of the Asian water tower. Nat. Rev. Earth Environ. 2022, 3, 618–632. [Google Scholar] [CrossRef]
- Lei, J.; Shi, Z.; Xie, X.; Sha, Y.; Li, X.; Liu, X.; An, Z. Seasonal Variation of the Westerly Jet over Asia in the Last Glacial Maximum: Role of the Tibetan Plateau Heating. J. Clim. 2021, 34, 2723–2740. [Google Scholar] [CrossRef]
- Huang, J.; Zhou, X.; Wu, G.; Xu, X.; Zhao, Q.; Liu, Y.; Duan, A.; Xie, Y.; Ma, Y.; Zhao, P.; et al. Global Climate Impacts of Land-Surface and Atmospheric Processes Over the Tibetan Plateau. Rev. Geophys. 2023, 61, e2022RG000771. [Google Scholar] [CrossRef]
- Yang, K.; Wu, H.; Qin, J.; Lin, C.; Tang, W.; Chen, Y. Recent climate changes over the Tibetan Plateau and their impacts on energy and water cycle: A review. Glob. Planet. Change 2014, 112, 79–91. [Google Scholar] [CrossRef]
- Zou, D.; Zhao, L.; Sheng, Y.; Chen, J.; Hu, G.; Wu, T.; Wu, J.; Xie, C.; Wu, X.; Pang, Q.; et al. A new map of permafrost distribution on the Tibetan Plateau. Cryosphere 2017, 11, 2527–2542. [Google Scholar] [CrossRef]
- Cheng, G.; Wu, T. Responses of permafrost to climate change and their environmental significance, Qinghai-Tibet Plateau. J. Geophys. Res. Earth Surf. 2007, 112, 14450823. [Google Scholar] [CrossRef]
- Wu, Q.; Zhang, T.; Liu, Y. Permafrost temperatures and thickness on the Qinghai-Tibet Plateau. Glob. Planet. Change 2010, 72, 32–38. [Google Scholar] [CrossRef]
- Lu, Q.; Zhao, D.; Wu, S. Simulated responses of permafrost distribution to climate change on the Qinghai-Tibet Plateau. Sci. Rep. 2017, 7, 3845. [Google Scholar] [CrossRef]
- Zhu, X.; Wu, T.; Ni, J.; Wu, X.; Hu, G.; Wang, S.; Li, X.; Wen, A.; Li, R.; Shang, C.; et al. Increased extreme warming events and the differences in the observed hydrothermal responses of the active layer to these events in China’s permafrost regions. Clim. Dyn. 2022, 59, 785–804. [Google Scholar] [CrossRef]
- Duan, J.; Li, L.; Fang, Y. Seasonal spatial heterogeneity of warming rates on the Tibetan Plateau over the past 30 years. Sci. Rep. 2014, 5, 11725. [Google Scholar] [CrossRef] [PubMed]
- Liu, X.; Chen, B. Climatic warming in the Tibetan plateau during recent decades. Int. J. Climatol. 2000, 20, 1729–2742. [Google Scholar] [CrossRef]
- Wang, B.; Bao, Q.; Hoskins, B.; Wu, G.; Liu, Y. Tibetan Plateau warming and precipitation changes in East Asia. Geophys. Res. Lett. 2008, 35, L14702. [Google Scholar] [CrossRef]
- Wang, X.; Yang, M.; Liang, X.; Pang, G.; Wan, G.; Chen, X.; Luo, X. The dramatic climate warming in the Qaidam Basin, northeastern Tibetan Plateau, during 1961–2010. Int. J. Climatol. 2014, 34, 1524–1537. [Google Scholar] [CrossRef]
- Guo, D.; Wang, H. The significant climate warming in the northern Tibetan Plateau and its possible causes. Int. J. Climatol. 2012, 32, 1775–1781. [Google Scholar] [CrossRef]
- Wang, X.; Pang, G.; Yang, M. Precipitation over the Tibetan Plateau during recent decades: A review based on observations and simulations. Int. J. Climatol. 2018, 38, 1116–1131. [Google Scholar] [CrossRef]
- You, Q.; Cai, Z.; Pepin, N.; Chen, D.; Ahrens, B.; Jiang, Z.; Wu, F.; Kang, S.; Zhang, R.; Wu, T.; et al. Warming amplification over the Arctic Pole and Third Pole: Trends, mechanisms and consequences. Earth-Sci. Rev. 2021, 217, 103625. [Google Scholar] [CrossRef]
- Duan, A.; Xiao, Z. Does the climate warming hiatus exist over the Tibetan Plateau? Sci. Rep. 2015, 5, 13711. [Google Scholar] [CrossRef]
- Li, R.; Zhao, L.; Ding, Y.; Wu, T.; Xiao, Y.; Du, E.; Liu, G.; Qiao, Y. Temporal and spatial variations of the active layer along the Qinghai-Tibet Highway in a permafrost region. Chin. Sci. Bull. 2012, 57, 4609–4616. [Google Scholar] [CrossRef]
- Cheng, G.; Zhao, L.; Li, R.; Wu, X.; Sheng, Y.; Hu, G.; Zou, D.; Jin, H.; Li, X.; Wu, Q. Characteristic, changes and impacts of permafrost on Qinghai-Tibet Plateau. Chin. Sci. Bull. 2019, 64, 2783–2795. [Google Scholar] [CrossRef]
- Muller, S.W.; Geological, S. Permafrost, Or Permanently Frozen Ground: And Related Engineering Problems; Army map service, U.S. Army: Washington, DC, USA, 1945. [Google Scholar]
- Hinkel, K.M.; Paetzold, F.; Nelson, F.E.; Bockheim, J.G. Patterns of soil temperature and moisture in the active layer and upper permafrost at Barrow, Alaska: 1993–1999. Glob. Planet. Change 2001, 29, 293–309. [Google Scholar] [CrossRef]
- Brown, J.; Hinkel, K.M.; Nelson, F.E. The circumpolar active layer monitoring (calm) program: Research designs and initial results. Polar Geogr. 2000, 24, 166–258. [Google Scholar] [CrossRef]
- Wu, Q.; Zhang, T. Changes in active layer thickness over the Qinghai-Tibetan Plateau from 1995 to 2007. J. Geophys. Res. Atmos. 2010, 115, D09107. [Google Scholar] [CrossRef]
- Li, C.; Wei, Y.; Liu, Y.; Li, L.; Peng, L.; Chen, J.; Liu, L.; Dou, T.; Wu, X. Active Layer Thickness in the Northern Hemisphere: Changes From 2000 to 2018 and Future Simulations. J. Geophys. Res. Atmos. 2022, 127, e2022JD036785. [Google Scholar] [CrossRef]
- Smith, M. Potential responses of permafrost to climatic change. J. Cold Reg. Eng. 1990, 4, 29–37. [Google Scholar] [CrossRef]
- Lachenbruch, A.H. Permafrost, the Active Layer, and Changing Climate; US Geological Survey Reston: Reston, VA, USA, 1994. [Google Scholar]
- Frauenfeld, O.W.; Zhang, T.; Barry, R.G.; Gilichinsky, D. Interdecadal changes in seasonal freeze and thaw depths in Russia. J. Geophys. Res. Atmos. 2004, 109, D05101. [Google Scholar] [CrossRef]
- Ma, W.; Mu, Y.; Wu, Q.; Sun, Z.; Liu, Y. Characteristics and mechanisms of embankment deformation along the Qinghai-Tibet Railway in permafrost regions. Cold Reg. Sci. Technol. 2011, 67, 178–186. [Google Scholar] [CrossRef]
- Wang, G.; Li, Y.; Wu, Q.; Wang, Y. Impacts of permafrost changes on alpine ecosystem in Qinghai-Tibet Plateau. Sci. China Ser. D Earth Sci. 2006, 49, 1156–1169. [Google Scholar] [CrossRef]
- Zhao, L.; Wu, Q.; Marchenko, S.S.; Sharkhuu, N. Thermal state of permafrost and active layer in Central Asia during the international polar year. Permafr. Periglac. Process. 2010, 21, 198–207. [Google Scholar] [CrossRef]
- Luo, D.; Jin, H.; Lin, L.; He, R.; Yang, S.; Chang, X. New Progress on Permafrost Temperature and Thickness in the Source Area of the Huanghe River. Sci. Geogr. Sin. 2012, 32, 898–904. [Google Scholar] [CrossRef]
- Luo, D.; Jin, H.; Bense, V.F. Ground surface temperature and the detection of permafrost in the rugged topography on NE Qinghai-Tibet Plateau. Geoderma 2019, 333, 57–68. [Google Scholar] [CrossRef]
- Cao, B.; Zhang, T.; Wu, Q.; Sheng, Y.; Zhao, L.; Zou, D. Brief communication: Evaluation and inter-comparisons of Qinghai-Tibet Plateau permafrost maps based on a new inventory of field evidence. Cryosphere 2019, 13, 511–519. [Google Scholar] [CrossRef]
- Deng, M.; Meng, X.; Lyv, Y.; Zhao, L.; Li, Z.; Hu, Z.; Jing, H. Comparison of Soil Water and Heat Transfer Modeling over the Tibetan Plateau Using Two Community Land Surface Model (CLM) Versions. J. Adv. Model. Earth Syst. 2020, 12, e2020MS002189. [Google Scholar] [CrossRef]
- Zhao, L.; Zou, D.; Hu, G.; Wu, T.; Du, E.; Liu, G.; Xiao, Y.; Li, R.; Pang, Q.; Qiao, Y.; et al. A synthesis dataset of permafrost thermal state for the Qinghai-Tibet (Xizang) Plateau, China. Geosci. Model Dev. 2021, 13, 4207–4218. [Google Scholar] [CrossRef]
- Lawrence, D.M.; Slater, A.G.; Romanovsky, V.E.; Nicolsky, D.J. Sensitivity of a model projection of near-surface permafrost degradation to soil column depth and representation of soil organic matter. J. Geophys. Res. Earth Surf. 2008, 113, F02011. [Google Scholar] [CrossRef]
- Lawrence, D.M.; Slater, A.G.; Swenson, S.C. Simulation of Present-Day and Future Permafrost and Seasonally Frozen Ground Conditions in CCSM4. J. Clim. 2012, 25, 2207–2225. [Google Scholar] [CrossRef]
- Li, R.; Xie, J.; Xie, Z.; Gao, J.; Jia, B.; Qin, P.; Wang, L.; Wang, Y.; Liu, B.; Chen, S. Simulated response of the active layer thickness of permafrost to climate change. Atmos. Ocean. Sci. Lett. 2021, 14, 100007. [Google Scholar] [CrossRef]
- Dirmeyer, P.A.; Koster, R.D.; Guo, Z. Do Global Models Properly Represent the Feedback between Land and Atmosphere? J. Hydrometeorol. 2006, 7, 1177–1198. [Google Scholar] [CrossRef]
- Parrish, M.A.; Moradkhani, H.; DeChant, C.M. Toward reduction of model uncertainty: Integration of Bayesian model averaging and data assimilation. Water Resour. Res. 2012, 48, W03519. [Google Scholar] [CrossRef]
- Zhang, G.; Chen, F.; Gan, Y. Assessing uncertainties in the Noah-MP ensemble simulations of a cropland site during the Tibet Joint International Cooperation program field campaign. J. Geophys. Res. Atmos. 2016, 121, 9576–9596. [Google Scholar] [CrossRef]
- Deng, M.; Meng, X.; Lu, Y.; Li, Z.; Zhao, L.; Hu, Z.; Chen, H.; Shang, L.; Wang, S.; Li, Q. Impact and Sensitivity Analysis of Soil Water and Heat Transfer Parameterizations in Community Land Surface Model on the Tibetan Plateau. J. Adv. Model. Earth Syst. 2021, 13, e2021MS002670. [Google Scholar] [CrossRef]
- Swenson, S.C.; Lawrence, D.M.; Lee, H. Improved simulation of the terrestrial hydrological cycle in permafrost regions by the Community Land Model. J. Adv. Model. Earth Syst. 2012, 4, M08002. [Google Scholar] [CrossRef]
- Cuntz, M.; Haverd, V. Physically Accurate Soil Freeze-Thaw Processes in a Global Land Surface Scheme. J. Adv. Model. Earth Syst. 2018, 10, 54–77. [Google Scholar] [CrossRef]
- Li, D.; Overeem, I.; Kettner, A.; Zhou, Y.; Lu, X.X. Air Temperature Regulates Erodible Landscape, Water, and Sediment Fluxes in the Permafrost-Dominated Catchment on the Tibetan Plateau. Water Resour. Res. 2021, 57, e2020WR028193. [Google Scholar] [CrossRef]
- Yang, K.; Wang, C.; Li, S. Improved Simulation of Frozen-Thawing Process in Land Surface Model (CLM4.5). J. Geophys. Res. Atmos. 2018, 123, 13238–13258. [Google Scholar] [CrossRef]
- Xie, Z.; Liu, S.; Zeng, Y.; Gao, J.; Qin, P.; Jia, B.; Xie, J.; Liu, B.; Li, R.; Wang, Y.; et al. A High-Resolution Land Model With Groundwater Lateral Flow, Water Use, and Soil Freeze-Thaw Front Dynamics and its Applications in an Endorheic Basin. J. Geophys. Res. Atmos. 2018, 123, 7204–7222. [Google Scholar] [CrossRef]
- Vogel, T.; Dohnal, M.; Votrubova, J.; Dusek, J. Soil water freezing model with non-iterative energy balance accounting. J. Hydrol. 2019, 578, 124071. [Google Scholar] [CrossRef]
- Wang, Z.; Fu, Q.; Jiang, Q.; Li, T. Numerical simulation of water–heat coupled movements in seasonal frozen soil. Math. Comput. Model. 2011, 54, 970–975. [Google Scholar] [CrossRef]
- Niu, G.; Yang, Z.; Mitchell, K.E.; Chen, F.; Ek, M.B.; Barlage, M.; Kumar, A.; Manning, K.; Niyogi, D.; Rosero, E.; et al. The community Noah land surface model with multiparameterization options (Noah-MP): 1. Model description and evaluation with local-scale measurements. J. Geophys. Res. Atmos. 2011, 116, D12109. [Google Scholar] [CrossRef]
- Yang, Z.; Niu, G.; Mitchell, K.E.; Chen, F.; Ek, M.B.; Barlage, M.; Longuevergne, L.; Manning, K.; Niyogi, D.; Tewari, M.; et al. The community Noah land surface model with multiparameterization options (Noah-MP): 2. Evaluation over global river basins. J. Geophys. Res. Atmos. 2011, 116, D12110. [Google Scholar] [CrossRef]
- Hu, W.; Ma, W.; Yang, Z.; Ma, Y.; Xie, Z. Sensitivity Analysis of the Noah-MP Land Surface Model for Soil Hydrothermal Simulations Over the Tibetan Plateau. J. Adv. Model. Earth Syst. 2023, 15, e2022MS003136. [Google Scholar] [CrossRef]
- You, Y.; Huang, C.; Yang, Z.; Zhang, Y.; Bai, Y.; Gu, J. Assessing Noah-MP Parameterization Sensitivity and Uncertainty Interval Across Snow Climates. J. Geophys. Res. Atmos. 2020, 125, e2019JD030417. [Google Scholar] [CrossRef]
- Ma, J.; Li, R.; Liu, H.; Huang, Z.; Wu, T.; Wu, X.; Zhao, L.; Hu, G.; Xiao, Y.; Jiao, Y.; et al. Evaluation of CLM5.0 for simulating surface energy budget and soil hydrothermal regime in permafrost regions of the Qinghai-Tibet Plateau. Agric. For. Meteorol. 2023, 332, 109380. [Google Scholar] [CrossRef]
- Zhao, L.; Hu, G.; Wu, X.; Wu, T.; Li, R.; Pang, Q.; Zou, D.; Du, E.; Zhu, X. Dynamics and characteristics of soil temperature and moisture of active layer in the central Tibetan Plateau. Geoderma 2021, 400, 115083. [Google Scholar] [CrossRef]
- Li, X.; Wu, T.; Wu, X.; Chen, J.; Zhu, X.; Hu, G.; Li, R.; Qiao, Y.; Yang, C.; Hao, J.; et al. Assessing the simulated soil hydrothermal regime of the active layer from the Noah-MP land surface model (v1.1) in the permafrost regions of the Qinghai-Tibet Plateau. Geosci. Model Dev. 2021, 14, 1753–1771. [Google Scholar] [CrossRef]
- Chen, F.; Manning, K.W.; LeMone, M.A.; Trier, S.B.; Alfieri, J.G.; Roberts, R.; Tewari, M.; Niyogi, D.; Horst, T.W.; Oncley, S.P.; et al. Description and Evaluation of the Characteristics of the NCAR High-Resolution Land Data Assimilation System. J. Appl. Meteorol. Climatol. 2007, 46, 694–713. [Google Scholar] [CrossRef]
- Nayak, H.P.; Sinha, P.; Satyanarayana, A.N.V.; Bhattacharya, A.; Mohanty, U.C. Performance Evaluation of High-Resolution Land Data Assimilation System (HRLDAS) Over Indian Region. Pure Appl. Geophys. 2019, 176, 389–407. [Google Scholar] [CrossRef]
- Xia, Y.; Sheffield, J.; Ek, M.B.; Dong, J.; Chaney, N.; Wei, H.; Meng, J.; Wood, E.F. Evaluation of multi-model simulated soil moisture in NLDAS-2. J. Hydrol. 2014, 512, 107–125. [Google Scholar] [CrossRef]
- Zhang, G.; Luo, W.; Chen, W.; Zheng, G. A robust but variable lake expansion on the Tibetan Plateau. Sci. Bull. 2019, 64, 1306–1309. [Google Scholar] [CrossRef]
- Rgi, C.; Nosenko, G. Randolph Glacier Inventory(RGI): A Dataset of Global Glacier Outlines: Version 6.0. Technical Report. In Global Land Ice Measurements from Space; National Snow and Ice Data Center: Boulder, CO, USA, 2017. [Google Scholar]
- Chen, F.; Mitchell, K.; Schaake, J.; Xue, Y.; Pan, H.; Koren, V.; Duan, Q.; Ek, M.; Betts, A. Modeling of land surface evaporation by four schemes and comparison with FIFE observations. J. Geophys. Res. Atmos. 1996, 101, 7251–7268. [Google Scholar] [CrossRef]
- Chen, F.; Janjić, Z.; Mitchell, K. Impact of Atmospheric Surface-layer Parameterizations in the new Land-surface Scheme of the NCEP Mesoscale Eta Model. Bound.-Layer Meteorol. 1997, 85, 391–421. [Google Scholar] [CrossRef]
- Chen, F.; Dudhia, J. Coupling an Advanced Land Surface-Hydrology Model with the Penn State-NCAR MM5 Modeling System. Part I: Model Implementation and Sensitivity. Mon. Weather Rev. 2001, 129, 569–585. [Google Scholar] [CrossRef]
- Ek, M.B.; Mitchell, K.E.; Lin, Y.; Rogers, E.; Grunmann, P.; Koren, V.; Gayno, G.; Tarpley, J.D. Implementation of Noah land surface model advances in the National Centers for Environmental Prediction operational mesoscale Eta model. J. Geophys. Res. Atmos. 2003, 108, 8851. [Google Scholar] [CrossRef]
- Li, J.; Zhang, G.; Chen, F.; Peng, X.; Gan, Y. Evaluation of Land Surface Subprocesses and Their Impacts on Model Performance With Global Flux Data. J. Adv. Model. Earth Syst. 2019, 11, 1329–1348. [Google Scholar] [CrossRef]
- Arsenault, K.R.; Nearing, G.S.; Wang, S.; Yatheendradas, S.; Peters-Lidard, C.D. Parameter Sensitivity of the Noah-MP Land Surface Model with Dynamic Vegetation. J. Hydrometeorol. 2018, 19, 815–830. [Google Scholar] [CrossRef]
- Gan, Y.; Liang, X.; Duan, Q.; Chen, F.; Li, J.; Zhang, Y. Assessment and Reduction of the Physical Parameterization Uncertainty for Noah-MP Land Surface Model. Water Resour. Res. 2019, 55, 5518–5538. [Google Scholar] [CrossRef]
- Li, J.; Chen, F.; Lu, X.; Gong, W.; Zhang, G.; Gan, Y. Quantifying Contributions of Uncertainties in Physical Parameterization Schemes and Model Parameters to Overall Errors in Noah-MP Dynamic Vegetation Modeling. J. Adv. Model. Earth Syst. 2020, 12, e2019MS001914. [Google Scholar] [CrossRef]
- Li, Q.; Yang, T.; Li, L. Quantitative assessment of the parameterization sensitivity of the WRF/Noah-MP model of snow dynamics in the Tianshan Mountains, Central Asia. Atmos. Res. 2022, 277, 106310. [Google Scholar] [CrossRef]
- Wu, W.; Yang, Z.; Barlage, M. The Impact of Noah-MP Physical Parameterizations on Modeling Water Availability during Droughts in the Texas-Gulf Region. J. Hydrometeorol. 2021, 22, 1221–1233. [Google Scholar] [CrossRef]
- Yang, Q.; Dan, L.; Lv, M.; Wu, J.; Li, W.; Dong, W. Quantitative assessment of the parameterization sensitivity of the Noah-MP land surface model with dynamic vegetation using ChinaFLUX data. Agric. For. Meteorol. 2021, 307, 108542. [Google Scholar] [CrossRef]
- Zhang, G.; Chen, F.; Chen, Y.; Li, J.; Peng, X. Evaluation of Noah-MP Land-Model Uncertainties over Sparsely Vegetated Sites on the Tibet Plateau. Atmosphere 2020, 11, 458. [Google Scholar] [CrossRef]
- Zheng, D.; Van Der Velde, R.; Su, Z.; Wen, J.; Wang, X. Assessment of Noah land surface model with various runoff parameterizations over a Tibetan river. J. Geophys. Res. Atmos. 2017, 122, 1488–1504. [Google Scholar] [CrossRef]
- Zheng, D.; van der Velde, R.; Su, Z.; Wen, J.; Wang, X.; Yang, K. Evaluation of Noah Frozen Soil Parameterization for Application to a Tibetan Meadow Ecosystem. J. Hydrometeorol. 2017, 18, 1749–1763. [Google Scholar] [CrossRef]
- Seck, A.; Welty, C.; Maxwell, R.M. Spin-up behavior and effects of initial conditions for an integrated hydrologic model. Water Resour. Res. 2015, 51, 2188–2210. [Google Scholar] [CrossRef]
- Cosgrove, B.A.; Lohmann, D.; Mitchell, K.E.; Houser, P.R.; Wood, E.F.; Schaake, J.C.; Robock, A.; Sheffield, J.; Duan, Q.; Luo, L.; et al. Land surface model spin-up behavior in the North American Land Data Assimilation System (NLDAS). J. Geophys. Res. Atmos. 2003, 108, 8845. [Google Scholar] [CrossRef]
- Lavin-Gullon, A.; Milovac, J.; García-Díez, M.; Fernández, J. Spin-up time and internal variability analysis for overlapping time slices in a regional climate model. Clim. Dyn. 2023, 61, 47–64. [Google Scholar] [CrossRef]
- Cai, X.; Yang, Z.; David, C.H.; Niu, G.; Rodell, M. Hydrological evaluation of the Noah-MP land surface model for the Mississippi River Basin. J. Geophys. Res. Atmos. 2014, 119, 23–38. [Google Scholar] [CrossRef]
- Gao, Y.; Li, K.; Chen, F.; Jiang, Y.; Lu, C. Assessing and improving Noah-MP land model simulations for the central Tibetan Plateau. J. Geophys. Res. Atmos. 2015, 120, 9258–9278. [Google Scholar] [CrossRef]
- Oleson, K.W.; Dai, Y.; Bosilovich, M.; Dickinson, R.; Dirmeyer, P. Technical Description of the Community Land Model (CLM); University Corporation for Atmospheric Research: Boulder, CO, USA, 2004. [Google Scholar]
- Xue, Y.; Sellers, P.J.; Kinter, J.L.; Shukla, J. A Simplified Biosphere Model for Global Climate Studies. J. Clim. 1991, 4, 345–364. [Google Scholar] [CrossRef]
- Brutsaert, W. Evaporation into the Atmosphere: Theory, History and Applications; Springer Science & Business Media: Berlin/Heidelberg, Germany, 1982; Volume 1. [Google Scholar]
- Niu, G.; Yang, Z. Effects of Frozen Soil on Snowmelt Runoff and Soil Water Storage at a Continental Scale. J. Hydrometeorol. 2006, 7, 937–952. [Google Scholar] [CrossRef]
- Koren, V.; Schaake, J.; Mitchell, K.; Duan, Q.Y.; Chen, F.; Baker, J.M. A parameterization of snowpack and frozen ground intended for NCEP weather and climate models. J. Geophys. Res. Atmos. 1999, 104, 19569–19585. [Google Scholar] [CrossRef]
- Niu, G.; Yang, Z. Effects of vegetation canopy processes on snow surface energy and mass balances. J. Geophys. Res. Atmos. 2004, 109, D23111. [Google Scholar] [CrossRef]
- Yang, Z.; Dickinson, R.E.; Robock, A.; Vinnikov, K.Y. Validation of the Snow Submodel of the Biosphere-Atmosphere Transfer Scheme with Russian Snow Cover and Meteorological Observational Data. J. Clim. 1997, 10, 353–373. [Google Scholar] [CrossRef]
- Verseghy, D.L. Class-A Canadian land surface scheme for GCMS. I. Soil model. Int. J. Climatol. 1991, 11, 111–133. [Google Scholar] [CrossRef]
- Jordan, R. A One-Dimensional Temperature Model for a Snow Cover: Technical Documentation for SNTHERM.89; Cold Regions Research and Engineering Laboratory, U.S. Army Corps of Engineers: Hanover, NH, USA, 1991. [Google Scholar]
- Wang, Y.; Broxton, P.; Fang, Y.; Behrangi, A.; Barlage, M.; Zeng, X.; Niu, G. A Wet-Bulb Temperature-Based Rain-Snow Partitioning Scheme Improves Snowpack Prediction Over the Drier Western United States. Geophys. Res. Lett. 2019, 46, 13825–13835. [Google Scholar] [CrossRef]
- Sakaguchi, K.; Zeng, X. Effects of soil wetness, plant litter, and under-canopy atmospheric stability on ground evaporation in the Community Land Model (CLM3.5). J. Geophys. Res. Atmos. 2009, 114, D1. [Google Scholar] [CrossRef]
- Sellers, P.J.; Heiser, M.D.; Hall, F.G. Relations between surface conductance and spectral vegetation indices at intermediate (100 m2 to 15 km2) length scales. J. Geophys. Res. Atmos. 1992, 97, 19033–19059. [Google Scholar] [CrossRef]
- Niu, G.; Yang, Z.; Dickinson, R.E.; Gulden, L.E. A simple TOPMODEL-based runoff parameterization (SIMTOP) for use in global climate models. J. Geophys. Res. Atmos. 2005, 110, D21106. [Google Scholar] [CrossRef]
- Schaake, J.C.; Koren, V.I.; Duan, Q.; Mitchell, K.; Chen, F. Simple water balance model for estimating runoff at different spatial and temporal scales. J. Geophys. Res. Atmos. 1996, 101, 7461–7475. [Google Scholar] [CrossRef]
- Yang, Z.; Dickinson, R.E. Description of the Biosphere-Atmosphere Transfer Scheme (BATS) for the Soil Moisture Workshop and evaluation of its performance. Glob. Planet. Change 1996, 13, 117–134. [Google Scholar] [CrossRef]
- Dickinson, R.E.; Henderson-Sellers, A.; Kennedy, P.J. Biosphere-Atmosphere Transfer Scheme (BATS) Version le as Coupled to the NCAR Community Climate Model; Technical Note; National Center for Atmospheric Research, Climate and Global Dynamics Division: Boulder, CO, USA, 1993. [Google Scholar]
- Wood, E.F.; Lettenmaier, D.P.; Zartarian, V.G. A land-surface hydrology parameterization with subgrid variability for general circulation models. J. Geophys. Res. Atmos. 1992, 97, 2717–2728. [Google Scholar] [CrossRef]
- Liang, X.; Xie, Z. A new surface runoff parameterization with subgrid-scale soil heterogeneity for land surface models. Adv. Water Resour. 2001, 24, 1173–1193. [Google Scholar] [CrossRef]
- Tukey, J.W. Comparing individual means in the analysis of variance. Biometrics 1949, 5, 99–114. [Google Scholar] [CrossRef]
- Bretz, F.; Hothorn, T.; Westfall, P. Multiple Comparisons Using R; Chapman and Hall/CRC: London, UK, 2010. [Google Scholar]
- Chen, S.; Hwang, C.L.; Beckmann, M.J.; Krelle, W. Fuzzy Multiple Attribute Decision Making: Methods and Applications; Springer: Berlin/Heidelberg, Germany, 1992. [Google Scholar]
- Opricovic, S.; Tzeng, G.-H. Compromise solution by MCDM methods: A comparative analysis of VIKOR and TOPSIS. Eur. J. Oper. Res. 2004, 156, 445–455. [Google Scholar] [CrossRef]
- Jena, P.; Azad, S.; Rajeevan, M.N. Statistical Selection of the Optimum Models in the CMIP5 Dataset for Climate Change Projections of Indian Monsoon Rainfall. Climate 2015, 3, 858–875. [Google Scholar] [CrossRef]
- Komaragiri, S.R.; Kumar, D.N. Ranking general circulation models for India using TOPSIS. J. Water Clim. Change 2014, 6, 288–299. [Google Scholar] [CrossRef]
- Li, J.; Liu, Z.; Yao, Z.; Wang, R. Comprehensive assessment of Coupled Model Intercomparison Project Phase 5 global climate models using observed temperature and precipitation over mainland Southeast Asia. Int. J. Climatol. 2019, 39, 4139–4153. [Google Scholar] [CrossRef]
- Sikder, S.; Hossain, F. Assessment of the weather research and forecasting model generalized parameterization schemes for advancement of precipitation forecasting in monsoon-driven river basins. J. Adv. Model. Earth Syst. 2016, 8, 1210–1228. [Google Scholar] [CrossRef]
- Stergiou, I.; Tagaris, E.; Sotiropoulou, R.-E.P. Sensitivity Assessment of WRF Parameterizations over Europe. Proceedings 2017, 1, 119. [Google Scholar] [CrossRef]
- Wang, X.; Tolksdorf, V.; Otto, M.; Scherer, D. WRF-based dynamical downscaling of ERA5 reanalysis data for High Mountain Asia: Towards a new version of the High Asia Refined analysis. Int. J. Climatol. 2021, 41, 743–762. [Google Scholar] [CrossRef]
- Dirmeyer, P.A.; Gao, X.; Zhao, M.; Guo, Z.; Oki, T.; Hanasaki, N. GSWP-2: Multimodel Analysis and Implications for Our Perception of the Land Surface. Bull. Am. Meteorol. Soc. 2006, 87, 1381–1398. [Google Scholar] [CrossRef]
- Hinkel, K.M.; Outcalt, S.I.; Nelson, F.E. Temperature variation and apparent thermal diffusivity in the refreezing active layer, Toolik Lake, Alaska. Permafr. Periglac. Process. 1990, 1, 265–274. [Google Scholar] [CrossRef]
- Gayler, S.; Wöhling, T.; Grzeschik, M.; Ingwersen, J.; Wizemann, H.-D.; Warrach-Sagi, K.; Högy, P.; Attinger, S.; Streck, T.; Wulfmeyer, V. Incorporating dynamic root growth enhances the performance of Noah-MP at two contrasting winter wheat field sites. Water Resour. Res. 2014, 50, 1337–1356. [Google Scholar] [CrossRef]
- Galik, A.; Bąk, M.; Bałandynowicz-Panfil, K.; Cirella, G.T. Evaluating Labour Market Flexibility Using the TOPSIS Method: Sustainable Industrial Relations. Sustainability 2022, 14, 526. [Google Scholar] [CrossRef]
- Chang, M.; Liao, W.; Wang, X.; Zhang, Q.; Chen, W.; Wu, Z.; Hu, Z. An optimal ensemble of the Noah-MP land surface model for simulating surface heat fluxes over a typical subtropical forest in South China. Agric. For. Meteorol. 2020, 281, 107815. [Google Scholar] [CrossRef]
- Wang, Y.; Liu, X.; Lv, M.; Zhang, Z. Mechanisms and influencing factors of hydrothermal processes in active layer soils on the Qinghai-Tibet Plateau under freeze-thaw action. CATENA 2023, 220, 106694. [Google Scholar] [CrossRef]




| Experiment | Freeze–Thaw Cycle | Thawed Period | Frozen Period | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Soil Layer | 1 | 2 | 3 | 4 | 1 | 2 | 3 | 4 | 1 | 2 | 3 | 4 | |
| Def | RMSE (°C) | 5.13 | 3.44 | 3.80 | 5.63 | 4.74 | 1.60 | 1.05 | 2.15 | 5.49 | 4.62 | 5.26 | 7.12 |
| MBE (°C) | −4.42 | −1.81 | −2.28 | −4.31 | −4.27 | 0.21 | −0.08 | −1.93 | −4.57 | −3.89 | −4.44 | −5.98 | |
| R | 0.95 | 0.98 | 0.98 | 0.90 | 0.66 | 0.86 | 0.91 | 0.50 | 0.80 | 0.92 | 0.93 | 0.80 | |
| Ens1 | RMSE (°C) | 5.09 | 2.33 | 2.36 | 3.24 | 4.97 | 1.54 | 1.33 | 1.51 | 5.20 | 2.93 | 3.06 | 4.04 |
| MBE (°C) | −4.48 | −1.44 | −1.65 | −2.49 | −4.40 | −0.54 | −0.95 | −0.99 | −4.57 | −2.36 | −2.34 | −3.55 | |
| R | 0.96 | 0.98 | 0.97 | 0.97 | 0.72 | 0.88 | 0.91 | 0.34 | 0.79 | 0.89 | 0.87 | 0.98 | |
| Ens2 | RMSE (°C) | 4.93 | 2.62 | 2.57 | 3.57 | 4.49 | 1.62 | 1.08 | 1.41 | 5.34 | 3.35 | 3.46 | 4.51 |
| MBE (°C) | −4.34 | −1.25 | −1.34 | −2.37 | −3.92 | 0.31 | 0.19 | −0.23 | −4.76 | −2.85 | −2.84 | −3.87 | |
| R | 0.96 | 0.98 | 0.98 | 0.97 | 0.72 | 0.89 | 0.92 | 0.34 | 0.82 | 0.90 | 0.90 | 0.98 | |
| Ens3 | RMSE (°C) | 5.28 | 2.28 | 2.56 | 3.04 | 5.47 | 1.93 | 2.29 | 1.98 | 5.08 | 2.59 | 2.80 | 3.61 |
| MBE (°C) | −4.63 | −1.63 | −1.96 | −2.61 | −4.88 | −1.39 | −2.09 | −1.74 | −4.37 | −1.87 | −1.84 | −3.23 | |
| R | 0.95 | 0.98 | 0.96 | 0.97 | 0.70 | 0.87 | 0.88 | 0.34 | 0.76 | 0.87 | 0.81 | 0.97 | |
| Opt1 | RMSE (°C) | 4.22 | 3.60 | 3.96 | 4.54 | 3.93 | 4.21 | 5.06 | 6.62 | 4.50 | 2.83 | 2.44 | 2.07 |
| MBE (°C) | −2.31 | 2.25 | 3.09 | 3.07 | −2.96 | 3.70 | 4.46 | 5.67 | −1.66 | 0.75 | 1.74 | 1.24 | |
| R | 0.90 | 0.96 | 0.96 | 0.91 | 0.56 | 0.73 | 0.62 | 0.53 | 0.67 | 0.83 | 0.90 | 0.89 | |
| Opt2 | RMSE (°C) | 4.15 | 3.74 | 4.47 | 5.42 | 3.35 | 4.63 | 5.98 | 8.14 | 4.83 | 2.51 | 2.09 | 1.86 |
| MBE (°C) | −2.30 | 2.43 | 3.47 | 3.52 | −2.30 | 4.21 | 5.61 | 7.68 | −2.29 | 0.60 | 1.37 | 0.59 | |
| R | 0.92 | 0.97 | 0.98 | 0.96 | 0.66 | 0.81 | 0.82 | 0.71 | 0.69 | 0.87 | 0.94 | 0.95 | |
| Experiment | Freeze–Thaw Cycle | Thawed Period | Frozen Period | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Soil Layer | 1 | 2 | 3 | 4 | 1 | 2 | 3 | 4 | 1 | 2 | 3 | 4 | |
| Def | RMSE (m3/m3) | 0.084 | 0.052 | 0.030 | 0.100 | 0.096 | 0.061 | 0.036 | 0.139 | 0.071 | 0.040 | 0.023 | 0.057 |
| MBE (m3/m3) | −0.081 | −0.047 | −0.019 | −0.072 | −0.092 | −0.057 | −0.029 | −0.121 | −0.070 | −0.036 | −0.009 | −0.038 | |
| R | 0.929 | 0.956 | 0.967 | 0.325 | 0.455 | 0.300 | 0.894 | −0.425 | 0.578 | 0.669 | 0.900 | 0.166 | |
| Ens1 | RMSE (m3/m3) | 0.107 | 0.057 | 0.014 | 0.046 | 0.135 | 0.074 | 0.017 | 0.067 | 0.065 | 0.031 | 0.011 | 0.021 |
| MBE (m3/m3) | −0.098 | −0.051 | −0.005 | −0.032 | −0.132 | −0.073 | −0.014 | −0.064 | −0.064 | −0.028 | 0.003 | −0.010 | |
| R | 0.903 | 0.983 | 0.992 | 0.973 | 0.254 | 0.786 | 0.976 | 0.666 | 0.702 | 0.887 | 0.985 | 0.987 | |
| Ens2 | RMSE (m3/m3) | 0.096 | 0.052 | 0.029 | 0.051 | 0.118 | 0.066 | 0.039 | 0.074 | 0.066 | 0.031 | 0.015 | 0.024 |
| MBE (m3/m3) | −0.090 | −0.047 | −0.017 | −0.037 | −0.114 | −0.065 | −0.033 | −0.068 | −0.065 | −0.029 | −0.001 | −0.015 | |
| R | 0.907 | 0.987 | 0.985 | 0.947 | 0.305 | 0.828 | 0.928 | 0.332 | 0.721 | 0.918 | 0.974 | 0.988 | |
| Ens3 | RMSE (m3/m3) | 0.118 | 0.063 | 0.017 | 0.042 | 0.153 | 0.082 | 0.022 | 0.062 | 0.065 | 0.032 | 0.010 | 0.019 |
| MBE (m3/m3) | −0.107 | −0.054 | 0.006 | −0.028 | −0.150 | −0.081 | 0.005 | −0.059 | −0.064 | −0.027 | 0.007 | −0.006 | |
| R | 0.789 | 0.972 | 0.981 | 0.982 | 0.065 | 0.661 | 0.964 | 0.841 | 0.619 | 0.803 | 0.990 | 0.982 | |
| Opt1 | RMSE (m3/m3) | 0.083 | 0.045 | 0.033 | 0.075 | 0.104 | 0.058 | 0.028 | 0.088 | 0.053 | 0.027 | 0.038 | 0.065 |
| MBE (m3/m3) | −0.074 | −0.030 | 0.007 | 0.062 | −0.097 | −0.054 | −0.006 | 0.079 | −0.051 | −0.004 | 0.021 | 0.049 | |
| R | 0.831 | 0.874 | 0.911 | 0.917 | 0.071 | 0.454 | 0.830 | 0.463 | 0.611 | 0.751 | 0.708 | 0.878 | |
| Opt2 | RMSE (m3/m3) | 0.070 | 0.041 | 0.036 | 0.053 | 0.081 | 0.051 | 0.039 | 0.060 | 0.057 | 0.027 | 0.032 | 0.047 |
| MBE (m3/m3) | −0.065 | −0.028 | 0.009 | 0.041 | −0.075 | −0.046 | −0.002 | 0.052 | −0.056 | −0.010 | 0.020 | 0.033 | |
| R | 0.919 | 0.903 | 0.893 | 0.934 | 0.202 | 0.215 | 0.438 | 0.574 | 0.742 | 0.829 | 0.831 | 0.880 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jiao, Y.; Li, R.; Wu, T.; Wu, X.; Wang, S.; Yao, J.; Hu, G.; Zhu, X.; Shi, J.; Xiao, Y.; et al. Physical Parameterization Sensitivity of Noah-MP for Hydrothermal Simulation Within the Active Layer on the Qinghai–Tibet Plateau. Land 2025, 14, 247. https://doi.org/10.3390/land14020247
Jiao Y, Li R, Wu T, Wu X, Wang S, Yao J, Hu G, Zhu X, Shi J, Xiao Y, et al. Physical Parameterization Sensitivity of Noah-MP for Hydrothermal Simulation Within the Active Layer on the Qinghai–Tibet Plateau. Land. 2025; 14(2):247. https://doi.org/10.3390/land14020247
Chicago/Turabian StyleJiao, Yongliang, Ren Li, Tonghua Wu, Xiaodong Wu, Shenning Wang, Jimin Yao, Guojie Hu, Xiaofan Zhu, Jianzong Shi, Yao Xiao, and et al. 2025. "Physical Parameterization Sensitivity of Noah-MP for Hydrothermal Simulation Within the Active Layer on the Qinghai–Tibet Plateau" Land 14, no. 2: 247. https://doi.org/10.3390/land14020247
APA StyleJiao, Y., Li, R., Wu, T., Wu, X., Wang, S., Yao, J., Hu, G., Zhu, X., Shi, J., Xiao, Y., Du, E., & Qiao, Y. (2025). Physical Parameterization Sensitivity of Noah-MP for Hydrothermal Simulation Within the Active Layer on the Qinghai–Tibet Plateau. Land, 14(2), 247. https://doi.org/10.3390/land14020247









