The multi-methodological background of these two approaches will be illustrated in detail in the remaining part of this section.
2.1. The System of Landscape Economic Indicators
Systems of indicators constitute the most used evaluation tool to assess and monitor a landscape. Generally, an indicator is a parameter used to measure a certain phenomenon by providing information on its characteristics and on its global form [
15]. Economic assessment experiences have been included in landscape research, with emphasis on the use of landscape economic indicators [
5] because these provide a mean for measuring the value of landscape focusing on its utility or functionality for the people use [
16]. As far as landscape economic indicators are considered, these can be referred to quantitative and/or qualitative economic evaluation methods. The quantitative economic evaluation methods (i.e., monetary approach) estimate the willingness to pay to use a landscape to be evaluated. Within this family of methods, it is possible to recall the Contingent Valuation method, the Choice Experiments technique [
17,
18], the Stated Preferences methods [
19,
20] or the Hedonic Pricing method [
21,
22].
The qualitative economic evaluation methods (i.e., non-monetary approach) is finalized to calculate an average score of landscape by considering a set of qualitative and quantitative criteria and including the opinion of experts and society in the evaluation [
23].
Table 1 summarizes the main economic evaluation methodologies shared in literature for assessing a landscape.
This research work chooses a non-monetary evaluation by employing a set of indicators that are finalized to evaluate the landscape economic attractiveness as it concerns its elements. As noticed by Gómez-Sal et al. (2013) [
24], indicators are not a panacea and there is a need to research them with reference to their importance, structure, relations, and place them into a hierarchy. This allows the indicators system to be used for evaluating the territory under examination and to see how it addresses future possible scenarios. Therefore, we have structured the system of landscape economic indicators according to the Analytic Hierarchy Process (AHP) because it allows the evaluation of both qualitative and quantitative aspects of complex problems [
25,
26]. Therefore, we have defined the following elements: The goal, that is the assessment of the landscape economic attractiveness; the criteria which are represented by four economic categories and these are further subdivided into economic indicators; and the alternatives that correspond to a set of territorial clusters. The economic categories chosen for this evaluation represent the most important aspects that contribute to the economic attractiveness of a landscape and arise from the relevant literature in the domain of economic evaluation of landscape [
27]: Agriculture (A), Tourism (T), Real estate market (R) and Forestry (F). The Agriculture category concerns the existing relations between agricultural landscapes and the economic system, considering rural employment and local investment [
28,
29]. The Tourism category aims at analyzing the role of landscape in attracting tourism flows [
30]. As far as the Real estate category is considered, landscape and general natural amenities have a fundamental role in generating benefits on property values considering both buildings and agricultural fields [
31]. All this research agrees in considering landscape as a positive externality that generates benefits on property values. Finally, the Forestry category represents the benefits delivered by forestry management and activities for local economic development.
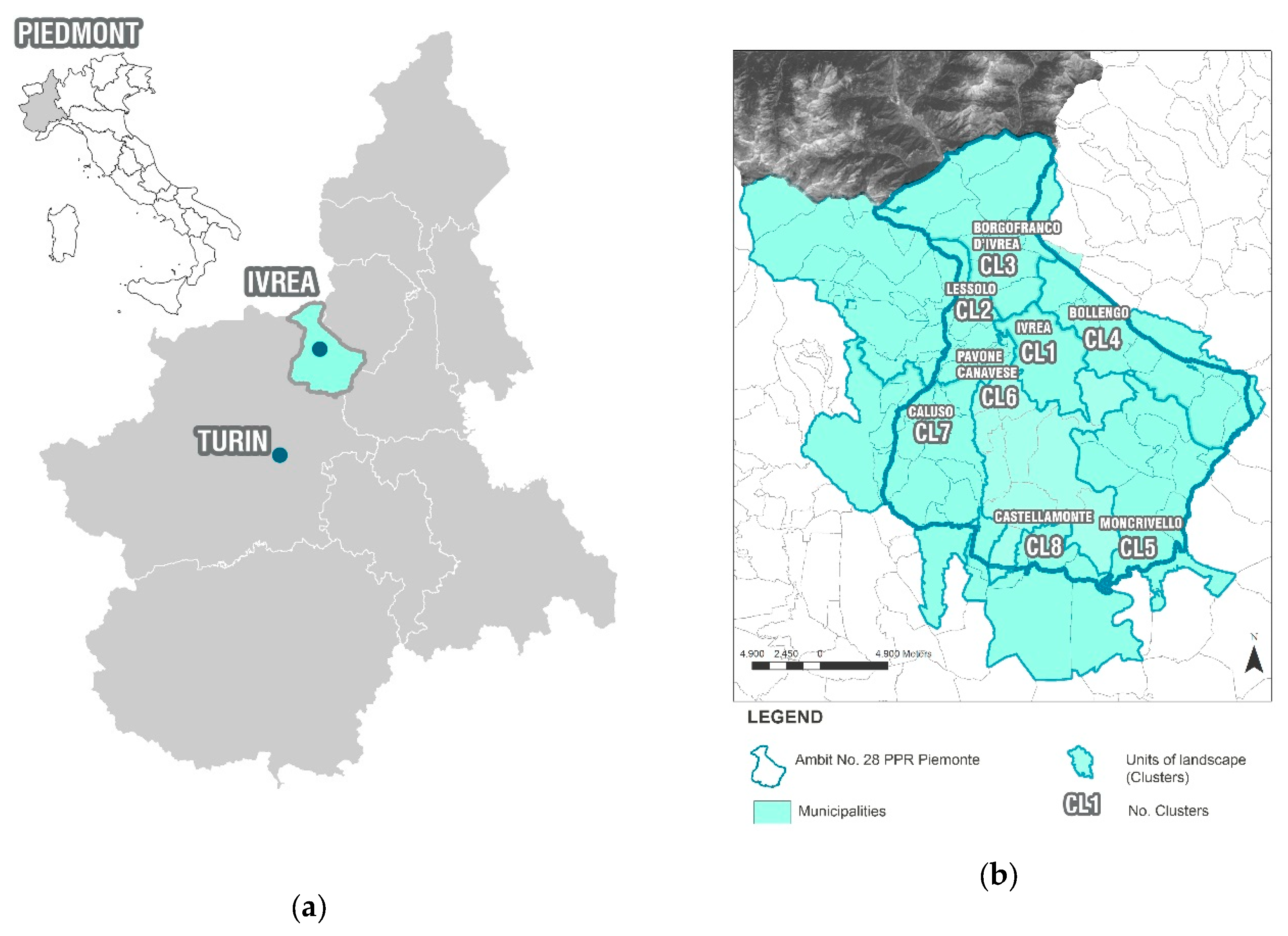
Table 2 represents the system of landscape economic indicators employed in the present research. The landscape economic indicators are then aggregated following the subsequent levels of the hierarchy thus obtaining a synthetic index called LEA (Landscape Economic Attractiveness).
It can be observed that the LEA index is something different from other economic indices such as the Gross Domestic Product index (GDP). In fact, the GDP is a parameter for measuring the economic performance of a territory, without considering sustainability issues or quality of life. Many drawbacks and limitations have been recognized in using the GDP as a measure of the economic well-being of an area and so other aggregated sustainability measures have been proposed [
32]. It has to be noticed that, compared to GDP, the LEA is a non-dimensional index that is constructed considering multidimensional indicators which contribute, at different degrees of importance, to the definition of the landscape value. In fact, while GDP can be useful in the tackling the specific problems of economic development in a region, the borders of landscape value are certainly vaster and a number of indicators is required. In this sense, indicators and composite indicators are increasingly recognized as a useful tool for policy making and public communication [
33]. Following the latest initiatives in the context of suitability indicators frameworks, a number of components of a landscape (e.g., agriculture, tourism, real estate market and forestry) and the economic benefits that it provides to people, are included in this model. Municipal data have been collected and then organized in a system of territorial clusters (also known as Landscape Units), according to the territorial and landscape continuity of the considered Municipalities. As far as the LEA is considered, the purpose is to provide an integrated evaluation of the economic attractiveness of a landscape, focusing on the different benefits provided to people.
The subsequent phases provide the estimation of the landscape economic attractiveness, through normalization and aggregation formulas.
Normalization is employed to relate a certain numeric value
xi with the maximum value
ximax recorded in the same category among clusters, whose result is a normalized indicator
Ii. As shown in Equation (1), the normalization allows all indicators to be comparable in an interval between 0 and 1.
Weighting is an important step to know the importance of the different evaluated elements. It is important to notice that the set of weights used in this evaluation has been determined by the utilization of the analytic hierarchy process [
25] with a panel of experts. In this case, it was presented to a panel of experts in agriculture, tourism, real estate, and forestry fields, the importance of the economic elements of landscape [
11,
34] using the pairwise comparison method. The experts expressed a value through the Saaty’s scale values from 1 to 9, where 1 means same importance and 9 means extremely strong importance. Subsequently, the values have been converted into a set of weights through the software Expert Choice.
Table 3 reports the set of weights obtained.
Once the set of weights is obtained, it is possible to aggregate the sub-criteria in partial indices by calculating the weighted average sum, as shown in Equations (2) and (3).
Finally, a synthetic index named the Landscape Economic Attractiveness index is obtained through the aggregation of partial indices using the following formula:
This synthetic index is a non-dimensional value between zero and one, where zero means a lesser economic attractiveness, and one is the maximum economic attractiveness in the landscape under investigation.
Finally, the LEA indices are related to the clusters surface (
Km2), thus obtaining the Specific Landscape Economic Attractiveness index (SLEA).
In order to better differentiate LEA and SLEA indices, the numerical figures were normalized, translating the original scores into the 0–1 scale and awarding 1 the maximum value within the considered set. The LEA indices will be used in such parameter within the dynamic model. In the following paragraph, the relation between landscape evaluation and mathematical modeling is examined.
2.2. The Dynamic Model
In order to test the influence of the economic attractiveness on the possible people mobility throughout the landscape under observation, a suitable mathematical model has been used. Such a model consists of a system of differential equations, used in the 1980s [
10] to study the city and its issues, according to the idea that the population changes depending on both the environment and mobility, which is the level of proximity of a generic
i center of the neighboring cities, and the economic attractiveness value, represented by their own economic, social, and cultural components. The present survey is about the possible dynamic fluxes of population, moving permanently for a change of residence. Such a model [
35] has been recently adapted for a problem concerning gross leasable areas in the valley communities of the autonomous province of Trento in Italy [
36].
In this study, people mobility is closely related to landscape economic attractiveness, as a high LEA value in a given center implies a high number of people living in the neighboring centers who will be willing to move to that center.
Given a system composed of a number of urban centers, linked by a regular road network, whose reciprocal distances (
dij) and the attractiveness coefficients (respectively,
Ai that is the attractiveness exerted by the
i center on its own population, and
Aij, the attractiveness of the
i center as perceived by the populations of the other
j centers) are known, it is possible to formulate a system of differential equations which may be viewed as a special type of the cooperative Lotka–Volterra system [
35,
37].
The state variable of the mathematical model is the number of residents
pi of each cluster. The mathematical system which will be employed for the simulations proposed further on is then given by
The variation of population (
p’i is the time derivative) of the
i cluster is determined by the two terms of the second member of Equation (5). The first term is of the logistic type and depends on the carrying capacity 1/
si,
si being a suitable threshold which takes into account that the
i cluster may suffer if it is overcrowded, while the second member depends on the attractiveness parameters
Aij. According to the properties of the cooperative Lotka–Volterra type equations, the differential system has always at least one stable equilibrium solution [
38].
As it concerns the coefficients
Aij, they have been calculated according to the following formula:
where
dM is the maximum value of the distances
dij in the road network for any value of
i and
j. Observe that the attractiveness
Bij of the
i cluster perceived by the other ones depends directly on
Ai and is inverse proportional to
Aj so that the relative strength of the cluster
i is conditioned by the attractiveness of the cluster
j.
In conclusion, the dynamics of the model depends on the attractiveness coefficients of the clusters, on their threshold values, and on the reciprocal distances among the clusters themselves, so that the model expresses the limitation of people mobility in the territory. As it will be shown in the simulations, the attractiveness coefficients characterize the trends of fluxes during the transient times of simulation, while the threshold values and the reciprocal distances between clusters determine the repartition of the population values among the clusters themselves in a standard condition.