Real-Time Video Stitching Using Camera Path Estimation and Homography Refinement
Abstract
:1. Introduction
2. Related Work
2.1. Image Stitching
2.2. Video Stitching
3. Overview of the Proposed Method
3.1. Notation
3.2. Basic Theory
3.3. Proposed Method
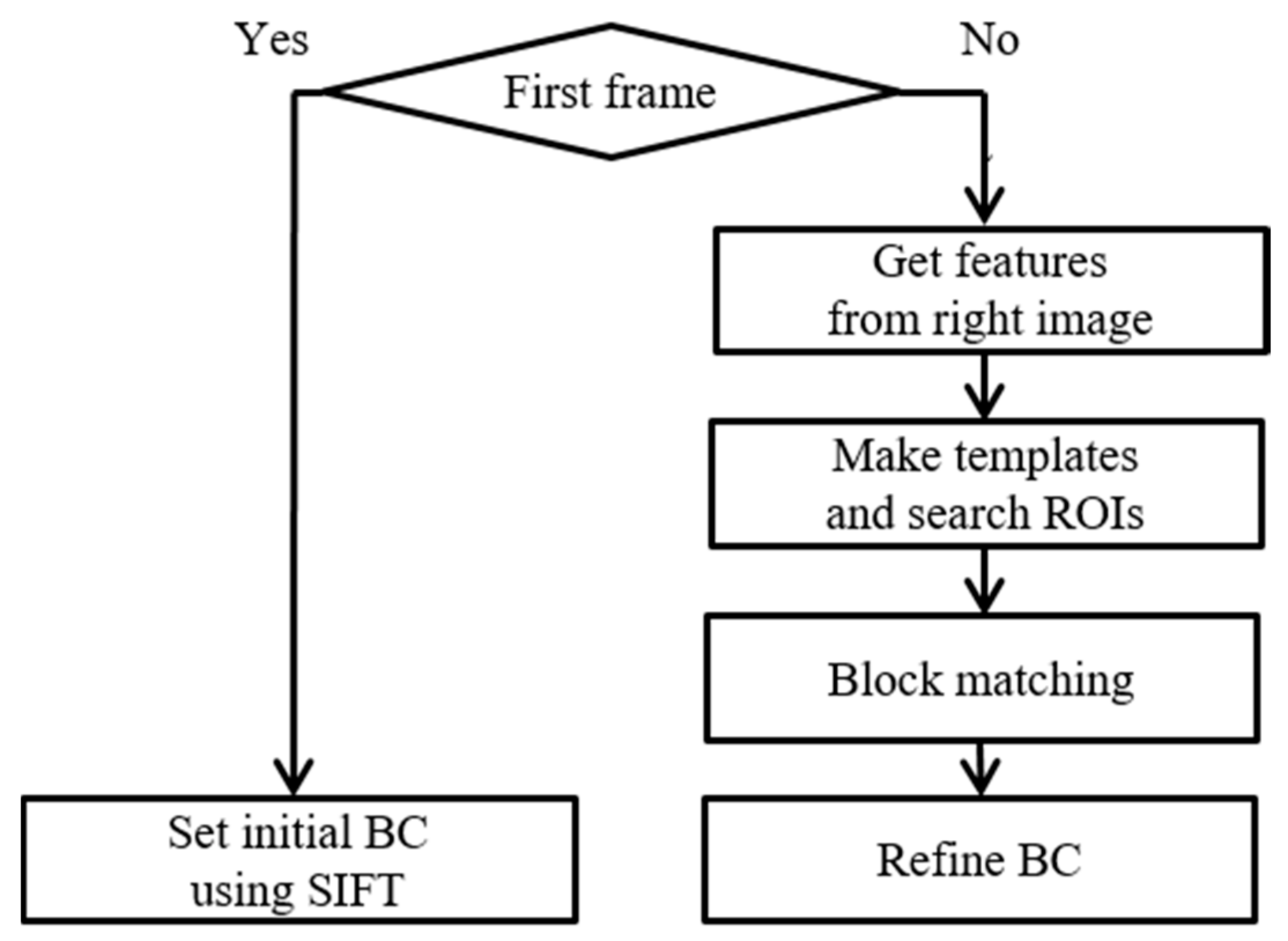
4. Camera Path Estimation
4.1. Feature Extraction
4.2. Feature Matching
4.3. Feature Selection
5. Homography Refinement
6. Experimental Results
6.1. Processing Time and Stitching Quality
6.2. Comparison with Other Methods
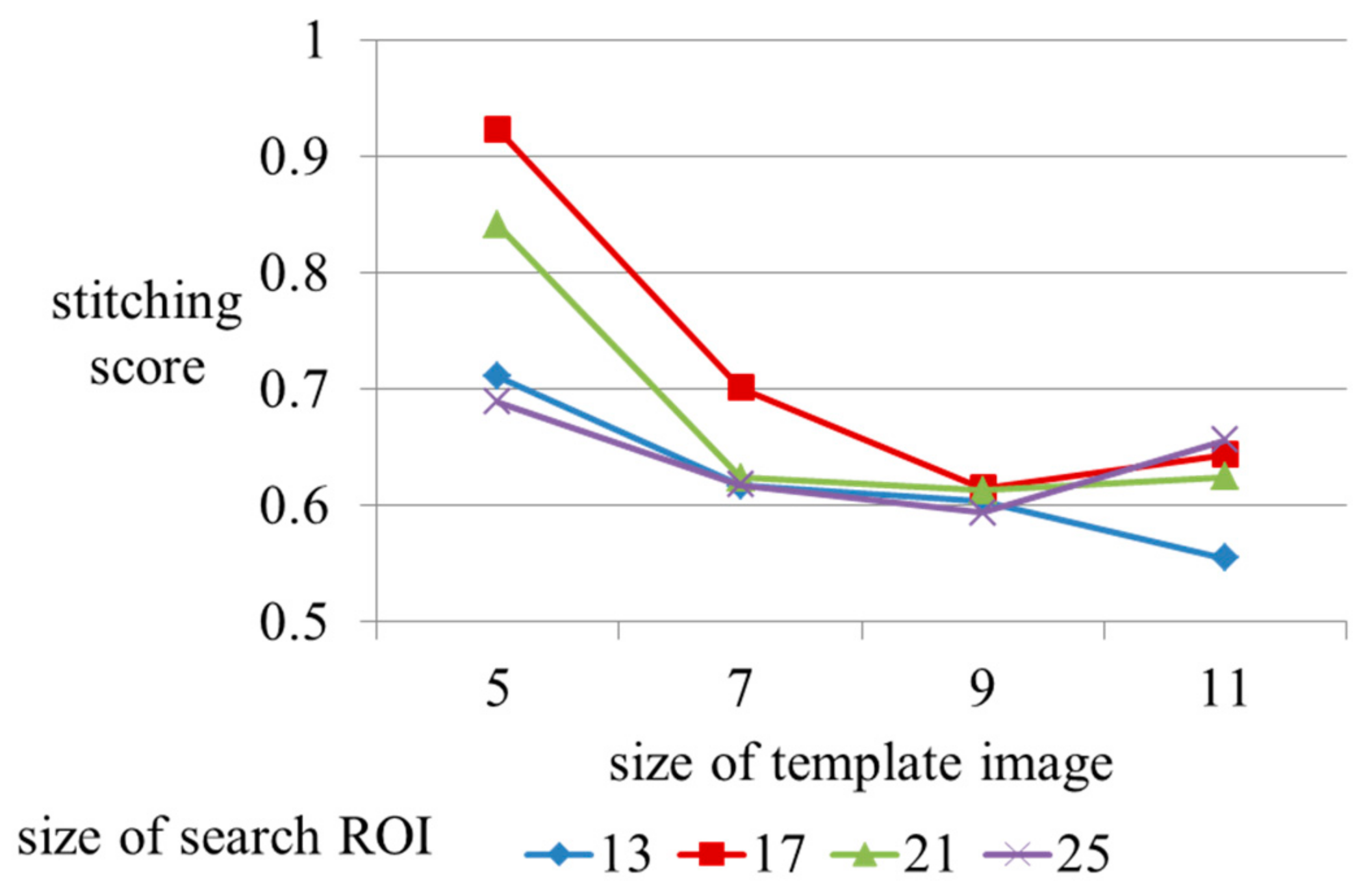
6.3. Parameter Optimization
7. Discussion
8. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- He, B.; Yu, S. Parallax-Robust Surveillance Video Stitching. Sensors 2016, 16, 7. [Google Scholar] [CrossRef] [PubMed]
- He, B.; Zhao, G.; Liu, Q. Panoramic Video Stitching in Multi-Camera Surveillance System. In Proceedings of the 25th International Conference of Image and Vision Computing New Zealand (IVCNZ), Queenstown, New Zealand, 8–9 November 2010; pp. 1–6. [Google Scholar]
- Amiri, A.J.; Moradi, H. Real-Time Video Stabilization and Mosaicking for Monitoring and Surveillance. In Proceedings of the 4th International Conference on Robotics and Mechatronics (ICROM), Tehran, Iran, 26–28 October 2016; pp. 613–618. [Google Scholar]
- Li, J.; Xu, W.; Zhang, J.; Zhang, M.; Wang, Z.; Li, X. Efficient Video Stitching Based on Fast Structure Deformation. IEEE Trans. Cybern. 2015, 45, 2707–2719. [Google Scholar] [CrossRef] [PubMed]
- Lin, K.; Liu, S.; Cheong, L.; Zeng, B. Seamless Video Stitching from Hand-held Camera Inputs. Comput. Graphics Forum 2016, 35, 479–487. [Google Scholar] [CrossRef]
- Guo, H.; Liu, S.; He, T.; Zhu, S.; Zeng, B.; Gabbouj, M. Joint Video Stitching and Stabilization from Moving Cameras. IEEE Trans. Image Process. 2016, 25, 5491–5503. [Google Scholar] [CrossRef] [PubMed]
- Bouguet, J. Pyramidal Implementation of the Affine Lucas Kanade Feature Tracker Description of the Algorithm. Intel. Corpor. 2001, 5, 4. [Google Scholar]
- Szeliski, R. Image Alignment and Stitching: A Tutorial. In Foundations and Trends® in Computer Graphics and Vision; Now Publishers Inc.: Hanover, MA, USA, 2007; Volume 2, pp. 1–104. [Google Scholar]
- Lowe, D.G. Distinctive Image Features from Scale-Invariant Keypoints. Int. J. Comput. Vis. 2004, 60, 91–110. [Google Scholar] [CrossRef]
- Bay, H.; Tuytelaars, T.; Van Gool, L. Surf: Speeded Up Robust Features. In Computer Vision–ECCV 2006, Proceedings of the European Conference on Computer Vision; Springer: Berlin, German, 2006; pp. 404–417. [Google Scholar]
- Muja, M.; Lowe, D.G. Scalable Nearest Neighbor Algorithms for High Dimensional Data. IEEE Trans. Pattern Anal. Mach. Intell. 2014, 36, 2227–2240. [Google Scholar] [CrossRef] [PubMed]
- Fischler, M.A.; Bolles, R.C. Random Sample Consensus: A Paradigm for Model Fitting with Applications to Image Analysis and Automated Cartography. Commun ACM 1981, 24, 381–395. [Google Scholar] [CrossRef]
- Agarwala, A.; Dontcheva, M.; Agrawala, M.; Drucker, S.; Colburn, A.; Curless, B.; Salesin, D.; Cohen, M. Interactive Digital Photomontage. In Proceedings of the ACM Transactions on Graphics (TOG), New York, NY, USA, November 2017; pp. 294–302. [Google Scholar]
- Gao, J.; Li, Y.; Chin, T.; Brown, M.S. Seam-Driven Image Stitching. In Eurographics; Short Papers; The Eurographics Association: Lyon, France, 2013; pp. 45–48. [Google Scholar]
- Zomet, A.; Levin, A.; Peleg, S.; Weiss, Y. Seamless Image Stitching by Minimizing False Edges. IEEE Trans. Image Process. 2006, 15, 969–977. [Google Scholar] [CrossRef] [PubMed]
- Lee, S.; Park, Y.; Lee, D. Seamless Image Stitching using Structure Deformation with HoG Matching. In Proceedings of the International Conference on the Information and Communication Technology Convergence (ICTC), Jeju, Korea, 28–30 October 2015; pp. 933–935. [Google Scholar]
- Gao, J.; Kim, S.J.; Brown, M.S. Constructing Image Panoramas using Dual-Homography Warping. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Colorado Springs, CO, USA, 20–25 June 2011; pp. 49–56. [Google Scholar]
- Lin, W.; Liu, S.; Matsushita, Y.; Ng, T.; Cheong, L. Smoothly Varying Affine Stitching. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Colorado Springs, CO, USA, 20–25 June 2011; pp. 345–352. [Google Scholar]
- Zaragoza, J.; Chin, T.; Brown, M.S.; Suter, D. As-Projective-as-Possible Image Stitching with Moving DLT. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Portland, OR, USA, 23–28 June 2013; IEEE: Piscataway, NJ, USA, 2013; pp. 2339–2346. [Google Scholar]
- Chang, C.; Sato, Y.; Chuang, Y. Shape-Preserving Half-Projective Warps for Image Stitching. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Columbus, OH, USA, 23–28 June 2004; pp. 3254–3261. [Google Scholar]
- Jiang, W.; Gu, J. Video Stitching with Spatial-Temporal Content-Preserving Warping. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition Workshops, Boston, MA, USA, 7–12 June 2015; pp. 42–48. [Google Scholar]
- El-Saban, M.; Izz, M.; Kaheel, A.; Refaat, M. Improved Optimal Seam Selection Blending for Fast Video Stitching of Videos Captured from Freely Moving Devices. In Proceedings of the 18th IEEE International Conference on Image Processing (ICIP), Brussels, Belgium, 11–14 September 2011; pp. 1481–1484. [Google Scholar]
- Shimizu, T.; Yoneyama, A.; Takishima, Y. A Fast Video Stitching Method for Motion-Compensated Frames in Compressed Video Streams. In Proceedings of the 2006 Digest of Technical Papers. International Conference on Consumer Electronics (ICCE’06), Las Vegas, NV, USA, 7–11 January 2006; pp. 173–174. [Google Scholar]
- El-Saban, M.; Izz, M.; Kaheel, A. Fast Stitching of Videos Captured from Freely Moving Devices by Exploiting Temporal Redundancy. In Proceedings of the 17th IEEE International Conference on Image Processing (ICIP), Hong Kong, China, 26–29 September 2010; pp. 1193–1196. [Google Scholar]
- Chen, L.; Wang, X.; Liang, X. An Effective Video Stitching Method. In Proceedings of the International Conference on Computer Design and Applications (ICCDA), Qinhuangdao, China, 25–27 June 2010; pp. V1-297–V1-301. [Google Scholar]
- Shum, H.; Szeliski, R. Construction of panoramic image mosaics with global and local alignment. In Panoramic Vision; Springer: Berlin, Germany, 2001; pp. 227–268. [Google Scholar]
- Szeliski, R.; Shum, H. Creating Full View Panoramic Image Mosaics and Environment Maps. In Proceedings of the 24th Annual Conference on Computer Graphics and Interactive Techniques, Los Angeles, CA, USA, 3–8 August 1997; pp. 251–258. [Google Scholar]
- Harris, C.; Stephens, M. A Combined Corner and Edge Detector. In Proceedings of the Alvey Vision Conference, Hong Kong, China, 31 August–2 September 1988; pp. 147–151. [Google Scholar]
- Original Videos and Results. Available online: http://sites.google.com/site/khuaris/home/video-stitching (accessed on 26 December 2017).
- Shi, J. Good Features to Track. In Proceedings of the IEEE Computer Society Conference on Computer Vision and Pattern Recognition (CVPR’94), Seattle, WA, USA, 21–23 June 1994; pp. 593–600. [Google Scholar]
- Wang, O.; Schroers, C.; Zimmer, H.; Gross, M.; Sorkine-Hornung, A. Videosnapping: Interactive Synchronization of Multiple Videos. ACM Trans. Graphics (TOG) 2014, 33, 77. [Google Scholar] [CrossRef]
- Liu, F.; Gleicher, M.; Jin, H.; Agarwala, A. Content-Preserving Warps for 3D Video Stabilization. ACM Trans. Graphics (TOG) 2009, 28, 44. [Google Scholar] [CrossRef]
- Litvin, A.; Konrad, J.; Karl, W.C. Probabilistic Video Stabilization using Kalman Filtering and Mosaicking. Proc. SPIE 2003, 5022, 663–675. [Google Scholar] [CrossRef]





















| Dataset | Camera Path Estimation (ms) | Homography Refinement (ms) | Frame Warping (ms) | Multi-Band Blending (ms) | Total (ms) |
|---|---|---|---|---|---|
| Sample 1 | 10.5 | 6.3 | 16.9 | 46.1 | 80.5 |
| Sample 2 | 11.6 | 6.2 | 14.7 | 39.1 | 72.4 |
| Sample 3 | 10.3 | 6.4 | 15.3 | 41.6 | 74.6 |
| Sample 4 | 10.8 | 6.1 | 17.1 | 49.4 | 83.9 |
| Sample 5 | 11.5 | 5.8 | 15.4 | 34.7 | 68.2 |
| Sample 6 | 11.5 | 6.3 | 14.5 | 40.7 | 73.8 |
| Average | 11.0 | 6.2 | 15.6 | 42.0 | 75.6 |
| Stitching Score | Sample 1 | Sample 2 | Sample 3 | Sample 4 | Sample 5 | Sample 6 | Average |
|---|---|---|---|---|---|---|---|
| Without refinement | 3.031 | 3.315 | 7.187 | 17.126 | 6.533 | 1.434 | 6.433 |
| Homography refinement | 0.621 | 0.623 | 0.576 | 0.595 | 2.695 | 1.051 | 1.027 |
| Methods | Stitching Score (without Homography Refinement) | Processing Time (ms) (Camera Path Estimation) |
|---|---|---|
| Proposed method | 3.031 | 14.2 |
| GFTT | 2.565 | 63.2 |
| Harris corner detection | 3.157 | 69.5 |
| Methods | Stitching Score (with Homography Refinement) | Processing Time (ms) (Homography Refinement) |
|---|---|---|
| Proposed method | 0.649 | 12.4 |
| NNS | 103.106 | 11.5 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yoon, J.; Lee, D. Real-Time Video Stitching Using Camera Path Estimation and Homography Refinement. Symmetry 2018, 10, 4. https://doi.org/10.3390/sym10010004
Yoon J, Lee D. Real-Time Video Stitching Using Camera Path Estimation and Homography Refinement. Symmetry. 2018; 10(1):4. https://doi.org/10.3390/sym10010004
Chicago/Turabian StyleYoon, Jaeyoung, and Daeho Lee. 2018. "Real-Time Video Stitching Using Camera Path Estimation and Homography Refinement" Symmetry 10, no. 1: 4. https://doi.org/10.3390/sym10010004
APA StyleYoon, J., & Lee, D. (2018). Real-Time Video Stitching Using Camera Path Estimation and Homography Refinement. Symmetry, 10(1), 4. https://doi.org/10.3390/sym10010004




