Impact of Collisional Matter on the Late-Time Dynamics of f(R,T) Gravity
Abstract
:1. Introduction
2. Gravity: Basic Formalism
- ,
- .
3. Collisional Matter Model within Theory and Late-Time Dynamics
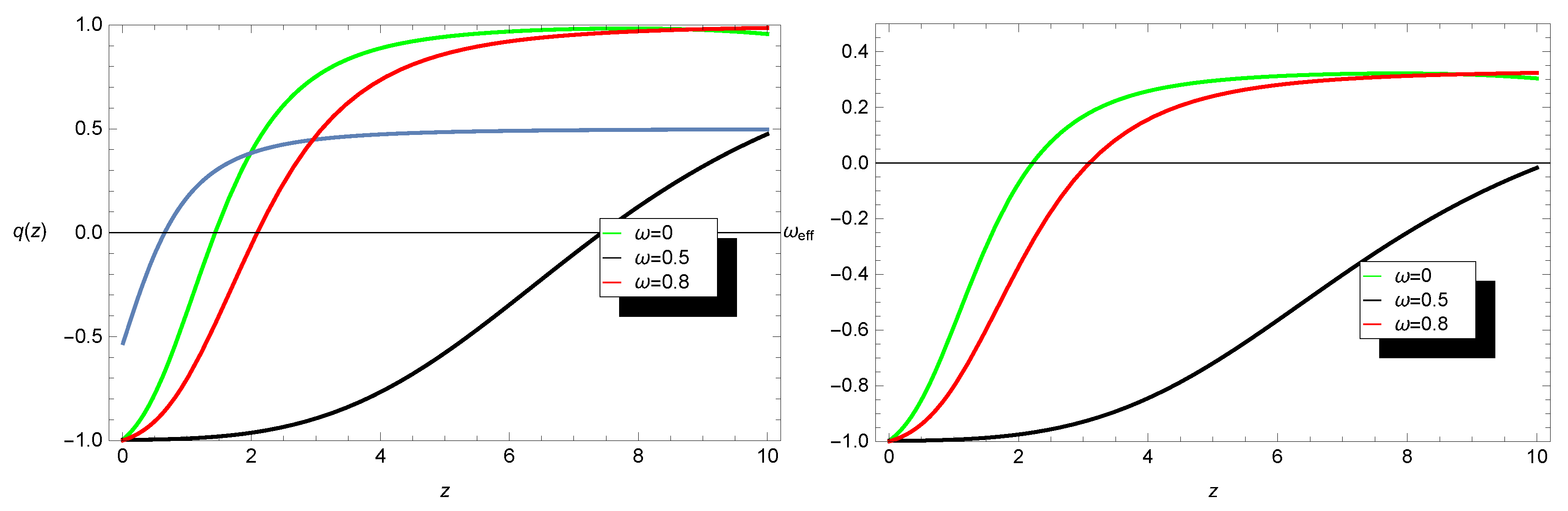
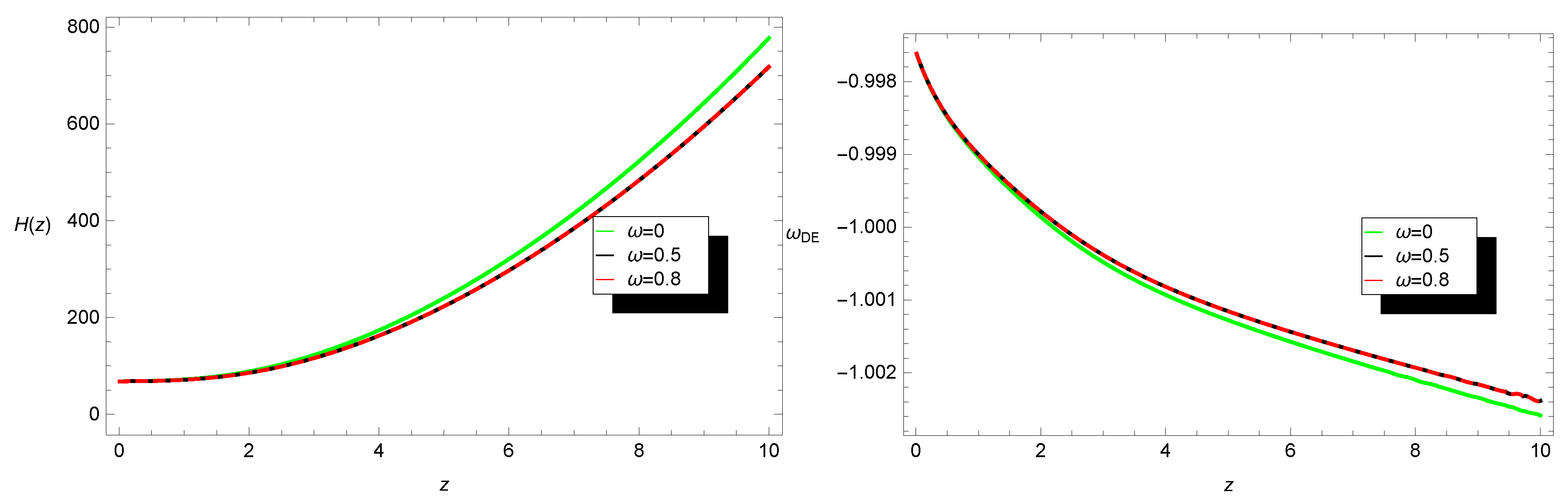
3.1. Model I
- .
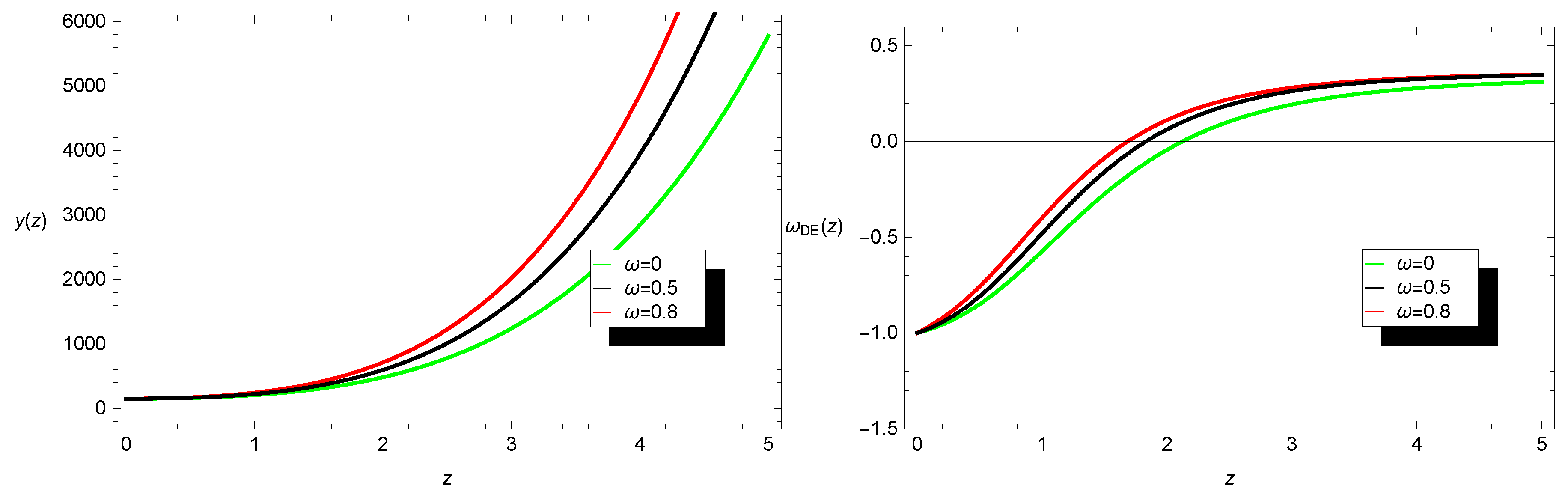
3.2. Model II
3.3. Another Perspective of the Late-Time Cosmological Evolution of Dark Energy with Collisional Matter Fluid
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Perlmutter, S.; Aldering, G.; Goldhaber, G.; Knop, R.A.; Nugent, P.; Castro, P.G.; Deustua, S.; Fabbro, S.; Goobar, A.; Groom, D.E.; et al. Measurements of Ω and Λ from 42 High-Redshift Supernovae. Astrophys. J. 1999, 517, 565–586. [Google Scholar] [CrossRef]
- Riess, A.G.; Filippenko, A.V.; Challis, P.; Clocchiattia, A.; Diercks, A.; Garnavich, P.M.; Gilliland, R.L.; Hogan, C.J.; Jha, S.; Kirshner, R.P.; et al. Observational Evidence from Supernovae for an Accelerating Universe and a Cosmological Constant. Astron. J. 1998, 116, 1009–1038. [Google Scholar] [CrossRef] [Green Version]
- Ade, P.A.R.; Aikin, R.W.; Barkats, D.; Benton, S.J.; Bischoff, C.A.; Bock, J.J.; Brevik, J.A.; Buder, I.; Bullock, E.; Dowell, C.D.; et al. Detection of B-Mode Polarization at Degree Angular Scales by BICEP2. Phys. Rev. Lett. 2014, 112, 241101. [Google Scholar] [CrossRef] [PubMed]
- Nojiri, S.; Odintsov, S.D. Modified gravity with negative and positive powers of the curvature: Unification of the inflation and of the cosmic acceleration. Phys. Rev. D 2003, 68, 123512. [Google Scholar] [CrossRef]
- Nojiri, S.; Odintsov, S.D.; Oikonomou, V.K. Modified Gravity Theories on a Nutshell: Inflation, Bounce and Late-time Evolution. Phys. Rep. 2017, 692, 1–104. [Google Scholar] [CrossRef]
- Nojiri, S.; Odintsov, S.D. Unified cosmic history in modified gravity: From F(R) theory to Lorentz non-invariant models. Phys. Rep. 2011, 505, 59–144. [Google Scholar] [CrossRef]
- Weinberg, S. The cosmological constant problem. Rev. Mod. Phys. 1989, 61, 1. [Google Scholar] [CrossRef]
- Ade, P.A.R.; Aghanim, N.; Armitage-Caplan, C.; Arnaud, M.; Ashdown, M.; Atrio-Barandela, F.; Aumont, J.; Baccigalupi, C.; Banday, A.J.; Barreiro, R.B.; et al. Planck 2013 results. XVI. Cosmological parameters. Astron. Astrophys. 2014, 571, A16. [Google Scholar]
- Spergel, D.N.; Bean, R.; Dor, O.; Nolta, M.R.; Bennett, C.L.; Dunkley, J.; Hinshaw, G.; Jarosik, N.; Komatsu, E.; Page, L.; et al. Three-Year Wilkinson Microwave Anisotropy Probe (WMAP) Observations: Implications for Cosmology. Astrophys. J. Suppl. 2007, 170, 377. [Google Scholar] [CrossRef]
- Eisenstein, D.J.; Zehavi, I.; Hogg, D.W.; Scoccimarro, R.; Blanton, M.R.; Nichol, R.C.; Scranton, R.; Seo, H.-J.; Tegmark, M.; Zheng, S.; et al. Detection of the Baryon Acoustic Peak in the Large-Scale Correlation Function of SDSS Luminous Red Galaxies. Astrophys. J. 2005, 633, 560–574. [Google Scholar] [CrossRef]
- Capozziello, S.; Faraoni, V. Beyond Einstein Gravity: A Survey of Gravitational Theories for Cosmology and Astrophysics; Springer: Berlin, Germany, 2011. [Google Scholar]
- Ferraro, R.; Fiorini, F. Modified teleparallel gravity: Inflation without an inflaton. Phys. Rev. D 2007, 75, 084031. [Google Scholar] [CrossRef]
- Faraoni, V. Cosmology in Scalar-Tensor Gravity; Kluwer Academic Publishers: Alphen aan den Rijn, The Netherlands, 2004. [Google Scholar]
- Sharif, M.; Zubair, M. Effects of Electromagnetic Field on the Dynamics of Bianchi type VI0 Universe with Anisotropic Dark Energy. Int. J. Mod. Phys. D 2010, 19, 1957–1972. [Google Scholar] [CrossRef]
- Sharif, M.; Zubair, M. Dynamics of a magnetized Bianchi VI0 universe with anisotropic fluid. Astrophys. Space Sci. 2012, 339, 45. [Google Scholar] [CrossRef]
- Sharif, M.; Zubair, M. Study of Bianchi I anisotropic model in f(R,T) gravity. Astrophys. Space Sci. 2014, 349, 457. [Google Scholar] [CrossRef]
- Brevik, I.; Gron, O.; de Haro, J.; Odintsov, S.D.; Saridakis, E.N. Viscous Cosmology for Early- and Late-Time Universe. Int. J. Mod. Phys. D 2017, 26, 1730024. [Google Scholar] [CrossRef]
- Brevik, I.; Elizalde, E.; Odintsov, S.D.; Timoshkin, A.V. Inflationary universe in terms of a van der Waals viscous fluid. Int. J. Geom. Meth. Mod. Phys. 2017, 14, 1750185. [Google Scholar] [CrossRef] [Green Version]
- Brevik, I.; Obukhov, V.V.; Timoshkin, A.V. Inflation in Terms of a Viscous van der Waals Coupled Fluid. Int. J. Geom. Meth. Mod. Phys. 2018, 15, 1850150. [Google Scholar] [CrossRef]
- Buchdahl, H.A. Non-linear Lagrangians and cosmological theory. Mon. Notice R. Astron. Soc. 1970, 150, 1. [Google Scholar] [CrossRef]
- Harko, T.; Lobo, F.S.N.; Nojiri, S.; Odintsov, S.D. f(R,T) gravity. Phys. Rev. D 2011, 84, 024020. [Google Scholar] [CrossRef]
- Azmat, H.; Zubair, M.; Noureen, I. Dynamics of shearing viscous fluids in f(R,T) gravity. Int. J. Mod. Phys. D 2017, 27, 1750181. [Google Scholar] [CrossRef]
- Baffou, E.H.; Salako, I.G.; Houndjo, M.J.S. Viscous Generalized Chaplygin Gas Interacting with f(R,T) gravity. Int. J. Geom. Meth. Mod. Phys. 2017, 14, 1750051. [Google Scholar] [CrossRef]
- Barrientos, E.; Lobo, F.S.N.; Mendoza, S.; Olmo, G.J.; Rubiera-Garcia, D. Metric-affine f(R,T) theories of gravity and their applications. Phys. Rev. D 2018, 97, 104041. [Google Scholar] [CrossRef]
- Pradhan, A.; Jaiswal, R. Magnetized string cosmological models of accelerated expansion of the Universe in f(R,T) theory of gravity. Int. J. Geom. Meth. Mod. Phys. 2018, 15, 1850076. [Google Scholar] [CrossRef]
- Zubair, M.; Azmat, H.; Noureen, I. Anisotropic stellar filaments evolving under expansion-free condition in f(R,T) gravity. Int. J. Mod. Phys. D 2018, 27, 1850047. [Google Scholar] [CrossRef]
- Shabani, H.; Ziaie, A.H. Bouncing cosmological solutions from f(R,T) gravity. Eur. Phys. J. C 2018, 78, 397. [Google Scholar] [CrossRef]
- Jamil, M.; Momenil, D.; Raza, M.; Myrzakulov, R. Reconstruction of some cosmological models in f(R,T) cosmology. Eur. Phys. J. 2012, 72, 1999. [Google Scholar] [CrossRef]
- Zubair, M.; Waheed, S.; Ahmad, Y. Static spherically symmetric wormholes in f(R,T) gravity. Eur. Phys. J. C 2016, 76, 444. [Google Scholar] [CrossRef]
- Zubair, M.; Mustafa, G.; Waheed, S.; Abbas, G. Existence of stable wormholes on a non-commutative-geometric background in modified gravity. Eur. Phys. J. C 2017, 77, 680. [Google Scholar] [CrossRef] [Green Version]
- Moraes, P.H.R.S.; Sahoo, P.K. The simplest non-minimal matter-geometry coupling in the f(R,T) cosmology. Eur. Phys. J. C 2017, 77, 480. [Google Scholar] [CrossRef]
- Moraes, P.H.R.S.; Correa, R.A.C.; Lobato, R.V. Analytical general solutions for static wormholes in f(R,T) gravity. JCAP 2017, 7, 29. [Google Scholar] [CrossRef]
- Moraes, P.H.R.S.; Sahoo, P.K. Modelling wormholes in f(R,T) gravity. Phys. Rev. D 2017, 96, 044038. [Google Scholar] [CrossRef]
- Sharif, M.; Zubair, M. Thermodynamics in f(R,T) theory of gravity. JCAP 2012, 3, 028. [Google Scholar] [CrossRef]
- Sharif, M.; Zubair, M. Thermodynamics behavior of particular f(R,T) gravity models. J. Exp. Theor. Phys. 2013, 117, 248. [Google Scholar] [CrossRef]
- Sharif, M.; Siddiqa, A. Interaction of viscous modified Chaplygin gas with f(R,T) gravity. Mod. Phys. Lett. A 2017, 32, 1750151. [Google Scholar] [CrossRef]
- Myrzakulov, R. FRW Cosmology in F(R,T) gravity. Eur. Phys. J. C 2012, 72, 2203. [Google Scholar] [CrossRef]
- Odintsov, S.D.; Saez-Gomez, D. f(R,T,RμνTμν) gravity phenomenology and ΛCDM universe. Phys. Lett. B 2013, 725, 437. [Google Scholar] [CrossRef]
- Haghani, Z.; Harko, T.; Lobo, F.S.N.; Sepangi, H.R.; Shahidi, S. Further matters in space-time geometry: f(R,T,RμνTμν) gravity. Phys. Rev. D 2013, 88, 044023. [Google Scholar] [CrossRef]
- Sharif, M.; Zubair, M. Study of thermodynamics laws in f(R,T,RμνTμν) gravity. JCAP 2013, 11, 042. [Google Scholar] [CrossRef]
- Sharif, M.; Zubair, M. Energy conditions in f(R,T,RμνTμν) gravity. JHEP 2013, 12, 079. [Google Scholar] [CrossRef]
- Riess, A.G.; Strolger, L.-G.; Tonry, J.; Casertano, S.; Ferguson, H.C.; Mobasher, B.; Challis, P.; Filippenko, A.V.; Jha, S.; Li, W.; et al. Type Ia Supernova Discoveries at z>1 from the Hubble Space Telescope: Evidence for Past Deceleration and Constraints on Dark Energy Evolution. Astrophys. J. 2004, 607, 665–687. [Google Scholar] [CrossRef]
- Appleby, S.A.; Battye, R.A. Do consistent F(R) models mimic General Relativity plus Λ? Phys. Lett. B 2007, 654, 7–12. [Google Scholar] [CrossRef]
- Appleby, S.A.; Battye, R.A. Aspects of cosmological expansion in F(R) gravity models. J. Cosmol. Astropart. Phys. 2008. [Google Scholar] [CrossRef]
- Sharif, M.; Zubair, M. Cosmological evolution of pilgrim dark energy. Astrophys. Space Sci. 2014, 352, 263. [Google Scholar] [CrossRef]
- Sharif, M.; Zubair, M. Evolution of the universe in inverse and ln f(R) gravity. Astrophys. Space Sci. 2012, 342, 511–520. [Google Scholar] [CrossRef]
- Mukherjee, A.; Banerjee, N. Acceleration of the Universe in f(R) Gravity Models. Astrophys. Space Sci. 2014, 352, 893. [Google Scholar] [CrossRef]
- Oikonomou, V.K.; Karagiannakis, N. Late-time cosmological evolution in f(R) theories with ordinary and collisional matter. Class. Quant. Grav. 2015, 32, 085001. [Google Scholar] [CrossRef]
- Oikonomou, V.K.; Karagiannakis, N.; Park, M. Dark energy and equation of state oscillations with collisional matter fluid in exponential modified gravity. Phys. Rev. D 2015, 91, 064029. [Google Scholar] [CrossRef]
- Zubair, M. Phantom crossing with collisional matter in f(T) gravity. Int. J. Mod. Phys. D 2016, 25, 1650057. [Google Scholar] [CrossRef]
- Linder, E.V. Einsteins other gravity and the acceleration of the Universe. Phys. Rev. D 2010, 81, 127301. [Google Scholar] [CrossRef]
- Wu, P.; Yu, H. Observational constraints on f(T) theory. Phys. Lett. B 2010, 693, 415–420. [Google Scholar] [CrossRef]
- Baffou, E.H.; Houndjo, M.J.S.; Rodrigues, M.E.; Kpadonou, A.V.; Tossa, J. Cosmological evolution in f(R,T)theory with collisional matter. Phys. Rev. D 2015, 92, 084043. [Google Scholar] [CrossRef]
- Houndjo, M.J.S. Reconsrtruction of f(R,T) gravity describing matter dominated and acelereated phases. Int. J. Mod. Phys. D 2012, 21, 1250003. [Google Scholar] [CrossRef]
- Sharif, M.; Zubair, M.J. Cosmology of holographic and new Agegraphic f(R,T) models. Phys. Soc. Jpn. 2013, 82, 064001. [Google Scholar] [CrossRef]
- Sharif, M.; Zubair, M. Reconstruction and stability of f(R,T) gravity with Ricci and modified Ricci dark energy. Astrophys. Space Sci. 2014, 349, 529–537. [Google Scholar] [CrossRef]
- Jamil, M.; Momeni, D.; Raza, M.; Myrzakulov, R. Reconstruction of some cosmological models in f(R,T) gravity. Eur. Phys. J. C 2012, 72, 1999. [Google Scholar] [CrossRef]
- Sharif, M.; Zubair, M. Anisotropic Universe Models with Perfect Fluid and Scalar Field in f(R,T) Gravity. J. Phys. Soc. Jpn. 2012, 81, 114005. [Google Scholar] [CrossRef]
- Sharif, M.; Zubair, M. Energy Conditions Constraints and Stability of Power Law Solutions in f(R,T) Gravity. J. Phys. Soc. Jpn. 2013, 82, 014002. [Google Scholar] [CrossRef]
- Alvarenga, F.G.; Houndjo, M.J.S.; Monwanou, A.V.; Orou, J.B.C. Testing some f(R,T) gravity models from energy conditions. J. Mod. Phys. 2013, 4, 130–139. [Google Scholar] [CrossRef]
- Sharif, M.; Zubair, M. Cosmological reconstruction and stability in f(R,T) gravity. Gen. Relat. Grav. 2014, 46, 1723. [Google Scholar] [CrossRef]
- Jos Barrientos, O.; Guillermo, F. Comment on f(R,T) gravity. Phys. Rev. D 2014, 90, 028501. [Google Scholar] [CrossRef]
- Chang, J.; Adams, J.H.; Ahn, H.S.; Bashindzhagyan, G.L.; Christl, M.; Ganel, O.; Guzik, T.G.; Isbert, J.; Kim, K.C.; Kuznetsov, E.N.; et al. An excess of cosmic ray electrons at energies of 300–800 GeV. Nature 2008, 456, 362–365. [Google Scholar] [CrossRef] [PubMed]
- Spergel, D.N.; Steinhardt, P.J. Observational Evidence for Self-Interacting Cold Dark Matter. Phys. Rev. Lett. 2000, 84, 3760. [Google Scholar] [CrossRef] [PubMed]
- Kleidis, K.; Spyrou, N.K. A conventional approach to the dark-energy concept. Astron. Astrophys. 2011, 529, A26. [Google Scholar] [CrossRef]
- Ernazarov, K.K. On non-exponential cosmological solutions with two factor spaces of dimensions m and 1 in the Einstein-Gauss-Bonnet model with a Λ-term. Mod. Phys. Lett. A 2017, 32, 1750202. [Google Scholar] [CrossRef]


© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zubair, M.; Zeeshan, M.; Hasan, S.S.; Oikonomou, V.K. Impact of Collisional Matter on the Late-Time Dynamics of f(R,T) Gravity. Symmetry 2018, 10, 463. https://doi.org/10.3390/sym10100463
Zubair M, Zeeshan M, Hasan SS, Oikonomou VK. Impact of Collisional Matter on the Late-Time Dynamics of f(R,T) Gravity. Symmetry. 2018; 10(10):463. https://doi.org/10.3390/sym10100463
Chicago/Turabian StyleZubair, M., Muhammad Zeeshan, Syed Sibet Hasan, and V. K. Oikonomou. 2018. "Impact of Collisional Matter on the Late-Time Dynamics of f(R,T) Gravity" Symmetry 10, no. 10: 463. https://doi.org/10.3390/sym10100463
APA StyleZubair, M., Zeeshan, M., Hasan, S. S., & Oikonomou, V. K. (2018). Impact of Collisional Matter on the Late-Time Dynamics of f(R,T) Gravity. Symmetry, 10(10), 463. https://doi.org/10.3390/sym10100463




