Design and Application of Fuzzy Logic Based Fire Monitoring and Warning Systems for Smart Buildings

Abstract

Typical fire monitoring and warning systems use a single smoke detector that is connected to a fire management system to give early warnings before the fire spreads out up to a damaging level. However, it is found that only smoke detector-based fire monitoring systems are not efficient and intelligent since they generate false warnings in case of a person is smoking, etc. There is need of a multi-sensor based intelligent and smart fire monitoring system that employs various parameters, such as presence of flame, temperature of the room, smoke, etc. To achieve such a smart solution, a multi-sensor solution is required that can intelligently use the data of sensors and generate true warnings for further fire control and management. This paper presents an intelligent Fire Monitoring and Warning System (FMWS) that is based on Fuzzy Logic to identify the true existence of dangerous fire and send alert to Fire Management System (FMS). This paper discusses design and application of a Fuzzy Logic Fire Monitoring and Warning System that also sends an alert message using Global System for Mobile Communication (GSM) technology. The system is based on tiny, low cost, and very small in size sensors to ensure that the solution is reproduceable. Simulation work is done in MATLAB ver. 7.1 (The MathWorks, Natick, MA, USA) and the results of the experiments are satisfactory.

1. Introduction

Fire is very useful, it serves a lot of purpose for us as long as it is under control, but when it goes out of control, it can be the cause of a big disasters. Since, for household activities, like cooking, heating, or lighting, fire is a common solution however such fire-based activities result in a high mortality rate and damage of property of almost $8.6 billion per year. The available solutions of home based Fire Monitoring and Warning System (FMWS) are of two types; smoke alarm and vision based Camera systems. The first one, smoke alarm is not reliable while the second one, vision based camera systems are highly expensive. For developing countries, there is need of cheap and reproduceable solutions that can also be provided on commercial basis.

There is an urgent need to design and develop an intelligent and smart Fire Monitoring and Warning System (FMES) using Fuzzy Logic [1,2,3,4] that plays an important role in achieving the safe environments and buildings. To achieve the above-mentioned goals, a home based Fire Monitoring and Warning System (FMWS) is introduced in this paper that uses Arduino Uno R3 (Arduino, Somerville, TX, USA) that is economical and affordable and a set of easy-to-buy sensors. The proposed system is efficient in detecting fire during the presence of smoke and flame at a level with the particular increase in the room temperature. The proposed systems uses a fuzzy logic based system to identify the true incidents of fire that can result in a critical and dangerous situation and send alerts via GSM to the concerning person. The proposed system is efficient in detecting false-fire incidents and report only the true-fire incidents as previous solutions [5,6,7,8] do not identify false-fire incidents. Here, the false-fire incidents are those incidents that is not actual fire but a fir-detecting system gives an alarm for true-fire.

In the literature, researchers proposed different methods [6,7,8,9,10] to detect and control fire, whereas these methods are fire alarm system, autonomous fire fighting Robots, Fire Monitoring and Warning System using wireless sensor networks (WSN) and Global System for Mobile Communication (GSM) technology, and videos and images based fire detection systems. Many controllers have good effects as well as negative like false alarm which can be due to any environmental changes, smoking, etc. and such false alarms result in consumption of lots of energy. Due to these reasons, a system is much needed that is less expensive and can detect fire at early stages, uses multiple sensors to detect true incidents of fire, reduce false alarm rate and reliability, which can be used in houses, buildings, and offices. The proposed system also sends alerts to the concerning people for better and in-time control and management of fire incidents. In this study, the novel idea is the use of Fuzzy Logic method for identification of true incidents of fire. Fuzzy Logic was originally proposed by Dr. Lotfi Zadeh of the University of California at Berkeley in 1960s. He gave idea of membership function and in 1964 which had become the backbone of fuzzy set theory. In 1965, [2,3,4], the idea of fuzzy set theory and fuzzy logic technology was introduced to define membership function and rule set, which plays an important role in simulation work to construct a FMWS.

The previous studies show that the existing fire detection and warning systems are mostly uni-sensor systems that only decide on the base of presence of smoke. However, smoke cannot always be a reason of a true fire incident. There is need to consider the other parameters of fire in design of an intelligent and fully automatic system for detecting incidents of true fire. To fill this research gap, a multi-sensor system is presented in this paper that uses the decision making power of fuzzy logic techniques for the purpose of decision making and implementing the system in MATLAB. The experiments show that the proposed system is accurate and reliable in identification of incidents of true fire.

The rest of the paper is structured, as follows: Section 2 discusses the outcomes of the detailed literature review carried out during the research and a course of related work; Section 3 describes the materials and methods of the presented research along the used fuzzy logic system for the proposed Fire Monitoring and Warning System; Section 4 provides details of the experiments their results and discussions to show the performance testing and outcomes of the presented approach; and, Section 5 presents a conclusion of the presented research.

Related Work

Several years before, fuzzy control became one of the most beneficial area where the focus of the research was applications of fuzzy set theory. There were many technologies which were proposed for early fire detection for safety, such as Neural Networks, Image Processing, Video-based techniques, Fuzzy Logic, etc. Fire detection has become an important research topic for the safety of human life, many other technologies are used for the surveillance of early fire detection.

Faisal et al. designed and evaluated wireless sensor network using multiple sensors for early fire detection of a house fire. The author also used GSM to avoid false alarms. The system was tested in a smart home [5]. Hamdy et al. build “Smart Forest Fire Early Detection Sensory System (SFFEDSS)”, by combining wireless sensor networks with artificial neural networks (ANNs). In this system, low-cost sensor nodes, temperature, light, and smoke data spread out on the forest in order to get information, and this information is taken as input to ANN models that is converted into intelligence. Without any human involvement, this SFFEDSS system monitors the forest [6]. Giovanni Laneve et al. discussed that in the Mediterranean regions, to detect fire at the early stage, author analysis the application of Spinning Enhanced Visible and Infrared Imager SEVIRI images. In this techniques, two or more images are compared with each other after the interval (15-min) [7].

Digvijay Singh et al. proposed a fire alarm system, by using less expensive instruments, connectivity, and wireless communication. It is real-time monitoring system, in which system detects the presence of fire as well as captures images by using the camera and display images on the screen. In this system two controllers are used, Controller 1 sends signals to GSM and Controller 2, and Controller 2 will turn ON the screen. When it finds that temperature, humidity, CO2, and fire are increased above the threshold, these outputs are taken from sensors. One or more Arduino is connected and trigger automatically [8]. Md Iftekharul Mobin et al. proposed a System Safe from Fire (SFF) by using multi-sensor, actuators, and operated by micro-controller unit (MCU) is an intelligent self-controlled smart fire extinguisher system. Sensors placed in different areas for monitoring purpose and input signals are taken from that sensors and combine integrated fuzzy logic to detect fire breakout location and severity and discard false fire situation, such as cigarette, smoke, welding etc. SFF notifies fire services and other by text messages and telephone calls when the fire is detected [9].

Navyanth et al. presented a system design for fire-fighting robots, which detect the fire and reach the target area without hitting any obstacle for preventing damage lives and property using the Fuzzy Logic techniques. In another contribution, there are many ultrasonic sensors mounted on the robot, which sensed turn angle between the robot head and the target, distance of the obstacles around the robot (front, left, and right, including other mobile robots) and used as input fuzzy members. The objective of designing the fire-fighting robots is to reach at fire area zone without hitting any obstacle to prevent any damage in the unknown environment [10]. Liu et al. describe a smart bushfire monitoring system that alerts through warning message in case of a bushfire. Global system for mobile (GSM) communication technology is used as a communication medium for sending short message service (SMS). The temperature and humidity sensors are connected to a microcontroller composed of a device. To report module position, Microcontroller interfaces with a GPS as well as GSM module to communicate the sensory information. Sent message through GSM is received by other mobile phones for further processing [11].

Vikshant et al. presented a work in the detection of forest fire using wireless sensor networks (WSNs) [12,13,14,15] with the idea of implementing Fuzzy Logic. Multiple sensors are used for detecting the probability of fire and fire direction as well. Information that is collected from different sensors will be passed on the cluster head using Event Detection Mechanism. Multiple sensors temperature, Humidity, light, and CO density are used to detect fire probability and fire direction and these all sensors are mounted in each nod in order to improve accuracy and reduce false alarm rate as well [16]. Muralidharan et al. develop a simple way of detecting fire using multi-sensor instead of the single sensor with the use of Artificial Intelligence technology Fuzzy Logic. Results were presented in MATLAB. The developed system was simpler work in a human way of thinking and closely related to the real model concept [17]. Mirjana et al. developed a system with the internet of things (IoT) concept for making right decision according to the situation for monitoring and determining fire confidence and reduce the number of rules by doing so sensor activities also reduced and extend battery life time as well as improve efficiency [18].

Robert et al. describe a system for detecting fire in automobiles while using Arduino microcontroller and Artificial Intelligence technology Fuzzy Logic in order to avoid any damages in an automobile due to fire. Temperature sensors, flame sensors, and smoke sensors are used, when the fire is detected then sound alarm and provide carbon dioxide to location. A system is implemented and tested on a medium sized physical car and 2 kg Cylinder is mounted behind the rear seats of the passenger [19]. Hongliang et al. proposed a multi-features fusion (MFF) algorithm with self-adaptive, self-learning, and fault tolerance, the probability of burning fire is detected by taking flame’s twinkling frequency and its dynamic contour into account. For detecting fire areas, first dynamic video of fire picked up, detect fire area, and build a quantified distinguishing rule using disperse to the eigenvector. In complex situations, the MFF algorithm has an ability to detect white spots from moving and static objects, with a spotlight, automobile light, and illumination changing [20].

Harjinder et al. describe a solution of an early detection of the forest fire with the wireless sensors. Data is collected from sensors using Arduino development board and it is sent to the base station wirelessly after detecting fire also alert message is sent using GSM module [21]. Turgay et al. present a model for detecting fire and smoke without using any sensor, this approach is based on image processing. The system is designed in which color information with motion analysis are combined by using the extracted model [22].

Wang et al. describe the idea of automatic fire alarm and fire control linkage system in the intelligent building. The system predicts fire intelligently, it controls gas, automatic fire alarm, and linkage function as well [23]. Viktor et al. describes the architecture for fire detection using social media networks. Author said that as social network and services are increasing there has been large amount of information sharing on the internet. Author proposed architecture of wildfire social sensor (WSS) platform. In result of this work, a human-centric sensor network can be provided by social media for the early detection of disasters like fire [24].

2. Materials and Methods

In this paper, the fuzzy control algorithm is used to detect fire in the residential area which is placed where it is needed and used to detect any abnormal behavior. Whenever any abnormal behavior is detected, FMWS are used to set an alarm and other control mechanisms. Rule-based fuzzy logic is implemented in this approach on data that is collected from different sensors. In FMWS, MATLAB Fuzzy Logic Toolbox is used for simulation work with more accuracy, flexibility, and scalability with other systems. To process the Fuzzy Logic in this research Fuzzy Rule, Fuzzy Inference System, and Defuzzification process are involved.

2.1. Nomenclature of Proposed Fuzzy Logic Control

In the implementation of fuzzy logic control, the fuzzification component, the inference rules component and the defuzzification component are implemented and each component have different methods, such as singleton fuzzification, min-max inference, and centroid defuzzification methods with different characteristics. In general, fuzzy logic control method of each components can be represented by the number of operations and memory requirements. In Fuzzy Logic Control, program is implemented in the C language in Arduino IDE (Integrated Development Environment), which is integrated with Arduino UNO microcontroller and model is ATmega328P. Basic operation that is, addition, subtraction, and division is used to count number of operations.

Table 1. Nomenclature of proposed fuzzy logic.

Symbol	Description
K	Kernal of Fuzzification
x	The number of input fuzzy sets
µ	The number of inputs
R	The number of rules
X	The number of output fuzzy sets
x*	Defuzzified output
C-R-Temp	The change rate of temperature
C-R-humidity	The change rate of humidity

presents the symbols which is used in this paper.

2.2. Architecture of the Proposed Fuzzy Logic System

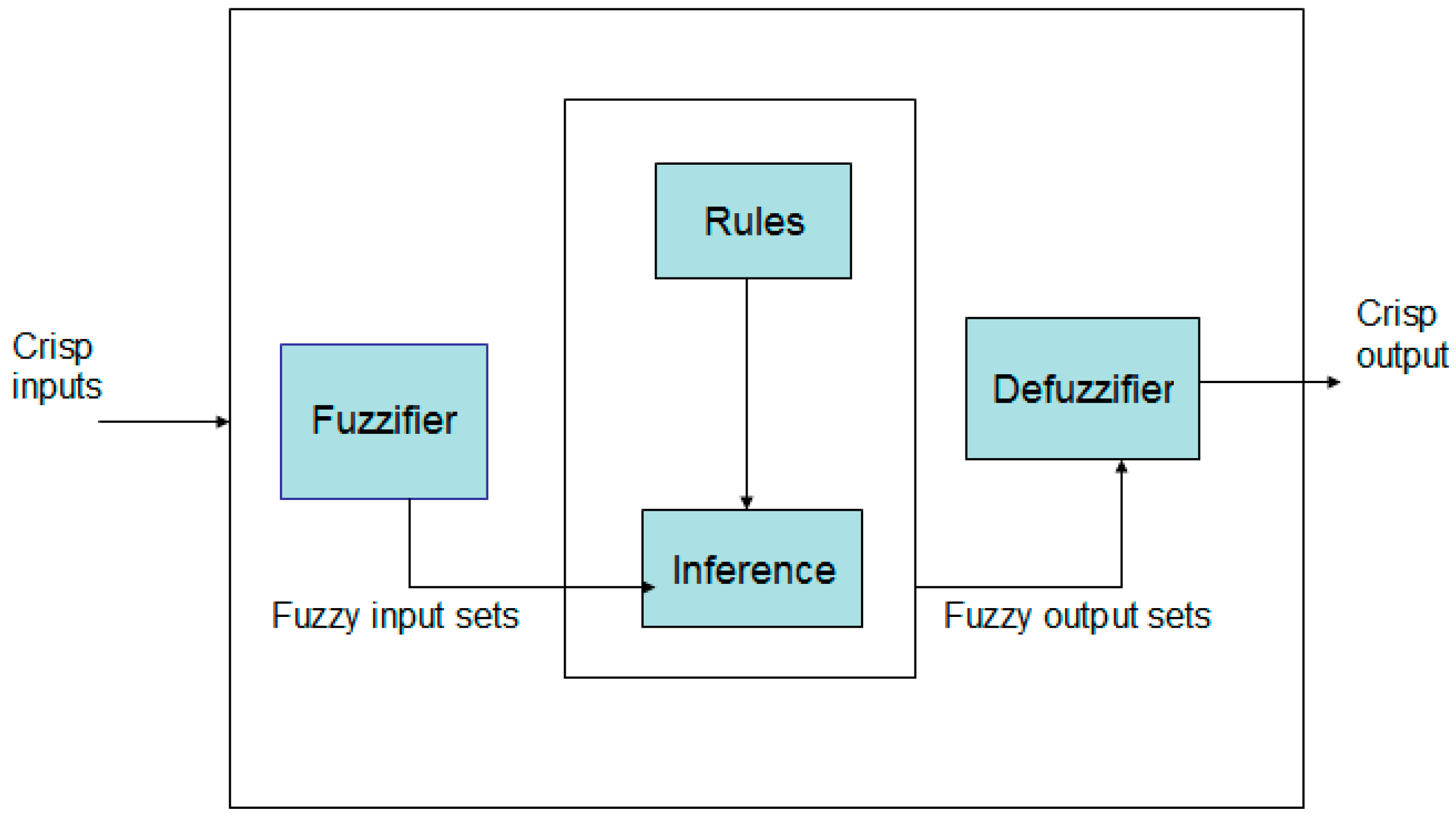
The general architecture of a proposed FLS is shown in Figure 1. In a broader sense, the fuzzy logic refers to a fuzzy set [25]. Typically, a fuzzy set S is a pair (U,m) where universe of discourse U is a set and characterized by a membership function where m_S takes the value in the interval [0, 1], i.e., m_S:U → [0, 1]. Whereas, the Universe of Discourse and the membership function plays a vital role in this approach. The fuzzy set can be represented as a set of ordered pairs of elements e and its degree of membership function, as described in [19] and the same is shown in Equation (1):

S = {(e, m_S(e), e Є U)}

(1)

The probability that e belongs to S is the membership function mS(e). Here, three parameters (three fuzzy subset of S (A, B, and C)) are used in the proposed approach. In Equations (2) and (3), the m_A(x) is the degree of membership of x in A, mB (x), the degree of membership function of x in B and m_C(x) is the degree of membership of x in C. Here, a variable A represents temperature, variable B represents time and Variable C represents humidity. Considering this, the fuzzy union set and fuzzy intersection set are defined as:

A ∪ B ∪ C = { x, max(m_A(x), m_B(x), m_C(x))|x is an element of S}

(2)

A ∩ B ∩ C = { x, min(m_A(x), m_B(x), m_C(x))|x is an element of S}

(3)

The Equations (2) and (3) are implemented in this approach to compute rules strength. In Equation (2), the union of three fuzzy subsets is computed by using fuzzy operator “or” by combining the fuzzified inputs using fuzzy combination. Similarly, in Equation (3), to compute the intersection of three subsets, the fuzzy “and” operator is used by clipping the output membership function at the rule strength. According to the proposed work, Equation (3) is implemented with three inputs because in this approach, we need to obtain rule strength by combining the fuzzified inputs, and it clips the output membership function at the rule strength. Typically, a fuzzy set describes the values of linguistic variables as quantitatively and qualitatively. A membership functions defines that each point is mapped to a membership value between 0 and 1 in the defined Universe of Discourse. In the proposed FMWS, the fuzzy rules are implemented using if-then rules, which are used to express a piece of knowledge. The fuzzy rules are most widely and commonly used for interpretation also used in this approach, like

“if x is A and y is B then z is C”

For the collection of fuzzy rules,

“if x is A_i and y is B_i then z is C_i”, where i = 1....n,

The proposed fuzzy logic expert system in this paper consists of the four basic components: fuzzification, inference, knowledge base, rules, and defuzzification. Every component is involved in the decision making process by the proposed FMWS.

Fuzzy logic system with its components is shown in Figure 1 and working of the proposed fuzzy logic system is described in Algorithm 1 that is based on [26]. This algorithm implements the fuzzy logic system in the proposed Fire Management and Warning System (FMWS).

Algorithm 1 Proposed Algorithm for proposed Fuzzy Logic System

1. Define: Linguistic variables and terms (initialization) 2. Construct: Membership Functions (initialization) 3. Construct: Rule base (initialization) 4. Construct: Crisp input data to fuzzy values using Membership Function (fuzzification) 5. Evaluate: Rules in the rule base (inference) 6. Combine: Results of each rule (inference) 7. Convert: Output data to non-fuzzy values (defuzzification)

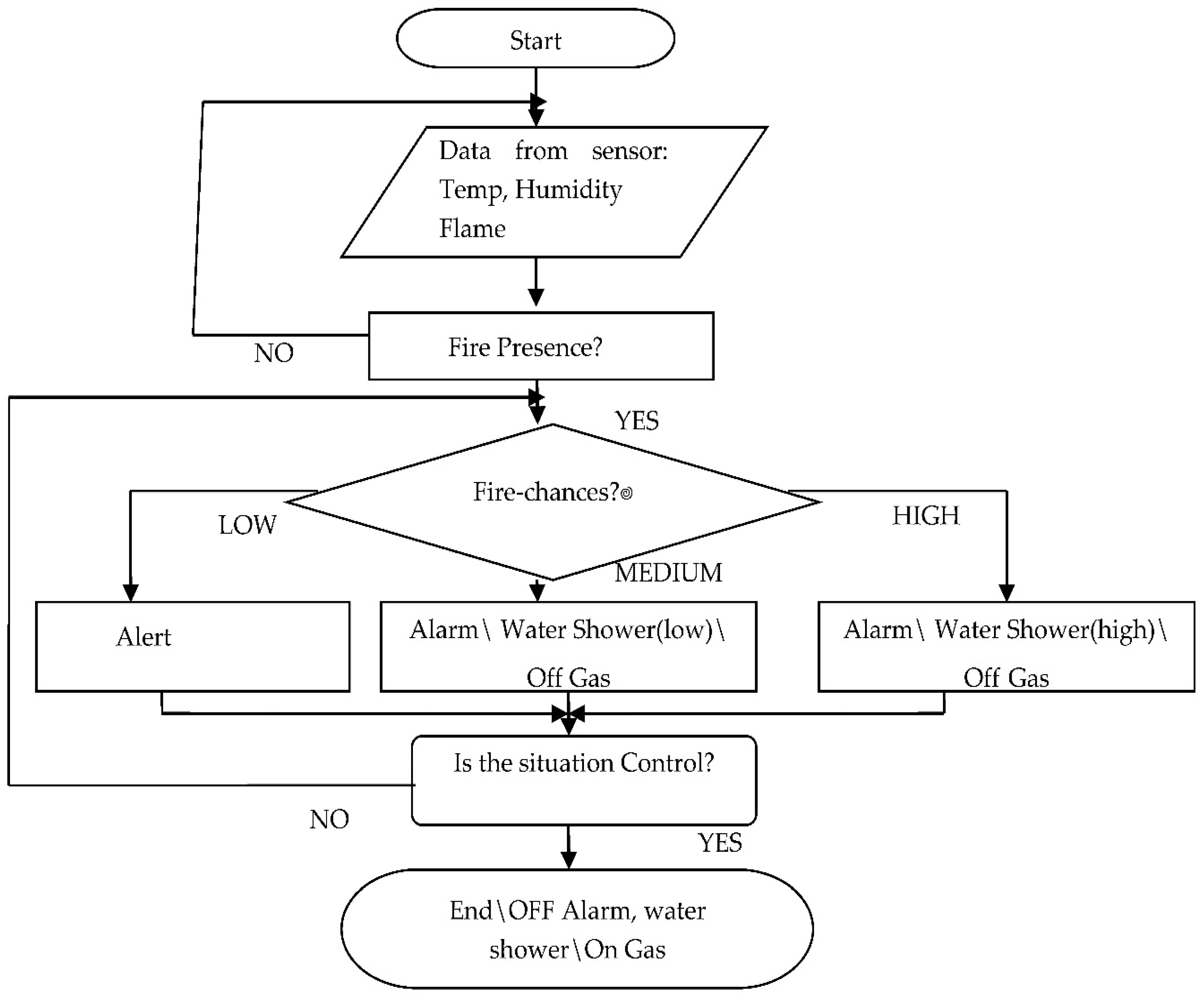
According to the Algorithm 1, a set of input data was collected from sensors and using data variables, fuzzy linguistic terms, and membership function set is converted to a fuzzy set and this process is called as fuzzification. Afterwards, using a set of rules an inference is made. In the last, step which is called as defuzzifictaion, fuzzy output is mapped to an output using the membership functions. The description of each components of the proposed fuzzy logic systems is given below:

2.2.1. Used Fuzzification Method

The fuzzification is the first phase in the proposed fuzzy logic based FMWS. In this fuzzification process, the crisp values are converted into fuzzy set using a set of membership functions that are described in next section. Each membership function represents quality of the sensor variables being fuzzified, e.g., the membership function of a variable “Change rate of Temperature” and “Change rate of Humidity” are valued as “Low”, “Mid”, and “High”, whereas the membership function of variable “Time” is “short” and “long”, The fuzzified set can be described, as shown in Equation (4):

à = µ₁ K(x₁) + µ₂ K(x₂) +...... + µ_n K(x_n)

(4)

In this relation, the fuzzy set K(xi) is called as kernel of fuzzification. To implement this method, µi constant and xi is being transformed to a fuzzy set K(xi). In the proposed work, the Equation (4) is used in the process of fuzzification where the universe of discourse and the membership functions are implemented.

2.2.2. Used Membership Function

In the proposed fuzzy logic based FMWS, a membership function is defined as µ_A:X [0, 1] for a fuzzy set A and X is a universe of discourse, and each element of X is mapped to a degree of membership function between 0 to 1. In the proposed approach, a fuzzy set can be represented graphically using a membership function. The x-axis represents universe of discourse and y-axis represents the degree of membership function from 0 to 1. In the proposed approach, the triangular membership function is used, and the details of the triangular membership function. The reason of using the triangular membership function in the proposed approach is that it is simple to implement in MATLAB and it provides accurate results. It is available with the function name “trimf” in MATLAB. The triangular membership function [19] can be defined by a lower limit a, an upper limit b and a value mean m, where a < m < b, as shown in Figure 2 and Equation (5).

$${\mathsf{\mu }}_{\mathrm{A}}(\mathrm{X})=\{\begin{array}{c}0,\\ \left(\mathrm{x}-\mathrm{a}\right)/\left(\mathrm{m}-\mathrm{a}\right),\\ \left(\mathrm{b}-\mathrm{x}\right)/\left(\mathrm{b}-\mathrm{m}\right),\\ 0,\end{array}\begin{array}{c}\mathrm{x}\le \mathrm{a}\\ \mathrm{a}<\mathrm{x}\le \mathrm{m}\\ \mathrm{m}<\mathrm{x}<\mathrm{b}\\ \mathrm{x}\ge \mathrm{b}\end{array}$$

(5)

There are three parameters in x-axis (a, m, b), as shown in Figure 2 that represents lower boundary, peak, and upper boundary of a membership function, y-axis represents the degree of membership function. Alternative expression for the preceding equation can be written using min and max operations, as shown in Equation (6):

$$\mathrm{triangle}\left(\mathrm{x};\mathrm{a},\mathrm{b},\mathrm{c}\right)=\max \left(\min \left(\begin{array}{cc}\frac{\mathrm{x}-\mathrm{a}}{\mathrm{b}-\mathrm{c}},& \frac{\mathrm{c}-\mathrm{x}}{\mathrm{c}-\mathrm{b}}\end{array}\right)\right)$$

(6)

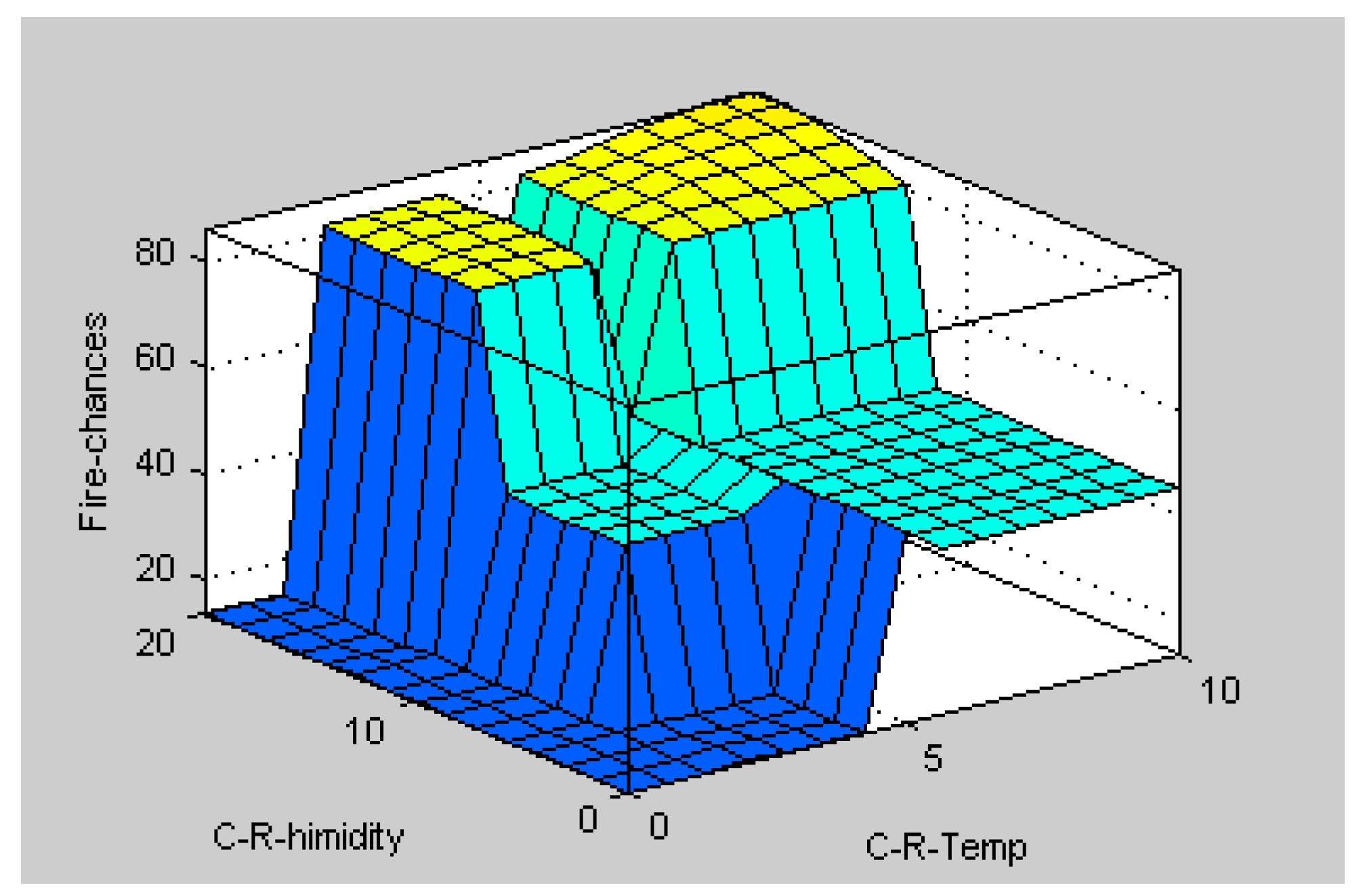
The Equation (6) shows that there are three parameters (a, b, c) with (a < b < c) that determines x coordinates of the three corners of the underlying triangular membership function. The Equations (5) and (6) are used to make membership functions for all four variables (three inputs and one output) of the used fuzzy logic system. The membership function is designed in this approach using above equations for each input linguistic variables, which are “change rate of temperature”, “change rate of humidity”, “time” and output linguistic variable “fire-chances”. The used membership functions are defined in MATLAB Fuzzy Logic toolbox, as explained in Section 3.

2.2.3. Used Fuzzy Inference System

In the architecture of the proposed FMWS, a fuzzy inference system is used that is based on a set of if-then rules, a set of membership functions and fuzzy logic operators, such as “and”, “or”. In the proposed approach, the fuzzy inference is mapped from an input to an output using fuzzy logic. The fuzzy inference has three types, such as Mamdani fuzzy inference system, Sugeno fuzzy inference system, and Tsukamoto fuzzy inference system. In the proposed approach, Mamdani and Sugeno fuzzy inference system [27] is used that was originally introduced by WeEbrahim Mamdani in 1975. The used Mamdani fuzzy inference system is implemented in the following six steps:

• Fuzzification of input using membership function
• According to fuzzy set theory the fuzzified inputs are combines
• Built fuzzy rules
• Finding outcomes of the rules by combining rule strength and output membership function
• Get an output distribution by combining the outcomes
• Defuzzification of the output membership function

IF (X₁ is A¹₁ AND y₁ is A¹₂ AND z₁ is A¹₃) THEN (w is B¹)

(7)

IF (X₂ is A²₁ AND y₂ is A²₂ AND z₂ is A²₃) THEN (w is B²)

(8)

In Figure 3, a detailed process of Mamdani FIS [28] using three inputs and two rules is illustrated and defined in Equations (7) and (8), where the input x₁, y₁, and z₁ is fuzzy, not crisp. The three inputs are fuzzified by applying intersection on crisp input value with the input membership function. For combining, the three fuzzified inputs to obtain rule strength by using operator “and”. The used Mamdani inference system uses a membership function for each rule and then according to the condition of the rule reaches to a conclusion.

2.2.4. Used Defuzzification Method

This is a last step in the implementation of FMWS whereas the output is evaluated from a rule set that is written in the form of if-then statements and is saved in a knowledge base of the system. Here, a scalar value of fuzzy system is fuzzified, rules are applied, and each rule generates a fuzzy output and converts it to a scalar quantity. The two typically used defuzzification methods are the Centroid Defuzzification method and Weighted Average Defuzzification method

This step is done by MATLAB fuzzy logic tool box and centroid method is implemented in this research and its details are described below:

Centroid Defuzzification Method: In this approach centroid defuzzification method is used because it gives an accurate result which is originally developed by Sugeno in 1985. This technique is expressed mathematically in Equation (9) as

$$\mathrm{x}*=\frac{\int {\mathsf{\mu }}_{\mathrm{i}}\left(\mathrm{x}\right)\mathrm{dx}}{\int {\mathsf{\mu }}_{\mathrm{i}}\left(\mathrm{x}\right)\mathrm{dx}}$$

(9)

where x* is the defuzzified output, µ_i(x) aggregated membership function, and x is the output variable in Equation (9). It is defined graphically in Figure 4 where x-axis represents the output variable x, y-axis represents µ_i(x) aggregated membership function and x* is the defuzzified output. The shape of output is obtained by applying fuzzy operator “and” by clipping the output membership function according to the rule strength.

3. Implementation of Fire Monitoring and Warning System (FMWS)

The proposed FMWS system is implemented with less-expensive and tiny sensors to detect true fire incidents. Input data is taken from different sensors, like temperature, humidity, and flame sensors. After collecting data from sensors, the first step is to check flame’s presence using flame sensor and if there is a flame found, then the decision systems goes to next step for further processing otherwise the system goes back to initial phase. In next step, a rule-based logic is applied on data to detect fire incidents and check its intensity. If the fire intensity is low then just an alert is generated to the people or management in order to take a particular action to control this respective kind of situation. However, if fire intensity is medium, then a fire control-mechanism is applied but the systems outputs a ‘medium’ signal, alarm sounds and turn off gas and turns on the water shower. However, if fire intensity is high then a solution similar to ‘medium’ mechanism is applied, but the level of application will be in high mode. The workflow of the proposed FMWS is shown in Figure 5.

In Figure 5, the incidents of true fire are identified by using a set of variables, such as temperature, humidity values, time-span, fire-presence, etc. and with respect to the identification, a respective action is taken. However, when situation become under control then system stops the control mechanism and moves back to the normal behaviour. The following sections explain the implementation with used hardware and software:

3.1. Used Hardware in Proposed FMWS (Fire Monitoring and Warning System)

In proposed FMWS, a temperature sensor DHT22 (Aosong Electronics, Shenzhen, China) is used that performs dual action by measuring both temperature and humidity, while a flame sensor is used to detect flame presence. These two sensors are attached with Arduino UNO microcontroller. The properties and working of sensors and microcontroller are discussed below:

Arduino UNO microcontroller: To implements the proposed FMWS, an ATmega328P microcontroller (see Figure 6) is used due to its special features, such as analog input, PWM output, etc. To access sensors data, the sensors were attached with microcontroller using USB cable.

In

Table 2. Properties of Arduino UNO microcontroller.

Model	ATmega328P
Operating Voltage	5 V
Input Voltage	6–20 V
Analog Input Pins	6 (A0–A5)
Digital I/O Pins	14 (out of which 6 provide PWM output)
DC Current on I/O Pins	40 mA
DC Current on 3.3 V Pin	50 mA
Flash memory	32 KB
SRAM	2 KB
EEPROM	1 KB
Clock Speed	16 MHz

Shows the key properties of microcontroller Ardunio UNO. The microcontroller consists of six analog input pins from A0 to A5 and 14 digital pins, out of which six provides PWM output. When the microcontroller is connected to computer using USB port, it appears on PC as virtual com port to software. In our implementation, the textual data is sent to and from Arduino board using serial monitor. Arduino IDE is used in this approach to program the Arduino UNO board.

Temperature and Humidity Sensor (DHT22): To detect presence of fire in the surroundings, the DHT22 (see Figure 7) was used as one of the sensors that gives two measurements, such as temperature and humidity, and these two values play an important role in the implementation of FMWS. After digitization, through serial port data is transferred to microcontroller.

DHT22 temperature sensor gives temperature value in °C and humidity value in %. The reason of using DHT22 in this approach is because of measuring two inputs using single sensor. DHT22 is attached with microcontroller with three pins, which are +ve, data and −ve pins.

In

Table 3. Properties of DHT22 sensor.

Model	AM2302
Power supply	3.3–6 V DC
Output Signal	Digital Signal via 1-wire bus
Sensing element	Polymer capacitor
Operating range	Humidity 0–100%RH, temperature −40~80 Celsius
Accuracy	Humidity ±2% RH (Max ±5% RH), Temperature < ±0.5 Celsius
Resolution of sensitivity	Humidity 0.1% RH; Temperature 0.1 Celsius
Repeatability	Humidity ±1% RH; Temperature ±0.2 Celsius
Humidity hystersis	±0.3% RH
Long-term stability	±0.5% RH/year
Sensing period	Average: 2 s
Interchange ability	Fully interchangeable
Dimensions	Small size 14,185.5 mm, Big size 22,285 mm

, the properties of DHT22 sensor are described. DHT22 measures temperature between −40 °C to 80 °C and 0 to 100% humidity. The model AM2302 is suitable for this type of systems, as it has small size, low energy-consumption, and long transformation distance (100 m). In the proposed work, DHT22 sensor is configured by using jumper wires with Arduino microcontroller. To code and configure DHT22 with Arduino IDE, the DHT22 library is used.

Flame sensor: In the implementation of FMWS, a flame sensor is also used as shown in Figure 8. The purpose of using flame sensor in proposed work, to check the presence of flame. It detects fire within short range, its detection range is 3 feet and angle is 60 degree.

In the implementation, the flame sensor is attached to microcontroller. The flame sensor VCC pin is connected to the Ardunio 5 V pin, GND pin of module is connected to Arduino GND pin, and module output pin is connected to A0 pin of Arduino using jumper wires. After configuring the flame sensor with Arduino, a program is written in Arduino IDE by altering the code of online code available for the flame-sensor. The properties of flame sensor are given in

Table 4. Properties of Flame sensor used in proposed work.

Positive supply	+5 V
Output	Digital and Analog
Flame wavelength	760 nm to 1100 nm
Power supply	3.3–5.5 V DC, DO, high/low electric level signal output
Detection angle range	about 60 degrees

.

3.2. Coding in Arduino IDE (Integrated Development Environment)

Once the hardware is configured with Arduino UNO microcontroller, the code is written on Arduino IDE that is available. However, the code was customized a bit to get desired format of the sensor’s data. Once the sensors’ data is obtained and the Universe of Discourse is defined that is necessary to perform simulation work in MATLAB. In implementation, only one DHT22 library is used that is also available online. The program is written using C language in Arduino IDE and then uploaded on board. The used IDE is shown in Figure 9.

In the implementation, Arduino 1.8.5 version is used for hardware configuration and programming. Once the code is written in Arduino IDE using C language, it is uploaded into Arduino IDE and output is achieved on serial monitor, as shown in Figure 9. Here, the data is collected from each sensor in an Excel sheet, and for integration between Arduino IDE and Excel sheet, another piece of code is written in Arduino IDE to access data from sensors.

3.3. Recording Sensor’s Data in Experiments

The simulation work is done in MATLAB using Fuzzy Logic toolbox is used for proposed FMWS to record readings of the sensors for real time situations. To test the proposed FMWS, a set of different scenarios were chosen, such as scenarios with no fire, scenarios with medium fire, and scenarios with high fire. Here, the actual data is gathered from sensors (Temperature, Humidity, and Flame) to find Universe of Discourse for simulation. For all different scenarios, the data is collected in an Excel sheet directly from sensors when fire is detected. This data helps in finding the Universe of Discourse. An extract of the collected data is shown in

Table 5. C-R-Temp, C-R-Temp, and time of fire detection with two experiments.

Sr. No.	Experiment 1			Experiment 2
	Time Interval (minutes)	C-R-Temp (°C)	C-R-Humidity (%)	Time Interval (minutes)	C-R-Temp (°C)	C-R-Humidity (%)
1	2	0	0	1.5	0.7	0.6
2	2	3	−2.4	1.10	2	1.8
3	3.4	3.5	−2.9	39 s	1	2
4	4	6.4	−10.6	2.38	2	1.5
5	2	3	6.1	2.12	2	3
6	2.3	3.6	9	1.56	3	5
7	1.2	2	5	2	3	8
8	2.35	4	6	2	3.2	6

.

In Table 5, the shown data is collected from sensors to find universe of discourse for simulation work in MATLAB for the proposed FMWS. The shown data is taken by two experiments. Here, the first column represents time interval of fire to occur and second column represent the change rate of temperature (C-R-Temp) that shows how much the temperature is affected and when the incident of true fire is detected. Column three represent the change rate of humidity (C-R-Humidity) that shows how much the humidity is affected when the fire is detected. The proposed system was tested with more than fifty (50) experiments with at least 500 values, however two of them are described in Table 5. In Experiment 1, first iteration shows that the change rate of temperature and the change rate of humidity is 0 and at this time no fire is detected, but in second iteration, the change rate of temperature is 3 which means that temperature is changed by 3 °C and humidity is changed by 3% within 2 min. In the third iteration, the value of change rate of temperature is 3.5, which means that temperature is changed by 3.5 °C and humidity is changed by −2.9% within 3.4 min. In 4th iteration, the value of change rate of temperature is 6.4, which means that temperature is changed by 36.4 °C and humidity is changed by −10.6% within 4 min. In experiment 2, in first iteration, the value of change rate of temperature is 0.7, which means temperature is changed by 0.7 °C and humidity is changed by 0.6% within 1.5 min. The value of change rate of temperature and change rate of humidity is changed according to the fire intensity. So, we conclude that the value of change rate of temperature and change rate of humidity is changed around 2 °C within 2 to 3 min, and 3 °C to 5 °C within 4 min, etc. So, according to these experiments, we find the Universe of Discourse illustrated in

Table 6. Universe of Discourse for each membership function.

Variable	Universe of Discourse for C-R-Temp (°C)	Universe of Discourse for C-R-Humidity	Universe of Discourse for Fire-Chances	Universe of Discourse for Time
Low	0–2	0–7	0–30	-
Mid	2–5	5–12	30–60	-
High	5–10	12–20	60–100	-
Short (Time)	-	-	-	0–4
Long (Time)	-	-	-	4–10

:

In Table 6, the first column represents the linguistic variable of each membership function, the second column represents the Universe of Discourse for input variable C-R-Temp for each variable. For example, if C-R-Temp is 4 it means change rate of temp lies between range of 2–5 and the change rate is medium and if C-R-humidity is 10 then it lies between range of 5–12 and C-R-humidity is also medium and if time interval of fire detection is 2 min, which is short time it lies in 0–4 and after that rules are applied then computed fire chances. The third column represents the Universe of Discourse for input variable C-R-humidity. The fourth column represents the Universe of Discourse for output Fire-chances, which represents the chances of fire as output, and according to it, fire-control mechanism will be activated. The fifth column represents the Universe of Discourse for Time, which represents the time interval at which the fire is detected. After data collection and the universe of discourse selection, the next step is to configuration of MATLAB for the simulation of the proposed FMWS.

3.4. Configuring MATLAB Implementation with Universe of Discourse

In the proposed FMWS, once the MATLAB simulation is ready, it is configured with the Universe of Discourse. In MATLAB, a fuzzy controller block is available to simulate a fuzzy logic control system [12]. Here, the values in the input vector and its respective fuzzy rules are defined, the values are assigned to the output vector that are interpreted using fuzzy inference method. A set of editors and viewers are used for simulation work of proposed FMWS in which a rules set is built, the membership functions are defined and then analyzed the behavior of a fuzzy inference system in fuzzy logic toolbox, as shown in Figure 10. All of these editors and viewers are implemented in MATLAB for FMWS and simulation work of this approach is described in this section. We used MATLAB 2014b x64 version in this approach for simulation work. In MATLAB Fuzzy Logic Toolbox is opened by writing “fuzzy” in command window. Afterwards, we entered the names of input and output variables.

In Figure 10, three inputs C-R-Temp, C-R-humidity, and Time, which are shown on left side and only one output Fire-chances on right side are added for simulation work of Fire Monitoring and Warning System (FMWS).

3.4.1. Implementing Fuzzification in MATLAB

In fuzzification, a crisp value is converted into fuzzy linguistic variables using membership functions. In this paper, four inputs are used the change rate of temperature, change rate of humidity, time, and flame, and one output is evaluated, which is fire-chances. Since the Flame- presence variable remains constant because we just use it to check flame is present or not, then the rules are applied after confirming flame’s presence. Further, three inputs, such as the change rate of temp and humidity and time are used in simulation work for the evaluation of fire-chances to be detected by the FMWS. Fuzzification of the input and output variables are presented below:

Membership Function of Change Rate of Temp (C-R-temp): In Figure 11, three linguistic variables of C-R-Temp Low, Mid, and High are used. x-axis represents the value of change rate of temp from 0 to 10 °C and y-axis represents the degree of membership from 0 to 1. The range of linguistic variables Low is from 0 to 2 °C, Mid is from 2 to 5 °C, and High is from 5 to 10 °C according to our defined Universe of Discourse of each variable in Table 5.

Membership Function of Change Rate of humidity (C-R-humidity): In Figure 12, three linguistic variables of C-R-humidity is Low, Mid and High are used and x-axis represent the value of change rate of humidity from 0 to 20% and y-axis represent the degree of membership from 0 to 1. The range of linguistic variable Low is from 0 to 5%, Mid is from 5 to 12%, and High is from 12 to 20% according to the Universe of Discourse of each variable, which we defined in Table 5.

Membership Function of Time: In Figure 13 three linguistic variables for Time is Short and Long are used and x-axis represent the value of Time from 0 to 10 min and y-axis represent the degree of membership from 0 to 1. The range of linguistic variable Time Short is from 0 to 4 and Long is from 4 to 10 min according to our defined Universe of Discourse of each variable in Table 5.

Membership Function of Output Fire-chances: In Figure 14 three linguistic variables of output Fire-chances Low, Mid and High are used and x axis represent the value of Fire-chances from 0 to 100% and y axis represent the degree of membership from 0 to 1. The range of linguistic variable Low is from 0 to 30%, Mid is from 30 to 60%, and High is from 60 to 100%, according to our defined universe of discourse of each variable in Table 5.

3.4.2. Defining Fuzzy Rules in MATLAB Rules Editor

Once the membership functions are designed, the fuzzy rules are defined using simple IF-Then rules, which are used to express piece of knowledge in MATLAB rules editor. The fuzzy rules are most widely and commonly used for interpretation.

Rules for FMWS (according to flame presence): The defined rules are applied when fire is detected otherwise FMWS again start sensing surroundings until the fire is not detected.

In

Table 7. Rules for FMWS (according to flame presence).

Flame	Go to Start	Go to Next Step
Flame is present	No	Yes
Flame is not present	Yes	No

flame is used as for Boolean value (Yes, No) to check the flame presence. It is because when the fire is detected, it means there must be flame, second column is “Go to Start” when flame is present it will go back until flame remains present, in column three “Go to next step” means when flame is present it will go to next step for further procedure for evaluating fire chances by using other inputs variables, otherwise will never go to next step until flame is not present. In the proposed work, we applied three and two linguistic variables consisting of three linguistic values each thereby resulting in 3 × 3 × 2 = 18 rules. Using these rules a controller system was designed.

Rules for FMWS (when input time is short): In

Table 8. Rules for FMWS (Short time).

C-R-Humidity	C-R-Temp
	Low	Mid	High
Low	Low	Mid	High
Mid	Low	Mid	High
High	Mid	Mid	High

, the rule set is formulated for short time according to two inputs C-R-Temp and C-R-Humidity by using variables Low, Mid, and High. Which means when C-R-Temp and C-R-Humidity values changed in short time:

Rules for FMWS (when input time is long):

Table 9. Rules for FMWS (Long time).

C-R-Humidity	C-R-Temp
	Low	Mid	High
Low	Low	Low	Mid
Mid	Low	Low	Mid
High	Low	High	High

is formulated similar to Table 8, but the only difference between them that in Table 9, rule set is applied when time is Long.

Apply solution mechanisms according to outcomes: Here,

Table 10. Solution of outcomes.

Outcome	Solution
Low	Alert
Mid	Alarm/Water Shower(Low)/Off Gas
High	Alarm/Water Shower(High)/Off Gas

, represents the solution mechanism according to outcome (Fire chances) for FMWS. If the outcome is Low, then FMWS alerts the people, if outcome is Mid then alarm is activated, water showers are turned ON but with High intensity Gas is turned Off, if outcome is High then alarm is activated, water showers are turned ON and Gas will turned Off until situation turns to under control.

Add rules in MATLAB using Rules Editor: Figure 15 represents MATLAB rule editor in which rule sets are added for FMWS. First box represents the rule set, second left box shows C-R-Temp variables, third represents C-R-humidity variables, and fourth box represents time variables, these sides of box represents the input variables and in right side box represents Fire-chances, which we used for output.

4. Results and Discussion

A set of experiments were conducted to test the performance of the proposed FMWS. The performance of the FMWS is defined with respect to the accuracy of flame detection. Here, the accuracy of flame detection is represented by the Fire-chances in the experiments discussed below. To test the performance of proposed FMWS, a set of twelve experiments was performed, as shown in

Table 11. Table of the FMWS results of 12 Experiments.

Sr. No.	C-R-Temp (°C)	Presence of Flame	C-R-Humidity (% age)	Time (minutes)	Chances of True Fire (% age)	Test Case	Actual Case	Accuracy (% age)
1	1.51	1	7.83	2.53	8.4	Low	Low	100%
2	5	1	10	5	50	Mid	Mid	100%
3	3.67	1	9.28	2.53	40	Mid	Mid	100%
4	7.41	1	12.9	1.99	61.2	High	High	100%
5	7.89	1	14.3	8.3	82.9	High	High	100%
6	1.87	1	3.01	1.39	14.3	Low	Low	100%
7	2.71	1	5.18	2.47	45	Mid	Mid	100%
8	7.29	1	7.35	1.39	67.7	High	High	100%
9	6.69	1	16.3	2.35	83.4	High	High	100%
10	1.27	1	15.8	2.35	45	Mid	Low	50%
11	5.48	1	11	1.39	65.9	High	High	100%
12	9.1	1	15.3	4.04	83.9	High	High	100%

. Out of these twelve experiments, the visual representation of three experiment cases is given in Figure 16, Figure 17 and Figure 18 as experiments with medium, lowest, and highest chances of fire, respectively. In the experiments discussed below, the fire-chance is calculated from 1 to 100 in terms of ratio to chances of true fire. The score of fire-chances in our experiments had a range from 8 to 83. At this point, FMWS is ready to accept input values and generate output value according to rule set.

4.1. Results of MATLAB Implementation

In Figure 16, the result of experiment 1 are shown in rule viewer. First column of rule viewer represents the change rate of temperature (C-R-Temp), second column represents the change rate of humidity (C-R-humidity), and third column represents the time, these three columns represented input values. The fourth column is for output, which represents the chances of Fire (how much chances of fire to occur). In Figure 16, the value of C-R-Temp is 5, C-R-humidity is 10 and Time is 5. The output of this experiment is 50, which is shown in the last column that means according to input values the fire-chances is 50% o, according to rules there is urgent need of activating fire control mechanisms discussed above.

In Figure 17, the results of experiment 2 in proposed work is shown in rule viewer. First column of rule viewer represents the change rate of temperature (C-R-Temp), second column represents the change rate of humidity (C-R-humidity) and third column represents the time, these three columns represented input values. The fourth column is for output which represents the chances of Fire (how much chances of fire to occur). In Figure 17 the value of C-R-Temp is 1.52, C-R-humidity is 7.83 and Time is 2.53. The output of this experiment is 13 which are shown in last column which means according to input values the fire- chances is 13, there are 13% chances of fire to occur, situation is normal and according to rules there is need to alert people using alarm or SMS.

Figure 18 represents the experiment result in rules viewer for FMWS, in which the first three columns represent input values and fourth represents output values, which is evaluated by input values and according to rule set. First column represents C-R-Temp, which means how much temperature is changed and value is set by 6.33. Second column represents C-R-humidity, which means how much humidity is changed within defined time interval and in value is set by 13.9. Third column show time which represents time interval and the value in this is 3.07. Fourth column represents output value of Fire-chances which is evaluated by input values. The input values in rule viewer can set manually in fuzzy logic toolbox to check rule set is working according to requirements and system accuracy. At this point, the construction of the FMWS is complete, because inference and defuzzification are built in function in the software, which is done by MATLAB. FMWS is ready to accept input values; we entered input values (6.33, 13.9, 3.03), as shown in Figure 18 the input values are related to fuzzy sets and decision rules are applied. The fuzzy results of the output variable are composed and defuzzified using Centroid Defuzzification method which are done by MATLAB. In Figure 18 the output is 82.4 which is High chances of fire. All of these steps are implemented by using MATLAB fuzzy logic toolbox based on fuzzy logic rules and operations.

Figure 19 represents FMWS results graphically in surface viewer. x-axis represents input value of C-R-Temp, y-axis represents input value of C-R-humidity, and z-axis represents the output value of Fire-chances. It is clearly shown in Figure 19 that C-R-temp and C-R-humidity gets higher value over fire regions and lower values over non-fire region.

After experiments, all the results are collected, now in this section results are discussed, and all experiment results are illustrated in Table 11.

Results are shown in Table 11. In experiment 1, the change rate of temp is 1.51, change rate of humidity is 7.83 and time is 2.53, and the chance of fire is 8.4%, which is low and actual case also Low, which means that the accuracy is 100%. In experiment 2, change rate of temp is 5, change rate of humidity is 10 and time is 5 and the chance of fire is 50% which mean there are 50% chances of fire to occur and actual case also Mid which means the accuracy is 100%. In experiment 3, change rate of temp is 3.67, change rate of humidity is 9.28, and time is 2.53, and chance of fire is 40 and actual case also Mid, which means in this case that accuracy is 100%. In experiment 4, change rate of temp is 7.41, change rate of humidity is 12.9, and time is 1.99 and chance of fire is 61.2, which is high and actual case also High which means the accuracy is 100%. But in exp 5, change rate of temp is 7.89, change rate of humidity is 14.3 and time is 8.3 and the chance of fire is 82.9, which is high chances of fire and actual case also High, which means that the accuracy is 100%. In experiment 6 to 12 few of them are High and few are Mid chances of fire. As it can be observed from Table 11 the accuracy of proposed FMWS in most of experiments is 100%, which means that the system is working according to our defined rules for FMWS. The overall FMWS is calculated below:

$$\mathrm{FMWS}\mathrm{accuracy}={\displaystyle \sum \frac{\mathsf{\mu }\left(\mathrm{ai}\right)}{\mathrm{n}}}$$

(10)

In Equation (10), we calculated the FMWS accuracy where µ(ai) represents the accuracy percentage of each experiment and n represents the total number of experiments. According to experiments we achieved accuracy 95.83%.

4.2. Computational Complexity of Proposed Approach

The computational complexity of the proposed system is examined when the control enters in loop and run in controller hardware then inference speed of fuzzy logic control can be observed. In

Table 12. Inference speed of CPU.

CPU (Clock Speed)	Instruction Cycle (Clocks)					Inference Speed
	Add.	Com.	Sub.	Mul.	Div.
Arduino UNO (16 MHz)	1	1	1	1	1	3 s
AM2302 (0.5 Hz)	1	16	2	1	1	250 ms
Flame Sensor	1	2	1	1	1	2 s

, the clock speed of CPU is described, which is observed when controller is running and instruction cycles represent the number of instruction which is executed.

4.3. Contribution to Knowledge

The comparison between existing work and proposed work is described in

Table 13. Comparison with existing work.

Features	Tan et al. [12]	Yunus et al. [13]	Son B. et al. [14]	Proposed Method
Multiple-sensors	No	No	No	Yes
Alarm	No	No	No	Yes
Decision on two Authentications	No	No	No	Yes
False Alarm Detection	No	No	No	Yes

that three existing works are compared to our proposed work. The feature, which is the base of this comparison, are multiple-sensors, alarm, decision on two authentications, and false alarm.

The proposed work is novel and important in multiple ways. A comparison between the presented work and previous work is shown in Table 13. First novelty is that existing work of Tan et al., Yunus et al. and Son B. et al., have many short comings in their work, such as the use of one or two sensors, which gives less accuracy, while the proposed work employs a multi sensor solution and it uses four inputs to provide more accurate and reliable results. Second, there was no alarm system to alert people but in proposed work alarm activation is used. Third, in existing work, the decision is not verified by two authentications but in proposed work multiple sensors are used as the flame is detected initially and then change rate of temp and humidity is calculated. Fourth, the major shortcoming in the previous work was false alarm, sometimes temperature is changed according to environmental changes and the system notifies fire detection, which consume lot of energy consumption and create hustle and disturbance, but in proposed work, it never produces false alarm. The results of the experiments are accurate up to 95.83%, as shown in Table 11, which outperforms the similar work in the domain.

4.4. Limitation of the Proposed Approach

The proposed system is designed to detect fire at early stage, it is very effective for this purpose, which is found in some previous solution, and it also has many advantages as well as few disadvantages. The advantage and disadvantages of proposed solution with traditional solution are described in

Table 14. Advantages of proposed solution and traditional solutions.

Proposed Solution	Traditional Solutions
Proposed system is less expensive. It reduce false alarm rate. It detects true fire at early stage. It can be used in residential areas. It detect fire automatically without any supervision.	Image processing and video based systems are good for fire detection on large scale but are expensive. In WSN, number of clusters are sensing environment and send information when fire is detected.

and

Table 15. Disadvantages of proposed solution and traditional solutions.

Proposed Solution

Traditional Solution

It is used only in small area such as rooms. Accuracy may differ in big halls. Flame sensor also detect sun light instead of flame or fire. The systems is effective for indoor solutions.

Some traditional solution can produce false alarm. Some system cannot work automatically. Single sensor is not enough to detect true fire. Some systems only suitable to detect fire in large scale like wildfire and not suitable for residential area. It can be very expensive. In WSN, if any cluster is not able to send information to cluster head due to any reason then it cannot detect fire until cluster head got information from that cluster.

.

5. Conclusions

In this research paper, the fuzzy logic based Fire Monitoring and Warning System (FMWS) is presented to save lives and property damages. The objective of this paper is to detect true-fire incidents at early stages, and alert people and extinguish fire as soon as possible. Researchers proposed different methods to monitor and detect fire incidents. In this paper, fuzzy logic is used as one of the latest technology in which it supported execution requirements very easily. Multiple sensors (Temperature sensor, flame sensor) are used to get the accurate results to reduce false alarm rate. Four parameters are used as input, such as the change rate of temperature, the change rate of humidity, presence of flame, and time. The purpose of using change rate is to make the system more general rather than specific because different countries have different temperatures, increase in temperature in short time shows that there is something wrong in environment. The system will alert people if any unwanted situation occurs anywhere. The output ‘chances of fire’ is achieved after applying rules when a fire is detected somewhere, then, according to situation alternative control mechanism, can be activated like water showers, etc. The proposed work also discards the false alarm rate. Simulation work is done in MATLAB Fuzzy Logic toolbox and satisfactory results are discussed in this paper as well.