Numerical Study of Dynamic Properties of Fractional Viscoplasticity Model
Abstract
:1. Introduction
2. Fractional Viscoplasticity
2.1. Remarks on Fractional Calculus
2.2. Basic Concepts
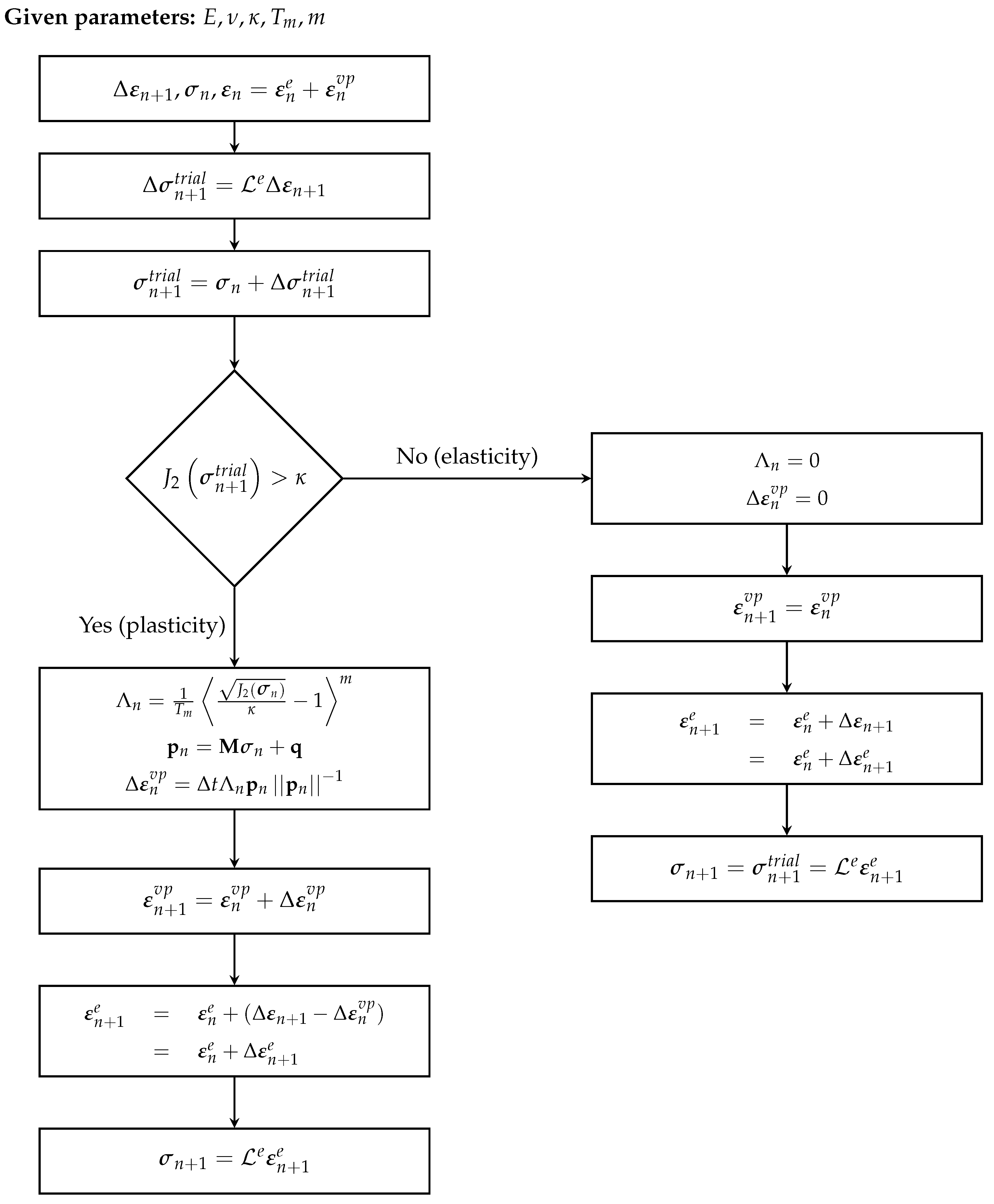
3. Implementation
4. Parametric Study: Uniaxial Tension
4.1. Description of the Numerical Experiment
4.2. Influence of the Order of FV and Non-Locality in a Stress State on Plastic Flow
4.2.1. Study of Intensified Plastic Flow in Tension Direction for Different Orders of Flow
4.2.2. Study of Intensified Plastic Flow Perpendicular to the Tension Direction for Different Orders of Flow
4.3. Influence of the Relaxation Time and the Overstress Power
4.3.1. Study of the Fractional Flow Under Different Dynamic Loading Rates for Intensified Plastic Flow in Tension Direction
4.3.2. Study of the Fractional Flow Under Different Dynamic Loading for the Intensified Plastic Flow Perpendicular to the Tension Direction
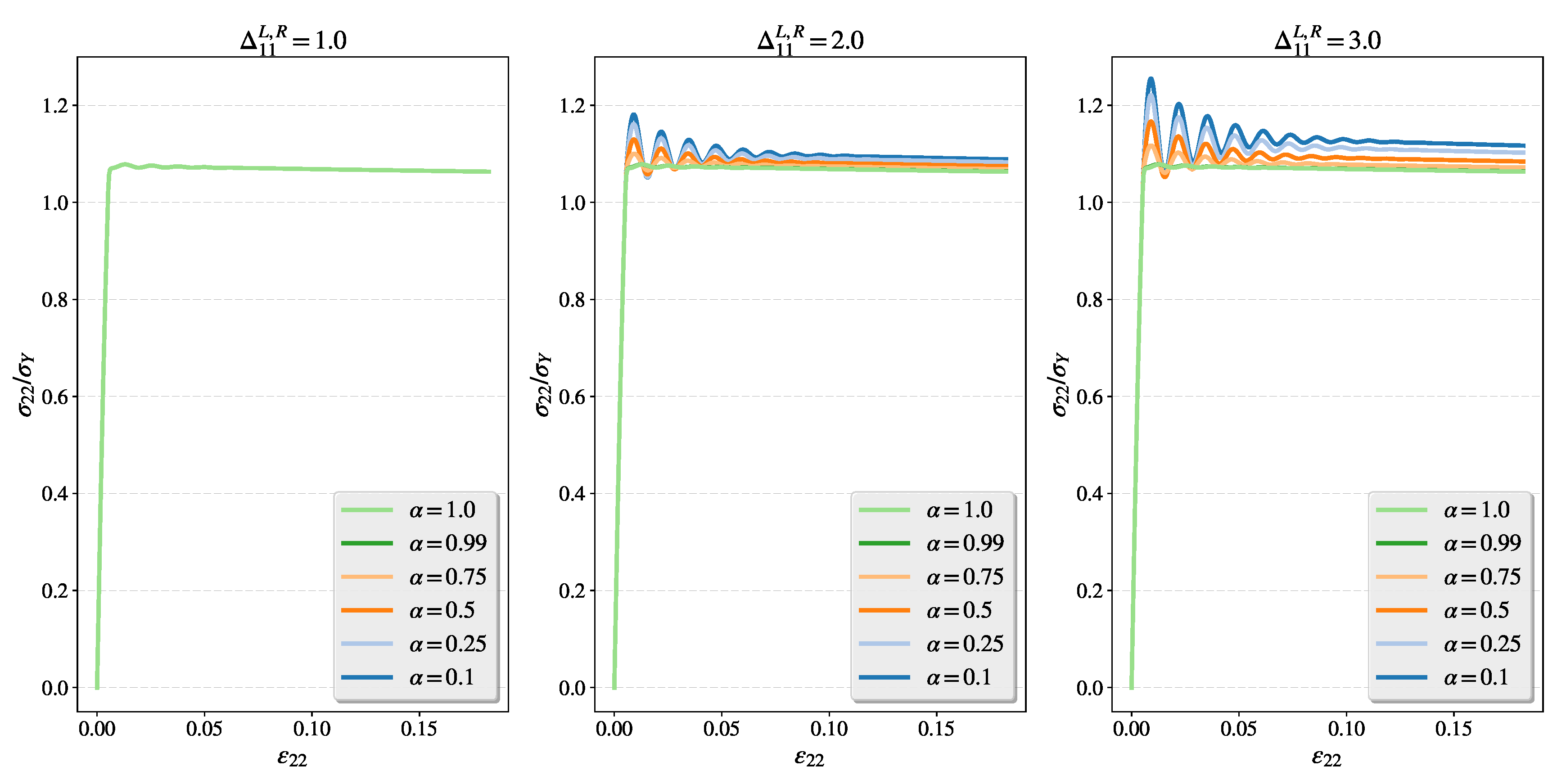
4.4. Study of the Disperse Character of the Fractional Viscoplastic Stress Waves
5. Conclusions
- Fractional viscoplasticity introduces an additional set of material parameters, namely flow order and virtual stress state surrounding .
- Fractional parameters and control the dynamic properties of the fractional model, especially hardening, the character of the stress waves, and plastic anisotropy.
- The direction of the flow vector is controlled by , which in general leads to non-normality of plastic flow.
- As in the classical Perzyna model, the relaxation time and the overstress power m affect the strain rate hardening and the character of the stress waves.
- Induced plastic anisotropy of the fractional model should be regarded not only in the classical sense as directional deformation but also as directional viscosity, which results in directional dispersive character.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Podlubny, I. Fractional Differential Equations. In Mathematics in Science and Engineering; Academin Press: Cambridge, MA, USA, 1999; Volume 198. [Google Scholar]
- Samko, S.; Kilbas, A.; Marichev, O. Fractional Integrals and Derivatives: Theory and Applications; Gordon and Breach: Amsterdam, The Netherlands, 1993. [Google Scholar]
- Meng, R.; Yin, D.; Zhou, C.; Wu, H. Fractional description of time-dependent mechanical property evolution in materials with strain softening behavior. Appl. Math. Modell. 2016, 40, 398–406. [Google Scholar] [CrossRef]
- Li, M. Three Classes of Fractional Oscillators. Symmetry 2018, 10, 40. [Google Scholar] [CrossRef]
- Zhao, J.; Zheng, L.; Zhang, X.; Liu, F. Convection heat and mass transfer of fractional MHD Maxwell fluid in a porous medium with Soret and Dufour effects. Int. J. Heat Mass Trans. 2016, 103, 203–210. [Google Scholar] [CrossRef]
- Jinhu, Z.; Liancun, Z.; Xinxin, Z.; Fawang, L. Mixed convection heat transfer of viscoelastic fluid along an inclined plate obeying the fractional constitutive laws. Heat Trans. Res. 2017, 48, 1165–1178. [Google Scholar]
- Zhang, X.; Liu, L.; Wu, Y. The uniqueness of positive solution for a fractional order model of turbulent flow in a porous medium. Appl. Math. Lett. 2014, 37, 26–33. [Google Scholar] [CrossRef]
- Cherniha, R.; Gozak, K.; Waniewski, J. Exact and Numerical Solutions of a Spatially-Distributed Mathematical Model for Fluid and Solute Transport in Peritoneal Dialysis. Symmetry 2016, 8, 50. [Google Scholar] [CrossRef]
- Atanackovic, T.; Janev, M.; Oparnica, L.; Pilipovic, S.; Zorica, D. Space–time fractional Zener wave equation. Proc. Math. Phys. Eng. Sci. 2015, 471, 20140614. [Google Scholar]
- Ren, T.; Li, S.; Zhang, X.; Liu, L. Maximum and minimum solutions for a nonlocal p-Laplacian fractional differential system from eco-economical processes. Bound. Value Probl. 2017, 2017, 118. [Google Scholar] [CrossRef]
- Sumelka, W.; Voyiadjis, G. A hyperelastic fractional damage material model with memory. Int. J. Solids Struct. 2017, 124, 151–160. [Google Scholar] [CrossRef]
- Klimek, M. Fractional sequential mechanics—Models with symmetric fractional derivative. Czechoslov. J. Phys. 2001, 51, 1348–1354. [Google Scholar] [CrossRef]
- Drapaca, C.; Sivaloganathan, S. A Fractional Model of Continuum Mechanics. J. Elast. 2012, 107, 107–123. [Google Scholar] [CrossRef]
- Sumelka, W.; Szajek, K.; Łodygowski, T. Plane strain and plane stress elasticity under fractional continuum mechanics. Arch. Appl. Mech. 2015, 89, 1527–1544. [Google Scholar] [CrossRef]
- Tomasz, B. Analytical and numerical solution of the fractional Euler–Bernoulli beam equation. J. Mech. Mater. Struct. 2017, 12, 23–34. [Google Scholar]
- Lazopoulos, K.; Lazopoulos, A. Fractional vector calculus and fluid mechanics. J. Mech. Behav. Mater. 2017, 26, 43–54. [Google Scholar] [CrossRef]
- Peter, B. Dynamical Systems Approach of Internal Length in Fractional Calculus. Eng. Trans. 2017, 65, 209–215. [Google Scholar]
- Sumelka, W. Fractional viscoplasticity. Mech. Res. Commun. 2014, 56, 31–36. [Google Scholar] [CrossRef]
- Sun, Y.; Shen, Y. Constitutive model of granular soils using fractional-order plastic-flow rule. Int. J. Geomech. 2017, 17, 04017025. [Google Scholar] [CrossRef]
- Sun, Y.; Xiao, Y. Fractional order model for granular soils under drained cyclic loading. Int. J. Numer. Anal. Meth. Geomech. 2017, 41, 555–577. [Google Scholar] [CrossRef]
- Sun, Y.; Xiao, Y. Fractional order plasticity model for granular soils subjected to monotonic triaxial compression. Int. J. Solids Struct. 2017, 118-119, 224–234. [Google Scholar] [CrossRef]
- Perzyna, P. The constitutive equations for rate sensitive plastic materials. Q. Appl. Math. 1963, 20, 321–332. [Google Scholar] [CrossRef] [Green Version]
- Glema, A.; Łodygowski, T. On importance of imperfections in plastic strain localization problems in materials under impact loading. Arch. Mech. 2002, 54, 411–423. [Google Scholar]
- Glema, A. Analysis of wave nature in plastic strain localization in solids. In Rozprawy; Publishing House of Poznan University of Technology: Poznan, Poland, 2004; Volume 379. (In Polish) [Google Scholar]
- Glema, A.; Łodygowski, T.; Perzyna, P. Interaction of deformation waves and localization phenomena in inelastic solids. Comput. Meth. Appl. Mech. Eng. 2000, 183, 123–140. [Google Scholar] [CrossRef] [Green Version]
- Glema, A.; Łodygowski, T.; Perzyna, P. Localization of plastic deformations as a result of wave interaction. Comput. Assist. Mech. Eng. Sci. 2003, 10, 81–91. [Google Scholar]
- Perzyna, P. The Thermodynamical Theory of Elasto-Viscoplasticity. Eng. Trans. 2005, 53, 235–316. [Google Scholar]
- Sumelka, W.; Nowak, M. Non-normality and induced plastic anisotropy under fractional plastic flow rule: A numerical study. Int. J. Numer. Anal. Meth. Geomech. 2016, 40, 651–675. [Google Scholar] [CrossRef]
- Sumelka, W.; Nowak, M. On a general numerical scheme for the fractional plastic flow rule. Mech. Mater. 2017, 116, 120–129. [Google Scholar] [CrossRef]
- Xiao, R.; Sun, H.; Chen, W. A finite deformation fractional viscoplastic model for the glass transition behavior of amorphous polymers. Int. J. Non-Linear Mech. 2017, 93, 7–14. [Google Scholar] [CrossRef]
- Odzijewicz, T.; Malinowska, A.; Torres, D. Green’s theorem for generalized fractional derivatives. Fract. Calc. Appl. Anal. 2013, 16, 64–75. [Google Scholar] [CrossRef] [Green Version]
- Ziegler, H. An Introduction to Thermomechanics; North Holland Series in Applied Mathematics and Mechanics; North-Holland Publishing Company: North Holland, The Netherlands, 1983; Volume 21. [Google Scholar]
- Dao, M.; Asaro, R. Non-Schmid effects and localized plastic flow in intermetallic alloys. Mater. Sci. Eng. A 1993, 170, 143–160. [Google Scholar] [CrossRef]
- Racherla, V.; Bassani, J. Strain burst phenomena in the necking of a sheet that deforms by non-associated plastic flow. Modell. Simul. Mater. Sci. Eng. 2007, 15, S297–S311. [Google Scholar] [CrossRef]
- Marin, E.; McDowell, D. Models for Compressible Elasto-Plasticity Based on Internal State Variables. Int. J. Damage Mech. 1998, 7, 47–83. [Google Scholar] [CrossRef] [Green Version]
- Leffers, T. Lattice rotations during plastic deformation with grain subdivision. Mater. Sci. Forum 1994, 157–162, 1815–1820. [Google Scholar] [CrossRef]
- Hughes, D.; Liu, Q.; Chrzan, D.; Hansen, N. Scaling of microstructural parameters: Misorientations of deformation induced boundaries. Acta Mater. 1997, 45, 105–112. [Google Scholar] [CrossRef]
- Steinmann, P.; Kuhl, E.; Stein, E. Aspects of non-associated single crystal plasticity: Influence of non-schmid effects and localization analysis. Int. J. Solids Struct. 1998, 35, 4437–4456. [Google Scholar] [CrossRef]
- McDowell, D. Viscoplasticity of heterogeneous metallic materials. Mater. Sci. Eng. R 2008, 62, 67–123. [Google Scholar] [CrossRef]













| 2.085 MHz | 2.085 MHz | ||
| 2.108 MHz | 1.996 MHz | ||
| 2.073 MHz | 2.073 MHz | ||
| 2.157 MHz | 2.028 MHz | ||
| 2.5e-7 | 2.5e-6 | 2.5e-5 | ||
|---|---|---|---|---|
| 2.073 MHz | 2.073MHz | 2.274 MHz | ||
| 2.157 MHz | 2.157 MHz | 2.288 MHz | ||
| 2.073 MHz | 2.085 MHz | 2.182 MHz | ||
| 2.157 MHz | 2.157 MHz | 2.207 MHz | ||
| 2.073 MHz | 2.085 MHz | 2.169 MHz | ||
| 2.157 MHz | 2.157 MHz | 2.182 MHz | ||
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Szymczyk, M.; Nowak, M.; Sumelka, W. Numerical Study of Dynamic Properties of Fractional Viscoplasticity Model. Symmetry 2018, 10, 282. https://doi.org/10.3390/sym10070282
Szymczyk M, Nowak M, Sumelka W. Numerical Study of Dynamic Properties of Fractional Viscoplasticity Model. Symmetry. 2018; 10(7):282. https://doi.org/10.3390/sym10070282
Chicago/Turabian StyleSzymczyk, Michał, Marcin Nowak, and Wojciech Sumelka. 2018. "Numerical Study of Dynamic Properties of Fractional Viscoplasticity Model" Symmetry 10, no. 7: 282. https://doi.org/10.3390/sym10070282
APA StyleSzymczyk, M., Nowak, M., & Sumelka, W. (2018). Numerical Study of Dynamic Properties of Fractional Viscoplasticity Model. Symmetry, 10(7), 282. https://doi.org/10.3390/sym10070282






