PUF Based Authentication Protocol for IoT
Abstract
:1. Introduction
2. Related Work
2.1. Key Agreement from IoT Device to Server
2.2. Key Agreement between Two IoT Devices
3. Preliminaries
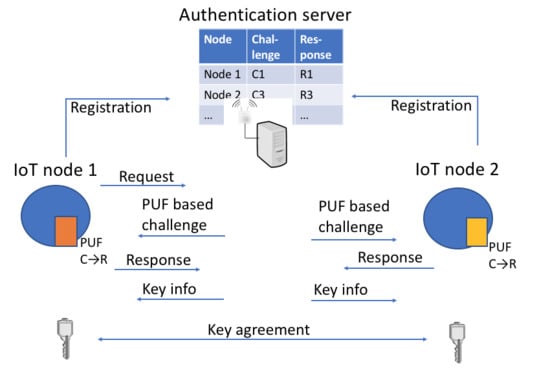
3.1. System Architecture
- In the enrolment phase, each IoT node shares through a secure channel challenge–response pairs with a server, which is considered as a trusted and authenticated party.
- In the authentication and key sharing phase, two nodes supervised by the same server are able to generate a private and public key pair. The public key of the one node is shared with the other with the help of the server to guarantee the authenticity. Note that we here also consider this simplified setting. In [3], details are given on how to deal with the situation where two nodes are registered with a different server.
- Finally, the secure communication phase allows both nodes to start a secure communication.
3.2. Cryptographic Operations
3.2.1. PUFs
3.2.2. Public Key Related Operations
- The Elliptic Curve Discrete Logarithm Problem (ECDLP). This problem states that, given two EC points R and Q of ), it is computationally hard for any polynomial-time bounded algorithm to determine a parameter , such that .
- The Elliptic Curve Diffie–Hellman Problem (ECDHP). Given two EC points with two unknown parameters and P, the base point generator of the defined EC, it is computationally hard for any polynomial-time bounded algorithm to determine the EC point .
3.2.3. Other Operations
4. Security Attacks on the System of Chatterjee et al.
4.1. Enrolment Phase
4.2. Description of the Authentication and Key Sharing Phase
- Node 1 sends a request to the server that it wants to communicate with Node 2.
- The server randomly selects two challenges related to Node 1 and two challenges related to Node 2 from its database. Next, it calculates the values by hashing the corresponding responses and , respectively, with the timestamp . Next, this is hidden for outsiders by xoring it with the concatenation of the responses of Node 1 and Node 2 in order to obtain and , respectively. Finally, the Server sends to Node 1 and to Node 2.
- Upon arrival of these messages, Node 1 and Node 2 perform similar actions in the rest of the protocol. Let us explain the steps of Node 1. First, it derives from after evaluating the PUF of and . Next, it computes by hashing the responses of the challenge with the obtained . Then, it calculates , which is the hash of the xor of the two challenges and results in an ECC point. Based on a randomly chosen value , the public key is computed as the EC multiplication of t with . The corresponding private key equals , which is transferred to an EC point. Next, a hash function of the xor of the different obtained values is computed to guarantee the integrity, resulting in . The message containing is sent to the server.
- The server first authenticates Node 1 by checking the equality of with the previously computed value and the correctness of . If so, the received public key of Node 2, together with and , is sent to Node 1. A hash function on the xor of these values, together with the responses , is sent to Node 1.
4.3. Security Attacks
- In a local network:
- -
- Anyone who is connected to the same Wi-Fi is able to read the traffic.
- -
- If the router (or some other part of the network) is hacked, the hacker can read and modify the traffic.
- -
- The person that legitimately controls the network, e.g., the responsibility of the authentication server can read and modify the traffic without even having to hack anything.
- Over the internet:
- -
- The Internet Service Provider (ISP) is able to read and modify all the traffic, since it controls the hardware it passes through. The traffic can also go through other networks owned by unknown companies, eventually of different countries, and those can also read and modify the traffic as well.
- -
- When a nation state hands over a court to one of these companies passing the traffic, it can also read and modify the data (e.g., NSA).
4.3.1. Man-in-the-Middle Attack
4.3.2. Impersonation Attack with Malicious Insider Node
4.3.3. Replay Attack
4.3.4. Denial of Service Attack
4.4. Conclusion of the Security Attacks
- The node identity used in the initial request should be utilised throughout the whole protocol.
- The timestamp should be verifiable by all entities in each step of the protocol up to the end.
- The integrity and authentication of the message should be checked at each single step in the protocol.
- The responses should only be sent under a hash value in order not to leak information on them and to allow reusability of the challenge–response pairs.
5. Proposed Solution
5.1. Authentication and Key Agreement Phase
- To start the key agreement phase, Node 1 shares with the server the identities of Nodes 1 and 2, respectively, together with the current timestamp . Node 1 opens a new session and stores the three parameters in it.
- Upon arrival of the request, the server checks its database for the existence of and . If so, it then selects two pairs of Node 1 and two pairs of Node 2 from its database. Based on this information, it computes bothIn addition, a hash value to ensure the integrity and authentication of the server needs to be included. This value for Nodes 1 and 2, respectively, is computed as follows:The message is sent to Node 1 and is sent to Node 2. The server opens a new session in which the parameters are stored.
- Upon arrival of the message, Node 1 first checks if the message consists of three parameters of the expected length. If so, it opens the stored session and retrieves the parameters . Then, Node 1 computes for in order to derive . This allows for verifying . If correct, Node 1 also derives and randomly chooses to compute . Next, it computes . The message is sent to the server and are additionally stored in the session. Similarly, Node 2 generates the message and the parameters are stored in a new session at Node 2.
- Upon arrival of messages consisting of two parameters of the expected length, the server first verifies for the identities involved in any of the open sessions stored on the server side, where the current timestamp is in a reasonable timeframe with the corresponding stored timestamp. The verification of ensures the integrity and authenticity of both nodes. If it is correct, it starts with the derivation of the certificates for both nodes. Therefore, it randomly chooses a variable and computes . Next, the two certificates of the nodes are computed as and :These certificates are used to compute the auxiliary information for Node 1 and Node 2 to compute their private and public key pair, respectively. Recall that is the private-public key pair of the server, where is publicly published:In addition, to guarantee the integrity of the communication, the values are also computed:The values are sent to Node 1. The values are sent to Node 2. The stored session is now closed on the server side.
- When a message of four parameters of expected length is received, Node 1 opens the stored session(s) where the current timestamp is in a reasonable timeframe with the stored timestamp. Node 1 first checks the hash value . If OK, it continues with the computation of its private key . Its public key equals , but also toConsequently, given the publicly available values , everybody is able to compute this key. The private key is only known by the node itself. Using , Node 1 is able to compute the public key of Node 2. Note that this mechanism is based on the ECQV Implicit Certificate Scheme [11]. After a successful generation of the key material, both nodes close the stored session and open a new session storing its private and public key pair together with the public key and identity of the other node.
5.2. Secure Communication Phase
6. Security Evaluation
- Integrity. Integrity is obtained in every step of the protocol since every message contains a hash, which includes the other parts (or derivations of it) of the message.
- Authentication of the Node. The nodes are authenticated if the check on the values are correct. These hash values contain the responses on the challenges, which can only be generated by the node possessing the PUF.
- Authentication of the Server. The server is authenticated by the node in both received messages. In the first received message by Node 1, the value , computed by the server, includes , while this value is not part of the received message. Instead, is masked by a hash value, which includes the response on the first challenge. Consequently, as only the server is aware of the challenge–response pairs, Node 1 ensures that the server has sent the message. In the second received message, the hash value is included. This hash value contains the responses on the two challenges, which is only known by the server. Due to the symmetry of the protocol, the same reasoning holds for Node 2.
- Resistance against man-in-the-middle attacks. As the authenticity of the sender is verified by the receiver in each step of the protocol, resistance against man-in-the middle attacks is guaranteed.
- Resistance against impersonation attacks. Even if Node 1 is malicious, it is not possible for the node to derive information on the challenge–response pairs of the other node from the messages exchanged between the server and Node 2. This follows from the fact that only hash values on the responses are included in the messages, which do not leak any information.
- Resistance against replay attacks. Replay attacks are avoided, due to the usage of the timestamp, which is included in all the hashes of the different transmitted messages.
- Protection against denial of service attacks. Besides the first message, both the nodes and the server can check at each step of the key agreement scheme the integrity and authentication by verifying the hash included in the messages. Consequently, in case a massive amount of false messages flow over the network, it will be very quickly discovered.
7. Performance
7.1. Computational Cost
7.2. Communication Cost
8. Conclusions
Conflicts of Interest
Abbreviations
| PUF | Physical Unclonable Function |
| IoT | Internet of Things |
| DoS | Denial of Service |
| ECC | Elliptic Curve Cryptography |
| EC | Elliptic Curve |
| ECQV | Elliptic Curve Qu Vanstone |
References
- Das, A.K.; Zeadally, S.; He, D. Taxonomy and analysis of security protocols for Internet of Things. Future Gener. Comput. Syst. 2018, 89, 110–125. [Google Scholar] [CrossRef]
- Pappu, S.R. Physical One-Way Functions. Ph.D. Thesis, Massachusetts Institute of Technology, Cambridge, MA, USA, 2001. [Google Scholar]
- Chatterjee, U.; Chakraborty, R.S.; Mukhopadhyay, D. A PUF-Based Secure Communication Protocol for IoT. ACM Trans. Embed. Comput. Syst. 2017, 16, 67. [Google Scholar] [CrossRef]
- Zheng, Y. Digital Signcryption or How to Achieve Cost (Signature & Encryption) << Cost (Signature) + Cost (Encryption). In Annual International Cryptology Conference; Springer: Berlin/Heidelberg, Germany, 1997; pp. 165–179. [Google Scholar]
- Braeken, A.; Shabisha, P.; Touhafi, A.; Steenhaut, K. Pairing free and implicit certificate based signcryption scheme with proxy re-encryption for secure cloud data storage. In CloudTech; IEEE: Rabat, Morocco, 2017. [Google Scholar]
- Tashi, J.J. Comparative analysis of smart card authentication schemes. IOSR J. Comput. Eng. 2014, 16, 91–97. [Google Scholar]
- Braeken, A. Efficient anonymous smart card based authentication scheme for multi-server architecture. Int. J. Smart Home 2015, 9, 177–184. [Google Scholar] [CrossRef]
- Shamir, A. Identity-Based Cryptosystems and Signature Schemes. In Workshop on the Theory and Application of Cryptographic Techniques; Springer: Berlin/Heidelberg, Germany, 1984; Volume 196, pp. 47–53. [Google Scholar]
- Al-Riyami, S.S.; Paterson, K.G. Certificateless Public Key Cryptography. In International Conference on the Theory and Application of Cryptology and Information Security; Springer: Berlin/Heidelberg, Germany, 2003; pp. 452–473. [Google Scholar]
- Gentry, C. Certificate-Based Encryption and the Certificate Revocation Problem. In International Conference on the Theory and Applications of Cryptographic Techniques; Springer: Berlin/Heidelberg, Germany, 2003; pp. 272–293. [Google Scholar]
- Certicom Research. 2013. SEC4: Elliptic Curve Qu-Vanstone Implicit Certificate Scheme, Standards for Efficient Cryptography Group. Version 1.0. Retrieved 30 October 2017. Available online: http://www.secg.org/sec4-1.0.pdf (accessed on 10 July 2018).
- Porambage, P.; Schmitt, C.; Kumar, P.; Gurtov, A.; Ylianttila, M. Two-phase Authentication Protocol for Wireless Sensor Networks in Distributed IoT Applications. In Proceedings of the 2014 IEEE Wireless Communications and Networking Conference (WCNC), Istanbul, Turkey, 6–9 April 2014; pp. 2728–2733. [Google Scholar]
- Delvaux, J. Security Analysis of PUF-Based Key Generation and Entity Authentication. Ph.D. Thesis, Katholieke Universiteit Leuven (KULeuven), Leuven, Belgium, 2017. [Google Scholar]
- Rostami, M.; Majzoobi, M.; Koushanfar, F.; Wallach, D.S.; Devadas, S. Robust and reverse-engineering resilient PUF authentication and key-exchange by substring matching. IEEE Trans. Emerg. Top. Comput. 2014, 2, 37–49. [Google Scholar] [CrossRef]
- Yu, M.D.; Verbauwhede, I.; Devadas, S.; M’Raihi, D. A noise bifurcation architecture for linear additive physical functions. In Proceedings of the 2014 IEEE International Symposium on Hardware-Oriented Security and Trust (HOST), Arlington, VA, USA, 6–7 May 2014; pp. 124–129. [Google Scholar]
- Yu, M.D.; Hiller, M.; Delvaux, J.; Sowell, R.; Devadas, S.; Verbauwhede, I. A lockdown technique to prevent machine learning on PUFs for lightweight authentication. IEEE Trans. Multiscale Comput. Syst. 2016, 2, 146–159. [Google Scholar] [CrossRef]
- Sadeghi, A.R.; Visconti, I.; Wachsmann, C. Enhancing RFID security and privacy by physically unclonable functions. In Towards Hardware Intrinsic Security—Foundations and Practice; Springer: Berlin/Heidelberg, Germany, 2010; pp. 281–305. [Google Scholar]
- Tuyls, P.; Batina, L. RFID-Tags for Anti-counterfeiting. In Topics in Cryptology—CT-RSA 2006; Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2006; Volume 3860. [Google Scholar]
- Guartime and Intrinsic ID. Internet of Things Authentication: A Blockchain solution using SRAM Physical Unclonable Functions. 2017. Retrieved 30 October 2017. Available online: https://www.intrinsic-id.com/wp-content/uploads/2017/05/gtKSI-PUF-web-1611.pdf (accessed on 10 July 2018).
- Simplicio, M.A., Jr.; Silva, M.V.; Alves, R.C.; Shibata, T.K. Lightweight and escrow-less authenticated key agreement for the internet of things. Comput. Commun. 2017, 98, 43–51. [Google Scholar] [CrossRef]
- Wouters, P.; Tschofenig, H.; Gilmore, J.; Weiler, S.; Kivinen, T. RFC 7250—Using Raw Public Keys in Transport Layer Security (TLS) and Datagram Transport Layer Security (DTLS), June 2014. Available online: https://www.rfc-editor.org/rfc/rfc7250.txt (accessed on 10 July 2018).
- Ha, D.A.; Nguyen, K.T.; Zao, J.K. Efficient authentication of resource-constrained IoT devices based on ECQV implicit certificates and datagram transport layer security protocol. In Proceedings of the Seventh Symposium on Information and Communication Technology, Ho Chi Minh City, Vietnam, 8–9 December 2016; pp. 173–179. [Google Scholar]
- Gao, Y.; Ma, H.; Al-Sarawi, S.F.; Abbott, D.; Ranasinghe, D.C. PUF-FSM: A Controlled Strong PUF. IEEE Trans. Comput.-Aided Des. Integr. Circuits Syst. 2017. [Google Scholar] [CrossRef]
- Hankerson, D.; Menezes, A.J.; Vanstone, S. Guide to Elliptic Curve Cryptography; Springer: New York, NY, USA, 2003; ISBN 038795273X. [Google Scholar]
- SEC 2: Recommended Elliptic Curve Domain Parameters, Certicom Research, Standards for Efficient Cryptography Version 1.0, September 2000. Available online: http://www.secg.org/collateral/sec2 final.pdf (accessed on 10 July 2018).
- Recommended Elliptic Curves for Federal Government Use, National Institute of Standards and Technology, August 1999. Available online: http://csrc.nist.gov/groups/ST/toolkit/documents/dss/NISTReCur.pdf (accessed on 10 July 2018).
- Dolev, D.; Yao, A. On the security of public key protocols. IEEE Trans. Inf. Theory 1983, 29, 198–208. [Google Scholar] [CrossRef] [Green Version]
- Lu, Y.; Li, J. Efficient Certificate-Based Signcryption Secure against Public Key Replacement Attacks and Insider Attacks. Sci. World J. 2014. [Google Scholar] [CrossRef] [PubMed]
- Le, M.-H.; Hwang, S.O. Certificate-Based Signcryption Scheme without Pairing: Directly Verifying Signcrypted Messages Using a Public Key. ETRI J. 2016, 38, 724–734. [Google Scholar] [CrossRef]
- He, D.; Zeadally, S.; Wang, H.; Liu, Q. Lightweight Data Aggregation Scheme against Internal Attackers in Smart Grid Using Elliptic Curve Cryptography. Wirel. Commun. Mob. Comput. 2017. [Google Scholar] [CrossRef]





| Key Agreement | ||||||
|---|---|---|---|---|---|---|
| Entity | This | [3] | Benchmark | |||
| Node | 5H + 3EM + 1EA | 2.967 s | 1HP + 2H + 2EM | 16.269 s | 1H + 1EM + 1S | 0.991 s |
| Server | 10H + 1EM + 2EA | 1.004 s | 4HP + 2H | 57.174 s | 2H + 2EM + 2S | 1.982 s |
| Communication Phase | ||||
|---|---|---|---|---|
| Entity | This | [3] | ||
| Node 1 | 1EM + 2H | 0.988 s | 2HP + 2H + 2P | 62.590 s |
| Node 2 | 3EM + 1EA + 2H | 2.96 s | 2HP + 2H + 2P | 62.590s |
| Key Agreement | ||||||
| Entity | This (Bits/Bytes) | [3] (Bits/Bytes) | Benchmark (Bits/Bytes) | |||
| Node 1 | 416 | 52 | 704 | 88 | 256 | 32 |
| Server | 1120 | 140 | 864 | 108 | 224 | 28 |
| total | 1536 | 192 | 1568 | 196 | 480 | 60 |
| Communication Phase | ||||||
| Entity | This (Bits/Bytes) | [3] (Bits/Bytes) | ||||
| Node | 480 | 60 | 480 | 60 | ||
© 2018 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Braeken, A. PUF Based Authentication Protocol for IoT. Symmetry 2018, 10, 352. https://doi.org/10.3390/sym10080352
Braeken A. PUF Based Authentication Protocol for IoT. Symmetry. 2018; 10(8):352. https://doi.org/10.3390/sym10080352
Chicago/Turabian StyleBraeken, An. 2018. "PUF Based Authentication Protocol for IoT" Symmetry 10, no. 8: 352. https://doi.org/10.3390/sym10080352
APA StyleBraeken, A. (2018). PUF Based Authentication Protocol for IoT. Symmetry, 10(8), 352. https://doi.org/10.3390/sym10080352