Accurate Age Estimation Using Multi-Task Siamese Network-Based Deep Metric Learning for Frontal Face Images
Abstract
1. Introduction
1.1. Motivation
1.2. Contribution
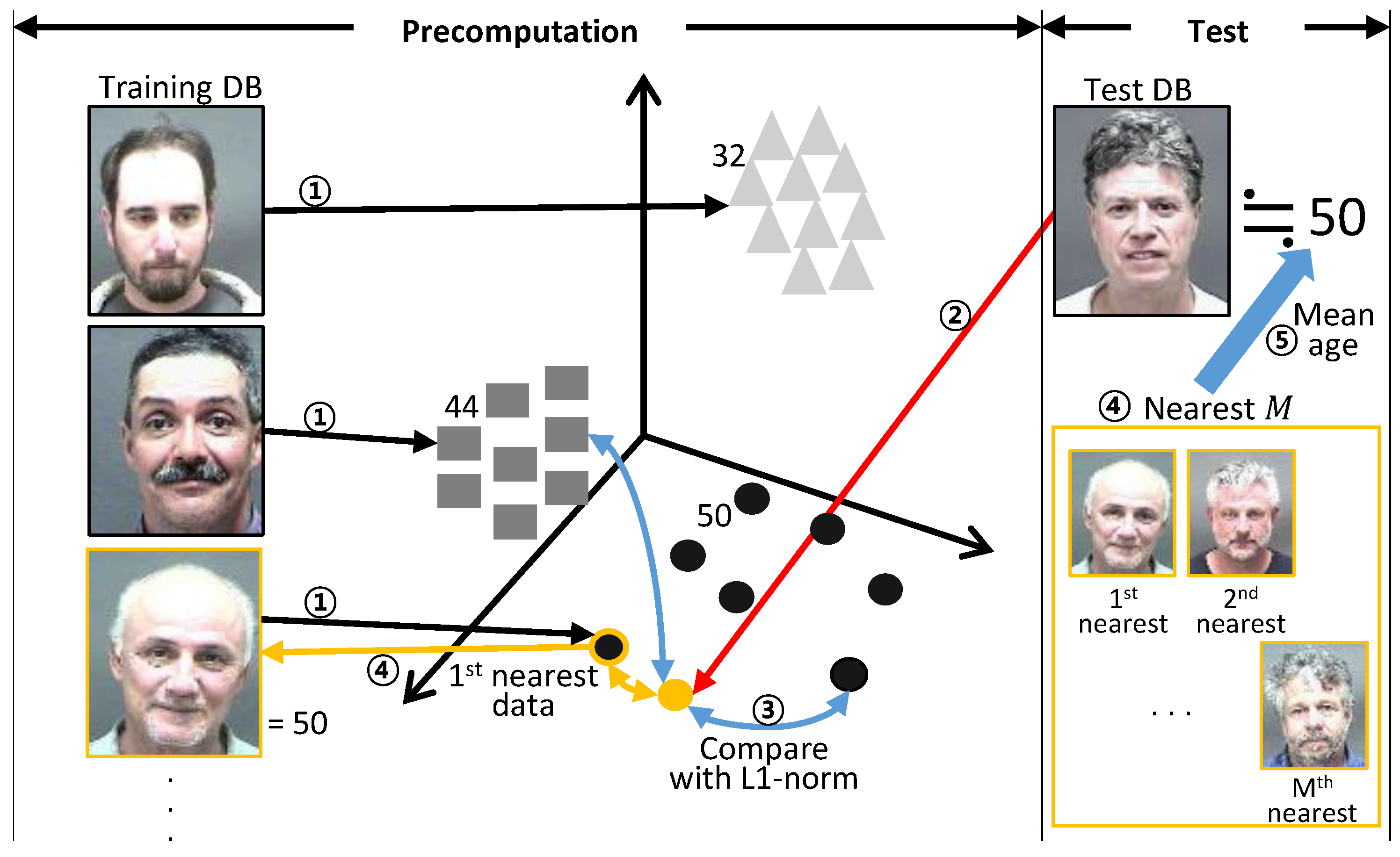
2. Proposed Architecture
2.1. Inception V3
2.2. Selection of Two Images and the Feature-Embedding Process
2.3. Distance as Similarity between Two Images
2.4. Loss Function for the Training Comparison Task
2.5. Age Estimation
2.6. Multi-Task Learning for Age and Gender Estimation
3. Experimental Results and Discussion
3.1. Toy Example: Visualization of Feature Embedding Computed by Our Method Using a Subset of the MORPH Dataset
3.2. Multi-Task Learning for Age and Gender Estimation
3.3. Comparison with Deep Metric Learning-Based Approaches on the MORPH Dataset
3.4. Comparison with State-of-Art Method on Each Dataset
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| CNN | Convolutional Neural Network |
| DEX | Deep EXpectation |
| CRCNN | Comparative Region Convolution Neural Network |
| MAE | Mean Absolute Error |
| CS | Cumulative Score |
References
- Ling, H.; Soatto, S.; Ramanathan, N.; Jacobs, D.W. A Study of Face Recognition as People Age. In Proceedings of the 2007 IEEE 11th International Conference on Computer Vision, Rio de Janeiro, Brazil, 14–21 October 2007; pp. 1–8. [Google Scholar] [CrossRef]
- Alkass, K.; Buchholz, B.A.; Ohtani, S.; Yamamoto, T.; Druid, H.; Spalding, K.L. Age estimation in forensic sciences: Application of combined aspartic acid racemization and radiocarbon analysis. Mol. Cell. Proteom. (MCP) 2010, 95, 1022–1030. [Google Scholar] [CrossRef] [PubMed]
- Han, H.; Otto, C.; Jain, A.K. Age estimation from face images: Human vs. machine performance. In Proceedings of the 2013 International Conference on Biometrics (ICB), Madrid, Spain, 4–7 June 2013; pp. 1–8. [Google Scholar]
- Rothe, R.; Timofte, R.; Van Gool, L. Deep Expectation of Real and Apparent Age from a Single Image without Facial Landmarks. Int. J. Comput. Vis. 2018, 126, 144–157. [Google Scholar] [CrossRef]
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. ImageNet Classification with Deep Convolutional Neural Networks. In Advances in Neural Information Processing Systems 25; Pereira, F., Burges, C.J.C., Bottou, L., Weinberger, K.Q., Eds.; Curran Associates, Inc.: Red Hook, NY, USA, 2012; pp. 1097–1105. [Google Scholar]
- Simonyan, K.; Zisserman, A. Very Deep Convolutional Networks for Large-Scale Image Recognition. arXiv, 2014; arXiv:1409.1556. [Google Scholar]
- Szegedy, C.; Liu, W.; Jia, Y.; Sermanet, P.; Reed, S.E.; Anguelov, D.; Erhan, D.; Vanhoucke, V.; Rabinovich, A. Going Deeper with Convolutions. arXiv, 2015; arXiv:1409.4842. [Google Scholar]
- Yin, X.; Liu, X. Multi-Task Convolutional Neural Network for Face Recognition. arXiv, 2017; arXiv:1702.04710. [Google Scholar]
- Chen, S.; Zhang, C.; Dong, M.; Le, J.; Rao, M. Using Ranking-CNN for Age Estimation. In Proceedings of the 2017 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017; pp. 742–751. [Google Scholar]
- Song, H.O.; Xiang, Y.; Jegelka, S.; Savarese, S. Deep Metric Learning via Lifted Structured Feature Embedding. arXiv, 2015; arXiv:1511.06452. [Google Scholar]
- Abousaleh, F.S.; Lim, T.; Cheng, W.H.; Yu, N.H.; Hossain, M.A.; Alhamid, M.F. A novel comparative deep learning framework for facial age estimation. EURASIP J. Image Video Process. 2016, 2016, 47. [Google Scholar] [CrossRef]
- Chopra, S.; Hadsell, R.; LeCun, Y. Learning a similarity metric discriminatively, with application to face verification. In Proceedings of the 2005 IEEE Computer Society Conference on Computer Vision and Pattern Recognition (CVPR’05), San Diego, CA, USA, 20–25 June 2005; pp. 539–546. [Google Scholar]
- Szegedy, C.; Vanhoucke, V.; Ioffe, S.; Shlens, J.; Wojna, Z. Rethinking the Inception Architecture for Computer Vision. arXiv, 2015; arXiv:1512.00567. [Google Scholar]
- Russakovsky, O.; Deng, J.; Su, H.; Krause, J.; Satheesh, S.; Ma, S.; Huang, Z.; Karpathy, A.; Khosla, A.; Bernstein, M.; et al. ImageNet Large Scale Visual Recognition Challenge. Int. J. Comput. Vis. (IJCV) 2015, 115, 211–252. [Google Scholar] [CrossRef]
- Abadi, M.; Barham, P.; Chen, J.; Chen, Z.; Davis, A.; Dean, J.; Devin, M.; Ghemawat, S.; Irving, G.; Isard, M.; et al. TensorFlow: A System for Large-Scale Machine Learning. In Proceedings of the OSDI’16 Proceedings of the 12th USENIX Conference on Operating Systems Design and Implementation, Savannah, GA, USA, 2–4 November 2016; pp. 265–283. [Google Scholar]
- Zeiler, M.D. ADADELTA: An Adaptive Learning Rate Method. arXiv, 2012; arXiv:1212.5701. [Google Scholar]
- Zhang, Y.; Yeung, D.Y. Multi-task warped Gaussian process for personalized age estimation. In Proceedings of the 2010 IEEE Computer Society Conference on Computer Vision and Pattern Recognition, San Francisco, CA, USA, 13–18 June 2010; pp. 2622–2629. [Google Scholar]
- Guo, G.; Mu, G. Simultaneous dimensionality reduction and human age estimation via kernel partial least squares regression. In Proceedings of the CVPR 2011, Colorado Springs, CO, USA, 20–25 June 2011; pp. 657–664. [Google Scholar]
- Guo, G.; Fu, Y.; Dyer, C.R.; Huang, T.S. Image-Based Human Age Estimation by Manifold Learning and Locally Adjusted Robust Regression. IEEE Trans. Image Process. 2008, 17, 1178–1188. [Google Scholar] [CrossRef] [PubMed]
- Ricanek, K.; Tesafaye, T. MORPH: A longitudinal image database of normal adult age-progression. In Proceedings of the 7th International Conference on Automatic Face and Gesture Recognition (FGR06), Southampton, UK, 10–12 April 2006; pp. 341–345. [Google Scholar]
- Kemelmacher-Shlizerman, I.; Seitz, S.M.; Miller, D.; Brossard, E. The MegaFace Benchmark: 1 Million Faces for Recognition at Scale. arXiv, 2015; arXiv:1512.00596. [Google Scholar]
- Liu, H.; Lu, J.; Feng, J.; Zhou, J. Label-Sensitive Deep Metric Learning for Facial Age Estimation. IEEE Trans. Inf. Forensics Secur. 2018, 13, 292–305. [Google Scholar] [CrossRef]
- Howard, A.G.; Zhu, M.; Chen, B.; Kalenichenko, D.; Wang, W.; Weyand, T.; Andreetto, M.; Adam, H. MobileNets: Efficient Convolutional Neural Networks for Mobile Vision Applications. arXiv, 2017; arXiv:1704.04861. [Google Scholar]
- Huang, G.; Liu, Z.; Weinberger, K.Q. Densely Connected Convolutional Networks. arXiv, 2016; arXiv:1608.06993. [Google Scholar]
- Zhang, Y.; Liu, L.; Li, C.; Loy, C.C. Quantifying Facial Age by Posterior of Age Comparisons. In Proceedings of the British Machine Vision Conference (BMVC), London, UK, 4–7 September 2017. [Google Scholar]
- Yang, T.Y.; Huang, Y.H.; Lin, Y.Y.; Hsiu, P.C.; Chuang, Y.Y. SSR-Net: A Compact Soft Stagewise Regression Network for Age Estimation. In Proceedings of the Twenty-Seventh International Joint Conference on Artificial Intelligence, IJCAI-18, Stockholm, Sweden, 13–19 July 2018; pp. 1078–1084. [Google Scholar]










| DB Name | The Number of Training Images | The Number of Test Images |
|---|---|---|
| MegaAge-Asian | 40,000 | 4000 |
| MORPH | 45,132 | 10,000 |
| Method | Accuracy (%) |
|---|---|
| Our method without gender data | 81.23 |
| Alexnet [5] with gender data | 97.38 |
| Inception V3 [7] with gender data | 99.1 |
| Method | Kinds of Loss Function | MORPH(MAE) |
|---|---|---|
| Our method | Revised contrastive loss function | 2.24 |
| Our method with multi-task learning | Revised contrastive loss function | 2.28 |
| CRCNN [11] | Contrastive loss function | 3.74 |
| M-LSDML [22] | Custom-defined loss function | 2.89 |
| ResNet (contrastive loss) [22] | Contrastive loss function | 3.72 |
| ResNet (triplet hinge loss) [22] | Triplet hinge loss function | 3.59 |
| ResNet (lifted structural loss) [22] | Lifted structural loss function | 3.24 |
| Method | ||
|---|---|---|
| Our method | 69.70 | 84.64 |
| MobileNet [23] | 44.0 | 60.6 |
| DenseNet [24] | 51.7 | 69.4 |
| Zhang et al. [25] ** | 64.08 | 82.43 |
| SSR-Net [26] * | 54.9 | 74.1 |
| Method | MAE |
|---|---|
| Our method | 2.24 |
| Our method with multi-task ** | 2.28 |
| Ranking-CNN [9] | 2.96 |
| DEX [4] * | 3.25 |
| DEX w IMDB [4] * | 2.68 |
| Zhang et al. [25] ** | 2.87 |
| Zhang et al. w IMDB-WIKI [25] ** | 2.52 |
| SSR-Net [26] * | 2.52 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jeong, Y.; Lee, S.; Park, D.; Park, K.H. Accurate Age Estimation Using Multi-Task Siamese Network-Based Deep Metric Learning for Frontal Face Images. Symmetry 2018, 10, 385. https://doi.org/10.3390/sym10090385
Jeong Y, Lee S, Park D, Park KH. Accurate Age Estimation Using Multi-Task Siamese Network-Based Deep Metric Learning for Frontal Face Images. Symmetry. 2018; 10(9):385. https://doi.org/10.3390/sym10090385
Chicago/Turabian StyleJeong, Yoosoo, Seungmin Lee, Daejin Park, and Kil Houm Park. 2018. "Accurate Age Estimation Using Multi-Task Siamese Network-Based Deep Metric Learning for Frontal Face Images" Symmetry 10, no. 9: 385. https://doi.org/10.3390/sym10090385
APA StyleJeong, Y., Lee, S., Park, D., & Park, K. H. (2018). Accurate Age Estimation Using Multi-Task Siamese Network-Based Deep Metric Learning for Frontal Face Images. Symmetry, 10(9), 385. https://doi.org/10.3390/sym10090385






