Spacetime Symmetry and LemaîTre Class Dark Energy Models
Abstract
:1. Introduction
2. Algebraic Structure of Tress-Energy Tensors for Vacuum Dark Energy and Spacetime Symmetry
3. The Lemaître Class Models for Relaxing Cosmological Constant
3.1. Basic Equations
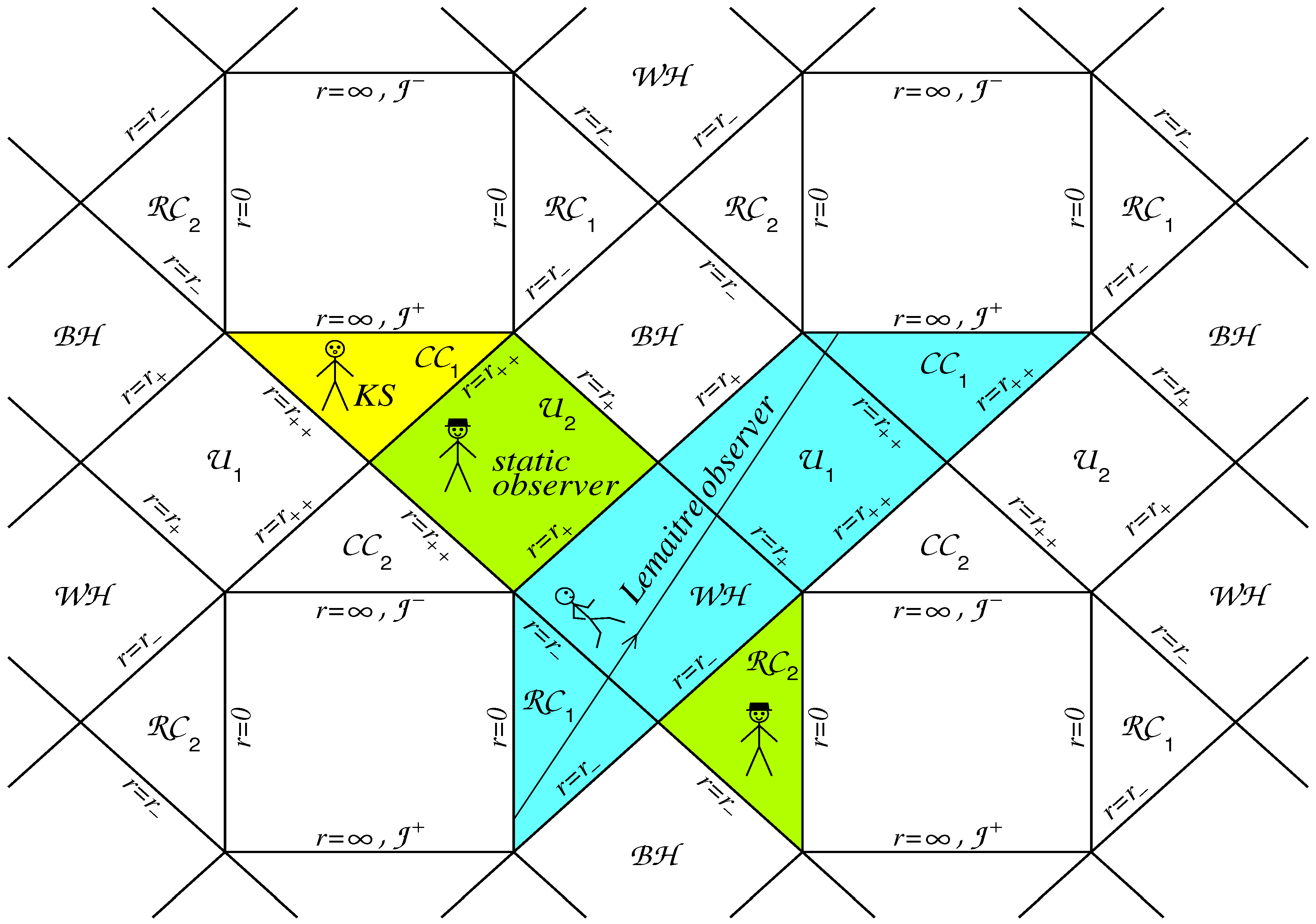
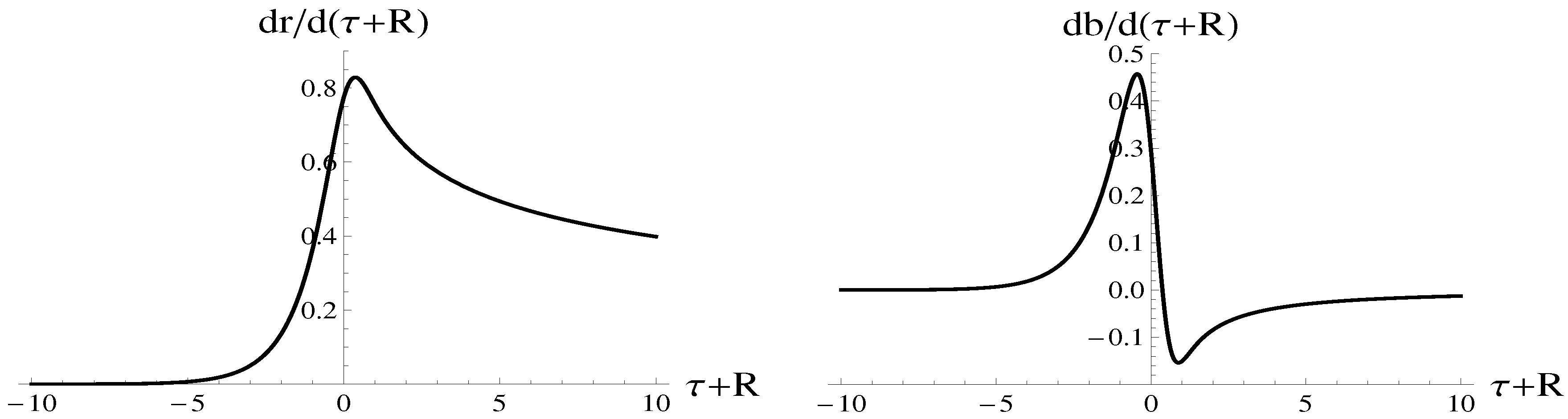
3.2. Basic Features of the Lemaître Cosmological Models With the Vacuum Dark Energy
3.3. The Lemaître Class Models Singled Out by the Holographic Principle
4. Summary and Discussion
Author Contributions
Funding
Conflicts of Interest
References
- Riess, A.G.; Kirshner, R.P.; Schmidt, B.P.; Jha, S.; Challis, P.; Garnavich, P.M.; Esin, A.A.; Carpenter, C.; Grashius, R. BV RI light curves for 22 type Ia supernovae. Astron. J. 1999, 117, 707–724. [Google Scholar] [CrossRef]
- Perlmutter, S.; Aldering, G.; Goldhaber, G.; Knop, R.A.; Nugent, P.; Castro, P.G.; Deustua, S.; Fabbro, S.; Goobar, A.; Groom, D.E.; et al. Measurements of Ω and Λ from 42 high-redshift supernovae. Astrophys. J. 1999, 517, 565–586. [Google Scholar] [CrossRef]
- Bahcall, N.A.; Ostriker, J.P.; Perlmutter, S.; Steinhardt, P.J. The cosmic triangle: Revealing the state of the universe. Science 1999, 284, 1481–1488. [Google Scholar] [CrossRef]
- Wang, L.; Caldwell, R.R.; Ostriker, J.P.; Steinhardt, P.J. Cosmic Concordance and Quintessence. Astrophys. J. 2000, 530, 17–35. [Google Scholar] [CrossRef] [Green Version]
- Sullivan, M.; Guy, J.; Conley, A.; Regnault, N.; Astier, P.; Balland, C.; Basa, S.; Carlberg, R.G.; Fouchez, D.; Hardin, D.; et al. SNLS3: Constraints on dark energy combining the supernova legacy survey three-year data with other probes. Astrophys. J. 2011, 737, 102–121. [Google Scholar] [CrossRef]
- Corasaniti, P.S.; Copeland, E.J. Constraining the quintessence equation of state with SnIa data and CMB peaks. Phys. Rev. D 2002, 65, 043004. [Google Scholar] [CrossRef]
- Hannestad, S.; Mortsell, E. Probing the dark side: Constraints on the dark energy equation of state from CMB, large scale structure, and type Ia supernovae. Phys. Rev. D 2002, 66, 063508. [Google Scholar] [CrossRef]
- Bassett, B.A.; Kunz, M.; Silk, J.; Ungarelli, C. A late-time transition in the cosmic dark energy? Mon. Not. R. Astron. Soc. 2002, 336, 1217–1222. [Google Scholar] [CrossRef] [Green Version]
- Tonry, J.L.; Schmidt, B.P.; Barris, B.; Candia, P.; Challis, P.; Clocchiatti, A.; Coil, A.L.; Filippenko, A.V.; Garnavich, P.; Hogan, C.; et al. Cosmological results from high-z supernovae. Astrophys. J. 2003, 594, 1–24. [Google Scholar] [CrossRef]
- Ellis, J. Dark matter and dark energy: Summary and future directions. Philos. Trans. A 2003, 361, 2607–2627. [Google Scholar] [CrossRef]
- Corasaniti, P.S.; Kunz, M.; Parkinson, D.; Copeland, E.J.; Bassett, B.A. Foundations of observing dark energy dynamics with the Wilkinson Microwave Anisotropy Probe. Phys. Rev. D 2004, 70, 083006. [Google Scholar] [CrossRef]
- Weinberg, S. The cosmological constant problem. Rev. Mod. Phys. 1989, 61, 1–23. [Google Scholar] [CrossRef] [Green Version]
- Wheeler, J.A.; Ford, K. Black Holes and Quantum Foam: A Life in Physics; W.W. Norton and Co.: New York, NY, USA, 1998. [Google Scholar]
- Hawking, S. Spacetime foam. Nucl. Phys. B 1978, 144, 349–362. [Google Scholar] [CrossRef]
- Coleman, S. Why There Is Nothing Rather Than Something: A Theory of the Cosmological Constant. Nucl. Phys. B 1988, 310, 643–668. [Google Scholar] [CrossRef]
- Klebanov, I.; Susskind, L.; Banks, T. Wormholes and the cosmological constant. Nucl. Phys. B 1989, 317, 665–692. [Google Scholar] [CrossRef] [Green Version]
- Feng, C.J.; Li, X.L. Towards a realistic solution of the cosmological constant fine-tuning problem. Phys. Rev. D 2014, 90, 103009. [Google Scholar] [CrossRef]
- Bousso, R.; Harnik, R.; Kribs, G.D.; Perez, G. Predicting the cosmological constant from the causal entropic principle. Phys. Rev. D 2007, 76, 043513–043530. [Google Scholar] [CrossRef]
- Krauss, L.M.; Dent, J.; Starkman, G.D. Late Time Decay of False Vacuum, Measurement, and Quantum Cosmology. Int. J. Mod. Phys. D 2009, 17, 2501–2505. [Google Scholar] [CrossRef]
- Guendelman, E.I. Non singular origin of the Universe and cosmological constant. Int. J. Mod. Phys. D 2012, 20, 2767–2771. [Google Scholar] [CrossRef]
- Cortes, J.L.; Lopez-Sarrion, J. Fine-tuning problem in quantum field theory and Lorentz invariance: A scalar-fermion model with a physical momentum cutoff. Int. J. Mod. Phys. A 2017, 32, 1750084. [Google Scholar] [CrossRef]
- Adler, R.J. Comment on the cosmological constant and a gravitational alpha. arXiv, 2011; arXiv:1110.3358. [Google Scholar]
- Ade, P.A.R.; Aghanim, N.; Arnaud, M.; Ashdown, M.; Aumont, J.; Baccigalupi, C.; Banday, A.J.; Barreiro, R.B.; Bartlett, J.G.; Bartolo, N.; et al. Planck 2015 results. Astron. Astrophys. 2016, 594, A13. [Google Scholar]
- Li, Y.H.; Zhang, J.F.; Zhang, X. Testing models of vacuum energy interacting with cold dark matter. Phys. Rev. D 2016, 93, 023002. [Google Scholar] [CrossRef] [Green Version]
- Peracanba, J.S.; Perez, J.D.C.; Gomez-Valent, A. Possible signals of vacuum dynamics in the Universe. Mon. Not. R. Astron. Soc 2018, 478, 4357–4373. [Google Scholar]
- Li, H.L.; Feng, L.; Zhang, J.F.; Zhang, X. Models of vacuum energy interacting with cold dark matter: Constraints and comparison. arXiv, 2018; arXiv:1812.00319. [Google Scholar]
- Sahni, V.; Starobinsky, A.A. The case for a positive cosmological Lambda term. Int. J. Mod. Phys. D 2000, 9, 373–444. [Google Scholar] [CrossRef]
- Bean, R.; Carroll, S.M.; Trodden, M. Insight into dark energy: Interplay between theory and observation. arXiv, 2005; arXiv:astro-ph/0510059. [Google Scholar]
- Tanabashi, M.; Hagiwara, K.; Hikasa, K.; Nakamura, K.; Sumino, Y.; Takahashi, F.; Tanaka, J.; Agashe, K.; Aielli, G.; Amsler, C.; et al. Dark Energy. Phys. Rev. D 2018, 98, 030001. [Google Scholar] [CrossRef]
- Caldwell, R.R.; Kamionkowski, M. The Physics of Cosmic Acceleration. Ann. Rev. Nucl. Part. Sci. 2009, 59, 397–429. [Google Scholar] [CrossRef]
- Copeland, E.J. Models of dark energy. In Proceedings of the Invisible Universe International Conference, Paris, France, 29 June–3 July 2009; AIP: New York, NY, USA, 2010; pp. 132–138. [Google Scholar]
- Bamba, K.; Capozziello, S.; Nojiri, S.; Odintsov, S.D. Dark energy cosmology: The equivalent description via different theoretical models and cosmography tests. Astrophys. Space Sci. 2012, 342, 155–228. [Google Scholar]
- Rivera, A.B.; Farieta, J.G. Exploring the Dark Universe: Constraint on dynamical dark energy models from CMB, BAO and Growth Rate Measurements. arXiv, 2016; arXiv:1605.01984. [Google Scholar]
- Aviles, A.; Bravetti, S.; Capozziello, S.; Luongo, O. Precision cosmology with Padé rational approximations: Theoretical predictions versus observational limits. Phys. Rev. D 2011, 90, 043531. [Google Scholar] [CrossRef]
- Capozziello, S.; D’Agostino, R.; Luongo, O. Model-independent reconstruction of f(T) teleparallel cosmology. Gen. Relativ. Gravit. 2017, 49, 141–162. [Google Scholar] [CrossRef]
- Cai, Y.F.; Saridakis, E.N.; Setare, M.R.; Xia, J. Quintom Cosmology: Theoretical implications and Observations. Phys. Rep. 2010, 493, 1–60. [Google Scholar] [CrossRef]
- Capozziello, S.; Predipalumbo, E.; Rubano, C.; Scudellaro, P. Noether symmetry approach in phantom quintessence cosmology. Phys. Rev. D 2009, 80, 104030. [Google Scholar] [CrossRef]
- Mishra, S.; Chakraborty, S. Dynamical system analysis of Quintom Dark Energy Model. Eur. Phys. J. C 2018, 78, 917–923. [Google Scholar] [CrossRef]
- Joyce, A.; Lombriser, L.; Schmidt, F. Dark Energy Versus Modified Gravity. Ann. Rev. Nucl. Part. Sci. 2016, 66, 95–122. [Google Scholar] [CrossRef] [Green Version]
- Cognola, G.; Elizalde, E.; Nojiri, S.; Odintsov, S.D.; Sebastiani, L.; Zerbini, S. Class of viable modified f(R) gravities describing inflation and the onset of accelerated expansion. Phys. Rev. D 2008, 77, 046009. [Google Scholar] [CrossRef]
- Horava, P.; Minic, D. Probable Values of the Cosmological Constant in a Holographic Theory. Phys. Rev. Lett. 2000, 85, 1610–1613. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Thomas, S. Holography Stabilizes the Vacuum Energy. Phys. Rev. Lett. 2002, 89, 81301–81304. [Google Scholar] [CrossRef] [PubMed]
- Setare, M.R. Interacting holographic dark energy model in non-flat universe. Phys. Lett. B 2006, 642, 1–4. [Google Scholar] [CrossRef] [Green Version]
- Li, E.K.; Zhang, Y.; Cheng, J.L. Modified holographic Ricci dark energy coupled to interacting relativistic and non-relativistic dark matter in the nonflat universe. Phys. Rev. D 2014, 90, 083534. [Google Scholar] [CrossRef]
- Wang, S.; Wu, J.; Li, M. Holographic Dark Energy. Phys. Rep. 2017, 696, 1–58. [Google Scholar] [CrossRef]
- Cruz, M.; Lepe, S. Holographic approach for dark energy-dark matter interaction in curved FLRW spacetime. Class. Quantum Gravity 2018, 35, 155013. [Google Scholar] [CrossRef]
- Nojiri, S.; Odintsov, S.D. Covariant Generalized Holographic Dark Energy and Accelerating Universe. Eur. Phys. J. C 2017, 77, 528. [Google Scholar] [CrossRef]
- Cruz, M.; Lepe, S. A holographic cut-off inspired in the apparent horizon. Eur. Phys. J. C 2018, 78, 994. [Google Scholar] [CrossRef]
- Cruz, M.; Lepe, S. Modeling holographic dark energy with particle and future horizons. arXiv, 2018; arXiv:1812.06373. [Google Scholar]
- Ade, P.A.R.; Aikin, R.W.; Barkats, D.; Benton, S.J.; Bischoff, C.A.; Bock, J.J.; Brevik, J.A.; Buder, I.; Bullock, E.; Dowell, C.D.; et al. Detection of B-Mode Polarization at Degree Angular Scales by BICEP2. Phys. Rev. Lett. 2014, 112, 241101. [Google Scholar] [CrossRef] [PubMed]
- Anderson, L.; Aubourg, E.; Bailey, S.; Beutler, F.; Bhardwaj, V.; Blanton, M.; Bolton, A.S.; Brinkmann, J.; Brownstein, J.R.; Burden, A.; et al. The clustering of galaxies in the SDSS-III Baryon Oscillation Spectroscopic Survey: Baryon acoustic oscillations in the Data Releases 10 and 11 Galaxy samples. Mon. Not. R. Astron. Soc 2014, 441, 24–62. [Google Scholar] [CrossRef]
- Suzuki, N.; Rubin, D.; Lidman, C.; Aldering, G.; Amanullah, R.; Barbary, K.; Barrientos, L.F.; Botyanszki, J.; Brodwin, M.; Connolly, N.; et al. The Hubble Space Telescope Cluster Supernova Survey: Improving the Dark Energy Constraints and Building an Early-Type-Hosted Supernova Sample. Astrophys. J. 2012, 746, 85–109. [Google Scholar] [CrossRef]
- Sahni, V.; Shafiello, A.; Starobinsky, A.A. Model-independent Evidence for Dark Energy Evolution from Baryon Acoustic Oscillations. Astrophys. J. 2014, 793, L40–L44. [Google Scholar] [CrossRef]
- Bauer, F.; Sola, J.; Štefancić, H. Dynamically avoiding fine-tuning the cosmological constant: The “Relaxed Universe”. J. Cosmol. Astropart. Phys. 2010, 1012, 29. [Google Scholar] [CrossRef]
- Bauer, F.; Sola, J.; Štefancić, H. Relaxing a large cosmological constant. Phys. Lett. B 2009, 678, 427–433. [Google Scholar] [CrossRef] [Green Version]
- Elizalde, E.; Odintsov, S.D.; Sebastiani, L.; Myrzakulov, R. Beyond-one-loop quantum gravity action yielding both inflation and late-time acceleration. Nucl. Phys. B 2017, 921, 411–435. [Google Scholar] [CrossRef]
- Anderson, P.R. Attractor states and infrared scaling in de Sitter space. Phys. Rev. D 2000, 62, 124019. [Google Scholar] [CrossRef]
- Bronnikov, K.A.; Dymnikova, I.; Galaktionov, E. Multihorizon spherically symmetric spacetimes with several scales of vacuum energy. Class. Quantum Gravity 2012, 29, 095025. [Google Scholar] [CrossRef] [Green Version]
- Petrov, A.Z. Einstein Spaces; Pergamon Press: Oxford, UK, 1969. [Google Scholar]
- Stephani, H.; Kramer, D.; MacCallum, V.; Hoenselaers, C.; Herlt, E. Exact Solutions of Einstein’s Field Equations; Cambridge University Press: Cambridge, UK, 2003. [Google Scholar]
- Gliner, E.B.; Dymnikova, I.G. Nonsingular Friedmann cosmology. Sov. Astron. Lett. 1975, 1, 93–95. [Google Scholar]
- Olive, K.A. Inflation. Phys. Rep. 1990, 190, 307–403. [Google Scholar] [CrossRef]
- Dymnikova, I. Vacuum nonsingular black hole. Gen. Relativ. Gravit. 1992, 24, 235–242. [Google Scholar] [CrossRef]
- Dymnikova, I.; Galaktionov, E. Vacuum dark fluid. Phys. Lett. B 2007, 645, 358–364. [Google Scholar] [CrossRef] [Green Version]
- Dymnikova, I. The algebraic structure of a cosmological term in spherically symmetric solutions. Phys. Lett. B 2000, 472, 33–38. [Google Scholar] [CrossRef] [Green Version]
- Dymnikova, I.; Galaktionov, E. Dark ingredients in one drop. Cent. Eur. J. Phys. 2011, 9, 644–653. [Google Scholar] [CrossRef] [Green Version]
- Dymnikova, I. Unification of dark energy and dark matter based on the Petrov classification and space-time symmetry. Intern. J. Mod. Phys. A 2016, 31, 1641005. [Google Scholar] [CrossRef]
- Dymnikova, I.; Khlopov, M. Regular black hole remnants and graviatoms with de Sitter interior as heavy dark matter candidates probing inhomogeneity of early universe. Int. J. Mod. Phys. D 2015, 24, 1545002. [Google Scholar] [CrossRef] [Green Version]
- Polnarev, A.G.; Khlopov, M.Y. Cosmology, primordial black holes, and supermassive particles. Sov. Phys. Uspekhi 1985, 28, 213–232. [Google Scholar] [CrossRef]
- MacGibbon, J.H. Can Planck-mass relics of evaporating black holes close the Universe? Nature 1987, 329, 308–309. [Google Scholar] [CrossRef]
- Dymnikova, I. Regular black hole remnants. In Proceedings of the Invisible Universe International Conference, Paris, France, 29 June–3 July 2009; AIP: New York, NY, USA, 2010; pp. 361–368. [Google Scholar]
- Dymnikova, I.; Korpusik, M. Regular black hole remnants in de Sitter space. Phys. Lett. B 2010, 685, 12–18. [Google Scholar] [CrossRef] [Green Version]
- Dymnikova, I. Generic Features of Thermodynamics of Horizons in Regular Spherical Space-Times of the Kerr-Schild Class. Universe 2018, 4, 63. [Google Scholar] [CrossRef]
- Dymnikova, I.; Fil’chenkov, M. Graviatoms with de Sitter Interior. Adv. High Energy Phys. 2013, 2013, 746894. [Google Scholar] [CrossRef]
- Gibbons, G.W. Phantom Matter and the Cosmological Constant; DAMTP-2003-19; Cambridge University: Cambridge, UK, 2003. [Google Scholar]
- Boyanovsky, D.; de Vega, H.J.; Schwarz, D.J. Phase transitions in the early and present universe. Ann. Rev. Nucl. Part. Sci. 2006, 56, 441–500. [Google Scholar] [CrossRef]
- Poisson, E.; Israel, W. Structure of the black hole nucleus. Class. Quantum Gravity 1988, 5, L201–L205. [Google Scholar] [CrossRef]
- Dymnikova, I. The cosmological term as a source of mass. Class. Quantum Gravity 2002, 19, 725–740. [Google Scholar] [CrossRef]
- Dymnikova, I. Spherically symmetric space-time with regular de Sitter center. Int. J. Mod. Phys. D 2003, 12, 1015–1034. [Google Scholar] [CrossRef]
- Frolov, V.P.; Markov, M.A.; Mukhanov, V.F. Black holes as possible sources of closed and semiclosed worlds. Phys. Rev. D 1990, 41, 383–394. [Google Scholar] [CrossRef]
- Dymnikova, I. Internal structure of nonsingular spherical black holes. Ann. Isr. Phys. Soc. 1997, 13, 422–440. [Google Scholar]
- Perez, A. Spin foam models for quantum gravity. Class. Quantum Gravity 2003, 20, R43–R104. [Google Scholar] [CrossRef]
- Rovelli, C. Quantum Gravity; Cambridge University Press: Cambridge, UK, 2004. [Google Scholar]
- Bonanno, A.; Reuter, M. Spacetime structure of an evaporating black hole in quantum gravity. Phys. Rev. D 2006, 73, 83005–83017. [Google Scholar] [CrossRef]
- Nicolini, P. Noncommutative black holes, the final appeal to quantum gravity: A review. Int. J. Mod. Phys. A 2009, 24, 1229–1308. [Google Scholar] [CrossRef]
- Arraut, I.; Batic, D.; Nowakowski, M. A noncommutative model for a mini black hole. Class. Quantum Gravity 2009, 26, 245006. [Google Scholar] [CrossRef] [Green Version]
- Arraut, I.; Batic, D.; Nowakowski, M. Maximal extension of the Schwarzschild spacetime inspired by noncommutative geometry. J. Math. Phys. 2010, 51, 022503. [Google Scholar] [CrossRef]
- Kerr, R.P.; Schild, A. Some algebraically degenerate solutions of Einstein’s gravitational field equations. Proc. Symp. Appl. Math 1965, 17, 199–207. [Google Scholar]
- Dymnikova, I.; Soltysek, B. Spherically symmetric space-time with two cosmological constants. Gen. Relativ. Gravit. 1998, 30, 1775–1793. [Google Scholar] [CrossRef]
- Dymnikova, I. De Sitter-Schwarzschild black hole: Its particlelike core and thermodynamical properties. Int. J. Mod. Phys. D 1996, 5, 529–540. [Google Scholar] [CrossRef]
- Dymnikova, I.; Sakharov, A.; Ulbricht, J. Appearance of a minimal length in e+e- annihilation. Adv. High Energy Phys. 2014, 2014, 707812. [Google Scholar] [CrossRef]
- Bażański, S.L.; Ferrari, V. Analytic Extension of the Schwarzschild-de Sitter Metric. Il Nuovo Cimento B 1986, 91, 126–142. [Google Scholar] [CrossRef]
- Balaguera Antolinez, A.; Böhmer, C.G.; Nowakowski, M. Scales set by the Cosmological Constant. Class. Quantum Gravity 2006, 23, 485–496. [Google Scholar] [CrossRef]
- Arraut, I.; Batic, D.; Nowakowski, M. Velocity and velocity bounds in static spherically symmetric metrics. Cent. Eur. J Phys. 2011, 9, 926–938. [Google Scholar] [Green Version]
- Vainshtein, A.I. To the problem of nonvanishing gravitation mass. Phys. Lett. B 1972, 39, 393–394. [Google Scholar] [CrossRef]
- Chkareuli, G.; Pirtskhalava, D. Vainshtein mechanism in Λ3-theories. Phys. Lett. B 2012, 713, 99–103. [Google Scholar] [CrossRef]
- Babichev, E.; Deffayet, C. An introduction to the Vainshtein mechanism. Class. Quantum Gravity 2013, 30, 184001. [Google Scholar] [CrossRef] [Green Version]
- Arraut, I. On the Black Holes in alternative theories of gravity: The case of non-linear massive gravity. Int. J. Mod. Phys. D 2015, 24, 1550022. [Google Scholar] [CrossRef]
- Arraut, I. The Astrophysical Scales Set by the Cosmological Constant, Black-Hole Thermodynamics and Non-Linear Massive Gravity. Universe 2017, 3, 45. [Google Scholar] [CrossRef]
- Bronnikov, K.A.; Dobosz, A.; Dymnikova, I. Nonsingular vacuum cosmologies with a variable cosmological term. Class. Quantum Gravity 2003, 20, 3797–3814. [Google Scholar] [CrossRef] [Green Version]
- Bronnikov, K.A.; Dymnikova, I. Regular homogeneous T-models with vacuum dark fluid. Class. Quantum Gravity 2007, 24, 5803–5816. [Google Scholar] [CrossRef] [Green Version]
- Lemaître, G. Evolution of the Expanding Universe. Proc. Natl. Acad. Sci. USA 1934, 20, 12–17. [Google Scholar] [CrossRef]
- Landau, L.D.; Lifshitz, E.M. Classical Theory of Fields, 4th ed.; Butterworth-Heinemann: Oxford, UK, 1975. [Google Scholar]
- Tolman, R.C. Effect of Inhomogeneity on Cosmological Models. Proc. Natl. Acad. Sc. USA 1934, 20, 169–176. [Google Scholar] [CrossRef]
- Dymnikova, I.; Dobosz, A.; Filchenkov, M.; Gromov, A. Universes inside a Λ black hole. Phys. Lett. B 2001, 506, 351–360. [Google Scholar] [CrossRef]
- Olson, D.W.; Silk, J. Primordial inhomogeneities in the expanding universe. II—General features of spherical models at late times. Astrophys. J. 1979, 233, 395–401. [Google Scholar] [CrossRef]
- Harko, T.; Mak, M.K. Bianchi Type I universes with dilaton and magnetic fields. Int. J. Mod. Phys. D 2002, 11, 1171–1189. [Google Scholar] [CrossRef]
- Bronnikov, K.A.; Chudayeva, E.N.; Shikin, G.N. Magneto-dilatonic Bianchi-I cosmology: Isotropization and singularity problems. Class. Quantum Gravity 2004, 21, 3389–3403. [Google Scholar] [CrossRef]
- Dymnikova, I.; Dobosz, A.; Sołtysek, B. Lemaître Class Dark Energy Model for Relaxing Cosmological Constant. Universe 2017, 3, 39. [Google Scholar] [CrossRef]
- Wald, R.M. General Relativity; University of Chicago Press: Chicago, IL, USA; London, UK, 1984. [Google Scholar]
- ’t Hooft, G. Dimensional reduction in quantum gravity. arXiv, 1999; arXiv:9310026. [Google Scholar]
- Susskind, L. The World as a hologram. J. Math. Phys. 1995, 36, 6377–6396. [Google Scholar] [CrossRef]
- Dymnikova, I. Triple-horizon spherically symmetric spacetime and holographic principle. Int. J. Mod. Phys. D 2012, 21, 1242007–12420016. [Google Scholar] [CrossRef]
- Sekino, Y.; Susskind, L. Fast scramblers. High Energy Phys. 2008, 810, 65–80. [Google Scholar] [CrossRef]
- Dymnikova, I.; Dobosz, A.; Soltysek, B. Lemaître dark energy model singled out by the holographic principle. Gravit. Cosmol. 2017, 23, 28–34. [Google Scholar] [CrossRef]
- Wiaux, Y.; Vielva, P.; Martinez-Gonzalez, E.; Vandergheynst, P. Global universe anisotropy probed by the alignment of structures in the cosmic microwave background. Phys. Rev. Lett. 2006, 96, 151303–151306. [Google Scholar] [CrossRef] [PubMed]
- Marochnik, L.; Usikov, D. Inflation and CMB anisotropy from quantum metric fluctuations. Gravit. Cosmol. 2015, 21, 118–122. [Google Scholar] [CrossRef] [Green Version]
- Sharma, M. Raychaudhuri equation in an anisotropic universe with anisotropic sources. Gravit. Cosmol. 2015, 21, 252–256. [Google Scholar] [CrossRef] [Green Version]
- Chang, Z.; Li, X.; Lin, H.-N.; Wang, S. Constraining anisotropy of the universe from different groups of type-Ia supernovae. Eur. Phys. J. C 2014, 74, 2821–2829. [Google Scholar] [CrossRef]
- Chang, Z.; Li, X.; Lin, H.-N.; Wang, S. Constraining anisotropy of the universe from Supernovae and Gamma-ray Bursts. Mod. Phys. Lett. A 2014, 29, 1450067. [Google Scholar] [CrossRef]
- Nikolaev, A.V.; Chervon, S.V. The effect of universe inhomogeneities on cosmological distance measurements. Gravit. Cosmol. 2016, 22, 208–216. [Google Scholar] [CrossRef]





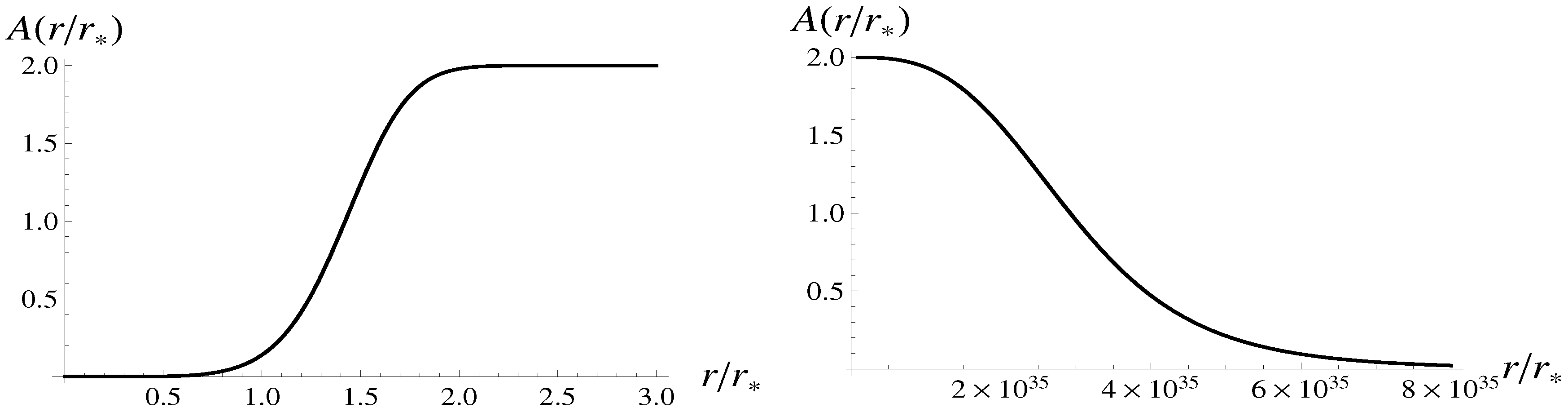
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dymnikova, I.; Dobosz, A. Spacetime Symmetry and LemaîTre Class Dark Energy Models. Symmetry 2019, 11, 90. https://doi.org/10.3390/sym11010090
Dymnikova I, Dobosz A. Spacetime Symmetry and LemaîTre Class Dark Energy Models. Symmetry. 2019; 11(1):90. https://doi.org/10.3390/sym11010090
Chicago/Turabian StyleDymnikova, Irina, and Anna Dobosz. 2019. "Spacetime Symmetry and LemaîTre Class Dark Energy Models" Symmetry 11, no. 1: 90. https://doi.org/10.3390/sym11010090
APA StyleDymnikova, I., & Dobosz, A. (2019). Spacetime Symmetry and LemaîTre Class Dark Energy Models. Symmetry, 11(1), 90. https://doi.org/10.3390/sym11010090



