Space Independent Image Registration Using Curve-Based Method with Combination of Multiple Deformable Vector Fields
Abstract
:1. Introduction
2. The Proposed Image Registration Method
2.1. Polynomial Fitting and Its Conversion to Cubic B-Spline
2.2. Transformation Function
2.3. Weighting Mask Creation
2.4. Combination of Multiple Masks/Multiple Deformable Vector Fields
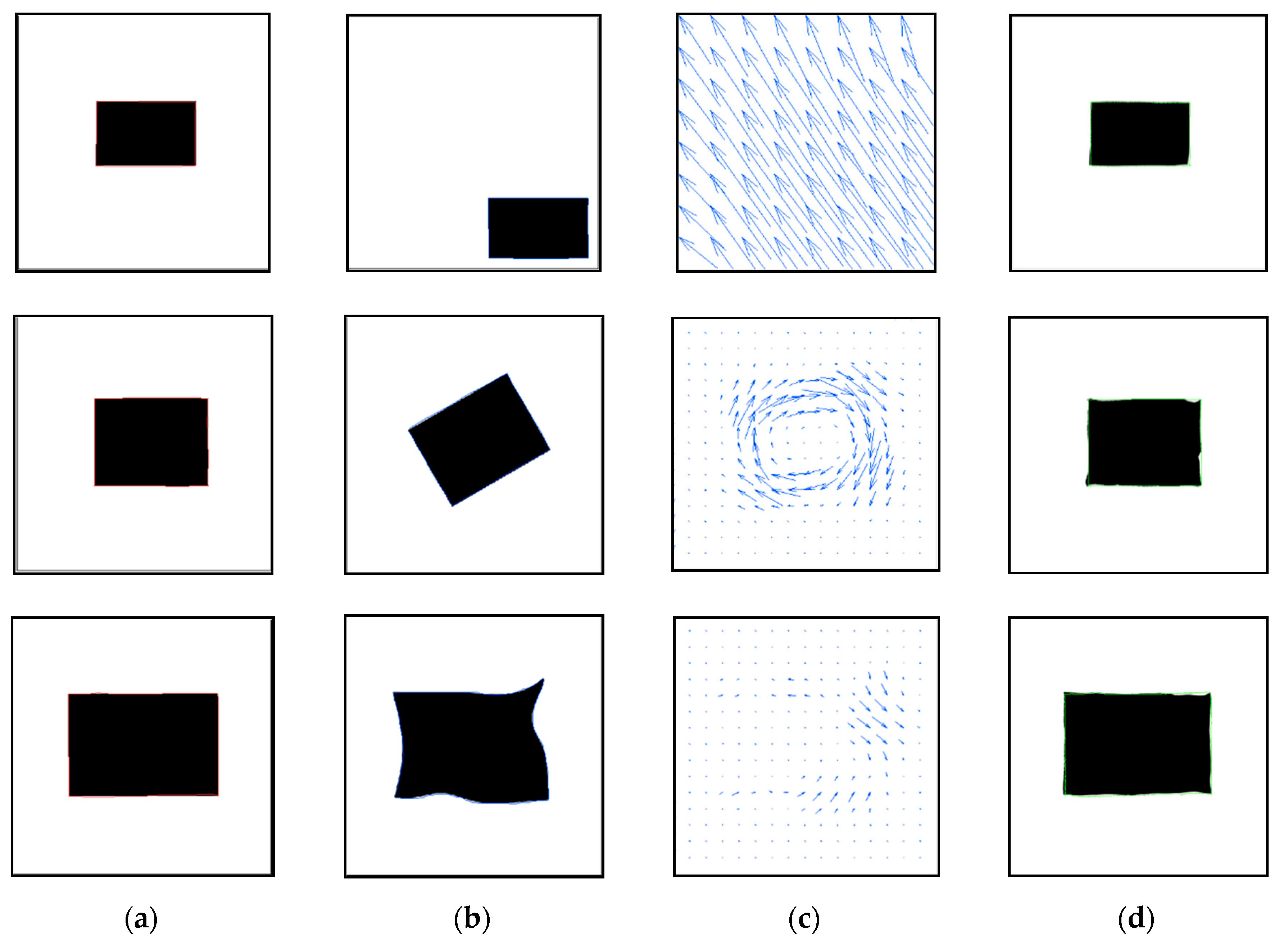
3. Experimental Results and Discussion
3.1. Performance Evaluation for Curve Transformation
3.2. Performance Evaluation for Binary Image Registration
3.3. Performance Evaluation for Grayscale Image Registration
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Ye, Y.; Shan, J.; Bruzzone, L. Robust registration of multimodal remote sensing images based on structural similarity. IEEE Trans. Geosci. Remote Sens. 2017, 55, 2941–2958. [Google Scholar] [CrossRef]
- Ma, J.; Zhou, H.; Zhao, J. Robust feature matching for remote sensing image registration via locally linear transforming. IEEE Trans. Geosci. Remote Sens. 2015, 53, 6469–6481. [Google Scholar] [CrossRef]
- Su, Y.; Liu, Z.; Ban, X. Symmetric face normalization. Symmetry 2019, 11, 96. [Google Scholar] [CrossRef]
- Liu, L.; Jiang, T.; Yang, J. Fingerprint registration by maximization of mutual information. IEEE Trans. Image Process. 2006, 15, 1100–1110. [Google Scholar] [PubMed]
- Sariyanidi, E.; Gunes, H.; Cavallaro, A. Robust registration of dynamic facial sequences. IEEE Trans. Image Process. 2017, 26, 1708–1722. [Google Scholar] [CrossRef] [PubMed]
- Li, H.; Manjunath, B.; Mitra, S.H. Registration of 3D multimodality brain images by curve matching. In Proceedings of the 1993 IEEE Conference Record Nuclear Science Symposium and Medical Imaging Conference, San Francisco, CA, USA, 31 October–6 November 1993; pp. 1744–1748. [Google Scholar]
- Liang, Z.; He, X.; Teng, Q. 3D MRI image super-resolution for brain combining rigid and large diffeomorphic registration. IET Image Process. 2017, 11, 1291–1301. [Google Scholar] [CrossRef]
- Dong, G.; Yan, H.; Lv, G.; Dong, X. Exploring the utilization of gradient information in SIFT based local image descriptors. Symmetry 2019, 11, 998. [Google Scholar] [CrossRef]
- Liu, X.; Tao, X.; Ge, N. Fast remote-sensing image registration using priori information and robust feature extraction. Tsinghua Sci. Technol. 2016, 21, 552–560. [Google Scholar]
- Brock, K.K. Image Processing in Radiation Therapy; Taylor & Francis Group: New York, NY, USA, 2013. [Google Scholar]
- Li, Y.; Stevenson, R.L. Multimodal image registration with line segments by selective search. IEEE Trans. Cybern. 2017, 47, 1285–1298. [Google Scholar] [CrossRef]
- Li, J.; Hu, Q.; Ai, M. Robust feature matching for remote sensing image registration based on Lq-estimator. IEEE Geosci. Remote Sens. Lett. 2016, 13, 1989–1993. [Google Scholar] [CrossRef]
- Razlighi, Q.R.; Kehtarnavaz, N. Spatial mutual information as similarity measure for 3-D brain image registration. IEEE J. Transl. Eng. Health Med. 2014, 2, 27–34. [Google Scholar] [CrossRef] [PubMed]
- Tagare, H.D.; Rao, M. Why does mutual-information work for image registration? A deterministic explanation. IEEE Trans. Pattern Anal. Mach. Intell. 2015, 37, 1286–1296. [Google Scholar] [CrossRef] [PubMed]
- Heinrich, M.P.; Jenkinson, M.; Bhushan, M. MIND: Modality independent neighbourhood descriptor for multi-modal deformable registration. Med. Image Anal. 2012, 16, 1423–1435. [Google Scholar] [CrossRef] [PubMed]
- Reaungamornrat, S.; de Silva, T.; Uneri, A.; Vogt, S.; Kleinszig, G.; Khanna, A.J.; Wolinsky, J.-P.; Prince, J.L.; Siewerdsen, J.H. MIND Demons: Symmetric diffeomorphic deformable registration of MR and CT for image-guided spine surgery. IEEE Trans. Med. Imaging 2016, 35, 2413–2424. [Google Scholar] [CrossRef] [PubMed]
- Ghassabi, Z.; Shanbehzadeh, J.; Sedaghat, A. An efficient approach for robust multimodal retinal image registration based on UR-SIFT features and PIIFD descriptors. EURASIP J. Image Video Process. 2013, 2013, 25. [Google Scholar] [CrossRef] [Green Version]
- Cao, W.; Lyu, F.; He, Z. Multi-modal medical image registration based on feature spheres in geometric algebra. IEEE Access 2018, 6, 21164–21172. [Google Scholar] [CrossRef]
- Xia, M.; Liu, B. Image registration by ‘super-curves’. IEEE Trans. Image Process. 2004, 13, 720–732. [Google Scholar] [CrossRef] [PubMed]
- Khoualed, S.; Sarbinowski, A.; Samir, C. A new curves-based method for adaptive multimodal registration. In Proceedings of the 5th International Conference on Image Processing, Theory, Tools and Applications, Orleans, France, 10–13 November 2015; pp. 391–396. [Google Scholar]
- Senneville, B.D.D.; Zachiu, C.; Moonen, C. EVolution: An edge-based variational method for non-rigid multi-modal image registration. Phys. Med. Biol. 2016, 61, 7377–7396. [Google Scholar] [CrossRef]
- Peng, W.; Tong, R.; Qian, G. A new curves-based local image registration method. In Proceedings of the 1st International Conference on Bioinformatics and Biomedical Engineering, Wuhan, China, 6–8 July 2007; pp. 984–988. [Google Scholar]
- Rawlings, J.O.; Pantula, S.G.; Dickey, D.A. Polynomial Regression. In Applied Regression Analysis: A Research Tool, 2nd ed.; Casella, G., Fienberg, S., Olkin, I., Eds.; Spinger: New York, NY, USA, 1998; Volume 18, pp. 235–261. [Google Scholar]
- Unser, M. Splines: A perfect fit for signal processing. Eur. Signal Process. Mag. 1999, 16, 22–38. [Google Scholar] [CrossRef]
- Chankong, T.; Theera-Umpon, N.; Auephanviriyakul, S. Automatic cervical cell segmentation and classification in Pap smears. Comput. Methods Programs Biomed. 2014, 113, 539–556. [Google Scholar] [CrossRef]
- Huttenlocher, D.P.; Klanderman, A.; Rucklidge, W.J. Comparing images using the Hausdroff distance. IEEE Trans. Pattern Anal. Mach. Intell. 1993, 15, 850–863. [Google Scholar] [CrossRef]
- Sorzano, C.O.S.; Thevenaz, P.; Unser, M. Elastic registration of biological images using vector spline regularization. IEEE Trans. Biomed. Eng. 2005, 52, 652–663. [Google Scholar] [CrossRef] [PubMed]
- Yang, D.; Brame, S.; Naqa, I. Technical Note: DIRART—A software suite for deformable image registration and adaptive radiotherapy research. Med. Phys. 2011, 38, 85–94. [Google Scholar]



















| Case | Hausdroff Distance (Pixels) | |||
|---|---|---|---|---|
| Translation | Rotation | Scaling | Complex | |
| 1 | 3.995 | 3.775 | 5.885 | 4.180 |
| 2 | 4.066 | 3.524 | 3.837 | 4.606 |
| 3 | 4.368 | 4.366 | 2.864 | 5.727 |
| 4 | 4.352 | 5.731 | 5.638 | 4.809 |
| 5 | 4.154 | 4.349 | 3.248 | 5.801 |
| 6 | 4.417 | 6.182 | 3.315 | 6.807 |
| 7 | 5.582 | 6.475 | 2.988 | 7.070 |
| 8 | 3.671 | 7.136 | 4.338 | 7.143 |
| 9 | 5.755 | 7.792 | 4.177 | 5.064 |
| 10 | 5.862 | 6.471 | 3.981 | 6.993 |
| Average | 4.622 | 5.580 | 4.027 | 5.820 |
| Standard Deviation | 0.799 | 1.482 | 1.041 | 1.127 |
| Lena Image no. | No Registration | Proposed Method | bUnwarpJ | DIRART | ||||
|---|---|---|---|---|---|---|---|---|
| RMSE | NCC (%) | RMSE | NCC (%) | RMSE | NCC (%) | RMSE | NCC (%) | |
| 1 | 3252.10 | 90.41 | 1607.64 | 97.65 | 2220.25 | 94.20 | 1631.68 | 97.57 |
| 2 | 2690.98 | 93.38 | 1579.81 | 97.72 | 1668.53 | 96.74 | 1715.67 | 97.30 |
| 3 | 3010.36 | 91.69 | 1579.81 | 97.72 | 1697.29 | 96.45 | 2020.65 | 96.25 |
| 4 | 3249.89 | 90.27 | 1738.55 | 97.23 | 1828.23 | 95.98 | 1926.09 | 96.58 |
| 5 | 2829.80 | 92.77 | 1667.60 | 97.46 | 2177.10 | 94.81 | 1772.41 | 97.13 |
| 6 | 2897.92 | 92.32 | 1545.06 | 97.84 | 2118.51 | 94.58 | 1880.80 | 96.76 |
| 7 | 2392.20 | 94.81 | 1344.48 | 98.35 | 1814.05 | 96.30 | 1355.07 | 98.32 |
| 8 | 3258.11 | 90.30 | 1762.44 | 97.16 | 1680.99 | 96.74 | 1887.11 | 96.74 |
| 9 | 2939.54 | 92.14 | 1971.31 | 96.48 | 2280.70 | 93.93 | 2104.41 | 95.95 |
| 10 | 3185.72 | 90.64 | 1982.70 | 96.41 | 2227.62 | 94.39 | 2218.27 | 95.47 |
| Average | 2970.66 | 91.87 | 1677.94 | 97.40 | 1971.32 | 95.41 | 1851.21 | 96.81 |
| Standard Deviation | 284.13 | 1.52 | 195.20 | 0.60 | 254.66 | 1.13 | 248.16 | 0.82 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Watcharawipha, A.; Theera-Umpon, N.; Auephanwiriyakul, S. Space Independent Image Registration Using Curve-Based Method with Combination of Multiple Deformable Vector Fields. Symmetry 2019, 11, 1210. https://doi.org/10.3390/sym11101210
Watcharawipha A, Theera-Umpon N, Auephanwiriyakul S. Space Independent Image Registration Using Curve-Based Method with Combination of Multiple Deformable Vector Fields. Symmetry. 2019; 11(10):1210. https://doi.org/10.3390/sym11101210
Chicago/Turabian StyleWatcharawipha, Anirut, Nipon Theera-Umpon, and Sansanee Auephanwiriyakul. 2019. "Space Independent Image Registration Using Curve-Based Method with Combination of Multiple Deformable Vector Fields" Symmetry 11, no. 10: 1210. https://doi.org/10.3390/sym11101210
APA StyleWatcharawipha, A., Theera-Umpon, N., & Auephanwiriyakul, S. (2019). Space Independent Image Registration Using Curve-Based Method with Combination of Multiple Deformable Vector Fields. Symmetry, 11(10), 1210. https://doi.org/10.3390/sym11101210





