A Robust Color Image Watermarking Algorithm Based on APDCBT and SSVD

Abstract

With the wide application of color images, watermarking for the copyright protection of color images has become a research hotspot. In this paper, a robust color image watermarking algorithm based on all phase discrete cosine biorthogonal transform (APDCBT) and shuffled singular value decomposition (SSVD) is proposed. The host image is transformed by the 8 × 8 APDCBT to obtain the direct current (DC) coefficient matrix, and then, the singular value decomposition (SVD) is performed on the DC matrix to embed the watermark. The SSVD and Fibonacci transform are mainly used at the watermark preprocessing stage to improve the security and robustness of the algorithm. The watermarks are color images, and a color quick response (QR) code with error correction mechanism is introduced to be a watermark to further improve the robustness. The watermark embedding and extraction processes are symmetrical. The experimental results show that the algorithm can effectively resist common image processing attacks, such as JPEG compression, Gaussian noise, salt and pepper noise, average filter, median filter, Gaussian filter, sharpening, scaling attacks, and a certain degree of rotation attacks. Compared with the color image watermarking algorithms considered in this paper, the proposed algorithm has better performance in robustness and imperceptibility.

1. Introduction

With the rapid development of the information age, digital images, as important information carriers, have been widely spread on the network. Images are easy to copy and spread in large quantities, which brings convenience to people, but also makes piracy and infringement more and more serious. In recent years, endless piracy and infringement incidents have emerged, seriously affecting the legitimate rights and interests of copyright owners and disrupting the normal market order and social public order. Improving the level of copyright protection and information security for digital images has become a research hotspot. Techniques for copyright protection include cryptography [1], steganography [2], digital fingerprinting [3], and digital watermarking [4]. Among them, digital watermarking is the most commonly used copyright protection technology for digital products due to its good concealment, robustness, and stability. Until now, digital watermarking has been applied to the copyright protection of texts [5], images [6,7,8], audios [9], videos [10,11,12], and so on, especially images.

Since the advent of color displays, black-and-white displays have been rapidly replaced. With the rise of this technology, color images have replaced black-and-white images and gray images. As a result, the watermarking technology for copyright protection of color images has gradually developed. Depending on the difference of the embedding locations, image watermarking can be divided into two categories: watermarking in the spatial domain [13,14,15] and watermarking in the transform domain [16,17,18,19,20,21,22,23,24,25,26,27,28]. Chou and Wu [13] embedded the color watermark image into the color host images uniformly by modifying the quantization indices of color pixels. This algorithm cannot effectively resist various attacks. Su et al. [14] calculated the approximate maximum eigenvalue of the Schur decomposition in the spatial domain to embed the watermark without true Schur decomposition. Su et al. [15] embedded the watermark into the direct current (DC) coefficient of two-dimensional (2D) discrete Fourier transform (DFT) obtained in the spatial domain. These two algorithms have both the advantages of the spatial domain and frequency domain.

Watermarking algorithms in the spatial domain are easy to implement but have poor robustness, while watermarking algorithms in the transform domain are robust and have wide application range. Barni et al. [16] embedded the watermark by changing all discrete cosine transform (DCT) coefficients of each color channel. A threshold was used in this algorithm to minimize the difference of extracted watermark information. Liu [17] extended the perceptual model used in gray images to the color images, and estimated the noise attack threshold of each wavelet coefficient in the luminance and chrominance of the color image to meet the requirements of imperceptibility and robustness. Patvardhan et al. [18] took the quick response (QR) code as the carrier of watermark information, and combined discrete wavelet transform (DWT) and singular value decomposition (SVD) to embed the watermark into the luminance component of host images. Roy and Pal [19] proposed a color multiple watermarking method based on DCT and repetition code. Two watermarks were embedded into green and blue components, respectively. The computational complexity of this algorithm is high. Based on the local invariant significant bit-plane histogram, Niu et al. [20] presented a new robust color image watermarking algorithm, which embedded the watermark into the affine invariant local feature regions. Its limitation is that it has lower watermark capacity. In addition, it cannot be used effectively in real-time applications. Liu et al. [21] proposed a robust hybrid color image watermarking algorithm by fusing a local KAZE feature-based watermarking scheme with a conventional watermarking scheme based on integer wavelet transform (IWT). Its watermark capacity is limited. Chang et al. [22] converted the color host image into the YIQ color space, and embedded two binary watermarks into the DCT domain of the quadrature chrominance component. The imperceptibility of this algorithm is relatively poor. Lakrissi et al. [23] proposed a novel dynamic color image watermarking algorithm combining the DWT with SVD. The watermark was randomly embedded into LL sub-bands based on the human visual system (HVS) to choose an adaptive scaling factor. Li et al. [24] proposed a novel color image watermarking scheme based on the quaternion Hadamard transform (QHT) and Schur decomposition. Rosales-Roldan et al. [25] used SVD, DWT, and DCT to transform the luminance component of host images and embedded the watermark using the quantization index modulation (QIM). Roy and Pal [26] embedded the watermark into the luminance component of host images based on DWT and SVD. Vaidya and Mouli [27] used multiple decompositions, including DWT, contourlet transform (CT), Schur decomposition, and SVD, to embed the watermark into the luminance component of the host image. Mohammad and Gholamhossein [28] adopted the teaching-learning-based optimization (TLBO) method to automatically determine the embedding parameters and suitable locations for inserting the watermark. Laur et al. [29] proposed a non-blind color image watermarking scheme based on DWT, chirp Z-transform (CZT), QR decomposition, SVD, and entropy, which embedded the watermark into low entropy parts of all three RGB components. Cedillo-Hernandez et al. [30] proposed a robust-encoded color image watermarking algorithm using the image normalization procedure and DCT transform. To improve the security of the algorithm, a convolutional encoder was used to encode the watermark. All of these algorithms used gray or binary images as the watermark.

With the development of color image watermarking algorithms, color images have gradually been implemented as watermarks [31,32,33]. Su et al. [31] performed two-level DCT on the color host image and embedded the color watermark into DC coefficients and alternating current (AC) coefficients. Su and Chen [32] proposed an improved dual color image watermarking scheme based on the Schur decomposition, using the features obtained by the Schur decomposition to embed or extract the watermark images. Pandey et al. [33] embedded the singular values of the watermark into the luminance component of host images using variable scaling factors. This algorithm has high payload capacity, while it is also a non-blind watermarking algorithm. Jia et al. [34] proposed a color image watermarking algorithm based on DWT and QR decomposition, using the features obtained by QR decomposition to embed the watermark. Taking color images as watermarks poses more challenges to the watermark capacity and the imperceptibility of the algorithm.

In this paper, a robust color image watermarking algorithm based on all phase discrete cosine biorthogonal transform (APDCBT) and shuffled singular value decomposition (SSVD) is proposed. The better low-frequency energy accumulation characteristics of the APDCBT and the stability of SSVD are combined to ensure the robustness of the algorithm. Firstly, the host image is divided into nonoverlapping 8 × 8 blocks, and the APDCBT is performed to obtain the DC coefficient matrix. Then, SVD is performed on the DC matrix to embed the watermark. The SSVD is mainly used at the watermark preprocessing stage to improve the security and robustness of the algorithm.

The main contributions of the proposed algorithm are as follows. (1) The APDCBT transform is introduced into the color image watermarking algorithm, and its better low-frequency energy accumulation characteristic is used to find the watermark embedding locations. (2) Fibonacci transform with larger key space is used to improve the security of the algorithm. (3) The watermarks for embedding are color images, not gray or binary images. Additionally, the color QR code with error correction mechanism is introduced to be a watermark, which can further improve the robustness of the algorithm. (4) The proposed algorithm has high robustness to common image processing attacks, such as JPEG compression, Gaussian noise, salt and pepper noise, average filter, median filter, Gaussian filter, sharpening, and scaling attacks.

The rest of this paper is organized as follows. Preliminary concepts are provided in Section 2, including the concepts and characteristics of APDCBT, SSVD, Fibonacci transform, and QR code. Section 3 details the proposed algorithm, including the preprocessing, embedding, and extraction of the watermark. The experimental results and discussions are presented in Section 4. Finally, the conclusions and future work are discussed in Section 5.

2. Preliminary Concepts

To improve the robustness of the algorithm, the advantages of the APDCBT and SSVD are combined to determine the appropriate locations for watermark embedding. To improve the security of the algorithm, the Fibonacci transform is adopted to scramble the watermark image. In addition, the QR code is introduced to further improve the robustness of the algorithm. This section mainly introduces the concepts and characteristics of these three transforms and the QR code.

2.1. APDCBT

The APDCBT was proposed to solve the serious block artifacts caused by DCT at low bit rates in image compression [35]. Compared with DCT, the APDCBT has better low-frequency energy accumulation and high-frequency energy attenuation characteristics. Due to these characteristics, the APDCBT has been applied in many fields, such as image compression and digital watermarking [36]. The transform matrix of APDCBT can be expressed as Equation (1):

$$B(i,j)=\{\begin{array}{ll}\frac{N-i}{N^2},& i=0,1,\cdots ,N-1,\hspace{0.17em}j=0\\ \frac{1}{N^2}\left[(N-i)\cos \frac{ij\mathsf{\pi }}{N}-\csc \frac{j\mathsf{\pi }}{N}\sin \frac{ij\mathsf{\pi }}{N}\right],& i=0,1,\cdots ,N-1,\hspace{0.17em}j=1,2,\cdots ,N-1\end{array},$$

(1)

where $N$ is the size of the image block $X$. Performing the APDCBT on $X$ can be presented as Equation (2):

$$A=BX{B}^{\mathrm{T}},$$

(2)

where $A$ is the transform coefficient matrix and $B$ is the transform matrix of APDCBT.

2.2. SSVD

The SSVD [37] was developed on the basis of the standard SVD. Different from the SVD, SSVD adds a scrambling process, which can be expressed as $Y=\widehat{S}\hspace{0.17em}\left\{X\right\}$, where $X$ is the input image, $Y$ is the scrambled image, and $\widehat{S}$ is the shuffled operator. In other words, SSVD scrambles the input image first, and then performs standard SVD on the scrambled image $Y$. The scrambling method used in the proposed algorithm is the Fibonacci transform, which will be introduced in Section 2.3.

SVD is a type of matrix decomposition that can be applied to any matrix. By performing SVD on a complex matrix, three smaller and simpler submatrices can be obtained, which can describe the important characteristics of the complex matrix. For a matrix $Y$, its SVD can be expressed as Equation (3):

$$Y=US{V}^{\mathrm{T}},$$

(3)

where $U$ and $V$ are orthogonal matrices and $S$ is a diagonal matrix. The matrix $S$ contains the singular values of matrix $Y$, which can represent the main information of matrix $Y$ and has high stability. Due to this characteristic, SVD is widely used in the watermarking field.

2.3. Fibonacci Transform

Matrix transform is one of the most commonly used image scrambling methods. For an image $F$ of size $N\times N$, its Fibonacci transform [11] can be shown as Equation (4):

$$\left[\begin{array}{l}{x}^{\prime }\\ y^{\prime }\end{array}\right]=\left[\begin{array}{cc}1& 1\\ 1& 0\end{array}\right]\left[\begin{array}{l}x\\ y\end{array}\right]\mathrm{mod}(N),$$

(4)

where $(x,y)$ is the coordinate of image $F$ and $(x^{\prime },y^{\prime })$ is the coordinate after the transform. The Fibonacci transform is periodic, and its transform periods for images with different sizes are shown in

Table 1. The periods of the Fibonacci transform for images with different sizes.

Size of Image	4 × 4	8 × 8	16 × 16	32 × 32	64 × 64	128 × 128	256 × 256
Period	6	12	24	48	96	192	384

. When the images are the same size, the period of Fibonacci transform is twice as long as an Arnold transform [38]. Therefore, the Fibonacci transform can provide more key space and improve the security of watermarking algorithms.

2.4. QR Code

The QR code is a two-dimensional bar code that can be read quickly. Compared with the traditional bar code, the QR code can store more data information. Due to this characteristic, QR codes have been widely used in the information identification of intelligent devices. The size of QR codes can range from 21 × 21 to 177 × 177, mainly including data area, alignment pattern, timing pattern, finder pattern, quit zone, dark module, and separator. Since QR codes have four levels of error correction capability and its maximum fault tolerance can reach 30%, it can still be read correctly even if it is damaged. In addition, QR codes also have strong bending resistance.

Due to the error correction algorithm of the QR code, it can ensure the security of the information to be hidden. In watermarking algorithms, embedding the hidden information into the QR code and using the generated QR code as the watermark can improve the robustness of the algorithm. Even if the extracted QR code image is destroyed, the hidden information can still be decoded.

3. Proposed Color Image Watermarking Algorithm

In this section, the specific steps of the proposed color image watermarking algorithm are explained. The algorithm consists of three parts: watermark preprocessing, watermark embedding, and watermark extraction. The APDCBT is introduced into the color image watermarking algorithm, and its better low-frequency energy accumulation characteristic is used to find the watermark embedding locations, which is the main contribution of the proposed algorithm. In addition, the Fibonacci transform and the QR code are used to improve the security and the robustness of the proposed algorithm, which are also the contributions of the proposed algorithm. The frameworks of watermark embedding and watermark extraction are shown in Figure 1, and the specific steps are explained in the following subsections.

3.1. Watermark Preprocessing

The watermark preprocessing is performed to improve the security of the watermarking algorithm. SSVD is used to preprocess the watermark image. Here, the Fibonacci transform is used to scramble the color watermark image, and the scrambling process is shown in Figure 2.

The specific watermark preprocessing process is presented below.

Step 1: Divide the color watermark image $W$ of size 64 × 64 into $R_{\mathrm{W}}$, $G_{\mathrm{W}}$, and $B_{\mathrm{W}}$ components.

Step 2: Apply the Fibonacci transform to scramble the three color components.

Step 3: Perform SVD on the scrambled components, as shown in Equation (5):

$$C_{\mathrm{s}}=U_{C\mathrm{s}}{S}_{C\mathrm{s}}{V}_{C\mathrm{s}}^{\mathrm{T}},\hspace{0.17em}\hspace{0.17em}C=\{R,\hspace{0.17em}G,\hspace{0.17em}B\},$$

(5)

where $C_{\mathrm{s}}$ are the three scrambled color components, $U_{C\mathrm{s}}$ and $V_{C\mathrm{s}}$ are orthogonal matrices for $C_{\mathrm{s}}$, and $S_{C\mathrm{s}}$ are singular value matrices for $C_{\mathrm{s}}$.

Step 4: Generate embedded watermark using Equation (6):

$$W_C=U_{C\mathrm{s}}{S}_{C\mathrm{s}},\hspace{0.17em}\hspace{0.17em}C=\{R,\hspace{0.17em}G,\hspace{0.17em}B\},$$

(6)

where $W_C$, namely $W_{\mathrm{R}}$, $W_{\mathrm{G}}$, and $W_{\mathrm{B}}$, are the generated watermarks for embedding.

To more comprehensively illustrate the watermark preprocessing process, its pseudocode is shown in Algorithm 1.

Algorithm 1.Watermark Preprocessing Algorithm
Variable Declaration:
	SDUW: color watermark image
	W: read the watermark image
	RW, GW, and BW: three components of the color watermark image
	Rs, Gs, and Bs: three scrambled components using Fibonacci transform
	URs, VRs, UGs, VGs, UBs, and VBs: orthogonal matrices for Rs, Gs, and Bs
	SRs, SGs, and SBs: singular value matrices for Rs, Gs, and Bs
	WR, WG, and WB: three watermark components for embedding
Watermark Preprocessing Procedure:
Start Procedure:
1:	Read the color watermark image
	W ← SDUW.png (color watermark image of size 64 × 64);
	RW ← W (:, :, 1); GW ← W (:, :, 2); BW ← W (:, :, 3);
2:	Scramble the three color components of the watermark image
	Rs ← Fibonacci transform (RW); Gs ← Fibonacci transform (GW); Bs ← Fibonacci transform (BW);
3:	Perform SVD on each scrambled color components
	[URs, SRs, VRs] ← SVD (Rs); [UGs, SGs, VGs] ← SVD (Gs); [UBs, SBs, VBs] ← SVD (Bs);
4:	Obtain watermark for embedding
	WR = URs × SRs; WG = UGs × SGs; WB = UBs × SBs;
End Procedure

3.2. Watermark Embedding

The watermark embedding process is shown in Figure 1a, and the detailed steps are given below.

Step 1: Divide the color host image $I$ of size 512 × 512 into $R$, $G$, and $B$ components.

Step 2: Divide each component into nonoverlapping 8 × 8 blocks, and apply the APDCBT to each block to obtain the DC coefficient, and then the DC coefficient matrices $M_C$ can be obtained, where $C=\{R,\hspace{0.17em}G,\hspace{0.17em}B\}$.

Step 3: Perform SVD on $M_C$ to obtain singular value matrices $S_C$, where $C=\{R,\hspace{0.17em}G,\hspace{0.17em}B\}$.

Step 4: Use Algorithm 1 to preprocess the color watermark image and obtain $W_C$, where $C=\{R,\hspace{0.17em}G,\hspace{0.17em}B\}$.

Step 5: Embed $W_C$ into $S_C$ according to Equation (7):

$$S_{C\mathrm{W}}=S_C+\alpha \times W_C,\hspace{0.17em}{S}_{C\mathrm{W}}=U_{C\mathrm{W}}{S}_{C\mathrm{W}1}{V}_{C\mathrm{W}}^{\mathrm{T}},\hspace{0.17em}\hspace{0.17em}C=\{R,\hspace{0.17em}G,\hspace{0.17em}B\},$$

(7)

where $\alpha$ is the embedding strength of the watermark, and $S_{C\mathrm{W}}$ are three singular value matrices with the embedded watermark. $U_{C\mathrm{W}}$ and $V_{C\mathrm{W}}$ are orthogonal matrices for $S_{C\mathrm{W}}$, and $S_{C\mathrm{W}1}$ are the singular value matrices for $S_{C\mathrm{W}}$. Save $U_{C\mathrm{W}}$, $V_{C\mathrm{W}}$, and $S_C$ for watermark extraction process.

Step 6: Apply the inverse SVD to $S_{C\mathrm{W}1}$, then the watermarked $M_C^{*}$ can be obtained.

Step 7: After performing the inverse APDCBT, three watermarked color components can be obtained. Use the concatenate (cat) operator to stack them, and then the watermarked color image $I^{*}$ can be obtained.

To more comprehensively illustrate the watermark embedding process, its pseudocode is shown in Algorithm 2.

Algorithm 2.Watermark Embedding Algorithm
Variable Declaration:
	Lena: color host image
	I: read the color host image
	R, G, and B: three color components of the host image
	MC: three DC coefficient matrices obtained by APDCBT, where C = {R, G, B}
	UC and VC: orthogonal matrices for MC
	SC: singular value matrices for MC
	WC: three preprocessed color components of the watermark image, where C = {R, G, B}
	α: scaling factor
	SCW: three singular value matrices with the embedded watermark
	UCW and VCW: the orthogonal matrices for SCW
	SCW1: the singular value matrices for SCW
	$M_C^{*}$: watermarked DC coefficient matrices
	$C^{*}$: three watermarked color components, including $R^{*}$, $G^{*}$, and $B^{*}$
	$I^{*}$: watermarked image
Watermark Embedding Procedure:
Start Procedure:
1:	Read the color host image
	I ← Lena.ppm (color host image of size 512 × 512);
	R ← I (:, :, 1); G ← I (:, :, 2); B ← I (:, :, 3);
2:	Perform 8 × 8 APDCBT to three color components
	MC ← APDCBT (C) //C = {R, G, B}
3:	Perform SVD on MC
	[UC, SC, VC] ← SVD (MC)
4:	Watermark Embedding
	SCW = SC + α × WC
	[UCW, SCW1, VCW] ← SVD (MC)
	$M_C^{*}$ ← $U_C{S}_{C\mathrm{W}1}{V}_C^{\mathrm{T}}$
5:	Perform the inverse APDCBT
	$C^{*}$ ← inverse APDCBT ($M_C^{*}$) //$C^{*}=\{R^{*},\hspace{0.17em}{G}^{*},\hspace{0.17em}{B}^{*}\}$
	$I^{*}$ ← cat (3, $R^{*},\hspace{0.17em}{G}^{*},\hspace{0.17em}{B}^{*}$)
End Procedure

3.3. Watermark Extraction

The watermark extraction process is shown in Figure 1b, and the detailed steps are given below.

Step 1: Divide the suspicious color image $I^{\prime }$ into $R^{\prime }$, $G^{\prime }$, and $B^{\prime }$ components.

Step 2: Divide each component into nonoverlapping 8 × 8 blocks, and apply the APDCBT to each block to obtain the DC coefficient matrices ${M^{\prime }}_C$, where $C=\{R^{\prime },\hspace{0.17em}{G}^{\prime },\hspace{0.17em}{B}^{\prime }\}$.

Step 3: Perform SVD on ${M^{\prime }}_C$ to obtain singular value matrices ${S^{\prime }}_{C\mathrm{W}1}$, which can be presented as Equation (8):

$${M^{\prime }}_C={U^{\prime }}_C{S^{\prime }}_{C\mathrm{W}1}{\left({V^{\prime }}_C\right)}^{\mathrm{T}},\hspace{0.17em}\hspace{0.17em}C=\{R^{\prime },\hspace{0.17em}{G}^{\prime },\hspace{0.17em}{B}^{\prime }\},$$

(8)

where ${U^{\prime }}_C$ and ${V^{\prime }}_C$ are orthogonal matrices for ${M^{\prime }}_C$.

Step 4: The embedded watermark ${W^{\prime }}_C$ can be obtained according to Equation (9):

$${S^{\prime }}_C=U_{C\mathrm{W}}{S^{\prime }}_{C\mathrm{W}1}{\left(V_{C\mathrm{W}}\right)}^{\mathrm{T}},\hspace{0.17em}{W^{\prime }}_C=({S^{\prime }}_C-\hspace{0.17em}{S}_C)/\alpha ,\hspace{0.17em}\hspace{0.17em}C=\{R^{\prime },\hspace{0.17em}{G}^{\prime },\hspace{0.17em}{B}^{\prime }\},$$

(9)

Step 5: Obtain the three color components ${C^{\prime }}_{\mathrm{W}}$ using Equation (10):

$${C^{\prime }}_{\mathrm{W}}={W^{\prime }}_C{\left(V_{C\mathrm{s}}\right)}^{\mathrm{T}},\hspace{0.17em}\hspace{0.17em}C=\{R^{\prime },\hspace{0.17em}{G}^{\prime },\hspace{0.17em}{B}^{\prime }\},$$

(10)

Step 6: Apply inverse Fibonacci transform on ${C^{\prime }}_{\mathrm{W}}$ to obtain the reconstructed color components ${C^{\prime }}_{\mathrm{WR}}$.

Step 7: Reconstruct the final watermark image $W^{\prime }$ by using the concatenate operator to stack the three color components ${C^{\prime }}_{\mathrm{WR}}$, that is, ${R^{\prime }}_{\mathrm{WR}}$, ${G^{\prime }}_{\mathrm{WR}}$, and ${{{\rm B}}^{\prime }}_{\mathrm{WR}}$.

To more comprehensively illustrate the watermark extraction process, its pseudocode is shown in Algorithm 3.

Algorithm 3. Watermark Extraction Algorithm
Variable Declaration:
	$I^{\prime }$: the suspicious color image
	$R^{\prime }$, $G^{\prime }$, and $B^{\prime }$: three color components of $I^{\prime }$
	${M^{\prime }}_C$: three DC coefficient matrices obtained by APDCBT, where $C=\{R^{\prime },\hspace{0.17em}{G}^{\prime },\hspace{0.17em}{B}^{\prime }\}$
	${U^{\prime }}_C$ and ${V^{\prime }}_C$: orthogonal matrices for ${M^{\prime }}_C$
	${S^{\prime }}_{C\mathrm{W}1}$: singular value matrices for ${M^{\prime }}_C$
	SC: saved singular value matrices for MC of host image
	UCW and VCW: saved orthogonal matrices for SCW in watermark embedding process
	${S^{\prime }}_C$: watermarked singular value matrices
	α: scaling factor
	${W^{\prime }}_C$: extracted watermark
	${C^{\prime }}_{\mathrm{W}}$: three reconstructed color components of watermark image
	${C^{\prime }}_{\mathrm{WR}}$: three inverse scrambled color components of watermark image
	$W^{\prime }$: reconstructed watermark image
Watermark Embedding Procedure:
Start Procedure:
1:	Read the suspicious color image
	$I^{\prime }$ ← Suspicious image.ppm
	$R^{\prime }$ ← $I^{\prime }$(:, :, 1); $G^{\prime }$ ← $I^{\prime }$(:, :, 2); $B^{\prime }$ ← $I^{\prime }$(:, :, 3);
2:	Perform 8 × 8 APDCBT to three color components
	${M^{\prime }}_C$ ← APDCBT (C) //$C=\{R^{\prime },\hspace{0.17em}{G}^{\prime },\hspace{0.17em}{B}^{\prime }\}$
3:	Perform SVD on${M^{\prime }}_C$
	[${U^{\prime }}_C$, ${S^{\prime }}_{C\mathrm{W}1}$, ${V^{\prime }}_C$] ← SVD (${M^{\prime }}_C$)
4:	Watermark Extraction
	${S^{\prime }}_C$ ← $U_{C\mathrm{W}}{S^{\prime }}_{C\mathrm{W}1}{\left(V_{C\mathrm{W}}\right)}^{\mathrm{T}}$ //$C=\{R^{\prime },\hspace{0.17em}{G}^{\prime },\hspace{0.17em}{B}^{\prime }\}$
	${W^{\prime }}_C$ ← $({S^{\prime }}_C-\hspace{0.17em}{S}_C)/\alpha$
	${C^{\prime }}_{\mathrm{W}}$ ← ${W^{\prime }}_C{\left(V_{C\mathrm{s}}\right)}^{\mathrm{T}}$
5:	Apply inverse Fibonacci transform on${C^{\prime }}_{\mathrm{W}}$
	${C^{\prime }}_{\mathrm{WR}}$ ← inverse Fibonacci transform (${C^{\prime }}_{\mathrm{W}}$) //$C=\{R^{\prime },\hspace{0.17em}{G}^{\prime },\hspace{0.17em}{B}^{\prime }\}$
6:	Reconstruct the final watermark image
	$W^{\prime }$ ← cat (3, ${R^{\prime }}_{\mathrm{WR}},\hspace{0.17em}{G^{\prime }}_{\mathrm{WR}},\hspace{0.17em}{B^{\prime }}_{\mathrm{WR}}$)
End Procedure

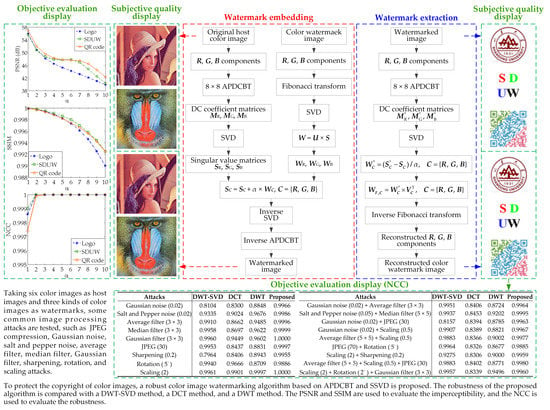
4. Experimental Results and Analysis

In this section, to evaluate the performance of the proposed algorithm, several experiments are performed using MATLAB R2014a on an Intel Core i5-4590 3.30 GHz CPU. All 24-bit color images of size 512 × 512 in the CVG-UGR image database [39] are prepared as host images. In this paper, six color images, including “Lena”, “Baboon”, “Airplane”, “Sailboat”, “House”, and “Peppers”, are selected to illustrate the experimental results, which are shown in Figure 3. In addition, three 24-bit color images of size 64 × 64 are used as the watermarks, which are shown in Figure 4. Among them, Figure 4a is the school badge of Shandong University; Figure 4b is the English abbreviation of Shandong University (Weihai) drawn with Microsoft Visio 2010; and Figure 4c is a color QR code containing a personal website [40] generated by a QR code generator. The imperceptibility and robustness of the proposed algorithm are tested and compared with algorithms [18,31,34].

4.1. Evaluation Indexes

In general, peak signal-to-noise ratio (PSNR) and structural similarity index (SSIM) [41] are used to evaluate the imperceptibility of watermarking algorithms, while the normalized correlation coefficient (NCC) is used to evaluate the robustness of watermarking algorithms [31]. The definition of PSNR is shown as Equation (11):

$$\mathrm{PSNR}=10{\log }_{10}\frac{{255}^2}{\mathrm{MSE}}\hspace{0.17em}(\mathrm{dB}),$$

(11)

where the mean square error (MSE) can be defined as Equation (12):

$$\mathrm{MSE}=\frac{1}{M\times N}{\displaystyle \sum _{m=1}^M{\displaystyle \sum _{n=1}^N[f(m,n)-f_{\mathrm{w}}}}(m,n){]}^2,$$

(12)

where $f$ and $f_{\mathrm{w}}$ are the original host and watermarked images of size $M\times N$, respectively. In this paper, the PSNR of color images is calculated by averaging the PSNRs of R, G, and B components (${\mathrm{PSNR}}_{\mathrm{R}}$, ${\mathrm{PSNR}}_{\mathrm{G}}$, and ${\mathrm{PSNR}}_{\mathrm{B}}$), which can be defined as Equation (13):

$${\mathrm{PSNR}}_{\mathrm{c}}=\frac{1}{3}({\mathrm{PSNR}}_{\mathrm{R}}+{\mathrm{PSNR}}_{\mathrm{G}}+{\mathrm{PSNR}}_{\mathrm{B}}),$$

(13)

where ${\mathrm{PSNR}}_{\mathrm{c}}$ is the PSNR value of color images. The definition of SSIM is shown as Equation (14):

$$\mathrm{SSIM}(f,f_{\mathrm{w}})=\frac{(2{\mu }_f{\mu }_{f_{\mathrm{w}}}+C_1)(2{\sigma }_{f{f}_{\mathrm{w}}}+C_2)}{({\mu }_f^2+{\mu }_{f_{\mathrm{w}}}^2+C_1)({\sigma }_f^2+{\sigma }_{f_{\mathrm{w}}}^2+C_2)},$$

(14)

where $f$ and $f_{\mathrm{w}}$ are the original host and watermarked images, respectively. ${\mu }_f$ and ${\mu }_{f_{\mathrm{w}}}$ represent the mean values of $f$ and $f_{\mathrm{w}}$, respectively; ${\sigma }_f$ and ${\sigma }_{f_{\mathrm{w}}}$ are the variances of $f$ and $f_{\mathrm{w}}$, respectively; ${\sigma }_{f{f}_{\mathrm{w}}}$ is the covariance between $f$ and $f_{\mathrm{w}}$; and $C_1$ and $C_2$ are two constants to maintain the stability. Usually, the larger the PSNR and SSIM are, the better the imperceptibility is.

The definition of NCC is shown as Equation (15):

$$\mathrm{NCC}=\frac{{\displaystyle \sum _{p=1}^3{\displaystyle \sum _{i=1}^M{\displaystyle \sum _{j=1}^N[W(i,j,p)\times W^{\prime }(i,j,p)]}}}}{\sqrt{{\displaystyle \sum _{p=1}^3{\displaystyle \sum _{i=1}^M{\displaystyle \sum _{j=1}^N{[W(i,j,p)]}^2}}}}\sqrt{{\displaystyle \sum _{p=1}^3{\displaystyle \sum _{i=1}^M{\displaystyle \sum _{j=1}^N{[W^{\prime }(i,j,p)]}^2}}}}},$$

(15)

where $W$ and $W^{\prime }$ are the original color watermark image and extracted watermark image of size $M\times N$, respectively. The NCC values range from 0 to 1, and the larger the NCC is, the stronger the robustness is.

4.2. Imperceptibility

Imperceptibility means that the watermark embedded into the image cannot be perceived by the human eyes, that is, the embedded watermark cannot affect the visual quality of the image. The embedding strength of the watermark plays an important role in the performance of a watermarking algorithm. The selection of it must take the imperceptibility and robustness of the watermark into account. Here, taking “Lena” as the host image, the changes of PSNR, SSIM, and NCC with the embedding strength $\alpha$ are shown in Figure 5.

To show the imperceptibility of the algorithm more comprehensively, taking “Baboon”, “Airplane”, “Sailboat”, “House”, and “Peppers” as objects, the change of the imperceptibility with the embedding strength is tested, and the test results are shown in

Table 2. The change of the proposed algorithm’s imperceptibility with the embedding strength $\alpha$.

Host Images	$\mathit{\alpha }$	Logo			SDUW			QR Code
		PSNR (dB)	SSIM	NCC	PSNR (dB)	SSIM	NCC	PSNR (dB)	SSIM	NCC
Baboon	1	55.90	1.0000	0.9992	55.49	1.0000	0.9993	56.88	1.0000	0.9980
	3	47.88	0.9998	1.0000	48.25	0.9998	1.0000	49.20	0.9998	1.0000
	5	44.84	0.9992	1.0000	46.53	0.9995	1.0000	46.78	0.9995	1.0000
	7	42.91	0.9982	1.0000	45.97	0.9988	1.0000	45.80	0.9989	1.0000
Airplane	1	55.69	0.9997	0.9979	55.20	0.9998	0.9986	56.63	0.9998	0.9965
	3	47.17	0.9979	1.0000	47.15	0.9984	1.0000	48.32	0.9984	1.0000
	5	43.63	0.9942	1.0000	44.34	0.9955	1.0000	45.15	0.9960	1.0000
	7	41.43	0.9877	1.0000	43.11	0.9914	1.0000	43.40	0.9922	1.0000
Sailboat	1	55.98	0.9999	0.9995	55.46	0.9999	0.9998	56.85	0.9999	0.9992
	3	48.09	0.9993	1.0000	48.18	0.9994	1.0000	49.09	0.9995	1.0000
	5	45.43	0.9979	1.0000	46.52	0.9986	1.0000	46.62	0.9985	1.0000
	7	44.10	0.9960	1.0000	46.56	0.9973	1.0000	45.78	0.9970	1.0000
House	1	55.78	0.9997	0.9991	55.29	0.9998	0.9995	56.71	0.9998	0.9975
	3	47.49	0.9972	1.0000	47.57	0.9984	1.0000	48.60	0.9985	1.0000
	5	44.25	0.9934	1.0000	45.22	0.9963	1.0000	45.73	0.9965	1.0000
	7	42.33	0.9879	1.0000	44.45	0.9932	1.0000	44.36	0.9936	1.0000
Peppers	1	56.13	0.9826	0.9984	55.79	0.9844	0.9990	57.16	0.9843	0.9977
	3	48.80	0.9729	1.0000	49.70	0.9793	1.0000	50.36	0.9775	1.0000
	5	46.34	0.9685	1.0000	48.89	0.9808	1.0000	49.07	0.9777	1.0000
	7	44.13	0.9662	1.0000	46.06	0.9824	1.0000	46.21	0.9806	1.0000

.

As can be seen from Figure 5 and Table 2, under the same conditions, the imperceptibility of the watermark using a QR code is better than the other two types of watermarks, which shows that QR code can be used as the carrier of watermark information to achieve the watermark embedding. When the embedding strength $\alpha$ equals 5, most PSNR values are larger than 44 dB and most SSIM values are larger than 0.99, while all the NCC values equal 1. Therefore, the embedding strength in the proposed algorithm is set to 5. Taking “Lena” and “Baboon” as objects, the subjective effects of the watermarked images and the extracted watermark images when without performing any attacks on host images are shown in

Table 3. The subjective effects of the proposed algorithm with three color watermark images.

Watermarks	Logo	SDUW	QR Code
Watermarked images (PSNR (dB)/SSIM)	45.24/0.9982	47.66/0.9986	47.70/0.9982
Extracted watermarks (NCC)	1.0000	1.0000	1.0000
Watermarked images (PSNR (dB)/SSIM)	44.84/0.9992	46.53/0.9995	46.78/0.9995
Extracted watermarks (NCC)	1.0000	1.0000	1.0000

.

From Table 3, we can see that the watermarked images have no trace of watermark embedding, and the watermarks can be completely extracted. To compare the proposed algorithm with other three robust image watermarking algorithms, the PSNR, SSIM, NCC, and the watermark capacity of them are listed in

Table 4. Comparisons of the PSNR, SSIM, NCC, and the watermark capacity among different color image watermarking algorithms.

Algorithms	Patvardhan et al. [18]	Su et al. [31]	Jia et al. [34]	Proposed
Host images	512 × 512 × 3	512 × 512 × 3	512 × 512 × 3	512 × 512 × 3
Watermark images	gray	color	color	color
PSNR (dB)	52.13	46.07	41.45	49.03
SSIM	0.9975	0.9913	0.9842	0.9992
NCC	0.9962	0.9999	1.0000	1.0000
Capacity	128 × 128	64 × 64 × 3	32 × 32 × 3	64 × 64 × 3

.

From Table 4, we can see that the watermarks in algorithm [18] are gray images, while algorithms [31,34] and the proposed algorithm embed color watermark images into color host images. Although the PSNR of the proposed algorithm is less than algorithm [18] and larger than algorithms [31,34], the SSIM and NCC of the proposed algorithm are both better than those of the other three algorithms.

4.3. Robustness

Robustness means that the watermark image can still be extracted from the watermarked image after suffering various attacks. In the storage and transmission processes, it is inevitable for color images to undergo various attacks. To test the robustness of the proposed algorithm, various common image processing attacks and geometric attacks are performed on the watermarked color images, including JPEG compression, Gaussian noise, salt and pepper noise, average filter, median filter, Gaussian filter, sharpening, rotation, and scaling attacks. Taking “Lena”, “Baboon”, and “Sailboat” as objects, when “SDUW” is used as the watermark, the results of extracted watermarks and the NCC values under various attacks are shown in

Table 5. The results of extracted watermarks (SDUW) and the NCC values under various attacks.

Attacks	Parameter	Lena	Baboon	Sailboat
JPEG	QF = 30	0.9999	0.9999	0.9998
	QF = 60	1.0000	1.0000	1.0000
Gaussian noise	0.01	0.9997	0.9998	0.9997
	0.02	0.9986	0.9994	0.9990
Salt and Pepper noise	0.01	0.9998	0.9999	0.9999
	0.02	0.9995	0.9998	0.9997
Average filter	5 × 5	0.9991	0.9988	0.9984
Median filter	5 × 5	0.9999	0.9988	0.9995
Gaussian filter	5 × 5	1.0000	1.0000	1.0000
Sharpening	0.2	0.9977	0.9971	0.9974
Rotation	$5^{\circ }$	0.9922	0.9905	0.9941
Scaling	0.5	1.0000	1.0000	1.0000

; when “QR code” is used as the watermark, the results of extracted watermarks and the NCC values under various attacks are shown in

Table 6. The results of extracted watermarks (QR code) and the NCC values under various attacks.

Attacks	Parameter	Lena	Baboon	Sailboat
JPEG	QF = 30	0.9997	0.9998	0.9996
	QF = 60	0.9999	0.9999	0.9999
Gaussian noise	0.01	0.9991	0.9994	0.9994
	0.02	0.9966	0.9979	0.9978
Salt and Pepper noise	0.01	0.9996	0.9998	0.9999
	0.02	0.9986	0.9993	0.9991
Average filter	5 × 5	0.9978	0.9971	0.9963
Median filter	5 × 5	0.9996	0.9972	0.9988
Gaussian filter	5 × 5	1.0000	0.9999	0.9999
Sharpening	0.2	0.9955	0.9932	0.9941
Rotation	$5^{\circ }$	0.9886	0.9855	0.9900
Scaling	0.5	1.0000	1.0000	1.0000

.

It can be seen from Table 5 and Table 6 that the proposed algorithm has high robustness to JPEG compression, noise, filtering, sharpening, and scaling attacks. Although the proposed algorithm can resist a small degree of rotation attacks, it will fail when the rotation angle increases. In the actual image transmission process, images are usually affected by more than one attack. Most color image watermarking algorithms did not consider the robustness when multiple attacks are combined. In this paper, to more comprehensively prove the effectiveness of the proposed algorithm, taking “Lena” as the host image and “QR code” as the watermark, the robustness of the proposed algorithm is compared with algorithms [18,31,34]. In addition, hybrid attacks, which include two or three kinds of attacks, are also considered. The comparison results are shown in

Table 7. Comparisons of the NCC values of the watermarks extracted by different robust color image watermarking algorithms.

Attacks	Patvardhan et al. [18]	Su et al. [31]	Jia et al. [34]	Proposed
Gaussian noise (0.02)	0.8104	0.8300	0.8848	0.9966
Salt and Pepper noise (0.02)	0.9335	0.9024	0.9676	0.9986
Average filter (3 × 3)	0.9910	0.8662	0.9485	0.9996
Median filter (3 × 3)	0.9958	0.8697	0.9622	0.9999
Gaussian filter (3 × 3)	0.9960	0.9449	0.9602	1.0000
JPEG (30)	0.9953	0.8437	0.8831	0.9997
Sharpening (0.2)	0.7964	0.8406	0.8943	0.9955
Rotation ($5^{\circ }$)	0.9940	0.9666	0.8709	0.9886
Scaling (2)	0.9961	0.9901	0.9997	1.0000
Gaussian noise (0.02) + Average filter (3 × 3)	0.9951	0.8406	0.8724	0.9964
Salt and Pepper noise (0.05) + Median filter (5 × 5)	0.9937	0.8453	0.9202	0.9995
Gaussian noise (0.02) + JPEG (30)	0.8157	0.8394	0.8785	0.9963
Salt and Pepper noise (0.05) + JPEG (50)	0.8402	0.8432	0.8923	0.9934
Average filter (3 × 3) + JPEG (30)	0.9910	0.8413	0.8801	0.9995
Median filter (3 × 3) + JPEG (70)	0.9950	0.8405	0.9062	0.9999
Gaussian noise (0.02) + Scaling (0.5)	0.9907	0.8389	0.8821	0.9967
Salt and Pepper noise (0.05) + Scaling (2)	0.9639	0.8580	0.9668	0.9938
Average filter (5 × 5) + Scaling (0.5)	0.9883	0.8366	0.9002	0.9977
Median filter (5 × 5) + Scaling (2)	0.9917	0.8826	0.9260	0.9996
JPEG (30) + Scaling (0.5)	0.9895	0.8424	0.8822	0.9998
JPEG (50) + Sharpening (0.2)	0.9394	0.8462	0.8801	0.9969
JPEG (70) + Rotation ($5^{\circ }$)	0.9964	0.8326	0.8677	0.9885
Scaling (2) + Sharpening (0.2)	0.9275	0.8306	0.9000	0.9959
Gaussian noise (0.02) + Median filter (3 × 3) + Sharpening (0.2)	0.8190	0.8320	0.8777	0.9925
Salt and Pepper noise (0.05) + Average filter (3 × 3) + Scaling (0.5)	0.9889	0.8306	0.8849	0.9936
Average filter (5 × 5) + Scaling (0.5) + JPEG (30)	0.9883	0.8402	0.8771	0.9980
Scaling (2) + Rotation ($2^{\circ }$) + Gaussian filter (3 × 3)	0.9957	0.8339	0.9496	0.9960

.

As can be seen from Table 7, for JEPG compression, noise, filtering, sharpening, scaling, and most hybrid attacks, the NCC values of the proposed algorithm are higher than the other three algorithms, which means that the proposed algorithm is more robust than the other three algorithms. However, when the watermarked image is attacked by rotation attacks, the robustness of the proposed algorithm is slightly weaker than algorithm [18]. In general, SVD-based watermarking algorithms have stronger robustness than DCT-based watermarking algorithms, and the comparison results in Table 7 are no exception. When suffering noise attacks, sharpening attacks, and some hybrid attacks, the robustness of the proposed algorithm is much better than the other three algorithms.

4.4. Real-Time Analysis

To compare the real-time performance of the four algorithms, we take “Lena”, “Baboon”, “Airplane”, “Sailboat”, “House”, and “Peppers” as objects to test the average execution time for watermark embedding and extraction. The test results are given in

Table 8. Comparisons of the embedding time, extraction time, and total time among different algorithms (second).

Algorithms	Embedding Time	Extraction Time	Total Time
Patvardhan et al. [18]	1.4668	0.6477	2.1145
Su et al. [31]	5.0233	2.2093	7.2326
Jia et al. [34]	1.9622	0.4170	2.3792
Proposed	1.1560	0.3880	1.5440

, including embedding time, extraction time, and total time. All values in Table 8 are obtained by averaging the execution time of six objects, and the execution time of each object is obtained by averaging 10 test results.

From Table 8, we can see that the embedding time, extraction time, and total time of the proposed algorithm are all shorter than those of the other three algorithms. The execution time of reference [31] is the longest, and the execution time of reference [18] is similar to that of reference [34]. As for reference [31], its watermark preprocessing and embedding processes prolong the total execution time. In conclusion, the real-time performance of the proposed algorithm is better than the other three algorithms.

5. Conclusions

In this paper, a double color image watermarking algorithm is proposed. The main contributions are as follows. (1) The APDCBT transform is introduced into the color image watermarking algorithm. The better low-frequency energy accumulation characteristics of the APDCBT and the stability of SSVD are combined to ensure the robustness of the algorithm. (2) The Fibonacci transform with larger key space is used to improve the security of the algorithm. (3) The watermarks for embedding are color images, not gray or binary images. Additionally, the color QR code with error correction mechanism is introduced to be a watermark, which can further improve the robustness of the algorithm. The experimental results show that the algorithm can effectively resist common image processing attacks, such as JPEG compression, Gaussian noise, salt and pepper noise, average filter, median filter, Gaussian filter, sharpening, and scaling attacks, while its robustness to rotation attacks is relatively weak. In the future, we will consider how to improve the resistance of the algorithm to high-intensity rotation attacks.