A Novel Lattice-Based CP-ABPRE Scheme for Cloud Sharing
Abstract
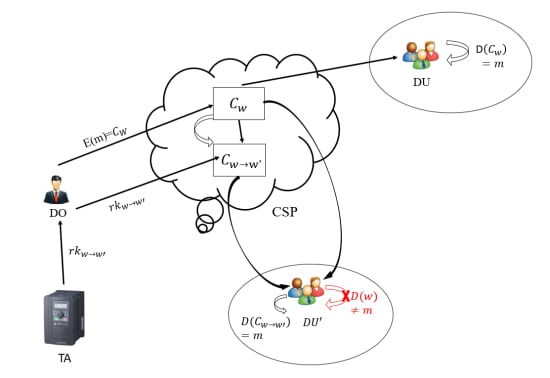
:1. Introduction
1.1. Related Work
1.2. Our Contributions
2. Preliminaries
2.1. Notation
2.2. Gaussian Distributions and the LWE Hardness Assumption
- (1)
- A is statistically close to uniform in ;
- (2)
- T is a basis for ;
- (3)
- and .
2.3. Attribute and Access Structure
2.4. Definition and Security Model of CP-ABPRE Scheme
- 1.
- Setup(): For a set L of attribute and security parameter κ, the TA outputs public parameters and master secret key .
- 2.
- KeyGen(): For and an attribute set S of user (DO or DU), the TA outputs secret key for S. Note that each secret key is associated with an attribute set S.
- 3.
- Encrypt(): For , a message μ, and an access structure W over the attribute set L, the DO outputs ciphertext . Note that each ciphertext is associated with an access structure W.
- 4.
- Decrypt(): For and its corresponding secret key , the user (DO or DU) outputs plaintext μ if or a symbol ⊥ indicating either is invalid or .
- 5.
- ReKeyGen(): For , two access structures and an attribute set S, if , and W and are disjoint, the TA outputs the re-encryption key , and otherwise outputs a symbol ⊥.
- 6.
- ReEnc(): For , , , the CSP outputs the re-encrypted ciphertext .
- 1.
- Decrypt(= μ, where and .
- 2.
- Decrypt()= μ, where , , , .
- (1)
- Secret key oracle : The adversary inputs an attribute set S. If , then the challenger returns , and otherwise returns ⊥.
- (2)
- Re-encryption key oracle : The adversary inputs two access structures and S. If , W and are disjoint, and has been accessed for any , then the challenger returns , and otherwise returns ⊥.
- (3)
- Re-encryption oracle : The adversary inputs , , . If , , , then the challenger returns , and otherwise returns ⊥.
3. A CP-ABPRE Scheme
3.1. Concrete Scheme
- Setup(): Given positive integers , and a set of attributes L, the TA samples , computes for , where and returns public parameters and master secret key .
- KeyGen(): Given and an attribute set S of the DU, where , the TA lets , computes , and returns secret key , where , , is the basis for , .
- Encrypt(): Given , a message , and an access structure W, the DO denotes as the positive (negative) attribute set in W, computes, and returns ciphertextwhere , , .
- Decrypt(): After receiving the cipthertext from the CSP, the DU computes by , and then outputs 0 if is closer to 0 than to modulo q, and 1 otherwise.
- ReKeyGen(): After receiving , two access structures from the DO, if are not disjoint or , then the TA outputs ⊥, and otherwise denotes the positive (negative) attribute set in as , noting , then computeswhere , , , and finally returns the re-encryption key .
- ReEnc(): Given , the CSP computeswhere , and outputs the re-encrypted ciphertext
3.2. Correctness and Parameters
- Algorithm TrapGen requires .
- Algorithm SamplePre requires .
- Decrypting the ciphertext requires 2.
- Decrypting the re-encrypted ciphertext requires 2.
- The hardness of LWE requires .
3.3. Security
- –
- If , output .
- –
- If , output .
3.4. Comparison
4. Extension
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Castiglione, A.; De Santis, A.; Masucci, B.; Palmieri, F.; Huang, X.; Castiglione, A. Supporting dynamic updates in storage clouds with the Akl-Taylor scheme. Inf. Sci. 2017, 387, 56–74. [Google Scholar] [CrossRef]
- Crampton, J.; Gagarin, A.; Gutin, G.; Jones, M.; Wahlström, M. On the workflow satisfiability problem with class-independent constraints for hierarchical organizations. ACM Trans. Priv. Secur. 2016, 19, 3. [Google Scholar] [CrossRef]
- Goyal, V.; Pandey, O.; Sahai, A.; Waters, B. Attribute-based encryption for finegrained access control of encrypted data. In Proceedings of the 13th ACM Conference on Computer and Communications Security, Alexandria, VA, USA, 30 October–3 November 2006; pp. 89–98. [Google Scholar]
- Xhafa, F.; Li, J.; Zhao, G.; Li, J.; Chen, X.; Wong, D.S. Designing cloud-based electronic health record system with attribute-based encryption. Multimed. Tools Appl. 2015, 74, 3441–3458. [Google Scholar] [CrossRef]
- Wang, D.; Ma, C.; Shi, L.; Wang, Y. On the Security of an Improved Password Authentication Scheme Based on ECC. In Information Computing and Applications, ICICA 2012; Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2012; Volume 7473, pp. 181–188. [Google Scholar]
- He, D.; Wang, D.; Wu, S. Cryptanalysis and improvement of a password-based remote user authentication scheme without smart cards. Inf. Technol. Control. 2013, 42, 105–112. [Google Scholar] [CrossRef]
- Wang, D.; Ma, C.; Zhang, Q.; Zhao, S. Secure password-based remote user authentication scheme against smart card security breach. J. Netw. 2013, 8, 148–155. [Google Scholar] [CrossRef]
- Ma, C.; Li, J.; Ouyang, W. Lattice-Based Identity-Based Homomorphic Conditional Proxy Re-Encryption for Secure Big Data Computing in Cloud Environment. Int. J. Found. Comput. Sci. 2017, 28, 645–660. [Google Scholar] [CrossRef]
- Ma, C.; Li, J.; Ouyang, W. A Homomorphic Proxy Re-encryption from Lattices. In Provable Security. ProvSec 2016; Lecture Notes in Computer Science; Springer: Cham, Switzerland, 2016; Volume 10005, pp. 353–372. [Google Scholar]
- Li, J.; Ma, C.; Zhang, L.; Yuan, Q. Unidirectional FHPRE Scheme from Lattice for Cloud Computing. Int. J. Netw. Secur. 2019, 21, 592–600. [Google Scholar]
- Singh, K.; Rangan, C.P.; Banerjee, A.K. Lattice Based Identity Based Proxy Re-Encryption Scheme. J. Internet Serv. Inf. Secur. 2013, 3, 38–51. [Google Scholar]
- Yang, Y.; Zheng, X.; Chang, V.; Tang, C. Semantic keyword searchable proxy re-encryption for postquantum secure cloud storage. Concurr. Comput. Pract. Exp. 2017, 29, e4211. [Google Scholar] [CrossRef]
- Liang, X.; Cao, Z.; Lin, H.; Shao, J. Attribute based proxy re-encryption with delegating capabilities. In Proceedings of the 4th International Symposium on Information, Computer, and Communications Security, Sydney, Australia, 10–12 March 2009; pp. 276–286. [Google Scholar]
- Luo, S.; Hu, J.; Chen, Z. Ciphertext Policy Attribute-Based Proxy Re-encryption. In Information and Communications Security, ICICS 2010; Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2010; Volume 6476, pp. 401–415. [Google Scholar]
- Liang, K.; Man, H.; Liu, J.; Susilo, W.; Wong, D.S.; Yang, G.; Yu, Y.; Yang, A. A secure and efficient Ciphertext-Policy Attribute-Based Proxy Re-Encryption for cloud data sharing. Future Gener. Comput. Syst. 2015, 52, 95–108. [Google Scholar] [CrossRef]
- Zhang, J.; Zhang, Z.; Ge, A. Ciphertext policy attribute-based encryption from lattices. In Proceedings of the 7th ACM Symposium on Information, Computer and Communications Security, Seoul, Korea, 2–4 May 2012; pp. 16–17. [Google Scholar]
- Zeng, F.; Xu, C. A novel model for lattice-based authorized searchable encryption with special keyword. Math. Probl. Eng. 2015, 314621. [Google Scholar] [CrossRef]
- Boneh, D.; Di Crescenzo, G.; Ostrovsky, R.; Persiano, G. Public key encryption with keyword search. In Proceedings of the International Conference on the Theory and Applications of Cryptographic Techniques, Interlaken, Switzerland, 2–6 May 2004; pp. 506–522. [Google Scholar]
- Shao, J.; Cao, Z.; Liang, X.; Lin, H. Proxy re-encryption with keyword search. Inf. Sci. 2010, 180, 2576–2587. [Google Scholar] [CrossRef]
- Wang, X.; Huang, X.; Yang, X.; Liu, L.; Wu, X. Further observation on proxy re-encryption with keyword search. J. Syst. Softw. 2012, 85, 643–654. [Google Scholar] [CrossRef]
- Shi, Y.; Liu, J.; Han, Z.; Zheng, Q.; Zhang, R.; Qiu, S. Attribute-Based Proxy Re-Encryption with Keyword Search. PLoS ONE 2015, 9, e116325. [Google Scholar] [CrossRef] [PubMed]
- Hong, H.; Sun, Z. Towards secure data sharing in cloud computing using attribute based proxy re-encryption with keyword search. In Proceedings of the 2017 IEEE 2nd International Conference on Cloud Computing and Big Data Analysis, ICCCBDA2017, Chengdu, China, 28–30 April 2017; pp. 218–223. [Google Scholar]
- Alwen, J.; Peikert, C. Generating shorter bases for hard random lattices. Theory Comput. Syst. 2011, 48, 535–553. [Google Scholar] [CrossRef]
- Agrawal, S.; Boneh, D.; Boyen, X. Efficient Lattice (H)IBE in the Standard Model. In Advances in Cryptology-EUROCRYPT 2010, EUROCRYPT 2010; Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2010; Volume 6110, pp. 553–572. [Google Scholar]
- Micciancio, D.; Peikert, C. Trapdoors for Lattices: Simpler, Tighter, Faster, Smaller. In Advances in Cryptology-EUROCRYPT 2012, EUROCRYPT 2012; Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2012; Volume 7237, pp. 700–718. [Google Scholar]
- Regev, O. On lattices, learning with errors, random linear codes, and cryptography. J. ACM 2005, 56, 34. [Google Scholar]
- Liang, K.; Fang, L.; Susilo, W.; Wong, D.S. A ciphertext-policy attribute-based proxy re-encryption with chosen-ciphertext security. In Proceedings of the 5th International Conference on Intelligent Networking and Collaborative Systems, INCoS2013, Xi’an, China, 9–11 September 2013; pp. 55–559. [Google Scholar]
- Zhang, J.; Zhang, Z. A Ciphertext Policy Attribute-Based Encryption Scheme without Pairings. In Information Security and Cryptology. Inscrypt 2011; Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2011; Volume 7537, pp. 324–340. [Google Scholar]
- Zeng, P.; Choo, K. A New Kind of Conditional Proxy Re-Encryption for Secure Cloud Storage. IEEE Access 2018, 6, 70017–70024. [Google Scholar] [CrossRef]
- Xagawa, K. Cryptography with Lattices. Ph.D. Thesis, Department of Mathematical and Computing Sciences, Tokyo Institute of Technology, Tokyo, Japan, 2010. [Google Scholar]
- Jiang, M.; Hu, Y.; Wang, B.; Wang, F.H.; Lai, Q.Q. Lattice-based multi-use unidirectional proxy re-encryption. Secur. Commun. Netw. 2016, 8, 3796–3803. [Google Scholar] [CrossRef]
- Hou, J.; Jiang, M.; Guo, Y.; Song, W. Identity-Based Multi-bit Proxy Re-encryption Over Lattice in the Standard Model. In Frontiers in Cyber Security, FCS 2018, Communications in Computer and Information Science; Springer: Singapore, 2018; Volume 879, pp. 110–118. [Google Scholar]


| x | scalar |
| vector | |
| A | matrix or set |
| norm of | |
| norm of | |
| set | |
| the order of set L | |
| attribute set S satisfies (or does not satisfy) access structure W | |
| the concatenation of the columns of | |
| the concatenation of the rows of | |
| x is sampled according to a probability distribution | |
| x is sampled uniformly from a set S | |
| X and Y are computationally (statistically) indistinguishable |
| Cryptosystem | The Size of pp | Sizeof sk | Sizeof Ciphertext | Support and-Gateson Positive and Negative Attributes | LWE Assumption |
|---|---|---|---|---|---|
| [28] | YES | YES | |||
| [17] | 1+ | YES | YES | ||
| Our scheme | 1+ | YES | YES |
| Cryptosystem | Interactivity | Directionality | Security | LWE Assumption | Access Control |
|---|---|---|---|---|---|
| [8] | NO | Unidirectional | CPA | YES | NO |
| [9] | NO | Unidirectional | CPA | YES | NO |
| [10] | NO | Unidirectional | CPA | YES | NO |
| [30] | YES | Bidirectional | CPA | YES | NO |
| [31] | NO | Unidirectional | CPA | YES | NO |
| [32] | NO | Unidirectional | CPA | YES | NO |
| Our scheme | NO | Unidirectional | CPA | YES | YES |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, J.; Ma, C.; Zhang, K. A Novel Lattice-Based CP-ABPRE Scheme for Cloud Sharing. Symmetry 2019, 11, 1262. https://doi.org/10.3390/sym11101262
Li J, Ma C, Zhang K. A Novel Lattice-Based CP-ABPRE Scheme for Cloud Sharing. Symmetry. 2019; 11(10):1262. https://doi.org/10.3390/sym11101262
Chicago/Turabian StyleLi, Juyan, Chunguang Ma, and Kejia Zhang. 2019. "A Novel Lattice-Based CP-ABPRE Scheme for Cloud Sharing" Symmetry 11, no. 10: 1262. https://doi.org/10.3390/sym11101262
APA StyleLi, J., Ma, C., & Zhang, K. (2019). A Novel Lattice-Based CP-ABPRE Scheme for Cloud Sharing. Symmetry, 11(10), 1262. https://doi.org/10.3390/sym11101262