Diffusion Correntropy Subband Adaptive Filtering (SAF) Algorithm over Distributed Smart Dust Networks
Abstract
:1. Introduction
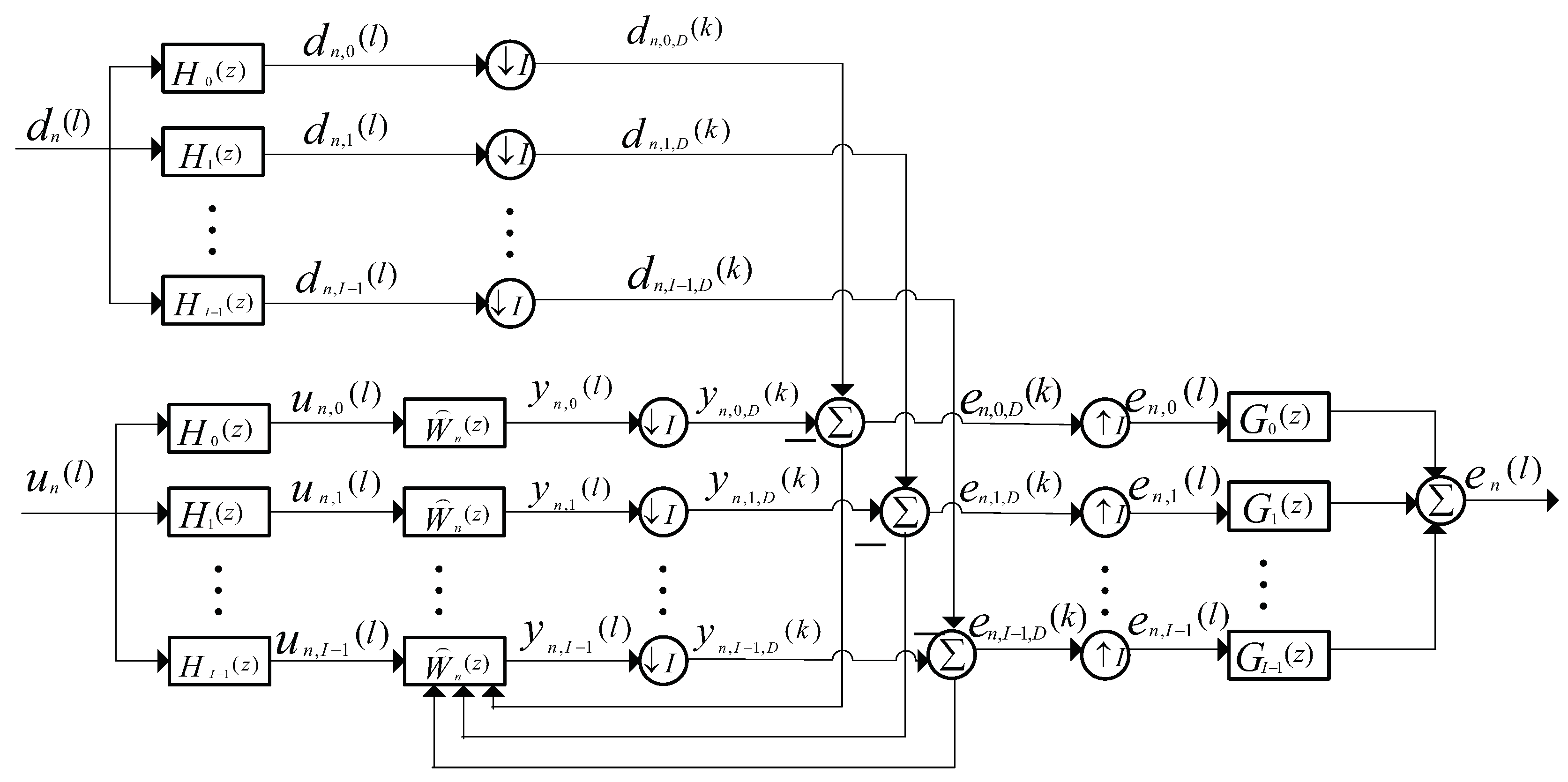
2. The Proposed Algorithms
2.1. Review of the DSAF Algorithm
2.2. The Proposed MCC-DSAF Algorithm
2.3. The Proposed MCC-IPDSAF Algorithm
3. Performance Analysis
3.1. Data Model and Assumption
3.2. Convergence Analysis
3.3. Steady-State Performance
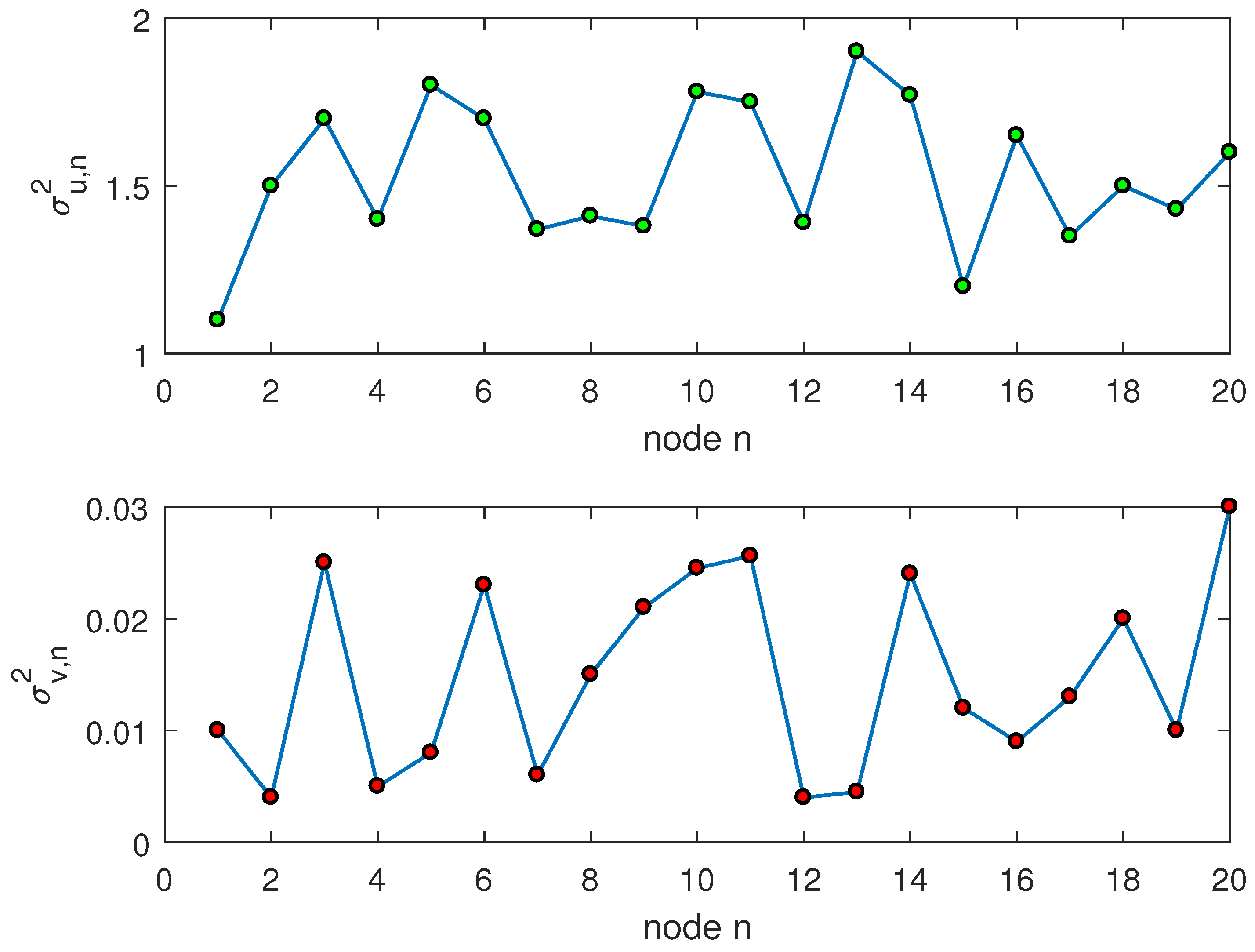
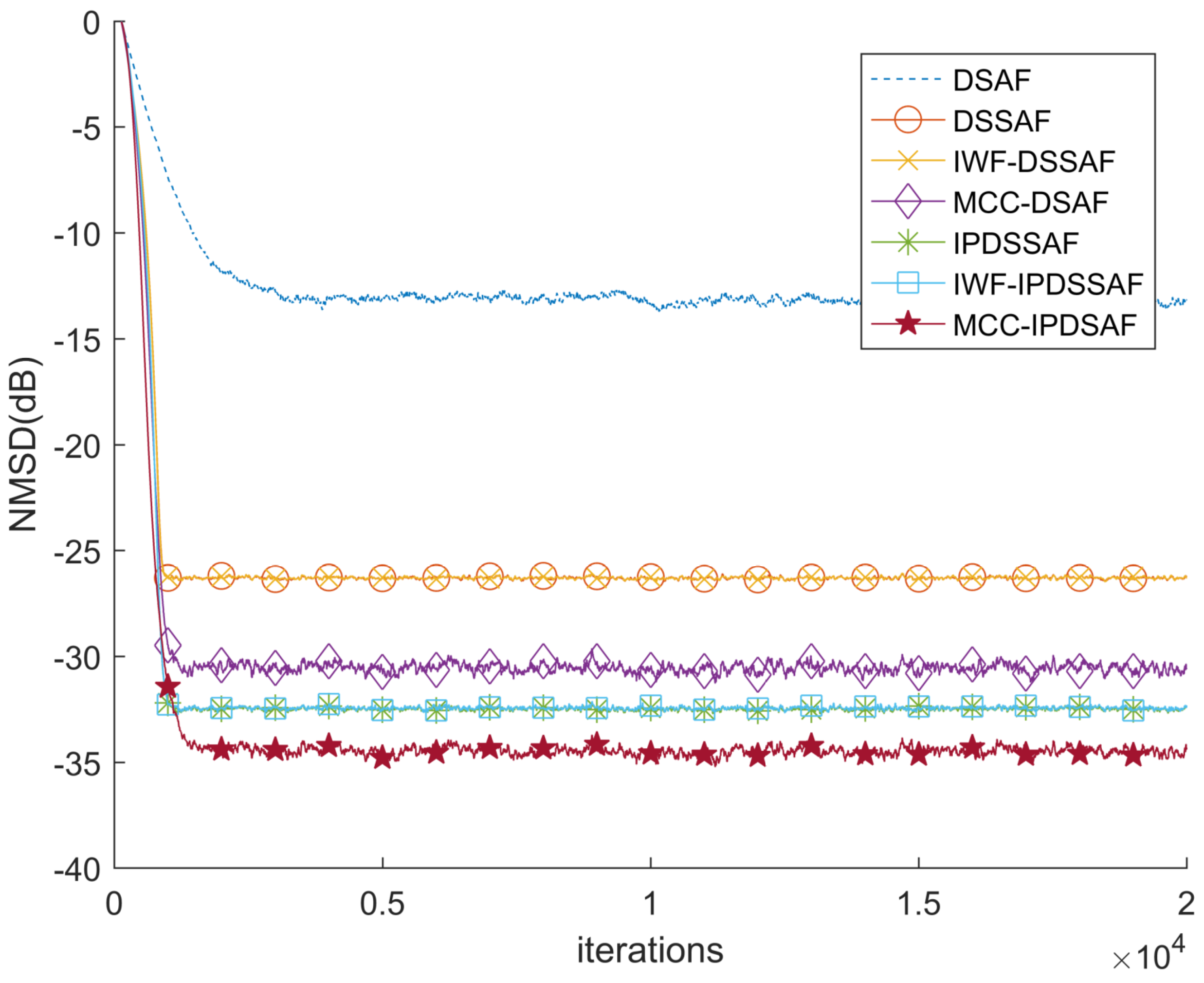
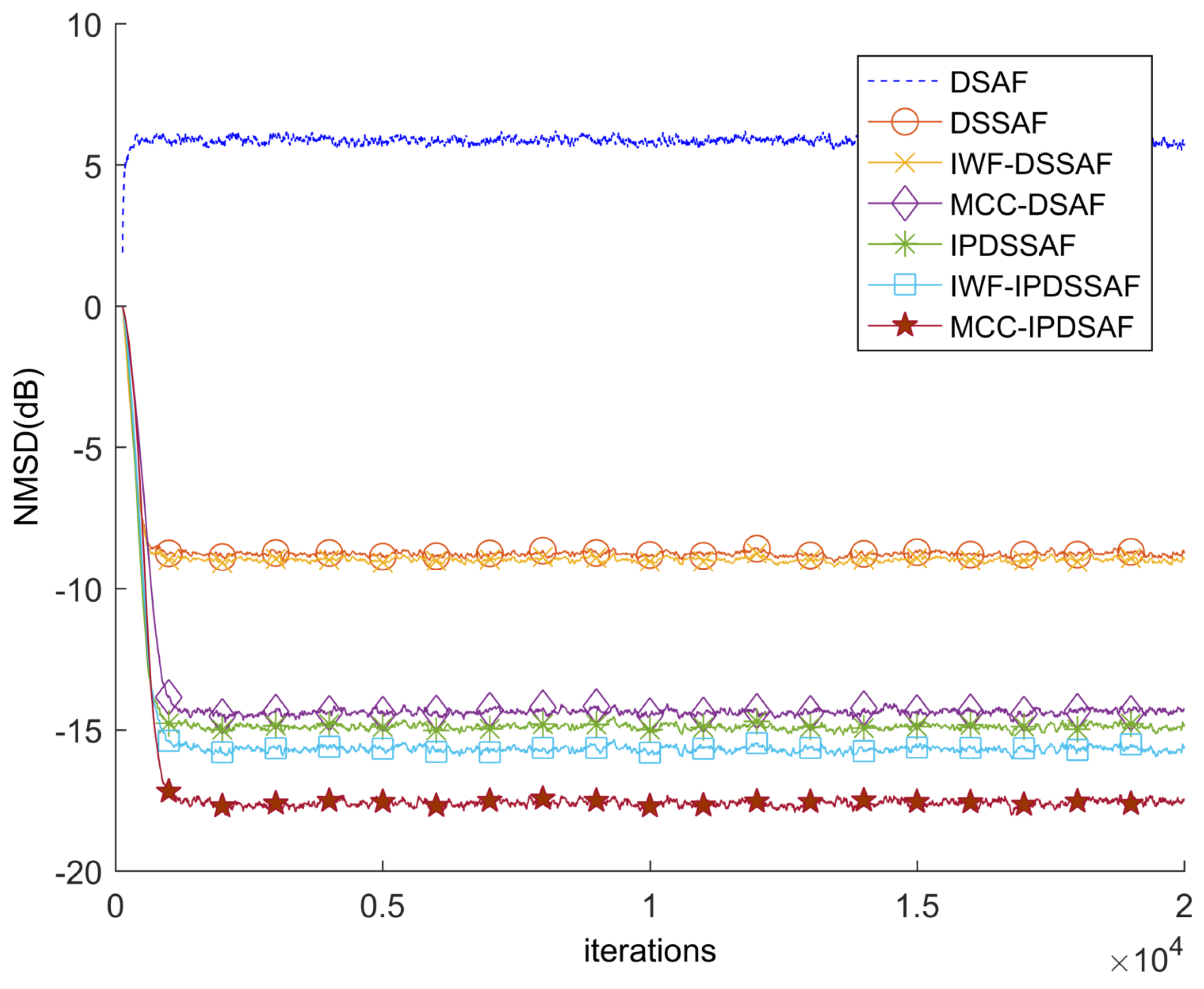
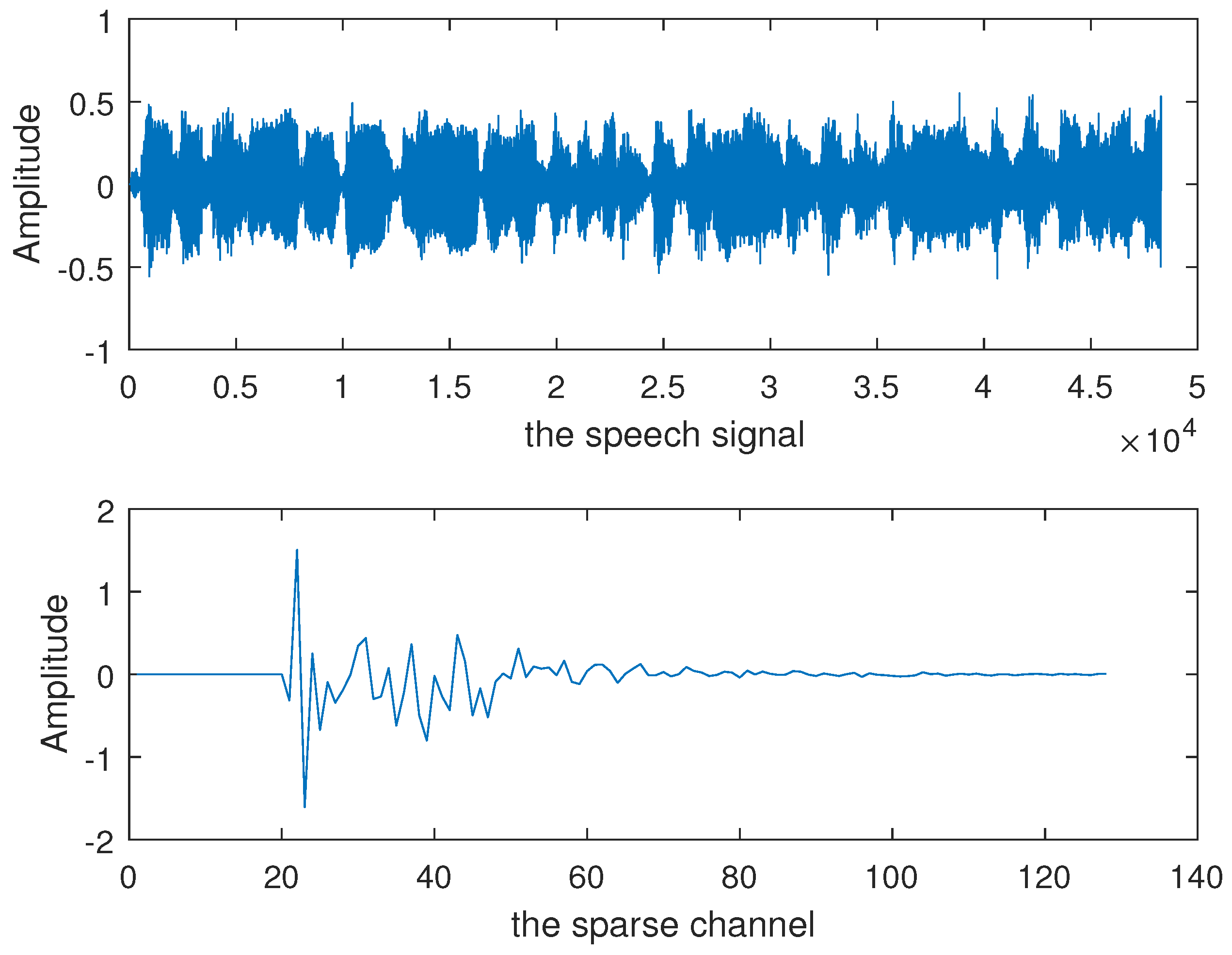
4. Simulation
System Identification
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Sayed, A.H. Adaptive, networks. Procs. IEEE 2014, 102, 460–497. [Google Scholar] [CrossRef]
- Rossi, L.A.; Krishnamachai, B.; Kuo, C.C.J. Distributed parameter estimation for monitoring diffusion phenomena using physical models. In Proceedings of the 2004 First Annual IEEE Communications Society Conference on Sensor and Ad Hoc Communications and Networks, Santa Clara, CA, USA, 4–7 October 2004. [Google Scholar]
- Li, J.; AlRegib, G. Rate-constrained distributed estimation in wireless sensor network. IEEE Trans. Signal Process. 2007, 55, 1624–1643. [Google Scholar] [CrossRef]
- Culler, D.; Estrin, D.; Srivastava, M. Overview of sensor networks. Computer 2004, 37, 41–49. [Google Scholar] [CrossRef]
- Tu, S.Y.; Sayed, A.H. Mobile adaptive networks. IEEE J. Sel. Top. Signal Process. 2011, 5, 649–664. [Google Scholar]
- Sayed, A.H. Adaptive, learning, and optimization over networks. Found. Trends Mach. Learn. 2014, 7, 311–801. [Google Scholar] [CrossRef]
- Chen, F.; Shi, T.; Duan, S.; Wang, L.; Wu, J. Diffusion Least Logarithmic Absolute Difference Algorithm for Distributed estimation. Signal Process. 2018, 142, 423–430. [Google Scholar] [CrossRef]
- Li, L.; He, J.; Zhang, Y. Affine projection algorithms over distributed wireless networks. J. Commun. Univ. China (Sci. Technol.) 2012, 19, 34–43. [Google Scholar]
- Lopes, C.G.; Sayed, A.H. Diffusion least-mean squares over adaptive networks: formulation and performance analysis. IEEE Trans. Signal Process. 2008, 56, 3122–3136. [Google Scholar] [CrossRef]
- Jin-gen, N.I.; Lan-shen, M.A. Distributed subband adaptive filtering algorithms. Chin. J. Electron. 2015, 43, 2222–2231. [Google Scholar]
- Seo, J.H.; Jung, S.M.; Park, P.G. A diffusion subband adaptive filtering algorithm for distributed estimation using variable step size and new combination method based on the MSD. Digit. Signal Process. 2016, 48, 361–369. [Google Scholar] [CrossRef]
- Abadi, M.S.E.; Ahmadi, M.J. Diffusion Improved Multiband-Structured Subband Adaptive Filter Algorithm with Dynamic Selection of Nodes Over Distributed Networks. IEEE Trans. Circuits Syst. 2019, 66, 507–511. [Google Scholar] [CrossRef]
- Abadi, M.S.E.; Shafiee, M.S. A family of diffusion normalized subband adaptive filter algorithms over distributed networks. Int. J. Commun. Syst. 2017, 30, 1–15. [Google Scholar]
- Abadi, M.S.E.; Shafiee, M.S. Diffusion Normalized Subband Adaptive Algorithmfor Distributed Estimation Employing Signed Regressor of Input Signal. Digit. Signal Process. 2017, 70, 73–83. [Google Scholar] [CrossRef]
- Wen, P.; Zhang, J. Widely-Linear Complex-Valued Diffusion Subband Adaptive Filter Algorithm. IEEE Trans. Signal Inf. Process. Netw. 2018, 47, 90–95. [Google Scholar] [CrossRef]
- Mathews, V.J.; Cho, S.H. Improved convergence analysis of stochastic gradient adaptive filters using the sign algorithm. IEEE Trans. Acoust. Speech Signal Process. 1987, 35, 450–454. [Google Scholar] [CrossRef]
- Ni, J. Diffusion sign subband adaptive filtering algorithm for distributed estimation. IEEE Signal Process. Lett. 2015, 11, 2029–2033. [Google Scholar] [CrossRef]
- Shi, J.; Ni, J. Diffusion sign subband adaptive filtering algorithm with enlarged cooperation and its variant. Circuits Syst. Signal Process. 2016, 36, 1714–1724. [Google Scholar] [CrossRef]
- Wang, W.Y.; Zhao, H.Q.; Liu, Q.Q. Diffusion Sign Subband Adaptive Filtering Algorithm with Individual Weighting Factors for Distributed Estimation. Circuits Syst. Signal Process. 2017, 36, 2605–2621. [Google Scholar] [CrossRef]
- Chen, B.; Principe, J.C. Maximum correntropy estimation is a smoothed MAP estimation. IEEE Signal Process. Lett. 2012, 19, 491–494. [Google Scholar] [CrossRef]
- Ma, W.; Chen, B.; Duan, J.; Zhao, H. Diffusion maximum correntropy criterion algorithms for robust distributed estimation. Digit. Signal Process. 2016, 58, 10–19. [Google Scholar] [CrossRef] [Green Version]
- Li, C.; Shen, P.; Liu, Y. Diffusion information theoretic learning for distributed estimation over network. IEEE Trans. Signal Process. 2013, 61, 4011–4024. [Google Scholar] [CrossRef]
- Singh, A.; Principe, J.C. Using correntropy as a cost function in linear adaptive filters. In Proceedings of the International Joint Conference, Neural Networks (IJCNN), Atlanta, GA, USA, 14–19 June 2009; pp. 2950–2955. [Google Scholar]
- Li, Y.; Jiang, Z.; Shi, W.; Han, X.; Chen, B. Blocked maximum correntropy criterion algorithm for cluster-sparse system identifi-cations. IEEE Trans. Circuits Syst. II Exp. Briefs 2019. [Google Scholar] [CrossRef]
- Shi, W.; Li, Y.; Wang, Y. Noise-free maximum correntropy criterion algorithm in non-Gaussian environment. IEEE Trans. Circuits Syst. II Exp. Briefs 2019. [Google Scholar] [CrossRef]
- Haykin, S.; Widrom, B. Least-Mean-Square Adaptive Filters; Wiley: Hoboken, NJ, USA, 2005. [Google Scholar]
- Li, Y.; Wang, Y.; Jiang, T. Sparse least mean mixed-norm adaptive filtering algorithms for sparse channel estimation applications. Int. J. Commun. Syst. 2017, 30, e3181. [Google Scholar] [CrossRef]
- Li, Y.; Wang, Y.; Jiang, T. Norm-adaption penalized least mean square/fourth algorithm for sparse channel estimation. Signal Process. 2016, 128, 243–251. [Google Scholar] [CrossRef]
- Li, Y.; Jiang, Z.; Osman, O.; Han, X.; Yin, J. Mixed norm constrained sparse APA algorithm for satellite and network echo channel estimation. IEEE Access 2018, 6, 65901–65908. [Google Scholar] [CrossRef]
- Shi, W.; Li, Y.; Zhao, L.; Liu, X. Controllable sparse antenna array for adaptive beamforming. IEEE Access 2019, 7, 6412–6423. [Google Scholar] [CrossRef]
- Zhang, X.; Jiang, T.; Li, Y.; Zakharov, Y. A novel block sparse reconstruction method for DOA estimation with unknown mutual coupling. IEEE Commun. Lett. 2019, 23, 1845–1848. [Google Scholar] [CrossRef]
- Jin, Z.; Li, Y.; Wang, Y. An enhanced set-membership PNLMS algorithm with a correntropy induced metric constraint for acoustic channel estimation. Entropy 2017, 19, 281. [Google Scholar] [CrossRef]
- Guo, Y.; Gao, Y. Comparative Study of Several Sparse Adaptive Filtering Algorithms. Microcomput. Appl. 2014, 33, 1–3. [Google Scholar]
- Shi, L.; Zhao, H.Q. Two Diffusion Proportionate Sign Subband Adaptive Filtering Algorithms. Circuits Syst. Signal Process. 2017, 36, 4244–4259. [Google Scholar] [CrossRef]
- Chen, B.; Xing, L.; Liang, J.; Zheng, N.; Principe, J.C. Steady-statemean-square error analysisfor adaptive filtering under the maximum correntropy criterion. IEEE Signal Process. Lett. 2014, 21, 880–884. [Google Scholar]
- Wu, Q.; Li, Y.; Zakharov, Y.; Xue, W.; Shi, W. A kernel affine projection-like algorithm in reproducing kernel hilbert space. IEEE Trans. Circuits Syst. II Exp. Briefs 2019. [Google Scholar] [CrossRef]
- Ma, W.T.; Duan, J.D.; Man, W.S.; Liang, J.L.; Chen, B.D. General Mixed Norm Based Diffusion Adaptive Filtering Algorithm for Distributed Estimation over Network. IEEE Access 2017, 5, 1090–1102. [Google Scholar] [CrossRef]
- Saeed, M.O.B.; Zerguine, A.; Zummo, S.A. A variable step-size strategy for distributed estimation over adaptive networks. EURASIP J. Adv. Signal Process. 2013, 2013, 135. [Google Scholar] [CrossRef]
- Xu, X.G.; Qu, H.; Zhao, J.H.; Yan, F.Y.; Wang, W.H. Diffusion Maximum Correntropy Criterion Based Robust Spectrum Sensing in Non-Gaussian Noise Environments. Entropy 2018, 20, 246. [Google Scholar] [CrossRef]
- Tracy, D.S.; Singh, R.P. A new matrix product and its applications in partitioned matrix differentiation. Stat. Neerl. 1972, 26, 143–157. [Google Scholar] [CrossRef]
- Cattivelli, F.; Sayed, A.H. Diffusion LMS Strategies for Distributed Estimation. IEEE Trans. Signal Process. 2010, 58, 1035–1048. [Google Scholar] [CrossRef]
- Guo, Y.; Bai, Y. Robust Affine Projection Sign Adaptive Filtering Algorithm. J. Instrum. Instrum. 2017, 38, 23–32. [Google Scholar]
- Li, Y.; Wang, Y.; Jiang, T. Sparse-aware set-membership NLMS algorithms and their application for sparse channel estimation and echo cancelation. AEU Int. J. Electron. Commun. 2016, 70, 895–902. [Google Scholar] [CrossRef]
- Ni, J.; Chen, J.; Chen, X. Diffusion sign-error LMS algorithm: Formulation and stochastic behavior analysis. Signal Process. 2016, 128, 142–149. [Google Scholar] [CrossRef]
- Ni, J.; Ma, L. Distributed affine projection algorithms against impulsive interferences. Tien Tzu Hsueh Pao/Acta Electron. Sin. 2016, 44, 1555–1560. [Google Scholar]








© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guo, Y.; Li, J.; Li, Y. Diffusion Correntropy Subband Adaptive Filtering (SAF) Algorithm over Distributed Smart Dust Networks. Symmetry 2019, 11, 1335. https://doi.org/10.3390/sym11111335
Guo Y, Li J, Li Y. Diffusion Correntropy Subband Adaptive Filtering (SAF) Algorithm over Distributed Smart Dust Networks. Symmetry. 2019; 11(11):1335. https://doi.org/10.3390/sym11111335
Chicago/Turabian StyleGuo, Ying, Jingjing Li, and Yingsong Li. 2019. "Diffusion Correntropy Subband Adaptive Filtering (SAF) Algorithm over Distributed Smart Dust Networks" Symmetry 11, no. 11: 1335. https://doi.org/10.3390/sym11111335
APA StyleGuo, Y., Li, J., & Li, Y. (2019). Diffusion Correntropy Subband Adaptive Filtering (SAF) Algorithm over Distributed Smart Dust Networks. Symmetry, 11(11), 1335. https://doi.org/10.3390/sym11111335




