Analytical Solution of Heat Conduction in a Symmetrical Cylinder Using the Solution Structure Theorem and Superposition Technique
Abstract
:1. Introduction
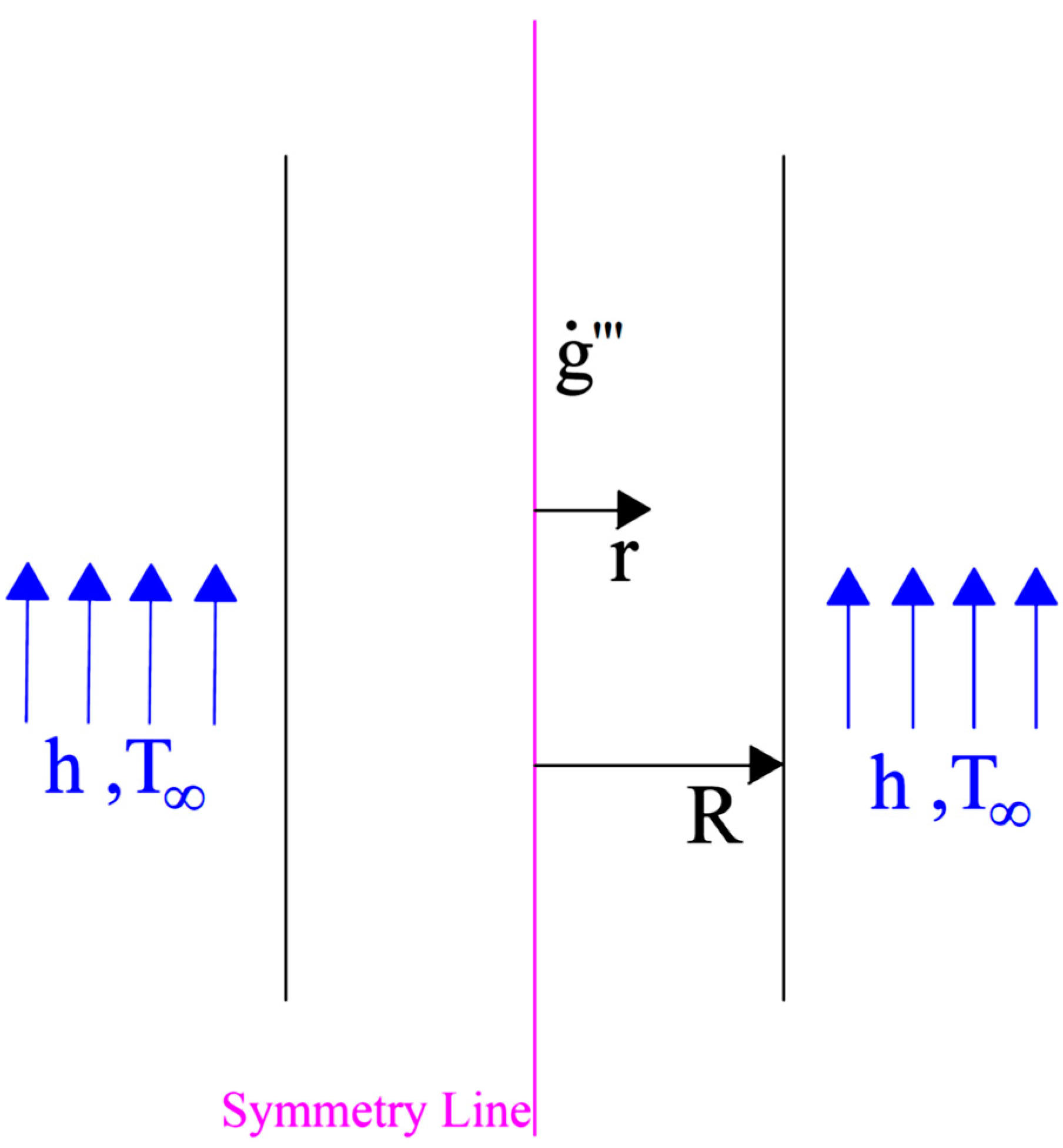
2. Formulation
2.1. Hyperbolic Heat Conduction
2.2. Solution Structure Theorems and Superposition Approach
2.3. Formulation of the Problem
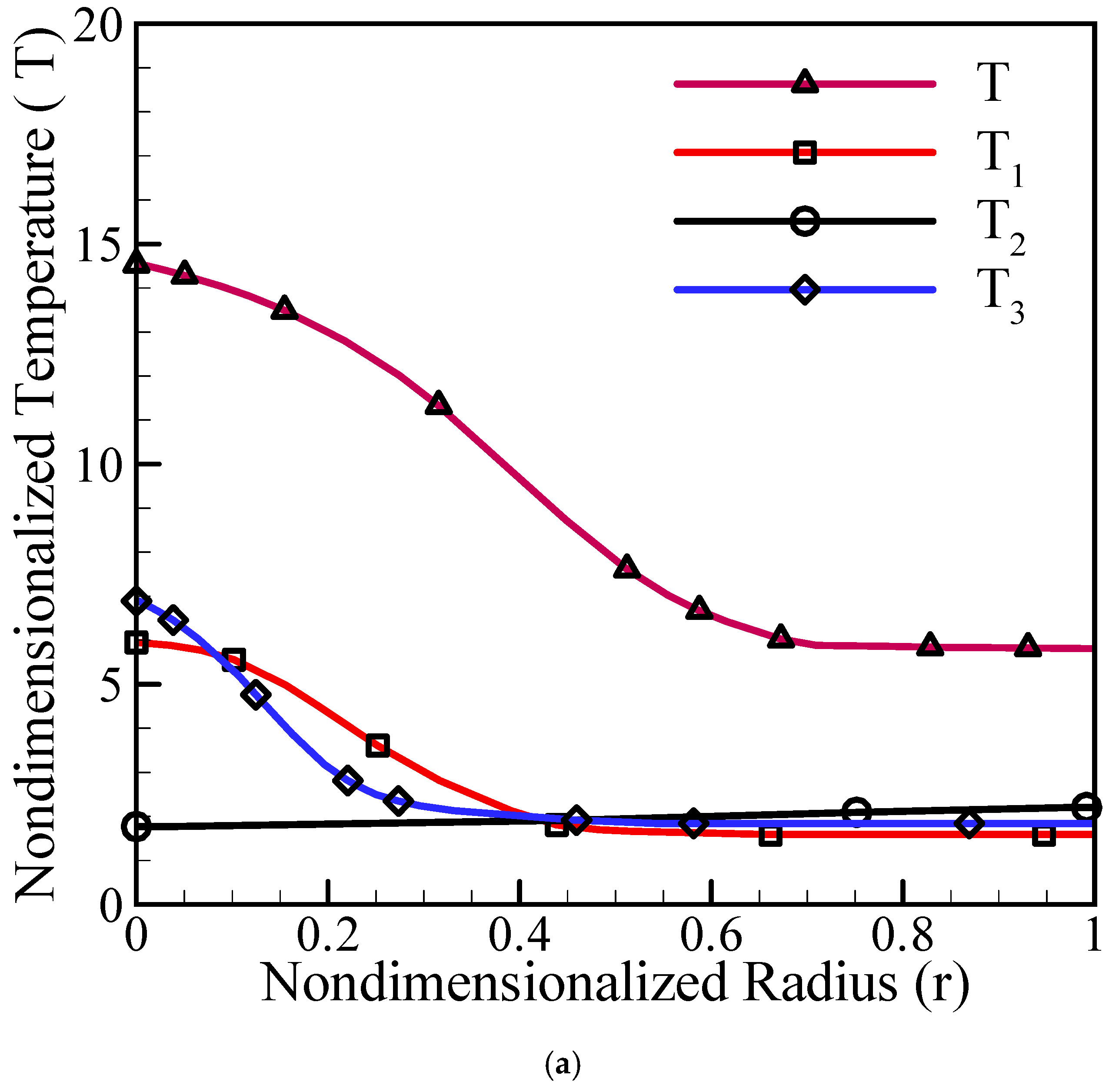
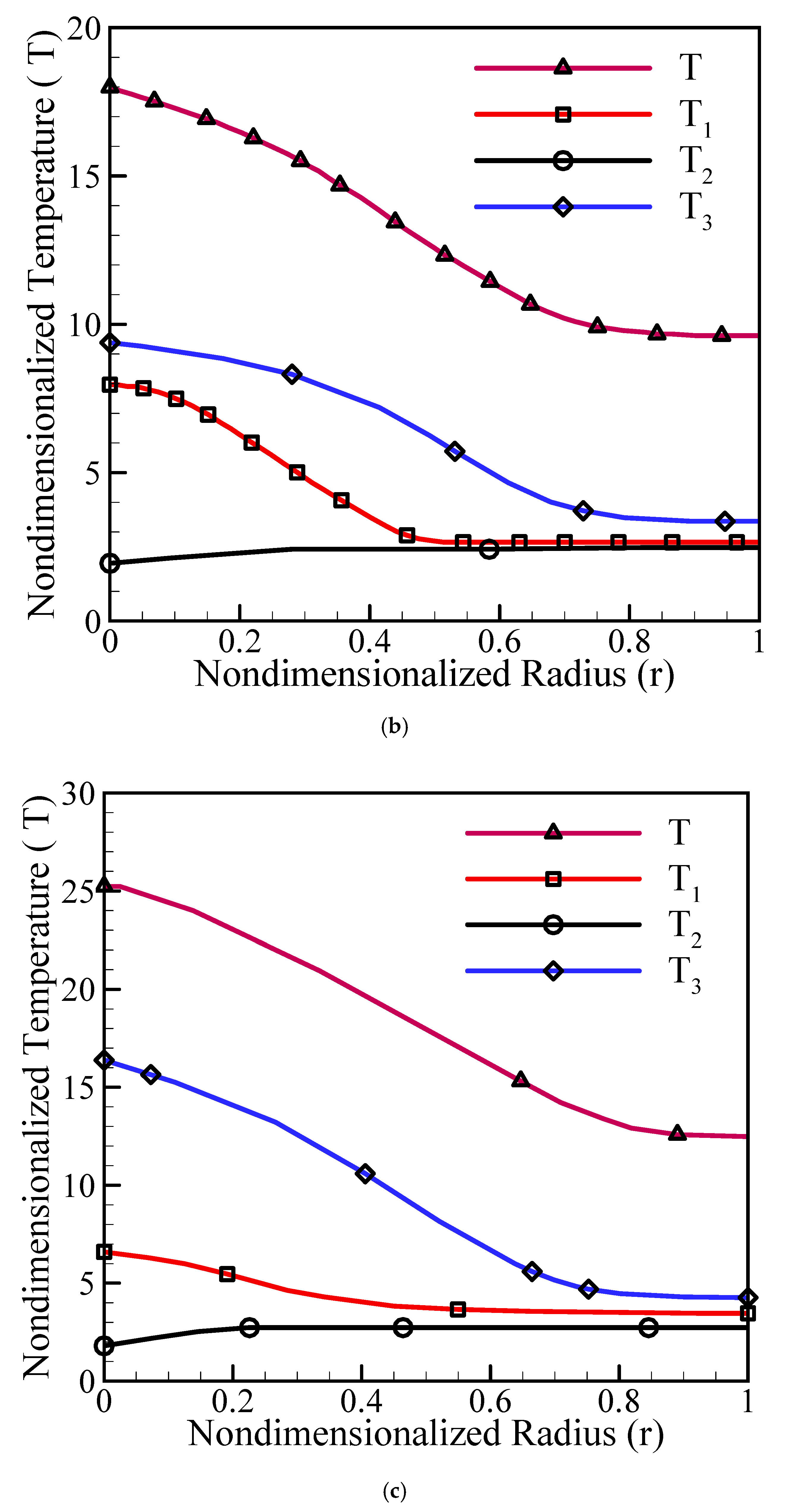
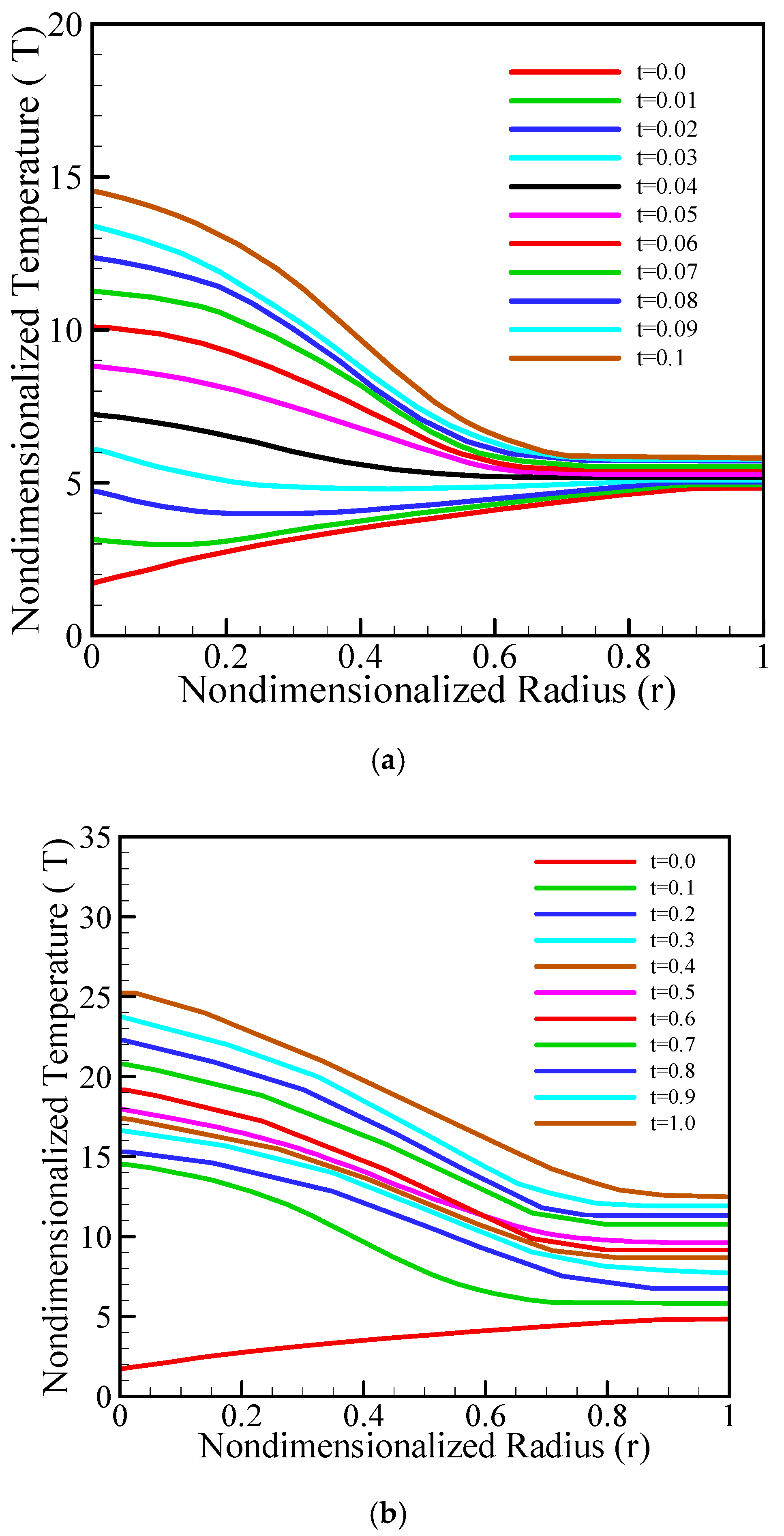
3. Results and Discussions
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| Nomenclature | |
| Thermal Wave Propagation Speed, m/s | |
| Specific Heat, J/kg K | |
| Total Internal Heat Generation in System | |
| Reference Laser Power Density, | |
| Dimensionless Internal Heat Generation | |
| Transmitted Energy Strength | |
| Internal Heat Generation, | |
| Laser peak Power Density, | |
| Thermal Conductivity, | |
| Convection Heat Transfer Coefficient, | |
| Dimensionless Convection Heat Transfer Coefficient | |
| Heat Flux, c | |
| Dimensionless Heat Flux, | |
| Dimensionless Source Term | |
| Surface Reflectivity of the Solid | |
| Dimensionless Time, | |
| Time, s | |
| Dimensionless Temperature, | |
| Dimensionless Ambient Temperature, | |
| Temperature, K | |
| Ambient Temperature, K | |
| r-coordinate, m | |
| Dimensionless Space Coordinate, | |
| Greek symbols | |
| Thermal Diffusivity , | |
| Eigen Value, | |
| Relative Error | |
| Dimensionless Absorption Coefficient, | |
| Density () | |
| Relaxation Time , s | |
| Dimensionless Initial Condition Function | |
| Dimensionless Initial rate of Temperature Change Function | |
| Dummy Index | |
References
- Dabby, F.W.; Paek, U.-C. High-intensity laser-induced vaporization and explosion of solid material. IEEE J. Quantum Electron. 1972, 8, 106–111. [Google Scholar] [CrossRef]
- Yeung, W.K.; Lam, T.T. Thermal analysis of anisotropic thin-film superconductors. Adv. Electron. Packag. 1999, 26, 1261–1268. [Google Scholar]
- Lundell, J.H.; Dickey, R.R. Vaporization of graphite in the temperature range of 4000 to 4500 K. In Proceedings of the NASA Ames Research Center, Moffett Field, CA, USA, 26–28 January 1976; pp. 76–166. [Google Scholar]
- Robin, J.E.; Nordin, P. Enhancement of CW laser melt-through of opaque solid materials by supersonic transverse gas flow. Appl. Phys. Lett. 1975, 26, 289–292. [Google Scholar] [CrossRef]
- Chen, J.K.; Tzou, D.Y.; Beraun, J.E. Numerical investigation of ultrashort laser damage in semiconductors. Int. J. Heat Mass Transf. 2005, 48, 501–509. [Google Scholar] [CrossRef]
- Cattaneo, C. Sur une former de l’equation de la chaleur elinant le paradoxe d’une propagation instance. Comptes Rendus Acad. Sci. 1958, 247, 431–432. [Google Scholar]
- Vernotte, P. Les paradoxes de la theories continue de l’equation de la chaleur. Comptes Rendus Acad. Sci. 1958, 246, 3154–4155. [Google Scholar]
- Wang, B.L.; Han, J.C.; Sun, Y.G. A finite element/finite difference scheme for the non-classical heat conduction and associated thermal stresses. Finite Elem. Anal. Des. 2012, 50, 201–206. [Google Scholar] [CrossRef]
- Lee, H.L.; Chen, W.L.; Chang, W.J.; Wei, E.J.; Yang, Y.C. Analysis of dual-phase-lag heat conduction in short-pulse laser heating of metals with a hybrid method. Appl. Therm. Eng. 2013, 52, 275–283. [Google Scholar] [CrossRef]
- Mishra, S.C.; Sahai, H. Analysis of non-Fourier conduction and radiation in a cylindrical medium using lattice Boltzmann method and finite volume method. Int. J. Heat Mass Transf. 2013, 61, 41–55. [Google Scholar] [CrossRef]
- Qui, T.; Juhasz, T.; Suarez, C.; Bron, W.; Tien, C. Femto second laser heating of multi-layer II experiments. Int. J. Heat Mass Transf. 1994, 37, 2799–2808. [Google Scholar]
- Ozisik, M.; Vick, B. Propagation and Reflection of Thermal Waves in a Finite Medium. Int. J. Heat Mass Transf. 1984, 27, 1845–1855. [Google Scholar] [CrossRef]
- Jiang, F. Solution and analysis of hyperbolic heat propagation in hollow spherical objects. Heat Mass Transf. 2006, 42, 1083–1091. [Google Scholar] [CrossRef]
- Moosaie, A. Non Fourier heat conduction in a finite medium with insulated boundaries and arbitrary initial condition. Int. Commun. Heat Mass Transf. 2008, 35, 103–111. [Google Scholar] [CrossRef]
- Moosaie, A. Non Fourier heat conduction in a finite medium subjected to arbitrary non-periodic surface disturbance. Int. Commun. Heat Mass Transf. 2008, 35, 376–383. [Google Scholar] [CrossRef]
- Ahmadikia, H.; Rismanian, M. Analytical solution of non-Fourier heat conduction problem on a fin under periodic boundary conditions. J. Mech. Sci. Technol. 2011, 25, 2919–2926. [Google Scholar] [CrossRef]
- Bamdad, K.; Azimi, A.; Ahmadikia, H. Thermal performance analysis of arbitrary-profile fins with non-fourier heat conduction behavior. J. Eng. Math. 2012, 76, 181–193. [Google Scholar] [CrossRef]
- lam, T.T.; Fong, E. Application of solution structure theorem to non-Fourier heat conduction problems: Analytical Approach. Int. J. Heat Mass Transf. 2011, 54, 1–11. [Google Scholar] [CrossRef]
- Liu, F.; Chen, Q.; Kang, Z.; Pan, W.; Zhang, D.; Wang, L. Non-Fourier heat conduction in oil-in-water emulsions. Int. J. Heat Mass Transf. 2019, 135, 323–330. [Google Scholar] [CrossRef]
- Daneshjou, K.; Bakhtiari, M.; Parsania, H.; Fakoor, M. Non-Fourier heat conduction analysis of infinite 2D orthotropic FG hollow cylinders subjected to time-dependent heat source. Appl. Therm. Eng. 2016, 98, 582–590. [Google Scholar] [CrossRef]
- Ma, J.; Sun, Y.; Yang, J. Analytical solution of non-Fourier heat conduction in a square plate subjected to a moving laser pulse. Int. J. Heat Mass Transf. 2017, 115, 606–610. [Google Scholar] [CrossRef]
- Wankhade, P.A.; Kundu, B.; Das, R. Establishment of non-Fourier heat conduction model for an accurate transient thermal response in wet fins. Int. J. Heat Mass Transf. 2018, 126, 911–923. [Google Scholar] [CrossRef]
- Hana, S.; Peddieson, J. Non-Fourier heat conduction/convection in moving medium. Int. J. Therm. Sci. 2018, 130, 128–139. [Google Scholar] [CrossRef]
- Liu, Y.; Li, L.; Lou, Q. A hyperbolic lattice Boltzmann method for simulating non-Fourier heat conduction. Int. J. Heat Mass Transf. 2019, 131, 772–780. [Google Scholar] [CrossRef]
- Kalbasi, R.; Afrand, M.; Alsarraf, J.; Tran, M.D. Studies on optimum fins number in PCM-based heat sinks. Energy 2019, 171, 1088–1099. [Google Scholar] [CrossRef]
- Li, Z.; Al-Rashed, A.A.; Rostamzadeh, M.; Kalbasi, R.; Shahsavar, A.; Afrand, M. Heat transfer reduction in buildings by embedding phase change material in multi-layer walls: Effects of repositioning, thermophysical properties and thickness of PCM. Energy Convers. Manag. 2019, 195, 43–56. [Google Scholar] [CrossRef]
- Li, Z.; Shahsavar, A.; Al-Rashed, A.A.; Kalbasi, R.; Afrand, M.; Talebizadehsardari, P. Multi-objective energy and exergy optimization of different configurations of hybrid earth-air heat exchanger and building integrated photovoltaic/thermal system. Energy Convers. Manag. 2019, 195, 1098–1110. [Google Scholar] [CrossRef]
- Nadooshan, A.A.; Kalbasi, R.; Afrand, M. Perforated fins effect on the heat transfer rate from a circular tube by using wind tunnel: An experimental view. Heat Mass Transf. 2018, 54, 3047–3057. [Google Scholar] [CrossRef]
- Salimpour, M.R.; Kalbasi, R.; Lorenzini, G. Constructal multi-scale structure of PCM-based heat sinks. Contin. Mech. Thermodyn. 2017, 29, 477–491. [Google Scholar] [CrossRef]
- Shanazari, E.; Kalbasi, R. Improving performance of an inverted absorber multi-effect solar still by applying exergy analysis. Appl. Therm. Eng. 2018, 143, 1–10. [Google Scholar] [CrossRef]
- Yari, M.; Kalbasi, R.; Talebizadehsardari, P. Energetic-exergetic analysis of an air handling unit to reduce energy consumption by a novel creative idea. Int. J. Numer. Methods Heat Fluid Flow 2019, 29, 3959–3975. [Google Scholar] [CrossRef]

© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kalbasi, R.; Alaeddin, S.M.; Akbari, M.; Afrand, M. Analytical Solution of Heat Conduction in a Symmetrical Cylinder Using the Solution Structure Theorem and Superposition Technique. Symmetry 2019, 11, 1522. https://doi.org/10.3390/sym11121522
Kalbasi R, Alaeddin SM, Akbari M, Afrand M. Analytical Solution of Heat Conduction in a Symmetrical Cylinder Using the Solution Structure Theorem and Superposition Technique. Symmetry. 2019; 11(12):1522. https://doi.org/10.3390/sym11121522
Chicago/Turabian StyleKalbasi, Rasool, Seyed Mohammadhadi Alaeddin, Mohammad Akbari, and Masoud Afrand. 2019. "Analytical Solution of Heat Conduction in a Symmetrical Cylinder Using the Solution Structure Theorem and Superposition Technique" Symmetry 11, no. 12: 1522. https://doi.org/10.3390/sym11121522
APA StyleKalbasi, R., Alaeddin, S. M., Akbari, M., & Afrand, M. (2019). Analytical Solution of Heat Conduction in a Symmetrical Cylinder Using the Solution Structure Theorem and Superposition Technique. Symmetry, 11(12), 1522. https://doi.org/10.3390/sym11121522






