Application of Neutrosophic Logic to Evaluate Correlation between Prostate Cancer Mortality and Dietary Fat Assumption

Abstract

This paper presents an epidemiological study on the dietary fat that causes prostate cancer in an uncertainty environment. To study this relationship under the indeterminate environment, data from 30 countries are selected for the prostate cancer death rate and dietary fat level in the food. The neutrosophic correlation and regression line are fitted on the data. We note from the neutrosophic analysis that the prostate cancer death rate increases as the dietary fat level in the people increases. The neutrosophic regression coefficient also confirms this claim. From this study, we conclude that neutrosophic regression is a more effective model under uncertainty than the regression model under classical statistics. We also found a statistical correlation between dietary fat and prostate cancer risk.

1. Introduction

In modern society, cancer is the most widespread disease in both developed and under-developing countries. The cancer disease, its symptoms and treatment impact the victim patients. Lin et al. [1] pointed out that high anxiety and depression is noted in cancer patients. According to Siegel et al. [2], cancer is the disease that is the leading cause of death in the USA. As mentioned by Rahib et al. [3], in 2030, it is expected the sufficient deaths because of cancer. In men, worldwide, prostate cancer is the second common type of cancer. Prostate cancer increases slowly and is not harmful during the initial stage. The main symptoms of prostate cancer are troubling in urine, blood during urination and pain in the bones. Cao et al. [4] mentioned, “Prostate cancer is the third highest cause of male mortality in the developed world”. Torre et al. [5] pointed out that more than 37,000 prostate cancer cases are recorded every year in the UK. According to Jemal et al. [6], prostate cancer increases with the increase in age. Lin et al. [1] described that prostate cancer is a common urologic malignancy and results in a high death rate. In Taiwan, it is the fifth most common cancer. Arnold et al. [7] studied the effect of smoking and weight on cancer. [8] studied the factors that contribute significantly to the cancer. Cao et al. [4] presented seven new biomarkers for the diagnosis of cancer. Applegate et al. [9] studied the relationship between soy food and prostate cancer. More information on cancer can be seen in Carter et al. [10].

Regression analysis, principle components analysis and partial least square analysis have been widely used for analyzing the data in a variety of fields. The regression analysis study is applied to see the effect of the independent variable (s) on the dependent variable (s). The regression analysis is a powerful statistical method to use for examining the relationship between one or more explanatory variables and dependent variables. This method is widely used for prediction and forecasting purposes. The applications of these methods can be seen in Abdul-Wahab et al. [11], Cervigón et al. [12], Kumar and Chong [13] and Karamacoska et al. [14].

Fuzzy logic is applied when there is uncertainty in the observations or in the parameters. Fuzzy logic has been widely applied in epidemical studies. Saritas et al. [15] introduced the fuzzy system to analyze prostate cancer. Benecchi [16] used the fuzzy logic and artificial neural network to develop a system to predict prostate cancer. Saritas et al. [17] described the fuzzy approach to determine prostate cancer. Yuksel et al. [18] introduced the soft expert system to diagnose this cancer. Fu et al. [19] studied the risk evaluation of prostate cancer. More information of this topic can be read in Cosma et al. [20], Al-Dmour et al [21] and Ludwig et al. [22]. More details about the use of fractal geometry and wavelet analysis in the cancer study can be seen in Rodrigo et al. [23], Rodrigo Capobianco Guido [24], Guariglia [25], Guariglia [26] and Guariglia [27].

According to Smarandache [28], neutrosophic logic is the generalized form of the fuzzy logic. The neutrosophic logic also considered an indeterminacy interval for the analysis. Smarandache [29] introduced neutrosophic statistics, which is the extension of classical statistics and is applied for the analysis under the uncertainty environment. Neutrosophic regression is the extension of classical regression analysis. Neutrosophic regression is applied when some observations in the sample are uncertain. Details of neutrosophic regression can be seen in Smarandache [29]. The applications of the neutrosophic statistics can be seen in Chen et al. [30], Chen et al. [30], Aslam [31] and Aslam [32].

Many studies on prostate cancer in social and biological sciences are available using classical statistics. The existing studies are not helpful when the data is recorded in an indeterminate environment. In this paper, we will study the relationship between prostate cancer and dietary fat level using the neutrosophic interval method. By exploring the literature on prostate cancer and according to the best of our knowledge, there is no study on the relationship between the death rate due to prostate cancer and dietary fat level using neutrosophic statistics. In this paper, we aim to present the analysis for these variables using the data of 30 countries under neutrosophic statistics. We expect that the proposed method will be more adequate and effective in analyzing the relation between the prostate cancer death rate and the dietary fat level than the analysis under classical statistics.

2. Material Methods

In this section, we will give details about the source of data, material and methods under the neutrosophic statistical interval method.

2.1. Data Description

The epidemiological studies showed that the dietary fat level causes an increase in the prostate cancer rate across countries, see [33]. The dietary fat can measure through the fat by each ingredient in our daily food or by calculating the per percentage of calories using glucose machines through blood in our daily food. In the earlier case, it was not possible to keep the record of exact or determined dietary fat level, and in the latter case it is was also not determined. Measuring the diet through these methods is not a determined value and recorded in the interval rage. When the variables are expressed in an interval, the relationship between dietary level and prostate cancer cannot be studied using the classical regression model. Therefore, under an uncertain environment, when the dietary fat level and prostate cancer rate are in the interval range, the neutrosophic statistics can be applied to study the relationship between the dietary fat level and prostate cancer. By following [33], the data on dietary fat level and prostate cancer from the 30 countries under the uncertainty level is reported in

Table 1. Prostate cancer death rate of 30 countries.

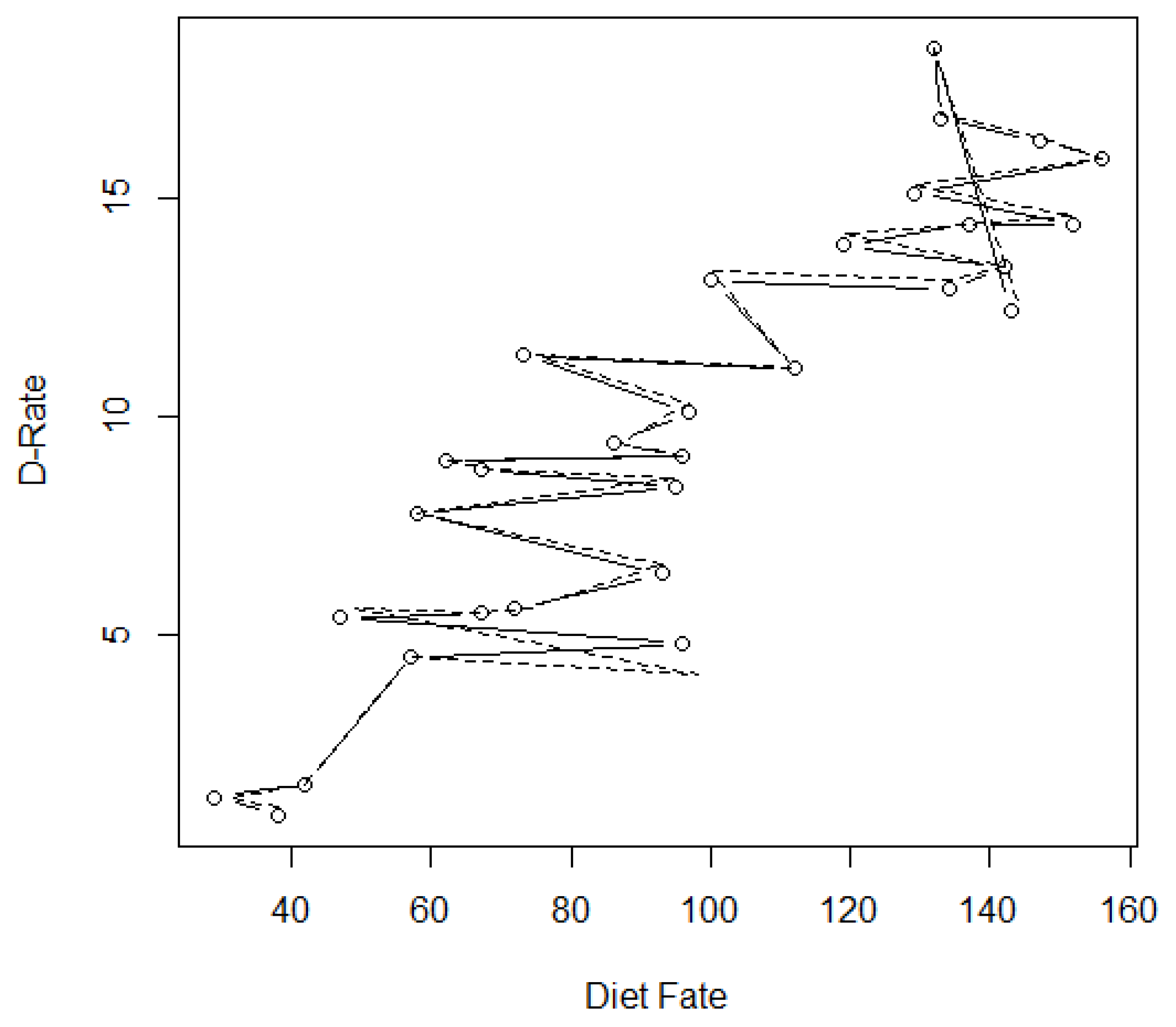
D-Rate	Diet Fat	County No.	D-Rate	Diet Fat	County No.
[10.1,10.3]	[97,97]	16	[0.9,1.1]	[38,38]	1
[11.4,11.4]	[73,75]	17	[1.3,1.3]	[29,31]	2
[11.1,11.1]	[112,112]	18	[1.6,1.6]	[42,42]	3
[13.1,13.3]	[100,100]	19	[4.5,4.5]	[57,57]	4
[12.9,13.1]	[134,134]	20	[4.8,4.10]	[96,98]	5
[13.4,13.4]	[142,142]	21	[5.4,5.6]	[47,49]	6
[13.9,14.2]	[119,119]	22	[5.5,5.5]	[67,67]	7
[14.4,14.4]	[137,137]	23	[5.6,5.6]	[72,74]	8
[14.4,14.6]	[152,152]	24	[6.4,6.6]	[93,93]	9
[15.1,15.3]	[129,129]	25	[7.8,7.8]	[58,58]	10
[15.9,15.9]	[156,156]	26	[8.4,8.6]	[95,95]	11
[16.3,16.4]	[147,147]	27	[8.8,8.8]	[67,69]	12
[16.8,16.9]	[133,133]	28	[9,9]	[62,62]	13
[18.4,18.4]	[132,132]	29	[9.1,9.1]	[96,96]	14
[12.4,12.6]	[143,144]	30	[9.4,9.4]	[86,87]	15

. The variable prostrate death rate is expressed per 100,000 and dietary fat consumption is expressed in gram/day.

2.2. Study Participants

[33] presented data on the prostate cancer death rate and consumption of fat in the 30 countries. The data presented in Table 1 is the extension of the data provided by [33] under the neutrosophic statistics. The data was collected from the 30 countries. The data given in Table 1 becomes the same as in [33] if no indeterminate observations are found in the dietary fat level and prostate cancer.

2.3. Study Outcomes

In this study, the neutrosophic dietary fat level is an explanatory variable and the neutrosophic death rate due to prostate cancer in the 30 countries is a response variable. The aim of this study is to see the effect on the prostate cancer death rate due to an increase in the dietary fat level under the neutrosophic statistical interval method. Therefore, the objective of the study is to measure the prostate cancer death rate. We defined the neutrosophic death due to prostate cancer may cause of increase in fat. The data given in Table 1 is the extension of the data provided by [33] in the neutrosophic interval rage.

2.4. Statistical Methods

We will study the effect of the death rate using the fat level as an explanatory variable. The relationship between the two variables is studied using the neutrosophic regression proposed by [29]. The neutrosophic regression is the extension of the classical regression used to see the relationship between variables when the data is taken from an incomplete, indeterminate or uncertain sample of the population. Let the neutrosophic variable $X_Nϵ\left\{X_L,X_U\right\}$ represent the dietary fat level and neutrosophic variable $Y_{NN}ϵ\left\{Y_L,Y_U\right\}$ denote the death rate due to prostate cancer. By following [29], the neutrosophic regression which expressed the relation between these two variables is given as

$$Y_N=a_N+b_N{X}_N;a_Nϵ\left\{a_L,a_U\right\}, b_Nϵ\left\{b_L,b_U\right\}$$

(1)

where $a_N$ and $b_N$ are the neutrosophic intercept and rate of change per unit, respectively. The neutrosophic regression given in Equation (1) can be written as follows

$$D.rate=a_N+b_{N}Diet Fat; a_Nϵ\left\{a_L,a_U\right\} b_Nϵ\left\{b_L,b_U\right\}$$

(2)

The neutrosophic correlation coefficient $r_Nϵ\left\{r_L,r_U\right\}$ between the two variables is defined as

$$r_N=\frac{n_N{{\displaystyle \sum }}^{}xy-{{\displaystyle \sum }}^{}x{{\displaystyle \sum }}^{}y}{\sqrt{\left\{n_N{{\displaystyle \sum }}^{}{x}^2-{\left({{\displaystyle \sum }}^{}x\right)}^2\right\}\left\{n_N{{\displaystyle \sum }}^{}{y}^2-{\left({{\displaystyle \sum }}^{}y\right)}^2\right\}}}; n_Nϵ\left\{n_L,n_U\right\}$$

(3)

We presented the scatter plot under the neutrosophic statistical interval methods. We presented the neutrosophic regression models to measure the prostate cancer death rate. We presented the fitted model and determined the residual sum of squares for using the neutrosophic regression model. We used a 5% level of significance to test the null hypothesis that the neutrosophic regression coefficient is zero. We also made a comparison between the neutrosophic regressions with a regression under the classical statistics. The data is analyzed using EXCEL and R.

3. Results

We plotted the death rate (D. rate) and dietary fat (Diet Fat) on the scatter diagram in Figure 1. We note from Figure 1 that there is an increasing trend in the D. rate as the fat level increases. Therefore, Figure 1 indicates that a relationship between the death rate due to prostate cancer and the dietary fat level exists. The neutrosophic correlation between two variables is $r_Nϵ\left\{0.8811,0.8851\right\}$. The fitted neutrosophic regression model of two variables is given as

$$Y_N=\left[28.36,29.95\right]+\left[6.757,6.911,\right]X_N$$

(4)

From Equation (3), we note that for a unit of change in dietary fat, the death rate due to prostate cancer increases between 6.75 to 6.911. We also observe from the model given in Equation (3) that when dietary fat is zero, the death rate due to prostate cancer can be expected to be between 28.38 to 29.95 per 100,000. The 95% neutrosophic confidence interval for the neutrosophic slope (rate of change) $b_Nϵ\left\{b_L,b_U\right\}$ is $\left(\left[5.35,5.50\right],\left[8.16,8.31\right]\right)$. This confidence interval shows that one can expect that the minimum death rate per 10,000 will be between 5.35 to 5.50 and the maximum death rate per 10,000 will be between 8.16 to 8.31. The neutrosophic p-values [0.0001,0.0001]$\le 0.05$ show the significance of death due to prostate cancer.

4. Discussion

The relationship between two variables using the regression model under classical statistics is given as: $Y=28.38+6.911X$. By comparing the neutrosophic regression with the classical regression, we note that the neutrosophic regression provides the parameters, confidence interval and p-values in the indeterminacy interval range. The regression model using the classical statistics provides the determined values of all parameters involved in the regression line. Therefore, under uncertainty, the proposed neutrosophic regression analysis will be more helpful to see the significance of death due to the increase in fate rate. Further, the forecasting of a death rate due to cancer can be expected in the indeterminacy interval rage rather than the exact or the determined values. The neutrosophic regression model is more flexible and adequate under the uncertainty environment than the classical regression model.

Study Limitations

The proposed neutrosophic regression model is the extension of the classical regression. The neutrosophic regression becomes the regression model in the classical statistics if no uncertain observations are in the sample or in the population. The proposed neutrosophic regression can be applied adequately in the uncertainty environment.

5. Conclusions

The present study showed that there is a strong relationship between the prostate cancer rate and dietary fat. We presented a neutrosophic regression model that can be used more effectively in the uncertainty environment than the classical regression model. The neutrosophic regression provides the parameters estimation in the indeterminacy interval rage. The neutrosophic regression shows a significant effect on the death rate due to the inverse in the fat. We also found a statistical correlation between dietary fat and prostate cancer risk. We conclude from this study that the use of the neutrosophic regression model for the estimation and forecasting of prostate cancer death will be helpful to make an adequate decision to control the death rate. We recommend that a health manager should adopt the neutrosophic regression model for better and more effective analysis under an uncertainty environment. The proposed study using multiple regression analysis, principal component analysis or partial least squares analysis can be extended for future research.