Experimental Investigation of the Mechanical Behavior of Layer-Crack Specimens under Cyclic Uniaxial Compression
Abstract
:1. Introduction
2. Specimen Preparation and Testing
2.1. Specimen Preparation
2.2. Test Scheme and System
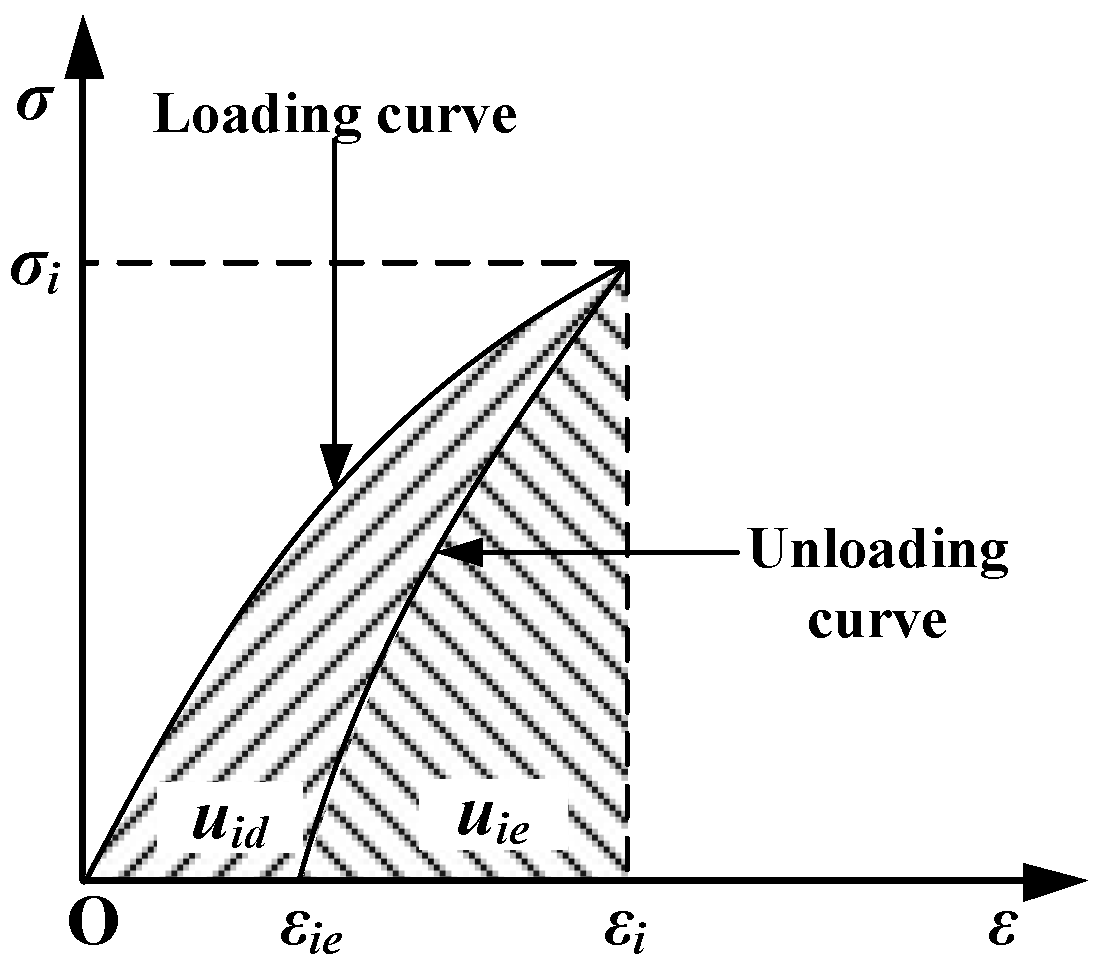
3. Determination of Fatigue Property
4. Experimental Results and Discussions
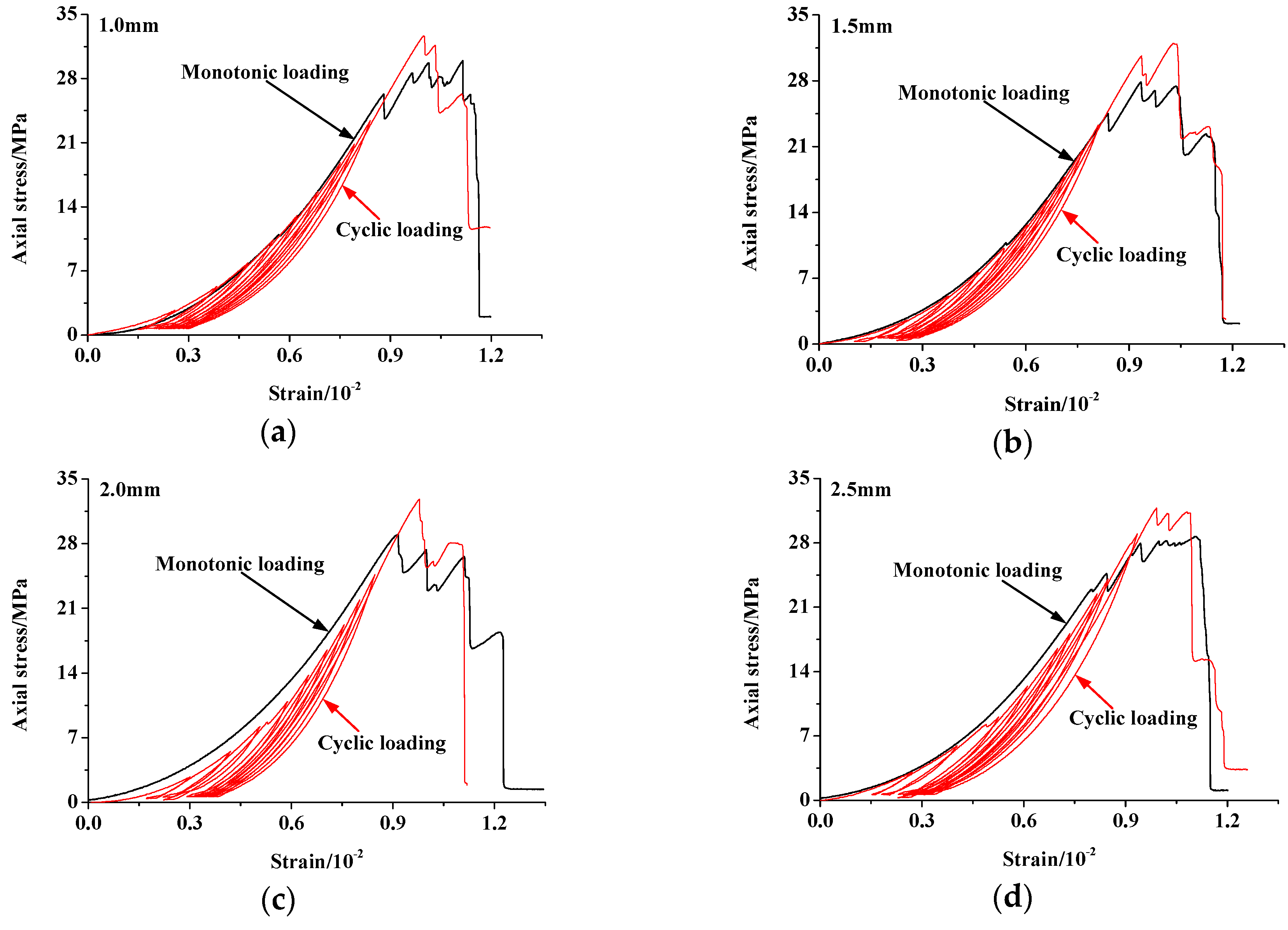
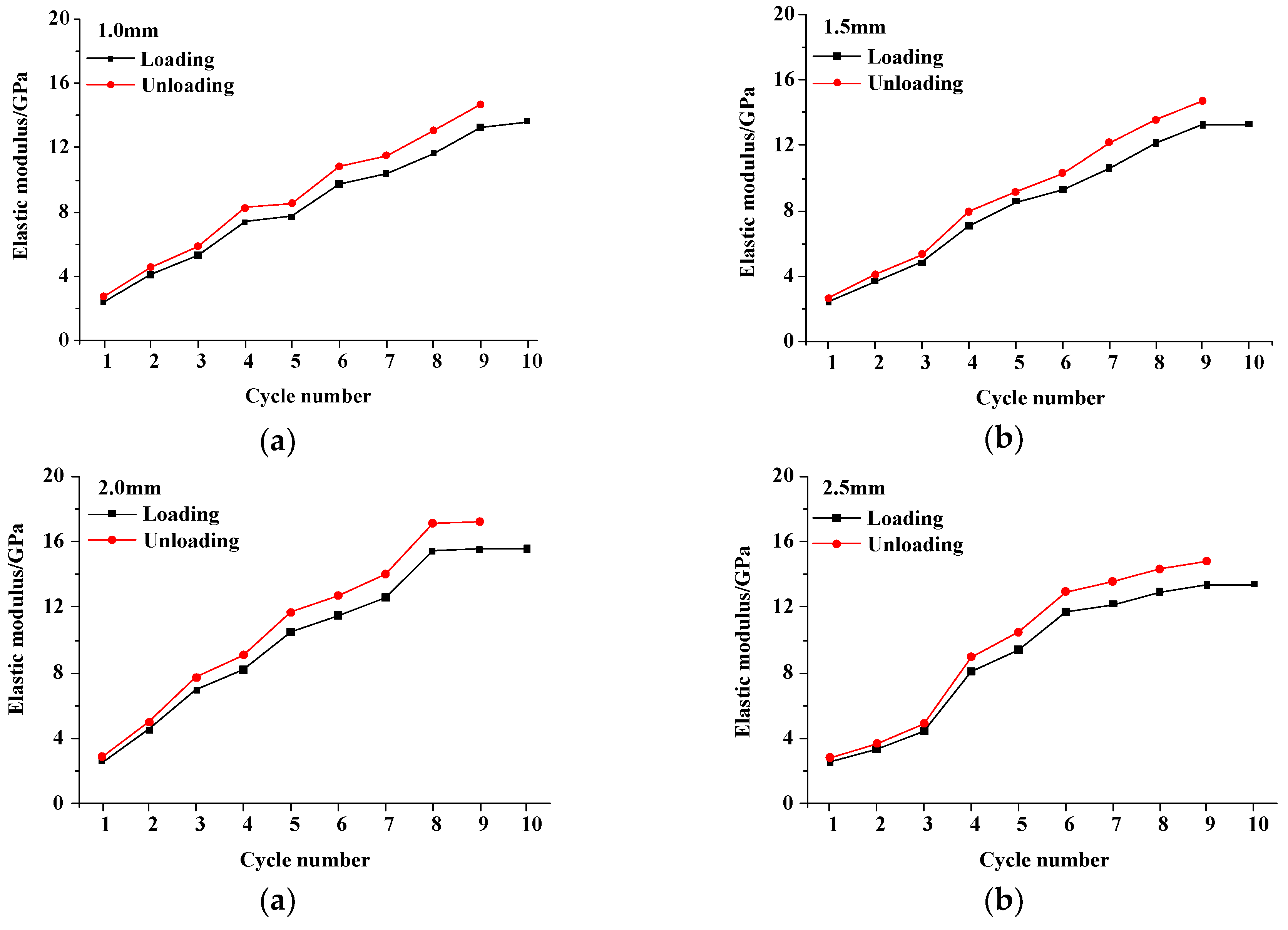
4.1. Influence of Fissure Width
4.1.1. Strength, Deformation and Failure Characteristics
4.1.2. Energy and Damage Evolution
4.1.3. AE Evolution Characteristics
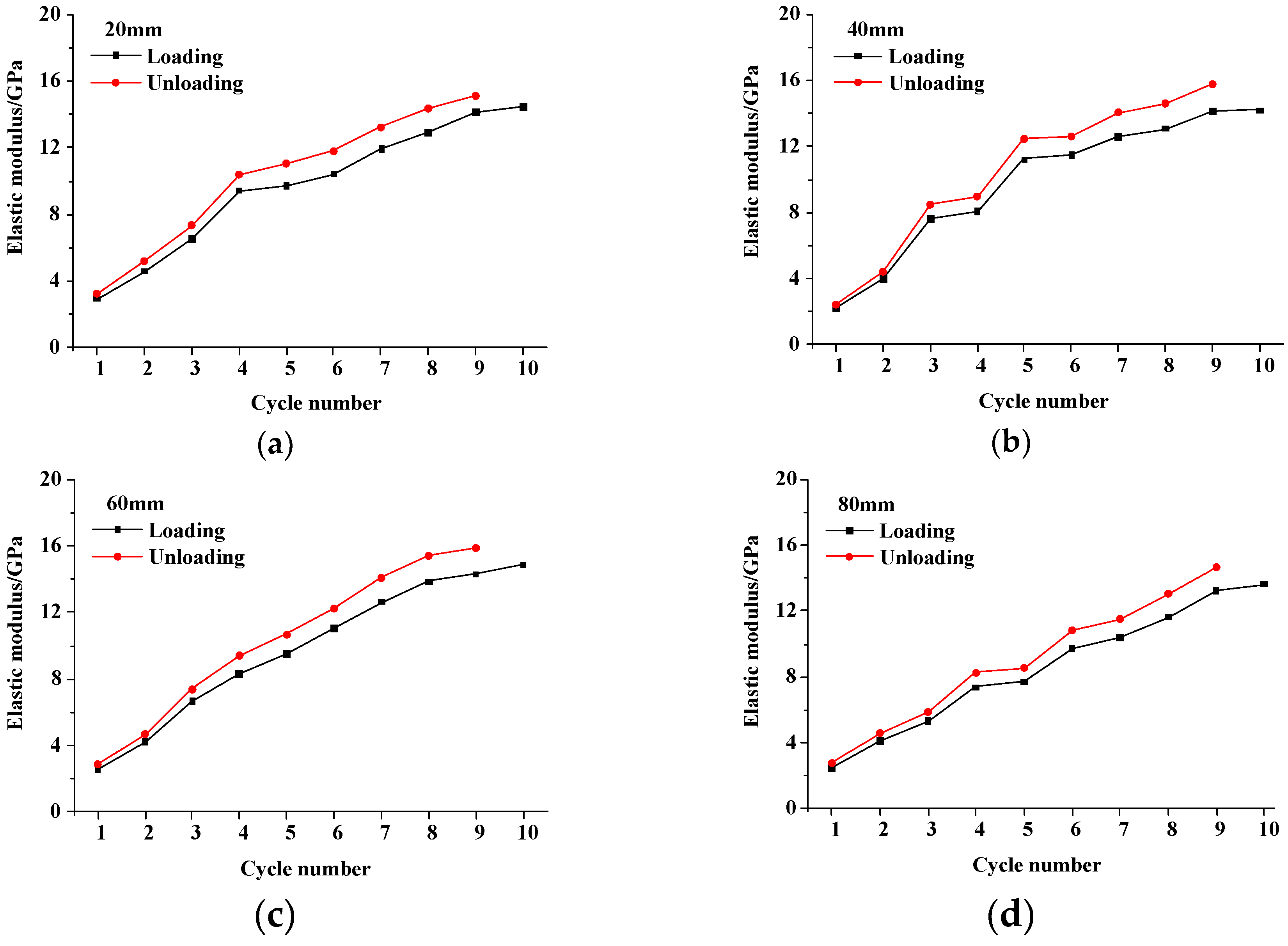
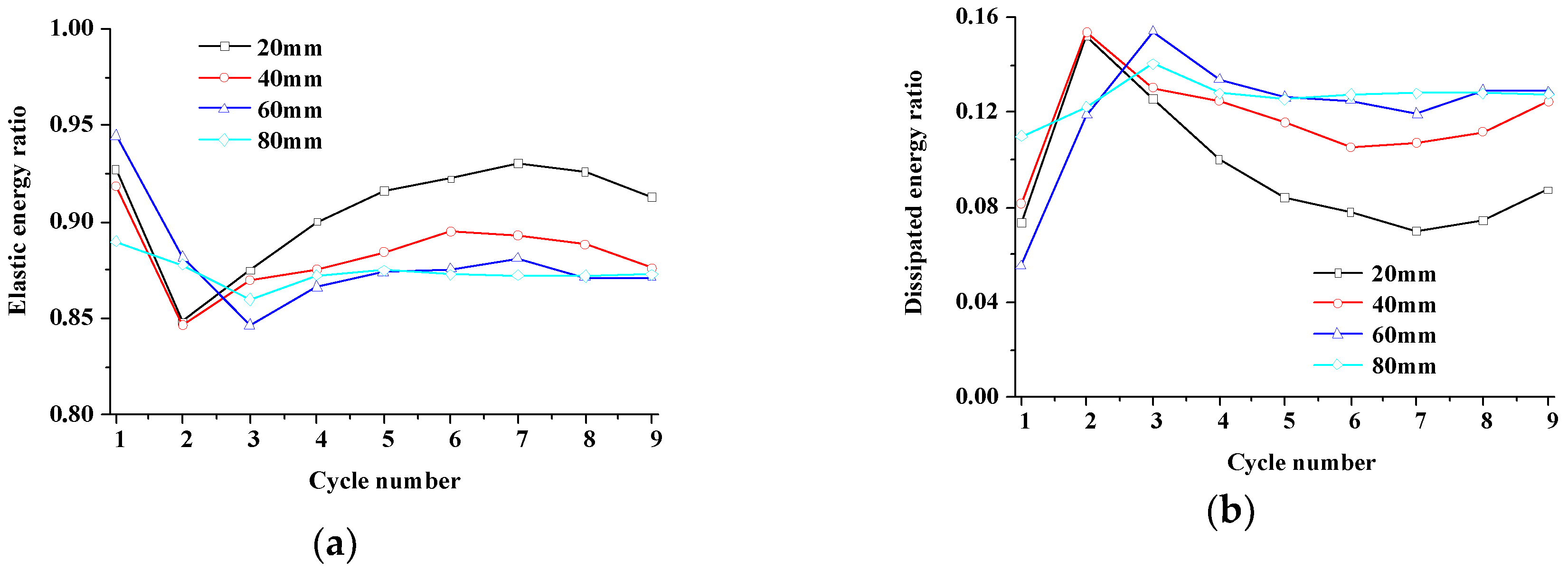
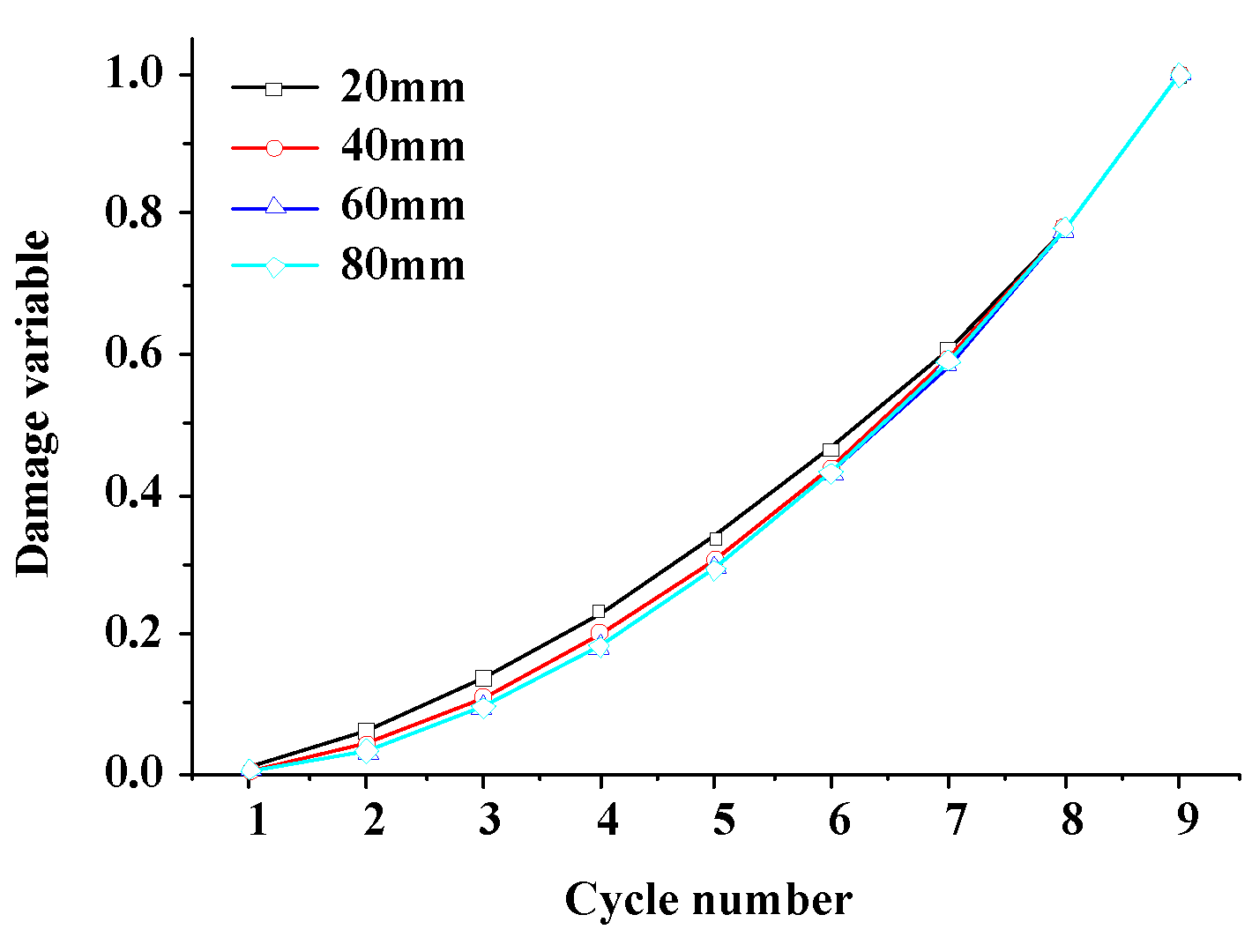
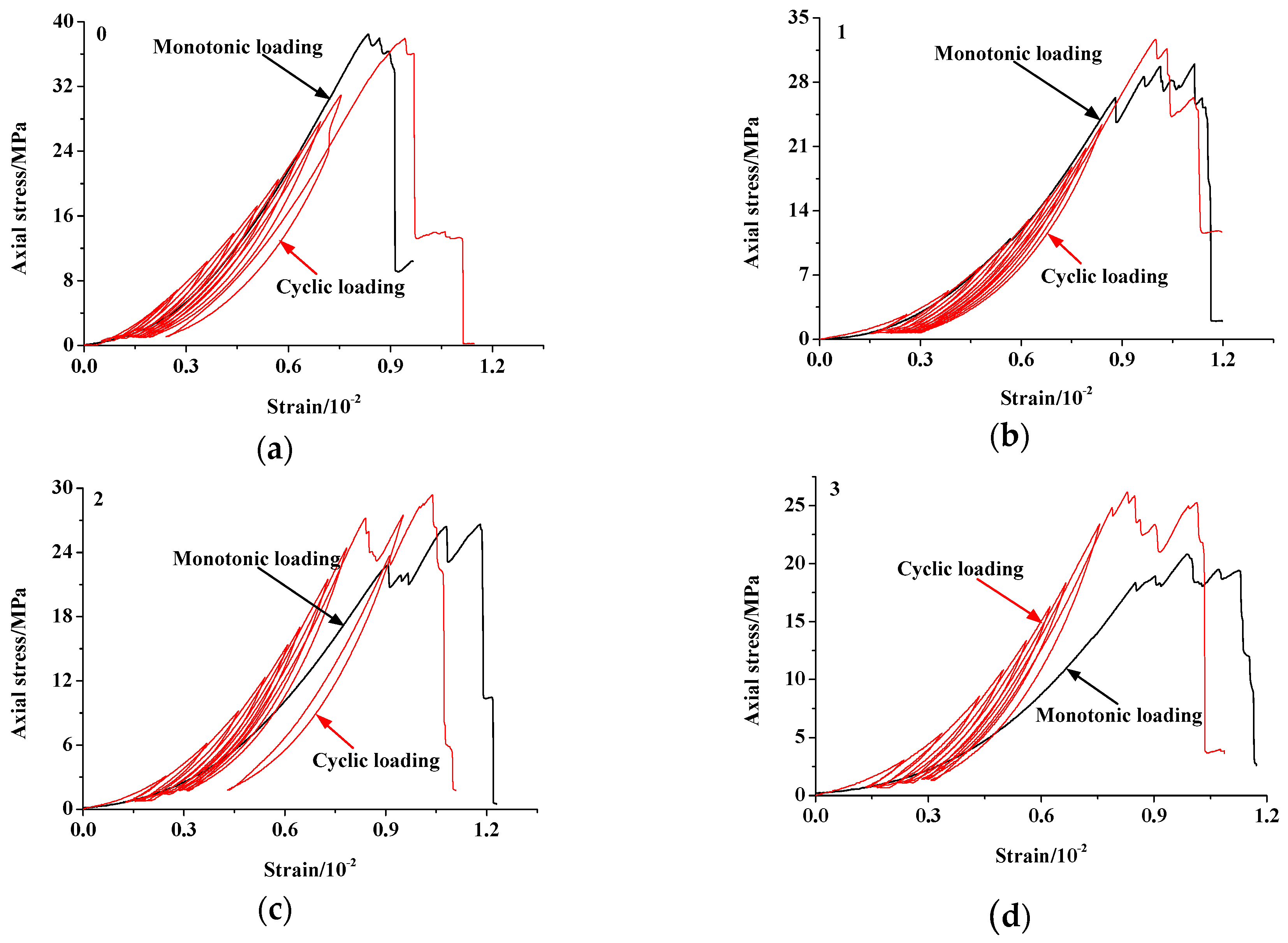
4.2. Influence of Fissure Length
4.2.1. Strength, Deformation and Failure Characteristics
4.2.2. Energy and Damage Evolution
4.2.3. AE Evolution Characteristics
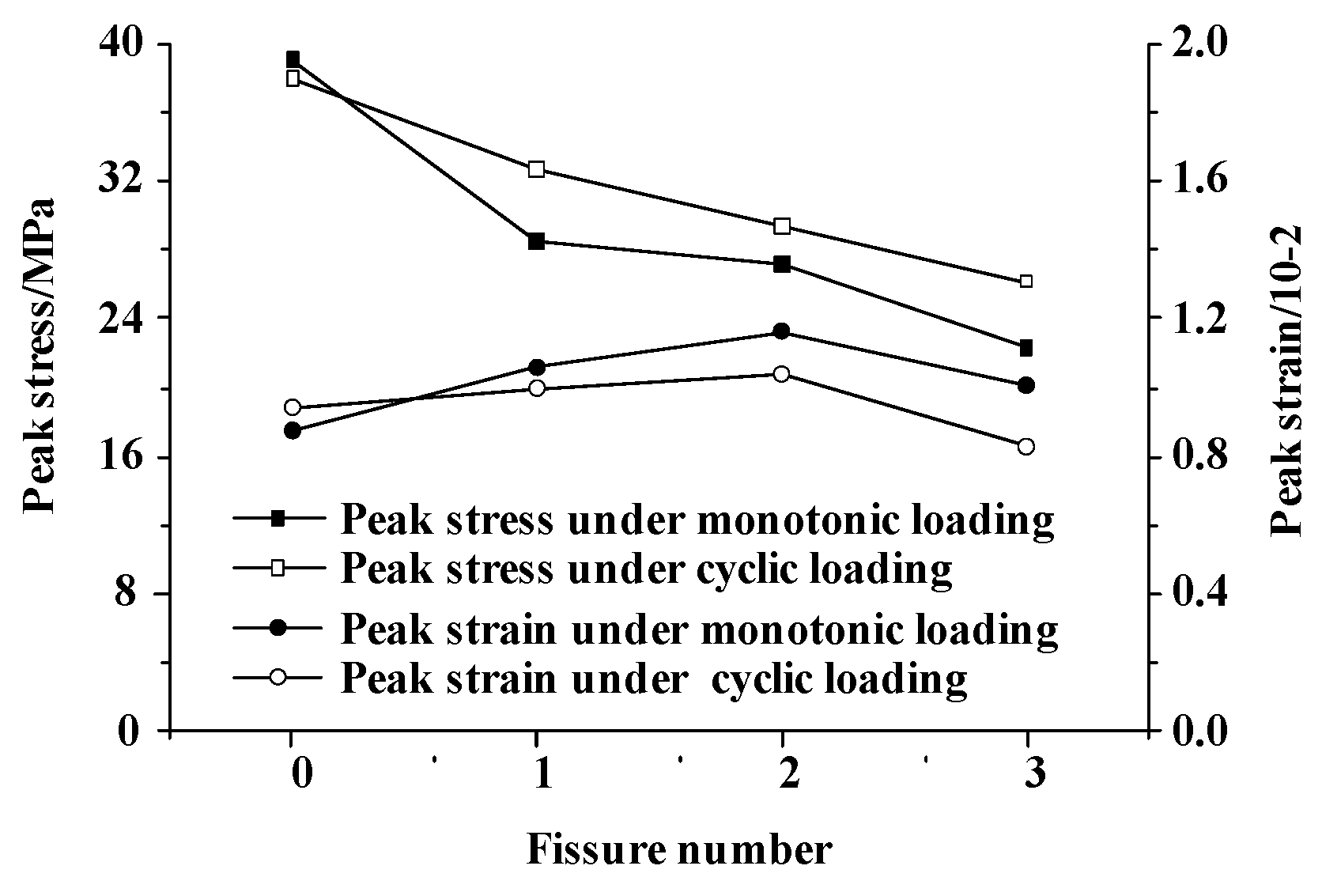
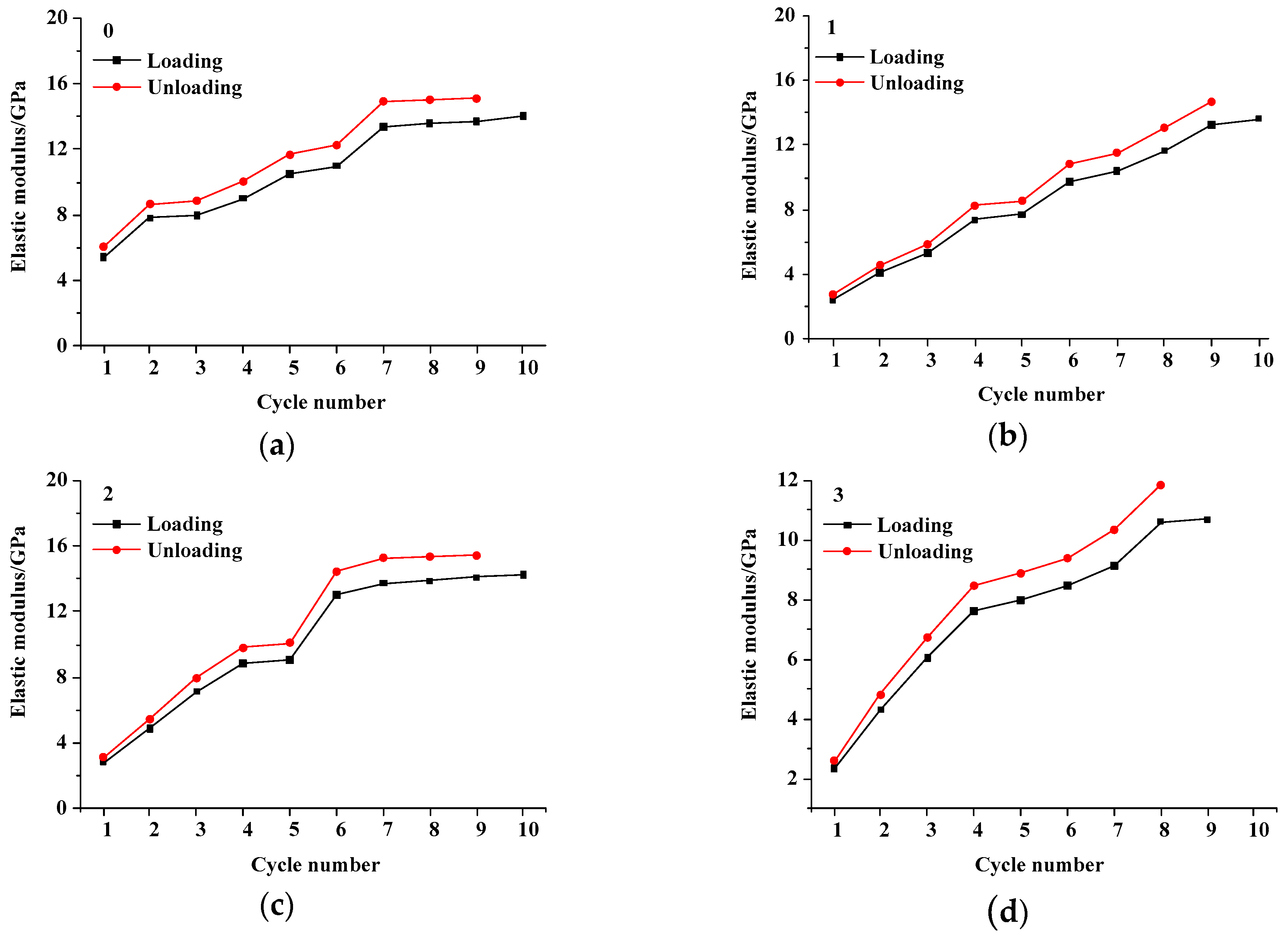
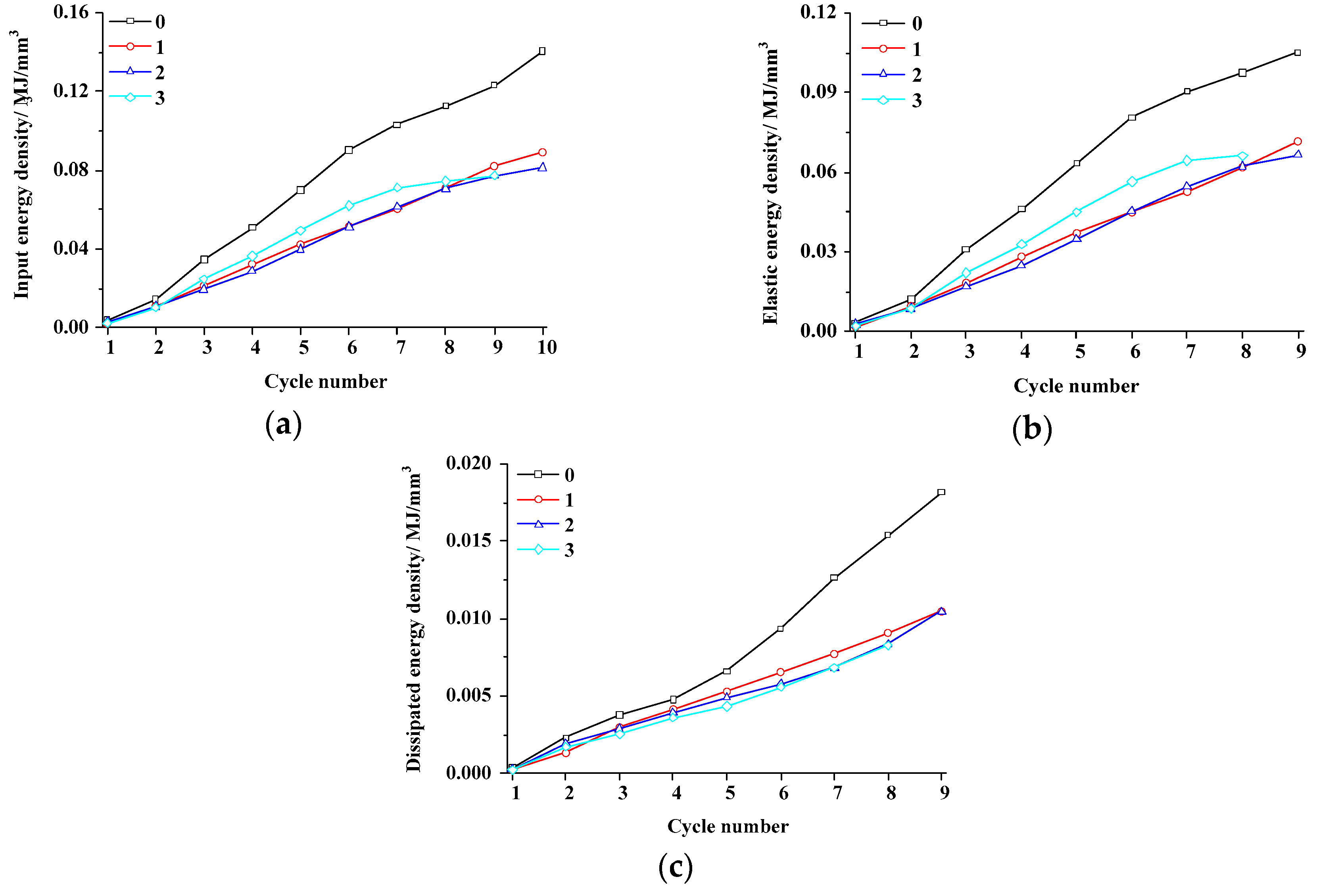
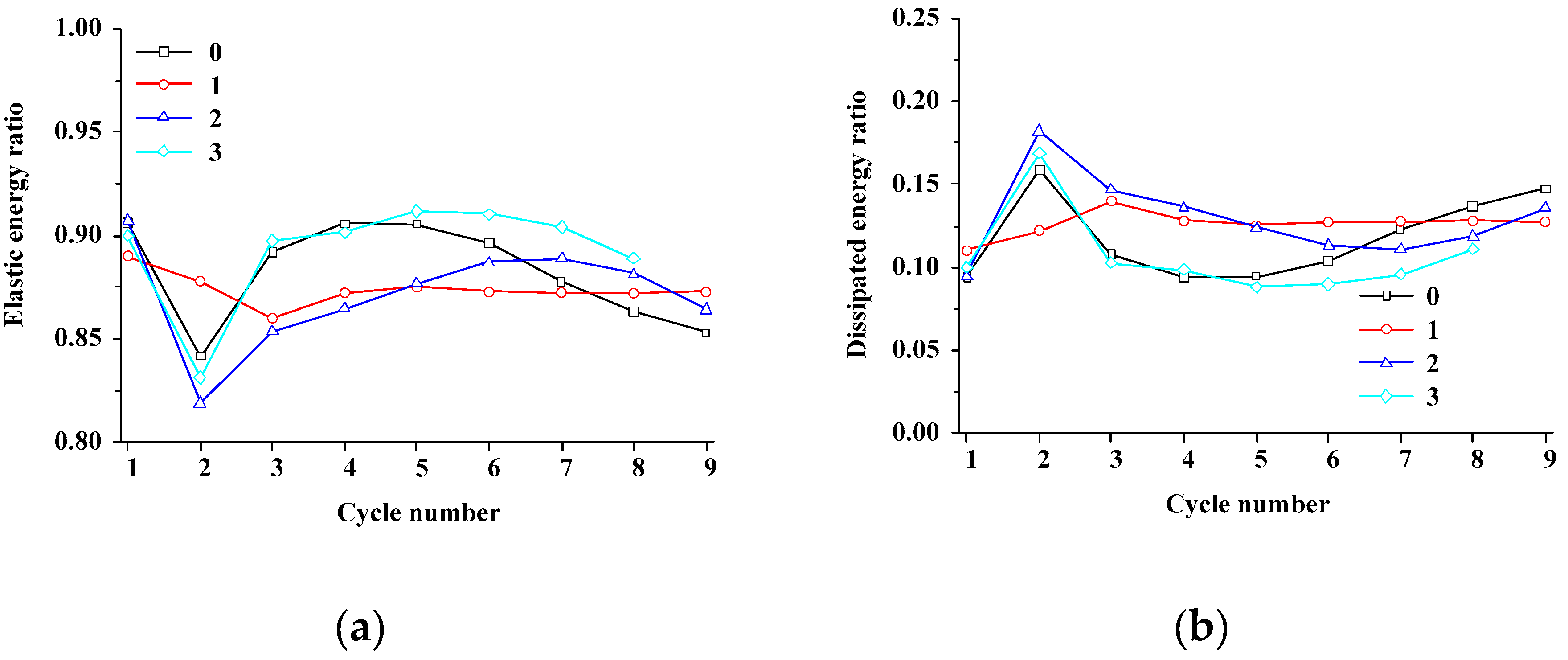
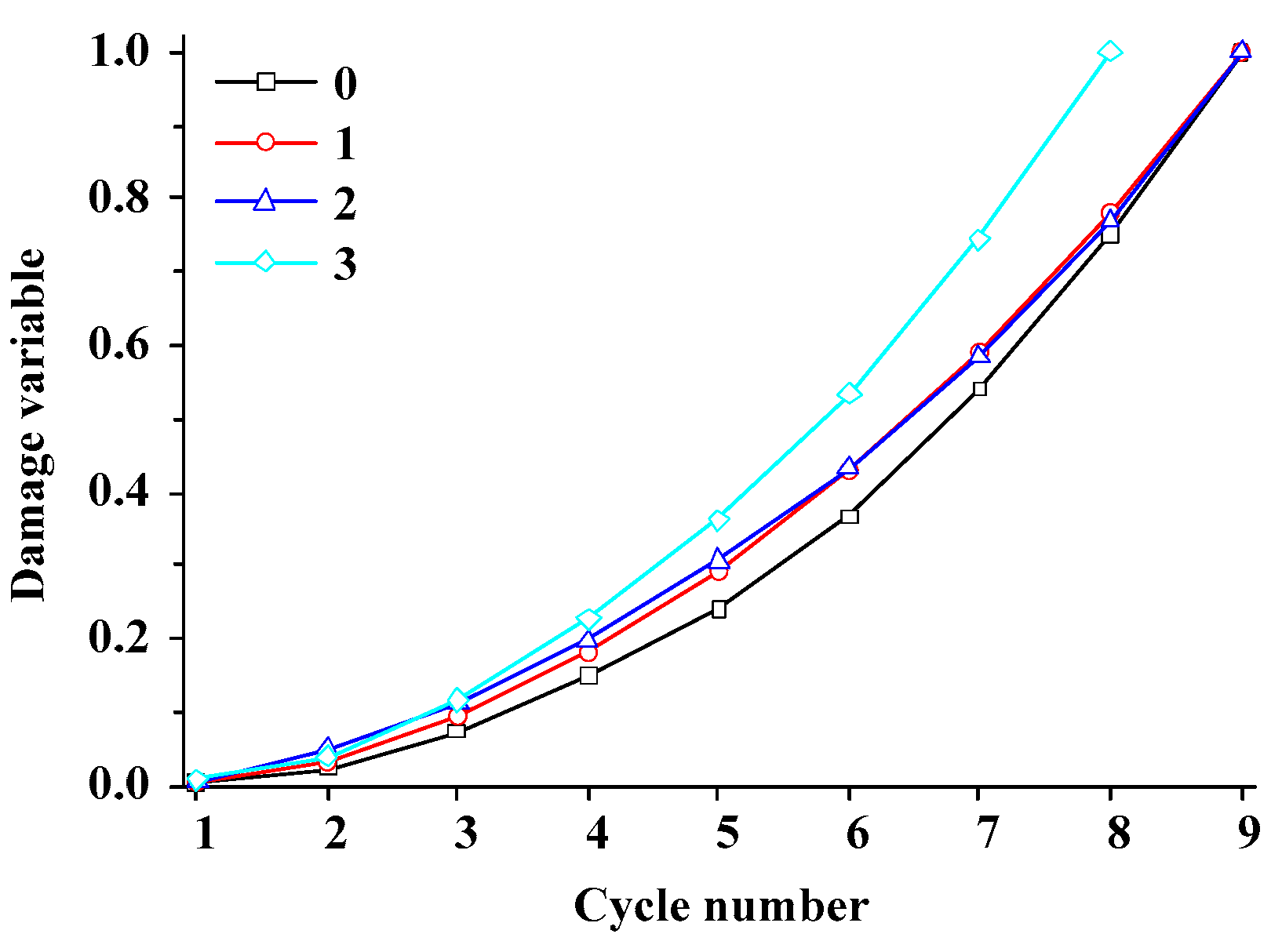
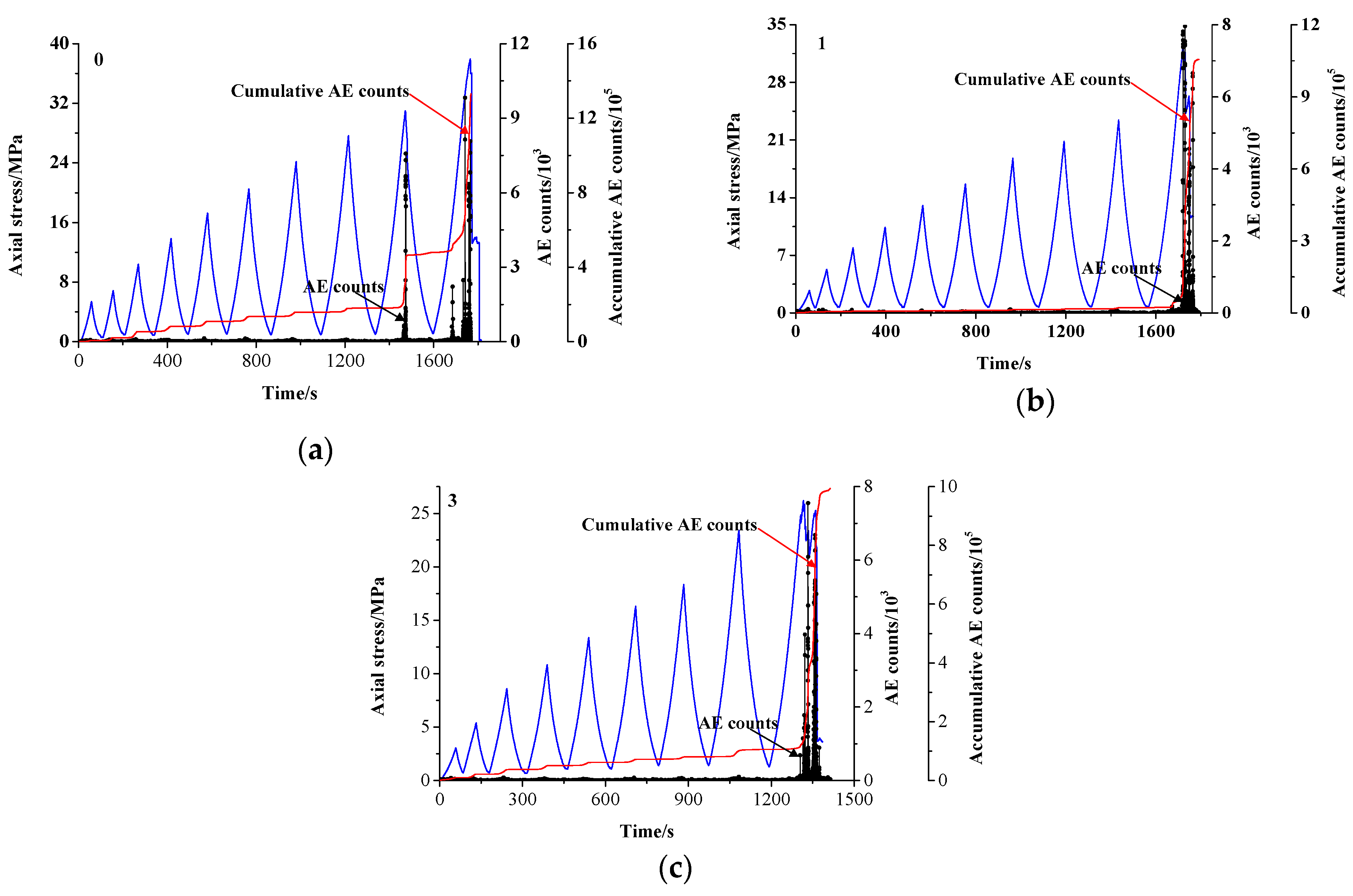
4.3. Influence of the Number of Fissures
4.3.1. Strength, Deformation and Failure Characteristics
4.3.2. Energy and Damage Evolution
4.3.3. AE Evolution Characteristics
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Guo, W.-Y.; Zhao, T.-B.; Tan, Y.-L.; Yu, F.-H.; Hu, S.-C.; Yang, F.-Q. Progressive mitigation method of rock bursts under complicated geological conditions. Int. J. Rock Mech. Min. Sci. 2017, 96, 11–22. [Google Scholar] [CrossRef]
- Guo, W.Y.; Tan, Y.L.; Yu, F.H.; Zhao, T.B.; Hu, S.C.; Huang, D.M.; Qin, Z. Mechanical behavior of rock-coal-rock specimens with different coal thicknesses. Geomech Eng. 2018, 5, 1017–1027. [Google Scholar]
- Zhao, T.B.; Guo, W.Y.; Tan, Y.L.; Lu, C.P.; Wang, C.W. Case histories of rock bursts under complicated geological conditions. Bull. Eng. Geol. Environ. 2018, 77, 1529–1545. [Google Scholar] [CrossRef]
- Tan, Y.; Yu, F.; Ning, J.; Zhao, T. Design and construction of entry retaining wall along a gob side under hard roof stratum. Int. J. Rock Mech. Min. Sci. 2015, 77, 115–121. [Google Scholar] [CrossRef]
- Martini, C.; Read, R.; Martino, J. Observations of brittle failure around a circular test tunnel. Int. J. Rock Mech. Min. Sci. Géoméch. Abstr. 1997, 34, 1065–1073. [Google Scholar] [CrossRef]
- Diederichs, M.S. The 2003 Canadian Geotechnical Colloquium: Mechanistic interpretation. Can. Geotech. J. 2007, 44, 1082–1116. [Google Scholar] [CrossRef]
- Gong, Q.; Yin, L.; Wu, S.; Zhao, J.; Ting, Y. Rock burst and slabbing failure and its influence on TBM excavation at headrace tunnels in Jinping II hydropower station. Eng. Geol. 2012, 124, 98–108. [Google Scholar] [CrossRef]
- Zhou, H.; Meng, M.Z.; Zhang, C.Q.; Lu, J.J.; Xu, R.C. Effect of structural plane on rockburst in deep hard rock tunnels. Chin J. Rock Mech Eng. 2015, 34, 720–727. [Google Scholar]
- Yin, Y.; Zhao, T.; Zhang, Y.; Tan, Y.; Qiu, Y.; Taheri, A.; Jing, Y. An Innovative Method for Placement of Gangue Backfilling Material in Steep Underground Coal Mines. Minerals 2019, 9, 107. [Google Scholar] [CrossRef]
- Tan, Y.-L.; Guo, W.-Y.; Zhao, T.-B.; Yu, F.-H.; Huang, B.; Huang, D.-M. Influence of Fissure Number on the Mechanical Properties of Layer-Crack Rock Models under Uniaxial Compression. Adv. Civ. Eng. 2018, 2018, 1–12. [Google Scholar] [CrossRef]
- Zhou, G.; Zhang, Q.; Bai, R.; Fan, T.; Wang, G. The diffusion behavior law of respirable dust at fully mechanized caving face in coal mine: CFD numerical simulation and engineering application. Process Saf Env. 2017, 106, 117–128. [Google Scholar] [CrossRef]
- Xie, H.P.; Ju, Y.; Li, L.Y.; Peng, R.D. Energy mechanism of deformation and failure of rock masses. Chin J. Rock Mech. Eng. 2008, 27, 1729–1740. [Google Scholar]
- Rezaei, M.; Hossaini, M.F.; Majdi, A. Determination of Longwall Mining-Induced Stress Using the Strain Energy Method. Rock Mech. Rock Eng. 2015, 48, 2421–2433. [Google Scholar] [CrossRef]
- Wang, J.; Ning, J.; Jiang, L.; Jiang, J.-Q.; Bu, T. Structural characteristics of strata overlying of a fully mechanized longwall face: a case study. J. South. Afr. Inst. Min. Met. 2018, 118, 1195–1204. [Google Scholar] [CrossRef]
- Mohamed, K.M.; Murphy, M.M.; Lawson, H.E.; Klemetti, T. Analysis of the current rib support practices and techniques in U.S. coal mines. Int. J. Min. Sci. Technol. 2016, 26, 77–87. [Google Scholar] [CrossRef] [PubMed]
- Xu, M.A. The energy variety analysis of rock under biaxial compression. J. Chin. Coal. Soc. 2010, 35, 2033–2038. [Google Scholar]
- Liu, J.F.; Xu, J.; Li, Q.S.; Li, L.G. Experimental research on damping parameters of rock under cyclic loading. Chin. J. Rock Mech. Eng. 2010, 29, 1036–1041. [Google Scholar]
- Xu, J.; Zhang, Y.; Yang, H.W.; Wang, J.N. Energy evolution law of deformation and damage of sandstone under cyclic pore water pressures. Chin. J. Rock Mech. Eng. 2011, 30, 141–148. [Google Scholar]
- Zhang, Z.Z.; Gao, F. Research on nonlinear characteristics of rock energy evolution under uniaxial compression. Chin. J. Rock Mech. Eng. 2012, 31, 1198–1207. [Google Scholar]
- Zou, J.P.; Chen, W.Z.; Yang, D.S.; Yuan, J.Q.; Tan, X.J. Mechanical properties and damage evolution of coal under cyclic loading conditions. J. Chin. Coal Soc. 2016, 41, 1675–1682. [Google Scholar]
- Wang, H.; Yang, T.H.; Liu, H.L.; Zhao, Y.C.; Deng, W.X.; Hou, X.G. Mechanical properties and energy evolution of dry and saturated sandstones under cyclic loading. Rock Soil Mech. 2017, 38, 1600–1608. [Google Scholar]
- Masoudian, M.S.; Saadabad, M.M. Multiphysics of carbon dioxide sequestration in coalbeds: A review with a focus on geomechanical characteristics of coal. J. Rock Mech. Geotech. Eng. 2016, 8, 93–112. [Google Scholar] [CrossRef]
- Guo, W.-Y.; Tan, Y.-L.; Zhao, T.-B.; Liu, X.-M.; Gu, Q.-H.; Hu, S.-C. Compression Creep Characteristics and Creep Model Establishment of Gangue. Geotech. Geol. Eng. 2016, 34, 1193–1198. [Google Scholar] [CrossRef]
- Fu, B.; Zhou, Z.H.; Wang, H.Q.; Wang, Y.X. Precursor information study on acoustic emission characteristics of marble under uniaxial cyclic loading-unloading. J. Chin. Coal Soc. 2016, 41, 1946–1953. [Google Scholar]
- Liu, X.; Tan, Y.; Ning, J.; Lu, Y.; Gu, Q. Mechanical properties and damage constitutive model of coal in coal-rock combined body. Int. J. Rock Mech. Min. Sci. 2018, 110, 140–150. [Google Scholar] [CrossRef]
- Xiao, J.-Q.; Ding, D.-X.; Jiang, F.-L.; Xu, G. Fatigue damage variable and evolution of rock subjected to cyclic loading. Int. J. Rock Mech. Min. Sci. 2010, 47, 461–468. [Google Scholar] [CrossRef]
- You, M.Q.; Su, C.D. Experimental study on strengthening of marble specimen in cyclic loading of uniaxial or pseudo-triaxial compression. Chin. J. Solid Mech. 2008, 10, 66–72. [Google Scholar]
- Guo, W.-Y.; Tan, Y.-L.; Huang, B.; Zhang, L.-S.; Zhao, T.-B.; Yu, F.-H. Failure mechanism of layer-crack rock models with different vertical fissure geometric configurations under uniaxial compression. Adv. Mech. Eng. 2017, 9, 1–15. [Google Scholar]
- Cao, A.Y.; Dou, L.M.; Jiang, H.; Lv, C.G.; Guo, X.Q.; Wang, Y. Characteristics of energy radiation and stress drop in different failure modes of mining-induced coal-rock mass. J. Min. Safety Eng. 2011, 28, 350–355. [Google Scholar]
- Chen, X.G.; Zhang, Q.Y. Research on the energy dissipation and release in the process of rock shear failure. J. Min. Safety Eng. 2010, 27, 179–184. [Google Scholar]
- Zhang, Q.; Zhou, G.; Qian, X.; Yuan, M.; Sun, Y.; Wang, D.; Yuan, M. Diffuse pollution characteristics of respirable dust in fully-mechanized mining face under various velocities based on CFD investigation. J. Clean. Prod. 2018, 184, 239–250. [Google Scholar] [CrossRef]






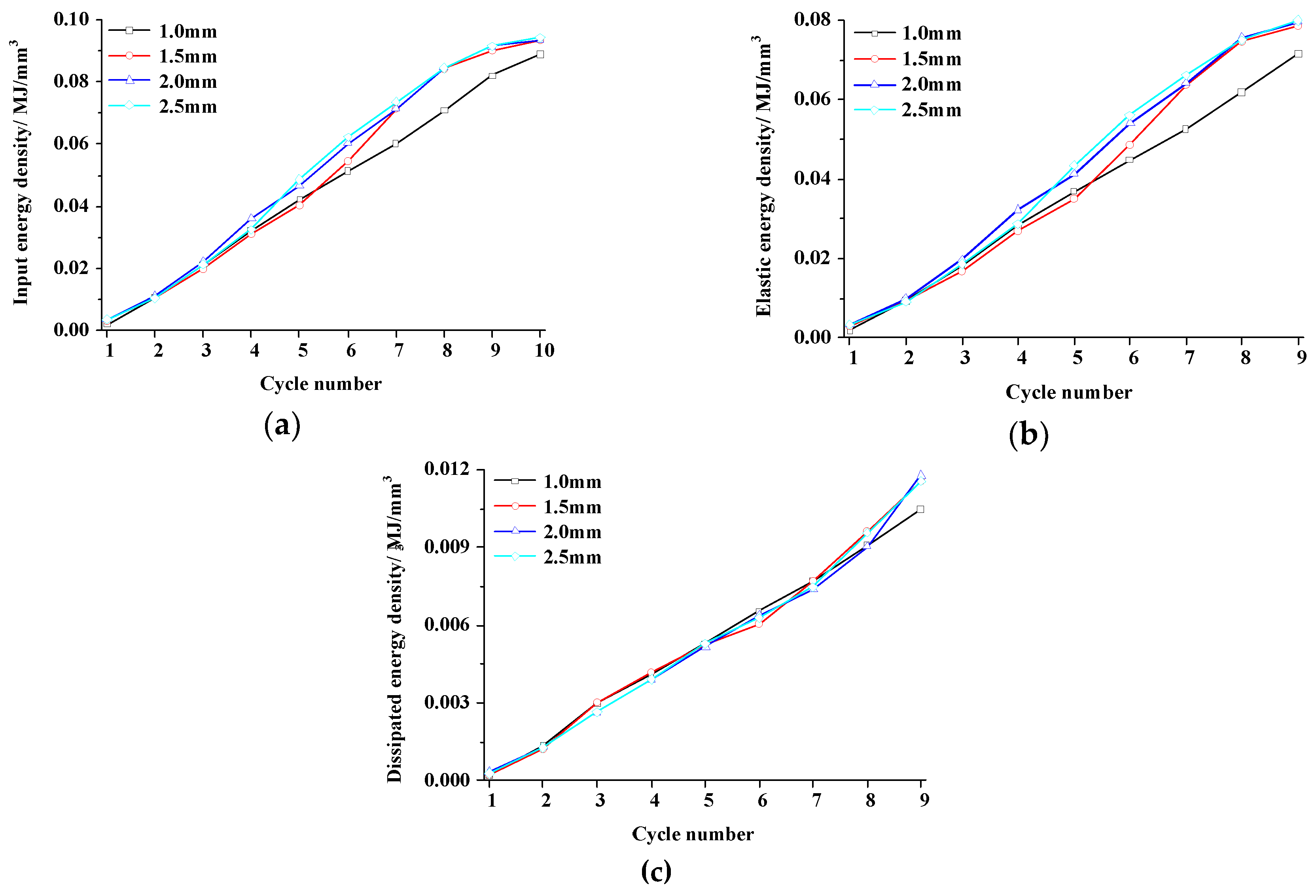
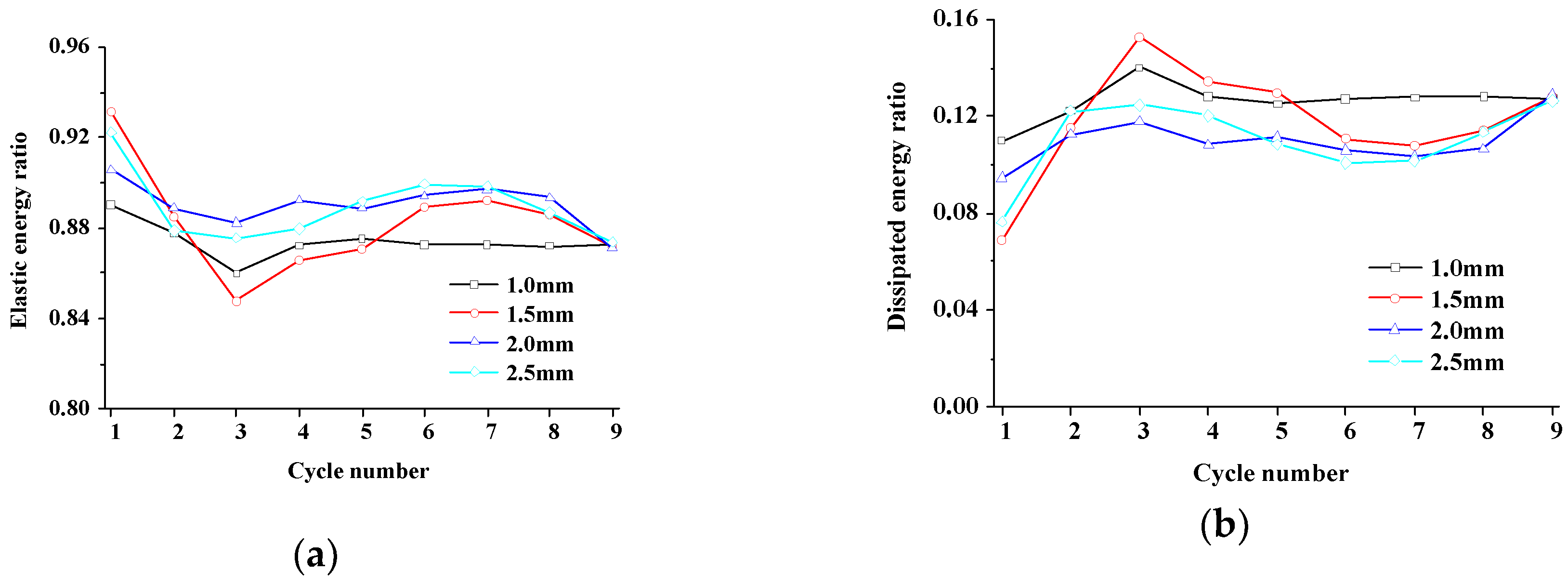
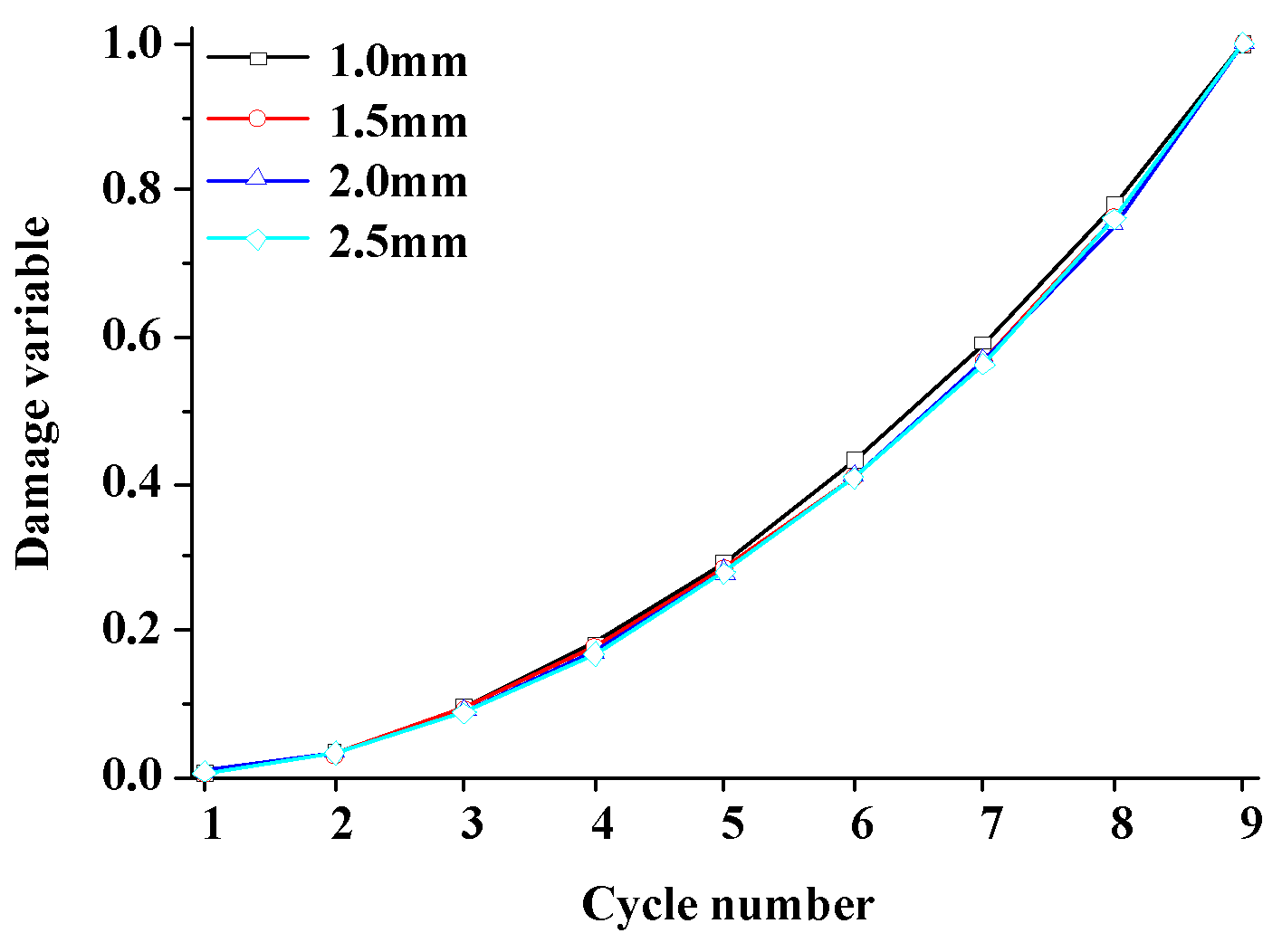

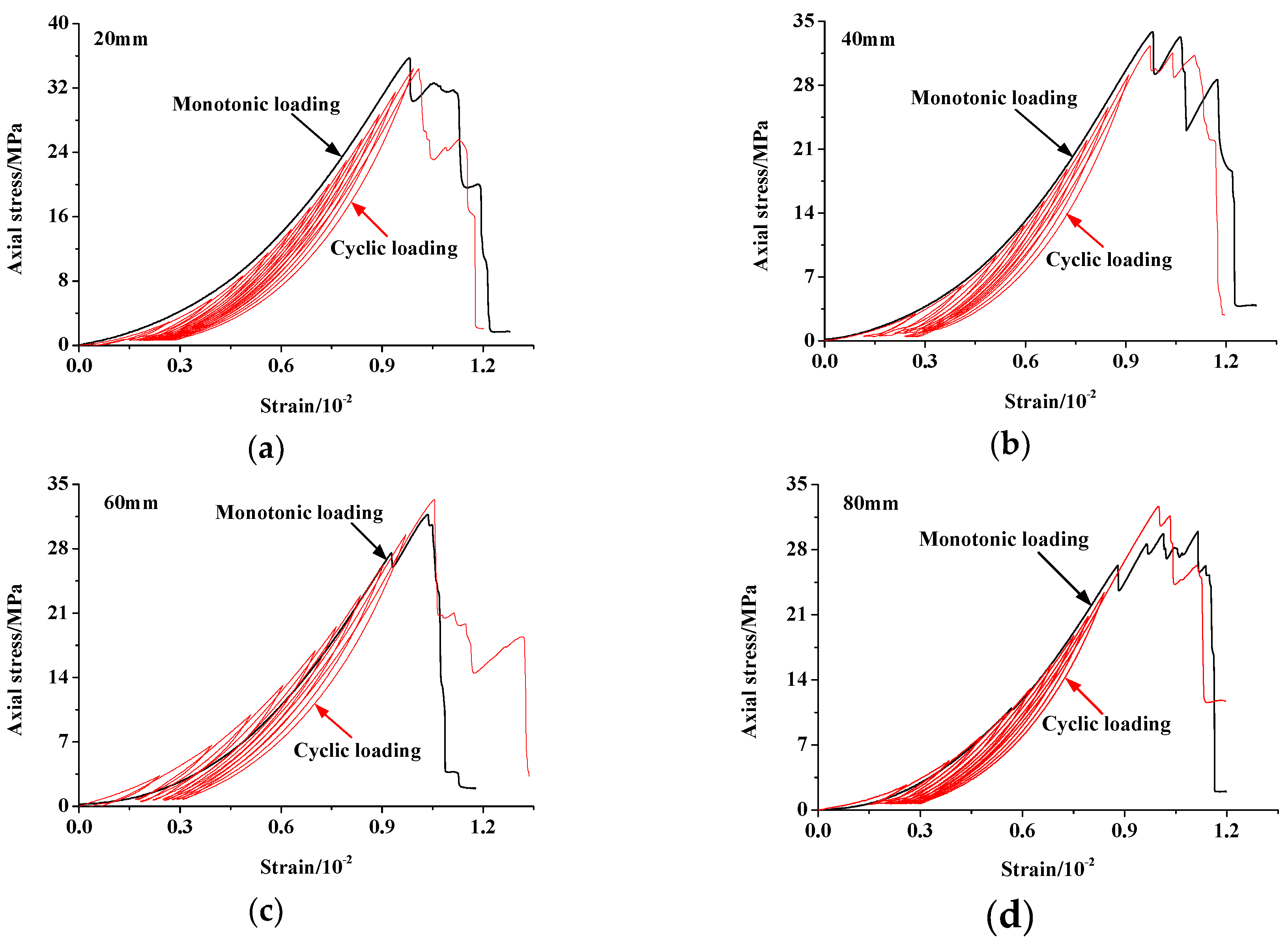
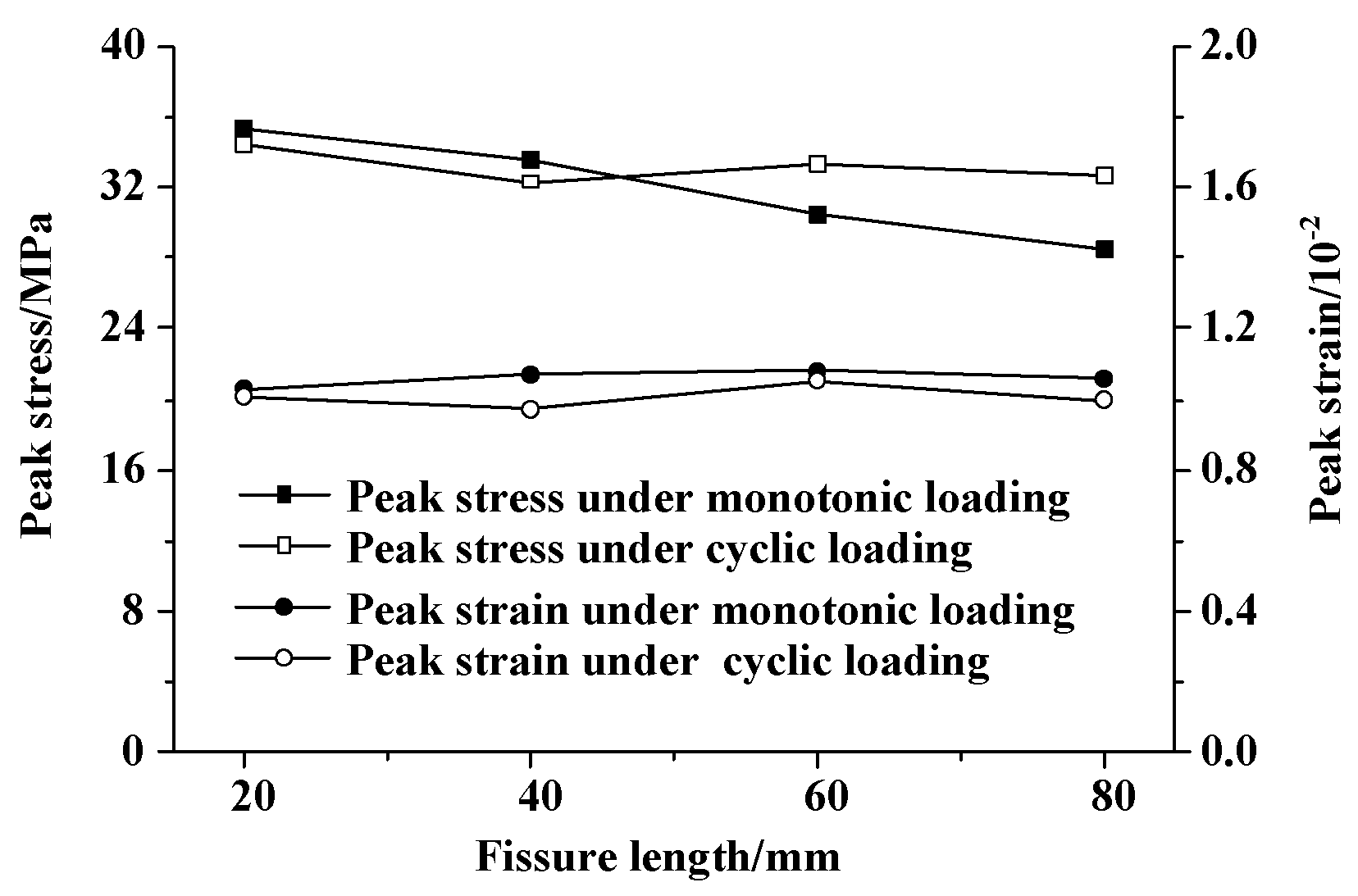




| Cycle Number | Fissure Width/mm | Fissure Width/mm | ||||||
|---|---|---|---|---|---|---|---|---|
| 1.0 | 1.5 | 2.0 | 2.5 | 1.0 | 1.5 | 2.0 | 2.5 | |
| Elastic Energy Density (uie)/MJ/mm3 | Dissipated Energy Density (uid)/MJ/mm3 | |||||||
| 1 | 0.0018 | 0.0030 | 0.0032 | 0.0033 | 0.0002 | 0.0002 | 0.0003 | 0.0003 |
| 2 | 0.0056 | 0.0093 | 0.0101 | 0.0091 | 0.0013 | 0.0012 | 0.0013 | 0.0013 |
| 3 | 0.0094 | 0.0168 | 0.0198 | 0.0186 | 0.0029 | 0.0031 | 0.0026 | 0.0026 |
| 4 | 0.0181 | 0.0269 | 0.0322 | 0.0286 | 0.0041 | 0.0042 | 0.0039 | 0.0039 |
| 5 | 0.0266 | 0.0351 | 0.0413 | 0.0434 | 0.0053 | 0.0052 | 0.0052 | 0.0053 |
| 6 | 0.0361 | 0.0486 | 0.0539 | 0.0559 | 0.0065 | 0.0061 | 0.0064 | 0.0063 |
| 7 | 0.0447 | 0.0637 | 0.0641 | 0.0661 | 0.0077 | 0.0077 | 0.0074 | 0.0075 |
| 8 | 0.0532 | 0.0746 | 0.0756 | 0.0749 | 0.0091 | 0.0096 | 0.0091 | 0.0096 |
| 9 | 0.0614 | 0.0786 | 0.0796 | 0.0799 | 0.0105 | 0.0116 | 0.0118 | 0.0116 |
| Cycle Number | Fissure Length/mm | Fissure Length/mm | ||||||
|---|---|---|---|---|---|---|---|---|
| 20 | 40 | 60 | 80 | 20 | 40 | 60 | 80 | |
| Elastic Energy Density (uie)/MJ/mm3 | Dissipated Energy Density (uid)/MJ/mm3 | |||||||
| 1 | 0.0028 | 0.0028 | 0.0021 | 0.0018 | 0.0002 | 0.0002 | 0.0002 | 0.0002 |
| 2 | 0.0095 | 0.0096 | 0.0064 | 0.0056 | 0.0017 | 0.0020 | 0.0013 | 0.0013 |
| 3 | 0.0173 | 0.0163 | 0.0118 | 0.0094 | 0.0025 | 0.0036 | 0.0030 | 0.0030 |
| 4 | 0.0272 | 0.0261 | 0.0209 | 0.0181 | 0.0031 | 0.0048 | 0.0040 | 0.0041 |
| 5 | 0.0372 | 0.0359 | 0.0322 | 0.0266 | 0.0034 | 0.0055 | 0.0052 | 0.0053 |
| 6 | 0.0482 | 0.0443 | 0.0442 | 0.0361 | 0.0041 | 0.0069 | 0.0063 | 0.0065 |
| 7 | 0.0608 | 0.0525 | 0.0546 | 0.0447 | 0.0046 | 0.0083 | 0.0071 | 0.0077 |
| 8 | 0.0688 | 0.0613 | 0.0635 | 0.0532 | 0.0055 | 0.0099 | 0.0091 | 0.0091 |
| 9 | 0.0749 | 0.0699 | 0.0714 | 0.0614 | 0.0072 | 0.0116 | 0.0103 | 0.0105 |
| Cycle Number | Number of Fissures | Number of Fissures | ||||||
|---|---|---|---|---|---|---|---|---|
| 0 | 1 | 2 | 3 | 0 | 1 | 2 | 3 | |
| Elastic Energy Density (uie)/MJ/mm3 | Dissipated Energy Density (uid)/MJ/mm3 | |||||||
| 1 | 0.0032 | 0.0018 | 0.0026 | 0.0020 | 0.0003 | 0.0002 | 0.0003 | 0.0002 |
| 2 | 0.0122 | 0.0056 | 0.0087 | 0.0086 | 0.0023 | 0.0013 | 0.0019 | 0.0017 |
| 3 | 0.0309 | 0.0094 | 0.0166 | 0.0221 | 0.0037 | 0.0030 | 0.0029 | 0.0025 |
| 4 | 0.0461 | 0.0181 | 0.0248 | 0.0327 | 0.0048 | 0.0041 | 0.0039 | 0.0036 |
| 5 | 0.0632 | 0.0266 | 0.0347 | 0.0449 | 0.0066 | 0.0053 | 0.0049 | 0.0043 |
| 6 | 0.0806 | 0.0361 | 0.0453 | 0.0563 | 0.0094 | 0.0065 | 0.0058 | 0.0056 |
| 7 | 0.0904 | 0.0447 | 0.0546 | 0.0643 | 0.0127 | 0.0077 | 0.0068 | 0.0068 |
| 8 | 0.0972 | 0.0532 | 0.0621 | 0.0661 | 0.0154 | 0.0091 | 0.0084 | 0.0083 |
| 9 | 0.1051 | 0.0614 | 0.0665 | 0.0182 | 0.0105 | 0.0105 | ||
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guo, W.-y.; Yu, F.-h.; Qiu, Y.; Zhao, T.-b.; Tan, Y.-l. Experimental Investigation of the Mechanical Behavior of Layer-Crack Specimens under Cyclic Uniaxial Compression. Symmetry 2019, 11, 465. https://doi.org/10.3390/sym11040465
Guo W-y, Yu F-h, Qiu Y, Zhao T-b, Tan Y-l. Experimental Investigation of the Mechanical Behavior of Layer-Crack Specimens under Cyclic Uniaxial Compression. Symmetry. 2019; 11(4):465. https://doi.org/10.3390/sym11040465
Chicago/Turabian StyleGuo, Wei-yao, Feng-hai Yu, Yue Qiu, Tong-bin Zhao, and Yun-liang Tan. 2019. "Experimental Investigation of the Mechanical Behavior of Layer-Crack Specimens under Cyclic Uniaxial Compression" Symmetry 11, no. 4: 465. https://doi.org/10.3390/sym11040465
APA StyleGuo, W.-y., Yu, F.-h., Qiu, Y., Zhao, T.-b., & Tan, Y.-l. (2019). Experimental Investigation of the Mechanical Behavior of Layer-Crack Specimens under Cyclic Uniaxial Compression. Symmetry, 11(4), 465. https://doi.org/10.3390/sym11040465






