Next Article in Journal
Solution Models Based on Symmetric and Asymmetric Information
Next Article in Special Issue
Electrochirogenesis: The Possible Role of Low-Energy Spin-Polarized Electrons in Creating Homochirality
Previous Article in Journal
Symmetrical Uncertainty-Based Feature Subset Generation and Ensemble Learning for Electricity Customer Classification
Previous Article in Special Issue
The Chirality Induction and Modulation of Polymers by Circularly Polarized Light
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Symmetry
Volume 11
Issue 4
10.3390/sym11040499
symmetry-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Characterization of Hidden Chirality: Two-Fold Helicity in β-Strands

by
Toshiyuki Sasaki
1,* and
Mikiji Miyata
2,*
1
Department of Materials System Science, Graduate School of Nanobioscience, Yokohama City University, 22-2 Seto, Kanazawa-ku, Yokohama, Kanagawa 236-0027, Japan
2
The Institute of Scientific and Industrial Research, Osaka University, 8-1 Mihogaoka, Ibaraki, Osaka 567-0047, Japan
*
Authors to whom correspondence should be addressed.
Symmetry 2019, 11(4), 499; https://doi.org/10.3390/sym11040499
Submission received: 27 March 2019 / Revised: 3 April 2019 / Accepted: 4 April 2019 / Published: 5 April 2019
(This article belongs to the Special Issue Possible Scenarios for Homochirality on Earth)
Browse Figures
Versions Notes

Abstract

:
A β-strand is a component of a β-sheet and is an important structural motif in biomolecules. An α-helix has clear helicity, while chirality of a β-strand had been discussed on the basis of molecular twists generated by forming hydrogen bonds in parallel or non-parallel β-sheets. Herein we describe handedness determination of two-fold helicity in a zig-zag β-strand structure. Left- (M) and right-handedness (P) of the two-fold helicity was defined by application of two concepts: tilt-chirality and multi-point approximation. We call the two-fold helicity in a β-strand, whose handedness has been unrecognized and unclarified, as hidden chirality. Such hidden chirality enables us to clarify precise chiral characteristics of biopolymers. It is also noteworthy that characterization of chirality of high dimensional structures like a β-strand and α-helix, referred to as high dimensional chirality (HDC) in the present study, will contribute to elucidation of the possible origins of chirality and homochirality in nature because such HDC originates from not only asymmetric centers but also conformations in a polypeptide chain.

1. Introduction

Chirality bestows variety and complexity to functions of substances and is one of the most important and fundamental properties in nature. In this context, elucidation of the origins of chirality and homochirality is a challenge of great importance for scientists, and there have been several theories [1,2] such as mechanical stirring [3] and photo reaction [4]. One of the possible answers to the challenge is chirality generation by chiral crystallization [5,6,7,8] with enantiomeric excess, or chiral symmetry breaking [9], followed by amplification [10,11] and transcription [12,13] of the excessed chirality.
In chiral crystallization, chirality is generated by assembling achiral components in chiral manners and is fixed in crystals. Such a phenomenon is observed in both inorganic [5] and organic materials [7,14,15,16,17,18]. A two-fold helix is an especially important structural motif [19] because a large number of chiral crystals belong to P21 and P212121 Sohncke groups having two-fold helices, according to space group statistics of the Cambridge Structural Database [20]. It is surprising, however, that a two-fold helix is achiral as a symmetry operation from the viewpoint of ‘mathematical’ crystallography [21]. This fact brought us a question “what is the origin of chirality in two-fold helix-based crystals?” The supramolecular-tilt-chirality method based on two concepts, tilt chirality and multi-point approximation, answered the question as described below (Figure 1) [22,23,24,25,26].
A two-fold helix is a symmetry operation of 180° rotation around a helical axis combined with one-half unit translation and is achiral in ‘mathematical’ crystallography (Figure 1a–c) [21]. On the other hand, a two-fold helix is chiral and has clear left- and right-handedness in ‘chemical/material’ crystallography [18,27] by considering molecular shapes (Figure 1d). This difference is attributed to an approximation method of molecules: one-point and multi-point approximation in the former and the latter, respectively. We call the chirality, whose handedness cannot be recognized in a general way by mathematical crystallography but definitely exists in materials, as hidden chirality. Not only clear helices, including three-fold, four-fold, and six-fold helices in crystals as well as α-helices in proteins, but also helices having hidden chirality like two-fold helices, may serve as the origin of chirality [17,18,28].
Inspired by the discovery of hidden chirality in a two-fold helix, we have been seeking for further hidden chirality not only in supermolecules [29] but also in a wide range of materials, including polymers. Consequently, we noticed the fact that chirality of a β-strand has been discussed according to twist of a β-strand generated by forming hydrogen bonds in a β-sheet [30,31,32], while the structure of a β-strand is recognized as a two-fold helix [33]. We can say that the fundamental chirality of a β-strand is two-fold helicity rather than the twist, which is a kind of secondary chirality. Herein we describe two-fold helicity as hidden chirality in a β-strand, which is a part of a β-sheet in biopolymers. Handedness of the two-fold helix is clarified and characterized by applying concepts of tilt-chirality, which is handedness determination based on the tilt of molecules, and multi-point approximation, which is consideration of molecules as multi-point rather than one-point. The unveiled fundamental chirality in a β-strand will give new clues for the origins of chirality generation, homochirality, and chiral properties of proteins.

2. Materials and Methods

Model molecules, pentaglycine and pentaalanine, having various dihedral angles, φ and ψ according to the Ramachandran plot [34], were constructed by using Gauss View5.0.8 [35] and Mercury CSD 4.0.0 [36].

3. Results

Polypeptides construct high dimensional structures, e.g., α-helices [37] and β-sheets [38], by changing dihedral angles of φ and ψ in the main chain [39]. Due to the simplicity of having no chiral centers, pentaglycine was firstly focused on as a model polypeptide. In addition, pentaalanine was also used to clarify effects of chiral centers and side chains by comparing with pentaglycine.

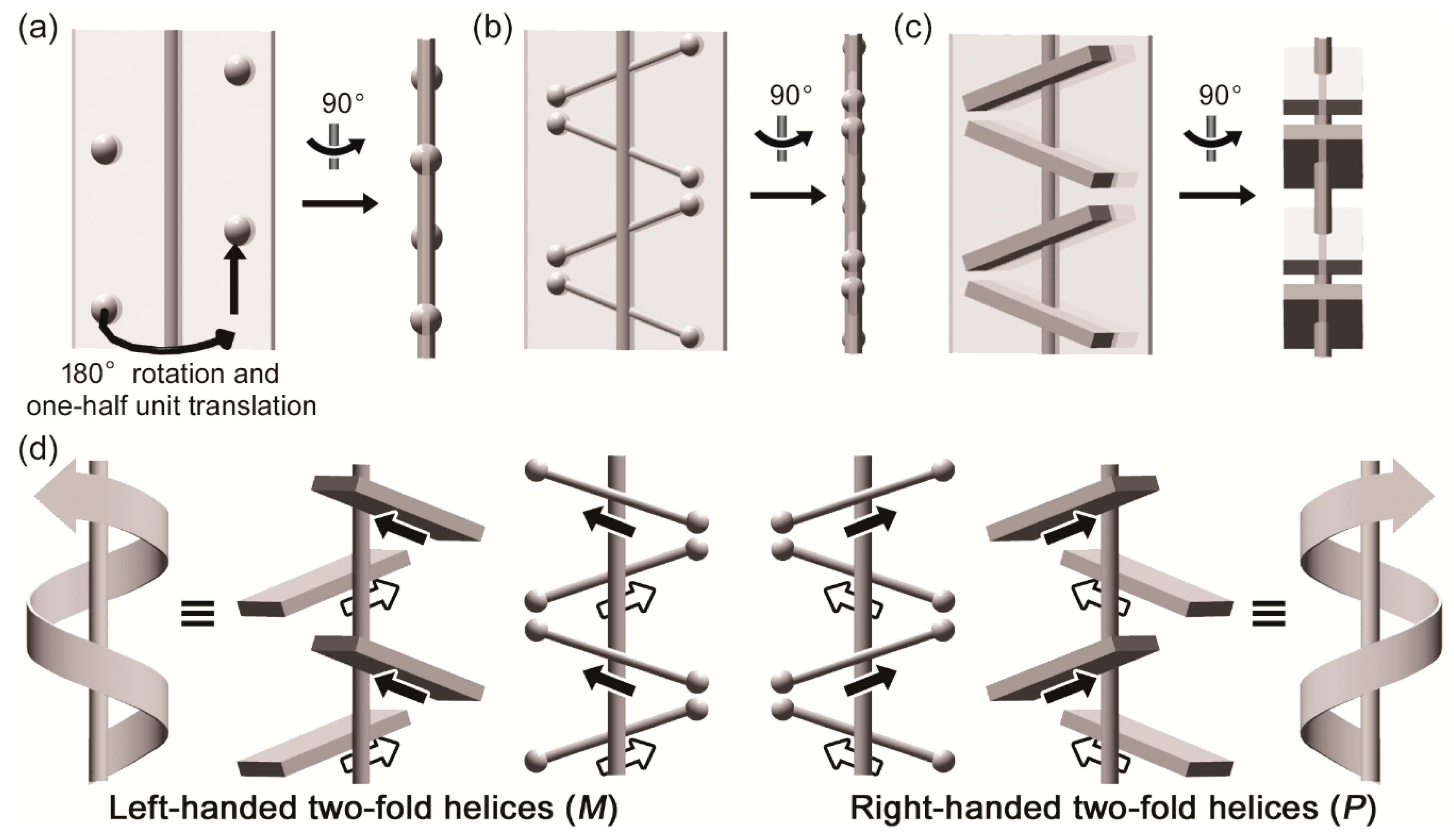
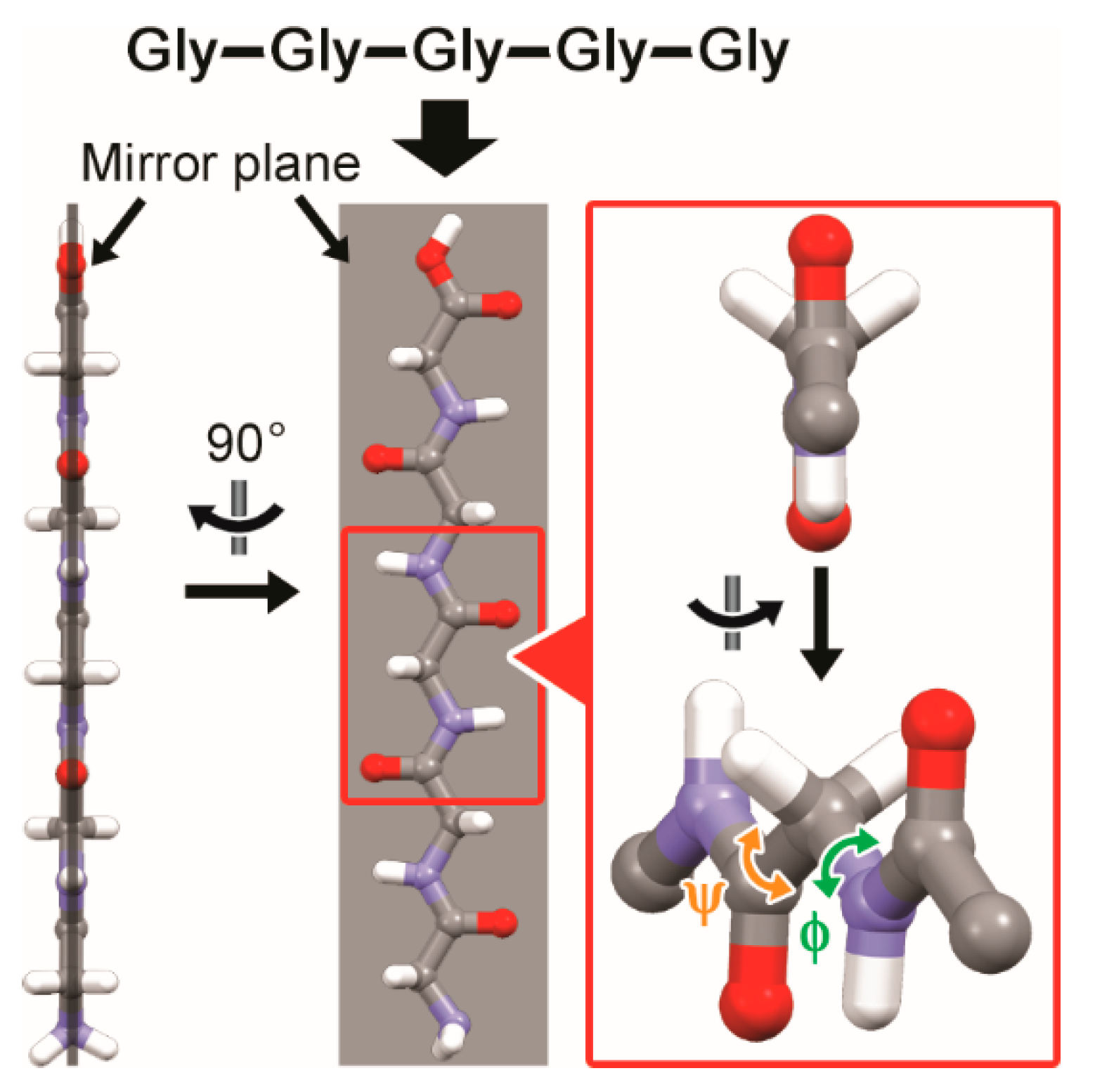
3.1. Two-Fold Helicity of Extended Linear Pentaglycine

Pentaglycine with all trans (φ = 180° and ψ = −180° (or φ = −180° and ψ = 180°)) formed an extended linear structure (Figure 2). The linear structure had two-fold helical symmetry, i.e., a glycine moiety corresponds to the neighboring one by the operation: 180° rotation around the two-fold axis chain followed by translation along the main chain. Such a two-fold helix was achiral because there was a mirror plane along the two-fold helical axis.

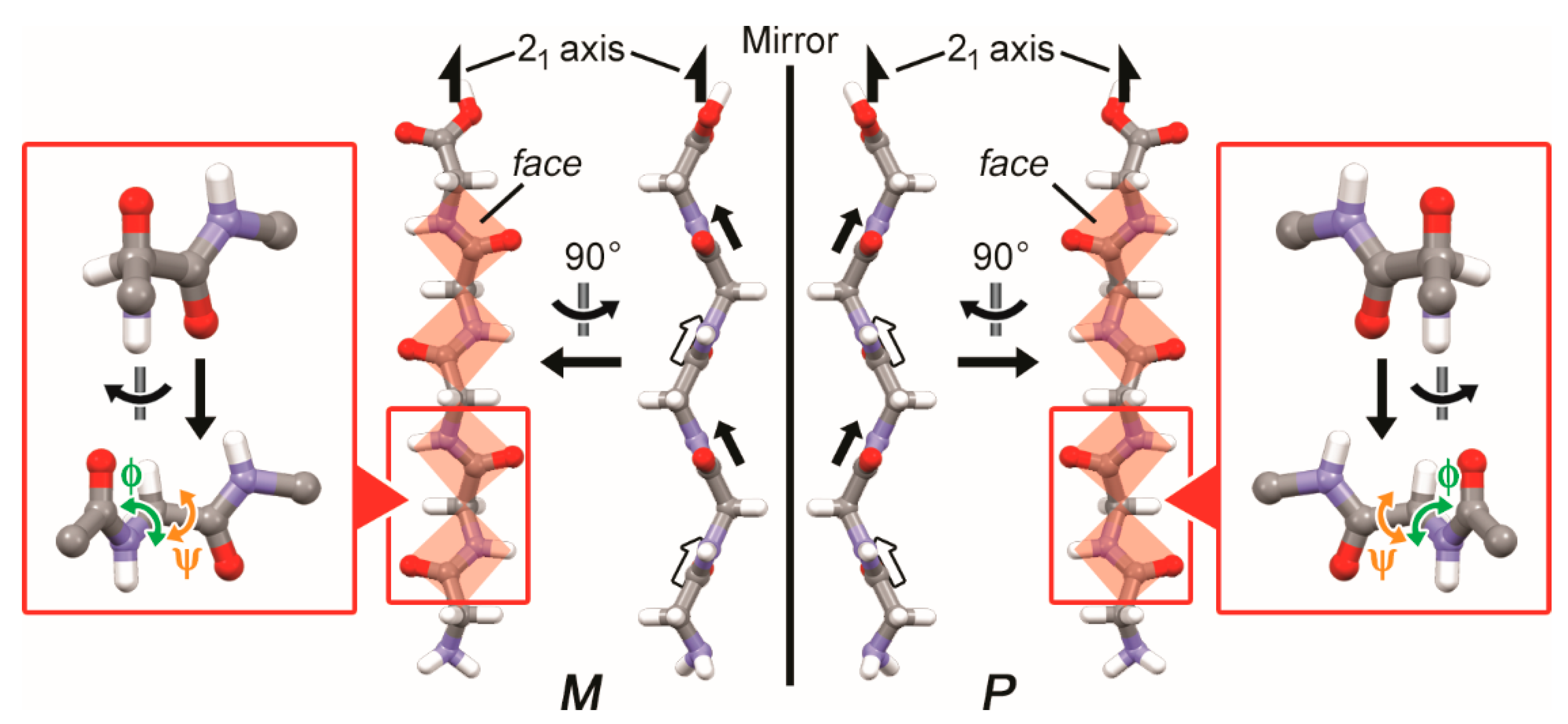
3.2. Two-Fold Helicity of Zig-Zag Pentaglycine

When the dihedral angles became φ = 120° and ψ = −120° (or φ = −120° and ψ = 120°), the linear pentaglycine transformed into a zig-zag structure (Figure 3 left (or right)). Each chain was a so-called β-strand, which is a substructure of a β-sheet. The β-strand had no mirror plane along the two-fold helical axis and constituted a two-fold helix having handedness. Handedness of the two-fold helicity was defined by focusing on lines or faces in the β-strand. Here we defined a face by a peptide bond, which is a well-known planar structure in polypeptides and neighboring alpha carbons of glycine residues.
Handedness of the two-fold helicity in the β-strand was defined by application of the same concept of the supramolecular-tilt-chirality method, i.e., helical handedness was defined based on tilt of lines or faces in front of helical axes. Relative positions of the faces against the helical axis, front and back, were distinguished based on the position of an oxygen atom in the face when the β-strand was viewed from the direction that was vertical to the helical axis and parallel to the faces. When the faces in front of the helical axis were tilted to the left, the β-strand was defined as a left-handed (M) two-fold helix (φ = 120° and ψ = −120°, Figure 3 left). Its mirror-imaged one was a right-handed (P) two-fold helix having faces tilted to the right in front of the helical axis (Figure 3 right). In this case, dihedral angles of the β-strand were φ = −120° and ψ = 120°.

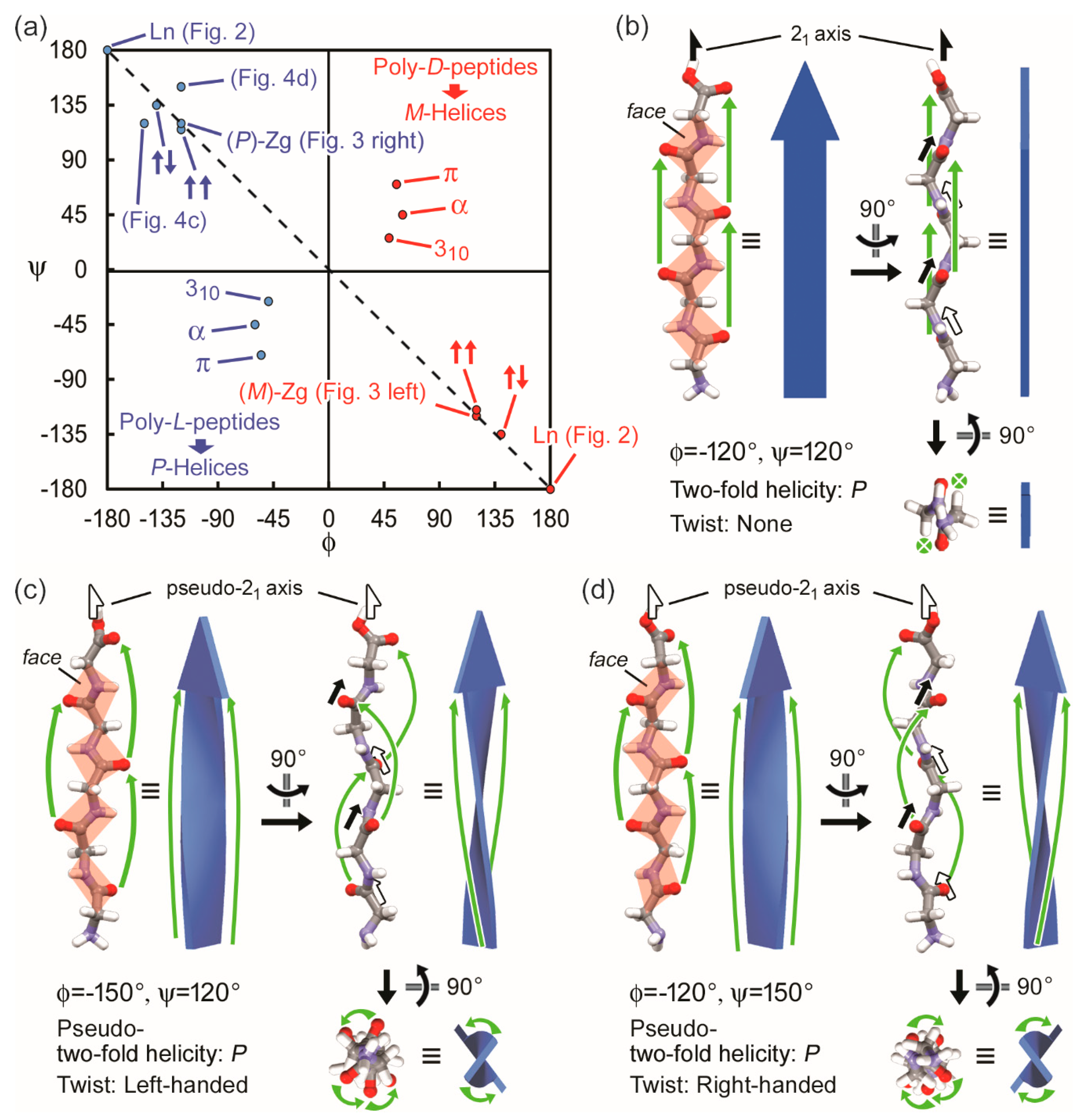
4. Discussion

4.1. Two-Fold Helicity and Twists of β-Strands in Real Polypeptides

The φ and ψ values of the above mentioned linear structure (Ln) and zig-zag β-strand (Zg) are shown on the Ramachandran plot in addition to the representative secondary structures: β-strands in a parallel β-sheet (↑↑), antiparallel β-sheet (↑↓), α-helix (α), 310-helix (310), and π-helix (π) (Figure 4). The blue and red circles are used to distinguish observed structures in real polypeptides composed of L-amino acids and their mirror-imaged structures, respectively. In real polypeptides, β-strands exhibit similar structures to the two-fold helical linear and zig-zag chains. From the viewpoint of symmetry, however, β-strands do not correspond to two-fold helices, with the exception of the case |φ| = |ψ| (dotted line in Figure 4).
Instead, they have pseudo-two-fold helicity with twists along the two-fold helical axes. For example, a β-strand shows a left- or right-handed twist when its dihedral angles are φ = −150° and ψ = 120° or φ = −120° and ψ = 150°, respectively (Figure 4c,d). Handedness of pseudo-two-fold helicity, or tilt of the faces, is unchanged by twists of polypeptide chains. Conventionally, on the other hand, a zig-zag β-strand having a left- (|φ| > |ψ|) or right-handed twist (|φ| < |ψ|) is defined as P or M helices because neighboring amino acid residues in a polypeptide chain are related by less than 180° rotation about the helical axis combined with a unit translation [31].

4.2. Correlation Between Molecular Chirality and Chirality of High Dimensional Structures

In characterization of chiral properties, it is important to consider not only molecular chirality (MC) but also high dimensional chiral structures, which we call high dimensional chirality (HDC) in the present study, because both of the chirality affect chiral functions. Previously, we succeeded in elucidating the linkage between MC and supramolecular chirality (SMC) [40]. At the same time, dependence of chiral characteristics on MC as well as SMC was confirmed by vibrational circular dichroism spectroscopy, which has been used in characterization of chirality in biopolymers [41,42,43]. This success demonstrated that geometrical characterization of MC and HDC leads to prediction and control of HDC. In the same way with the previous study, we investigated the correlation between MC of each amino acid residue and HDC, helicity in the present case, of β-strands and α-helices.
Structures of pentamers comprised of achiral glycine and chiral alanine were compared with each other to clarify effects of chiral centers on chiral secondary structures. In the case of pentaglycine (RCH(NH2)COOH, R = H), M and P two-fold helices are formed almost equally without external chiral sources. On the other hand, there is clear selectivity between M and P two-fold helices in the other polypeptides (RCH(NH2)COOH, R≠H). The selectivity is attributable to steric hindrance between the oxygen atom in a peptide bond and neighboring substituent R (Figure 5a). For example, linear penta-L-alanine (Figure 5a(i)) tends to form a zig-zag β-strand with P two-fold helicity (φ = −120° and ψ = 120°) (Figure 5a(ii)) by letting a methyl group be away from the oxygen atom of a neighboring peptide bond rather than that with M two-fold helicity (φ = 120° and ψ = −120°) (Figure 5a(iii)) by making a methyl group be close to the oxygen atom of a neighboring peptide bond. This fact suggests a correlation between MC and HDC, i.e., absolute structures of amino acids and helicity in polypeptides.
In the same way, handedness selectivity of α-helices is explained. A zig-zag β-strand with P two-fold helicity can be formed from an extended linear poly-L-amino acid by rotating dihedral angles, φ = −180°→−120° (+60°) and ψ = 180°→120° (−60°), in which rotation directions are determined by chirality of component amino acid residues as mentioned above. The β-strand then becomes a right-handed α-helix by further rotation of the dihedral angles: φ = −120°→−60° (+60°) and ψ = 120°→−45° (−165°). The rotation directions, clockwise and counterclockwise in φ and ψ, respectively, are the same as those in the formation of the β-strand from an extended linear poly-L-amino acid, even though the value of rotation angle ψ is relatively large. This coincidence in the rotation directions suggests a structural relationship, or possibility of an inter-structural transition, between a β-strand and α-helix. In fact, there is a region, sometimes called the bridge region, which bridges the regions of β-strand (β-sheet) and α-helix in the Ramachandran plot [39].

5. Conclusions

Two-fold helicity as hidden chirality in a β-strand, which is an important structural motif in proteins, was successfully clarified and characterized by applying the concepts of tilt-chirality and multi-point approximation. We suggest that two-fold helicity is fundamental chirality of a β-strand. The geometric viewpoint brings us a new perspective to explain linkages between handedness of two-fold helicity and that of molecular chirality of amino acid residues in polypeptides. Helicity of an α-helix, twists in a β-strand and β-sheet, as well as central chirality of component amino acids are chiral structures in general polypeptides. The two-fold helicity in a β-strand is also a chiral structure of great importance observed in most polypeptides. Furthermore, the concepts are also applicable to chiral structures of other biopolymers, e.g., polysaccharides [44] and nucleic acids [45], and synthetic crystalline polymers [46] of which chirality is non-negligible. Our findings bring important knowledge for elucidating origins of chirality and homochirality in nature and chiral properties of proteins including amyloid fibrils [47] and also give new insights into the transition from prebiotic chemistry to protobiology [48,49,50].

Author Contributions

Conceptualization, T.S. and M.M.; Investigation, T.S. and M.M.; Supervision, M.M.; Writing—original draft, T.S.; Writing—review and editing, M.M.

Funding

This research received no external funding.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Mason, S.F. Origins of Biomolecular Handedness. Nature 1984, 311, 19–23. [Google Scholar] [CrossRef] [PubMed]
  2. Feringa, B.L.; van Delden, R.A. Absolute Asymmetric Synthesis: the Origin, Control, and Amplification of Chirality. Angew. Chem. Int. Ed. 1999, 38, 3418–3438. [Google Scholar] [CrossRef]
  3. Okano, K.; Taguchi, M.; Fujiki, M.; Yamashita, T. Circularly Polarized Luminescence of Rhodamine B in a Supramolecular Chiral Medium Formed by a Vortex Flow. Angew. Chem. Int. Ed. 2011, 50, 12474–12477. [Google Scholar] [CrossRef]
  4. Inoue, Y. Asymmetric Photochemical Reactions in Solution. Chem. Rev. 1992, 92, 741–770. [Google Scholar] [CrossRef]
  5. Lowry, T.M. Optical Rotatory Power; Dover Publications: New York, NY, USA; London, UK, 1964. [Google Scholar]
  6. Jacques, J.; Collet, A.; Wilen, S.H. Enantiomers, Racemates, and Resolutions; Krieger: Malabar, ‎India, 1991. [Google Scholar]
  7. Matsuura, T.; Koshima, H. Introduction to Chiral Crystallization of Achiral Organic Compounds Spontaneous Generation of Chirality. J. Photochem. Photobiol. C 2005, 6, 7–24. [Google Scholar] [CrossRef]
  8. Vogl, O. Chiral Crystallization and the Origin of Chiral Life on Earth. J. Polym. Sci. Part A Polym. Chem. 2011, 49, 1299–1308. [Google Scholar] [CrossRef]
  9. Weissbuch, I.; Leiserowitz, L.; Lahav, M. Stochastic “Mirror Symmetry Breaking” via Self-Assembly, Reactivity and Amplification of Chirality: Relevance to Abiotic Conditions. Top. Curr. Chem. 2005, 259, 123–165. [Google Scholar]
  10. Soai, K.; Shibata, T.; Morioka, H.; Choji, K. Asymmetric Autocatalysis and Amplification of Enantiomeric Excess of a Chiral Molecule. Nature 1995, 378, 767–768. [Google Scholar] [CrossRef]
  11. Viedma, C. Chiral Symmetry Breaking During Crystallization: Complete Chiral Purity Induced by Nonlinear Autocatalysis and Recycling. Phys. Rev. Lett. 2005, 94, 065504. [Google Scholar] [CrossRef] [PubMed]
  12. Green, B.S.; Lahav, M.; Rabinovich, D. Asymmetric Synthesis via Reactions in Chiral Crystals. Acc. Chem. Res. 1979, 12, 191–197. [Google Scholar] [CrossRef]
  13. Hazen, R.M.; Sholl, D.S. Chiral Selection on Inorganic Crystalline Surfaces. Nat. Mater. 2003, 2, 367–374. [Google Scholar] [CrossRef] [PubMed]
  14. Azumaya, I.; Yamaguchi, K.; Okamoto, I.; Kagechika, H.; Shudo, K. Total Asymmetric Transformation of an N-Methylbenzamide. J. Am. Chem. Soc. 1995, 117, 9083–9084. [Google Scholar] [CrossRef]
  15. Iitaka, Y. The Crystal Structure of β-Glycine. Acta Cryst. 1960, 13, 35–45. [Google Scholar] [CrossRef]
  16. Iitaka, Y. The Crystal Structure of γ-Glycine. Acta Cryst. 1961, 14, 1–10. [Google Scholar] [CrossRef]
  17. Sasaki, T.; Ida, Y.; Tanaka, A.; Hisaki, I.; Tohnai, N.; Miyata, M. Chiral Crystallization by Non-Parallel Face Contacts on the Basis of Three-Axially Asymmetric Twofold Helices. Cryst. Eng. Comm. 2013, 15, 8237–8240. [Google Scholar] [CrossRef]
  18. Sasaki, T.; Miyata, M.; Tsuzuki, S.; Sato, H. Experimental and Theoretical Analysis of Two-fold Helix-Based Chiral Crystallization by Confined Interhelical CH/π Contacts. Cryst. Growth Des. 2019, 19, 1411–1417. [Google Scholar] [CrossRef]
  19. Kitaigorodskii, A.I. Molecular Crystals and Molecules; Academic Press: London, UK, 1973. [Google Scholar]
  20. Groom, C.R.; Bruno, I.J.; Lightfoot, M.P.; Ward, S.C. The Cambridge Structural Database. Acta Cryst. 2016, 72, 171–179. [Google Scholar] [CrossRef] [PubMed]
  21. International Tables for Crystallography Volume A: Space-Group Symmetry. 2016. Available online: https://it.iucr.org/A/ (accessed on 27 March 2019).
  22. Hisaki, I.; Sasaki, T.; Sakaguchi, K.; Liu, W.-L.; Tohnai, N.; Miyata, M. Right- and Left-Handedness of 21 Symmetrical Herringbone Assemblies of Benzene. Chem. Commun. 2012, 48, 2219–2221. [Google Scholar] [CrossRef] [PubMed]
  23. Hisaki, I.; Sasaki, T.; Tohnai, N.; Miyata, M. Supramolecular-Tilt-Chirality on Twofold Helical Assemblies. Chem. Eur. J. 2012, 18, 10066–10073. [Google Scholar] [CrossRef] [PubMed]
  24. Miyata, M.; Tohnai, N.; Hisaki, I.; Sasaki, T. Generation of Supramolecular Chirality around Twofold Rotational or Helical Axes in Crystalline Assemblies of Achiral Components. Symmetry 2015, 7, 1914–1928. [Google Scholar] [CrossRef]
  25. Miyata, M.; Tohnai, N.; Hisaki, I. Crystalline Host–Guest Assemblies of Steroidal and Related Molecules: Diversity, Hierarchy, and Supramolecular Chirality. Acc. Chem. Res. 2007, 40, 694–702. [Google Scholar] [CrossRef] [PubMed]
  26. Miyata, M.; Hisaki, I. Twofold Helical Molecular Assemblies in Organic Crystals: Chirality Generation and Handedness Determination. In Advances in Organic Crystal Chemistry: Comprehensive Reviews; Tamura, R., Miyata, M., Eds.; Springer: Tokyo, Japan, 2015; pp. 371–390. [Google Scholar]
  27. Sasaki, T.; Miyata, M.; Sato, H. Helicity and Topological Chirality in Hydrogen-Bonded Supermolecules Characterized by Advanced Graph Set Analysis and Solid-State Vibrational Circular Dichroism Spectroscopy. Cryst. Growth Des. 2018, 18, 4621–4627. [Google Scholar] [CrossRef]
  28. Kawasaki, T.; Hakoda, Y.; Mineki, H.; Suzuki, k.; Soai, K. Generation of Absolute Controlled Crystal Chirality by the Removal of Crystal Water from Achiral Crystal of Nucleobase Cytosine. J. Am. Chem. Soc. 2010, 132, 2874–2875. [Google Scholar] [CrossRef] [PubMed]
  29. Sasaki, T.; Ida, Y.; Hisaki, I.; Yuge, T.; Uchida, Y.; Tohnai, N.; Miyata, M. Characterization of Supramolecular Hidden Chirality of Hydrogen-Bonded Networks by Advanced Graph Set Analysis. Chem. Eur. J. 2014, 20, 2478–2487. [Google Scholar] [CrossRef]
  30. Chothia, C. Conformation of Twisted β-Pleated Sheets in Proteins. J. Mol. Biol. 1973, 75, 295–302. [Google Scholar] [CrossRef]
  31. Weatherford, D.W.; Salemme, F.R. Conformations of Twisted Parallel β-Sheets and the Origin of Chirality in Protein Structures. Proc. Natl. Acad. Sci. USA 1979, 76, 19–23. [Google Scholar] [CrossRef]
  32. Ho, B.K.; Curmi, P.M.G. Twist and Shear in β-Sheets and β-Ribbons. J. Mol. Biol. 2002, 317, 291–308. [Google Scholar] [CrossRef]
  33. Salemme, F.R. Structural Properties of Protein β-Sheets. Prog. Biophys. Mol. Biol. 1983, 42, 95–133. [Google Scholar] [CrossRef]
  34. Ramachandran, G.N.; Ramakrishnan, C.; Sasisekharan, V. Stereochemistry of Polypeptide Chain Configurations. J. Mol. Biol. 1963, 7, 95–99. [Google Scholar] [CrossRef]
  35. Dennington, R.D., II; Keith, T.A.; Millam, J.M. Gauss View, Version 5; Semichem Inc.: Shawnee Mission, KS, USA, 2009. [Google Scholar]
  36. Macrae, C.F.; Bruno, I.J.; Chisholm, J.A.; Edgington, P.R.; McCabe, P.; Pidcock, E.; Rodriguez-Monge, L.; Taylor, R.; van de Streek, J.; Wood, P.A. Mercury CSD 2.0—New Features for the Visualization and Investigation of Crystal Structures. J. Appl. Cryst. 2008, 41, 466–470. [Google Scholar] [CrossRef]
  37. Pauling, L.; Corey, R.B.; Branson, H.R. The Structure of Proteins: Two Hydrogen-Bonded Helical Configurations of the Polypeptide Chain. Proc. Natl. Acad. Sci. USA 1951, 37, 205–211. [Google Scholar] [CrossRef] [PubMed]
  38. Pauling, L.; Corey, R.B. Configurations of Polypeptide Chains with Favored Orientations Around Single Bonds: Two New Pleated Sheets. Proc. Natl. Acad. Sci. USA 1951, 37, 729–740. [Google Scholar] [CrossRef] [PubMed]
  39. Hollingsworth, S.A.; Karplus, A. A Fresh Look at the Ramachandran Plot and the Occurrence of Standard Structures in Proteins. Biomol. Concepts 2010, 1, 271–283. [Google Scholar] [CrossRef] [PubMed]
  40. Sasaki, T.; Hisaki, I.; Miyano, T.; Tohnai, N.; Morimoto, K.; Sato, H.; Tsuzuki, S.; Miyata, M. Linkage Control between Molecular and Supramolecular Chirality in 21−Helical Hydrogen-Bonded Networks using Achiral Components. Nat. Commun. 2013, 4, 1787. [Google Scholar] [CrossRef]
  41. Kurouski, D. Advances of Vibrational Circular Dichroism (VCD) in Bioanalytical Chemistry. A Review. Anal. Chim. Acta 2017, 990, 54–66. [Google Scholar] [CrossRef] [PubMed]
  42. Nafie, L.A.; Freedman, T.A. Biological and Pharmaceutical Applications of Vibrational Optical Activity. Pract. Spectrosc. 2001, 24, 15–54. [Google Scholar]
  43. Keiderling, T.A. Vibrational Circular Dichroism of Peptides and Proteins. Survey of Techniques, Qualitative and Quantitative Analyses, and Applications. Pract. Spectrosc. 2001, 24, 55–100. [Google Scholar]
  44. Moon, R.J.; Martini, A.; Nairn, J.; Simonsen, J.; Youngblood, J. Cellulose Nanomaterials Review: Structure, Properties and Nanocomposites. Chem. Soc. Rev. 2011, 40, 3941–3994. [Google Scholar] [CrossRef]
  45. Saenger, W. Principles of Nucleic Acid Structure; Springer: New York, NY, USA, 1984. [Google Scholar]
  46. Rosa, C.D.; Auriemma, F. Structure and Physical Properties of Syndiotactic Polypropylene: A Highly Crystalline Thermoplastic Elastomer. Prog. Polym. Sci. 2006, 31, 145–237. [Google Scholar]
  47. Sipe, J.D.; Cohen, A.S. Review: History of the Amyloid Fibril. J. Struct. Biol. 2000, 130, 88–98. [Google Scholar] [CrossRef]
  48. Orgel, L.E. Prebiotic Chemistry and the Origin of the RNA World. Crit. Rev. Biochem. Mol. Biol. 2004, 39, 99–123. [Google Scholar]
  49. Ruiz-Mirazo, K.; Briones, C.; de la Escosura, A. Prebiotic Systems Chemistry: New Perspectives for the Origins of Life. Chem. Rev. 2014, 114, 285–366. [Google Scholar] [CrossRef]
  50. Krishnamurthy, R. Giving Rise to Life: Transition from Prebiotic Chemistry to Protobiology. Acc. Chem. Res. 2017, 50, 455–459. [Google Scholar] [CrossRef]
Symmetry 11 00499 g001 550
Figure 1. Concepts of supramolecular-tilt-chirality method and multi-point approximation method for chirality characterization of two-fold helices. Achiral two-fold helices represented by approximating components as (a) one-point (sphere); (b) two-point (line); (c) three-point (face) on a mirror plane; (d) Chirality of two-fold helices in two-point and three-point approximation methods. The lines or faces in front of the helical axes are tilted to the left or right in the left-(M) or right-handed (P) two-fold helices, respectively.
Figure 1. Concepts of supramolecular-tilt-chirality method and multi-point approximation method for chirality characterization of two-fold helices. Achiral two-fold helices represented by approximating components as (a) one-point (sphere); (b) two-point (line); (c) three-point (face) on a mirror plane; (d) Chirality of two-fold helices in two-point and three-point approximation methods. The lines or faces in front of the helical axes are tilted to the left or right in the left-(M) or right-handed (P) two-fold helices, respectively.
Symmetry 11 00499 g001
Symmetry 11 00499 g002 550
Figure 2. A structure of extended linear pentaglycine. Dihedral angles are φ = 180° and ψ = −180° (or φ = −180° and ψ = 180°).
Figure 2. A structure of extended linear pentaglycine. Dihedral angles are φ = 180° and ψ = −180° (or φ = −180° and ψ = 180°).
Symmetry 11 00499 g002
Symmetry 11 00499 g003 550
Figure 3. Left- (M) and right-handed (P) two-fold helicity in a zig-zag β-strand of which dihedral angles are φ = 120°, ψ = −120° and φ = −120°, ψ = 120°, respectively. Faces are comprised of peptide bonds and neighboring alpha carbons of glycine residues. Relative positions of the faces, front, and back are defined based on the relative position of an oxygen atom in each face against the two-fold helical axis.
Figure 3. Left- (M) and right-handed (P) two-fold helicity in a zig-zag β-strand of which dihedral angles are φ = 120°, ψ = −120° and φ = −120°, ψ = 120°, respectively. Faces are comprised of peptide bonds and neighboring alpha carbons of glycine residues. Relative positions of the faces, front, and back are defined based on the relative position of an oxygen atom in each face against the two-fold helical axis.
Symmetry 11 00499 g003
Symmetry 11 00499 g004 550
Figure 4. (a) The Ramachandran plot indicating φ and ψ values of the linear polypeptide (Ln, φ = 180° and ψ = −180° or φ = −180° and ψ = 180°), the zig-zag β-strands ((M)-Zg, φ = 120° and ψ = −120°; (P)-Zg, φ = −120° and ψ = 120°), the representative secondary structures: β-strands in a parallel β-sheet (↑↑, φ = −120° and ψ = 115°), antiparallel β-sheet (↑↓, φ = −140° and ψ = 135°), α-helix (α, φ = −60° and ψ = −45°), 310-helix (310, φ = −49° and ψ = −26°), and π-helix (π, φ = −55° and ψ = −70°). The linear pentaglycine (Figure 2) and (M)- or (P)-zig-zag pentaglycine (Figure 3) correspond with Ln and (M)- or (P)-Zg, respectively. Blue and red circles are in mirror-imaged relation to each other. (b–d) Relationship among dihedral angles (φ, ψ), (pseudo-)two-fold helicity, and twist: (b) (P)-Zg (φ = −120° and ψ = 120°) with no twist; (c) a β-strand with P pseudo-two-fold helicity and left-handed twist (φ = −150° and ψ = 120°); (d) a β-strand with P pseudo-two-fold helicity and right-handed twist (φ = −120° and ψ = 150°).
Figure 4. (a) The Ramachandran plot indicating φ and ψ values of the linear polypeptide (Ln, φ = 180° and ψ = −180° or φ = −180° and ψ = 180°), the zig-zag β-strands ((M)-Zg, φ = 120° and ψ = −120°; (P)-Zg, φ = −120° and ψ = 120°), the representative secondary structures: β-strands in a parallel β-sheet (↑↑, φ = −120° and ψ = 115°), antiparallel β-sheet (↑↓, φ = −140° and ψ = 135°), α-helix (α, φ = −60° and ψ = −45°), 310-helix (310, φ = −49° and ψ = −26°), and π-helix (π, φ = −55° and ψ = −70°). The linear pentaglycine (Figure 2) and (M)- or (P)-zig-zag pentaglycine (Figure 3) correspond with Ln and (M)- or (P)-Zg, respectively. Blue and red circles are in mirror-imaged relation to each other. (b–d) Relationship among dihedral angles (φ, ψ), (pseudo-)two-fold helicity, and twist: (b) (P)-Zg (φ = −120° and ψ = 120°) with no twist; (c) a β-strand with P pseudo-two-fold helicity and left-handed twist (φ = −150° and ψ = 120°); (d) a β-strand with P pseudo-two-fold helicity and right-handed twist (φ = −120° and ψ = 150°).
Symmetry 11 00499 g004
Symmetry 11 00499 g005 550
Figure 5. (a) Selectivity in rotation direction of dihedral angles for transformation of poly-L-alanine: (i) an extended linear structure to (ii) a favored and (iii) unfavored zig-zag structure (β-strand); (b) Two-fold helicity of zig-zag pentaalanine β-strands: left-handed (M, φ = 120° and ψ = −120°) and right-handed two-fold helices (P, φ = −120° and ψ = 120°) comprised of D-alanine and L-alanine, respectively; (c) Left-handed (M, φ = 60° and ψ = 45°) and right-handed (P, φ = −60° and ψ = −45°) α-helices of penta-D-alanine and penta-L-alanine, respectively.
Figure 5. (a) Selectivity in rotation direction of dihedral angles for transformation of poly-L-alanine: (i) an extended linear structure to (ii) a favored and (iii) unfavored zig-zag structure (β-strand); (b) Two-fold helicity of zig-zag pentaalanine β-strands: left-handed (M, φ = 120° and ψ = −120°) and right-handed two-fold helices (P, φ = −120° and ψ = 120°) comprised of D-alanine and L-alanine, respectively; (c) Left-handed (M, φ = 60° and ψ = 45°) and right-handed (P, φ = −60° and ψ = −45°) α-helices of penta-D-alanine and penta-L-alanine, respectively.
Symmetry 11 00499 g005

Share and Cite

MDPI and ACS Style

Sasaki, T.; Miyata, M. Characterization of Hidden Chirality: Two-Fold Helicity in β-Strands. Symmetry 2019, 11, 499. https://doi.org/10.3390/sym11040499

AMA Style

Sasaki T, Miyata M. Characterization of Hidden Chirality: Two-Fold Helicity in β-Strands. Symmetry. 2019; 11(4):499. https://doi.org/10.3390/sym11040499

Chicago/Turabian Style

Sasaki, Toshiyuki, and Mikiji Miyata. 2019. "Characterization of Hidden Chirality: Two-Fold Helicity in β-Strands" Symmetry 11, no. 4: 499. https://doi.org/10.3390/sym11040499

APA Style

Sasaki, T., & Miyata, M. (2019). Characterization of Hidden Chirality: Two-Fold Helicity in β-Strands. Symmetry, 11(4), 499. https://doi.org/10.3390/sym11040499

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop