Configuration Equilibrium Model of Product Variant Design Driven by Customer Requirements
Abstract
1. Introduction
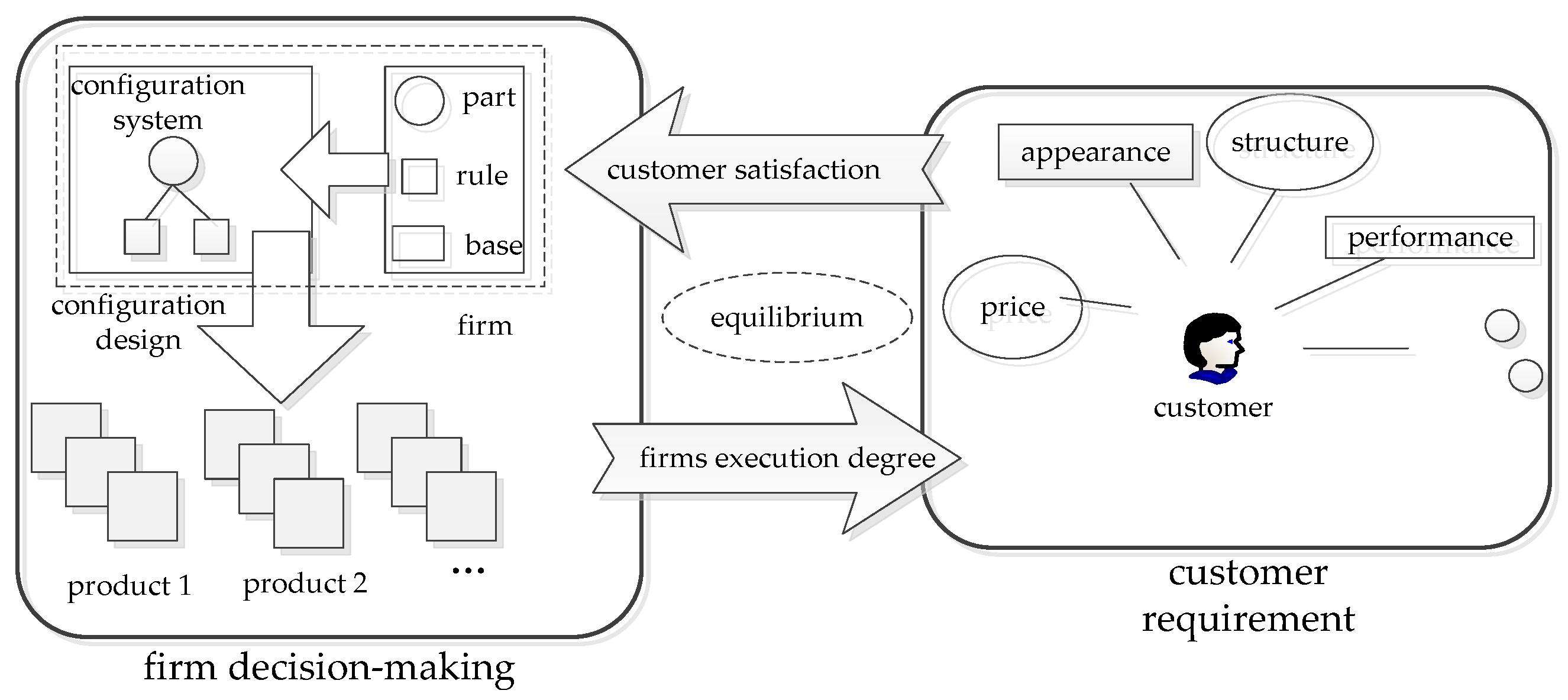
2. Research Background
2.1. Solutions to Customer Requirements (CRs)
2.2. Decision-Making of the Scheme
3. Product Variant Design Driven by CRs
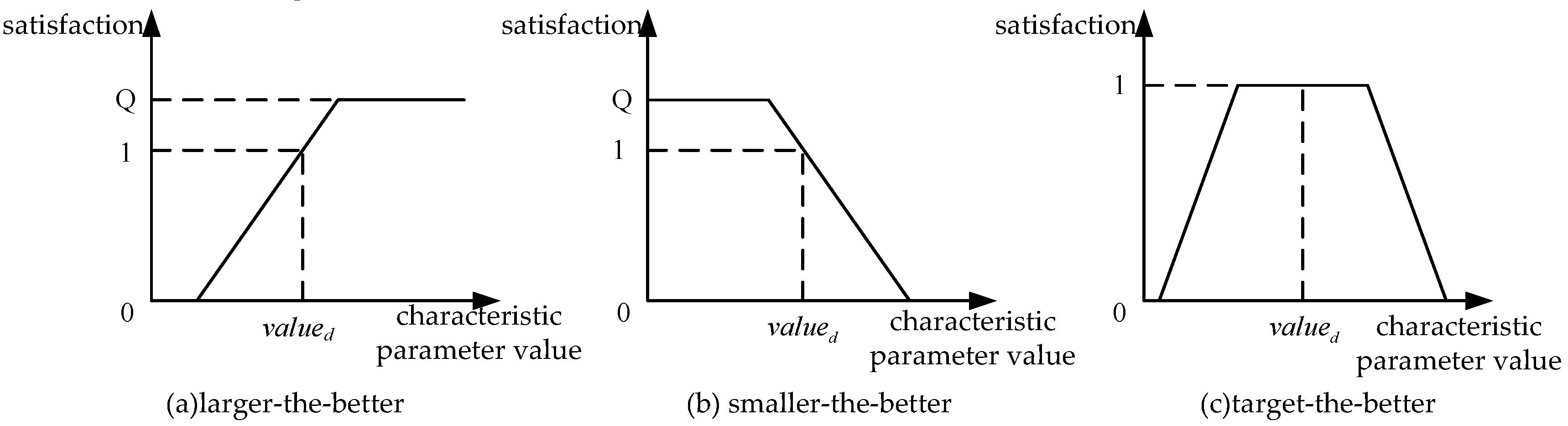
3.1. Customer Dynamic Requirements Acquisition and Transformation
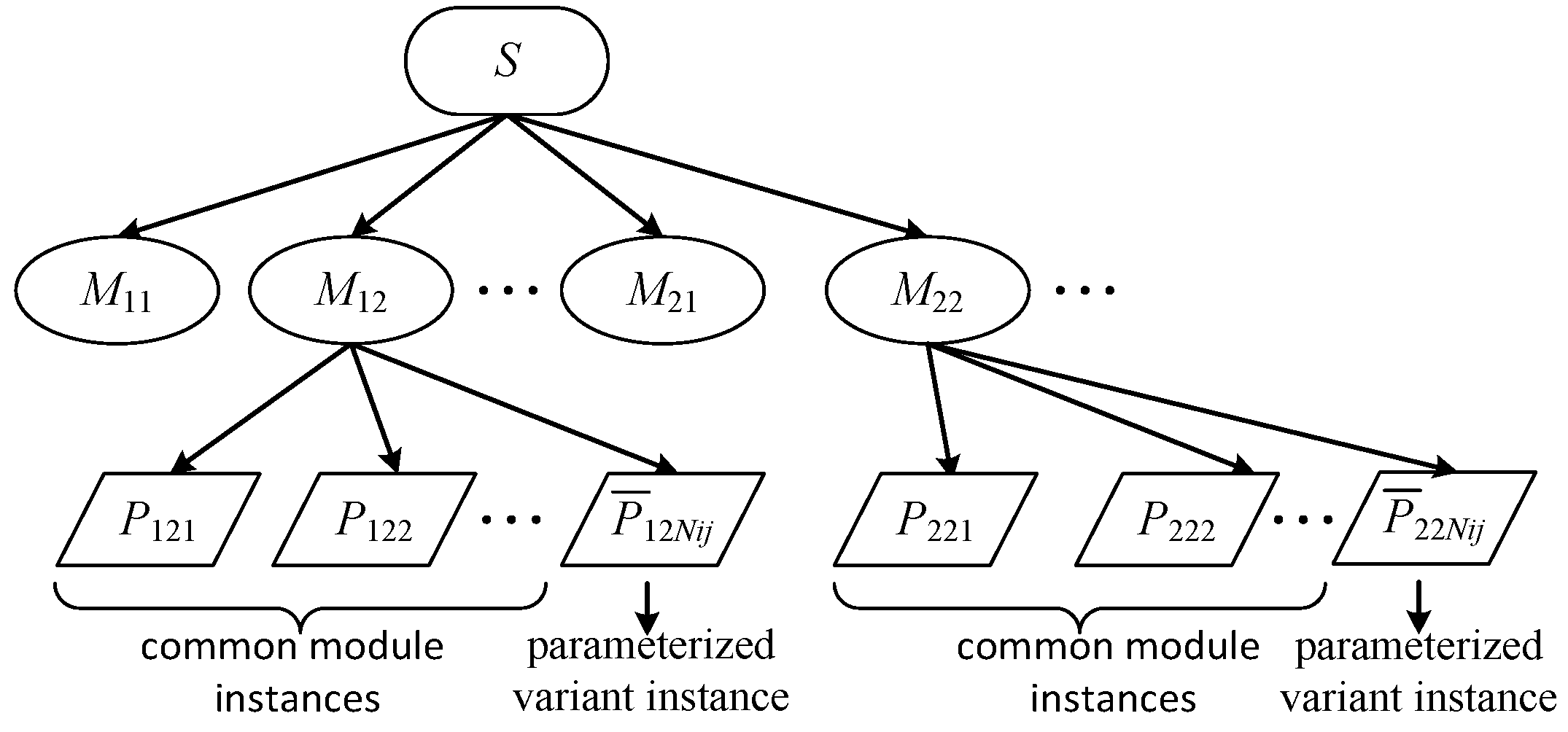
3.2. Modularization and Parameterized Variant Design Method
4. Configuration Model Based on the Bayesian Nash Equilibrium
4.1. The Model of the Bayesian Nash Equilibrium Theory
4.2. Determination of Product Strategy Set
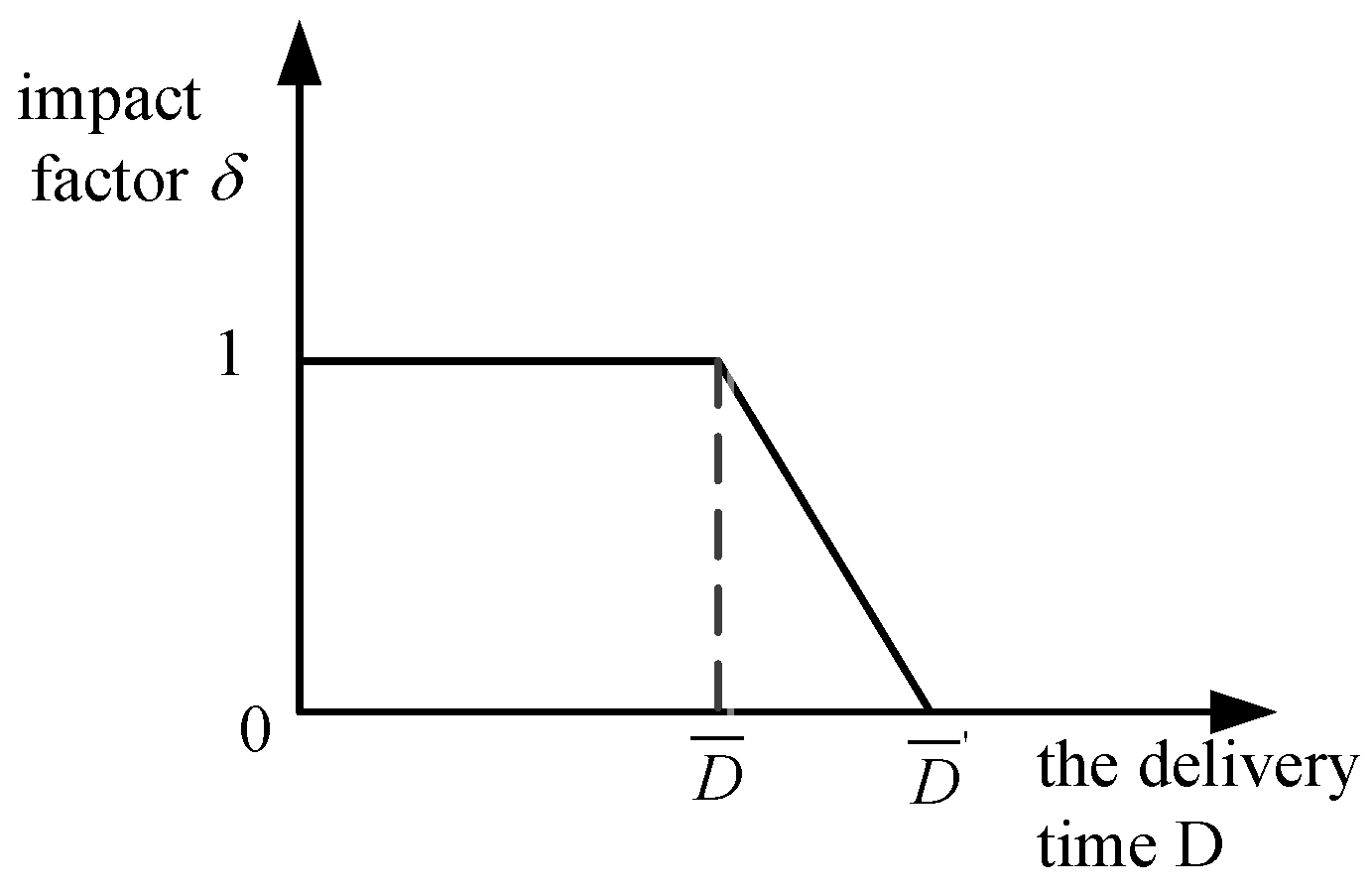
4.3. Construction of Payoff Function
4.4. Game Tree and Payoff Matrix
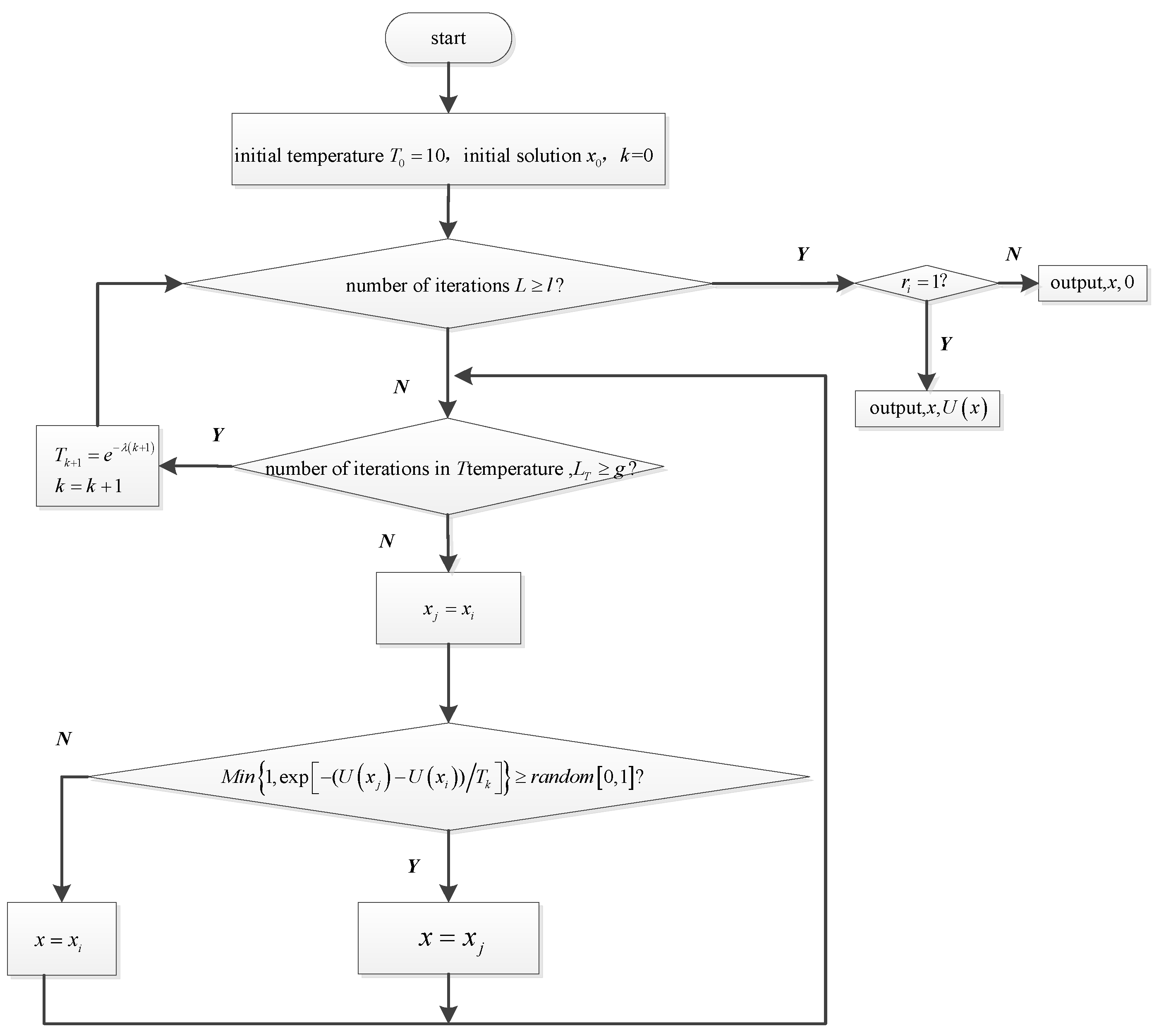
4.5. Calculation of Nash Equilibrium Based on an Improved Simulated Annealing (SA)
5. Case Study
5.1. Transformation of CRs
5.2. Variant Design Modules
5.3. Determination of Strategy Sets
5.4. Calculation of Nash Equilibrium Based on SA
6. Conclusions
- Based on the variant requirements of products, a virtual parameterized variable example is presented to realize the product variant design which combines modularization and parameterization.
- A Bayesian Nash equilibrium game model with customer satisfaction and reduced cost as the objectives is established based on the configuration decision problem of the product variant module, and the equilibrium solution of the scheme decision is realized.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Du, X.; Jiao, J.; Tseng, M.M. Understanding customer satisfaction in product customization. Int. J. Adv. Manuf. Technol. 2006, 31, 396–406. [Google Scholar] [CrossRef]
- Chen, C.; Wang, L. Integrating rough set clustering and grey model to analyse dynamic customer requirements. Proc. Inst. Mech. Eng. Part B J. Eng. Manuf. 2008, 222, 319–332. [Google Scholar] [CrossRef]
- Oddsson, G.; Ladeby, K.R. From a literature review of product configuration definitions to a reference framework. Artif. Intel. Eng. Des. Anal. Manuf. 2014, 28, 413–428. [Google Scholar] [CrossRef]
- Bonvoisin, J.; Halstenberg, F.; Buchert, T.; Stark, R. A systematic literature review on modular product design. J. Eng. Des. 2016, 27, 488–514. [Google Scholar] [CrossRef]
- Jia, W.; Liu, Z.; Lin, Z.; Qiu, C.; Tan, J. Quantification for the importance degree of engineering characteristics with a multi-level hierarchical structure in QFD. Int. J. Prod. Res. 2016, 54, 1627–1649. [Google Scholar] [CrossRef]
- Ma, J.; Kremer, G.E. A systematic literature review of modular product design (MPD) from the perspective of sustainability. Int. J. Adv. Manuf. Technol. 2016, 86, 1509–1539. [Google Scholar] [CrossRef]
- Lo, C.H.; Tseng, K.C.; Chu, C.H. One-Step QFD based 3D morphological charts for concept generation of product variant design. Expert Syst. Appl. 2010, 37, 7351–7363. [Google Scholar] [CrossRef]
- Yu, G.; Yang, Y.; Liu, A. Joint optimization of complex product variant design responding to customer requirement changes. J. Intell. Fuzzy Syst. 2016, 30, 397–408. [Google Scholar]
- Levandowski, C.E.; Jiao, J.R.; Johannesson, H. A two-stage model of adaptable product platform for engineering-to-order configuration design. J. Eng. Des. 2015, 26, 220–235. [Google Scholar] [CrossRef]
- Vianello, G.; Ahmed-Kristensen, S. A comparative study of changes across the lifecycle of complex products in a variant and a customised industry. J. Eng. Des. 2012, 23, 99–117. [Google Scholar] [CrossRef]
- Luh, D.B.; Ko, Y.T.; Ma, C.H. A structural matrix-based modelling for designing product variety. J. Eng. Des. 2011, 22, 1–29. [Google Scholar] [CrossRef]
- Feng, Y.X.; Hao, H.; Tan, J.R.; Hagiwara, I. Variant design for mechanical parts based on extensible logic theory. Int. J. Mech. Mater. Des. 2010, 6, 123–134. [Google Scholar] [CrossRef]
- Simpson, T.W.; Siddique, Z.; Jiao, R.J. Product Platform and Product Family Design: Methods and Applications; Springer: New York, NY, USA, 2005. [Google Scholar]
- Tseng, H.E.; Chang, C.C.; Chang, S.H. Applying case-based reasoning for product configuration in mass customization environments. Expert Syst. Appl. 2005, 29, 913–925. [Google Scholar] [CrossRef]
- Li, B.; Chen, L.; Huang, Z. Product configuration optimization using a multiobjective genetic algorithm. Int. J. Adv. Manuf. Technol. 2006, 30, 20–29. [Google Scholar] [CrossRef]
- Baldwin, C.Y.; Clark, K.B. Managing in an age of modularity. Harv. Bus. Rev. 1997, 75, 84–93. [Google Scholar] [PubMed]
- Inoue, M.; Lindow, K.; Stark, R.; Tanaka, K.; Nahm, Y.-E.; Ishikawa, H. Decision-making support for sustainable product creation. J. Adv. Eng. Inform. 2012, 26, 782–792. [Google Scholar] [CrossRef]
- Nepal, B.; Yadav, O.P.; Murat, A. A fuzzy-AHP approach to prioritization of CS attributes in target planning for automotive product development. Expert Syst. Appl. 2010, 37, 6775–6786. [Google Scholar] [CrossRef]
- Ma, H.; Chu, X.; Xue, D.; Chen, D. A systematic decision making approach for product conceptual design based on fuzzy morphological matrix. Expert Syst. Appl. 2017, 81, 444–456. [Google Scholar] [CrossRef]
- Wang, D.; Hong, K.L. Multi-fleet ferry service network design with passenger preferences for differential services. Transp. Res. Part B Methodol. 2008, 42, 798–822. [Google Scholar] [CrossRef]
- Gebauer, H.; Gustafsson, A.; Witell, L. Competitive advantage through service differentiation by manufacturing companies. J. Bus. Res. 2011, 64, 1270–1280. [Google Scholar] [CrossRef]
- Hartline, J.D. Bayesian mechanism design. Found. Trends Theor. Comput. Sci. 2013, 8, 143–263. [Google Scholar] [CrossRef]
- Alid-Vaccarezza, M.; Soto, M.E. Bayesian Nash equilibria using extended Werner-like states. Quantum Inf. Process. 2016, 15, 4337–4346. [Google Scholar] [CrossRef]
- Hougaard, J.L.; Tvede, M. Truth-telling and Nash equilibria in minimum cost spanning tree models. European. J. Oper. Res. 2012, 222, 566–570. [Google Scholar] [CrossRef]
- Solmeyer, N.; Dixon, R.; Balu, R. Characterizing the Nash equilibria of a three-player Bayesian quantum game. Quantum Inf. Process. 2017, 16, 146. [Google Scholar] [CrossRef]
- Sadeghi, A.; Zandieh, M. A game theory-based model for product portfolio management in a competitive market. Expert Syst. Appl. 2011, 38, 7919–7923. [Google Scholar] [CrossRef]
- Mu, H.; Jiang, P.; Leng, J. Costing-based coordination between mt-iPSS customer and providers for job shop production using game theory. Int. J. Prod. Res. 2017, 55, 430–446. [Google Scholar] [CrossRef]
- Sousa-Zomer, T.T.; Miguel, P.A.C. A QFD-based approach to support sustainable product-service systems conceptual design. Int. J. Adv. Manuf. Technol. 2016, 88, 701–717. [Google Scholar] [CrossRef]
- Chan, L.K.; Wu, M.L. Quality Function Deployment: A Literature Review. Eur. J. Oper. Res. 2002, 143, 463–497. [Google Scholar] [CrossRef]
- Wang, S.S.; Kong, Z.K.; Xie, C.; Xiang, J. Bayesian Nash Equilibrium Analysis of Medical Market under Asymmetry Information. In Proceedings of the 2008 4th International Conference on Wireless Communications, Networking and Mobile Computing, Dalian, China, 2–14 October 2008. [Google Scholar]
- Zandt, T.V.; Vives, X. Monotone equilibria in Bayesian games of strategic comple-mentarities. J. Econ. Theory. 2007, 134, 339–360. [Google Scholar] [CrossRef]
- Nishimura, K.; Friedman, J. Existence of Nash equilibrium in n person games without quasiconcavity. Int. Econ. Rev. 1981, 22, 637–648. [Google Scholar] [CrossRef]
- Gabriel, S.A.; Kiet, S.; Zhuang, J. A mixed complementarity-based equilibrium model of natural gas markets. Oper. Res. 2005, 53, 799–818. [Google Scholar] [CrossRef]
- Liu, J.; Zhao, H.; Xu, Z.; Wu, Z. Research on Demand-overflowing Customer Satisfaction Model. China Mech. Eng. 2013, 24, 2880–2884. [Google Scholar]
- Allahyari, S.; Salari, M.; Vigo, D. A hybrid metaheuristic algorithm for the multi-depot covering tour vehicle routing problem. Eur. J. Oper. Res. 2015, 242, 756–768. [Google Scholar] [CrossRef]
- Oliveira, H.; Petraglia, A. Establishing Nash equilibria of strategic games: A multistart fuzzy adaptive simulated annealing approach. Appl. Soft Comput. 2014, 19, 188–197. [Google Scholar] [CrossRef]
- Wei, G.; Qin, Y. Framework of Rapid Product Cost Estimation Based on the Modular Product Family. In 2011 International Conference in Electrics, Communication and Automatic Control Proceedings; Chen, R., Ed.; Springer: New York, NY, USA, 2012. [Google Scholar]
- Wang, H.; Sun, B.; Zhang, Q.; Wang, J.; Wei, X. Variant configuration design upporting personalization product customization. Chin. J. Mech. Eng. 2006, 42, 90–97. (In Chinese) [Google Scholar] [CrossRef]



| Physical Annealing | Optimization Problem |
|---|---|
| State of matter | Solution |
| The lowest energy state of matter | Optimal solution |
| Annealing process | Solution procedure |
| Temperature | Controls parameter |
| Energy | Objective function |
| Constant temperature process | Metropolis Sampling process |
| Module Name | Module Instance | Cost (1000 Yuan) | Delivery Time (Days) | Module Attributes |
|---|---|---|---|---|
| M11 car body module | P111 | 8 | 4 | basic module |
| P112 | 12 | 5 | ||
| P113 | 14 | 6 | ||
| 13 | 7 | |||
| M12 battery module | P121 | 4.5 | 2.5 | basic module |
| P122 | 3 | 2 | ||
| P123 | 5 | 3.5 | ||
| 6 | 4 | |||
| M13 navigation module | P131 | 12 | 7 | basic module |
| P132 | 8 | 6.5 | ||
| 15 | 8 | |||
| M21 automatic charging module | P211 | 10 | 5 | optional module |
| P212 | 9 | 7 |
| Scheme | Component Module | Delivery Time (Days) | Customer Satisfaction S |
|---|---|---|---|
| x1 | , P131, P211 | 20 | 0.8692 |
| x2 | P111, P121, , P211 | 19.5 | 0.8684 |
| x3 | P112, P123, P132, P211, | 20 | 0.8637 |
| x4 | P112, P122, , P211, | 20 | 0.8625 |
| x5 | P113, P122, P131, P211 | 20 | 0.8548 |
| x6 | P112, P122, , P212 | 20.5 | 0.8528 |
| x7 | P111, , P132, P211 | 19.5 | 0.8520 |
| x8 | P111, P123, P131, P211, | 20 | 0.8516 |
| x9 | P113, P121, P132, P211 | 20 | 0.8431 |
| Strategy | Component Module | Payoff Value |
|---|---|---|
| x7 | , P132, P211 | 0.252 |
| x3 | P112, P123, P132, P211 | 0.419 |
| x8 | P111, P121, P131, P211 | 0.760 |
| x1 | P111, , P131, P211 | 1.375 |
| x9 | P113, P121, P132, P211 | 1.458 |
| Firm | ||||
|---|---|---|---|---|
| Strategy | Respective Strategies | Implement | Non-Implement | |
| Customer | x7 | accept | (8.520,8.889) | (0,0) |
| refuse | (0,0) | (0,0) | ||
| x3 | accept | (8.637,9.556) | (0,0) | |
| refuse | (0,0) | (0,0) | ||
| x8 | accept | (8.516,9.556) | (0,0) | |
| refuse | (0,0) | (0,0) | ||
| x1 | accept | (8.692,9.778) | (0,0) | |
| refuse | (0,0) | (0,0) | ||
| x9 | accept | (8.431,9.889) | (0,0) | |
| refuse | (0,0) | (0,0) | ||
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, Q.; Bian, X.; Stark, R.; Fresemann, C.; Song, F. Configuration Equilibrium Model of Product Variant Design Driven by Customer Requirements. Symmetry 2019, 11, 508. https://doi.org/10.3390/sym11040508
Yang Q, Bian X, Stark R, Fresemann C, Song F. Configuration Equilibrium Model of Product Variant Design Driven by Customer Requirements. Symmetry. 2019; 11(4):508. https://doi.org/10.3390/sym11040508
Chicago/Turabian StyleYang, Qin, Xianjun Bian, Rainer Stark, Carina Fresemann, and Fei Song. 2019. "Configuration Equilibrium Model of Product Variant Design Driven by Customer Requirements" Symmetry 11, no. 4: 508. https://doi.org/10.3390/sym11040508
APA StyleYang, Q., Bian, X., Stark, R., Fresemann, C., & Song, F. (2019). Configuration Equilibrium Model of Product Variant Design Driven by Customer Requirements. Symmetry, 11(4), 508. https://doi.org/10.3390/sym11040508





