A Multi-Objective Programming Approach to Design Feeder Bus Route for High-Speed Rail Stations
Abstract
:1. Introduction
2. Literature Review
3. Problem Formulation
3.1. Problem Description and Assumptions
3.2. Mathematical Formulation
4. Solution Method
| Input: stop location and route design instance of feeder bus system for high-speed rail stations |
| Output:ParetoSet: the Pareto optimal front |
| 1: |
| 2: Solve |
| 3: Solve |
| 4: Solve |
| 5: Solve |
| 6: |
| 7: Set |
| 8: while do |
| 9: Solve |
| 10: |
| 11: Set |
| 12: Remove dominated points from ParetoSet. |
5. Numerical Example
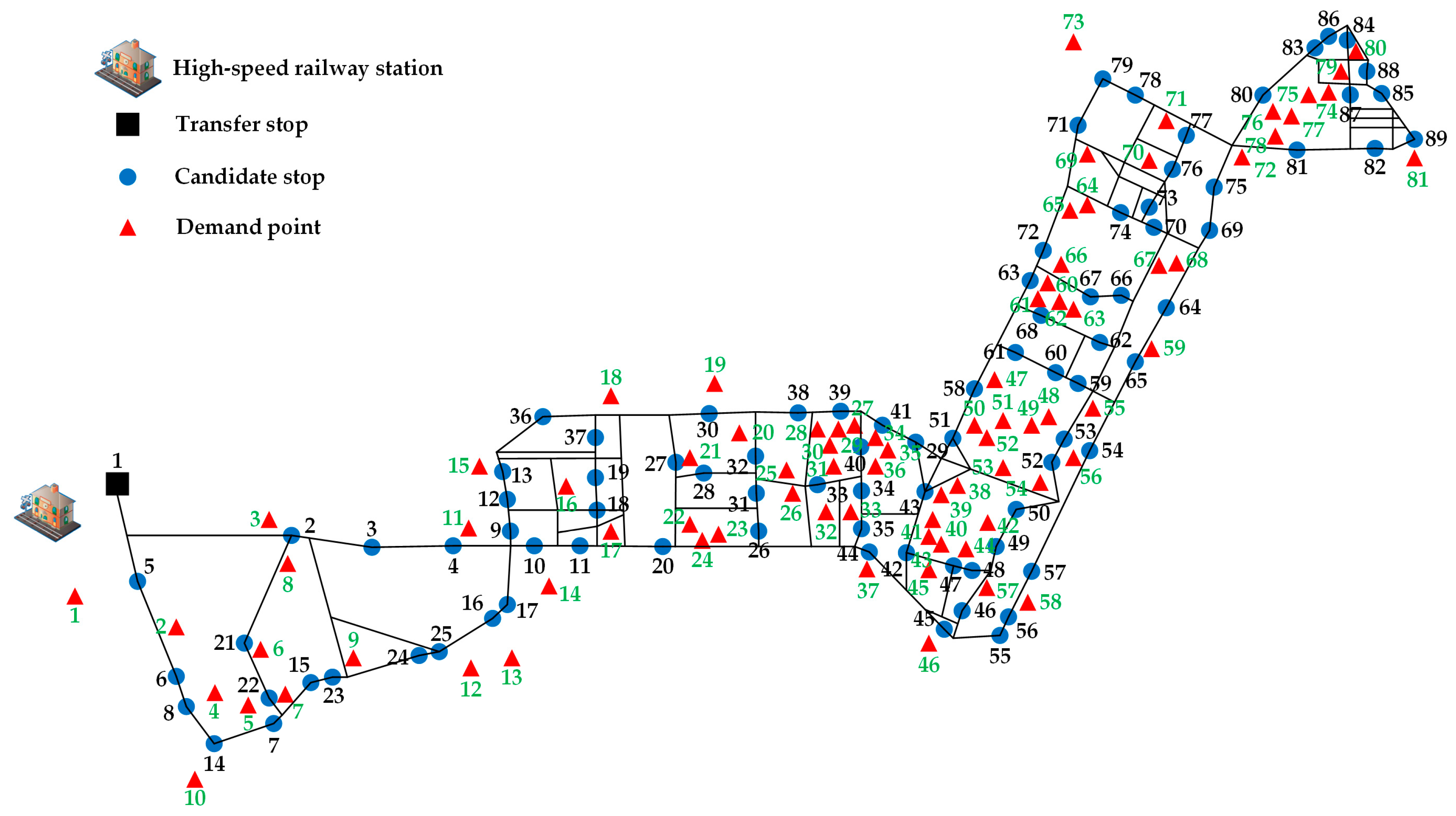
5.1. Scenario Studied
5.2. Computational Results
5.3. Effect of the Maximum Acceptable Walking Distance of Passengers
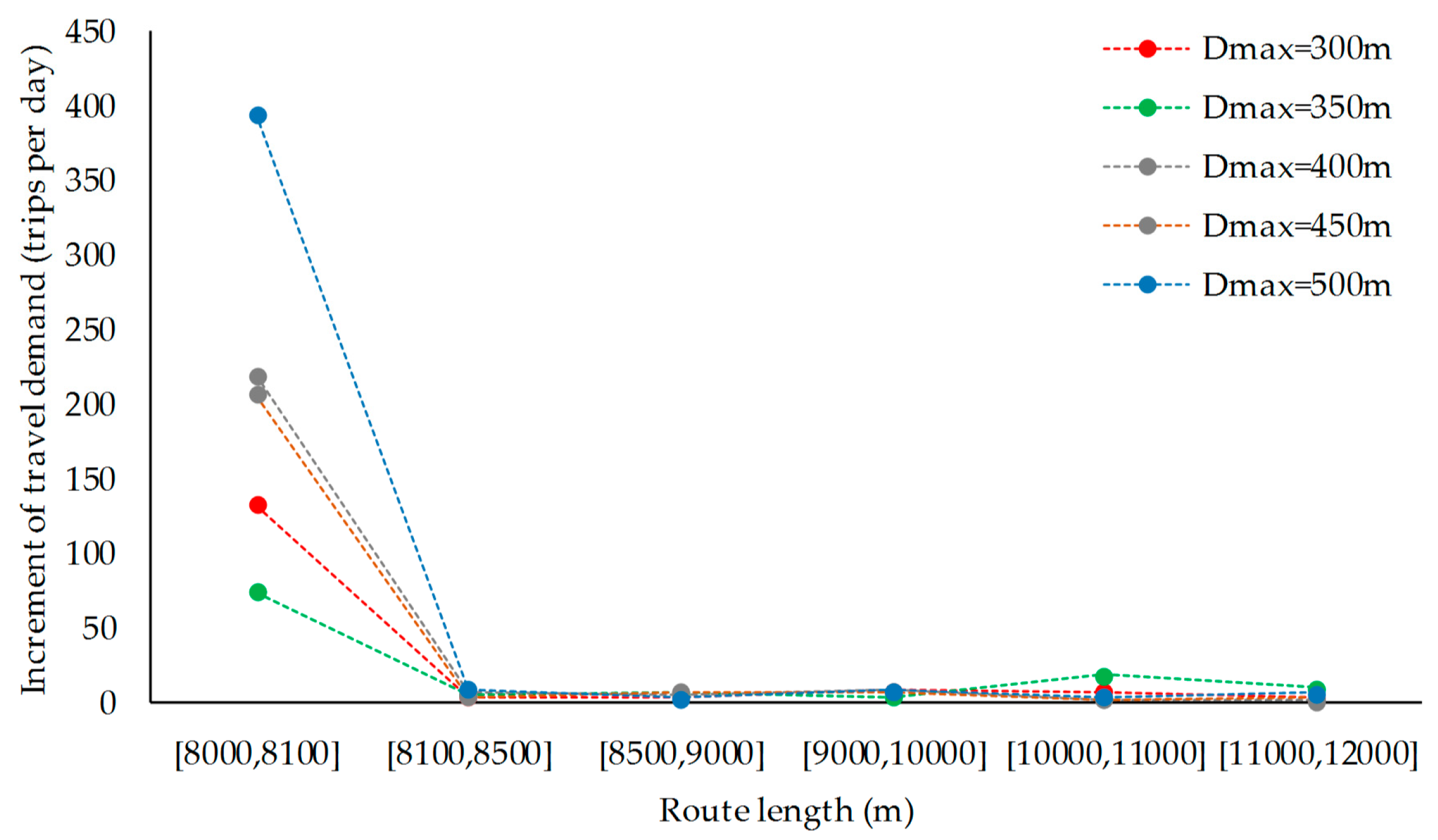
5.4. Benefits Brought by Increasing Feeder Bus Route Length
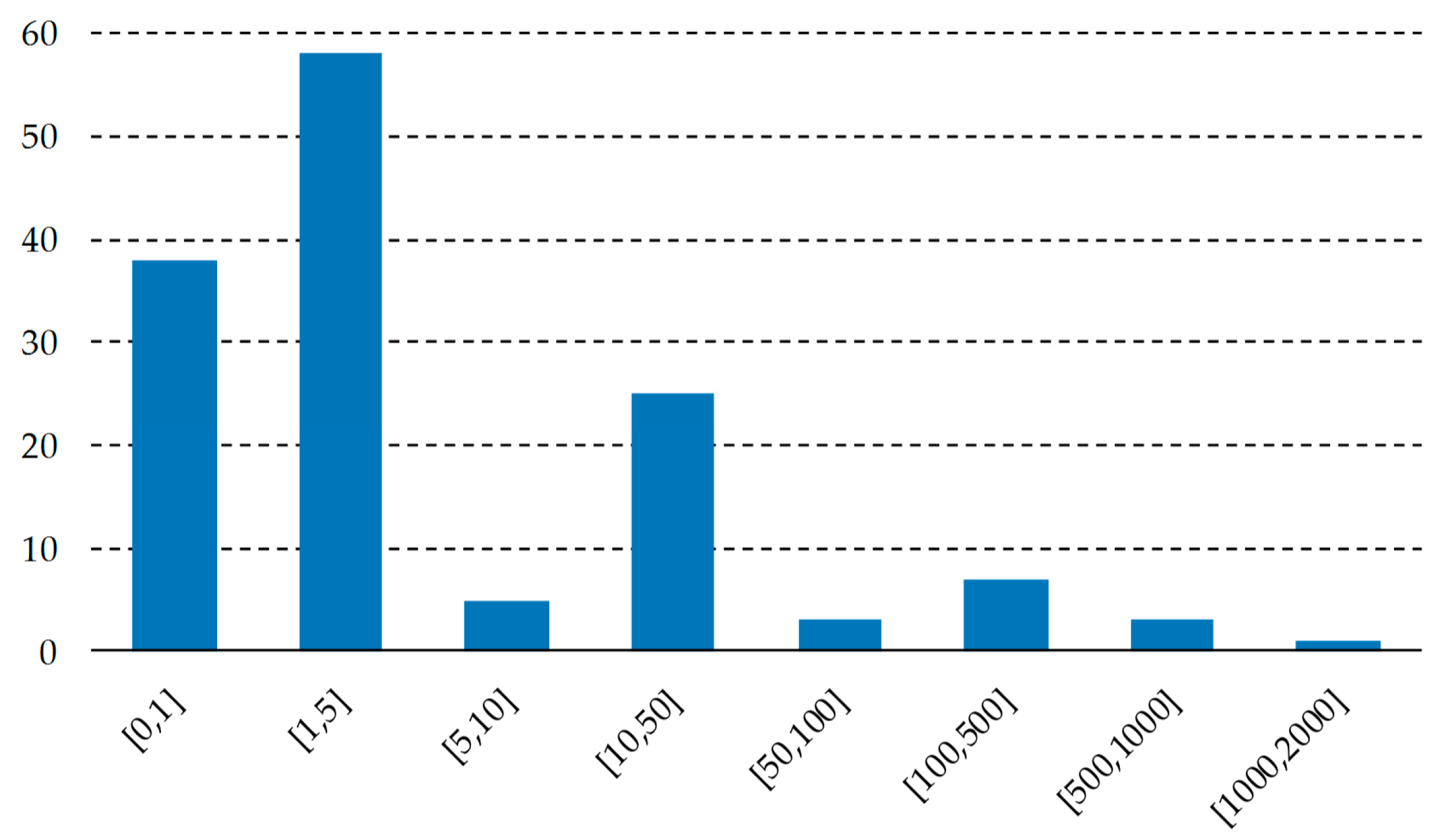
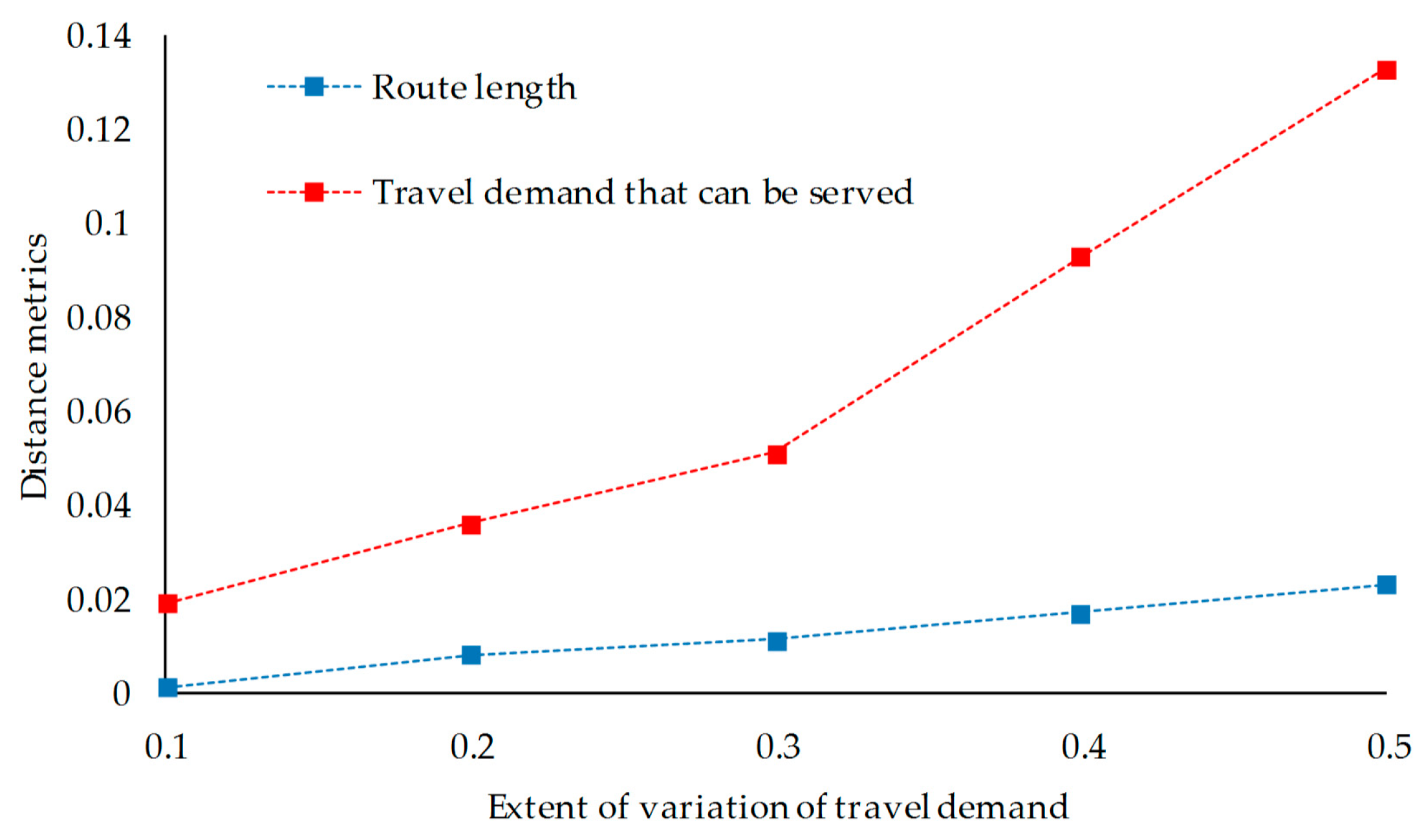
5.5. Robustness of the Pareto Optimal Solutions
5.6. Integrated Approach vs. Exisiting Approach
6. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Semler, C.; Hale, C. Rail station access—An assessment of options. In Proceedings of the 33rd Australasian Transport Research Forum Conference, Canberra, Australia, 29 Semptember–1 October 2010. [Google Scholar]
- Cheng, X.Y.; Cao, Y.; Huang, K.; Wang, Y.J. Modeling the satisfaction of bus traffic transfer service quality at a high-speed railway station. J. Adv. Transp. 2018, 2018, 7051789:1–7051789:12. [Google Scholar] [CrossRef]
- Teng, J.; Shen, B.; Fei, X.; Zhang, J.X.; Jiang, Z.B.; Ma, C. Designing feeder bus lines for high-speed railway terminals. Syst. Eng. Theory Pract. 2013, 33, 2937–2944. [Google Scholar] [CrossRef]
- Fan, W. Optimal transit route network design problem: Algorithms, implementations, and numerical results. Ph.D. Thesis, The University of Texas at Austin, Austin, TX, USA, 2004. [Google Scholar]
- Park, J.; Kim, B.I. The school bus routing problem: A review. Eur. J. Oper. Res. 2010, 202, 311–319. [Google Scholar] [CrossRef]
- Metcalf, D.D.; Bond, V.L. Bus stop guidelines to meet urban, suburban and rural conditions. In Proceedings of the ITE 2006 Technical Conference and Exhibit Compendium of Technical Papers, San Antonio, TX, USA, 19–22 March 2006. [Google Scholar]
- Chien, S.; Yang, Z.W. Optimal feeder bus routes on irregular street networks. J. Adv. Transpt. 2000, 34, 213–248. [Google Scholar] [CrossRef]
- Jerby, S.; Ceder, A. Optimal routing design for shuttle bus service. In Proceedings of the 85th Annual Meeting of the Transportation-Research-Board, Transportation Research Board Natl Research Council, Washington, DC, USA, 22–26 January 2006. [Google Scholar] [CrossRef]
- Xiong, J.; Guan, W.; Huang, A.L. Research on optimal routing of community shuttle connect rail transit line. J. Trans. Syst. Eng. Inf. Technol. 2014, 14, 166–173. [Google Scholar] [CrossRef]
- Zhu, Z.J.; Guo, X.C.; Zeng, J.; Zhang, S.R. Route design model of feeder bus service for urban rail transit stations. Math. Probl. Eng. 2017, 2017, 1090457:1–1090457:6. [Google Scholar] [CrossRef]
- Pan, S.L.; Yu, J.; Yang, X.F.; Liu, Y.; Zou, N. Designing a flexible feeder transit system serving irregularly shaped and gated communities: Determining service area and feeder route planning. J. Urban Plan. Dev. 2014, 141, 04014028:1–04014028:9. [Google Scholar] [CrossRef]
- Lin, J.J.; Wong, H.I. Optimization of a feeder-bus route design by using a multiobjective programming approach. Transpt. Plan. Technol. 2014, 37, 430–449. [Google Scholar] [CrossRef]
- Shrivastava, P.; Dhingra, S.L. Development of feeder routes for suburban railway stations using heuristic approach. J. Transp. Eng. 2001, 127, 334–341. [Google Scholar] [CrossRef]
- Kuan, S.N.; Ong, H.L.; Ng, K.M. Applying metaheuristics to feeder bus network design problem. Asia Pac. J. Oper. Res. 2004, 21, 543–560. [Google Scholar] [CrossRef]
- Kuan, S.N.; Ong, H.L.; Ng, K.M. Solving the feeder bus network design problem by genetic algorithms and ant colony optimization. Adv. Eng. Softw. 2006, 37, 351–359. [Google Scholar] [CrossRef]
- Shrivastava, P.; O’ Mahony, M. A model for development of optimized feeder routes and coordinated schedules—A genetic algorithms approach. Transp. Policy 2006, 13, 413–425. [Google Scholar] [CrossRef]
- Shrivastava, P.; O’ Mahony, M. Use of a hybrid algorithm for modeling coordinated feeder bus route network at suburban railway station. J. Transp. Eng. 2009, 135, 1–8. [Google Scholar] [CrossRef]
- Song, R.; Liu, Z.Q. Heuristic algorithm for feeder bus route generation in railway traffic system. J. Jilin Univ. 2011, 41, 1234–1239. [Google Scholar]
- Sun, Y.; Song, R.; He, S.W. Feeder bus network design under elastic demand. J. Jilin Univ. 2011, 41, 349–354. [Google Scholar] [CrossRef]
- Szeto, W.Y.; Wu, Y.Z. A simultaneous bus route design and frequency setting problem for Tin Shui Wai, Hong Kong. Eur. J. Oper. Res. 2011, 209, 141–155. [Google Scholar] [CrossRef] [Green Version]
- Liu, H.S.; Zhao, S.Z.; Zhu, Y.G.; Li, X.Y. Feeder bus network design model based on effective path. J. Jilin Univ. 2015, 45, 371–378. [Google Scholar] [CrossRef]
- Perugia, A.; Moccia, L.; Cordeau, J.F.; Laporte, G. Designing a home-to-work bus service in a metropolitan area. Transp. Res. B Methodol. 2011, 45, 1710–1726. [Google Scholar] [CrossRef]
- Li, H.G.; Chen, Y.S. Study on enterprise shuttle bus location and route optimization: An integrated approach. J. Univ. Electron. Sci. Technol. China 2016, 18, 68–73. [Google Scholar] [CrossRef]
- Leksakul, K.; Smutkupt, U.; Jintawiwat, R.; Phongmoo, S. Heuristic approach for solving employee bus routes in a large-scale industrial factory. Adv. Eng. Inf. 2017, 32, 176–187. [Google Scholar] [CrossRef]
- Xiong, J.; Guan, W.; Song, L.Y.; Huang, A.L.; Shao, C.F. Optimal routing design of a community shuttle for metro stations. J. Transp. Eng. 2013, 139, 1211–1223. [Google Scholar] [CrossRef]
- Schittekat, P.; Kinable, J.; Sorensen, K.; Sevaux, M.; Spieksma, F.; Springael, J. A metaheuristic for the school bus routing problem with bus stop selection. Eur. J. Oper. Res. 2013, 229, 518–528. [Google Scholar] [CrossRef]
- Chen, J.X.; Wang, S.A.; Liu, Z.Y.; Wang, W. Design of suburban bus route for airport access. Transp. A Transp. Sci. 2017, 13, 568–589. [Google Scholar] [CrossRef]
- Yan, S.Y.; Wang, S.S.; Wu, M.W. A model with a solution algorithm for the cash transportation vehicle routing and scheduling problem. Comput. Ind. Eng. 2012, 63, 464–473. [Google Scholar] [CrossRef]
- Yan, S.Y.; Wang, S.S.; Chang, Y.H. Cash transportation vehicle routing and scheduling under stochastic travel times. Eng. Optimiz. 2014, 46, 289–307. [Google Scholar] [CrossRef]
- Bányai, T. Real-time decision making in first mile and last mile logistics: How smart scheduling affects energy efficiency of hyperconnected supply chain solutions. Energies 2018, 11, 1833. [Google Scholar] [CrossRef]
- Bányai, T.; Illés, B.; Bányai, Á. Smart scheduling: An integrated first mile and last mile supply approach. Complexity 2018, 2018, 5180156:1–5180156:15. [Google Scholar] [CrossRef]
- Zhou, L.; Baldacci, R.; Vigo, D.; Wang, X. A multi-depot two-echelon vehicle routing problem with delivery options arising in the last mile distribution. Eur. J. Oper. Res. 2018, 265, 765–778. [Google Scholar] [CrossRef]
- Ramos, T.R.P.; Morais, C.S.D.; Barbosa-Póvoa, A.P. The smart waste collection routing problem: Alternative operational management approaches. Expert Syst. Appl. 2018, 103, 146–158. [Google Scholar] [CrossRef]
- Tirkolaee, E.B.; Mahdavi, I.; Esfahani, M.M.S. A robust periodic capacitated arc routing problem for urban waste collection considering drivers and crew’s working time. Waste Manag. 2018, 76, 138–146. [Google Scholar] [CrossRef]
- Bányai, T.; Tamás, P.; Illés, B.; Stankevičiūtė, Ž.; Bányai, Á. Optimization of municipal waste collection routing: Impact of industry 4.0 technologies on environmental awareness and sustainability. Int. J. Environ. Res. Public Health. 2019, 16, 634. [Google Scholar] [CrossRef]
- Riedler, M.; Raidl, G. Solving a selective dial-a-ride problem with logic-based Benders decomposition. Comput. Oper. Res. 2018, 96, 30–54. [Google Scholar] [CrossRef]
- Tellez, O.; Vercraene, S.; Lehuédé, F.; Péton, O. The fleet size and mix dial-a-ride problem with reconfigurable vehicle capacity. Transp. Res. C Emerg. Technol. 2018, 91, 99–123. [Google Scholar] [CrossRef] [Green Version]
- Chen, C.; Zhang, D.Q.; Li, N.; Zhou, Z.H. B-planner: Planning bidirectional night bus routes using large-scale taxi GPS traces. IEEE Trans. Intell. Transp. Syst. 2014, 15, 1451–1465. [Google Scholar] [CrossRef]
- Huang, C.H.; Galuski, J.; Bloebaum, C.L. Multi-objective Pareto concurrent subspace optimization for multidisciplinary design. AIAA J. 2007, 45, 1894–1906. [Google Scholar] [CrossRef]
- Berube, J.F.; Gendreau, M.; Potvin, J.Y. An exact ε-constraint method for bi-objective combinatorial optimization problems: Application to the traveling salesman problem with profits. Eur. J. Oper. Res. 2009, 194, 39–50. [Google Scholar] [CrossRef]
- Deb, K.; Agrawal, S.; Pratap, A.; Meyarivan, T. A fast elitist non-dominated sorting genetic algorithm for multi-objective optimization: NSGA-II. In Proceedings of the Sixth International Conference on Parallel Problem Solving From Nature, Paris, France, 18–20 September 2000. [Google Scholar]
- Liu, H.D. Research on Bus Transit Routes Network Design Theory and Implement Method. Ph.D. Thesis, Tongji University, Shanghai, China, 2008. [Google Scholar]
- Yan, P.; Song, R. Urban Public Transit Introduction, 1st ed.; China Machine Press: Beijing, China, 2011; p. 79. [Google Scholar]





| Publication | Objective | Decision Variables | Travel Demand Pattern | Optimization Method for Bus Stop and Route |
|---|---|---|---|---|
| Chien and Yang. 2000 | Minimize the summation of supplier cost and user cost | Bus route | Based on route links | - |
| Jerby and Ceder. 2006; Xiong et al. 2014; Zhu et al. 2017 | Maximize the demand potential of the route links | Bus route | Based on route links | - |
| Teng et al. 2013 | Maximize the population served by equivalent straight line of bus route | Bus route | Based on traffic zones | - |
| Lin and Wong. 2014 | Maximize service coverage, minimize the maximum bus route travel time, minimize bus route length | Bus route | Based on demand nodes | - |
| Shrivastava and Dhingra. 2001; Song and Liu. 2011 | Minimize bus route length | Bus route | Based on demand nodes (bus stops) | - |
| Kuan et al. 2004, 2006; Shrivastava and O’ Mahony. 2006, 2009 | Minimize the sum of operator and user costs | Bus route and frequency | Based on demand nodes (bus stops) | - |
| Sun et al. 2011 | Minimize the sum of operator, user costs and the opposite number of bus passengers | Bus route, timetable and choice behavior of passengers | Based on demand nodes (bus stops) | - |
| Szeto and Wu. 2011 | Minimize the sum of the number of transfers and total passengers’ travel time | Bus route and frequency | Based on demand nodes (bus stops) | - |
| Liu et al. 2015 | Minimize passengers’ travel time, maximize transport efficiency | Bus route | Based on demand nodes (bus stops) | - |
| Li and Chen. 2016 | Minimize bus route length and passengers’ travel cost | Bus stop location and route | Based on demand nodes | successive |
| Leksakul et al. 2017 | Minimize the sum of the distance between the bus stop and the passengers’ addresses, minimize route length | Bus stop location and route | Based on demand nodes | Successive |
| Perugia et al. 2011 | Minimize the total cost of bus service, minimize the total extra-time | Bus stop location and route | Based on demand nodes (bus stops) | Simultaneous |
| Xiong et al. 2013 | Minimize the sum of user cost and supplier cost | Bus stop location, route and headway | Based on demand nodes | Simultaneous |
| Schittekat et al. 2013 | Minimize the total distance travelled by buses | Bus stop location and route | Based on demand nodes | Simultaneous |
| Chen et al. 2017 | Minimize the total vehicular travel time | Bus stop location and route | neglected | Simultaneous |
| Yan et al. 2012, 2014 | Minimize the carrier’s operating cost | Vehicle route | Based on demand nodes | - |
| Bányai. 2018 | Minimize the energy use | Assignment of open tasks to delivery service provider, delivery route, scheduling of pickup and delivery operations | Based on pickup points and destinations | - |
| Bányai et al. 2018 | Minimize the costs of the whole delivery process | Assignment of open tasks to scheduled routes, assignment of picked up packages to delivery routes or hubs, scheduling of pickup operations | Based on pickup points and destinations | - |
| Zhou et al. 2018 | Minimize the sum of routing, connection and handling costs | Vehicle route | Based on demand nodes | - |
| Ramos et al. 2018 | Minimize transportation cost | Vehicle route | Based on demand nodes | - |
| Tirkolaee et al. 2018 | Minimize usage cost of vehicles and traversing cost | Vehicle route and optimal number of vehicles | Based on edges | - |
| Bányai et al. 2019 | Minimize energy use of collection process | Assignment of households to routes of garbage trucks and scheduling of garbage trucks | Based on demand nodes | - |
| Riedler and Raidl. 2018 | Maximize the number of served requests | Vehicle route, beginning-of-service time of vehicle, load of vehicle and ride time of request | Based on pick-up locations and drop-off locations | - |
| Tellez et al. 2018 | Minimize the total transportation cost | Vehicle route, location for vehicle to be reconfigured, load of vehicle and service time of vehicle at node | Based on pickup locations and delivery locations | - |
| Sets | |
| D | set of demand points, |
| H | set of candidate stops, |
| Parameters | |
| dkl | distance between candidate stops k and l |
| straight-line distance between the transfer stop and candidate stops k | |
| qi | travel demand of demand point i |
| lmax | the maximum length of feeder route |
| lmin | the minimum length of feeder route |
| smax | the maximum stop spacing |
| smin | the minimum stop spacing |
| c | the maximum nonlinear factor |
| Dmax | the maximum acceptable walking distance of passengers |
| aik | binary assistant parameter, (1 if distance between demand point i and candidate stop k does not exceed Dmax and 0 otherwise) |
| Decision variables | |
| xk | 0-1 decision variable, equals to 1 if candidate stop k is chosen as a stop, and 0 otherwise |
| vi | 0-1 variable, equals to 1 if demand point i can be served, and 0 otherwise |
| yik | binary variable (1 if demand point i can be served by candidate stop k and 0 otherwise) |
| zkl | binary variable (1 if candidate stop k and l are adjacent stops and 0 otherwise) |
| uk | nonnegative integer assistant variable to eliminate sub-tour |
| Solution | Route | Travel Demand That Can Be Served (trip/day) | Route Length (m) |
|---|---|---|---|
| 1 | 1-2-4-11-19-27-32-33-40-29 | 10,914 | 8000 |
| 2 | 1-2-3-10-20-26-33-40-44-51 | 11,098 | 8001 |
| 3 | 1-2-4-11-26-32-33-43-42-48 | 12,813 | 8002 |
| 4 | 1-2-3-4-9-11-20-26-33-40-35-43-58 | 13,204 | 8010 |
| 5 | 1-2-4-10-20-26-33-43-58-68 | 14,027 | 8042 |
| 6 | 1-2-4-10-20-26-33-35-43-58-68 | 14,470 | 8252 |
| 7 | 1-2-3-4-10-20-26-33-40-29-58-68 | 14,654 | 8304 |
| 8 | 1-2-4-10-20-26-32-33-43-58-68 | 14,676 | 8460 |
| 9 | 1-2-4-11-26-33-40-51-42-48 | 14,771 | 8468 |
| 10 | 1-2-3-10-20-26-33-40-43-58-68 | 15,591 | 8520 |
| 11 | 1-2-3-4-11-20-26-33-43-58-68-72 | 15,831 | 8634 |
| 12 | 1-2-3-4-10-20-26-33-40-35-43-58-68 | 16,034 | 8730 |
| 13 | 1-2-3-10-20-26-33-35-43-58-68-72 | 16,274 | 8844 |
| 14 | 1-2-4-10-20-26-33-40-29-58-68-72 | 16,458 | 8896 |
| 15 | 1-2-4-11-20-26-32-33-43-58-68-72 | 16,480 | 9052 |
| 16 | 1-5-2-4-11-20-26-33-40-43-58-68 | 16,613 | 9094 |
| 17 | 1-2-4-11-20-26-33-40-43-58-68-72 | 17,395 | 9112 |
| 18 | 1-2-3-4-11-26-33-40-35-43-58-68-72 | 17,838 | 9322 |
| 19 | 1-2-4-10-20-26-32-33-40-43-58-68-72 | 18,044 | 9530 |
| 20 | 1-5-2-4-11-26-33-40-43-58-68-72 | 18,417 | 9686 |
| 21 | 1-2-4-11-26-32-33-40-35-43-58-68-72 | 18,487 | 9740 |
| 22 | 1-2-3-4-11-26-33-40-42-43-58-68-72 | 18,634 | 9754 |
| 23 | 1-5-2-3-10-20-26-33-40-35-43-58-68-72 | 18,860 | 9896 |
| 24 | 1-2-3-4-11-20-26-32-33-40-43-58-68-72-73 | 18,879 | 10,612 |
| 25 | 1-2-4-11-26-33-40-42-43-58-68-72-71 | 18,951 | 10,636 |
| 26 | 1-5-2-3-4-11-20-26-33-40-43-58-68-72-73 | 19,252 | 10,768 |
| 27 | 1-2-3-4-10-20-26-32-33-40-35-43-58-68-72-73 | 19,322 | 10,822 |
| 28 | 1-2-4-11-26-33-40-42-43-58-68-72-73 | 19,469 | 10,836 |
| 29 | 1-5-2-3-4-10-20-26-33-40-35-43-58-68-72-73 | 19,695 | 10,978 |
| 30 | 1-5-2-3-10-20-26-33-40-43-58-68-72-73-69 | 19,771 | 11,389 |
| 31 | 1-2-4-10-20-26-32-33-40-35-43-58-68-72-73-69 | 19,841 | 11,443 |
| 32 | 1-2-3-4-11-26-33-40-42-43-58-68-72-73-69 | 19,988 | 11,457 |
| 33 | 1-5-2-4-10-20-26-33-40-35-43-58-68-72-73-77 | 20,078 | 11,648 |
| 34 | 1-2-3-4-11-26-33-40-43-58-68-72-73-77-81 | 20,139 | 11,655 |
| 35 | 1-2-4-11-26-33-40-35-43-58-68-72-74-77-81 | 20,332 | 11,846 |
| 36 | 1-2-4-11-20-26-33-40-35-43-58-68-72-73-77-81 | 20,582 | 11,865 |
| Solution | Situation of Matching Demand Points to Candidate Stops 1 |
|---|---|
| 1 | (3,8)-2,11-4,(16,18)-19,17-11,(20,25,26)-32,(21,22)-27,(25,26,28,30,31,32,33)-33,(27,34,35,39,40)-29,(27,31,34,36)-40 |
| 12 | 8-3,11-4,11-10,17-20,(23,24)-26,(25,26,28,30,31,32,33)-33,(27,31,34,36)-40,(33,37)-35,(38,39,40,41)-43,(47,50,51,52)-58,(60,61,62,63)-68 |
| 19 | (3,8)-2,11-4,11-10,17-20,(20,25,26)-32,(23,24)-26,(25,26,28,30,31,32,33)-33,(27,31,34,36)-40,(38,39,40,41)-43,(47,50,51,52)-58,(60,61,62,63)-68,(60,64,65,66)-72 |
| 23 | (1,2)-5,(3,8)-2,8-3,11-4,17-11,(23,24)-26,(25,26,28,30,31,32,33)-33,(27,31,34,36)-40,(33,37)-35,(38,39,40,41)-43,(47,50,51,52)-58,(60,61,62,63)-68,(60,64,65,66)-72 |
| 29 | (1,2)-5,(3,8)-2,11-4,17-11,(23,24)-26,(25,26,28,30,31,32,33)-33,(27,31,34,36)-40,(33,37)-35,(38,39,40,41)-43,(47,50,51,52)-58,(60,61,62,63)-68,(60,64,65,66)-72,(67,70)-73 |
| 36 | (3,8)-2,11-4,17-11,17-20,(23,24)-26,(25,26,28,30,31,32,33)-33,(27,31,34,36)-40,(33,37)-35,(38,39,40,41)-43,(47,50,51,52)-58,(60,61,62,63)-68,(60,64,65,66)-72,(67,70)-73,(70,71)-77,(72,78)-81 |
| Sets | |
| N | set of demand nodes, |
| N′ | set of candidate terminals, |
| A | set of road links, |
| Parameters | |
| length of road links (m,n) | |
| straight-line distance between the transfer stop and candidate terminals m | |
| Decision variables | |
| wmn | a binary variable (1 if road link (m,n) belongs to the route and 0 otherwise) |
| a binary variable which equals 1 if the route passes node m, and 0 otherwise | |
| a nonnegative integer assistant variable to eliminate sub-tour | |
| Solution | Situation of Matching Demand Points to Candidate Stops 1 |
|---|---|
| The solution of the existing approach | (3,8)-2,11-4,11-9,(16,17)-18,(16,18)-37,19-30,(27,28,29,30)-38,(27,34,35)-41,(38,39,40,41)-43 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guo, X.; Song, R.; He, S.; Hao, S.; Zheng, L.; Jin, G. A Multi-Objective Programming Approach to Design Feeder Bus Route for High-Speed Rail Stations. Symmetry 2019, 11, 514. https://doi.org/10.3390/sym11040514
Guo X, Song R, He S, Hao S, Zheng L, Jin G. A Multi-Objective Programming Approach to Design Feeder Bus Route for High-Speed Rail Stations. Symmetry. 2019; 11(4):514. https://doi.org/10.3390/sym11040514
Chicago/Turabian StyleGuo, Xiaole, Rui Song, Shiwei He, Sijia Hao, Lijie Zheng, and Guowei Jin. 2019. "A Multi-Objective Programming Approach to Design Feeder Bus Route for High-Speed Rail Stations" Symmetry 11, no. 4: 514. https://doi.org/10.3390/sym11040514





