Abstract
The steady boundary layer flow of a nanofluid past a thin needle under the influences of heat generation and chemical reaction is analyzed in the present work. The mathematical model has been formulated by using Buongiornos’s nanofluid model which incorporates the effect of the Brownian motion and thermophoretic diffusion. The governing coupled partial differential equations are transformed into a set of nonlinear ordinary differential equations by using appropriate similarity transformations. These equations are then computed numerically through MATLAB software using the implemented package called bvp4c. The influences of various parameters such as Brownian motion, thermophoresis, velocity ratio, needle thickness, heat generation and chemical reaction parameters on the flow, heat and mass characteristics are investigated. The physical characteristics which include the skin friction, heat and mass transfers, velocity, temperature and concentration are further elaborated with the variation of governing parameters and presented through graphs. It is observed that the multiple (dual) solutions are likely to exist when the needle moves against the direction of the fluid flow. It is also noticed that the reduction in needle thickness contributes to the enlargement of the region of the dual solutions. The determination of the stable solution has been done using a stability analysis. The results indicate that the upper branch solutions are linearly stable, while the lower branch solutions are linearly unstable. The study also revealed that the rate of heat transfer is a decreasing function of heat generation parameter, while the rate of mass transfer is an increasing function of heat generation and chemical reaction parameters.
1. Introduction
In recent decades, the performance of heat transfer of conventional fluids like ethylene glycol, lubricants, oil, kerosene and water, etc., has become less favorable in certain applications. Hence, new kinds of fluid are needed to reach the thermal efficiency for heat exchangers in the future. Choi [1] came out with a tactful idea to resolve the problem by adding dilute suspension of nanoparticles into conventional fluids and this mixture is known as ‘nanofluid’. Normally, nanoparticles consist of metals, carbides, oxides, nitrides or non-metals and have dimensions from 1 to 100 nm. Due to the tiny size of nanoelements, nanofluids possess strong suspension stability and able to move without clogging the flow system. Since nanoparticles have higher thermal conductivity than the base fluid, nanofluids are regarded as better coolants particularly in nuclear reactors, domestic refrigerators, transportations, cancer therapy, microelectronic devices, lubricants and also thin film solar energy collectors. A comprehensive literature on the nanofluid applications can be found in the works by Wong and Leon [2], Saidur et al. [3], Huminic and Huminic [4] and Colangelo et al. [5].
In view of above relevant applications, many researchers started to employ nanofluid as an alternative way to enhance the heat transfer efficacy. For instance, Buongiorno [6] established the non-homogeneous equilibrium model which is comprised of seven slip mechanisms; thermophoresis, Brownian diffusion, diffusiophoresis, inertia, gravity Magnus effect and fluid drainage. In this model, the Brownian movement and thermophoretic diffusion of nanoparticles are two notable effects that enhances the thermal conductivity of ordinary liquids. A year after the published work of Buongiorno [6], Tiwari and Das [7] proposed a homogeneous model which taking into account the effect of nanopartilces volume fractions. It is reported that the boundary layer flow of nanofluids over a stretching surface has been studied by Khan and Pop [8]. Makinde and Aziz [9] investigated the boundary layer flow of a nanofluid towards a stretching sheet with convective boundary conditions. Some relevant works on the homogeneous and non-homogeneous models can be seen in the references [10,11,12,13,14,15,16,17].
The study of chemical reactions has amazingly increased due to their wide range useful industrial and technological applications in polymer processing and electrochemistry. Such applications include chemical processing equipment, glass manufacturing, creation and distribution of fog, food processing, energy transfer in a wet cooling tower and evaporation at the surface of the water body [18,19,20]. The consideration of mixed convection flow past a vertical surface implanted in a porous medium carries species that are relatively soluble in the fluid. In fact, chemical reactions occur due to the presence of a foreign mass in a fluid. In many chemical reactions, the reaction rate relies on the concentration of the species itself. A chemical reactions between the conventional liquid and nanoparticles can be classified as a homogeneous reaction or heterogeneous reaction. Homogeneous reaction is a chemical reaction that occurs consistency in a single phase (gaseous, liquid, or solid). In addition, a heterogeneous reaction is a reaction that involves two or more phases (solid and gas, solid and liquid, two immiscible liquids) and takes place within the boundary of a phase. It is worth mentioning that a chemical reaction is said to be a first order reaction if the reaction rate is directly proportional to the concentration [21,22]. Some applications for the diffusion of species in the boundary layer flow include fibrous insulation, pollution studies and oxidation and synthesis materials. Furthermore, Mabood et al. [23] investigated the influence of chemical reaction on magnetohydrodynamics (MHD) stagnation point flow of nanofluid in porous medium by considering the additional effects of viscous dissipation and thermal radiation. Eid [24] analyzed the chemical reaction effect on MHD nanofluid flow past a stretching sheet with heat generation. It is noticed from his study that the presence of heat source and chemical reaction decrease the heat transfer rate and increase the mass transfer rate. The influence of chemical reaction and heat generation on mixed convection flow of a Casson nanofluid towards a permeable stretching sheet has been studied by Ibrahim et al. [25]. Inspired by the previous works, many authors have considered the chemical reaction effects on different flow concepts as can be seen in the references [26,27,28,29]. Very recently, Hayat et al. [30] discussed the mixed convection flow of Williamson nanofluid subject to chemical reaction.
Moreover, the boundary layer flow over a thin needle is of considerable importance in the biomedical and engineering purposes. For instance, it is commonly used in hot wire anemometer or protected thermocouple for calculating the wind velocity, transportations, circulatory problems and wire coating. The topic of thin needle seems very famous due to the movement of the needle that distracts the free-stream flow. This criterion is a primary point of the flow and heat transfer process to calculate the velocity and temperature distributions in experimental studies. Thin (or slender) needle is categorized as a rebellious body whose thicknesses are comparable to that of boundary layer or smaller. The boundary layer development adjacent to a thin needle in viscous fluid is first considered by Lee [31]. Narain and Uberoi [32] analyzed free and mixed convection flow along a thin needle. In extension to which, many works regarding slender needle in a viscous fluid are found in the existing literature [33,34,35,36]. Furthermore, the literature shows that researchers have also devoted their attention to the study of boundary layer flow near a slender needle in nanofluid. These situations are caused by the usage of nanofluid that enhance the heat transfer rate. In 2011, the study of the forced convection flow with variable surface temperature over a slender needle has been done by Grosan and Pop [37]. A collection of the boundary layer flow over a thin needle with various physical effects in nanofluid can be found in the work by Trimbitas et al. [38], Hayat et al. [39], Soid et al. [40], Krishna et al. [41] and Ahmad et al. [42]. Very recently, Salleh et al. [43] performed the numerical analysis of magnetohydrodynamics flow over a moving vertical slender needle in nanofluid using Buongiorno’s model with the revised boundary conditions.
Therefore, the novelty of the present work is to analyze the problem of the steady laminar nanofluid flow adjacent to a slender needle by considering the additional effects of chemical reaction and also heat source. Buongiorno’s model is chosen in the simulation of the nanofluid. The system of nonlinear ordinary differential equations is computed numerically using bvp4c package in MATLAB software. The graphical results are presented and discussed for the varying effect of emerging parameters.
2. Governing Formula and Modeling
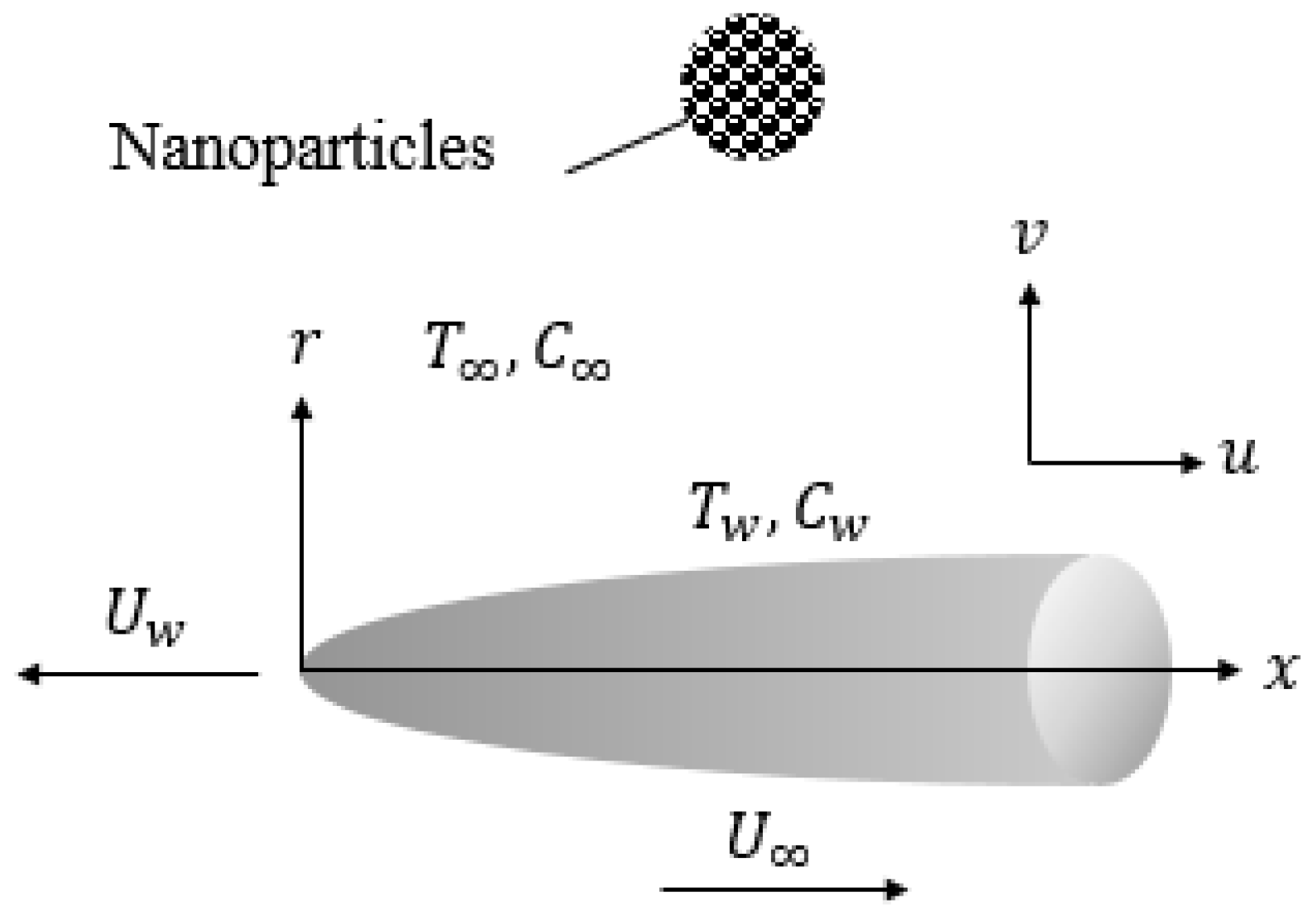
A steady nanofluid flow past a horizontal thin needle is examined. The geometry of the problem is illustrated in Figure 1 with u and v denoting x and r components of velocity, respectively, and represents the needle radius. The needle is considered to move with uniform velocity in the same or reverse direction of the external flow of constant velocity with the composite velocity . It is assumed that and are the constant wall temperature and nanoparticle concentration and as , the ambient temperature and nanoparticle fraction are and such that and . In view of small needle size, the pressure gradient is ignored, however, the transverse curvature effect is required.
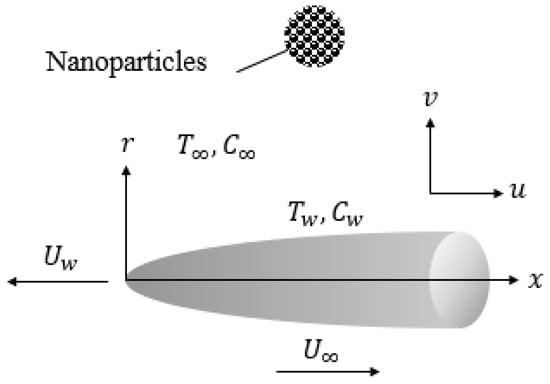
Figure 1.
Schematic view of the present study.
By using Buongiorno’s nanofluid model, the relevant governing boundary layer systems for the flow are [6,42]
The physical boundary restrictions are
in which is kinematic viscosity, T is the temperature of nanofluid, C is the concentration of nanoparticles, is the thermal diffusivity, is the density, is the heat capacity at uniform pressure, is the proportion of effectual heat capacity of nanofluid in which subscripts ‘s’ and ‘f’ refer to solid nanoparticle and base fluid, is the dimensionless heat generation, is the dimensionless reaction rate, is the heat generation coefficient and is the chemical reaction coefficient. It is worth mentioning that the dimensionless parameters and are the function of x and its value varies locally throughout the flow motion. Besides, and are Brownian and thermophoresis diffusion coefficients, respectively.
The similarity transformation technique has been used for obtaining the ordinary differential equations. Hence, the following non-dimensional parameters are introduced
where the stream functions are given as
The stream functions (7) satisfies the continuity Equation (1). Using Equations (6) and (7), we obtain the following equations
Also, the boundary condition could be rewritten as
where prime denotes the differentiation with regard to similarity variable . Besides, assume to represent size or thickness of the needle.
Here, , , , Q, and represent the Prandtl number, thermophoresis parameter, Brownian motion parameter, heat generation parameter, Lewis number and velocity ratio parameter. K is the chemical reaction parameter with represents a destructive reaction, and represents generative reaction. These non-dimension parameters are defined as follows:
The skin friction coefficient , local Nusselt number and local Sherwood number that relate to the shear stress, heat transfer rate and mass transfer rate are defined as
where is the local Reynold number.
3. Stability Analysis
The idea of the stability analysis came from Weidman et al. [44]. In their study, they noticed that there exists more than one solution called dual solutions. It is important to note that this analysis is introduced to determine which solution provides a good physical meaning to the flow (stable solution). Since we obtained the dual solutions, thus we are encouraged to determine which solutions are stable. To carry out this analysis, Equations (2)–(4) must be in unsteady case. Hence, the new dimensionless time variable is taken as . Thus, we have
and the new similarity transformations take the following form
Please note that the use of is related to an initial value problem that is consistent with the solution that will be attained in practice (physically realizable). Afterwards, encorporating Equation (19) into Equations (16)–(18), we obtains
together with the boundary conditions
Subsequently, we assume [44,45]
in order to specify the stability of solutions , and which meets the boundary value problem (20)–(23). Also, functions , and represent small relative to , and , respectively, and denotes an unknown eigenvalue parameter.
Then, introducing Equation (24) into Equations (20)–(23) yields the linear eigenvalue equations below:
The corresponds boundary conditions for these equations are given by
Next, to identify an early growth or decomposition of the solution (24), we have to set . Hence, functions F, G and H can be expressed as , and , respectively (see Weidman et al. [44] for the detail).
In the present work, we computed the numerical results for Equations (25)–(27) associated with conditions (28) by using the new boundary condition which is . This condition is obtained by relaxing the condition as (see [46] for details). It is to be noted that the flow will be stable if is positive, while the flow will be unstable if is negative.
4. Graphical Results and Discussion
In this section, the graphical outputs of our problem are interpreted for various effects of the involved parameters. All the computations have been carried out for a wide range of values of the governing parameters; , , , , , and for a fixed values of and . Equations (8)–(10) along with the conditions (11) are computed numerically via bvp4c function that implemented in MATLAB software. Besides the shooting method, there is a new effective method for solving the boundary value problem for ordinary differential equations that is bvp4c package. Mathematically, this package uses the finite difference methods, in which the output is attained using an initial guess provided at the starting mesh point and resize the step to obtain the particular certainty. Nevertheless, to use this package, the boundary value problem must reduce to first order system of ordinary differential equations. To validate the accuracy of the present results, we have initially compared our results to those of Ahmad et al. [42] and Salleh et al. [43]. In this respect, Table 1 shows a comparison value of shear stress for for some of the thickness of the needle c when . An excellent agreement is observed in these studies.

Table 1.
Comparison values of shear stress when for some of the thickness of the needle c when .
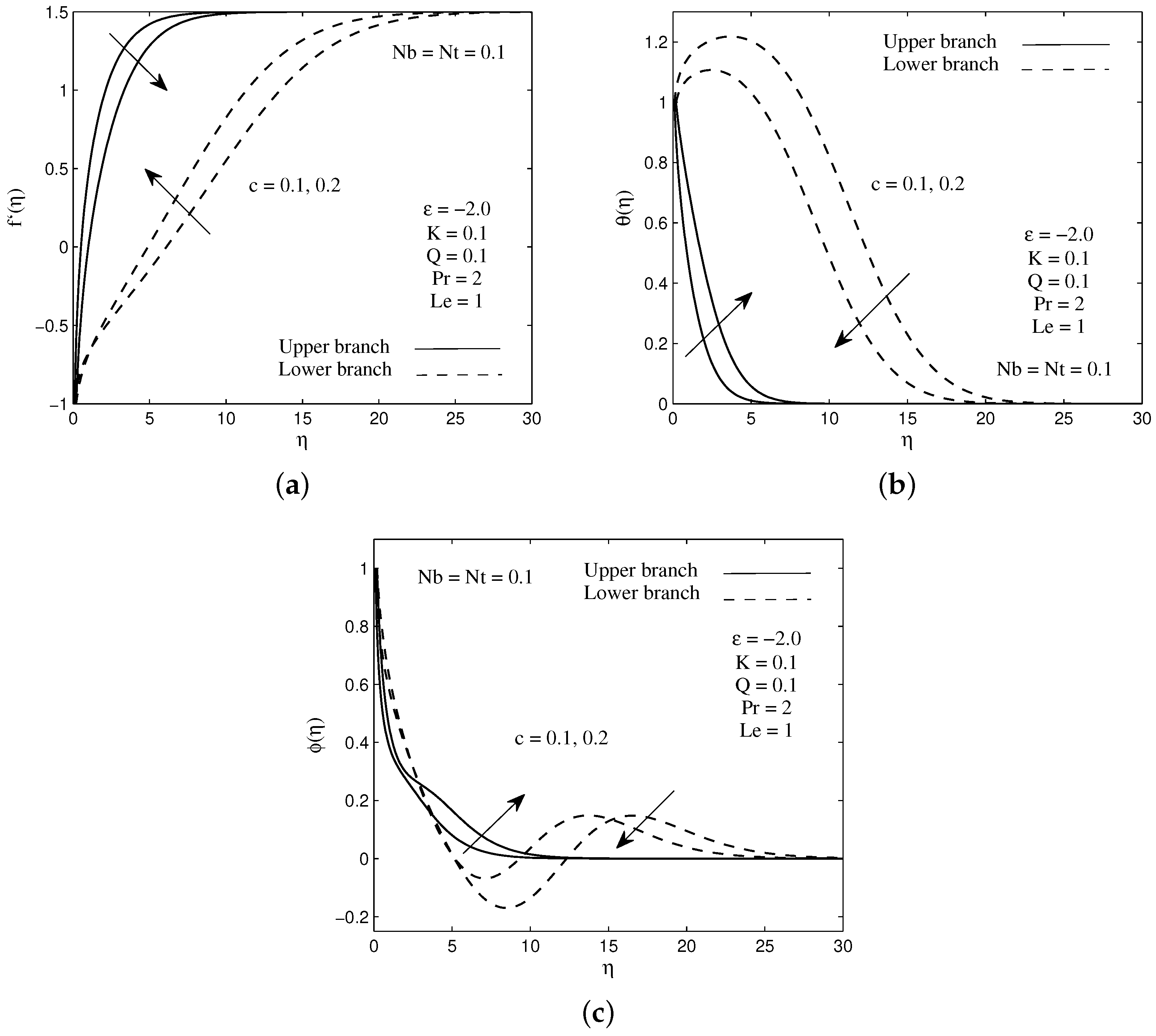
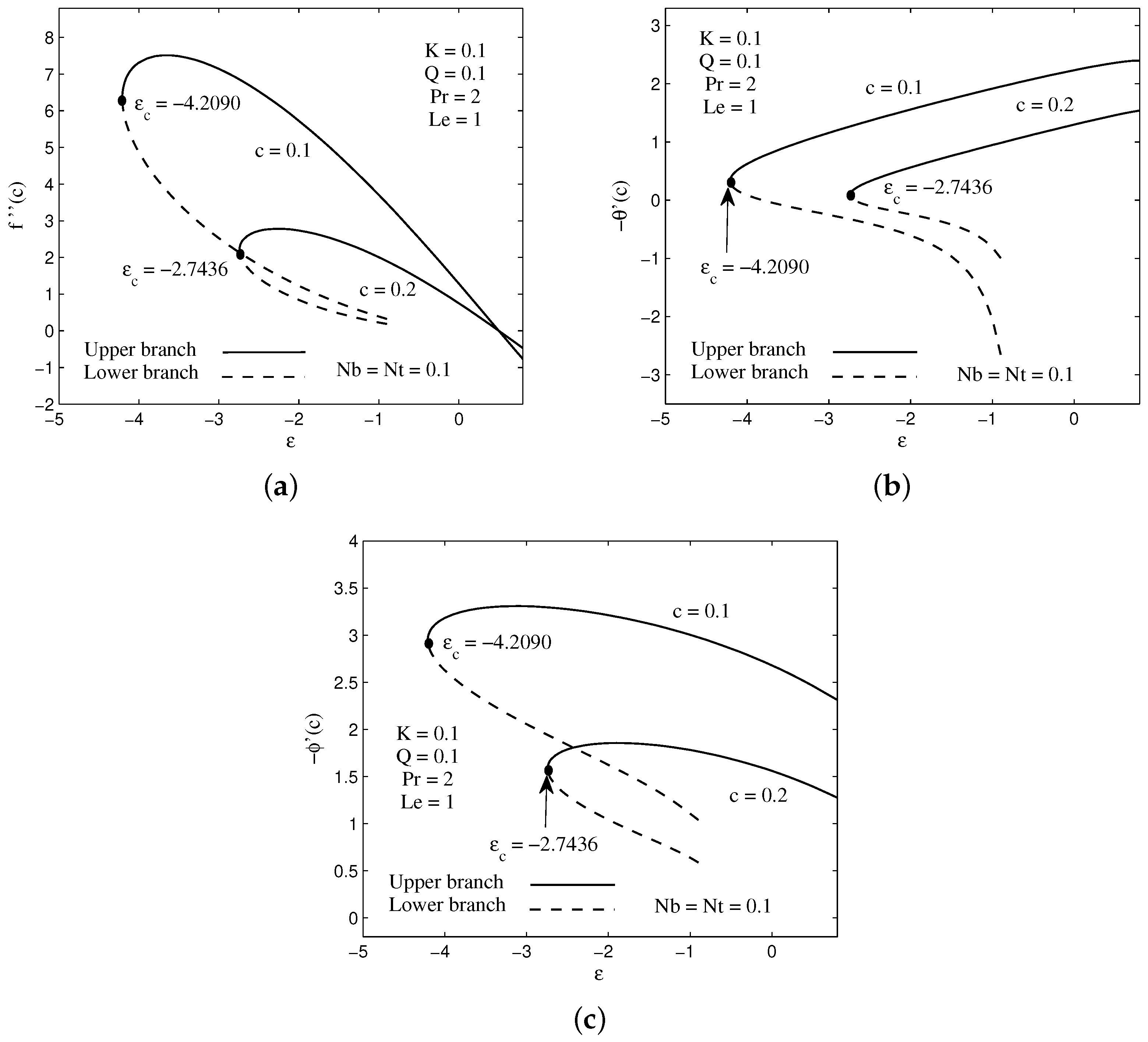
The effect of needle thickness c on the velocity, temperature and concentration profiles are graphically presented in Figure 2a–c. It is noticed from the plots that the velocity, temperature and concentration profiles for upper branch solution increase with the increasing value of needle thickness. Similar observation is found for momentum, thermal and concentration boundary layer thicknesses for the upper branch as the c increase. Mathematically, the shape of graphs obtained in these profiles has asymptote behaviors and it fulfills the requirement of boundary condition (11). One can see that an increment in the needle thickness decreases the numerical values of surface shear stress , heat flux and also mass flux . These phenomena are clearly shown in Figure 3a–c. This situation occurs due to an increase in the momentum, thermal and concentration boundary layer thicknesses on the surface, and consequently decline the shear stress and slow down the heat and mass transfers from the surface to the flow. Physically, the slender surface of the needle makes heat and mass to diffuse through it quickly compared to thick surface. In addition, the critical values of , by which the upper and lower branch solutions connected, are noticed to decrease as the needle thickness reduces. In other words, we can say that the needle thickness has a significant effect on the existence of the dual solutions.
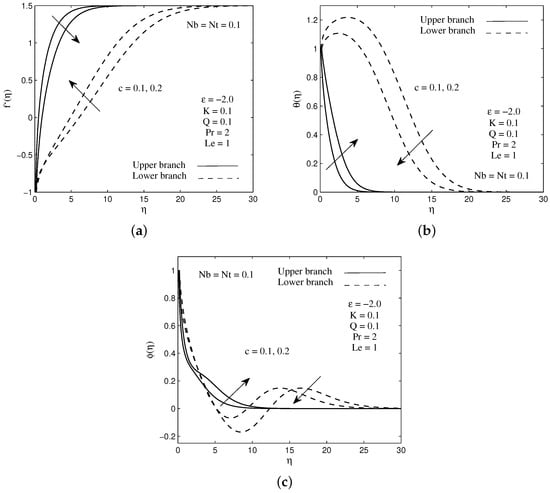
Figure 2.
Sample of (a) velocity, (b) temperature and (c) concentration profiles for several values of needle thickness c.
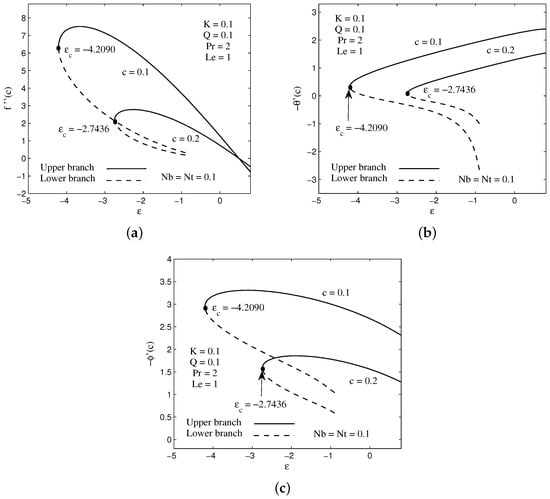
Figure 3.
Variation of surface (a) shear stress, (b) local heat flux and (c) local mass flux with velocity ratio parameter for several values of needle thickness c.
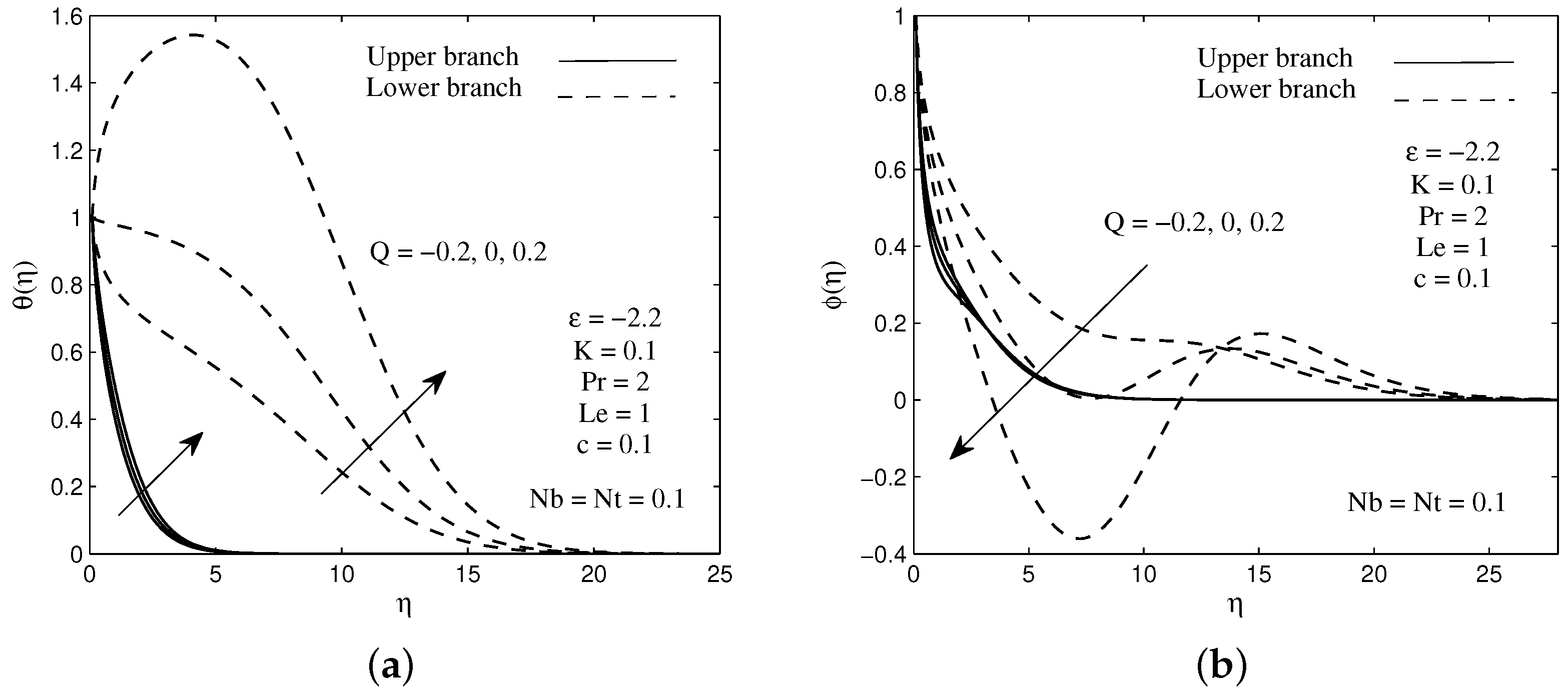
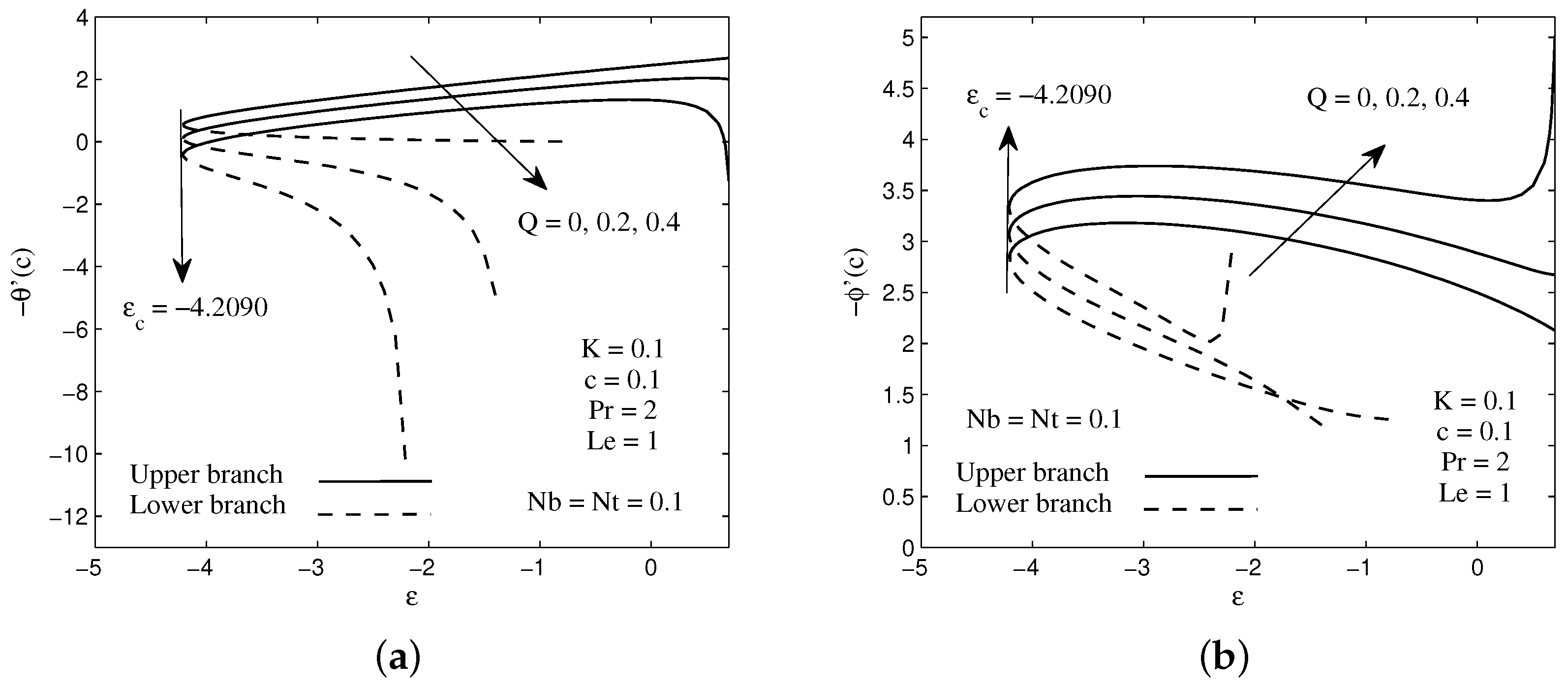
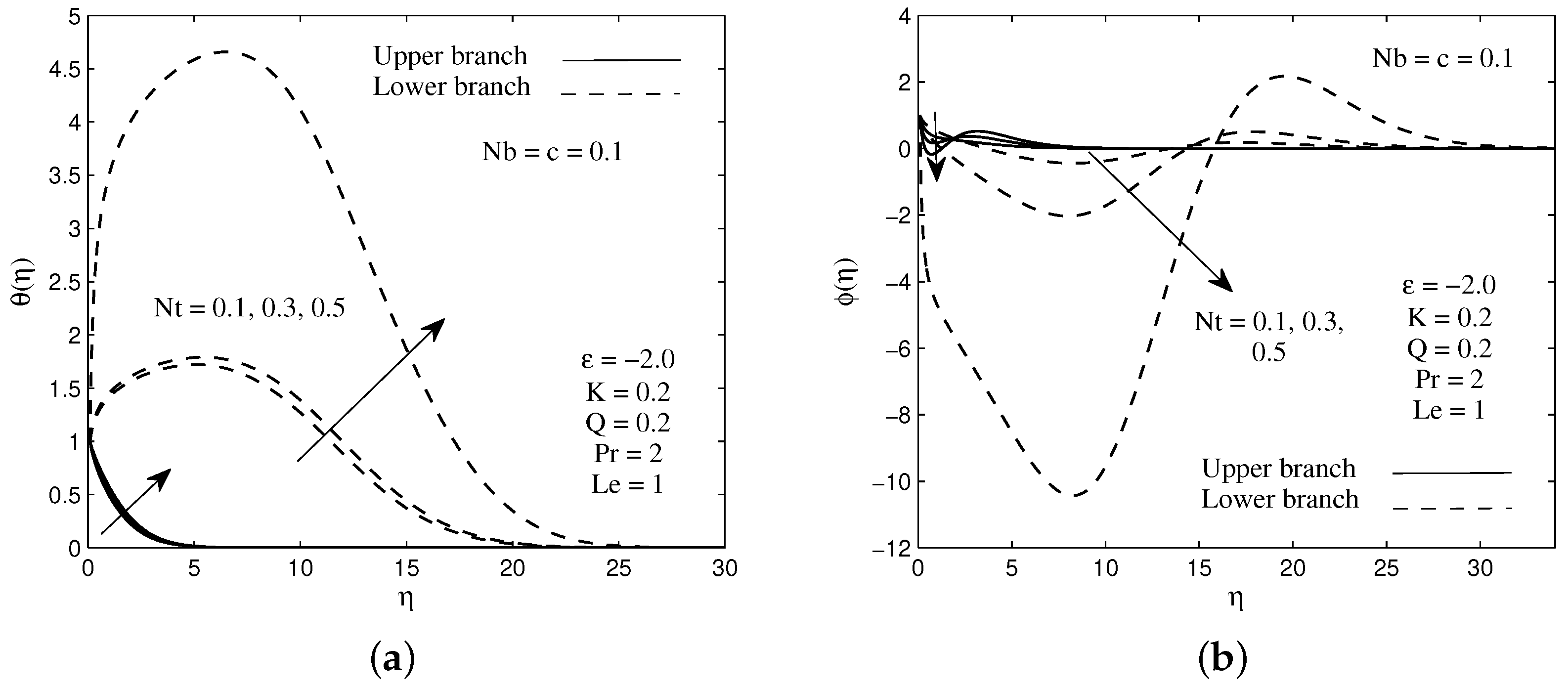
The distributions of the temperature and concentration for several values of heat generation parameter Q are illustrated in Figure 4a,b when . It is worth noticing from Figure 4a that the fluid temperature enhances significantly within the thermal boundary layer for higher values of heat generation parameter. However, the opposite effect is observed for the fluid concentration as the heat generation parameter increases. This characteristic can be seen in Figure 4b. Figure 5a,b visualize the effect of the heat generation parameter Q on the local heat and mass fluxes with velocity ratio parameter . It is found from the figures that increasing values of Q reduce the heat flux at the surface, while an opposite criterion is observed for the mass flux. Generally, the presence of the heat generator produces a hot fluid layer near the needle surface due to mechanism of heat generation. As a consequence, the rate of heat transfer decreases from the needle surface to the fluid flow. In addition, the decrement of heat transfer is also due to an increment in the thermal boundary layer thickness as Q increases (see Figure 4a). Moreover, the existence of the hot fluid in the system will accelerate the motion of nanoparticles, and as the result increases the rate of mass transfer on the needle surface. It is worth mentioning that the existence of the dual solutions is noted when the needle moves against the free stream direction, . In these variations, the presence of heat generation does not affect the flow. This statement can be proved by looking at Equation (8), where it does not contain the parameter Q inside.
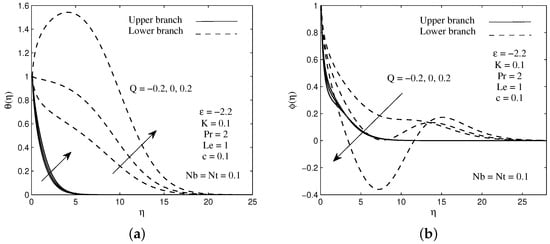
Figure 4.
Sample of (a) temperature and (b) concentration profiles for several values of heat generation parameter Q.
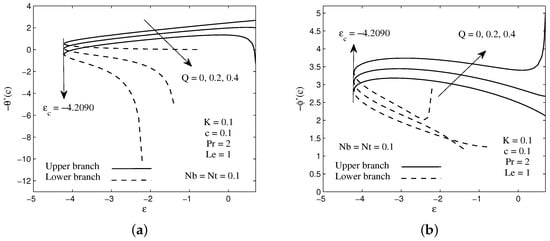
Figure 5.
Variation of surface (a) local heat flux and (b) local mass flux with velocity ratio parameter for several values of heat generation parameter Q.
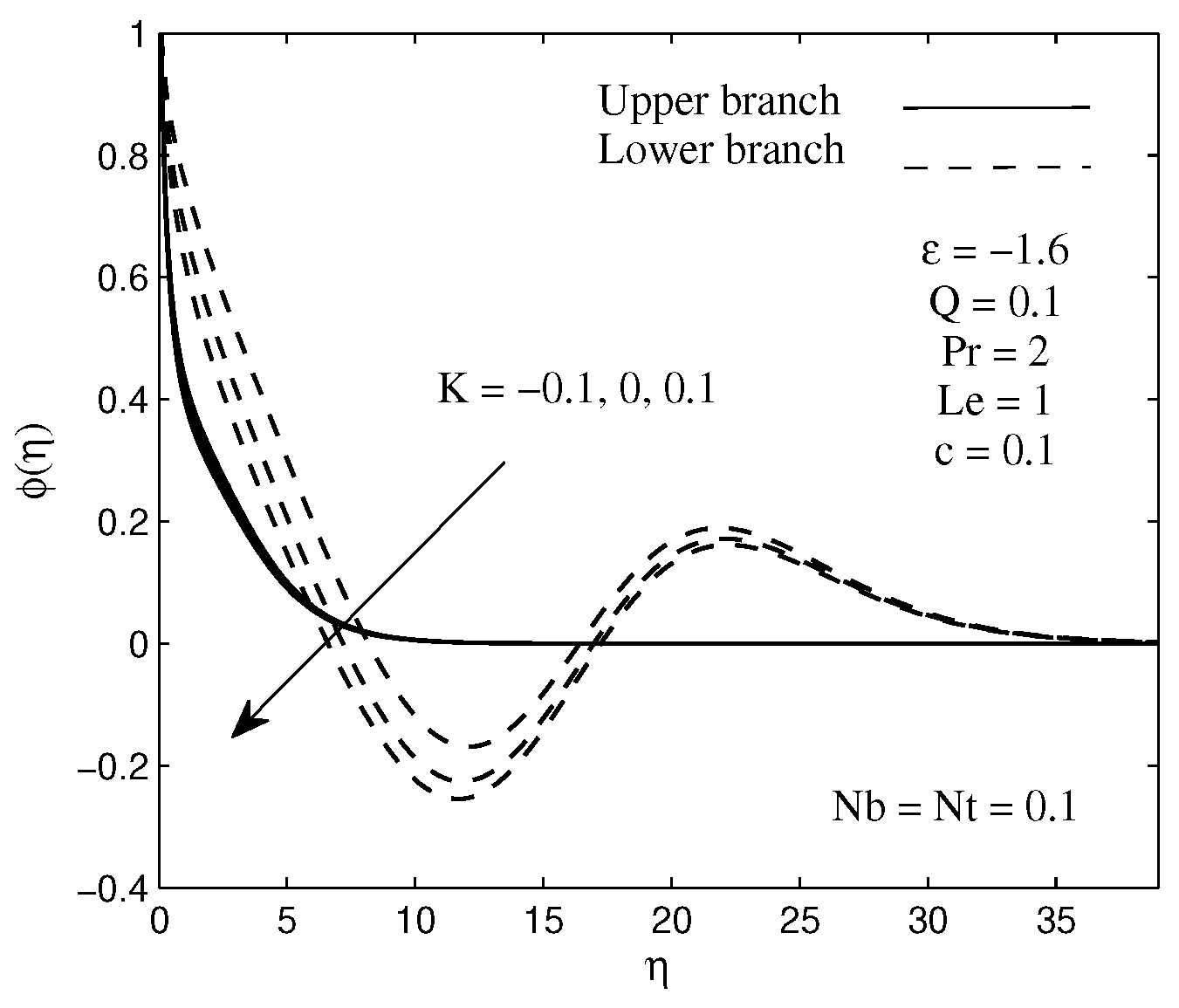
The concentration distributions for some values of chemical reaction parameter K are plotted in Figure 6 when . It is discerned from this figure that the fluid concentration is decreasing function of the chemical reaction parameter. It is important to know that the nanoparticle concentration as well as boundary layer thickness diminishes with the destructive chemical reaction, . Noteworthy, with the existence of destructive reaction, the change of the species as a cause of chemical reaction will reduce the nanoparticle concentration in the boundary layer thickness. Other than that, Figure 7 elucidates the influence of chemical reaction parameter on the local mass flux. This figure explains that increasing the chemical reaction parameter K results in an increase in the mass transfer rate on the surface. The reason behind this is that the reduction of the concentration boundary layer thickness causes the mass transfer takes place quickly between the needle surface and the fluid flow. Since the chemical reaction parameter exists in Equation (10), thus we present only the result for the mass flux here.
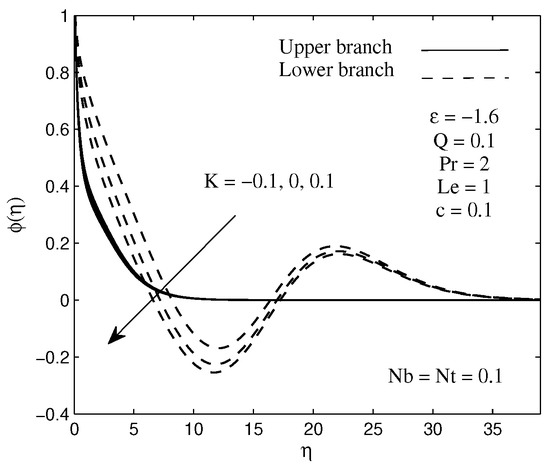
Figure 6.
Sample of concentration profiles for several values of chemical reaction parameter K.
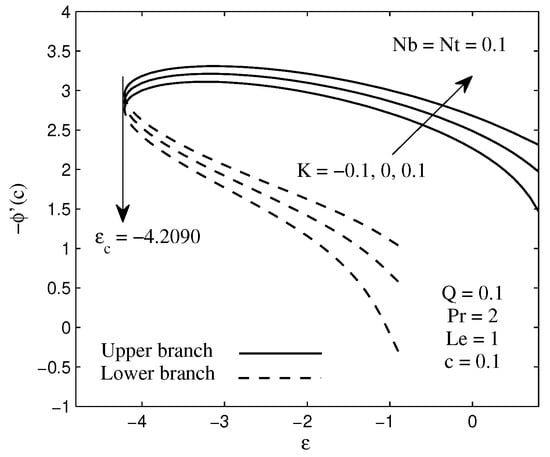
Figure 7.
Variation of surface local mass flux for several values of chemical reaction parameter K.
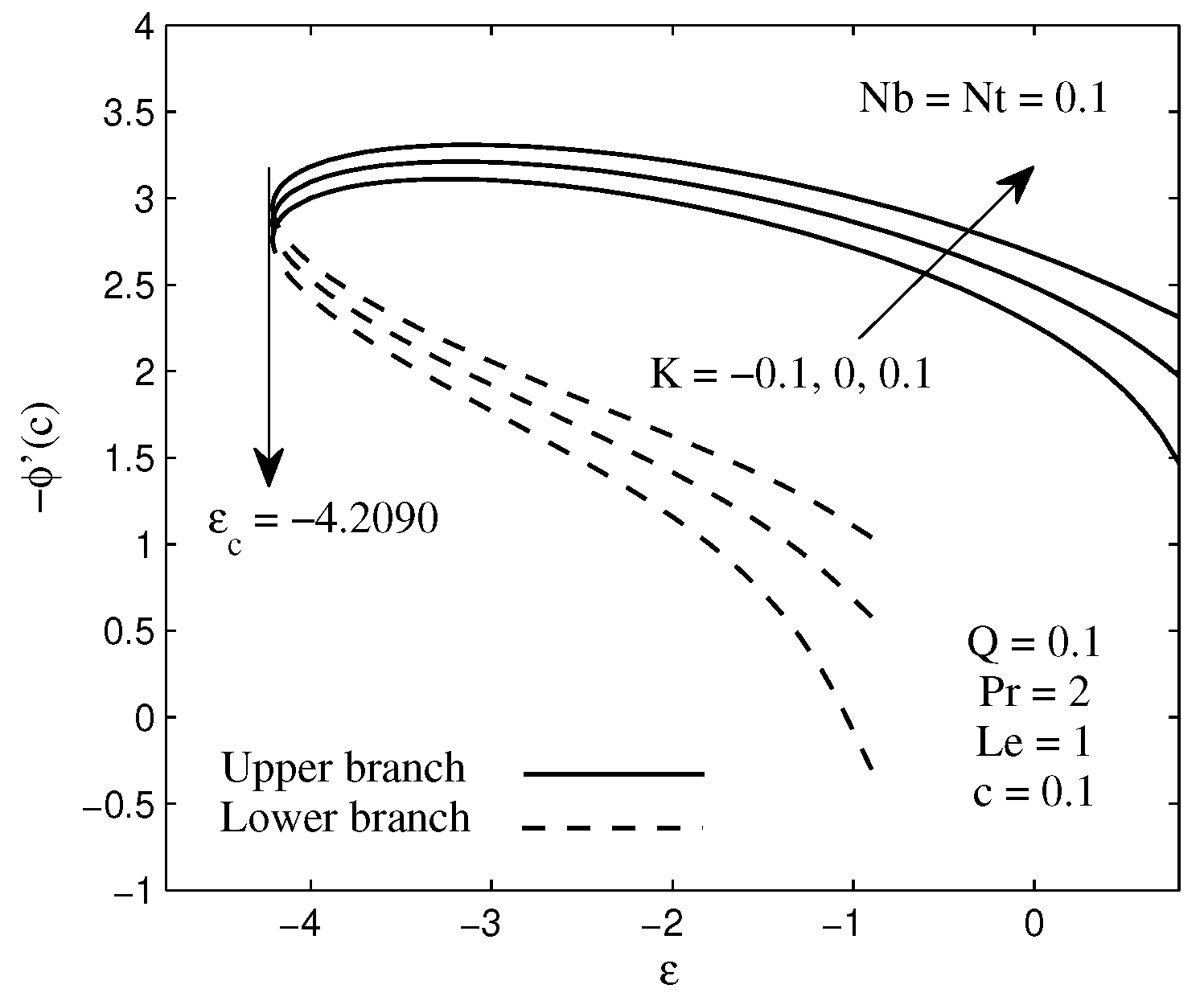
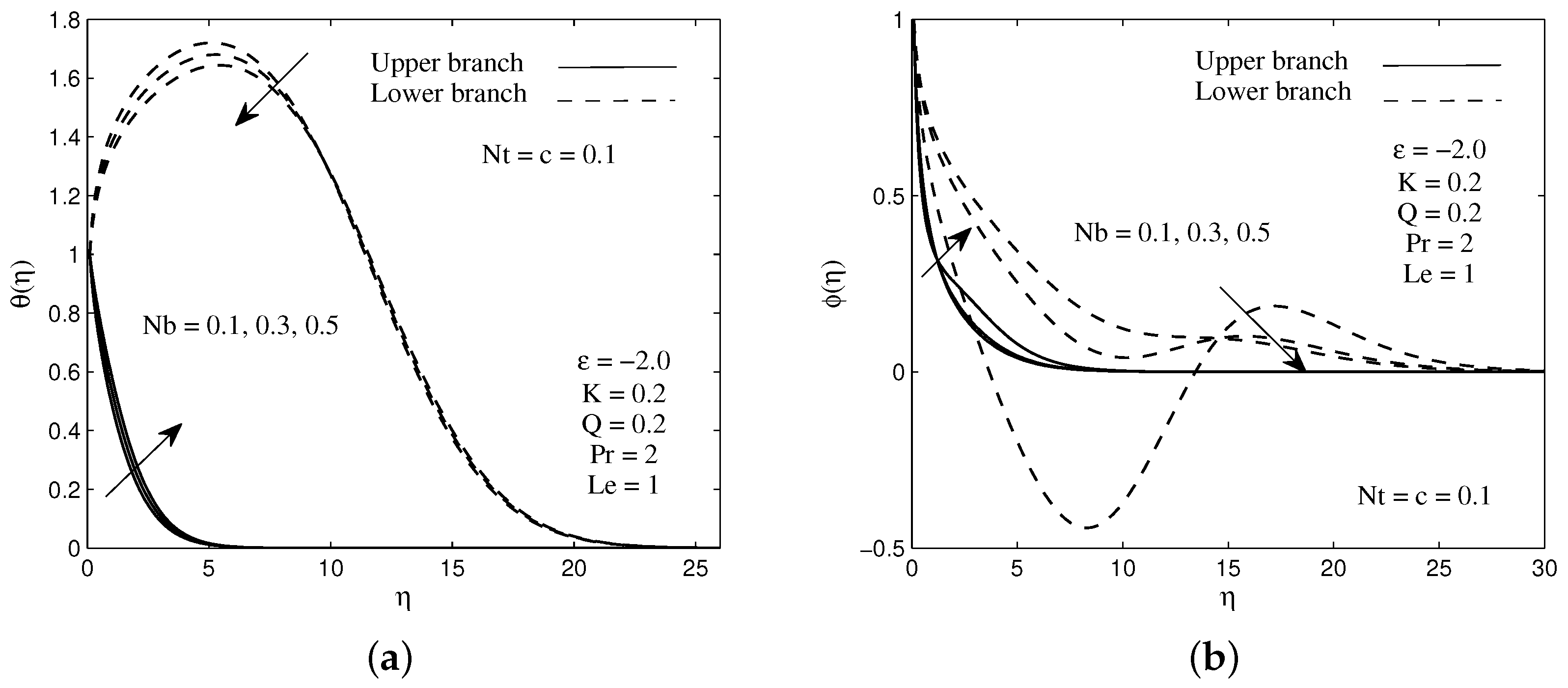
The variations of the local Nusselt number and local Sherwood number with thermophoresis parameter and Brownian motion parameter are presented in Table 2 and Table 3. Table 2 indicates that the higher values of and decrease the local Nusselt number or rate of heat transfer occurs on the needle surface. The same features can be seen as the heat generation parameter increases. It is quite clear from Figure 8a and Figure 9a that the higher rate of Brownian motion and thermophoresis enhance the temperature of the fluid as well as the thermal boundary layer thickness. This increment in the boundary layer thickness minimizes the rate of heat transfer from the needle to the flow. Furthermore, Table 3 clarifies that the rate of mass transfer (or local Sherwood number) increases with an increase in thermophoresis and chemical reaction parameters. Noticeably, the higher value of the Brownian motion parameter tends to slow down the rate of mass transfer in the system. This happens due to the continuous collision of base fluid particles and nanoparticles which cause the random movement of those particles in the fluid. In addition, it can be observed in Figure 8b that the presence of higher value of enhance the concentration profiles as well as the concentration boundary layer thickness. This criterion leads to the decrement in the mass transfer rate. In addition, as thermophoretic effect intensifies, nanoparticles with high thermal conductivity penetrate deeper in the fluid, hence, decreases the concentration boundary layer thickness as well as concentration profiles as can be seen in Figure 9b. This behavior leads to an increase in the local Sherwood Number.

Table 2.
Effects of thermphoresis parameter and Brownian motion parameter on the numerical values of local Nusselt number, for and when , , , and .

Table 3.
Effects of thermphoresis parameter and Brownian motion parameter on the numerical values of local Sherwood number, for and when , , , and .
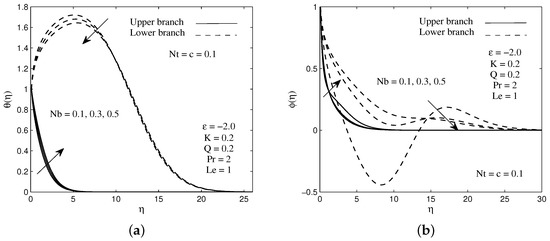
Figure 8.
Sample of (a) temperature and (b) concentration profiles for several values of Brownian motion parameter .
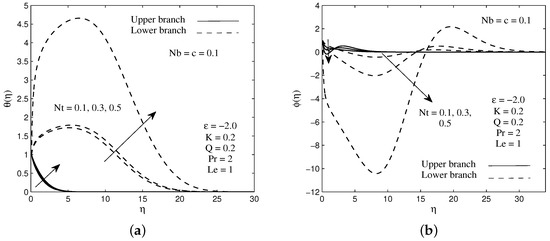
Figure 9.
Sample of (a) temperature and (b) concentration profiles for several values of thermophoresis parameter .
Since this study has more than one solution, we need to verify which of the solutions obtained are physically relevant (stable solution) by solving Equations (25)–(28). The determination of the stable solution count on the sign of the smallest eigenvalue gained through this analysis. Table 4 presents the smallest eigenvalue for several values of chemical reaction, heat generation and velocity ratio parameters when and . Table 4 indicates that the positive sign of for upper branch solution represents an initial decomposition of disturbance, while the negative sign of for lower branch solution represents an initial growth of disturbance in the system. Please note that the flow is said to be stable and physically relevant, if there is an initial decay of disturbance in the boundary layer separation. Otherwise, the flow is said to be unstable and not physically relevant.

Table 4.
Smallest eigenvalues for several values of chemical reaction parameter K, heat generation parameter Q and velocity ratio parameter for and when , and .
5. Final Remarks
In this work, the numerical model is developed to study the boundary layer flow of two-phase nanofluid on a moving slender needle. The influences of chemical reaction and heat generation on the flow have been taken into consideration. The governing flow equations are solved and validated numerically by applying bvp4c package through MATLAB software. The key findings of this analysis can be summarized as follows:
- The heat generation parameter reduces the local heat flux as well as the rate of heat transfer.
- The presence of a chemical reaction increases the rate of mass transfer on the needle surface.
- The Brownian motion parameter diminishes the rate of heat and mass transfers from the needle surface to the flow.
- An increase in the thermophoresis parameter results in an increase in the mass transfer rate, while the reverse effect is noted for the heat transfer rate.
- An increment in the needle thickness leads to decrease the magnitudes of the surface shear stress, local heat flux and local mass flux.
- The dual solutions are likely to exist when the needle surface moves against the free-stream direction, .
- The upper branch solution exhibits stable flow (or solution) and lower branch solution exhibits unstable flow.
Author Contributions
S.N.A.S. and N.B. designed the research; S.N.A.S. formulated the mathematical model and computed the numerical results; S.N.A.S. and N.B. analyzed the results; S.N.A.S. wrote the manuscript; S.N.A.S., N.B., N.M.A. and F.M.A. have read and approved this manuscript.
Funding
This research was funded by Fundamental Research Grant Scheme (FRGS/1/2018/STG06/UPM/ 02/4/5540155) from Ministry of Higher Education Malaysia and Putra Grant GP-IPS/2018/9667900 from Universiti Putra Malaysia.
Acknowledgments
The authors would like to express their gratitude to the anonymous reviewers for their valuable comments and suggestions for a betterment of this paper.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
| c | Needle size |
| C | Fluid concentration (kg m) |
| Skin friction coefficient | |
| Ambient nanoparticle volume fraction | |
| Surface volume fraction | |
| Specific heat at constant pressure | |
| Brownian diffusion coefficient (m s) | |
| Thermophoretic diffusion coefficient (m s) | |
| f | Similarity function for velocity |
| K | Chemical reaction parameter |
| Chemical reaction coefficient | |
| Dimensionless reaction rate | |
| Lewis number | |
| Brownian motion parameter | |
| Thermophoresis parameter | |
| Local Nusselt number | |
| Prandtl number | |
| Q | Heat generation parameter |
| Heat generation coefficient | |
| Dimensionless heat generation | |
| r | Cartesian coordinate |
| Local Reynolds number | |
| Local Sherwood number | |
| T | Fluid temperature (K) |
| Wall temperature (K) | |
| Ambient temperature (K) | |
| U | Composite velocity (ms) |
| Wall velocity (ms) | |
| Ambient velocity (ms) | |
| u | Velocity in x direction (ms) |
| v | Velocity in r direction (ms) |
| x | Cartesian coordinate |
| Thermal diffusivity (m s) | |
| Similarity independent variable | |
| Dimensionless temperature | |
| Velocity ratio parameter | |
| Ratio of effective heat capacity of nanofluid | |
| Volumetric heat capacity (J K) | |
| Kinematic viscosity (m s) | |
| Dynamic viscosity (kg ms) | |
| Fluid density (kg m) | |
| Dimensionless solid volume fraction | |
| w | Condition at the wall |
| ∞ | Ambient condition |
| Differentiative with respect to |
References
- Choi, S.U.S. Enhancing thermal conductivity of fluids with nanoparticles. Am. Soc. Mech. Eng. Fluids Eng. Div. 1995, 231, 99–105. [Google Scholar]
- Wong, K.V.; Leon, O.D. Applications of Nanofluids: Current and Future. Adv. Mech. Eng. 2010, 2010, 519659. [Google Scholar] [CrossRef]
- Saidur, R.; Leong, K.Y.; Mohammad, H.A. A review on applications and challenges of nanofluids. Renew. Sustain. Energy Rev. 2011, 15, 1646–1668. [Google Scholar] [CrossRef]
- Huminic, G.; Huminic, A. Application of nanofluids in heat exchangers: A review. Renew. Sustain. Energy Rev. 2012, 16, 5625–5638. [Google Scholar] [CrossRef]
- Colangelo, G.; Favale, E.; Milanese, M.; Risi, A.D.; Laforgia, D. Cooling of electronic devices: Nanofluids contribution. Appl. Ther. Eng. 2017, 127, 421–435. [Google Scholar] [CrossRef]
- Buongiorno, J. Convective transport in nanofluids. J. Heat Trans. 2006, 128, 240–250. [Google Scholar] [CrossRef]
- Tiwari, R.K.; Das, M.K. Heat transfer augmentation in a two-sided lid-driven differentially heated square cavity utilizing nanofluids. Int. J. Heat Mass Trans. 2007, 50, 2002–2018. [Google Scholar] [CrossRef]
- Khan, W.A.; Pop, I. Boundary-layer flow of a nanofluid past a stretching sheet. Int. J. Heat Mass Trans. 2010, 53, 2477–2483. [Google Scholar] [CrossRef]
- Makinde, O.D.; Aziz, A. Boundary layer flow of a nanofluid past a stretching sheet with a convective boundary condition. Int. J. Ther. Sci. 2011, 50, 1326–1332. [Google Scholar] [CrossRef]
- Bachok, N.; Ishak, A.; Pop, I. Unsteady boundary-layer flow and heat transfer of a nanofluid over a permeable stretching/shrinking sheet. Int. J. Heat Mass Trans. 2012, 55, 2102–2109. [Google Scholar] [CrossRef]
- Das, K.; Duari, P.R.; Kundu, P.K. Nanofluid flow over an unsteady stretching surface in presence of thermal radiation. Alex. Eng. J. 2014, 53, 737–745. [Google Scholar] [CrossRef]
- Mabood, F.; Khan, W.A.; Ismail, A.I.M. MHD boundary layer flow and heat transfer of nanofluids over a nonlinear stretching sheet: A numerical study. J. Magn. Magn. Mater. 2015, 374, 569–576. [Google Scholar] [CrossRef]
- Naramgari, S.; Sulochana, C. MHD flow over a permeable stretching/shrinking sheet of a nanofluid with suction/injection. Alex. Eng. J. 2016, 55, 819–827. [Google Scholar] [CrossRef]
- Pandey, A.K.; Kumar, M. Boundary layer flow and heat transfer analysis on Cu-water nanofluid flow over a stretching cylinder with slip. Alex. Eng. J. 2017, 56, 671–677. [Google Scholar] [CrossRef]
- Mustafa, M. MHD nanofluid flow over a rotating disk with partial slip effects: Buongiorno model. Int. J. Heat Mass Trans. 2017, 108, 1910–1916. [Google Scholar] [CrossRef]
- Jyothi, K.; Reddy, P.S.; Reddy, M.S. Influence of magnetic field and thermal radiation on convective flow of SWCNTs-water and MWCNTs-water nanofluid between rotating stretchable disks with convective boundary conditions. Adv. Powder Technol. 2018, 331, 326–337. [Google Scholar] [CrossRef]
- Bakar, N.A.A.; Bachok, N.; Arifin, N.M.; Pop, I. Stability analysis on the flow and heat transfer of nanofluid past a stretching/shrinking cylinder with suction effect. Results Phys. 2018, 9, 1335–1344. [Google Scholar] [CrossRef]
- Griffith, R.M. Velocity, temperature and concentration distributions during fiber spinning. Ind. Eng. Chem. Fundam. 1964, 3, 245–250. [Google Scholar] [CrossRef]
- Chin, D.T. Mass transfer to a continuousmoving sheet electrode. J. Electrochem. Soc. 1975, 122, 643–646. [Google Scholar] [CrossRef]
- Gorla, R.S.R. Unsteady mass transfer in the boundary layer on a continuous moving sheet electrode. J. Electrochem. Soc. 1978, 125, 865–869. [Google Scholar] [CrossRef]
- Damseh, R.A.; Al-Odat, M.Q.; Chamkha, A.J.; Shannak, B.A. Combined effect of heat generation or absorption and first-order chemical reaction on micropolar fluid flows over a uniformly stretched permeable surface. Int. J. Therm. Sci. 2009, 48, 1658–1663. [Google Scholar] [CrossRef]
- Magyari, E.; Chamkha, A.J. Combined effect of heat generation or absorption and first-order chemical reaction on micropolar fluid flows over a uniformly stretched permeable surface: The full analytical solution. Int. J. Therm. Sci. 2010, 49, 1821–1828. [Google Scholar] [CrossRef]
- Mabood, F.; Shateyi, S.; Rashidi, M.M.; Momoniat, E.; Freidoonimehr, N. MHD stagnation point flow heat and mass transfer of nanofluids in porous medium with radiation, viscous dissipation and chemical reaction. Adv. Powder Technol. 2016, 27, 742–749. [Google Scholar] [CrossRef]
- Eid, M.R. Chemical reaction effect on MHD boundary-layer flow of two-phase nanofluid model over an exponentially stretching sheet with a heat generation. J. Mol. Liq. 2016, 220, 718–725. [Google Scholar] [CrossRef]
- Ibrahim, S.M.; Lorenzini, G.; Vijaya Kumar, P.; Raju, C.S.K. Influence of chemical reaction and heat source on dissipative MHD mixed convection flow of a Casson nanofluid over a nonlinear permeable stretching sheet. Int. J. Heat Mass Trans. 2017, 111, 346355. [Google Scholar] [CrossRef]
- Nayak, M.K.; Akbar, N.S.; Tripathi, D.; Khan, Z.H.; Pandey, V.S. MHD 3D free convective flow of nanofluid over an exponentially stretching sheet with chemical reaction. Adv. Powder Technol. 2017, 28, 2159–2166. [Google Scholar] [CrossRef]
- Sithole, H.; Mondal, H.; Goqo, S.; Sibanda, P.; Motsa, S. Numerical simulation of couple stress nanofluid flow in magneto-porous medium with thermal radiation and a chemical reaction. Appl. Math. Comput. 2018, 339, 820–836. [Google Scholar] [CrossRef]
- Khan, M.; Shahid, A.; Malik, M.Y.; Salahuddin, T. Chemical reaction for Carreau-Yasuda nanofluid flow past a nonlinear stretching sheet considering Joule heating. Results Phys. 2018, 8, 1124–1130. [Google Scholar] [CrossRef]
- Zeeshan, A.; Shehzad, N.; Ellahi, R. Analysis of activation energy in Couette-Poiseuille flow of nanofluid in the presence of chemical reaction and convective boundary conditions. Results Phys. 2018, 8, 502–512. [Google Scholar] [CrossRef]
- Hayat, T.; Kiyani, M.Z.; Alsaedi, A.; Ijaz Khan, M.; Ahmad, I. Mixed convective three-dimensional flow of Williamson nanofluid subject to chemical reaction. Int. J. Heat Mass Trans. 2018, 127, 422–429. [Google Scholar] [CrossRef]
- Lee, L.L. Boundary layer over a thin needle. Phys. Fluids 1967, 10, 1820–1822. [Google Scholar] [CrossRef]
- Narain, J.P.; Uberoi, S.M. Combined forced and free-convection heat transfer from vertical thin needles in a uniform stream. Phys. Fluids 1973, 15, 1879–1882. [Google Scholar] [CrossRef]
- Wang, C.Y. Mixed convection on a vertical needle with heated tip. Phys. Fluids 1990, 2, 622–625. [Google Scholar] [CrossRef]
- Ishak, A.; Nazar, R.; Pop, I. Boundary layer flow over a continuously moving thin needle in a parallel free stream. Chin. Phys. Lett. 2007, 24, 2895–2897. [Google Scholar] [CrossRef]
- Ahmad, S.; Arifin, N.M.; Nazar, R.; Pop, I. Mixed convection boundary layer flow along vertical thin needles: Assisting and opposing flows. Int. Commun. Heat Mass Trans. 2008, 35, 157–162. [Google Scholar] [CrossRef]
- Afridi, M.I.; Qasim, M. Entropy generation and heat transfer in boundary layer flow over a thin needle moving in a parallel stream in the presence of nonlinear Rosseland radiation. Int. J. Therm. Sci. 2018, 123, 117–128. [Google Scholar] [CrossRef]
- Grosan, T.; Pop, I. Forced Convection Boundary Layer Flow Past Nonisothermal Thin Needles in Nanofluids. J. Heat Trans. 2011, 133. [Google Scholar] [CrossRef]
- Trimbitas, R.; Grosan, T.; Pop, I. Mixed convection boundary layer flow along vertical thin needles in nanofluids. Int. J. Numer. Methods Heat Fluid Flow 2014, 24, 579–594. [Google Scholar] [CrossRef]
- Hayat, T.; Khan, M.I.; Farooq, M.; Yasmeen, T.; Alsaedi, A. Water-carbon nanofluid flow with variable heat flux by a thin needle. J. Mol. Liq. 2016, 224, 786–791. [Google Scholar] [CrossRef]
- Soid, S.K.; Ishak, A.; Pop, I. Boundary layer flow past a continuously moving thin needle in a nanofluid. Appl. Therm. Eng. 2017, 114, 58–64. [Google Scholar] [CrossRef]
- Krishna, P.M.; Sharma, R.P.; Sandeep, N. Boundary layer analysis of persistent moving horizontal needle in Blasius and Sakiadis magnetohydrodynamic radiative nanofluid flows. Nucl. Eng. Technol. 2017, 49, 1654–1659. [Google Scholar] [CrossRef]
- Ahmad, R.; Mustafa, M.; Hina, S. Buongiorno’s model for fluid flow around a moving thin needle in a flowing nanofluid: A numerical study. Chin. J. Phys. 2017, 55, 1264–1274. [Google Scholar] [CrossRef]
- Salleh, S.N.A.; Bachok, N.; Arifin, N.M.; Ali, F.M.; Pop, I. Magnetohydrodynamics flow past a moving vertical thin needle in a nanofluid with stability analysis. Energies 2018, 11, 3297. [Google Scholar] [CrossRef]
- Weidman, P.D.; Kubitschek, D.G.; Davis, A.M.J. The effect of transpiration on self-similar boundary layer flow over moving surfaces. Int. J. Eng. Sci. 2006, 44, 730–737. [Google Scholar] [CrossRef]
- Rosca, A.V.; Pop, I. Flow and heat transfer over a vertical permeable stretching/shrinking sheet with a second order slip. Int. J. Heat Mass Trans. 2013, 60, 355–364. [Google Scholar] [CrossRef]
- Harris, S.D.; Ingham, D.B.; Pop, I. Mixed convection boundary-layer flow near the stagnation point on a vertical surface in a porous medium: Brinkman model with slip. Transp. Porous Media 2009, 77, 267–285. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).