Effect of Time Delay on Laser-Triggered Discharge Plasma for a Beyond EUV Source
Abstract
:1. Introduction
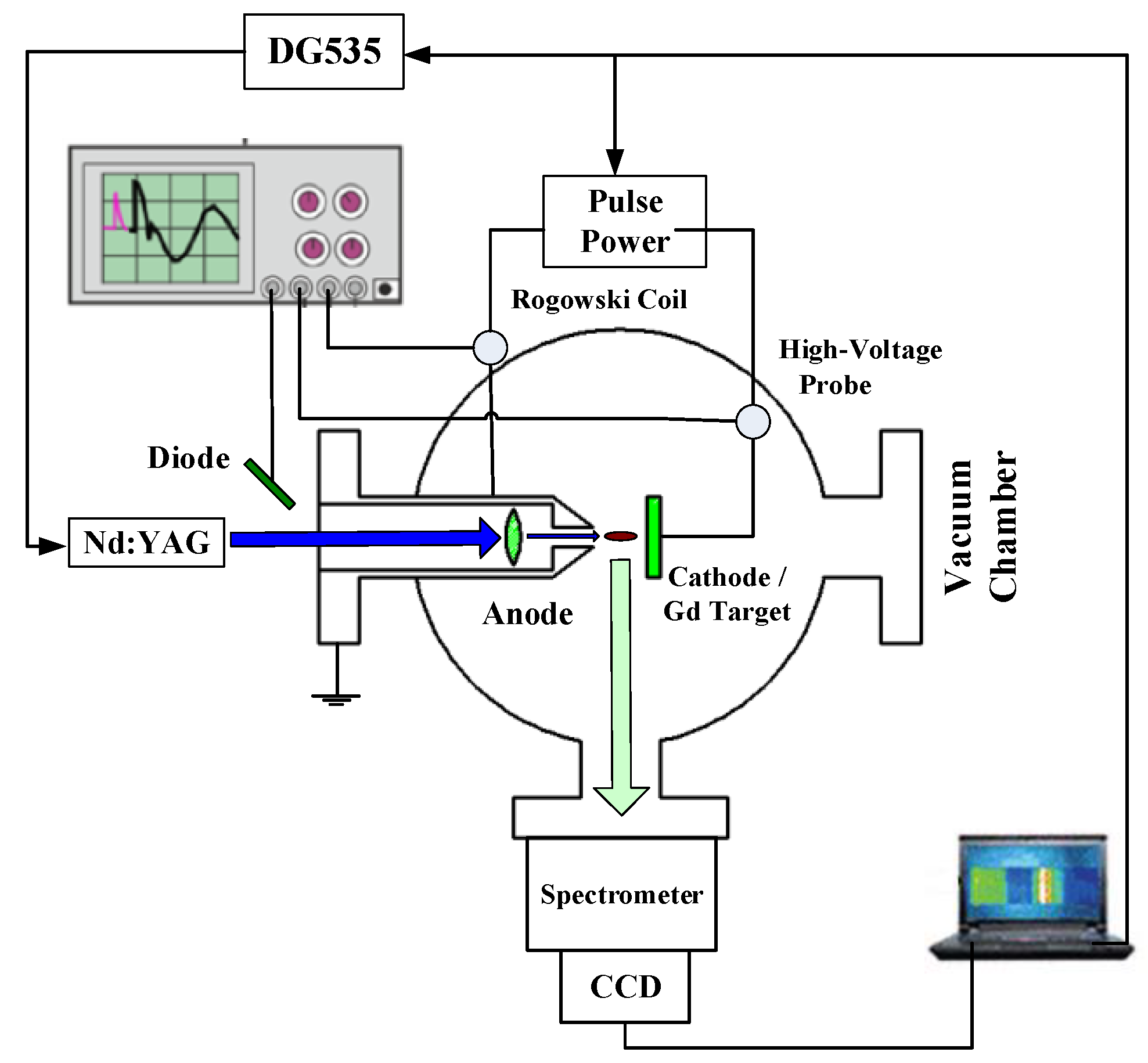
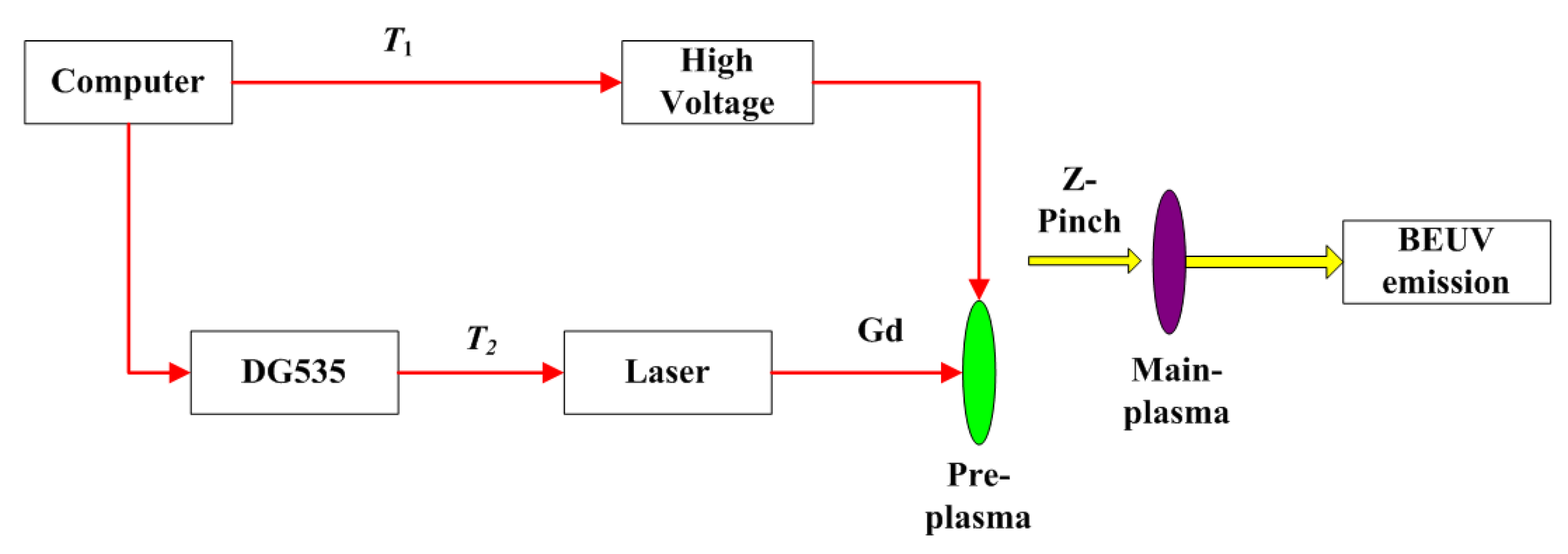
2. Experimental Apparatus
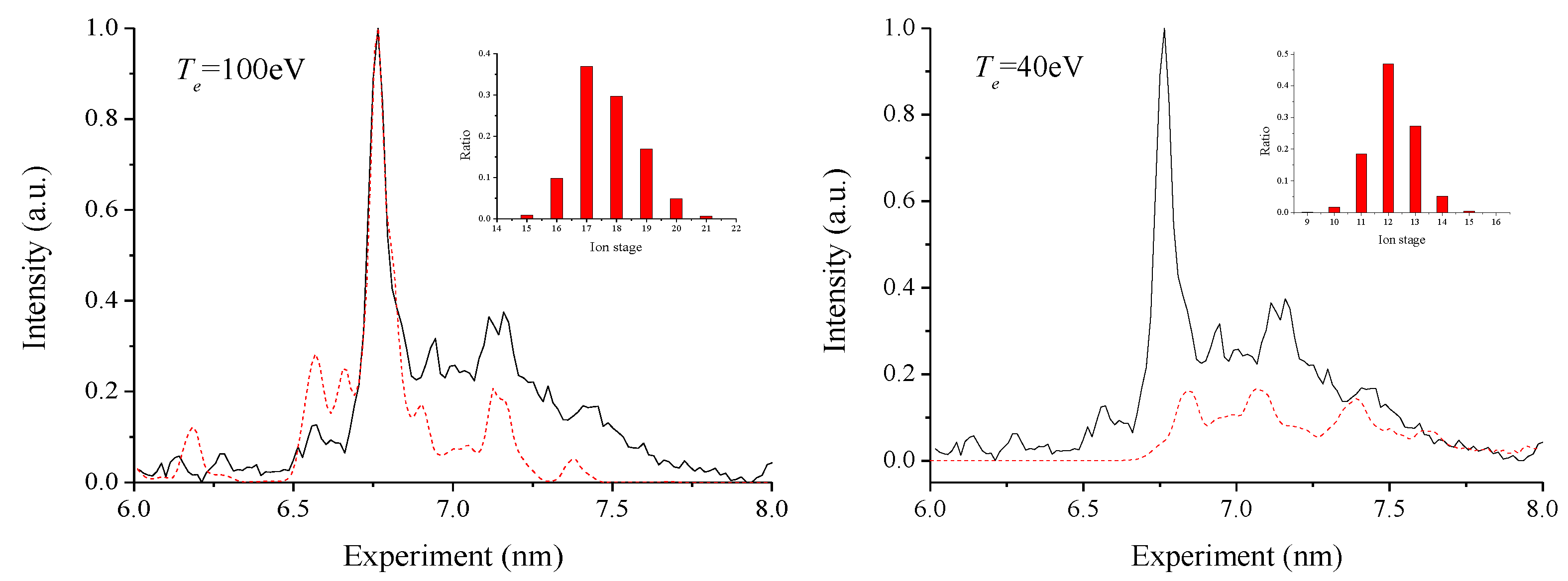
3. Theoretical Calculations
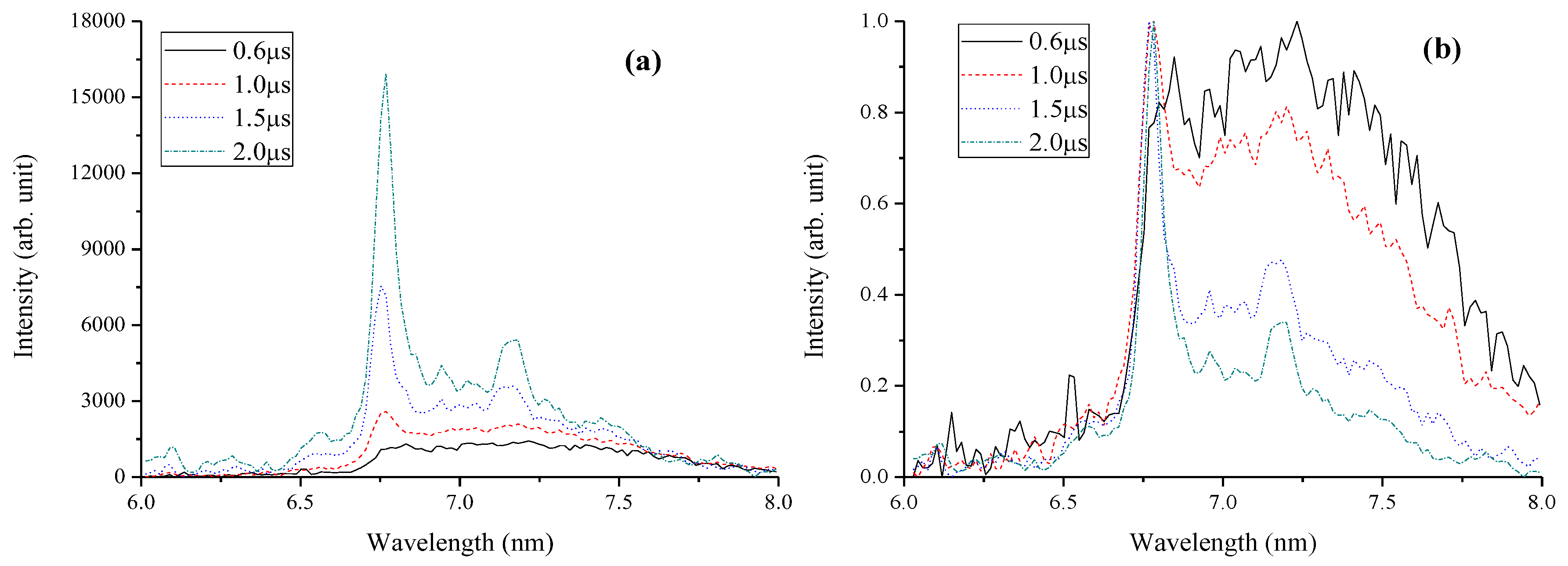
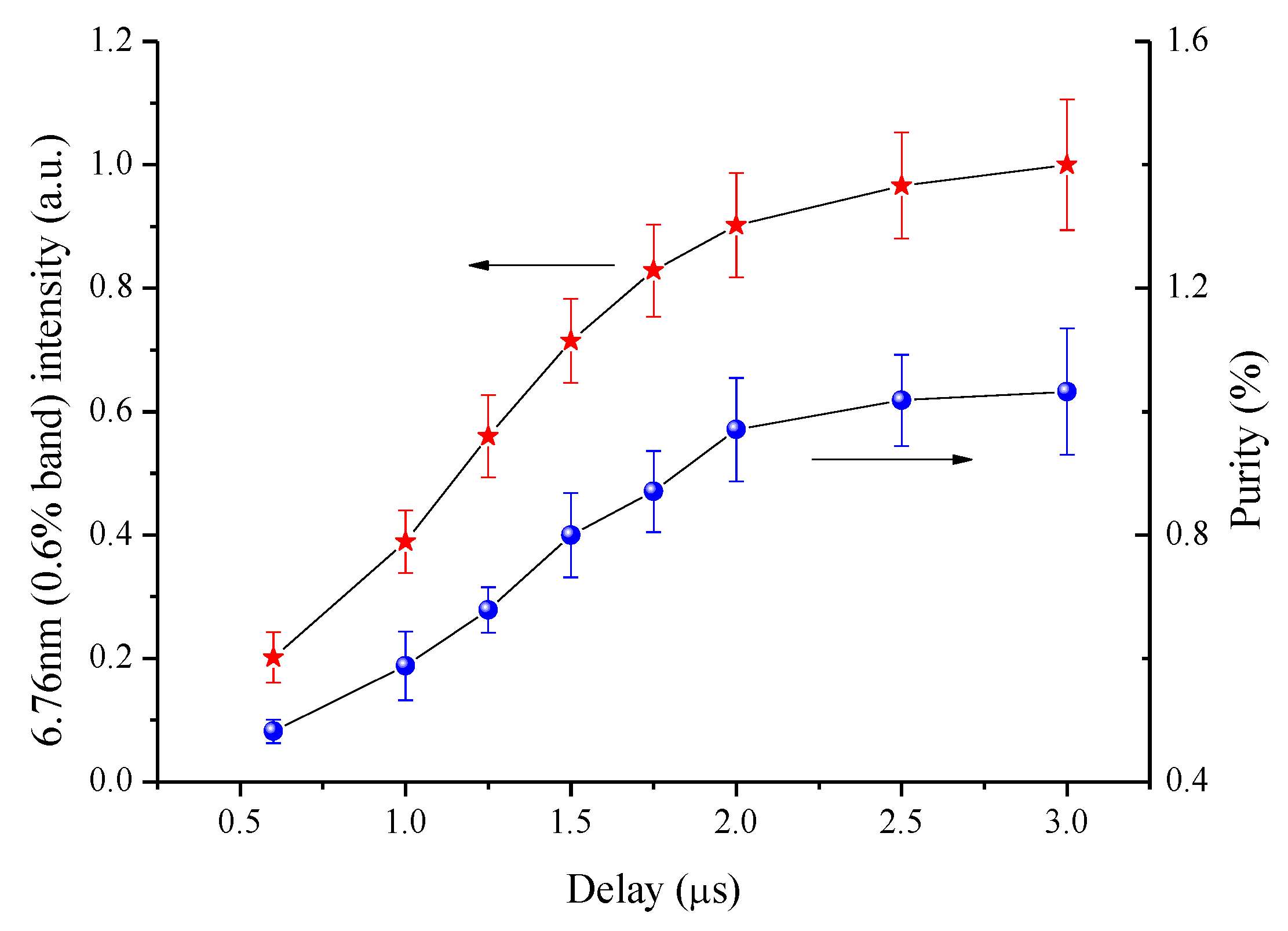
4. Experimental Results and Discussion
5. Summary
Author Contributions
Funding
Conflicts of Interest
References
- Musgrave, C.S.; Murakami, T.; Ugomori, T.; Yoshida, K.; Fujioka, S.; Nishimura, H.; Atarashi, H.; Iyoda, T.; Nagai, K. High-space resolution imaging plate analysis of extreme ultraviolet (EUV) light from tin laser-produced plasmas. Rev. Sci. Instrum. 2017, 88, 033506. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lim, S.; Kamohara, T.; Hosseini, S.H.R.; Katsuki, S. Dependence of current rise time on laser-triggered discharge plasma. J. Phys. D Appl. Phys. 2016, 49, 295207. [Google Scholar] [CrossRef]
- Churilov, S.S.; Ryabtsev, A.N. Analyses of the Sn IX–Sn XII spectra in the EUV region. Phys. Scr. 2006, 73, 614–619. [Google Scholar] [CrossRef]
- Zakharov, S.V.; Zakharov, V.S.; Novikov, V.G.; Mond, M.; Choi, P. Plasma dynamics in a hollow cathode triggered discharge with the influence of fast electrons on ionization phenomena and EUV emission. Plasma Sources Sci. Technol. 2008, 17, 024017. [Google Scholar] [CrossRef]
- Kuznetsov, D.S.; Yakshin, A.E.; Sturm, J.M.; Bijkerk, F. Grazing-incidence La/B-based multilayer mirrors for 6.x nm wavelength. J. Nanosci. Nanotechnol. 2019, 19, 585–592. [Google Scholar] [CrossRef] [PubMed]
- Naujok, P.; Yulin, S.; Bianco, A.; Mahne, N.; Kaiser, N.; Tunnermann, A. La/B4C multilayer mirrors with an additional wavelength suppression. Opt. Express 2015, 23, 4289–4295. [Google Scholar] [CrossRef]
- Belmonte, G.K.; Moura, C.A.D.; Reddy, P.G.; Gonsalves, K.E.; Weibel, D.E. EUV photofragmentation and oxidation of a polyarylene—Sulfonium resist: XPS and NEXAFS study. J. Photochem. Photobiol. Chem. 2018, 364, 373–381. [Google Scholar] [CrossRef]
- Oyama, T.G.; Oshima, A.; Washio, M.; Tagawa, S. Evaluation of resist sensitivity in extreme ultraviolet/soft x-ray region for next-generation lithography. AIP Adv. 2011, 1, 042153. [Google Scholar] [CrossRef] [Green Version]
- Li, B.; Otsuka, T.; Higashiguchi, T.; Yugami, N.; Jiang, W.; Endo, A.; Dunne, P.; O’Sullivan, G. Investigation of Gd and Tb plasmas for beyond extreme ultraviolet lithography based on multilayer mirror performance. Appl. Phys. Lett. 2012, 101, 013112. [Google Scholar] [CrossRef]
- Kilbane, D.; O’Sullivan, G. Extreme ultraviolet emission spectra of Gd and Tb ions. J. Appl. Phys. 2010, 108, 104905. [Google Scholar] [CrossRef] [Green Version]
- Higashiguchi, T.; Li, B.; Suzuki, Y.; Kawasaki, M.; Ohashi, H.; Torii, S.; Nakamura, D.; Takahashi, A.; Okada, T.; Jiang, W.; et al. Characteristics of extreme ultraviolet emission from mid-infrared laser-produced rare-earth Gd plasmas. Opt. Express 2013, 21, 31837–31845. [Google Scholar] [CrossRef]
- Ohashi, H.; Higashiguchi, T.; Li, B.; Suzuki, Y.; Kawasaki, M.; Kanehara, T.; Aida, Y.; Torii, S.; Makimura, T.; Jiang, W.; et al. Tuning extreme ultraviolet emission for optimum coupling with multilayer mirrors for future lithography through control of ionic charge states. J. Appl. Phys. 2014, 115, 033302. [Google Scholar] [CrossRef]
- Yin, L.; Wang, H.; Reagan, B.A.; Baumgarten, C.; Gullikson, E.; Berrill, M.; Shlyaptsev, V.N.; Rocca, J.J. 6.7-nm emission from Gd and Tb plasmas over a broad range of irradiation parameters using a single laser. Phys. Rev. Appl. 2016, 6, 034009. [Google Scholar] [CrossRef]
- Yoshida, K.; Fujioka, S.; Higashiguchi, T.; Ugomori, T.; Tanaka, N.; Ohashi, H.; Kawasaki, M.; Suzuki, Y.; Suzuki, C.; Tomita, K.; et al. Efficient extreme ultraviolet emission from one-dimensional spherical plasmas produced by multiple lasers. Appl. Phys. Express 2014, 7, 086202. [Google Scholar] [CrossRef]
- Tian, Y.; Song, X.L.; Xie, Z.; Gao, J.; Dou, Y.P.; Li, B.C.; Lin, J.Q.; Tomie, T. Sharpening of the 6.8 nm peak in an Nd: YAG laser produced Gd plasma by using a pre-formed plasma. AIP Adv. 2016, 6, 035108. [Google Scholar] [CrossRef]
- Xie, Z.; Wu, J.; Dou, Y.; Lin, J.; Tomie, T. Plasma dynamics in the initial stage of a laser-triggered discharge-plasma. J. Appl. Phys. 2018, 124, 213303. [Google Scholar] [CrossRef]
- Zhu, Q.; Yamada, J.; Kishi, N.; Watanabe, M.; Okino, A.; Horioka, K.; Hotta, E. Investigation of the dynamics of theZ-pinch imploding plasma for a laser-assisted discharge-produced Sn plasma EUV source. J. Phys. D Appl. Phys. 2011, 44, 145203. [Google Scholar] [CrossRef]
- Lu, P.; Katsuki, S.; Watanebe, T.; Akiyama, H. Electrical recovery after laser-assisted discharge for highly repetitive plasma EUV source. IEEE Trans. Plasma Sci. 2011, 39, 1849–1854. [Google Scholar] [CrossRef]
- Beyene, G.A.; Tobin, I.; Juschkin, L.; Hayden, P.; O’Sullivan, G.; Sokell, E.; Zakharov, V.S.; Zakharov, S.V.; O’Reilly, F. Laser-assisted vacuum arc extreme ultraviolet source: A comparison of picosecond and nanosecond laser triggering. J. Phys. D Appl. Phys. 2016, 49, 225201. [Google Scholar] [CrossRef]
- Vinokhodov, A.Y.; Krivtsun, V.M.; Lash, A.A.; Borisov, V.M.; Yakushev, O.F.; Koshelev, K.N. High-brightness laser-induced EUV source based on tin plasma with an unlimited lifetime of electrodes. Quantum Electron. 2016, 46, 81–87. [Google Scholar] [CrossRef]
- Lu, P.; Katsuki, S.; Tomimaru, N.; Ueno, T.; Akiyama, H. Dynamic characteristics of laser-assisted discharge plasmas for extreme ultraviolet light sources. Jpn. J. Appl. Phys. 2010, 49, 096202. [Google Scholar] [CrossRef]
- Kieft, E.R.; van der Mulen, J.J.A.M.; Banine, V. Subnanosecond thomson scattering on a vacuum arc discharge in tin vapor. Phys. Rev. E Stat. Nonlinear Soft Matter Phys. 2005, 72, 026415. [Google Scholar] [CrossRef] [PubMed]
- Su, M.G.; Min, Q.; Cao, S.Q.; Sun, D.X.; Hayden, P.; O’Sullivan, G.; Dong, C.Z. Evolution analysis of EUV radiation from laser-produced tin plasmas based on a radiation hydrodynamics model. Sci. Rep. 2017, 7, 45212. [Google Scholar] [CrossRef] [Green Version]
- Churilov, S.S.; Kildiyarova, R.R.; Ryabtsev, A.N.; Sadovsky, S.V. EUV spectra of Gd and Tb ions excited in laser-produced and vacuum spark plasmas. Phys. Scr. 2009, 80, 045303. [Google Scholar] [CrossRef]
- Colombant, D. X-ray emission in laser-produced plasmas. J. Appl. Phys. 1973, 44, 3524. [Google Scholar] [CrossRef]
- Masnavi, M.; Nakajima, M.; Sasaki, A.; Hotta, E.; Horioka, K. Potential of discharge-based lithium plasma as an extreme ultraviolet source. Appl. Phys. Lett. 2006, 89, 031503. [Google Scholar] [CrossRef]
- Yoshida, K.; Fujioka, S.; Higashiguchi, T.; Ugomori, T.; Tanaka, N.; Kawasaki, M.; Suzuki, Y.; Suzuki, C.; Tomita, K.; Hirose, R. Density and X-ray emission profile relationships in highly ionized high-Z laser-produced plasmas. Appl. Phys. Lett. 2015, 106, 121109. [Google Scholar] [CrossRef]
- Li, B.; Dunne, P.; Higashiguchi, T.; Otsuka, T.; Yugami, N.; Jiang, W.; Endo, A.; O’Sullivan, G. Gd plasma source modeling at 6.7 nm for future lithography. Appl. Phys. Lett. 2011, 99, 231502. [Google Scholar] [CrossRef]
- Otsuka, T.; Kilbane, D.; Higashiguchi, T.; Yugami, N.; Yatagai, T.; Jiang, W.; Endo, A.; Dunne, P.; O’Sullivan, G. Systematic investigation of self-absorption and conversion efficiency of 6.7 nm extreme ultraviolet sources. Appl. Phys. Lett. 2010, 97, 231503. [Google Scholar] [CrossRef] [Green Version]
- Makhotkin, I.A.; Zoethout, E.; Louis, E.; Yakunin, A.M.; Müllender, S.; Bijkerk, F. Spectral properties of La/B- based multilayer mirrors near the boron K absorption edge. Opt. Express 2012, 20, 11778–11786. [Google Scholar] [CrossRef]
- Hosokai, T.; Yokoyama, T.; Zhidkov, A.; Sato, H.; Hotta, E.; Horioka, K. Elongation of extreme ultraviolet (at 13.5 nm) emission with time-of-flight controlled discharges and lateral fuel injection. J. Appl. Phys. 2008, 104, 053306. [Google Scholar] [CrossRef]
- Song, X.L.; Song, X.W.; Dou, Y.P.; Tian, Y.; Xie, Z.; Gao, X.; Lin, J.Q.; Science, S.O. Out-of-band radiation and spatio-temporal characterization of Gd target laser plasma sources. Spectrosc. Spect. Anal. 2016, 36, 3114–3118. [Google Scholar]






© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, Q.; Tian, H.; Zhao, Y.; Wang, Q. Effect of Time Delay on Laser-Triggered Discharge Plasma for a Beyond EUV Source. Symmetry 2019, 11, 658. https://doi.org/10.3390/sym11050658
Xu Q, Tian H, Zhao Y, Wang Q. Effect of Time Delay on Laser-Triggered Discharge Plasma for a Beyond EUV Source. Symmetry. 2019; 11(5):658. https://doi.org/10.3390/sym11050658
Chicago/Turabian StyleXu, Qiang, He Tian, Yongpeng Zhao, and Qi Wang. 2019. "Effect of Time Delay on Laser-Triggered Discharge Plasma for a Beyond EUV Source" Symmetry 11, no. 5: 658. https://doi.org/10.3390/sym11050658
APA StyleXu, Q., Tian, H., Zhao, Y., & Wang, Q. (2019). Effect of Time Delay on Laser-Triggered Discharge Plasma for a Beyond EUV Source. Symmetry, 11(5), 658. https://doi.org/10.3390/sym11050658





