Influence of Symmetric and Asymmetric Voids on Mechanical Behaviors of Tunnel Linings: Model Tests and Numerical Simulations
Abstract
:1. Introduction
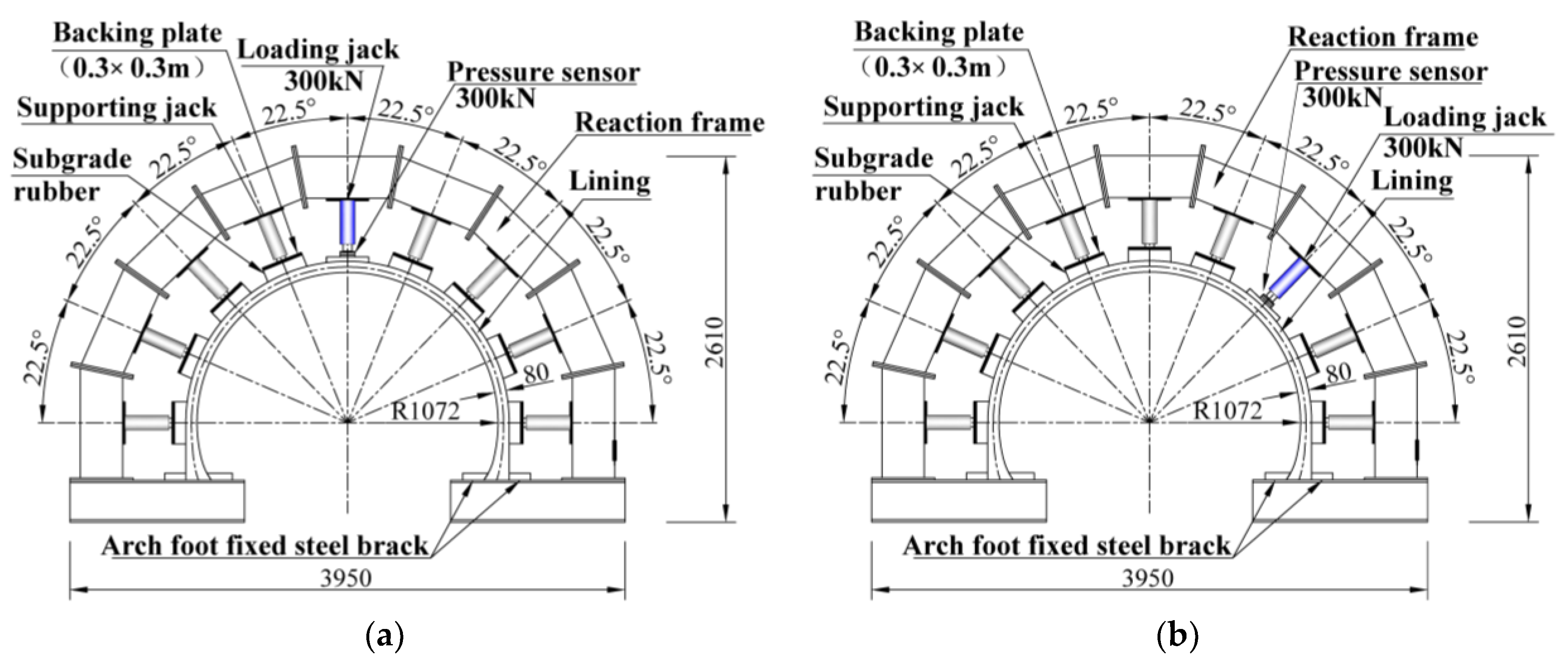
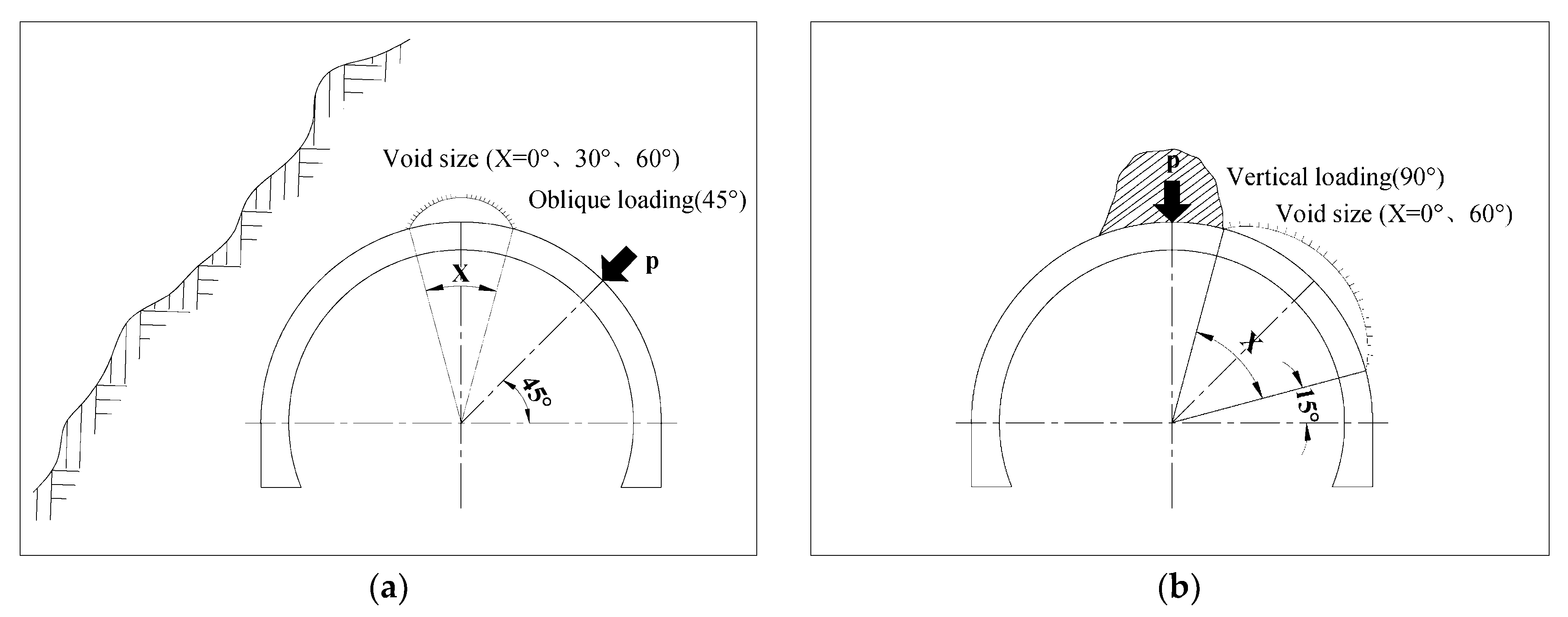
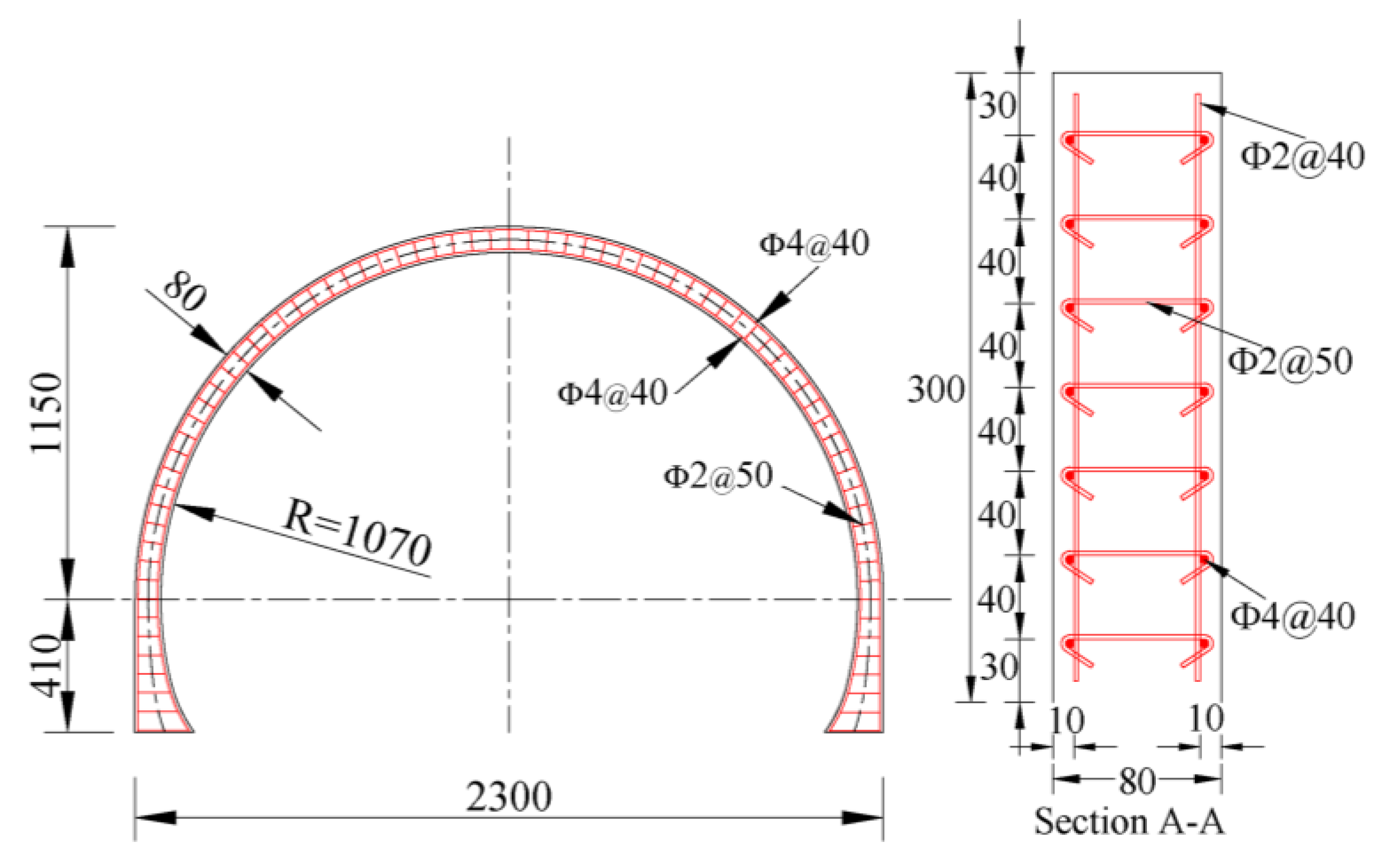
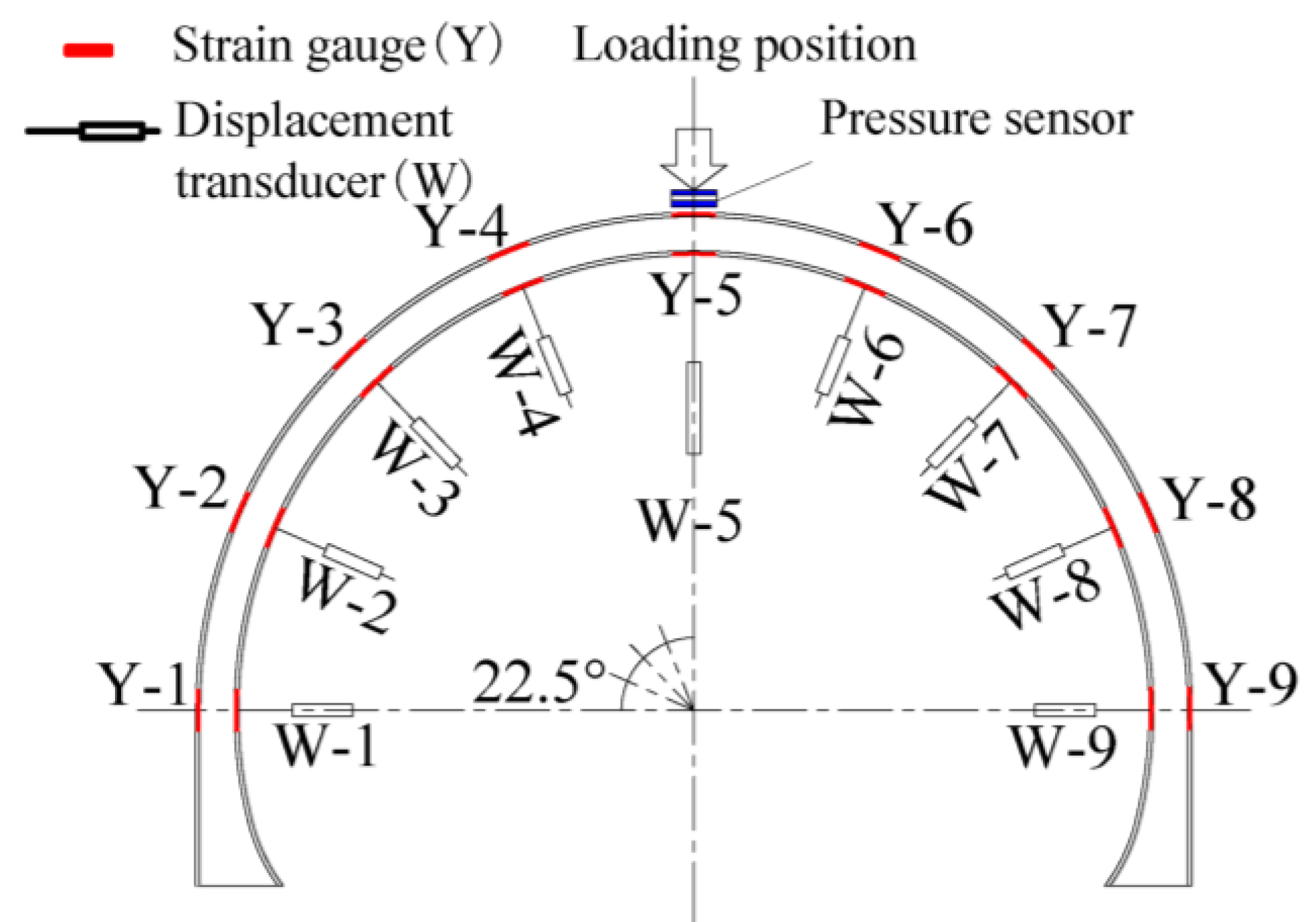
2. Model Test Scheme
3. Analysis of Test Results
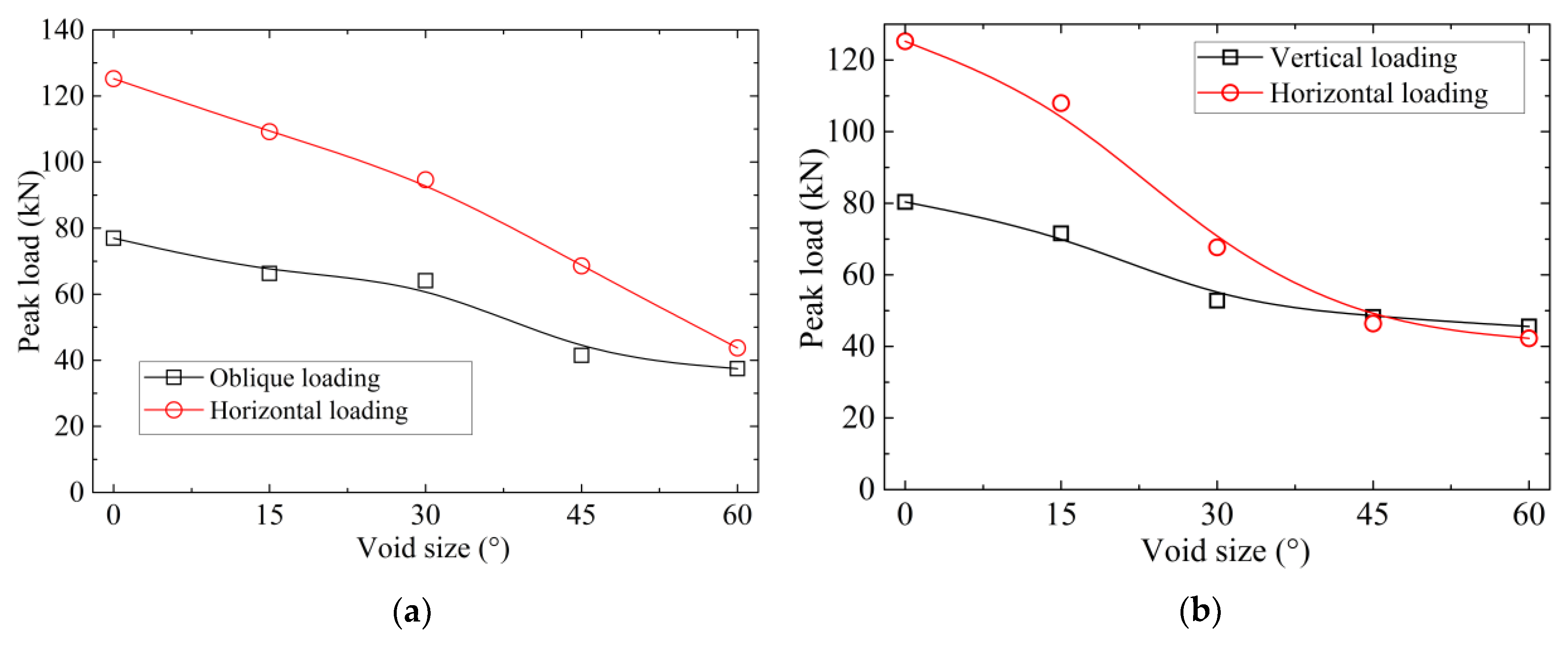
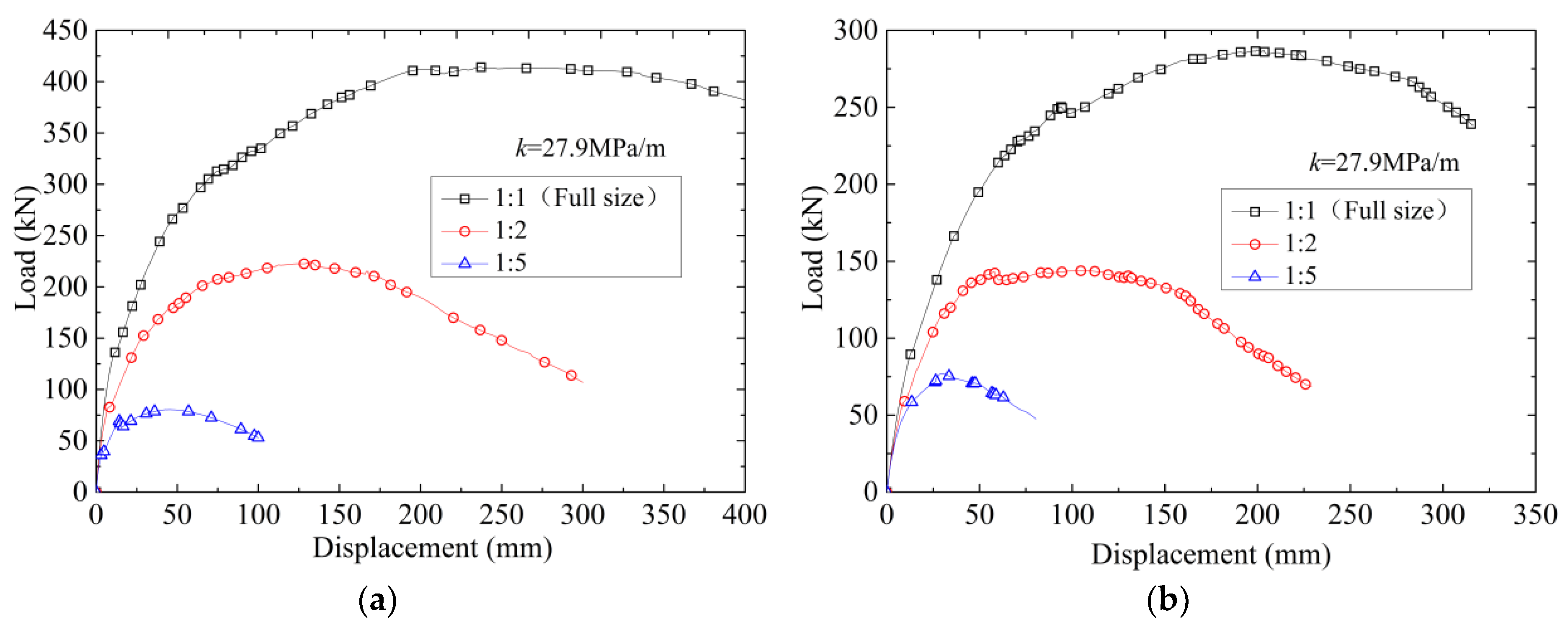
3.1. Bearing Capacity of Lining Under the Influence of Voids
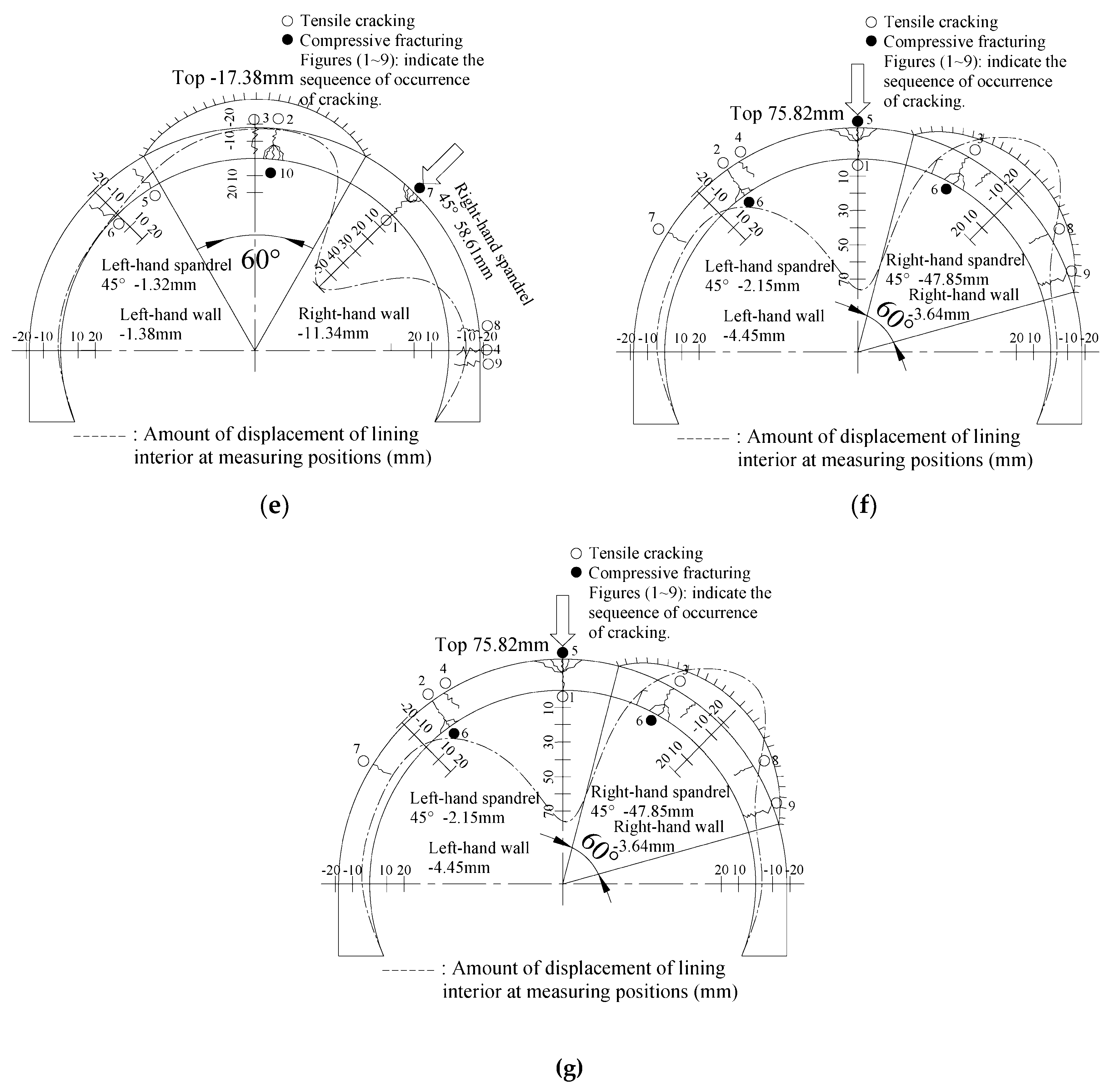
3.2. Failure Modes of Lining Under the Influence of Voids
4. Numerical Model
4.1. Material Model and Parameters
4.1.1. Modeling of Concrete
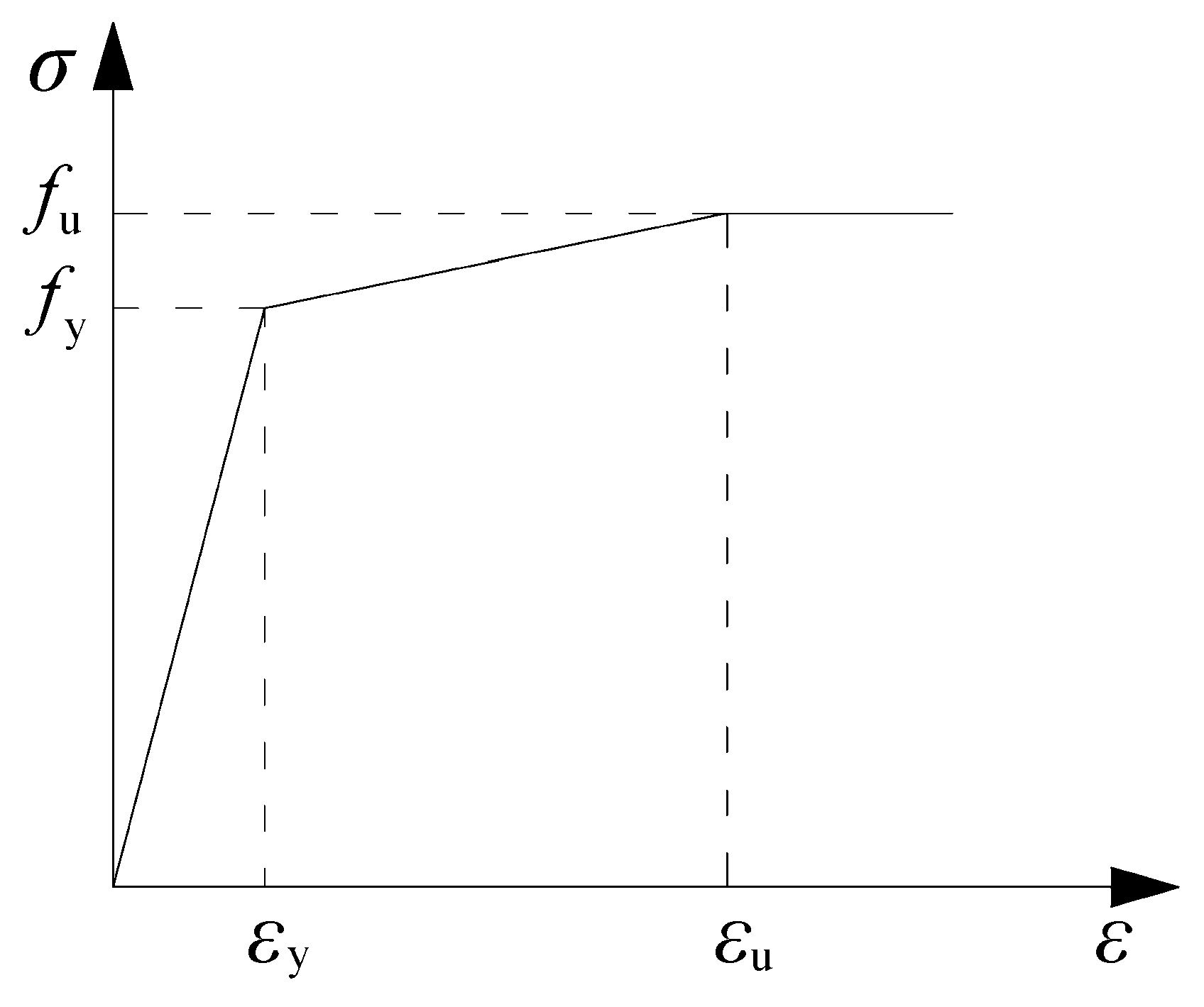
4.1.2. Modeling of Steel Bar
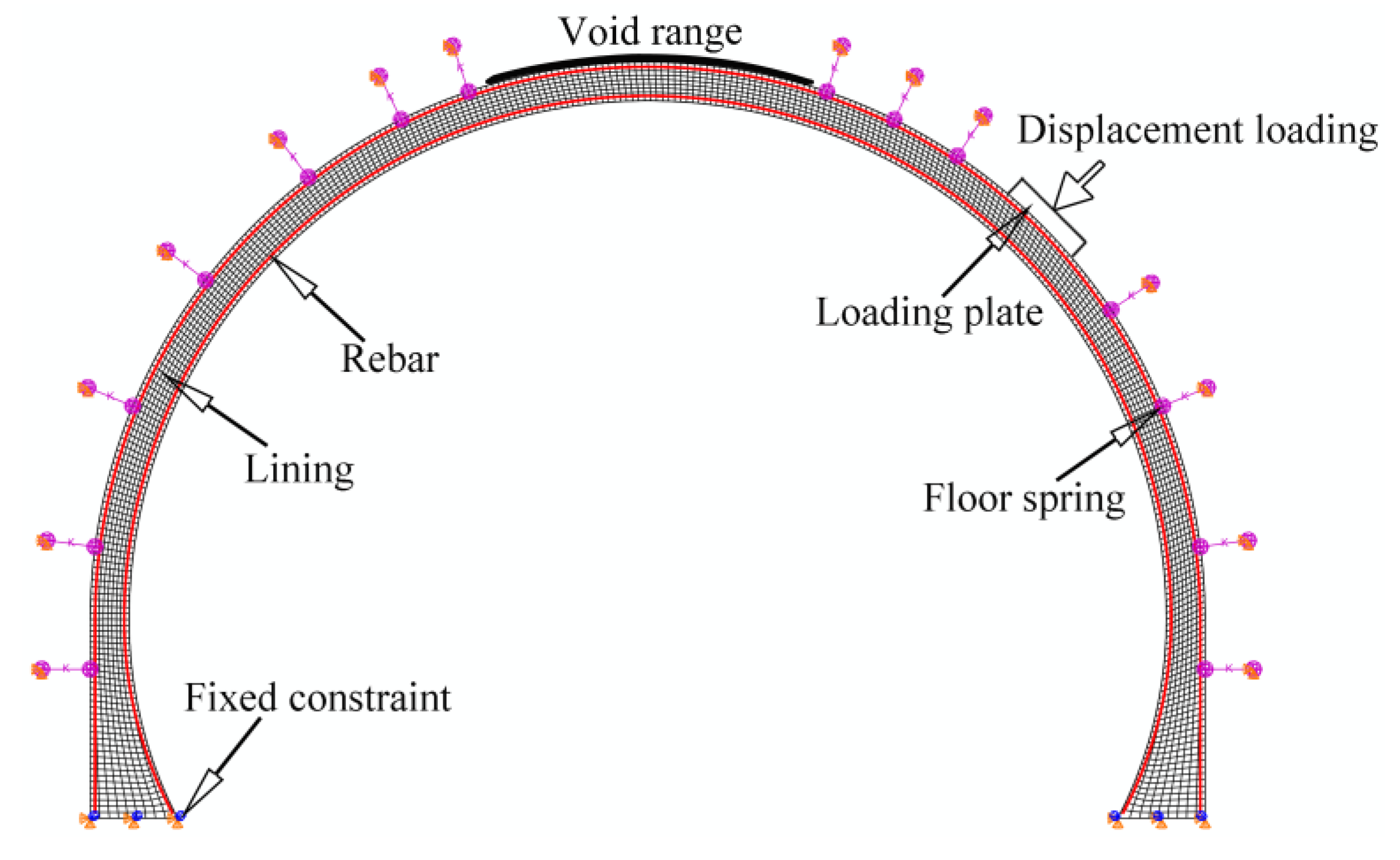
4.2. Structural Computational Model
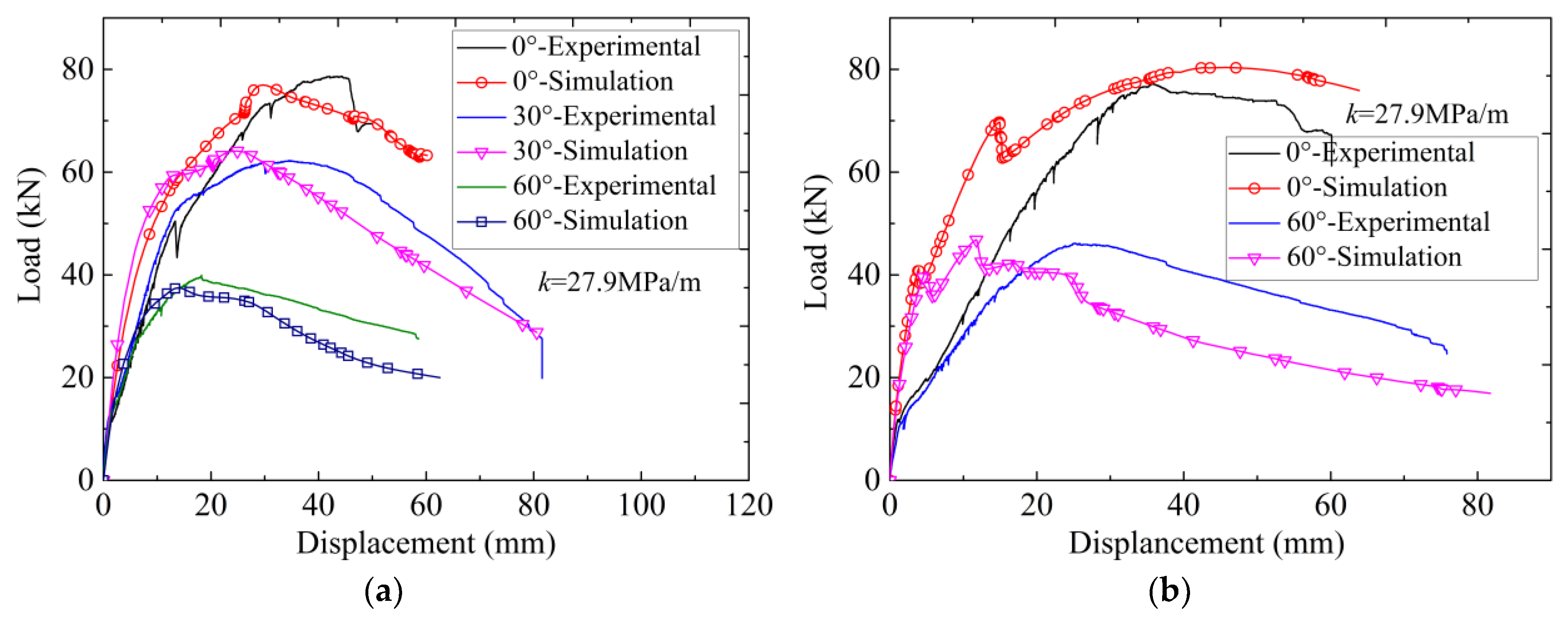
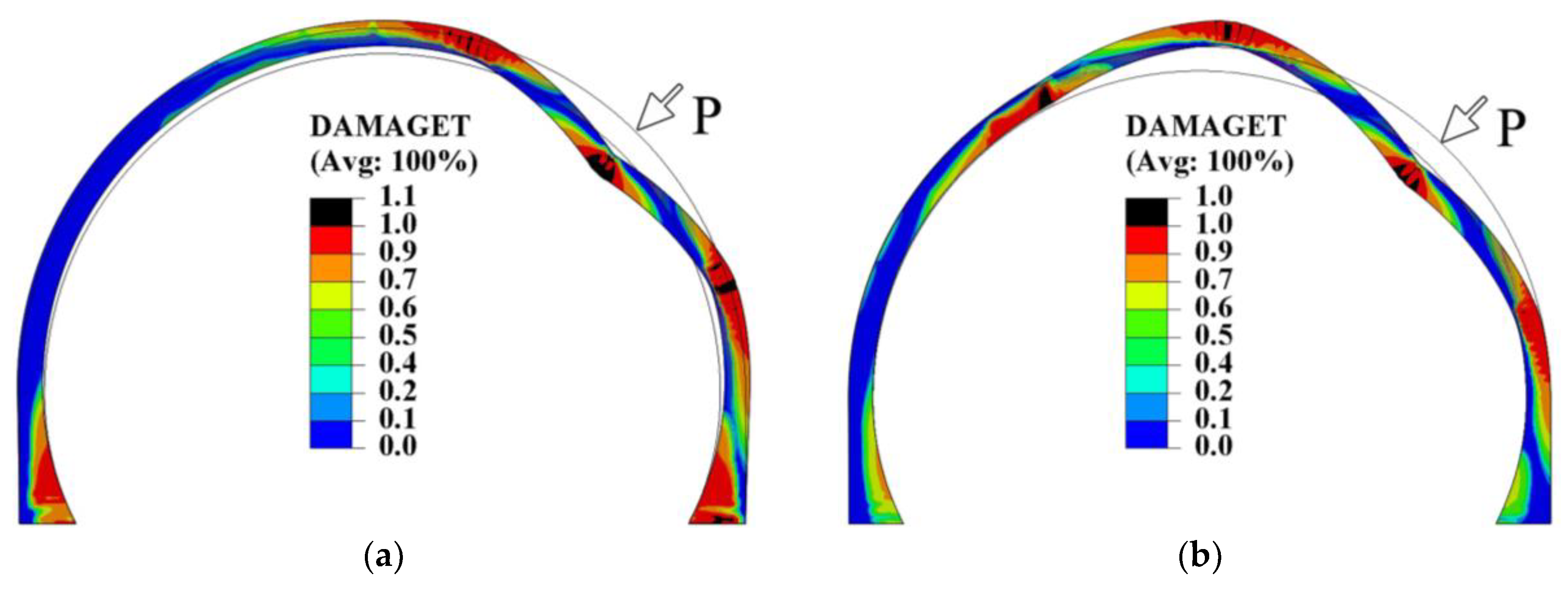
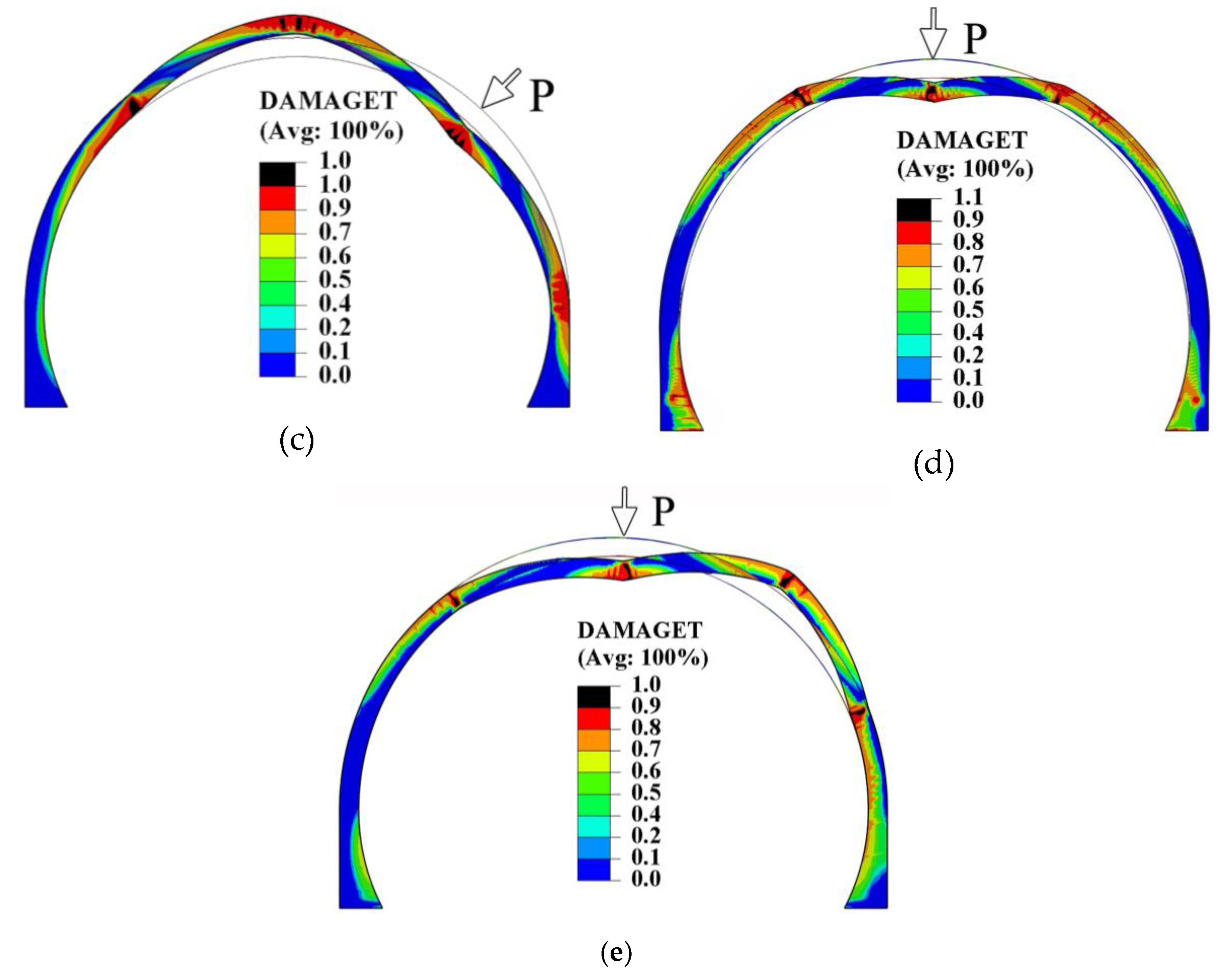
5. Verification of Numerical Models
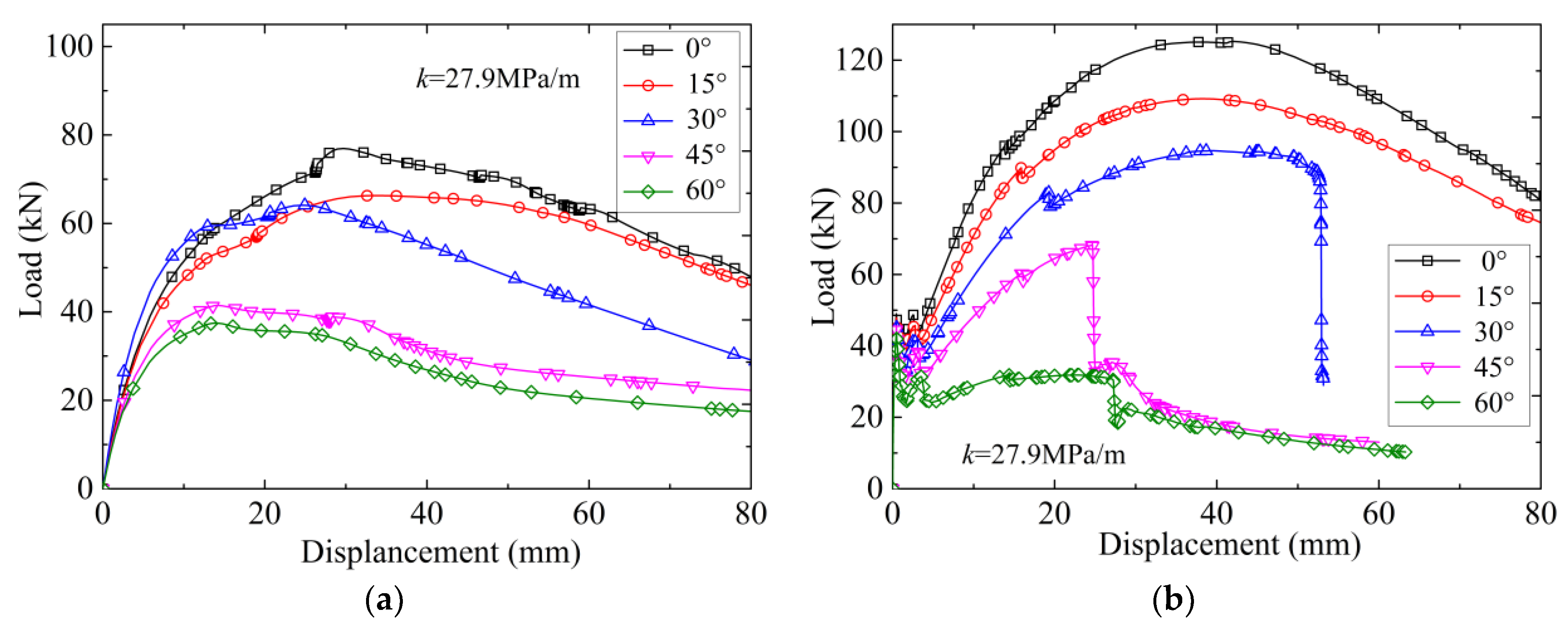
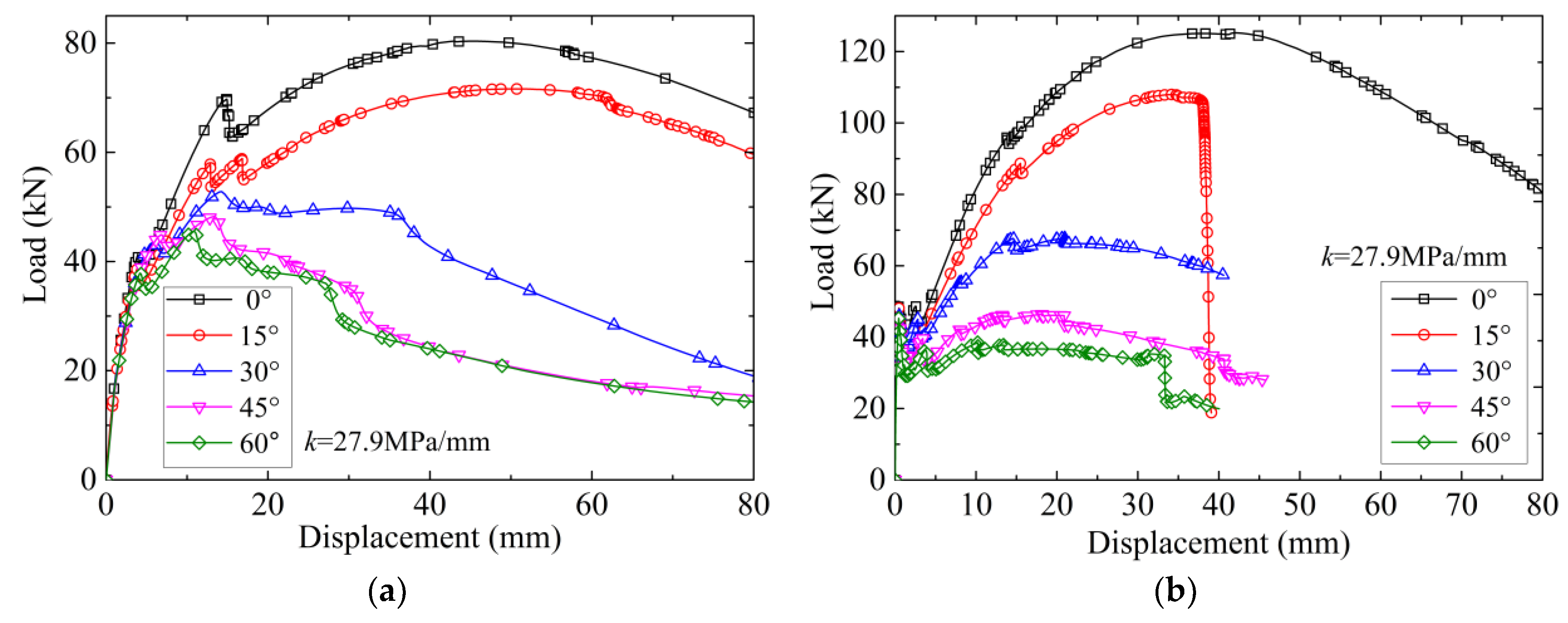
6. Parameter Analysis
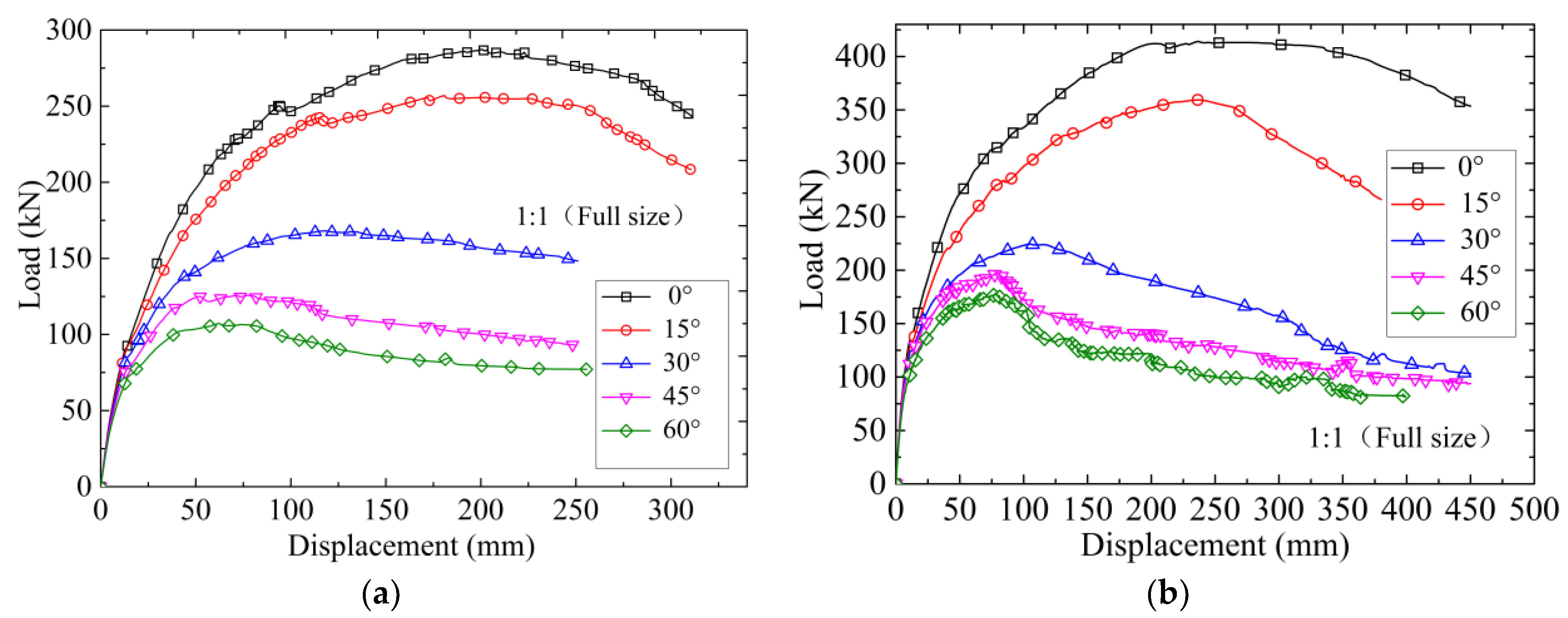
6.1. Effect of Void Location and Size
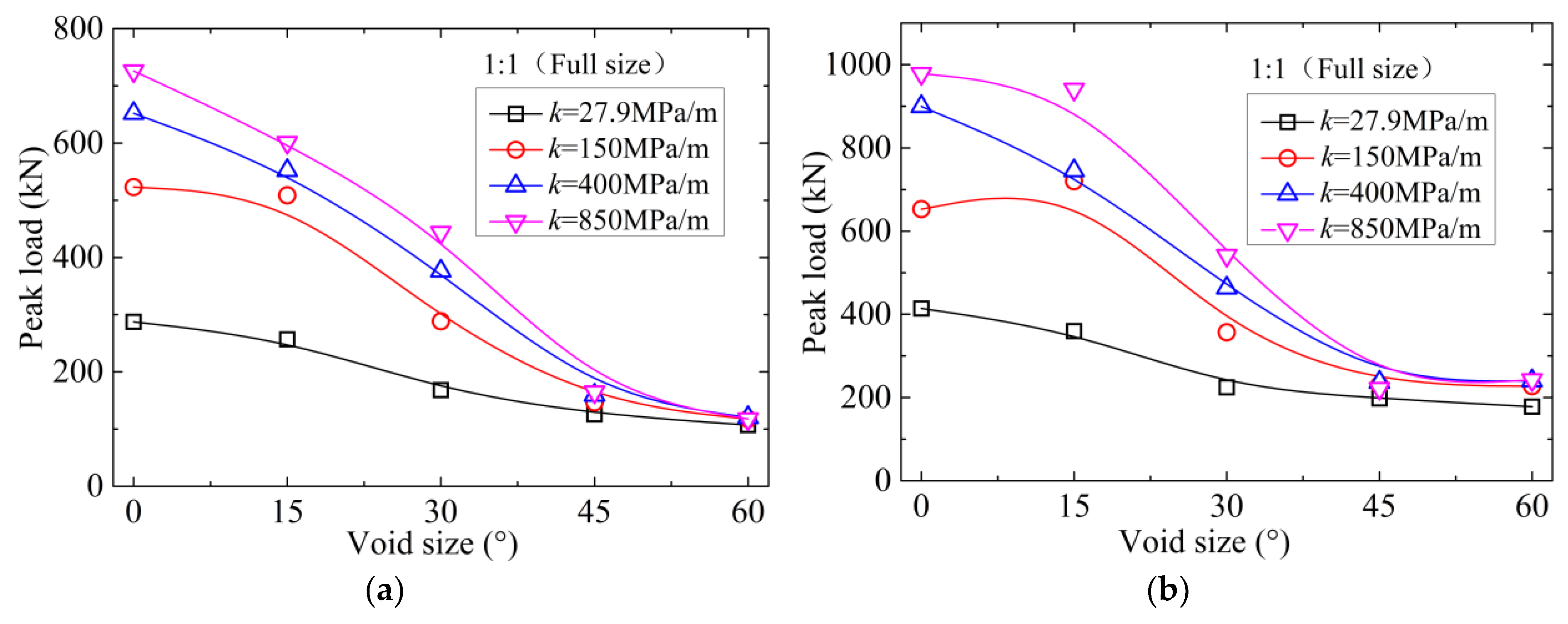
6.2. Effect of Soil Stiffness
6.3. Effect of Tunnel Lining Size
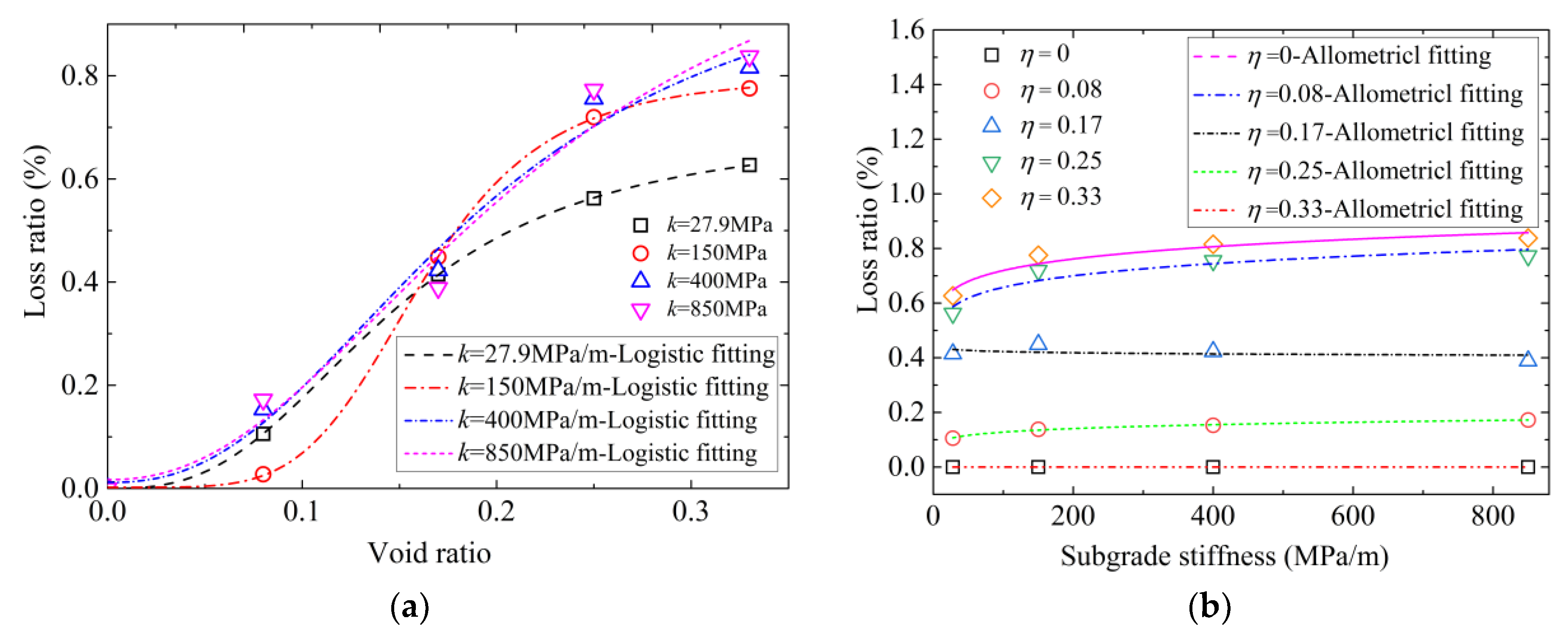
6.4. Analysis of Load-Carrying Capacity Loss Rate of RC Lining Considering the Void
6.4.1. Determination of Regression Equation
6.4.2. Determination of Model Parameters
7. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Zhao, Y. Tunnel Design Theory and Method; China Communications Press: Beijing, China, 2018; pp. 16–18. [Google Scholar]
- Inokuma, A.; Inano, S. Road tunnels in Japan: Deterioration and countermeasures. Tunn. Undergr. Space Technol. 1996, 11, 305–309. [Google Scholar] [CrossRef]
- Wang, H.; Huang, H.; Feng, Y.; Zhang, D. Characterization of Crack and Leakage Defects of Concrete Linings of Road Tunnels in China. J. Risk Uncertain. Eng. Syst. Part A Civ. Eng. 2018, 4, 1–14. [Google Scholar] [CrossRef]
- Amorim, D.L.N.F.; Proenca, S.P.B.; Florez-Lopez, J. Simplified modeling of cracking in concrete: Application in tunnel linings. Eng. Struct. 2014, 70, 23–35. [Google Scholar] [CrossRef]
- Mashimo, H.; Isago, N.; Kitani, T. Effect of fiber reinforced concrete on shrinkage crack of tunnel lining. Tunn. Undergr. Space Technol. 2006, 21, 382–383. [Google Scholar] [CrossRef]
- Vallini, P.; Chiaia, B.; Fantilli, A.P. Evaluation of crack width in FRC structures and application to tunnel linings. Mater. Struct. 2009, 42, 339–351. [Google Scholar]
- Gao, Y.; Jiang, Y.; Li, B. Voids delineation behind tunnel lining based on the vibration intensity of microtremors. Tunn. Undergr. Space Technol. 2015, 51, 338–345. [Google Scholar] [CrossRef]
- Huang, H.W.; Liu, D.J.; Xue, Y.D. Numerical analysis of cracking of tunnel linings based on extended finite element. Chin. J. Geotech. Eng. 2013, 35, 266–275. [Google Scholar]
- Empel, W.H.N.C.V.; Sip, J.W.; Haring, F.P. Design of repair measures of a damaged shield driven tunnel. Tunn. Undergr. Space Technol. 2006, 21, 338–339. [Google Scholar] [CrossRef]
- Pintado, X.; Barragán, B.E. Homogeneity of self-compacting concretes used in tunnel strengthening—A case study. Tunn. Undergr. Space Technol. 2009, 24, 647–653. [Google Scholar] [CrossRef]
- Zhang, S.L.; Zhang, D.L.; Liu, S.C. Discovering the main causes of tunnel lining damage based on correspondence analysis model. China Railw. Sci. 2012, 33, 54–58. [Google Scholar]
- Wang, Z.Z.; Jiang, Y.J.; Zhu, C.A. Shaking table tests of tunnel linings in progressive states of damage. Tunn. Undergr. Space Technol. 2015, 50, 109–117. [Google Scholar] [CrossRef]
- Leung, C.; Meguid, M.A. An experimental study of the effect of local contact loss on the earth pressure distribution on existing tunnel linings. Tunn. Undergr. Space Technol. 2011, 26, 139–145. [Google Scholar] [CrossRef]
- Yasuda, Y.; Tsukada, K.; Asakura, T. Elastic solutions for circular tunnel with void behind lining. Tunn. Undergr. Space Technol. 2017, 70, 274–285. [Google Scholar] [CrossRef]
- Wang, J.F.; Huang, H.W.; Xie, X.Y. Void-induced liner deformation and stress redistribution. Tunn. Undergr. Space Technol. 2014, 40, 263–276. [Google Scholar] [CrossRef]
- Peng, Y.; Wang, G.L.; Zhang, Y.X. Research about effect of cavity behind lining on structural safety of tunnel in active service. Chin. J. Undergr. Space Eng. 2008, 4, 1101–1104. [Google Scholar]
- Meguid, M.A.; Dang, H.K. The effect of erosion voids on existing tunnel linings. Tunn. Undergr. Space Technol. 2009, 24, 278–286. [Google Scholar] [CrossRef]
- Zhang, X.; Zhang, C.P.; Feng, G. Experimental studies on effect of voids behind tunnel linings on progressive failure process of tunnel structures. Chin. J. Geotech. Eng. 2017, 39, 1137–1144. [Google Scholar]
- Mashimo, H. State of the road tunnel safety technology in Japan. Tunn. Undergr. Space Technol. 2002, 17, 145–152. [Google Scholar] [CrossRef]
- Min, B.; Zhang, X.; Zhang, C.; Gong, Y.; Yuan, T. Mechanical behavior of double-arch tunnels under the effect of voids on the top of the middle wall. Symmetry 2018, 10, 703. [Google Scholar] [CrossRef]
- Okano, N. Development of a testing machine with a large tunnel lining model. Railw. Technol. Avalanche 2007, 19, 110. [Google Scholar]
- Huang, X.; Zhu, Y.; Zhang, Z. Mechanical behaviour of segmental lining of a sub-rectangular shield tunnel under self-weight. Tunn. Undergr. Space Technol. 2018, 74, 131–144. [Google Scholar] [CrossRef]
- Ding, Z.D.; Fu, J.; Li, X.Q. Mechanical behavior and its influencing factors on engineered cementitious composite linings. Adv. Mater. Sci. Eng. under review.
- Ding, Z.D.; Wen, J.C.; Li, X.Q.; Fu, J.; Ji, X.F. Mechanical behaviour of polyvinyl alcohol-engineered cementitious composite (PVA-ECC) tunnel linings subjected to vertical load. Tunn. Undergr. Space Technol. under review.
- He, W.; Wu, Z.; Kojima, Y. Failure mechanism of deformed concrete tunnels subject to diagonally concentrated loads. Comput.-Aided Civ. Infrastruct. Eng. 2010, 24, 416–431. [Google Scholar] [CrossRef]
- Yashiro, K.; Hirata, R.; Okano, N. Study on deformation and failure behavior of mountain tunnel linings which consist of various materials. J. Jpn. Soc. Civil Eng. Ser. F1 2015, 71, 78–94. [Google Scholar]
- Yuan, W.Z. Similarity Theory and Static Model Test; Southwest Jiaotong University Press: Leshan, China, 1998. [Google Scholar]
- Lee, J.; Fenves, G.L. Plastic-damage model for cyclic loading of concrete structures. J. Eng. Mech. 1998, 124, 892–900. [Google Scholar] [CrossRef]
- Lubliner, J.; Oliver, J.; Oller, S. A plastic-damage model for concrete. Int. J. Solids Struct. 1989, 25, 299–326. [Google Scholar] [CrossRef]
- Ministry of Housing and Urban-rural Development of the People’s Republic of China. GB50010-2010, Code for Design of Concrete Structures; China Architecture and Building Press: Beijing, China, 2011.
- Hordijk, D.A. Tensile and tensile fatigue behaviour of concrete; experiments, modelling and analyses. Heron 1992, 37, 1–79. [Google Scholar]
- Betonbau. Fib Model Code for Concrete Structures; Wiley: Hoboken, NJ, USA, 2013. [Google Scholar]
- Oller, J.A. Continuous Damage Model for Frictional Materials. Ph.D. Thesis, Technical University of Catalonia, Catalonia, Spain, 1998. [Google Scholar]
- Cao, M. Research on damage plastic calculation method of ABAQUS concrete damaged plasticity model. Transport. Res. 2012, 2, 51–54. [Google Scholar]
- Cai, J.M.; Pan, J.L.; Yuan, F. Experimental and numerical study on flexural behaviors of steel reinforced engineered cementitious composite beams. J. Southeast. Univ. 2014, 30, 330–335. [Google Scholar]
- Zhou, J.J.; Pan, J.L.; Leung, C.K.Y. Mechanical behavior of fiber reinforced engineered cementitious composites in uniaxial compression. J. Mater. Civ. Eng. 2015, 27, 1–10. [Google Scholar] [CrossRef]
- Yuan, F.; Pan, J.L.; Wu, Y.F. Numerical study on flexural behaviors of steel reinforced engineered cementitious composite (ECC) and ECC/concrete composite beams. Sci. China-Technol. Sci. 2014, 57, 637–645. [Google Scholar] [CrossRef]
- TB10003-2016, Code for Design on Tunnel of Railway; China Railway Publishing House: Beijing, China, 2016.
- Bazant, Z.P. Size effect in blunt fracture: Concrete, rock, metal. J. Eng. Mech. 1984, 110, 518–535. [Google Scholar] [CrossRef]
- Yang, T.; Li, G.W.; Yang, W.Q. Settlement prediction of stage construction embankment on soft ground based on the hyperbola method. Rock Soil Mech. 2004, 25, 1551–1554. [Google Scholar]
- Xu, H.Z.; Shi, B.; Li, X.H. Logistic growth model and its applicability for predicting settlement during the whole process. Rock Soil Mech. 2005, 26, 387–391. [Google Scholar]
- Kleefeld, A.; Martin, R. The Levenberg-Marquardt method applied to a parameter estimation problem arising from electrical resistivity tomography. Appl. Math. Comput. 2011, 217, 4490–4501. [Google Scholar] [CrossRef]




| Dilation Angle/ψ | Eccentricity/e | The Ratio of Yield Stress fb0/fc0 | The Ratio of the Second Stress Invariant on the Tensile meridian/K | Viscosity Parameter/ν |
|---|---|---|---|---|
| 30° | 0.1 | 1.16 | 0.667 | 1 × 10−5 |
| Elastic Modulus Es/GPa | Poisson Ratio μ | Yield Strength fy/MPa | Yield Strength Tensile Strain εy | Ultimate Strength fu/MPa | Ultimate Tensile Strain εu |
|---|---|---|---|---|---|
| 200 | 0.3 | 300 | 0.01675 | 420 | 0.025 |
| Fitting Parameters | a | b | p | m | n | R2 |
|---|---|---|---|---|---|---|
| Void at the crown | 0.507 | 0.180 | 2.259 | 1.333 | 0.067 | 0.974 |
| Void at the spandrel | 0.547 | 0.142 | 2.871 | 0.921 | 0.075 | 0.985 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ding, Z.; Ji, X.; Li, X.; Ren, Z.; Zhang, S. Influence of Symmetric and Asymmetric Voids on Mechanical Behaviors of Tunnel Linings: Model Tests and Numerical Simulations. Symmetry 2019, 11, 802. https://doi.org/10.3390/sym11060802
Ding Z, Ji X, Li X, Ren Z, Zhang S. Influence of Symmetric and Asymmetric Voids on Mechanical Behaviors of Tunnel Linings: Model Tests and Numerical Simulations. Symmetry. 2019; 11(6):802. https://doi.org/10.3390/sym11060802
Chicago/Turabian StyleDing, Zude, Xiafei Ji, Xiaoqin Li, Zhihua Ren, and Sen Zhang. 2019. "Influence of Symmetric and Asymmetric Voids on Mechanical Behaviors of Tunnel Linings: Model Tests and Numerical Simulations" Symmetry 11, no. 6: 802. https://doi.org/10.3390/sym11060802
APA StyleDing, Z., Ji, X., Li, X., Ren, Z., & Zhang, S. (2019). Influence of Symmetric and Asymmetric Voids on Mechanical Behaviors of Tunnel Linings: Model Tests and Numerical Simulations. Symmetry, 11(6), 802. https://doi.org/10.3390/sym11060802





