Fixed Coeficient A(?) Stable Block Backward Differentiation Formulas for Stiff Ordinary Differential Equations
Abstract
:1. Introduction
2. Derivation of the Method
2.1. Order of the Method
3. Stability Analysis
3.1. Zero Stability
3.2. Stability Region
3.3. Convergence of the Method
4. Implementation
- Step 1.
- Predict: are developed explicitly.
- Step 2.
- Evaluate:
- Step 3.
- Correct: by
- Step 4.
- Evaluate:
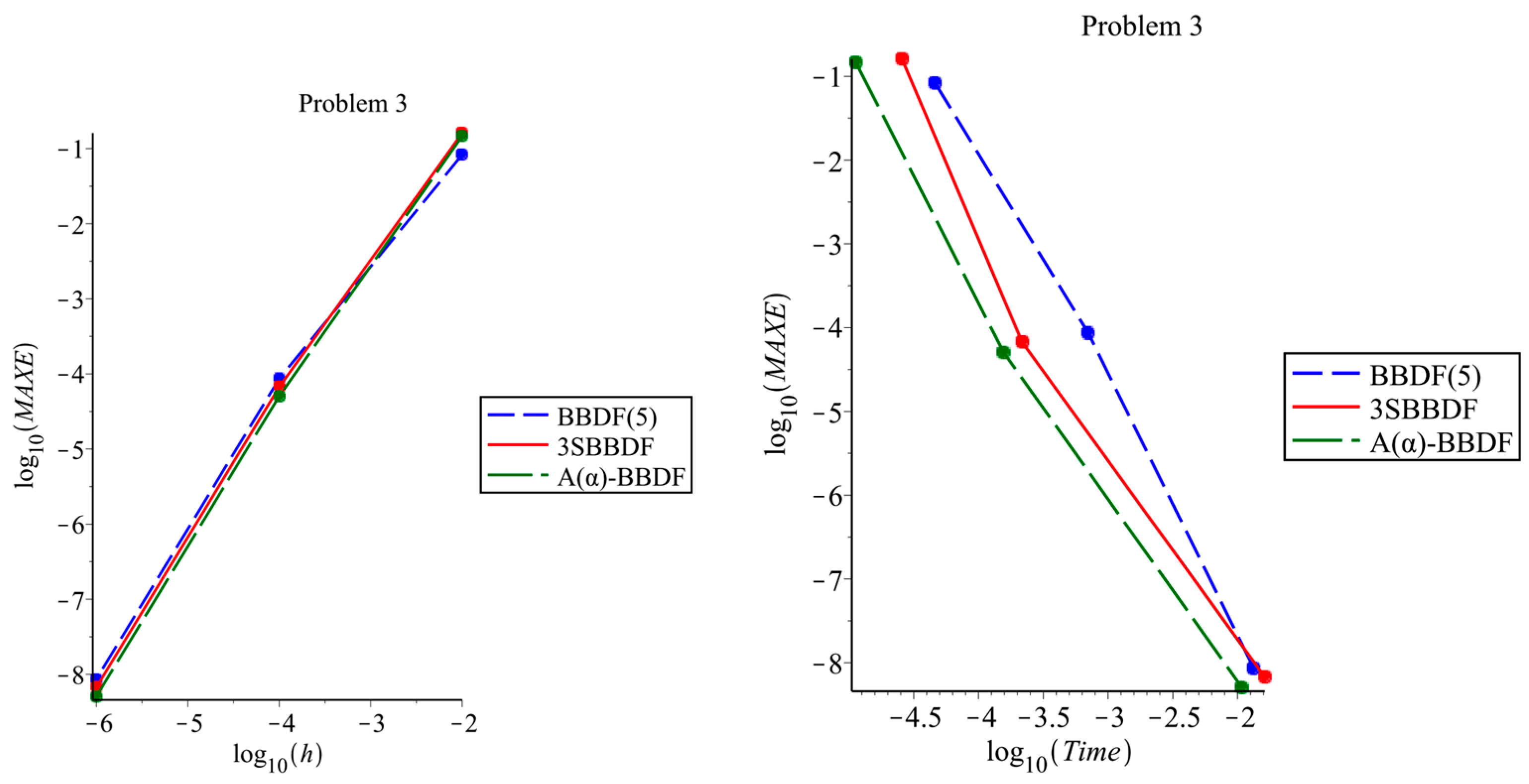
5. Numerical Results
| BBDF(5) | : | Fifth order Block Backward Differentiation Formula in [12] |
| 3SBBDF | : | 3-point Superclass of Block Backward Differentiation Formula in [14] |
| -BBDF | : | New 3-point BBDF |
| NS | : | Number of steps |
| : | Step size | |
| T | : | Computing time in seconds |
| MAXE | : | Maximum error |
6. Discussion and Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Bui, T.D. Solving stiff differential equations in the simulation of physical systems. Simulation 1981, 37, 37–46. [Google Scholar] [CrossRef]
- Aiken, J.C. Stiff Review. In Proceedings of the International Conference on Stiff Computation, Park City, UT, USA, 12–14 April 1982. [Google Scholar]
- Chu, M.T.; Hamilton, H. Parallel solution of ODE’s by multi-block methods. SIAM J. Sci. Stat. Comput. 1987, 8, 342–353. [Google Scholar] [CrossRef]
- Aceto, L.; Trigiante, D. On the A-stable methods in the GBDF class. Nonlinear Anal. Real World Appl. 2002, 3, 9–23. [Google Scholar] [CrossRef]
- Dahlquist, G. A Special Stability Problem for Linear Multistep Methods. BIT 1963, 3, 27–43. [Google Scholar] [CrossRef]
- Majid, Z.A.; Suleiman, M.B.; Ismail, F.; Othman, M. 2-Point Implicit Block One-Step Method Half Gauss-Seidel For Solving First Order Ordinary Differential Equations. Matematika 2003, 19, 91–100. [Google Scholar]
- Ibrahim, Z.B.; Othman, K.I.; Suleiman, M. Implicit r-point block backward differentiation formula for solving first-order stiff ODEs. Appl. Math. Comput. 2007, 186, 558–565. [Google Scholar] [CrossRef]
- Majid, Z.A.; Suleiman, M.; Omar, Z. 3-Point Implicit Block Method for solving ordinary differential equations. Bull. Malays. Math. Sci. Soc. Second Ser. 2006, 29, 29–31. [Google Scholar]
- Ismail, F.; Ken, Y.L.; Othman, M. Explicit and implicit 3-point block methods for solving special second order ordinary differential equations directly. Int. J. Math. Anal. 2009, 3, 239–254. [Google Scholar]
- Ibrahim, Z.B.; Othman, K.I.; Suleiman, M. 2-point block predictor-corrector of backward differentiation formulas for solving second order ordinary differential equations directly. Chiang Mai J. Sci. 2012, 39, 502–510. [Google Scholar]
- Ibrahim, Z.B.; Othman, K.I.; Suleiman, M. Derivation of diagonally implicit block backward differentiation formulas for solving stiff initial value problems. Math. Probl. Eng. 2015, 2015, 179231. [Google Scholar] [CrossRef]
- Shampine, L.F.; Watts, H.A. Block implicit one-step methods. Math. Comp. 1969, 23, 731–740. [Google Scholar] [CrossRef]
- Nasir, N.A.A.; Ibrahim, Z.B.; Othman, K.I.; Suleiman, M.B. Numerical Solution of First Order Ordinary Differential Equations Using Fifth Order Block Backward Differentiation Formulas. Sains Malays. 2012, 41, 489–492. [Google Scholar]
- Asnor, A.I.; Yatim, S.A.M.; Ibrahim, Z.B. Formulation of Modified Variable Step Block Backward Differentiation Formulae for Solving Stiff Ordinary Differential Equations. Indian J. Sci. Technol. 2017, 10, 1–7. [Google Scholar] [CrossRef]
- Iskandar Shah, M.Z.; Ibrahim, Z.B. Convergence Properties of pth Order Diagonally Implicit Block Backward Differentiation Formulas. Chiang Mai J. Sci. 2018, 45, 601–606. [Google Scholar]
- Musa, H.; Suleiman, M.B.; Senu, N. Fully Implicit 3-point Block Extended Backward Differentiation Formulas for Stiff Initial value Problems. Appl. Math. Sci. 2012, 6, 4211–4228. [Google Scholar]
- Babaginda, B.; Musa, H.; Ibrahim, L.K. A New Numerical Method For Solving Stiff Initial Value Problems. Fluid Mech. Open Access 2016, 3, 1–5. [Google Scholar]
- Lambert, J.D. Computational Methods in Ordinary Differential Equations, 3rd ed.; John Wiley and Sons: New York, NY, USA, 1973; pp. 154–196. [Google Scholar]
- Fatunla, S.O. Block methods for second order ODEs. Int. J. Comput. Math. 1991, 41, 55–63. [Google Scholar] [CrossRef]
- Butcher, J.C. Forty-Five Years of A-stability. J. Numer. Anal. Ind. Appl. Math. 2009, 4, 1–9. [Google Scholar]
- Burden, R.L.; Faires, J.D. Numerical Analysis, 7th ed.; Brooks/Cole: Belmont, CA, USA, 2001. [Google Scholar]
- Alvarez, J.; Rojo, J. An improved class of generalized Runge- Kutta methods for stiff problems. I. The scalar case. Appl. Math. Comput. 2002, 130, 537–560. [Google Scholar] [CrossRef]





| 1 | ||||||||
| 1 | ||||||||
| 1 |
| Method | NS | MAXE | TIME | |
|---|---|---|---|---|
| BBDF(5) | 50 | 1.22077 (02) | 3.38123 × 10−5 | |
| 3SBBDF | 34 | 1.25970 (02) | 7.97504 × 10−6 | |
| -BBDF | 34 | 9.80872 (03) | 5.74054 × 10−6 | |
| BBDF(5) | 5,000 | 3.61596 (06) | 1.95107 × 10−4 | |
| 3SBBDF | 3334 | 2.78963 (06) | 2.43208 × 10−5 | |
| -BBDF | 3334 | 2.10240 (06) | 1.81288 × 10−5 | |
| BBDF(5) | 500,000 | 3.65378 (10) | 1.19412 × 10−2 | |
| 3SBBDF | 333,334 | 2.84503 (10) | 2.40965 × 10−3 | |
| -BBDF | 333,334 | 2.15115 (10) | 1.24343 × 10−3 |
| Methods | NS | MAXE | TIME | |
|---|---|---|---|---|
| BBDF(5) | 250 | 8.22989 (05) | 3.13736 × 10−5 | |
| 3SBBDF | 167 | 6.27205 (05) | 1.42650 × 10−5 | |
| -BBDF | 167 | 4.80218 (05) | 5.55058 × 10−6 | |
| BBDF(5) | 25,000 | 9.13120 (09) | 6.23244 × 10−4 | |
| 3SBBDF | 16,667 | 7.10257 (09) | 2.84914 × 10−4 | |
| -BBDF | 16,667 | 5.36673 (09) | 3.00451 × 10−5 | |
| BBDF(5) | 2,500,000 | 4.75320 (11) | 8.99541 × 10−2 | |
| 3SBBDF | 1,666,667 | 3.20597 (11) | 1.71905 × 10−2 | |
| -BBDF | 1,666,667 | 2.04591 (11) | 3.01268 × 10−3 |
| Methods | NS | MAXE | TIME | |
|---|---|---|---|---|
| BBDF(5) | 50 | 8.31685 (02) | 4.61774 × 10−5 | |
| 3SBBDF | 34 | 1.60854 (01) | 2.57089 × 10−5 | |
| -BBDF | 34 | 1.46790 (01) | 1.13065 × 10−5 | |
| BBDF(5) | 5000 | 8.63685 (05) | 7.02594 × 10−4 | |
| 3SBBDF | 3334 | 6.71328 (05) | 2.17249 × 10−4 | |
| -BBDF | 3334 | 5.06905 (05) | 1.56282 × 10−4 | |
| BBDF(5) | 500,000 | 8.64038 (09) | 1.33371 × 10−2 | |
| 3SBBDF | 333,334 | 6.72941 (09) | 1.62222 × 10−2 | |
| -BBDF | 333,334 | 5.08898 (09) | 1.07846 × 10−2 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ibrahim, Z.B.; Mohd Noor, N.; Othman, K.I. Fixed Coeficient A(?) Stable Block Backward Differentiation Formulas for Stiff Ordinary Differential Equations. Symmetry 2019, 11, 846. https://doi.org/10.3390/sym11070846
Ibrahim ZB, Mohd Noor N, Othman KI. Fixed Coeficient A(?) Stable Block Backward Differentiation Formulas for Stiff Ordinary Differential Equations. Symmetry. 2019; 11(7):846. https://doi.org/10.3390/sym11070846
Chicago/Turabian StyleIbrahim, Zarina Bibi, Nursyazwani Mohd Noor, and Khairil Iskandar Othman. 2019. "Fixed Coeficient A(?) Stable Block Backward Differentiation Formulas for Stiff Ordinary Differential Equations" Symmetry 11, no. 7: 846. https://doi.org/10.3390/sym11070846
APA StyleIbrahim, Z. B., Mohd Noor, N., & Othman, K. I. (2019). Fixed Coeficient A(?) Stable Block Backward Differentiation Formulas for Stiff Ordinary Differential Equations. Symmetry, 11(7), 846. https://doi.org/10.3390/sym11070846





