A Numerical Solution of Fredholm Integral Equations of the Second Kind Based on Tight Framelets Generated by the Oblique Extension Principle
Abstract
:1. Introduction
2. Preliminary Results
3. Quasi-Affine B-Spline Tight Framelet Systems
3.1. Framelets by the UEP and Its Generalization
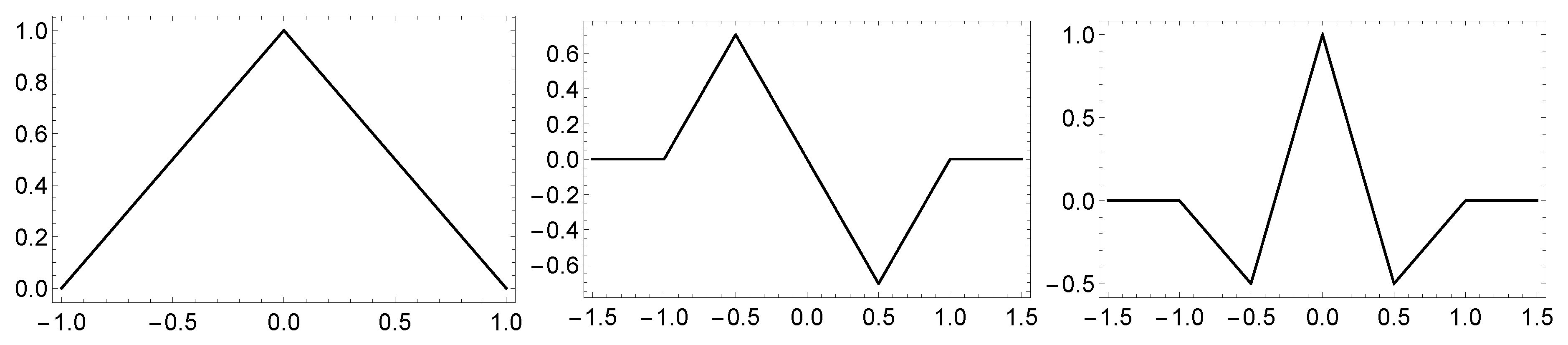
3.2. Examples of Quasi-Affine B-Spline Tight Framelets
4. Solving Fredholm Integral Equation via Tight Framelets
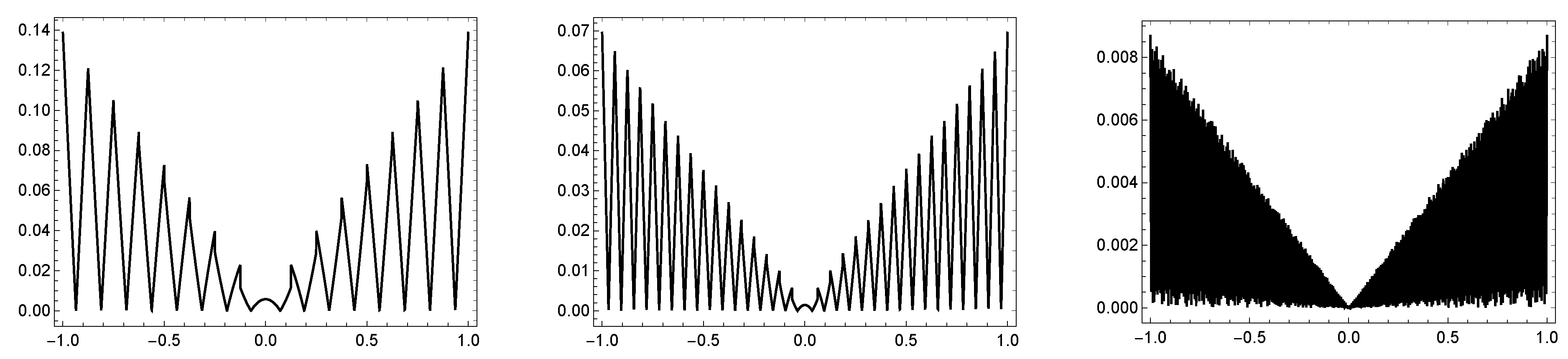
5. Error Analysis
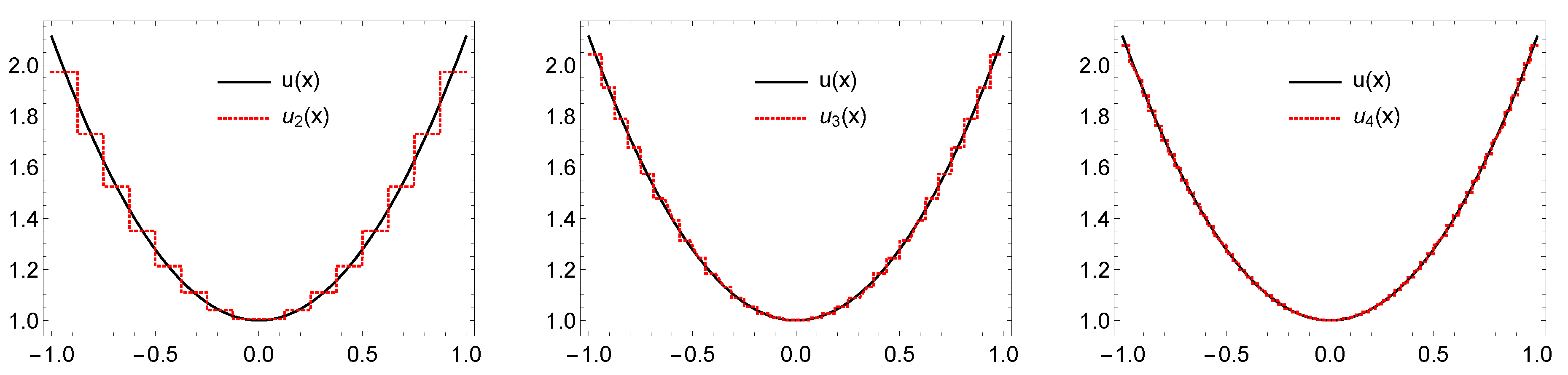
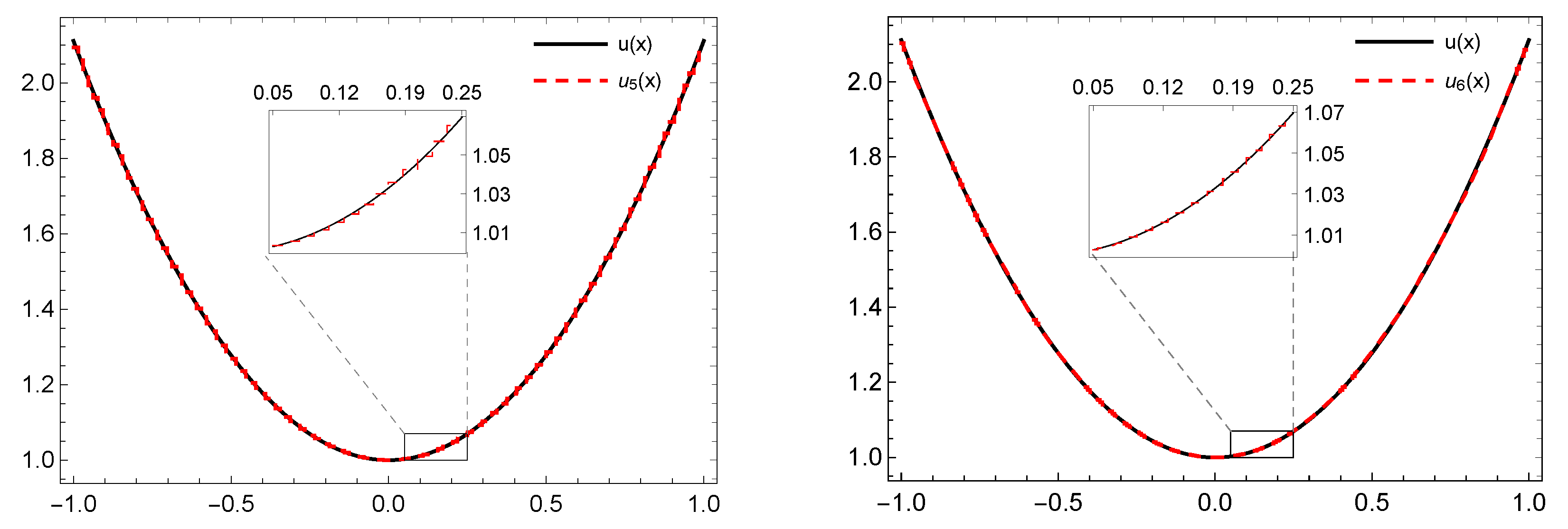
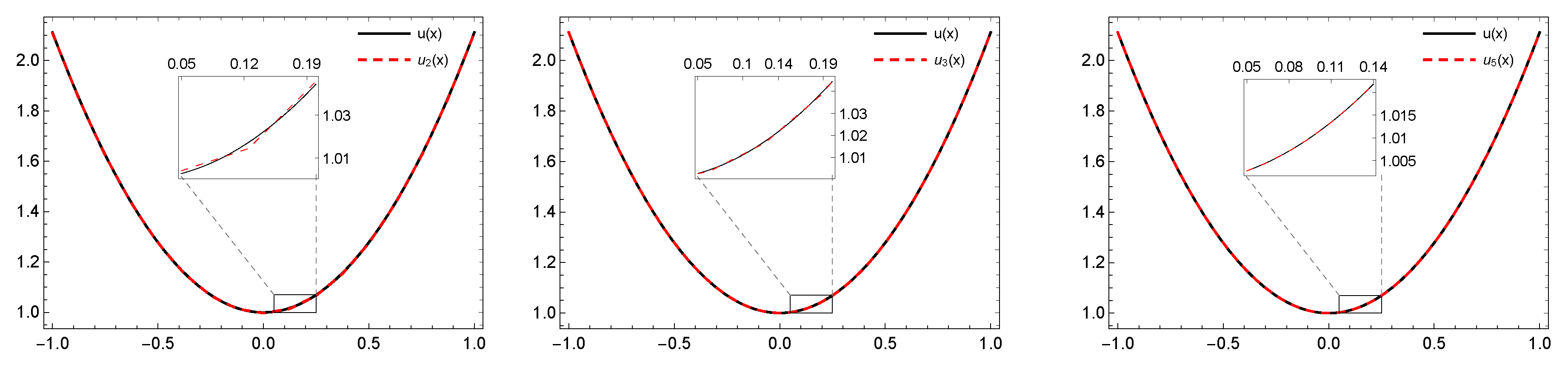
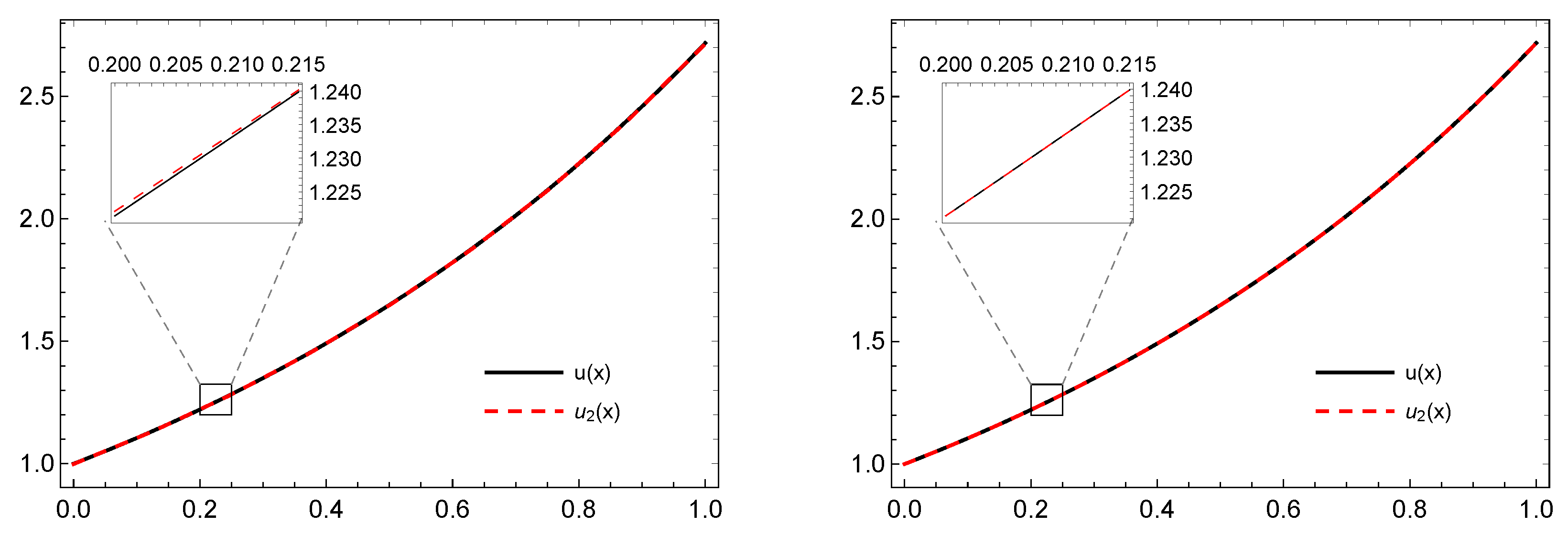
6. Numerical Performance and Illustrative Examples
7. Conclusions
Funding
Acknowledgments
Conflicts of Interest
References
- Ionescu, M.; Okoudjou, K.A.; Rogers, L.G. Some spectral properties of pseudo-differential operators on the Sierpinski gasket. Proc. Am. Math. Soc. 2017, 145, 2183–2198. [Google Scholar] [CrossRef]
- Daubechies, I. Ten Lectures on Wavelets; SIAM: Philadelphia, PA, USA, 1992. [Google Scholar]
- Grochenig, K. Foundations of Time-Frequency Analysis; Birkhäuser: Boston, MA, USA, 2001. [Google Scholar]
- Han, B. Framelets and wavelets: Algorithms, analysis, and applications. In Applied and Numerical Harmonic Analysis; Birkhäuser/Springer: Cham, Switzerland, 2017. [Google Scholar]
- Mallat, S.G. A Wavelet Tour of Signal Processing, 2nd ed.; Elsevier: Amsterdam, The Netherlands, 1999. [Google Scholar]
- Meyer, Y. Wavelets and Operators; Cambridge University Press: Cambridge, UK, 1992. [Google Scholar]
- Meyer, Y. Oscillating Patterns in Image Processing and Nonlinear Evolution Equations: The Fifteenth Dean Jacqueline B. Lewis Memorial Lectures. American Mathematical Society. Available online: https://bookstore.ams.org/ulect-22 (accessed on 21 May 2019).
- Duffin, R.; Schaeffer, A. A class of nonharmonic Fourier series. Trans. Am. Math. Soc. 1952, 72, 341–366. [Google Scholar] [CrossRef]
- Adeh, Z.; Heydari, M.; Loghman, G.B. Numerical solution of Fredholm integral equations of the second kind by using integral mean value theorem. Appl. Math. Model. 2011, 35, 2374–2383. [Google Scholar]
- Lepik, U.; Tamme, E. Application of the Haar wavelets for solution of linear integral equations. In Proceedings of the Dynamical Systems and Applications, Antalya, Turkey, 5–10 July 2005; pp. 395–407. [Google Scholar]
- Singh, B.; Bhardwaj, A.; Alib, R. A wavelet method for solving singular integral equation of MHD. Appl. Math. Comput. 2009, 214, 271–279. [Google Scholar] [CrossRef]
- Islam, M.S.; Shirin, A. Numerical Solutions of Fredholm Integral Equations of Second Kind Using Piecewise Bernoulli Polynomials. Dhaka Univ. J. Sci. 2011, 59, 103–107. [Google Scholar]
- Cai, J.; Dong, B.; Shen, Z. Image restorations: A wavelet frame based model for piecewise smooth functions and beyond. Appl. Comput. Harm. Anal. 2016, 41, 94–138. [Google Scholar] [CrossRef]
- Shen, Y.; Han, B.; Braverman, E. Adaptive frame-based color image denoising. Appl. Comput. Harm. Anal. 2016, 41, 54–74. [Google Scholar] [CrossRef]
- Yang, J.; Zhu, G.; Tong, D.; Lu, L.; Shen, Z. B-spline tight frame based force matching method. J. Comput. Phys. 2018, 362, 208–219. [Google Scholar] [CrossRef]
- Young, R. An Introduction to Non-Harmonic Fourier Series; Academic Press: New York, NY, USA, 1980. [Google Scholar]
- Daubechies, I.; Grossmann, A.; Meyer, Y. Painless nonorthogonal expansions. J. Math. Phys. 1986, 341, 1271–1283. [Google Scholar] [CrossRef]
- Ron, A. Factorization theorems of univariate splines on regular grids. Isr. J. Math. 1990, 70, 48–68. [Google Scholar] [CrossRef]
- Chui, C.K.; He, W.; Stockler, J. Compactly supported tight and sibling frames with maximum vanishing moments. Appl. Comput. Harmon. Anal. 2002, 341, 224–262. [Google Scholar] [CrossRef]
- Daubechies, I.; Han, B.; Ron, A.; Shen, Z. Framelets: MRA-based constructions of wavelet frames. Appl. Comput. Harmon. 2003, 14, 1–46. [Google Scholar] [CrossRef] [Green Version]
- Ron, A.; Shen, Z. Affine systems in II: Dual systems. J. Fourier Anal. Appl. 1997, 3, 617–637. [Google Scholar] [CrossRef]
- Ron, A.; Shen, Z. Affine systems in : The analysis of the analysis operators. J. Funct. Anal. 1997, 148, 408–447. [Google Scholar] [CrossRef]
- Mohammad, M.; Lin, E. Gibbs Phenomenon in Tight Framelet Expansions. Commun. Nonlinear Sci. Numer. Simul. 2018, 55, 84–92. [Google Scholar] [CrossRef]
- Mohammad, M.; Lin, E. Gibbs effects using Daubechies and Coiflet tight framelet systems, Frames and Harmonic Analysis. Contemp. Math. 2018, 706, 271–282. [Google Scholar]
- Atindehou, A.G.D.; Kouagou, Y.B.; Okoudjou, K.A. Frame sets for generalized B-splines. arXiv 2018, arXiv:1804.02450. [Google Scholar]
- He, T. Eulerian polynomials and B-splines. J. Comput. Appl. Math. 2012, 236, 3763–3773. [Google Scholar] [CrossRef]
- De Boor, C. A Practical Guide to Splines; Springer: New York, NY, USA, 1978. [Google Scholar]
- Dong, B.; Shen, Z. MRA Based Wavelet Frames and Applications. 2010. Available online: ftp://ftp.math.ucla.edu/pub/camreport/cam10-69.pdf (accessed on 21 May 2019).
- Bhatti, M.I.; Bracken, P. Solutions of differential equations in a Bernstein polynomial basis. J. Comput. Appl. Math. 2007, 205, 272–280. [Google Scholar] [CrossRef] [Green Version]
- Liang, X.Z.; Liu, M.C.; Che, X.J. Solving second kind integral equations by Galerkin methods with continuous orthogonal wavelets. J. Comput. Appl. Math. 2001, 136, 149–161. [Google Scholar] [CrossRef] [Green Version]
- De Boor, C.; DeVore, R.; Ron, A. Approximation from shift-invariant subspaces of . Trans. Am. Math. Soc. 1994, 341, 787–806. [Google Scholar]
- Borup, L.; Gribonval, R.; Nielsen, M. Bi-framelet systems with few vanishing moments characterize Besov spaces. Appl. Comput. Harmon. Anal. 2004, 17, 3–28. [Google Scholar] [CrossRef]





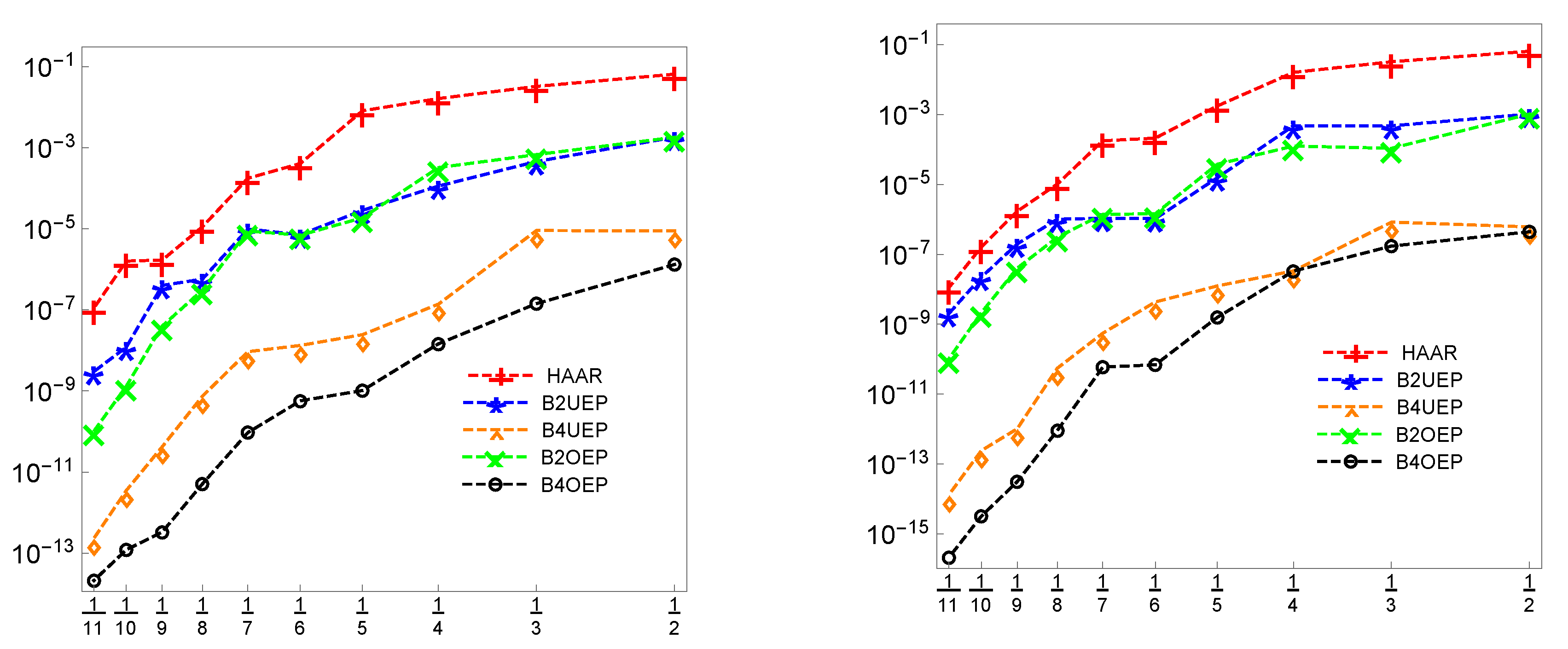
| n | HAAR Framelet | -UEP | -UEP | -OEP | -OEP |
|---|---|---|---|---|---|
| 2 | |||||
| 3 | |||||
| 4 | |||||
| 5 | |||||
| 6 | |||||
| 7 | |||||
| 8 | |||||
| 9 | |||||
| 10 |
| x | Exact | HAAR Framelet | -UEP | -UEP | -OEP | -OEP |
|---|---|---|---|---|---|---|
| n | HAAR Framelet | -UEP | -UEP | -OEP | -OEP |
|---|---|---|---|---|---|
| 2 | |||||
| 3 | |||||
| 4 | |||||
| 5 | |||||
| 6 | |||||
| 7 | |||||
| 8 | |||||
| 9 | |||||
| 10 |
| x | Exact | HAAR Framelet | -UEP | -UEP | -OEP | -OEP |
|---|---|---|---|---|---|---|
© 2019 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mohammad, M. A Numerical Solution of Fredholm Integral Equations of the Second Kind Based on Tight Framelets Generated by the Oblique Extension Principle. Symmetry 2019, 11, 854. https://doi.org/10.3390/sym11070854
Mohammad M. A Numerical Solution of Fredholm Integral Equations of the Second Kind Based on Tight Framelets Generated by the Oblique Extension Principle. Symmetry. 2019; 11(7):854. https://doi.org/10.3390/sym11070854
Chicago/Turabian StyleMohammad, Mutaz. 2019. "A Numerical Solution of Fredholm Integral Equations of the Second Kind Based on Tight Framelets Generated by the Oblique Extension Principle" Symmetry 11, no. 7: 854. https://doi.org/10.3390/sym11070854
APA StyleMohammad, M. (2019). A Numerical Solution of Fredholm Integral Equations of the Second Kind Based on Tight Framelets Generated by the Oblique Extension Principle. Symmetry, 11(7), 854. https://doi.org/10.3390/sym11070854





