Application of Fuzzy Sets to the Expert Estimation of Scrum-Based Projects

Abstract

The paper is basically dedicated to the problem of effort estimation for the Product Backlog items of IT projects led accordingly to the Scrum framework. The effort estimation issue is important, because low quality estimation decreases the efficiency of project implementation. The paper proposes an estimation method for the Product Backlog items of Scrum-based IT projects (which can be adapted also to other projects), which has two original elements with respect to the state of art in Scrum estimation: the usage of fuzzy numbers and strict rules for consensus forming, combined with a space for human interaction. The assumptions of the method should be complied with and were formulated on the basis of literature and authors experience. Two case studies were used for an initial method validation. The case studies confirmed a high potential of the method to increase estimation quality in Scrum-based projects, as well as in other project types. The case studies were conducted using research methods fulfilling the symmetry principle. The paper is thus an example of symmetry in management research.

1. Introduction

After a dozen years, both small organizations [1] and large multinationals ones [2] have been using Scrum in their daily operations [3]. Agile management methods, including Scrum, are seen as useful in achieving a shorter time-to-market and an increasing customer satisfaction with high quality software. However, although Scrum is already assessed fairly positively in the business context, it still requires further development and refinement [4]. This encompasses the project estimation issue, with a special emphasis on the estimation of the effort needed to accomplish the elements of the Product Backlog, performed before each Sprint. Demands in the industry set to estimating software development effort are nowadays considerably elevated [5,6,7] and it is general management knowledge that accurate (thus acceptably close to actual values) estimates increase the efficiency of project implementation. The problem seems thus to be essential for all organizations using Scrum.

All the known methods and techniques for Scrum estimation are expert methods—as opposed to methods using uniquely quantitative models, learning algorithms etc., where no human experts are asked to deliver estimates. Formally speaking, an expert estimation method is a method where the estimation task is conducted by persons recognized as experts in the area linked to the element being estimated, and a significant part of estimation is based on a non-explicit and non-recoverable reasoning process [8]. Expert based IT project estimation methods are generally considered to outperform, or in the worst case to equal purely quantitative estimation methods [9,10].

According to the authors of the present paper, the existing methods for Scrum estimation have two drawbacks. The first one is the requirement that uniquely crisp values are supposed to be selected for estimates. This rule excludes the possibility of conveying the message about the uncertainty or risk (we do not enter here into the complex discussion of their respective definitions, carried out in the literature, see e.g., [11]) linked to the estimates in the opinion of the experts. In addition, as the experience and the knowledge of the Development Team are crucial for the Scrum success, in our opinion, it is improper to disregard this information type in the estimation process, which statement will be justified more extensively in the subsequent part of this paper. Fuzzy estimates allow to take subjective and expert-related factors into account, because they are constructed on the basis of expert opinion (of individual experts or expert groups) [12,13,14]. Other known non-crisp estimation techniques, based on probability approaches (like three points estimation techniques, used in PERT), are much more limiting as probability distributions have to fulfil far more restrictive assumptions than fuzzy numbers. Moreover, in such approaches, as the one used in PERT, the probability distributions are imposed (betta distribution is used), whereas in case of fuzzy numbers the fuzzy distribution depends entirely on experts’ opinions/preferences or personal features and various types of fuzzy estimates can be applied.

The other drawback of the known Scrum estimation methods is, according to us, the fact that most of them are largely informal and their outcome, thus the finale estimate, which should represent a consensus of all the experts, is strongly influenced by non-controllable factors, like behavioural ones (e.g., the attitude or mood of the moderator) or external ones (like time pressure) [15].

Thus, the present paper aims at achieving the following objective: to propose a method of effort estimation basically for Scrum projects, focused, but not limited to, on the effort estimation for Product Backlog elements performed before Sprints, which would:

• Utilise fuzzy numbers as estimates;
• Be based on strict rules of achieving final consensus;
• Not disregard the human factor in the process of consensus elaboration.

To the knowledge of the authors, this objective constitutes a novelty in the literature. The only papers applying fuzziness to Scrum—or generally to agile project management [16,17,18]—use fuzzy logic to assess whether a value is good or acceptable or not, but do not allow experts to express their estimations of product backlogs in the form of fuzzy numbers. Other applications of fuzziness to agile project management, like for example those presented in [19] or [20], concern other issues and not estimation (they deal e.g., with project success measurement or agility assessment).

Fuzzy numbers (e.g., [12]) are a mathematical tool which allows to model the expert opinion or intuition about an estimate and its degree of uncertainty. As shown in the literature, fuzzy numbers can be successfully applied to the presentation of individual opinions, especially such ones which in the final analysis have to be aggregated in a single consensus opinion [21,22,23,24]. Their usage in the estimation of Scrum-based projects seems to be natural, as it is in numerous other areas, but according to our knowledge has not been suggested in the literature so far. Fuzzy numbers are one of numerous known tools to model uncertainty. However, they distinguish themselves, especially with respect to probability distributions, by relative application facility and reduced number of limiting assumptions.

Also, the problem of consensus elaboration has already been subject to vast investigation, whose results will be used in the proposed method construction. Basically, two approaches occur here: behavioural consensus and mathematical consensus [25]. The former one uses soft, informal methods, based on discussion and exchange between the experts involved and possibly a moderator. The latter one relies on formal models and calculations [26]. In the considered case both approaches will be combined.

Thus, in order to attain the objective formulated above, a method for the estimation of, in the first place, Scrum-led projects based on fuzzy numbers will be proposed. The managerial advantage of Scrum-based projects involving the fuzzy approach in the estimation process over those utilising uniquely crisp estimates will be discussed. An initial validation of the fuzzy method for the estimation of Scrum-based projects, by means of two single case studies, will be described. The validation consisted in an observer observing and evaluating the implementation of the proposed estimation method in two real world estimator groups.

In the scientific research, in a situation when we have an observer and an observed reality, we should, if possible, apply certain symmetry principles [27]. This was done in both case studies used in the paper. Thus, these case studies are examples of symmetry based research in management, while, after [27], “what symmetry actually boils down to in the final analysis is that the situation possesses the possibility of a change that leaves some aspect of the situation unchanged”. The actual translation of this symmetry concept into research principles will be described in detail later on.

The remainder of the paper is structured as follows. In Section 2 we review main approaches to effort estimation which can be used in Scrum. In Section 3 basic information about voting is given. In Section 4 we summarise theoretical foundations of fuzzy numbers. In Section 5 the state of art of the problem of reaching consensus by means of fuzzy numbers is presented. Section 6 is the beginning of the original part of the paper and presents assumptions for the fuzzy estimation method to be proposed, which have been derived from the literature and personal experience of the authors of the present paper (one of them has been involved in several Scrum-based IT projects). Section 7 describes in detail the main novelty of the present paper: the fuzzy estimation method for Scrum. Section 8 presents two case studies (a real-world international IT project and an R&D project), which were used to evaluate the proposed effort estimation method, and the symmetry principles used there. The paper terminates with a discussion and some conclusions.

2. Effort Estimation Methods for Scrum—State of Art

According to the Scrum framework [28], the effort estimation of Product Backlog items should be performed by the entire Development Team, whose members are considered to be experts. In the present section all the known expert project effort estimation methods, which have been assessed (in [26] and by the authors of the present paper) as usable in the Scrum framework, are shortly described.

2.1. Statistical Group Estimation Method

The method is based on the lack of interaction between the team members—each expert proposes an estimate of their own. The collection of individual estimates is presented as a group estimate using descriptive statistics: median, mean, and mode. This approach can be classified as a primitive method of expert opinion aggregation, and a purely mathematical one.

2.2. Unstructured Group

Effort estimation is performed here using brainstorming, while relations between the experts participating in the process are unspecified. The only element that is required is arriving at a consensus at some predefined time. Unfortunately, the diversity of social, psychological and political problems that may arise within an unstructured group significantly impede effective effort evaluation and may have a negative impact on communication in the team [29].

2.3. Planning Poker

The method was presented by the authors of [30]. To our knowledge, this is the estimation method used most often in Scrum-based projects. The method was given its name because it uses special playing cards. Each of the cards has on its inner side one estimate value.

In the first step [31,32] Product Backlog items are presented to the experts, who are Development Team members. A discussion follows, after which each member of the Development team, according to their own knowledge, selects for each Product Backlog item a card representing their estimate of the effort required to implement the item. All the cards are presented simultaneously. If uniquely cards with the same value have been selected, this value is considered as the result of the estimation and determines the assumed effort needed for the Product Backlog item in question. Otherwise, the Development Team continues the discussion and repeats the cards selection. The process is continued until a unanimous estimate has been reached. However, it is not clear how to avoid unnecessary lengthening of the process. As long as some experts are not ready to adapt themselves to the group, no consensus is possible.

2.4. Planning Game and Blitz Planning

The Planning Game was originally used in the agile method called eXtreme Programming [33], but is adequate for Scrum too. It is based on the assumption [34] that the knowledge about the to-be-produced IT project product is distributed between the Customer and the Developers. The Customer is usually most knowledgeable about the product requirements and the Developers are best informed on the requirements implementation. During the estimation process, Developers and Customer interact directly, responding mutually to any doubts about the estimates. The result of the Game is a list of requirements which are most important to the Customer, with assigned effort estimates. This method is characterized by a great freedom in its application. Lack of clearly defined structures and procedures can lead to difficult negotiations between Developers and Customers before a consensus is achieved. The literature also suggests a variation of Planning Game, called Blitz Planning [35]. Similar to the Planning Game method, it is not based on any strict structures or procedures.

2.5. Plan Delphi and Wideband Delphi

The Delphi method was developed by Helmer, Dalkey and Gordon [36]. It is based on repetitive expert panels, during which each member of the expert group individually determines their estimate, according to their own knowledge. After each panel, all the estimates are collected. Subsequently a moderator, not involved in the estimation process, aggregates the individual estimates in a kind of summary, not taking into account any personal information. The summary is presented to each of the experts and the process is repeated. It is up to the moderator to decide on the number of iterations, but it is recommended to repeat the process until consistent and stable results have been attained. The authors of the method do not define the results consistency and stability; hence the final outcome depends strongly on the moderator.

A variation of the Delphi method is the Wideband Delphi method [37]. The main difference between the Delphi method and the Wideband Delphi lies in the fact that in the former the experts perform the estimation in isolation, whereas in the latter they come in direct interaction with each other and exchange their opinions on the item being estimated.

The above overview of estimation methods that can be utilised for the estimation of Scrum-based projects, especially for the estimation of the effort required to implement individual items of the Product Backlog, shows that:

• Neither fuzzy approach nor any other modelling approach is employed by them for uncertainty/risk modelling;
• As for the consensus elaboration, two extremes are used: a purely mathematical or purely behavioural approach. No trade-off of both has been suggested.

One of families of methods which help groups to reach consensus is voting. As it will be used in the method to be proposed, it will be shortly discussed in the following section.

3. Voting

Voting is probably the most common way to make collective decisions in legislatures, international committees, corporations, associations, organization and product development process [38,39]. In the literature on voting, so-called fair voting procedures are distinguished as the most desirable to use.

According to the literature, fair voting procedures should, in the ideal case, fulfil the criteria [40] listed below, where the term “candidate” has a context-related interpretation:

• Majority criterion—each candidate which in a majority of votes is a winner should be the final winner;
• Condorcet criterion [41]—let us assume that all the candidates are combined in all the possible pairs for assessment. Then the winner shall be the candidate which is preferred by the majority of voters in this process;
• Monotonicity criterion—this criterion can be reduced to the requirement that it is neither possible to prevent the election of an elected candidate by ranking it higher in subsequent voting, nor it is possible to elect an otherwise unelected candidate by ranking it lower in subsequent voting (while nothing else is altered);
• Independence of irrelevant alternatives criterion—if the elections have been held and a winner has been chosen, the winning candidate should still be the winner in the event of recalculation of votes, when one or more of the losing candidates have been removed from voting.

Voting adaption possibilities are restricted (which is shown e.g., by the well-known Arrows impossibility theorem [42]). The authors of [40] demonstrate that no voting procedure exists which would satisfy all the above listed criteria simultaneously. However, it is usually possible to develop a quasi-fair estimation method. This will be done also in the method proposed further on in this paper.

In the following section, basic information about the selected uncertainty modelling tool, the fuzzy numbers, will be presented.

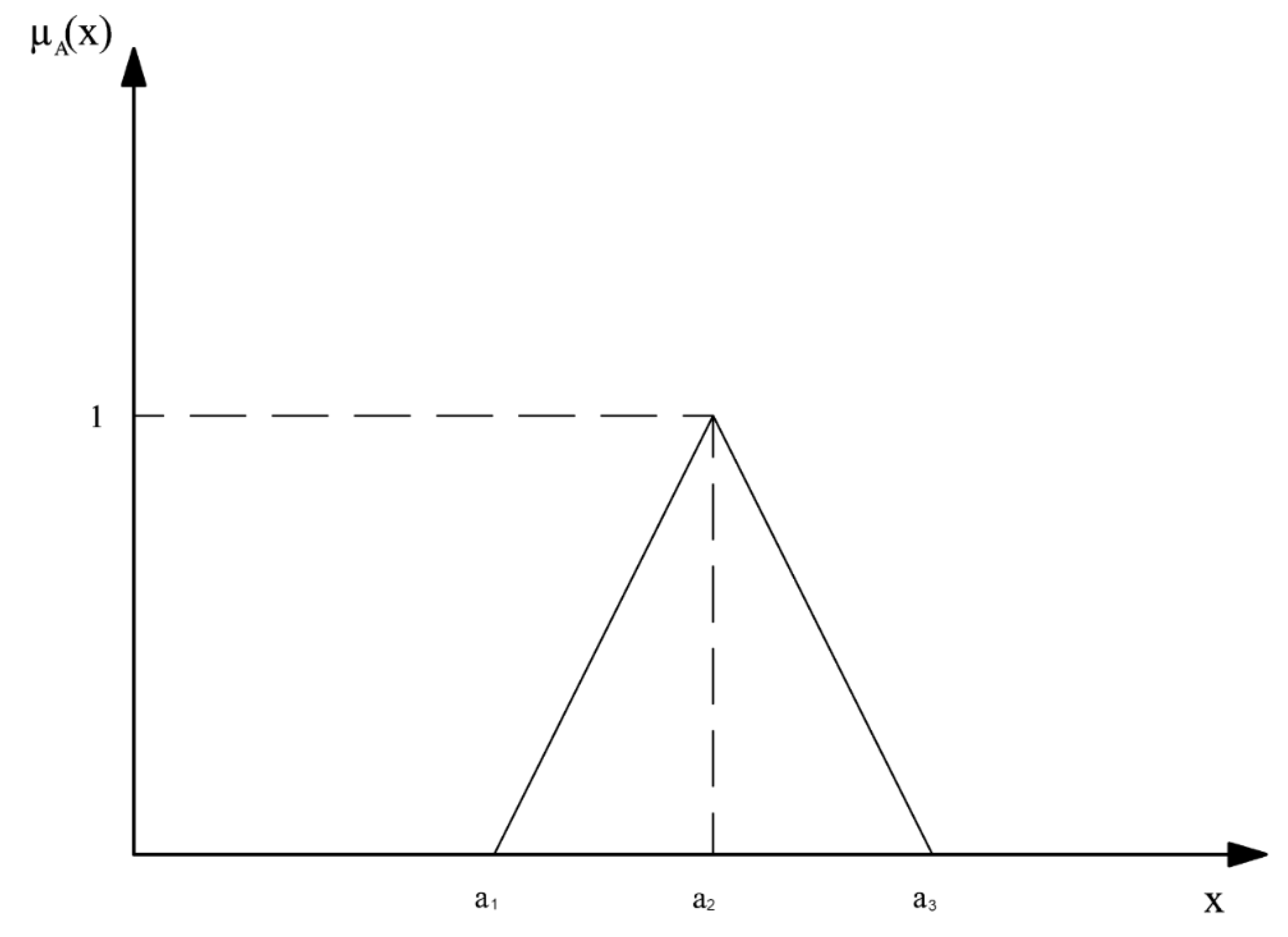
4. Theoretical Basis of Fuzzy Numbers

In the literature, there are many different definitions of fuzzy numbers [12,43,44]. For the purposes of this paper, the following notation will be used [43]:

Definition 1.

Fuzzy number à is a family of closed intervals $\left\{A^t\right\}\left(t\in \left[0,1\right]\right)$, satisfying the following conditions:

• $\mathrm{t}>\mathrm{r}\Rightarrow A^t\subset A^r$
• $\mathrm{I}\subseteq \left[0,1\right]\Rightarrow A^{supI}=\underset{\mathrm{r}\in \mathrm{I}}{{\displaystyle \cap }}{A}^r$(symbol ${\displaystyle \cap }$ means the common part of intervals)

For each t $\left(t\in \left[0,1\right]\right)$ interval $A^t$ is called the t-level of the fuzzy number Ã. Notation $A^t=\left[a_L^t,a_P^t\right]$ will be used.

The family of intervals forming a fuzzy number corresponds to more and more precise estimations of the magnitude A. $A^0$ is the interval containing all the values which are considered to be possible, even to a small degree, while $A^1$ is composed of only such values, which are possible to the highest degree.

Definition 2.

Let à be a fuzzy number. Function ${\mu }_A$, defined as ${\mu }_A\left(x\right)=sup\left\{t:x\in A^t\right\}$, is called the membership function of the fuzzy number Ã, and the value ${\mu }_A\left(x\right)$ represents the occurrence possibility of x in the role of actual value of an unknown magnitude A, estimated by means of Ã.

${\mu }_A\left(x\right)$ represents the degree to which the expert thinks it is possible that x will be the actual value of a not fully know magnitude A. The fuzzy number à is a representation of the incomplete knowledge about the magnitude A before it actually materializes itself and becomes fully know. à may stand for an estimation of the magnitude A.

In the framework of the present paper, we will basically assume that fuzzy number à expresses the subjective opinion of a selected Development Team member on the effort needed to perform a Product Backlog item and the degree of uncertainty linked to it. The value ${\mu }_A\left(x\right),$ reflects the degree of possibility (according to the Development Team member) that x will actually be the value of effort related to the Product Backlog item. The interval $A^t$ $\left(t\in \left[0,1\right]\right)$ is the set of all the values x which can be (still subjectively, according to the selected expert(s)) the actual effort value with the possibility at least t. Indeed, it can be proved that $A^t=\left\{x:{\mu }_A\left(x\right)\ge t\right\}$.

Various types of fuzzy numbers can be used. For the sake of simplicity we will limit ourselves to the simplest one: triangular fuzzy numbers, but experts can use numerous other shapes of membership functions, according to their preferences [45].

Definition 3.

Fuzzy number à =$\left(a_1,a_2,a_3\right)$ is a triangular fuzzy number if a triple ($a_1,a_2,a_3$) of real numbers exists such that $a_1\le a_2\le a_3$ and

$${\mu }_A\left(x\right)=\{\begin{array}{c}0\mathrm{for}x<a_1\\ \frac{x-a_1}{a_2-a_1}\mathrm{for}x\in \left[a_1,a_2\right]\\ \frac{a_3-x}{a_3-a_2}\mathrm{for}x\in \left[a_2,a_3\right]\\ 0\mathrm{for}x>a_3\\ \end{array}$$

(1)

A positive triangular fuzzy number is one fulfilling the condition $a_1>0$.

Figure 1 presents the shape of a positive triangular fuzzy number membership function:

Values smaller than $a_1$ and greater than $a_3$ are considered by the expert as impossible in the role of actual values of the magnitude in consideration, the occurrence of the other values in this role is seen as possible, although to various degrees. The most possible value of the item in question is, according to the expert, $a_2$.

Definition 4.

Let us define, for a given fuzzy number $\tilde{A}=\left(a_1,a_2,a_3\right)$, the in minus uncertainty degree $U^{-}\left(\tilde{A}\right)$ = $\frac{a_2-a_1}{a_2}$ and the in plus uncertainty degree$U^{+}\left(\tilde{A}\right)$ = $\frac{a_3-a_2}{a_2}$.

The uncertainty degrees represent the uncertainty about the actual value of an unknown magnitude A. The uncertainty may be negative or positive—not in the sense of the negativity or positivity of its value, but in the sense of its meaning for the decision maker. For example, if high values of the magnitude in question should be possibly avoided, then the in plus uncertainty degree represents the negative (undesired) uncertainty.

In the method to be proposed in the present paper, fuzzy estimates are going to be aggregated in order to construct a consensus. In this procedure arithmetical operations on fuzzy numbers will be needed.

Definition 5.

Let * represent the operation of addition or multiplication of real numbers, and let$\tilde{A}=\left(a_1,a_2,a_3\right)$and$\tilde{B}=\left(b_1,b_2,b_3\right)$be two positive triangular fuzzy numbers and g a positive real number. Then we define:

$$\tilde{A}\ast \tilde{B}=\left(a_1\ast b_1,a_2\ast b_2,a_3\ast b_3\right)$$

(2)

$$g\ast \tilde{A}=\left(g\ast a_1,g\ast a_2,g\ast a_3\right)$$

(3)

On top of that, we will need a method of comparing fuzzy numbers. This issue is rather complex and has been treated in a vast number of literature positions (e.g., [40,46,47]), as comparing fuzzy numbers is not unequivocal. Here, we propose to use one of many possible ways of defining the distance and the similarity degree between two triangular fuzzy numbers [48].

Definition 6.

Let$\tilde{A}=\left(a_1,a_2,a_3\right)$and$\tilde{B}=\left(b_1,b_2,b_3\right)$be two positive triangular fuzzy numbers.

(a) 

Distance between$\tilde{A}and\tilde{B},$denoted as$D\left(\tilde{A},\tilde{B}\right)$, is defined as$\frac{\left|b_1-a_1\right|+\left|b_2-a_2\right|+\left|b_3-a_3\right|}{3}$

(b) 

Similarity degree between$\tilde{A}and\tilde{B}$, denoted as$S\left(\tilde{A},\tilde{B}\right)$is defined as$\frac{{{\displaystyle \int }}_x^{}min\left({\mu }_A\left(x\right),{\mu }_B\left(x\right)\right)dx}{{{\displaystyle \int }}_x^{}max\left({\mu }_A\left(x\right),{\mu }_B\left(x\right)\right)dx}$.

Part (b) of the above definition is illustrated in Figure 2:

The similarity degree of the two fuzzy numbers shown in Figure 2, is the quotient of the area of the hatched surface by that of the union of both triangles. If the two triangles have no common area, the similarity degree will be zero. The distance is the arithmetical average of the differences of the three characterising parameters $a_1,a_2,a_3$, $b_1,b_2,b_3$ of the triangular fuzzy numbers.

In fact, in each case the decision maker has to select one from a vast number of methods of comparing fuzzy numbers. The literature on this subject is extremely rich. Each method reflects the decision maker preferences and intuition. For example, the distance between two fuzzy numbers defined above weights equally the three triangular fuzzy number characteristics $a_1,a_2,a_3$, but the decision maker might feel that e.g., the optimistic value should count less, because he or she is a pessimist. In this case another comparison method should be chosen. Similar considerations on the choice of fuzzy number comparison methods can be found in the literature, e.g., in items referred to above.

Fuzzy numbers are often used as a support to arrive at consensus, which will be needed also in the method to be developed and will be presented in the next section.

5. Theory of Consensus Using Fuzzy Numbers

Consensus is a term used for many centuries in different contexts and fields. It refers to the general situation in which we are facing a group of experts presenting opinions about a certain phenomenon. Consensus was originally defined as achieving a full and unanimous agreement of experts [49]. However, many researchers expressed their doubts whether in real-world conditions such consensus may be attained [50]. Consequently, another definition was formulated: consensus is an agreement which is considered to be beneficial for the whole group. Nevertheless, this definition does not presuppose that each person taking part in the consensus formation process identifies fully with the final result [51].

In the literature, the problem of obtaining a consensus while experts express their opinions using fuzzy numbers has been vastly investigated—with no relationship to Scrum, however. Researchers (more than 220 publications in Scopus, the findings are summarized in [52]) use a variety of approaches based on fuzzy numbers. One of the first papers describing consensus formation in group decision problems using fuzzy numbers is [53]. The author od that paper uses fuzziness to model such notions as “majority”, “a lot more than x%”, etc. The authors of [50] propose a method for measuring the degree of consensus calculated for each expert proposal, while the latter is expressed in the form of a fuzzy number. The authors of [54] use for expert proposals modelling a generalisation of fuzzy numbers, the so called intuitionistic fuzzy numbers. These numbers introduce the possibility to model expert opinion both on the question “to what degree it is possible that x is the searched final value” and on the question “to what degree it is impossible that x is the searched final value”. The authors of [54] define a similarity measure of expert opinions expressed in the form of intuitionistic fuzzy numbers. The consensus is then the value most similar to all the individual expert opinions. Likewise, the authors of [55] propose a similarity measure of intuitionistic fuzzy numbers and use it to calculate the agreement degree in the expert group. The consensus is a value which maximizes the agreement degree. The authors of [56] propose to calculate the consensus by means of a geometric aggregation operator applied to trapezoidal fuzzy numbers, which represent the expert opinions. Trapezoidal fuzzy numbers are a generalization of triangular fuzzy numbers and are characterized by a trapezoid-shape membership function (Figure 1). The authors of [57] present a consensus model based on a bicriterial decision problem. The first criterion (maximised) is a measure of agreement among the experts and the second one (minimised) is the distance of a given expert opinion (expressed by means of a fuzzy number) and a selected consensus value. The authors of [58] analyse the problem of constructing fuzzy numbers capable of measuring the consensus degree on a set of input data. The proposed final solution is calculated by means of two consensus operators.

One of the most popular ways to construct a consensus with the use of fuzzy numbers [57,59,60,61,62,63] is based on the degree of mutual trust among experts, whose opinions are expressed in a fuzzy form. We have decided to apply one of these methods, the one proposed in [64]. It was originally designed for solving multi-round decision making problems. In Section 6 it will be adapted to the problem of consensus forming in the effort estimation process for Product Backlog items.

Here, we have finished the literature-based part of the paper and are passing to our original proposal.

6. Assumptions and Basic Theory for Fuzzy Expert Estimation Method for Scrum

This section begins the presentation of the new method for effort estimation in Scrum-based projects, especially in their phase before Sprints, when Product Backlog items are to be assigned estimates of the effort needed for their completion. According to the Scrum philosophy, it is the Development Team whose responsibility is to perform the estimation. Its members are considered to be equally respected experts, knowledgeable about the items being estimated, but the Team is obliged to arrive at a consensus.

6.1. Assumptions to Be Fulfilled by the Method

Here we formulate, on the basis of literature and our own experience, a set of assumptions the method to be developed should satisfy:

(1)

Each member of the Development Team who is involved in the effort estimation gives their individual opinion about the estimate in subsequent interactions, and participates in the final decision. All the Development Team members share the general objective (a successful termination of the project in question), but may differ in their detailed views on how this objective should be achieved and on the amount of effort needed to do so;

(2)

No estimate value is preferred a priori;

(3)

Each member of the Development Team estimates the same set of feasible Product Backlog items;

(4)

Individual estimates are expressed in the form of fuzzy numbers;

(5)

There is a special actor (moderator), whose task is to ensure that the rules of the method are observed. She or he is responsible of informing the members of the Development Team about the results, but his or her opinion cannot affect the consensus;

(6)

Members of the Development Team accept the final decision obtained by means of the method as the final opinion of the entire Development Team.

(7)

The estimation method to be developed should use a quasi-fair voting procedure.

6.2. Fuzzy Representation of Effort Estimation for Product Backlog Items

Whenever fuzzy numbers are to be used for modelling experts’ opinions, it is indispensable to design the process of “translating” implicit opinions of experts into the mathematical form of a selected fuzzy number type. The earliest research on this issue was reported by [13]. Although such approaches are certainly valuable and worth considering, they are fairly complex. Thus, we propose to begin with an easier method, where the experts (indexed by the index i, i = 1, …, I) are instructed about the meaning of the membership function from Figure 1 and subsequently are asked three questions: What is the most optimistic value (the most likely, the most pessimistic) of effort estimation of Product Backlog item F_j, j = 1, …, J, where J is the number of elements in the Product Backlog. The answers can be expressed for example in a unit popular in Scrum, called user story points [32] and will be denoted, respectively, for the i-th (i = 1, …, I) expert, as (${\underset{\_}{P}}_i\left(F_j\right),{\widehat{P}}_i\left(F_j\right),{\overline{P}}_i\left(F_j\right)$). Of course we must have $0\le {\underset{\_}{P}}_i\left(F_j\right)$ $\le {\widehat{P}}_i\left(F_j\right)\le {\overline{P}}_i\left(F_j\right)$. In order to simplify the calculations, we assume that all used fuzzy numbers have triangular membership functions, although other shapes are also possible. The triangular fuzzy numbers (${\underset{\_}{P}}_i\left(F_j\right),{\widehat{P}}_i\left(F_j\right),{\overline{P}}_i\left(F_j\right))$ will be denoted as $\tilde{P}\left(i,F_j\right)$, j = 1,…, J, i = 1, …, I.

7. Fuzzy Method for Expert estimation of the Effort Needed to Accomplish Product Backlog Items

The method for the estimation of the effort needed to accomplish Product Backlog items proposed in this section is a modification of the method presented in [64]. In its construction we have taken into account the assumptions listed in Section 6.1.

As mentioned above, there are I experts—members of the Development Team, indexed by I = 1, 2, …, I. In subsequent rounds the i-th Development Team member (i = 1, …, I) proposes a fuzzy estimate $\tilde{P}\left(i,F_j\right)$ (i = 1, …, I, j = 1, …, J) of the j-th element of the Product Backlog. The estimates are selected without any interaction between the experts and afterwards presented to all of them. Subsequently, for each j = 1, …, J crisp weights $w_j^i\ge 0,$ i = 1, …, I, ${{\displaystyle \sum }}_{i=1}^I{w}_j^i=1$, are decided on in a group discussion. The weights are used to calculate the consensus (which is a mathematical consensus):

$${\tilde{P}}_j^{cons}={\displaystyle \sum }_{i=1}^I{w}_j^i\tilde{P}\left(i,F_j\right)$$

(4)

To start with, the weights are assumed as follows:

$$w_j^i=\frac{A\left(i,j\right)}{{{\displaystyle \sum }}_{i=1}^{I}A\left(i,j\right)}$$

(5)

$A\left(i,j\right)$ in (5) stands for the average degree of agreement of the i-th expert with all his or her colleagues regarding the estimate of the effort needed for the item $F_j$. $A\left(i,j\right)$ is defined on the basis of Definition 6b):

$$A\left(i,j\right)=\frac{{{\displaystyle \sum }}_{k=1,k\ne i}^{I}S\left(\tilde{P}\left(i,F_j\right),\tilde{P}\left(k,F_j\right)\right)}{I-1}$$

(6)

Formula (5) assigns more importance to the estimates of the experts whose relative agreement with the rest of the Development Team is higher.

However, as mentioned earlier, one of the novelties of our proposal is to combine mathematical consensus with a behavioural one. For this reason the weights values are subject to open discussion. If no agreement is found in the discussion after a pre-set period of time, weights (5) are accepted.

Once the final weights values have been agreed upon, the consensus of the entire team as to the estimate for the j-th Product Backlog element is taken as (4).

The consensus (4) is a triangular fuzzy number. It represents the opinion of the whole Development Team on possible values of the effort needed to accomplish the j-th Product Backlog element, together with the uncertainty associated to it.

Example. 

Let us assume that for a selected j-th Product Backlog element the following estimates were presented:

Table 1. Estimates presented by the members of the development team for the j-th Product Backlog—example.

	Estimates [User Story Point, Denoted as PP]
i-th Expert	${\underset{\_}{\mathit{P}}}_{\mathit{i}}\left({\mathit{F}}_{\mathit{j}}\right)$	${\widehat{\mathit{P}}}_{\mathit{i}}\left({\mathit{F}}_{\mathit{j}}\right)$	${\overline{\mathit{P}}}_{\mathit{i}}\left({\mathit{F}}_{\mathit{j}}\right)$
1	1	2	3
2	2	2	3
3	1.5	2	3
4	1	1.5	5
5	0.5	1.5	5

presented example value of estimation for the j-th Product Backlog item. For this example, ${\tilde{P}}_j^{cons}$ (with weights calculated according to (5)) is then equal to the triangular fuzzy number (1.18, 1.803, 3.789), presented in Figure 3 (the symbol PP stands for story points).

The estimate in Figure 3 shows that, according to the entire Development Team, the Product Backlog item in question will need about 1.8 story points to be completed. If the process of its completion does not encounter any obstacles, it may be accomplished using only about 1.18 story points. However, the Development team feels that the item is associated with a high uncertainty degree in the negative sense. Probably the Team reckons that some unexpected phenomena or questions may occur during its accomplishment. That is why the Team assessed that in the pessimistic case the item may need as many as almost 3.8 story points. This information has to be taken into account in the Sprint planning process. Buffers should be provided or other measures taken for the case when the pessimistic value materializes itself.

As far as the assumptions from Section 6.1 are concerned, the fulfilment of those numbered (1)–(6) follows directly from the above description of the method. The issue (7), concerning fair voting, is more complex. The conditions listed in Section 3 refer rather to voting in the sense of selecting a winner among the candidates according to expert preferences. It was mentioned in Section 3 that a fully fair voting does not exist. In the case considered here we face another type of voting: the final result may not be equal to any candidate number. It is rather a weighted average, and the voting may regard only the weights. However, the method proposed here fulfils modified versions of the requirements from Section 3, listed below and based on Definition 6a:

i*:

If the experts agree to give a high weight to an estimate $\tilde{P}\left(i_0,F_j\right)$, so that $w_j^{i_0}\ge 1-\epsilon$, where $\epsilon$ is a small number, then $D\left({\tilde{P}}_j^{cons},\tilde{P}\left(i_0,F_j\right)\right)\le \epsilon \left({\underset{\_}{P}}_{i_0}\left(F_j\right)+{\widehat{P}}_{i_0}\left(F_j\right)+{\overline{P}}_{i_0}\left(F_j\right)\right)$, thus the final solution is close to the estimate clearly preferred by the majority of experts. In other words, a candidate preferred by the majority of experts is the winner.

ii*:

for each pair of indices $i_0,i_1=1,\dots ,I$ it holds that if $w_j^{i_0}>w_j^{i_1}$ then $D\left({\tilde{P}}_j^{cons},\tilde{P}\left(i_0,F_j\right)\right)$ < $D\left({\tilde{P}}_j^{cons},\tilde{P}\left(i_1,F_j\right)\right)$, thus for each pair of candidate numbers the final solution is closer to the one which is more preferred by the Development Team. In other words, a candidate preferred by the majority of experts in pairwise comparisons is the winner;

iii*:

Let ${\tilde{P}}_j^{cons}={\displaystyle \sum }_{i=1}^I{w}_j^i\tilde{P}\left(i,F_j\right)$ and ${\tilde{P}}_j^{cons\ast }={\displaystyle \sum }_{i=1}^I{w}_j^{i\ast }\tilde{P}\left(i,F_j\right)$, where $w_j^{i\ast }=w_j^i$ for all $i\ne i_0$ and $i\ne i_1$ $w_j^{i_0\ast }=w_j^{i_0}+\mathsf{\Delta }$ $w_j^{i_1\ast }=w_j^{i_1}-\mathsf{\Delta }$ $w_j^{i_0\ast },w_j^{i_1\ast }\ge 0.$ Then we have, for $\mathsf{\Delta }>0$, $D\left({\tilde{P}}_j^{cons\ast },\tilde{P}\left(i_0,F_j\right)\right)<D\left({\tilde{P}}_j^{cons},\tilde{P}\left(i_0,F_j\right)\right)$ and $D\left({\tilde{P}}_j^{cons\ast },\tilde{P}\left(i_1,F_j\right)\right)$ $>D\left({\tilde{P}}_j^{cons},\tilde{P}\left(i_1,F_j\right)\right)$. In other words, an increase in the weight assigned to an estimate reduces its distance to the final solution and a decrease amplifies it, which means that increasing weights increases the chances of the relevant candidate to win and decreasing weights has the contrary effect;

iv:

removing a candidate reduces to assigning a zero weight to it. The same reasoning as for iii* shows that this decision decreases the distance of the final solution from the removed candidate number. In other words, the winner does not lose its position in case of the removal of some other candidates.

Proofs of the above statements consist in straightforward reformulations of respective inequalities.

The present section contains the proposal of estimation method for the effort of Product Backlog items. The method fulfils assumptions (1)–(7) from Section 6.1. It is a method which utilises fuzzy representation of the expert opinions and is based on unequivocal rules which determine the moment when the final decision, representing the opinion of the whole Development Team, has to be taken. Nevertheless, the method does not exclude soft decision making elements, like free discussion (on the weights assigned to individual proposals). However, the method offers a clear procedure in case the discussion does not lead to any consensus in a pre-set time limit. The method has been initially validated using the case study method.

8. Case Studies

Two case studies were used to evaluate the method proposed in the previous section. The case study method is particularly useful in the field of management sciences [65]. Frequently single case studies are used [66]. Single case studies are valuable in situations where the analysed problem is often encountered in practice, but the researchers do not have access to a higher number of cases [67]—due to the innovative nature of the problem or the reluctance of organizations to be the subject of such studies.

Both case studies used here correspond to this description:

• the first case study is an IT project in which the organisation used Scrum for the first time. Scrum is a fairly new method, still in the dynamic development stage, thus IT companies are generally little willing to reveal the data about their projects [68].
• the second case study is an R&D project of innovative and unique nature, which additionally put into question the financial management of a big university at that time. Such projects are encountered extremely rarely and organisations involved are rather reluctant to reveal detailed information.

Of course, the single case study method has considerable limitations: low representativeness and far reaching subjectivity of the results. However, it offers a possibility to scrutinize in depth a given research problem [69], to gather detailed data of various types: quantitative and qualitative ones, and to indicate future research directions.

In the case studies described here two basic ways of collecting data and information were used:

• participant observation—one of the authors was either an external coach supporting the implementation of Scrum in the project, conducting and moderating the estimation process for the whole project (first case study) or project manager (second case study);
• informal individual interviews with project team members and estimators.

The following symmetry principles were applied in the research [27]:

• all possible effort was put to ensuring that the behaviour of the observed reality (the team estimating the project) be unaffected by and independent of our observing and measuring. The coach and the project manager tried not to influence the project estimation process by their presence;
• the coach and the project manager also tried not to be affected in their observing and measuring by the behaviour of the project team and the estimators;
• an initial state (at the beginning of the case study) and evolution (modification of the estimation method) were distinguished, and the initial state definition was independent of the observing activity.

Naturally, as the observed reality was a group of human beings and not still objects, the independencies listed above were not always perfect, but in any case an approximate symmetry of the research [27] was guaranteed.

8.1. Case Study nb 1

8.1.1. Project Description

The project was implemented in a large international organization X with the headquarter in one of European capitals, providing services on the telecommunication market. The project was conducted on behalf of an Asian customer Y. The main goal of the project was the development of a billing platform. Three Development Teams were involved in the project execution. Scrum framework was selected for project management and it was the first time organisation X applied Scrum in one of their projects.

8.1.2. Implementation of Fuzzy Effort Estimation Method

According to the wish of the management of organization X, estimation of the effort needed to accomplish all the Product Backlog items was performed at the beginning of Sprint 0, thus the very first Sprint of the project.

The process map of estimating the effort linked to each Product Backlog item used in the case study is shown in Figure 4. The Product Backlog was the necessary prerequisite for the estimation process. In the case considered here it was composed of 49 items. Out of all the members of the three Development Teams, eight most experienced developers were selected (the company management wished to minimise the estimation cost and did not agree to the participation in the estimation process of all members of the three Development Teams). One of the authors of the present paper moderated the estimation process and instructed the members on the rules of the process and its double goal: to estimate Product Backlog items for the needs of the project realised by company X and to verify the application possibilities of a new, fuzzy numbers based estimation method.

The user story point units were used for estimation. The 8 experts conducted estimation in four rounds (thus we have $I=8)$, each time giving a crisp estimation for each Product Backlog item. Thus, for the j-th Product Backlog item, $j=1,\dots 49$, four crisp values were proposed by each expert i, i = 1, …, 8. Let us denote them as $T_{i,j}^k$, where k = 1, 2, 3, 4 stands for the round number. The Wideband Delphi approach was used here, thus after each round the estimates proposed by each experts were shown to all the other experts. The session took four hours. The final decision, i.e., the determination of one estimate for each Product Backlog item, was made in two ways:

• Traditional approach: no fuzzy numbers were applied, simple voting and majority rule after the 4th round determined the final estimate. This means that for the j-th Product Backlog item the crisp estimate from the set ${\left\{T_{i,j}^k\right\}}_{i=1,\dots ,8;k=1,\dots ,4}$ was selected which obtained the maximum number of expert votes. In case two or more estimates received the same number of votes, the highest of them (i.e., the most pessimistic one) was retained as the final result. Let us denote it as $T_j$, j = 1, …, 49.
• New, fuzzy numbers based approach: for each expert i = 1, …, 8 and Product Backlog item j = 1, …, 49, triangular fuzzy numbers $\tilde{P}\left(i,F_j\right)$ were constructed in the following way:

  ○

  ${\widehat{P}}_i\left(F_j\right)$, the most likely variant of the estimate, was the one proposed in the last round (i.e., it was equal to $T_{i,j}^4$);

  ○

  ${\overline{P}}_i\left(F_j\right)$, the pessimistic variant, was the maximum of the four relevant estimates (i.e., was set as $\underset{k=1,2,3,4}{\max }\left\{T_{i,j}^k\right\}$);

  ○

  analogously, ${\underset{\_}{P}}_i\left(F_j\right)$, the optimistic variant, was assumed to be equal to $\underset{k=1,2,3,4}{\min }\left\{T_{i,j}^k\right\}$.

Then weights (5) were assumed and fuzzy estimates for all the Product Backlog items were constructed according to (4). They will be denoted as ${\tilde{P}}_j^{cons}$. The results, after initial processing, are presented in

Table 2. Results of the estimation process in the case study.

j	${\displaystyle {\underset{\_}{\mathit{P}}}_{\mathit{j}}^{\mathit{c}\mathit{o}\mathit{n}\mathit{s}}}$	${\widehat{\mathit{P}}}_{\mathit{j}}^{\mathit{c}\mathit{o}\mathit{n}\mathit{s}}$	${\overline{\mathit{P}}}_{\mathit{j}}^{\mathit{c}\mathit{o}\mathit{n}\mathit{s}}$	${\mathit{T}}_{\mathit{j}}$	${\mathit{\mu }}_{{\mathit{P}}_{\mathit{j}}^{\mathit{c}\mathit{o}\mathit{n}\mathit{s}}}\left({\mathit{T}}_{\mathit{j}}\right)$	$1\mathbf{if}{\mathit{T}}_{\mathit{j}}\le {\widehat{\mathit{P}}}_{\mathit{j}}^{\mathit{c}\mathit{o}\mathit{n}\mathit{s}}$	${\mathit{U}}^{-}\left({\tilde{\mathit{P}}}_{\mathit{j}}^{\mathit{c}\mathit{o}\mathit{n}\mathit{s}}\right)$	${\mathit{U}}^{+}\left({\tilde{\mathit{P}}}_{\mathit{j}}^{\mathit{c}\mathit{o}\mathit{n}\mathit{s}}\right)$
1	13	13	13	13	1	1	0	0
2	0.90	2.23	3.62	3	0.45	0	0.60	0.62
3	16.32	28.87	69.70	20	0.29	1	0.43	1.41
4	4.16	5	5.47	5	1	1	0.17	0.09
5	2.96	4.63	6.18	5	0.76	0	0.36	0.34
6	0.92	1.61	2.61	1	0.11	1	0.43	0.62
8	15.81	22.87	34.07	20	0.59	1	0.31	0.49
9	13	13	13	13	1	1	0	0
10	8	8	8	8	1	1	0	0
11	5.20	8.22	13	8	0.93	1	0.37	0.58
12	14.89	25.18	56.59	20	0.50	1	0.41	1.25
13	2	2	2	2	1	1	0	0
14	2.20	3.67	5.22	5	0.14	0	0.40	0.42
15	7.78	10.39	13	13	0	0	0.25	0.25
16	6.84	8.37	12.81	8	0.76	1	0.18	0.53
17	7.34	9.13	12.68	8	0.37	1	0.20	0.39
18	11.33	11.90	13.47	13	0.30	0	0.05	0.13
19	5.75	7.53	11.82	8	0.89	0	0.24	0.57
20	2.87	3.76	6.55	5	0.55	0	0.24	0.74
21	6.65	9.09	11.61	8	0.55	1	0.27	0.28
22	5	5	5	5	1	1	0	0
23	2.62	3.82	6.26	3	0.32	1	0.31	0.64
24	28.31	35.46	40	40	0	0	0.20	0.13
25	20	20	20	20	1	1	0	0
26	4.27	5.38	6.54	5	0.66	1	0.21	0.22
27	6.21	9.90	12.44	8	0.48	1	0.37	0.26
28	8	8	8	8	1	1	0	0
29	8	8	8	8	1	1	0	0
30	15.97	18.24	21.06	18	0.89	1	0.12	0.15
31	9.11	19.23	31.71	20	0.94	0	0.53	0.65
32	5.38	8.40	12.90	8	0.87	1	0.36	0.54
33	10.07	12.56	17.81	13	0.92	0	0.20	0.42
34	13	13	13	13	1	1	0	0
35	8	8	8	8	1	1	0	0
36	8	8	8	8	1	1	0	0
37	8	8	8	8	1	1	0	0
38	3.97	5.21	7.70	5	0.83	1	0.24	0.48
39	2.46	3.71	5.54	3	0.43	1	0.34	0.49
40	7.97	12.31	21.31	13	0.92	0	0.35	0.73
41	4.27	6.25	8.88	5	0.37	1	0.32	0.42
42	3.21	4.87	7.93	5	0.96	0	0.34	0.63
43	4.27	6.25	8.88	8	0.33	0	0.32	0.42
44	5.37	7.17	9.86	8	0.69	0	0.25	0.38
45	5	5	5	5	1	1	0	0
46	10.99	21.01	40	20	0.90	1	0.48	0.90
47	17.74	24.71	37.87	20	0.32	1	0.28	0.53
48	13	13	13	13	1	1	0	0
49	10.83	15.58	28.97	20	0.67	0	0.30	0.86

.

The numbers from Table 2 are presented graphically in Figure 5.

The black line in Figure 5 represents column $T_j$ from Table 2, the other lines represent the fuzzy consensus (the first 3 columns from Table 2). It can be seen that for some Product Bakclog elements the uncertainty about their estimates is high, in terms of absolute values and in terms of the percentage of their crisp estimates $T_j.$

8.1.3. Results of Case Study nb 1

The most interesting aspect to discuss here is the relationship between the traditional estimation results and those following from the new, fuzzy numbers based method. The in plus and in minus uncertainty degrees (Definition 4) and the membership degrees of traditionally calculated estimates (Definition 3), as well as the information about the traditional estimate position on the axis with respect to ${\widehat{P}}_j^{cons}$ will be used to perform this comparison.

As mentioned above, the effort required to perform altogether 49 Product Backlog items was estimated.

• In 14 cases a fuzzy number with both uncertainty degrees equal to 0 was obtained (${\underset{\_}{P}}_j^{cons}={\widehat{P}}_j^{cons}={\overline{P}}_j^{cons})$ and the traditional, crisp estimate fully harmonised with this result (${\widehat{P}}_j^{cons}=T_j).$ For these items the usage of fuzzy numbers did not contribute any new information, it seems that the experts agreed that the production of these Product Backlog items was not linked to any uncertainty;
• In 7 cases the minimal uncertainty degree (of the in plus and in minus ones) was greater than 0.4, in two cases it was greater than 0.5, while it held ${\widehat{P}}_j^{cons}=T_j$. The accomplishment of these items was linked to a rather high uncertainty and the usage of fuzzy numbers indicates it clearly, contrary to the traditional approach. Decision makers should focus especially on them—their accomplishment may require substantially less or substantially more effort that indicated by the traditional approach. This knowledge was tacitly present in the expert team, but it was only the fuzzy approach which allowed it to come to light.
• In 14 cases the in plus uncertainty degree exceeded by at least 0.2 the in minus one. These cases correspond to those Product Backlog items where the possibility of exceeding the value ${\widehat{P}}_j^{cons}$ was substantially higher than the chances of being inferior to it. Also this type of information, made available thanks to the proposed method, is valuable, as it indicates the estimates which are more uncertain in the negative than in the positive sense;
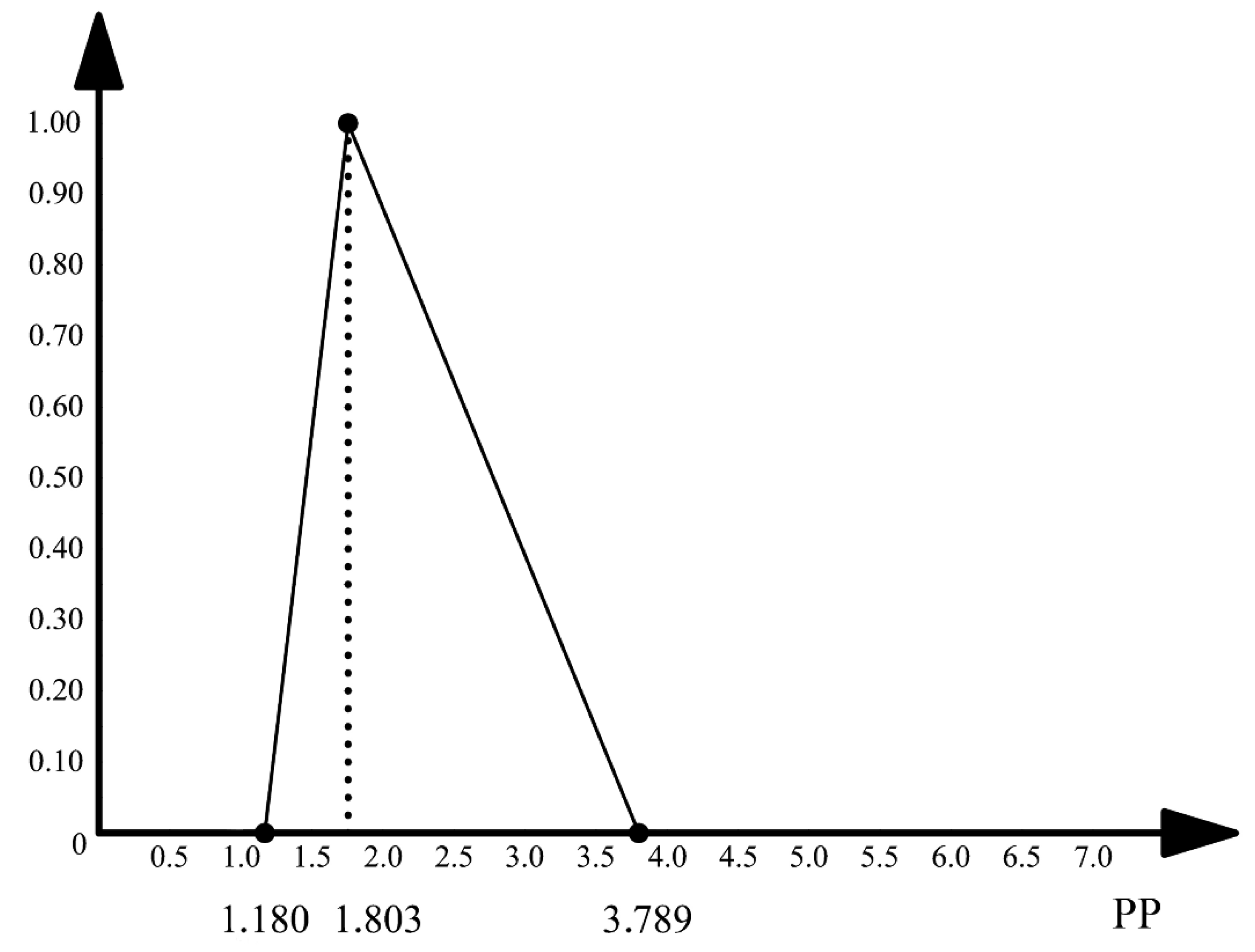
• In 7 cases it held ${\mu }_{P_j^{cons}}\left(T_j\right)<0.3$ (among them in 2 cases we had $T_j<{\widehat{P}}_j^{cons})$, in 11 cases ${\mu }_{P_j^{cons}}\left(T_j\right)<0.4$ (among which in 6 cases $T_j<{\widehat{P}}_j^{cons}$), in 15 cases ${\mu }_{P_j^{c\mathrm{o}ns}}\left(T_j\right)<0.5$ (among which in 9 cases $T_j<{\widehat{P}}_j^{cons})$ and in 18 ${\mu }_{P_j^{cons}}\left(T_j\right)<0.6$ (among which in 11 case $T_j<{\widehat{P}}_j^{cons}$). All these cases are a clear proof of the usefulness of the new method. Although both estimates, the traditional and the “new” one, were delivered by the same experts, in a considerable number of cases the occurrence of the traditional estimate (measured by means of the membership function ${\mu }_{P_j^{cons}}$) was, in the opinion of the experts, not very possible. The most alarming cases are those where ${\mu }_{P_j^{cons}}\left(T_j\right)$ was low and at the same time the inequality $T_j<{\widehat{P}}_j^{cons}$ held. In these cases the traditional estimates are in the left hand wing of the triangle from Figure 1 and as such, differ substantially from the most dangerous values, those from the right hand wing, which may occur with a positive possibility degree (according to the same experts). It means that in these cases decisions made on the basis of traditional estimates can be described as essentially biased with a high negative uncertainty and risk of exceeding the available resource pool or not being able to complete the items selected for the Sprint.
• Let us consider the estimation of the total effort (needed for the implementation of all the Product Backlog items):

  ○

  estimated in the traditional way as equal to (rounded to the nearest integer) $T={{\displaystyle \sum }}_{j=1}^{49}{T}_j=504$;

  ○

  estimated according to the new method as (also rounded to the nearest integer) as $\tilde{P}={{\displaystyle \sum }}_{j=1}^{49}{\tilde{P}}_j^{cons}=\left(397,514,736\right)$.

We can see that the traditional estimation returned a number characterized by a high possibility degree (${\mu }_P\left(T\right)=0.91$), but from the left hand wing of the membership function of $\tilde{P}.$ The 0.91-level (see Definition 1) of fuzzy number $\tilde{P}$, thus the set of all the values whose possibility degree is at least 0.91, is the interval [504, 716], which means that the same possibility degree is linked also to the value 716, which differs by more than 40% from the traditional estimate 504. A need for a substantial buffer in planning the Sprint on the basis of traditional estimation is evident. It has to be underlined that the traditional estimation process indicated neither the necessity of a buffer nor provided any suggestion as to its size.

8.1.4. Cancellation of the Project

As a result of business decisions (not related to the work progress in the project) the project was cancelled. Top management took this decision despite the financial expenditures incurred for the project. This decision was made on the 12th day of Sprint 0. Informal information obtained from the mid-level leadership of the organization indicated that the decision had been preceded by negotiations between the top management of organization X and that of customer Y. Unfortunately, they did not prevent the project breakdown.

It has to be underlined that cancellations of IT projects before their completion are not a rare phenomenon. The authors of [70] estimate that 5–15% of all IT projects are cancelled in the United States alone, and the total annual cost of cancelled IT projects may be about 75 billion dollars. In the literature authors quote different percentages of IT projects that have been cancelled: 9% [71], 11.5% [72]) or 19% [73].

8.1.5. Summary of Case Study nb 1

Because of the project cancelation, the estimated Product Backlog items were never accomplished. For this reason, the actual effort values are unknown and the accuracy of the estimation cannot be assessed. However, the case study proved that:

• The fuzzy approach brings to light the tacit knowledge and opinion of experts which in the traditional approach is revealed only partially and often in a distorted form (when for example an estimate is selected in the traditional approach which in the fuzzy approach turns off to be rather impossible and very different from the maximal possible values).
• The application of the proposed method in practice does not have to mean an additional effort for the experts. In the case study the experts worked as if only the traditional method was used. Uniquely the moderator additional task was to apply the respective formula from Section 7 and calculate the fuzzy estimates.
• The results, although not juxtaposed with actual values, intrigued the experts. They were surprised by the apparent defectiveness of their traditional estimates. If the necessary time had been available, they would have gladly discussed the fuzzy estimates—what is in fact a part of the proposed method (weights (5) can be changed by the experts).
• The idea of a buffer for the planned Sprint effort, which could be determined by means of the proposed method, was highly appreciated, as well as the possibility of $t$-levels application, which represent the estimates whose occurrence is characterized by the possibility equal to or exceeding $t.$ A maximal accepted uncertainty (risk) level 1-t can be selected and the values from unaccepted $t$-levels can be analysed, in order to prevent a too high uncertainty (risk) from occurring.

As the project used in the first case study was cancelled and no actual values were available, we decided (thanks to one of the Referees) to introduce an additional validation of the method, based on a completed R&D project, for which the actual task durations were known. Ii was not a Scrum based project, however, we tried to create Scrum similar conditions for the estimation process. The second case will be described in the next section.

8.2. Case study nb 2

8.2.1. Project Description

The project was implemented in a big university and financed by a governmental unit. It started in 2009 and took 1.5 years (the project duration was fixed and it could not be changed). Its budget equalled approximately 100,000 Euro. The project team was composed of 5 management researchers.

The objective of the project was to examine the existing costing system of a big university and to elaborate an improved system, which would deliver to all the university managers and decision makers the relevant information about the actual cost of all important cost objects, like faculties, departments, courses, students of different specialisations, projects, research workers, administration staff etc. The improved system was to be initially implemented in a selected division of the university.

The project was composed of four main tasks:

• Analysis of the organisational structure of the university in question. Analysis of the current cost structure. Identification of potential data sources.
• Elaboration of the system concept, definition of its basic elements and of cost flows. Initial validation of the concept.
• Analysis of costing systems existing in the market. Formulation of hardware requirements for the system. Formulation of recommendations and development plan for the university in terms of cost management.
• Implementation of the concept in EXCEL, selection of the university division to implement the system, analysis of the results, conclusions for future work.

The project was completed on time (no deadline postponing was possible) and, in spite of several problems, was assed positively by the financing institution. In the project documentation we can find the actual durations of the above tasks, entered into the final report in 2011.

8.2.2. Application of the Fuzzy Estimation Method

In 2019 six experienced management research workers who did not participate in the project were asked to estimate (in months) the duration of each of the above listed tasks. They knew the university and its situation in 2009. They were informed that the project duration was fixed (in this the situation resembled Scrum simulation, where the Sprint duration is fixed). They were asked to give four crisp estimates:

• An estimate they would enter in the application form for project funds (a crisp one);
• A fuzzy estimate, composed of three numbers: the optimistic, most possible and pessimistic duration;
• The consensus was reached through the application of arithmetical mean and rounding up or down to the closest integer or integer plus 0.5 value. In this way a crisp consensus $T_j$ (j = I, II, III, IV) and the fuzzy consensus $\left({\underset{\_}{P}}_j^{cons},{\widehat{P}}_j^{cons},{\overline{P}}_j^{cons}\right)$ (j = I, II, III, IV) were generated. The obtained numbers could be compared with the actual values from the final project report. The results are shown in

  Table 3. Results of the estimation process in the case study nb 2.

  j	${\displaystyle {\underset{\_}{\mathit{P}}}_{\mathit{j}}^{\mathit{c}\mathit{o}\mathit{n}\mathit{s}}}$	${\widehat{\mathit{P}}}_{\mathit{j}}^{\mathit{c}\mathit{o}\mathit{n}\mathit{s}}$	${\overline{\mathit{P}}}_{\mathit{j}}^{\mathit{c}\mathit{o}\mathit{n}\mathit{s}}$	${\mathit{T}}_{\mathit{j}}$	$\mathit{T}{\mathit{A}}_{\mathit{j}}$	Comment
  I	2.5	3	3.5	2.5	3	Fuzzy estimate closer to the actual value than the crisp estimate
  II	4	4.5	5	4	5	Fuzzy estimate closer to the actual value than the crisp estimate
  III	4	5	5,5	4.5	2	Crisp estimate closer to the actual value than the fuzzy estimate
  IV	5.5	6	7	5.5	7	Fuzzy estimate closer to the actual value than the crisp estimate

  , where $T{A}_j$ stands for the actual duration (all the durations are given in months).

It has to be underlined that for three of the four tasks the fuzzy estimate is closer to the actual value (in terms of Definition 6a) than the crisp estimate. Also, in case of the same three tasks the actual value is located in the middle or the right-hand part of the membership function of the corresponding triangular fuzzy number, which means that the fuzzy numbers would have allowed to be more aware of the risk of a relatively high task duration.

8.2.3. Results of Case Study nb 2

On the whole, the second case study indicates that fuzzy estimates give, in a number of cases, a better knowledge about the actual task duration than crisp estimates, and increase the ability of project manager to manage risk and uncertainty. The only task in the considered case for which the fuzzy estimation does not bring any visible advantage (but it does not bring any disadvantage either) is task III, which was completed in a much shorter time with respect to the opinion of the estimators, thus the risk information contained in the fuzzy estimate was not needed. But the overall assessment is favourable to the fuzzy estimation method as a tool to make use of expert opinions in project risk management, especially as far as the risk of exceeding deadlines is concerned.

9. Summary and Discussion

This present paper is an attempt to address the issue of effort estimation it IT projects following the Scrum framework (but also in projects generally). An expert method was proposed, which can be used in order to estimate the effort needed to accomplish Product Backlog items. The method has two features listed below. They distinguish it from the existing estimation methods which can be utilised for the Product Backlog items in Scrum:

• Fuzzy numbers are used as estimates, contrary to the existing methods, where crisp numbers are the only option. Fuzzy numbers allow the experts to express formally the whole knowledge and intuition they have about a Product Backlog item and the effort needed to produce it. As Product Backlog items are most often to a certain degree innovative, it seems natural that their estimation must, at least in numerous cases, encompass also the information about the inherent uncertainty. Fuzzy numbers introduce this possibility into the estimation process;
• Although, like in most existing estimation method, also the proposed method leaves to the experts some time for free discussion and interaction, contrary to most of the methods it proposes a fully defined solution for the case when, after a pre-set time, no consensus has been reached.

The method makes it possible to assess the uncertainty degree and risk (according to their different definitions) linked to the estimates, in order to provide for a buffer protecting the current Sprint and the whole project against serious underestimation effects. Also, chances linked to possible overestimation can be analysed.

The method was only tentatively validated using two single case studies - an international IT project and an R&D project—which were conducted using symmetry principles [27]. The first case study project, however, was closed prematurely, during the first Sprint, thus the data available does not encompass actual values and any accuracy assessment of the proposed method is impossible. In most researches on project estimation the same problem is encountered: incomplete, inconsistent, uncertain and unclear data [74]. Thus, further case studies are needed in order to verify the usefulness of the method. The second case study used here, an R&D project, allowed to juxtapose the fuzzy estimations with the actual results, but it did not allow either a complete validation of our proposal.

Further case studies will certainly point out to necessary modifications. The modifications may change the way of comparing and aggregating fuzzy numbers, as well as the form itself of fuzzy numbers used. Also, the description of the process of expert opinion translation into a fuzzy number has to be enhanced, using the vast available literature on the subject. The method might also be completed with new elements, like buffers, which are widely used in project planning (e.g., [75]), but not in Scrum-based project estimation yet. Also, it should be compared with other estimation methods used for projects.

On the whole, being aware of the incompleteness of the case studies used here, it has to be stated that they have firmly proven the following statement: experts in projects need a tool to express uncertainty and/or lack of knowledge in their estimates. During the estimation process they have the uncertainty in mind, but being constrained to giving crisp numbers, they choose them rather randomly (they even do not always choose crisp numbers corresponding to the highest occurrence possibility) and their expertise, experience and intuition are lost. Whether it is fuzzy numbers or another tool, estimators in projects should be able to take uncertainty and/or lack of knowledge into account.

That is why we can claim that initial results are promising. The method was applied in two real world projects with two groups of experts and they assessed the estimation process positively. The estimates obtained by means of the method were juxtaposed with the results of a traditional estimation and it was clear to all the participants of the experiments that the fuzzy method brought to light tacit knowledge about the estimated elements and significantly contributed to a better understanding of the uncertainty linked to the estimated items.

It has to be emphasized, that the fuzzy approach may be potentially used not only in the process of effort estimation of Product Backlog items, but also in other stages of Scrum and in other than Scrum related projects. However, this requires further research too.