Goal Recognition Control under Network Interdiction Using a Privacy Information Metric

Abstract

Goal recognition (GR) is a method of inferring the goals of other agents, which enables humans or AI agents to proactively make response plans. Goal recognition design (GRD) has been proposed to deliberately redesign the underlying environment to accelerate goal recognition. Along with the GR and GRD problems, in this paper, we start by introducing the goal recognition control (GRC) problem under network interdiction, which focuses on controlling the goal recognition process. When the observer attempts to facilitate the explainability of the actor’s behavior and accelerate goal recognition by reducing the uncertainty, the actor wants to minimize the privacy information leakage by manipulating the asymmetric information and delay the goal recognition process. Then, the GRC under network interdiction is formulated as one static Stackelberg game, where the observer obtains asymmetric information about the actor’s intended goal and proactively interdicts the edges of the network with a bounded resource. The privacy leakage of the actor’s actions about the real goals is quantified by a min-entropy information metric and this privacy information metric is associated with the goal uncertainty. Next in importance, we define the privacy information metric based GRC under network interdiction (InfoGRC) and the information metric based GRC under threshold network interdiction (InfoGRCT). After dual reformulating, the InfoGRC and InfoGRCT as bi-level mixed-integer programming problems, one Benders decomposition-based approach is adopted to optimize the observer’s optimal interdiction resource allocation and the actor’s cost-optimal path-planning. Finally, some experimental evaluations are conducted to demonstrate the effectiveness of the InfoGRC and InfoGRCT models in the task of controlling the goal recognition process.

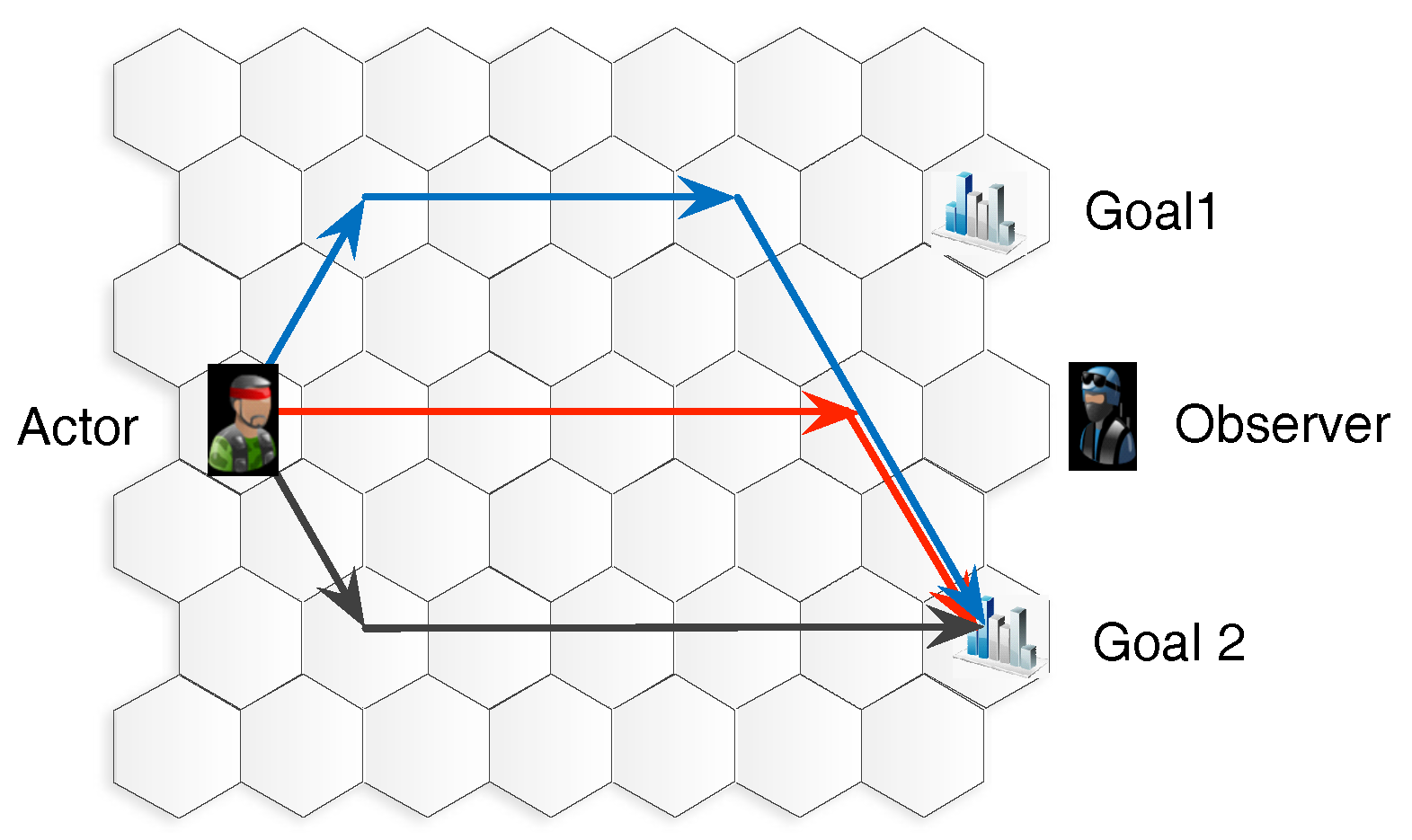
1. Introduction

Goal recognition (GR), also called intention recognition, or more generally plan recognition, is the task of recognizing other agents’ goals by analyzing the actions and/or the state (environment) changes caused by the actions [1], which has drawn the interest of researchers in the field of artificial intelligence and psychology for recent decades. Goal reasoning as one variant is the process in which intelligent agents continually reason about the goals they are pursuing [2]. Goal recognition design has been proposed to redesign the environment to facilitate goal recognition offline [3]. As one sub-problem of PAIR (plan activity and intent recognition) [4], goal recognition has been successfully applied to various applications, such as human–machine interaction (HMI) in social settings (home, offices, and hospitals) [5], agent modeling [6], critical infrastructure protection (CIP) [7], and some military applications about reasoning the goals of the terrorists or opponents [2,8]. Unlike manipulating asymmetric information in CIP, goal recognition is widely applied to “human–AI planning (HAIP)” [9], and “explainable planning (XAIP)” [10], where the focus is symmetric information understanding and explicit information sharing respectively. But, in a parallel thread, new problems arise, such as the goals uncertainty in a fully observable and deterministic environment, the hard environment redesign can be replaced by soft interdiction with additional cost to actions. One simplified CIP scenario is illustrated in Figure 1, first mentioned in [7], in which the defender’ objective is to protect critical infrastructure against the attacker whose goal (target) is unknown. The urban environment contains military and government facilities, physical (natural or artificial) obstacles and other environmental factors, where the ability of agents to perform certain actions is restricted. The actor is equipped with some explosive weapons, and these weapons enable the actor to carry out bomb attacks on vulnerable buildings. Owing to the different situation awareness of the urban environment, the defender has asymmetric information about the attacker’s real goals [11], but bridge interdiction still could be performed by the defender to facilitate the goal recognition process.

Explainability, as one key AI enabling technology, has been used to develop robust AI applications and systems [12]. Explainability and obfuscation of the behavior are a pair of opposite requirements, since sharing and hiding the goals depict the opposite choice of the agents. Sharing goals drives the actor’s behavior to be explainable (interpretable) with understandability [13], explicability [14], legibility [15], predictability [16], and transparency [17], while hiding goals drives the actor’s behavior to be uninterpretable with obfuscation, deception, privacy, and security [18]. In the cooperative setting, the explainability and interpretability of behavior remain significantly challenging in developing human-aware AI agents [18] and human-agent systems [19]. Goal signaling assists behavior explanation in human-robot teaming [20]. In order to share explainable behavior, the human-aware agent should not only consider his own model, but also the observer model and the differences thereof [5]. In the adversarial setting, such as military mission planning and counter-planning [21,22], keeping the goal obfuscated is the most important. Many recent pieces of work explore deception [23] and privacy [24]. For example, deception was investigated in two classes, simulation and dissimulation [23], privacy was investigated in five classes, agent privacy, model privacy, decision privacy, topology privacy, and constraint privacy [25,26]. In cooperative and adversarial environment, a goal-driven intelligent agent would manipulate the goals in the goal-pursuing process, such as sharing or revealing the goals among teammates and meanwhile hide the goals against adversaries. The recursive reasoning process shows the cruel twist of situation awareness between agents, who continually react to their evolving situation, possibly abandoning current goals and switching to other goals [27]. Many unified frameworks have been proposed for the cooperative and adversarial environment, such as information bottleneck based intention reveal and hide [28,29,30], cooperative-competitive processes (CCP)-based multi-agent decision-making [31]. In fact, many pieces of research revolved around the communication of goals implicitly using behavioral cues. The agents’ action could be treated as special cases of implicit signaling behavior [18,20]. The highly interwoven decision-making process of the opposing players situated in these settings motivates the need for a comprehensive strategic analysis, which would help the observer to recognize the agents’ real goals and identify the optimal interdiction strategies [32].

In different game models, the players are called differently. To be different from the pairing roles, such as attacker–defender, leader–follower, searcher–evader, and interdictor–intruder, in this paper, we use actor–observer as a more neutral pairing role to depict the interaction between the two players. When the actor performs an action privately in adversarial environment, the privacy information leakage from the actor’s behavior is closely related to the goal uncertainty. Similar to the behavioral probability weighting technique, which has been used in interdependent security game [33], the actions or states of the agents can be measured by information metrics. In this paper, we quantify the privacy information leakage of actions or states with a min-entropy information metric, which is tightly associated with the goal uncertainty and can be used to aid in recognizing the goals. Aiming at assisting the observer to control the goal recognition process, in this paper, we follow the multi-model models, such as share (reveal, signal) or hide information [28,29], delay predictability [34] or assist recognition [3], reduce or improve uncertainty [35], and define the goal recognition control (GRC) problem under network interdiction with a privacy information metric as InfoGRC. Here, the observer will reduce the goal uncertainty value through limiting the action space that an actor can perform under network interdiction, while the actor manages to delay the goal recognition process through adding the goal uncertainty value by performing abnormal actions.

In summary, the main contributions of this paper are as follows:

• We start by introducing one game-theoretic decision-making framework, and then present the generative inverse path-planning and network interdiction for goal recognition, and some information metrics for the signaling behavior.
• We adopt a min-entropy based privacy information metric to quantify the privacy information leakage of the actions and states about the goal.
• We define the InfoGRC and InfoGRCT using the privacy information metric, and provide a more compact solution method for the observer to control the goal uncertainty by incorporating the information metric as additional path cost.
• We conduct some experimental evaluations to demonstrate the effectiveness of the InfoGRC and InfoGRCT model in controlling the goal recognition process under network interdiction.

The rest of the paper is organized as follows: the background and related work are introduced in Section 2. In Section 3, the min-entropy based privacy information metric is presented, the InfoGRC and InfoGRCT problems are defined, and a Benders decomposition based solution method is introduced. Section 4 presents experimental results, evaluation, and analysis. Finally, conclusion and future work are summarized in Section 5.

2. Background and Related Work

In the defense and security domain, critical facility protection, privacy security, and convoy protection are in need of goal recognition. In such situations, the observer (decision-maker) is threatened by the actor with some conflicting goals and need one enabler to read the actor’s mind. Here, we first propose one game-theoretic decision-making framework for goal recognition under network interdiction, the goal recognition process can, therefore, be divided into two main subtasks, namely generative inverse planning, where the observer attempts to generate plans for the actor, and goal recognition for proactive response, where the observer has to identify the actor’s goal and make proactively response plans. As shown in Figure 2, the observer will get the game situation from the generative courses of action (COA) of the hostile opponents and friendly teammates, then attempts to recognize the actor’s goals under network interdiction. In fact, as one important carrier, the network can be used to represent “critical infrastructure network” (road network, railway network, power network, and cyber network), “task plans” (HTN, attack graph, and Petri Net). In this paper, we simply use the road network for path-planning and network interdiction.

2.1. Path-Planing and Network Interdiction

2.1.1. Path-Planning

Path-planning is a sub-problem of general task planning, which aims at finding a path through the map of a domain. One typical path planning scenario on the hexagonal grids is illustrated in Figure 3. Path-planning for an actor on the road network ( discrete grid or connected graph representation) finds a path from the start location to the final goals. The path-planning problem can be defined as follow:

Definition 1 (PPD).

A path planning domain is a tuple:

$$\mathcal{D}=〈\mathcal{N},\mathcal{E},\mathrm{c}〉$$

(1)

• $\mathcal{N}$ is a non-empty set of location nodes;
• $\mathcal{E}\subseteq \mathcal{N}\times \mathcal{N}$ is a set of actions related edges between nodes;
• $\mathrm{c}:\mathcal{E}\mapsto R_0^{+}$ returns the cost of traversing each edge.

Definition 2 (GDPP).

A goal-driven path planning problem is a tuple:

$${\mathcal{P}}_{GP}=〈\mathcal{D},s,\mathcal{G},{\mathcal{P}}_{po},\mathsf{\Omega },\mathcal{O}〉$$

(2)

• $\mathcal{D}$ is the path planning domain;
• $s\in \mathcal{N}$ is the start location;
• $\mathcal{G}=\{g_r,g_0,g_1,\dots \}$ is a set of candidate goals, where $g_r$ is the real goal;
• ${\mathcal{P}}_{po}\left(\mathcal{G}\right|{\mathcal{O}}_n)$ denotes the posterior probability of a goal given a sequence of observations (or last state in that sequence), which can be the model of the observer;
• $\mathsf{\Omega }=\left\{o_i|i=1,\cdots ,m\right\}$ is the set of m observations that can be emitted as results of the actions and the states;
• $\mathcal{O}:(\mathcal{N}\times \mathcal{E})\to \mathsf{\Omega }$ is a many-to-one observation function which maps the action taken and the next state reached to an observation in Ω.

2.1.2. Network Interdiction

In the defense and security domain, interdiction refers to actions that serve to block or otherwise inhibit an adversary’s operations [36]. Network interdiction is usually involved with two players, and it is a special class of network flow games [37], which has been widely studied in the fields of combinatorial optimization, artificial intelligence, and operations research. The interdiction and fortification between the two players can be described as one Stackelberg game model [38]. Generally, two basic models of network interdiction are considered: maximum-flow network interdiction (MXFI), shortest path network interdiction (SPNI). In this paper, we focus on maximizing the shortest path (MXSP), one variant of SPNI, where the actor attempts to travel along the shortest path through a road network from one start (origin) to one goal (destination), while the observer tries to interdict the edges to maximize the length of this shortest path. When the actor privately approaches a goal, the probability that the actor’s goal is correctly recognized by the observer would be inversely proportional to the path cost or time cost that the actor is willing to take. So, we formulate this road network interdiction problem with one Stackelberg game model, in which observer aims at maximizing the expectation of “start-goal” path cost in a directed path network by interdicting nodes (states) or edges (actions) under bounded resource. In fact, the node interdiction problem can be transformed into one edge interdiction problem [39,40]. In such environment, the actor’s past actions or states are increasingly difficult to conceal, the observer would proactively take some interdictions to accelerate the goal recognition process.

We consider that an actor executes a cost-critical task to travel from a start location S to a goal location G in minimum path cost, meanwhile, an observer seeks to interdict the actor path by choosing states (nodes) or actions (edges) along from S to G. The set of nodes between S and G define a secure road network represented by a directed graph $\mathcal{G}(\mathcal{N},\mathcal{E})$, as shown in Figure 4, where the set $\mathcal{N}$ is the set of $\left|\mathcal{N}\right|$ nodes between S and G, and the set $\mathcal{E}$ is the set of connections between nodes.

Each path will go through some nodes which are shared among different paths. An extremely patient actor without task but with a large time budget might start along a path that traverses the entire state space (e.g., a Hamiltonian path over the nodes) and stop when the goal is reached, so as to make the past actions reveal essentially nothing about the goal and make the observer’s recognition difficult [34]. But one goal-driven actor would lie somewhere in the middle, by combining a cost-optimal path with some wasteful actions of goal obfuscation. In addition, owing to the bounded resources for interdiction, the observer is unable to separate the goal and the start node by interdicting the minimum-cut set. The basic mathematical formulation of MXSP is defined as follows:

$$[MXSP-P]z^{*}=\underset{\mathbf{x}\in X}{max}\underset{\mathrm{y}}{min}\sum _{a\in \mathcal{E}}\left(c\left(a\right)+x\left(a\right)d\left(a\right)\right)y\left(a\right)$$

(3)

$$s.t.\sum _{a\in \mathrm{Out}\left(\mathrm{i}\right)}y\left(a\right)-\sum _{a\in \mathrm{In}\left(\mathrm{i}\right)}y\left(a\right)=\left\{\begin{array}{cc}1& \mathrm{for}i=s\\ 0& \forall i\in \mathcal{N}\setminus \left\{s,g\right\}\\ -1& \mathrm{for}i=t\end{array}\right.$$

(4)

where $X=\left\{\mathbf{x}\in {\{0,1\}}^{\left|\mathcal{E}\right|}|{\mathbf{r}}^T\mathbf{x}\le R\right\}$ with bounded resource R, $x\left(a\right),y\left(a\right)\in \{0,1\}$ indicate the observer’s interdiction resource allocation and the actor’s traverse respectively.

• ${\mathbf{x}}^{*}$ denotes an optimal interdiction solution for the observer.
• Flow-balance constraints of variables $\mathrm{y}$, route one unit of flow from s to g, the inner minimum is a standard shortest path model with edge cost $c\left(a\right)+\alpha x\left(a\right)d\left(a\right)$.
• $c\left(a\right)$ is the nominal cost of edge a and $c\left(a\right)+d\left(a\right)$ is the interdicted cost; $d\left(a\right)$ represents the additional path cost, if sufficiently large, represents complete destruction of edge a.
• $r\left(a\right)$ is a small positive integer, representing how many resources are required to interdict edge a.
• R is the total available resource, the observer has $C_R^{\left|x\right|}$ possible interdiction combinations, which will grow exponentially with R.
• y denotes a traverse path of the actor.

If the outer variable $\mathbf{x}$ is fixed, we can take the inner minimization using Karush–Kuhn–Tucker (KKT) conditions, then the dual formulation that releases $\mathbf{y}$ is defined as follows:

$$[MXSP-D]z^{*}=\underset{x\in X,\overrightarrow{\pi }}{max}\pi \left(t\right)-\pi \left(s\right)$$

(5)

$$s.t.\pi \left(j\right)-\pi \left(i\right)-d\left(a\right)x\left(a\right)\le c\left(a\right),\forall a=(i,j)\in \mathcal{E}$$

(6)

$$\pi \left(s\right)=0.$$

(7)

where we may interpret $\pi \left(i\right)$ as the post-interdiction shortest-path cost from s to i, $\pi \left(s\right)=0$.

2.2. Goal Recognition

The ability to recognize the goals of others enables humans to reason about what they are doing, why they are doing it, and what they will do next [4]. Goal recognition problems can be divided into three kinds according to the role of the actor whose intention is being inferred. In keyhole recognition [41], the actor is unaware of being observed and recognized as if the actor is looking through a keyhole. In intended recognition [42], the actor wants to convey the goal to be understood. In adversarial recognition [7], the actor is actively hostile to the observations of the actions and the inference of the goals, and would hide the intention and attempt to thwart the recognition process by deception and concealment. Different kinds of intention recognition bring different challenges. More generally, adversarial plan recognition has been applied to the recognition of strategies and tactics of opponents, in which adversarial reasoning is needed to understand the minds of the opponents. Generic methods for plan recognition are based on plan-library [43], inverse-planning [44], and learning [45].

2.2.1. Probabilistic Goal Recognition

Among the approaches proposed for goal recognition, the probabilistic goal recognition model is highly regarded, and it is defined as follows:

Definition 3 (PGR).

A probabilistic goal recognition problem for path-planning is a tuple:

$${\mathcal{P}}_{GR}=\langle \mathcal{D},\mathcal{G},s,O,{\mathcal{P}}_{pr}\rangle$$

(8)

• $\mathcal{D}=\langle \mathcal{N},\mathcal{E},\mathrm{c}\rangle$ is a path planning domain;
• $\mathcal{G}\subseteq \mathcal{N}$ is the set of candidate goals locations;
• $s\in \mathcal{N}$ is the start location;
• $\mathcal{O}=o_1,\dots ,o_k$, where $k\ge 0$ and $o_i\in \mathcal{N}$ for all $i\in \{1,\dots ,k\}$, is a sequence of observation;
• ${\mathcal{P}}_{pr}$ represents the prior probabilities of the goals.

The solution to a probabilistic goal recognition problem is a posterior probability distribution $P_{po}\left(\mathcal{G}\right|\mathcal{O})$ over the set of possible goals. Given the start location and the sequence of observations, the posterior goal distribution will be computed by the Bayesian rule. One cost difference-based [46] Boltzmann distribution of the posterior probability is defined as follow:

$${\mathcal{P}}_{po}\left(\mathcal{G}\right|\mathcal{O})=\alpha \mathcal{P}\left(\mathcal{O}\right|\mathcal{G}){\mathcal{P}}_{pr}\left(\mathcal{G}\right)=\alpha \frac{e^{-\lambda \delta }}{1+e^{-\lambda \delta }}$$

(9)

$$\delta ={\mathcal{C}}_{diff}(s,g,{\mathcal{O}}_n)=optc({\mathcal{O}}_n,g)-optc(s,g),$$

(10)

where $\alpha$ is a normalizing constant across all goals, $\lambda$ is a positive constant which captures a soft rationality assumption, s is the start, g is a goal, ${\mathcal{O}}_n$ is the most recently observed of the actor.

This cost difference-based recognition method provides one single-observation recognition paradigm, since the start and goal-related cost difference can be computed offline, we only need to compute the current location-related cost difference.

2.2.2. Goal Recognition Design

Goal recognition design focuses on one controllable environment by modifying the configuration of the domain [43]. As for the observer, redesigning the environment will improve explainability of the actor’s behavior. Many metrics have been proposed to redesign the environment, such as worst case distinctiveness ($wcd$) [3], expected-case distinctiveness (ecd) [47], all-goals $wcd$ ($wc{d}_{\left(ag\right)}$) [47], and relative goal uncertainty (rgu) [35]. As for more general plan recognition design problem, the worst-case distinctiveness for plans (wcpd) measures the number of observations needed to unambiguously identify the agent’s plan [43]. The $wcd$ and goal recognition design (GRD) problem are defined as follow:

Definition 4 (wcd).

Let ${\mathsf{\Pi }}_D=\left\{\pi \right|\pi \mathit{is}a\mathit{non}-\mathit{distinctive}\mathit{path}\mathit{of}D)$ and let $\left|\pi \right|$ denote the length of a path π, then, worst case distinctiveness ($wcd$) of a model $\mathcal{D}$, denoted by $wcd\left(\mathcal{D}\right)$, is:

$$\mathit{wcd}\left(\mathcal{D}\right)=\underset{\pi \in {\mathsf{\Pi }}_{\mathcal{D}}}{max}\left|\pi \right|$$

(11)

Definition 5 (GRD).

A goal recognition design problem is defined as a tuple:

$$\mathcal{D}=\langle {\mathcal{P}}_{\mathcal{D}},{\mathcal{G}}_{\mathcal{D}}\rangle$$

(12)

• ${\mathcal{P}}_{\mathcal{D}}$ is a planning domain formulated in STRIPS;
• ${\mathcal{G}}_{\mathcal{D}}$ is a set of possible goal;
• The output is ${\mathcal{P}}_{\mathcal{D}}^{\prime }$ such that $wcp\left({\mathcal{P}}_{\mathcal{D}}^{\prime }\right)\le wcp\left({{\mathcal{P}}_{\mathcal{D}}}^{″}\right)$,

where all actions have the same cost, the objective is to find a subset of actions and remove them from the action space, then the $wcd$ of the resulting problem is minimized.

These metrics for GRD are mainly formulated to optimize the maximum number of observations, which are required to unambiguously infer the goal or plan of the agent [43]. Such as the $wcd$ of a domain $\mathcal{D}$ is an upper bound of the action number that the actor can perform in a stable model, before selecting a distinctive path to reveal the goal [3]. Figure 5 portrays two possible solutions for placing barriers or blocks to interdict the passage of the actor.

In addition, the GRD problem can be reformulated into an optimization problem with some constraints: the cost of the cost-optimal plan to achieve each goal $g\in \mathcal{G}$ is the same before and after removing the subset of actions [48]. So, the objective is to find a subset of action $\delta \mathcal{E}\subset \mathcal{E}$, if they are removed from the set of actions $\mathcal{E}$, then the $wcd$ of the resulting problem is minimized.

$$\delta \mathcal{E}={argmin}_{\delta \mathcal{E}\subset \mathcal{E}}\mathit{wcd}\left(P\right)$$

(13)

$$s.t\mathcal{C}\left({\pi }_g^{*}\right)=\mathcal{C}\left({\widehat{\pi }}_g^{*}\right)\forall g\in \mathcal{G}$$

(14)

where $P=\langle \mathcal{D},\mathcal{G}\rangle$ is the problem with the resulting domain $\widehat{\mathcal{D}}=〈\mathcal{N},s_0,\mathcal{E}\setminus \delta \mathcal{E},f,\mathcal{C}〉$ after removing actions $\delta \mathcal{E}$, ${\pi }_g^{*}$ is a cost-optimal plan to achieve goal g in the original problem P, and ${\widehat{\pi }}_g^{*}$ is a cost-minimal plan to achieve goal g in problem $\widehat{P}$.

As for goal uncertainty, last deceptive point (LDP)-based deceptive path planning [23] and equidistant states based goal obfuscated plan [49] present two selective solutions. But, there are still a few standard assumptions in cryptography and multi-party computation. But what if the adversary knows the algorithms, which is realistic and complied with Kerckhoffs’ principle used in cryptography [50], these closed formulated solutions of the deceptive path-planning will not incorporate deception. Goal recognition design aims at facilitating the recognition process. In order to reduce the $wcd$, three types of modification, i.e., sensor refinement (SR), action removal (AR), and action conditioning (AC), are widely used [51]. Owing to the strategic interaction between the actor and the observer in the GR and GRD problems, the solutions with cost-minimal or $wcd$ do not reflect the strategic behaviors [52]. We are more interested in adopting soft measures such as additional action cost by interdiction so as to control the goal uncertainty.

2.2.3. Trend and Dual-Use

Three paradigms are widely used in recent research on goal recognition, such as the decision-theoretic paradigm based equi-reward utility maximizing design (ER-UMD) model, the environment is controlled by applying a sequence of modifications to maximize the agent’s utility [53]. The game-theoretic paradigm-based goal recognition and design models were used to reason the opponents’ minds, such as the adversarial intention recognition as inverse planning model, one generative stochastic game model was used for threat assessment [7]. As for the learning-based paradigm, inverse reinforcement learning [45], maximum entropy deep reinforcement learning [54], and information regularization-based deep reinforcement learning [30] are usually employed to explore the stochastic environment.

Network flow interdiction [55], plan interdiction games [56] and MDP interdiction [57] show one more potential research thread about interdiction. Network flow based game models such as network control under node disruptions and network routing under link disruptions [37] show one parallel thread of research about the goal and plan recognition.

From the perspective of explainability, goal obfuscation is the inverse problem of the goal legibility, while plan obfuscation is the inverse problem of the goal predictability [18]. Considering the duality property, road network interdiction is the inverse problem of network fortification [58].

2.3. Behavioral Information Metrics

Several information metrics for signaling behavior have been proposed in the literature. Such as the deception metric for deceptive path-planning, which involves finding a path such that the probability of an observer identifying the final destination is minimized [23]. As in the cost-optimal path-planning setting, simulation (simply deception) or dissimulation(concealment) can be employed to thwart the goal recognition process.

Simulation bound agents deliberately choose misleading actions to confuse the goal recognition process, i.e., there exists $g\in \mathcal{G}\setminus \left\{g_r\right\}$ s.t. the recognition probability $P\left(g_r|s_j\right)<P\left(g|s_j\right)$, where $s_j$ is the j-th node, $g_r$ is the real goal.

Definition 6 (S-SD).

The simulation based state information metric is defined as follows:

$${\mathcal{I}}_{S-SD}\left(s_j\right)=\underset{g_i\in G\setminus \left\{g_r\right\}}{max}P\left(g_i|s_j\right)-P\left(g_r|s_j\right).$$

(15)

Definition 7 (A-SD).

The simulation based action information metric is defined as follows:

$${\mathcal{I}}_{A-SD}\left(a_i\right)=1-\lambda {\mathcal{I}}_{S-SD}\left(s_j\right).$$

(16)

Dissimulation-bound agents act covertly or intentionally select actions that are hard to detect. That is, there exists $g\in \mathcal{G}\setminus \left\{g_r\right\}$ s.t. the recognition probability $P\left(g_r|s_j\right)\le P\left(g|s_j\right)$, where $s_j$ is the j-th node, $g_r$ is the real goal.

Definition 8 (S-DD).

The dissimulation-based state information metric is defined as follows:

$${\mathcal{I}}_{S-DD}\left(s_j\right)=-\kappa \sum _{g_i\in \mathcal{G}}P\left(g_i|s_j\right)\times log\left(P\left(g_i|s_j\right)\right)(\kappa ={log}_2\left|\mathcal{G}\right|)$$

(17)

Definition 9 (A-DD)

The dissimulation-based action information metric is defined as follows:

$${\mathcal{I}}_{A-DD}\left(a_i\right)=1-\lambda {\mathcal{I}}_{S-DD}\left(s_j\right)$$

(18)

Also, in some game-theoretic approaches of learning-based goal recognition frameworks, such as in [7], belief space and Kullback–Leibler (KL) divergence $D_{KL}$ have been adopted to measure the deception of strategy. Besides, in the reinforcement learning domain, the conditional mutual information between goal and action given state, ${\mathcal{I}}_{action}\left[\pi \right]:=\mathcal{I}(\mathcal{A};\mathcal{G}|\mathcal{S})$ was defined as the action information metric, and the mutual information between state and goal, ${\mathcal{I}}_{state}\left[\pi \right]:=\mathcal{I}(\mathcal{S};\mathcal{G})$ was defined as the state information metric [29]. Although these metrics have been defined for goal-related actions and states, the applicable scenarios and environment are diverse, we may need some neutral metrics if the actor knows the observer’s algorithms or deliberately reveals the goal.

3. Goal Recognition Control

In this section, we will define the GRC problem in the context of defense and security with the road network to connect start locations and goals. Different from the GRD problem, we employ more applicable and soft measure, network interdiction under bounded resource, to control the goal recognition process. We propose to model the GRC problem under network interdiction as one Stackelberg game, where the observer owns asymmetric information about the actor’s intended goal, and could proactively allocate security resources (such as road barrier, patrolling force) to protect goals against the actor.

3.1. Privacy Information Metrics

In the fully observable and deterministic environment with multiple goals, the observer may not be able to catch the real goal, since the actor’s actions and states contain goal uncertainty. Given the possible goals and current observations, the posterior probability distribution over the goals reflects the goal uncertainty that the actor will encounter after selecting an action and reaching the next state. This enlightens us to measure the goal uncertainty associated with the conveyed information of the actions and states, in which the leaked privacy information can be quantified as the difference between the initial uncertainty and the remaining uncertainty. In this paper, we consider the actions (the adjacent edges between the nodes in the road network) as quantitative information flow [59], the leakage of the privacy information is based on the uncertainty of the observer about the input. We propose to use the min-entropy (an instance of Rényi entropy [60]) as the privacy information leakage metric. How much information about H can be deduced by the observer who obtains the output L is computed as follows:

$$InformationLeakage=Initialuncertainty-Remaininguncertainty$$

(19)

• initial uncertainty: $H_{\infty }\left(H\right)=-logV\left(H\right)$
• remaining uncertainty: $H_{\infty }\left(H\right|L)=-logV\left(H\right|L)$.
• information leakage $=H_{\infty }\left(H\right)-H_{\infty }\left(H\right|L)$

where $V\left(\mathrm{x}\right)={max}_{x\in \mathcal{X}}p(\mathrm{X}=x)$.

This privacy leakage metric represents the rate of information transmission, which has been widely used in quantifying the privacy leakage in the privacy-preserving planning domain [28]. In this section, we will define the state and action privacy information metrics to control the goal recognition process. Under the requirement of privacy-preserving, the actor may deliberately choose misleading actions to obfuscate the goal, i.e., if there exists $g\in \mathcal{G}\setminus \left\{g_r\right\}$ s.t. the recognition probability $P\left(g_r|s_j\right)<P\left(g|s_j\right)$, where $s_j$ is the j-th node, $g_r$ is the real goal. So, we define the metric of action at each state as follows:

Definition 10 (S-PI).

The privacy information metric of the state is defined as follows:

$${\mathcal{I}}_{S-PI}\left(s_j\right)=H(\underset{g_i\in G\setminus \left\{g_r\right\}}{max}P\left(g_i|s_j\right)-P\left(g_r|s_j\right))=-log(\underset{g_i\in G\setminus \left\{g_r\right\}}{max}P\left(g_i|s_j\right)-P\left(g_r|s_j\right))$$

(20)

Definition 11 (A-PI)

The privacy information metric of action is defined as follows:

$${\mathcal{I}}_{A-PI}\left(a_i\right)=\frac{{\sum }_{a_j\in {\mathcal{E}}^{\prime }\left(s\right)}{I}_{S-PI}\left(s\right)}{\left|{\mathcal{E}}^{\prime }\left(s\right)\right|}$$

(21)

where $a_i\in \mathcal{E}\left(s\right)$, $a_j\in {\mathcal{E}}^{\prime }\left(s\right)$, and ${\mathcal{E}}^{\prime }\left(s\right)=\mathcal{E}\left(s\right)\setminus a_i$.

The metric ${\mathcal{I}}_{A-PI}\left(a_i\right)$ reflects the goal uncertainty associated with the action taken. The higher the privacy information metric is, more uncertainty the goal will be, which means the action taken by the actor gives less privacy information to the observer, and this will accelerate the goal recognition process. As shown in Figure 6, we compute the ${\mathcal{I}}_{A-PI}\left(a_i\right)$ of actions represented by arrow edges between nodes. As for the path-planning task, goal 1 and goal 2 are the actor’s two goals from the start node 2, we use $c^{\prime }\left(a\right)=c\left(a\right)+{\mathcal{I}}_{A-PI}\left(a\right)$ and $c\left(a\right)=1$ to represent the additional path cost, which will be employed by the observer to control the goal recognition process. Generally, the actor would choose $path=〈2,5,8,7〉$ for the goal 1 and $path=〈2,5,8,9〉$ for goal 2. After the additional path cost with ${\mathcal{I}}_{A-PI}\left(a\right)$, the actor will choose $path=〈2,1,4,7〉$ for the goal 1 and $path=〈2,3,6,9〉$ for goal 2.

3.2. InfoGRC and InfoGRCT

The GRC problem is a special case of static Stackelberg game. The observer attempts to facilitate the explainability of the actor’s behavior and accelerate goal recognition by reducing the goal uncertainty under network interdiction, while the actor wants to delay the goal recognition process. Without requiring the cost-optimal paths to the goals to be the same before and after redesign the environment, as investigated in GRD, we will attempt to change the goal uncertainty by proactively allocating interdiction resource to add the action cost. Adding the information metric $\mathcal{I}$ proportionally as additional cost to the original action cost: $c^{\prime }\left(a\right)=c\left(a\right)+{\mathcal{I}}_A\left(a\right)$, the GRC problem under network interdiction could be transformed into the problem of maximizing the expectation of “s-g” path cost. Here, we use optimization techniques to reformulate the GRC problems as mathematical programming problems. Some notations are shown in

Table 1. Notations for the information metric based goal recognition control (GRC) under network interdiction (InfoGRC) and information metric based GRC under threshold network interdiction (InfoGRCT) problem.

Parameters	Meaning
Sets and indices
$\mathcal{G}=(\mathcal{N},\mathcal{E})$	Road graph network with nodes $\mathcal{N}$ and edges $\mathcal{E}$
$i\in \mathcal{N}$	Node i in $\mathcal{G}$
$a=(i,j)\in \mathcal{E}$	Edge $(i,j)$ in $\mathcal{G}$
$s\in \mathcal{N}$	Start node s
$g\in \mathcal{N}$	Goal node g
$\mathrm{In}\left(\mathrm{i}\right)/\mathrm{Out}\left(\mathrm{i}\right)$	Edges set directed into or out of node i
Data
$0\le c\left(a\right)<\infty$	Cost of edge a, vector form $\mathbf{c}$
$0<d\left(a\right)<\infty$	Interdiction increment if edge a is interdicted, vector form $\mathbf{d}$
${\mathcal{I}}_A\left(a\right)$	The privacy information metric of action a
$r\left(a\right)>0$	Resource required to interdict edge a, vector form $\mathbf{r}$
R	Total amount of interdiction resource available
$\tilde{\theta }>0$	Threshold of the shortest path
$\overline{\theta }>0$	Upper bound with full interdiction
$\underline{\theta }>0$	Lower bound without interdiction
Decision Variables
$x\left(a\right)$	Observer’s interdiction resource allocation, $x\left(a\right)=1$ if edge a is interdicted
$y\left(a\right)$	Actor’s traveling edge, $y\left(a\right)=1$ if edge a is traveled by the actor

.

3.2.1. Accelerate and Delay

In order to formulate the accelerate model of the goal recognition process for the observer and the delay model of the goal recognition process for the actor, we use the network flow model to define these situations as follows:

$$\left[Accelerate\right]z^{*}=\underset{\mathbf{x}\in X}{max}\underset{\mathrm{y}}{min}\sum _{a\in \mathcal{E}}\left(c\left(a\right)+x\left(a\right)d\left(a\right)(1+\alpha {\mathcal{I}}_A\left(a\right))\right)y\left(a\right)$$

(22)

$$\left[Delay\right]z^{*}=\underset{\mathbf{x}\in X}{max}\underset{\mathrm{y}}{min}\sum _{a\in \mathcal{E}}\frac{\left(c\left(a\right)+x\left(a\right)d\left(a\right))\right)y\left(a\right)}{1+\beta {\mathcal{I}}_A\left(a\right)}$$

(23)

$$\begin{array}{c}\hfill s.t.\sum _{a\in Out\left(i\right)}y\left(a\right)-\sum _{a\in In\left(i\right)}y\left(a\right)=\left\{\begin{array}{cc}1& \mathrm{for}i=s\\ 0& \forall i\in \mathcal{N}\setminus \left\{s,g\right\}\\ -1& \mathrm{for}i=t\end{array}\right.\end{array}$$

(24)

where $X=\left\{\mathbf{x}\in {\{0,1\}}^{\left|\mathcal{E}\right|}|{\mathbf{r}}^T\mathbf{x}\le R\right\}$ with bounded resource R, $x\left(a\right),y\left(a\right)\in \{0,1\}$ indicate the observer’s interdiction resource allocation and the actor’s traverse path respectively, $\alpha ,\beta$ are the controlling parameters of two opposite objectives.

As shown in Figure 7, three paths of the actor under the observer’s interdiction with a barrier before the start node s. The observer proactively interdicts to reduce the goal uncertainty and accelerate goal recognition. The actor attempts to minimize the privacy information leakage, so as to improve the goal uncertainty and hide the real goal.

We need to know the metric ${\mathcal{I}}_A\left(a\right)$ associated with the goal uncertainty, which is defined over actions available at each state and can be computed offline. The single observation based probabilistic goal recognition approach will not encounter online inconsistency.

3.2.2. Control and Threshold

Instead of individually analyze the accelerate and delay model, we may want to control the goal recognition process by adding additional path cost under bounded resource. Here, we mainly focus on reformulating the GRC under network interdiction with bounded resource as one optimizing problem incorporating the metric ${\mathcal{I}}_A\left(a\right)$.

Definition 12 (InfoGRC).

The formulation of the action privacy information metric-based goal recognition control is defined as follows:

$$[InfoGRC]z^{*}=\underset{\mathbf{x}\in X}{max}\underset{\mathrm{y}}{min}\sum _{a\in \mathcal{E}}\frac{\left(c\left(a\right)+x\left(a\right)d\left(a\right)(1+\alpha {\mathcal{I}}_A\left(a\right))\right)y\left(a\right)}{1+\beta {\mathcal{I}}_A\left(a\right)}$$

(25)

$$\begin{array}{c}\hfill s.t.\sum _{a\in Out\left(i\right)}y\left(a\right)-\sum _{a\in In\left(i\right)}y\left(a\right)=\left\{\begin{array}{cc}1& \mathrm{for}i=s\\ 0& \forall i\in \mathcal{N}\setminus \left\{s,g\right\}\\ -1& \mathrm{for}i=t\end{array}\right.\end{array}$$

(26)

where $X=\left\{\mathbf{x}\in {\{0,1\}}^{\left|\mathcal{E}\right|}|{\mathbf{r}}^T\mathbf{x}\le R\right\}$ with bounded resource R, $x\left(a\right),y\left(a\right)\in \{0,1\}$ indicate the observer’s interdiction resource allocation and the actor’s traverse path respectively, $\alpha ,\beta$ are the controlling parameters of two opposite objectives. Equation (26) is the flow-balance constraint.

Here, we define one variant InfoGRCT, a novel extension of the InfoGRC with threshold interdiction [61], in which the actor attempts to minimize the length of the metric ${\mathcal{I}}_A\left(a\right)$ added path cost, while the observer interdicts the path so that the path cost exceeds a specific threshold with least resource consumption. We designate this critical threshold as a trade-off between the maximum shortest path and resource consumption for the observer, which represents the longest shortest path cost that the actor will tolerate.

Definition 13 (InfoGRCT).

The formulation of the action privacy information metric based goal recognition control with a threshold is defined as follows:

$$[InfoGRCT]r^{*}=\underset{\mathbf{x}\in X}{min}\sum _{a\in \mathcal{E}}x\left(a\right)r\left(a\right)$$

(27)

$$s.t.\underset{\mathrm{x},\mathrm{y}}{min}\sum _{a\in \mathcal{E}}\frac{\left(c\left(a\right)+x\left(a\right)d\left(a\right)(1+\alpha {\mathcal{I}}_A\left(a\right))\right)y\left(a\right)}{1+\beta {\mathcal{I}}_A\left(a\right)}\ge \tilde{\theta }$$

(28)

$$\begin{array}{c}\hfill \sum _{a\in Out\left(i\right)}y\left(a\right)-\sum _{a\in In\left(i\right)}y\left(a\right)=\left\{\begin{array}{cc}1& \mathit{for}i=s\\ 0& \forall i\in \mathcal{N}\setminus \left\{s,g\right\}\\ -1& \mathit{for}i=t\end{array}\right.\end{array}$$

(29)

where $x\left(a\right),y\left(a\right)\in \{0,1\}$ indicate the observer’s interdiction resource allocation and the actor’s traverse path respectively, $\alpha ,\beta$ are the controlling parameters of two opposite objectives, $\tilde{\theta }$ is the threshold. Equation (29) is the flow-balance constraint.

As illustrated in Figure 8a, one simple road graph network is composed of $\left|\mathcal{N}\right|=11$ nodes and $\left|\mathcal{E}\right|=21$ edges. Given that node S and node $G_i$ as part of each path, we label the 18 paths, from S to $G_1$, as follows: $[S,$$\dots ,$$G_1]$≜$\left[\right(A,D,F),$$(A,D,H),$$(A,D,I),$$(A,E,F),$$(A,E,H),$$(A,E,I),$$(B,D,F),$$(B,D,H),$$(B,D,I),$$(B,E,F),$$(B,E,H),$$(B,E,I),$$(C,D,F),$$(C,D,H),$$(C,D,I),$$(C,E,F),$$(C,E,H),$$(C,E,I)]$. We choose the path cost $c_i$ for the i-th edge to be equal to $[c_1,c_2,\dots ,c_{21}]$≜[6, 3, 7, 4, 3, 3, 5, 4, 4, 6, 5, 5, 7, 3, 6, 6, 7, 4, 5, 5, 3]. The three numbers in the tuple $(c,d,r)$ represent the original path cost of the edge, added cost after interdiction and the resource required for edge interdiction, respectively. The actor has one fixed starting node S and two possible goals ($G_1$ and $G_2$). We link the actor’s shortest path before and after the network interdiction using different lines with red arrows, and the interdicted edges are labeled with a red cross. Specifically, we assume that the observer has been assigned with a total of $R=5$ units of resource to interdict, and the threshold for interdiction is $\tilde{\theta }=20$.

The network interdiction solutions for the InfoGRC and InfoGRCT are shown in Figure 8. Taking the goal $G_1$ as an example, the actor would first traverse the optimal path $(S,B),(B,D),(D,H),(H,G_1)$ with a total length of 15. However, if the edge $(H,G_1)$ is interdicted, the path cost of the original path would be added to 18, and then the other path $(S,B),(B,D),(D,I),(I,G_1)$ with a cost of 16 will be selected, as shown in Figure 8b. Similarly, if the actor takes $G_2$ as the real goal, as shown in Figure 8c, a new path $(S,B),(B,D),(D,I),(I,G_2)$ would be taken to replace the original $(S,B),(B,E),(E,H),(H,G_2)$ after the edge $(7,8)$ being interdicted. In this case, the path cost before and after network interdiction are 16 and 22 respectively, while the newly selected path after interdiction is 18. As shown in Figure 8d,e, considering the interdiction threshold, the optimal interdiction solution for $G_1$ is $(H,G_1),(I,G_1)$, and the solution for $G_2$ is $(H,G_2),(I,G_2)$.

3.3. Dual Reformulation

The InfoGRC and InfoGRCT can be transformed into bi-level optimization programming (BMIP) problems, in which the observer’s interdiction resource allocation is transparent to the actor. Some algorithms cannot scale up to large road networks and are sensitive to network parameters, here we first propose to dual reformulate these problems. The matrix form of the InfoGRC problem is as follows:

$$[InfoGRC-P]z^{*}=\underset{\mathbf{x}\in X}{max}\underset{\mathbf{y}}{min}\sum _{a\in \mathcal{E}}{({\mathbf{c}}^{\prime }+\mathbf{M}\mathbf{x})}^T\mathbf{y}$$

(30)

$$\begin{array}{c}\hfill s.t.{\mathbf{K}}^T\mathbf{y}=\mathbf{b}\\ \hfill \mathbf{y}\ge \mathbf{0},\end{array}$$

(31)

where $c_a^{\prime }=c_a/\left(1+\beta {\mathcal{I}}_{AI}\left(a\right)\right)$ is the additional action cost, $\mathbf{M}=diag\left(m_1,\cdots ,m_{\left|\mathcal{E}\right|}\right)$, $\mathbf{b}=(1,0,\cdots ,0,-1)$, $m_a=d\left(a\right)(1+\alpha {\mathcal{I}}_A\left(a\right))/\left(1+\beta {\mathcal{I}}_A\left(a\right)\right)$, $\mathbf{K}$ is the network matrix. Equation (31) is the vector-form flow-balance constraint.

Fixing the outer variable x, we can take the dual of the inner minimization using KKT conditions, then the dual reformulation of the InfoGRC is as follows:

$$[InfoGRC-D]z^{*}=\underset{\mathbf{x}\in X,\overrightarrow{\pi }}{max}{\mathbf{b}}^T\overrightarrow{\pi }$$

(32)

$$\begin{array}{cc}\hfill s.t.{\mathbf{K}}^T\overrightarrow{\pi }& ={\mathbf{c}}^{\prime }+\mathbf{M}\mathbf{x}\hfill \\ \hfill {\pi }_s& =0,\hfill \end{array}$$

(33)

where $X=\left\{\mathbf{x}\in {\{0,1\}}^{\left|\mathcal{E}\right|}|{\mathbf{r}}^T\mathbf{x}\le R\right\}$ with bounded resource R, $\overrightarrow{\pi }$ is the dual variables. Hence, the dual problem can be solved by a standard branch-and-bound algorithm.

The matrix form and the dual reformulation of the InfoGRCT problem are as follows:

$$[InfoGRCT-P]r^{*}=\underset{\mathbf{x}\in X}{min}{\mathbf{r}}^T\mathbf{x}$$

(34)

$$s.t.{\mathbf{c}}^{\prime }T\mathbf{y}+{\mathbf{x}}^T\mathbf{M}\mathbf{y}\ge \tilde{\theta }\forall \mathbf{y}\in Y$$

(35)

$$\begin{array}{c}\hfill {\mathbf{K}}^T\mathbf{y}=\mathbf{b}\\ \hfill \mathbf{y}\ge \mathbf{0}.\end{array}$$

(36)

$$[InfoGRCT-D]r^{*}=\underset{\mathbf{x}\in X}{min}{\mathbf{r}}^T\mathbf{x}$$

(37)

$$s.t.\mathbf{A}\overrightarrow{\pi }\ge \tilde{\theta }$$

(38)

$$\begin{array}{c}\hfill {\mathbf{B}}^T\overrightarrow{\pi }+{\mathbf{M}}^T\mathbf{x}\ge -\mathbf{c}\\ \hfill \mathbf{x}\ge \mathbf{0},\end{array}$$

(39)

where $\tilde{\theta }$ is the threshold, $\mathbf{A}={[-1,0,\dots ,0,1]}_{1\times m}$, and ${\mathbf{B}}_{\left|\mathcal{N}\right|\times \left|\mathcal{E}\right|}=\left(b_{ik}\right)$ is the node-edge incidence matrix.

We will adopt a Benders decomposition based constraint generation approach [62]. The framework is depicted in Figure 9. The higher-level is the interdiction resource allocation problem for the observer, while the lower-level is the generative cost-optimal path-planning for the actor.

Benders decomposition is an efficient approach to solve large-scale optimization problems. The main idea is to separate the mixed decision variables into two-stage variables and generate two relatively independent problems denoted as the Master problem and the Subproblem respectively. Then we alternately solve the problems and iteratively update the results until a convergence condition is satisfied. Here, the InfoGRC and InfoGRCT can be reformulated to $[Master\left(\widehat{Y}\right)]-[Sub\left(\widehat{x}\right)]$ problems as follows:

$$[InfoGRC-Master]z^{*}=\underset{\mathbf{x}\in X}{max}z$$

(40)

$$\begin{array}{c}\hfill s.t.z\le {\mathbf{c}}^{\prime }T\widehat{y}+{\mathbf{x}}^T\mathbf{M}\widehat{y}\forall \widehat{y}\in \widehat{Y}\end{array}$$

(41)

$$[InfoGRC-Sub\left(\widehat{x}\right)]z_{\widehat{x}}=\underset{y}{min}\sum _{a\in \mathcal{E}}\left(c\left(a\right)+\widehat{x}\left(a\right)d\left(a\right)\right)y\left(a\right)$$

(42)

$$\begin{array}{c}\hfill s.t.{\mathbf{K}}^T\mathbf{y}=\mathbf{b}\\ \hfill x\left(a\right)\in \{0,1\}\forall a\in \mathcal{E}\end{array}$$

(43)

$$[InfoGRCT-Master\left(\widehat{Y}\right)]r_{\widehat{Y}}=\underset{x}{min}{\mathbf{r}}^T\mathbf{x}$$

(44)

$$\begin{array}{c}\hfill s.t.{\mathbf{c}}^{\prime }T\widehat{y}+{\mathbf{x}}^T\mathbf{M}\widehat{y}\ge \tilde{\theta }\forall \widehat{y}\in \widehat{Y}\\ \hfill x\left(a\right)\in \{0,1\}\forall a\in \mathcal{E}\end{array}$$

(45)

$$[InfoGRCT-Sub\left(\widehat{x}\right)]d_{\widehat{x}}=\underset{\mathbf{y}}{min}\sum _{a\in \mathcal{E}}\left(c\left(a\right)+\widehat{x}\left(a\right)d\left(a\right)\right)y\left(a\right)$$

(46)

$$\begin{array}{c}\hfill s.t.{\mathbf{K}}^T\mathbf{y}=\mathbf{b}\\ \hfill x\left(a\right)\in \{0,1\}\forall a\in \mathcal{E}\end{array}$$

(47)

where $\mathbf{Y}$ denotes the set of all simple $s-g$ paths, $\widehat{y}$ (temporary optimal actor path in $[Master(\widehat{Y})]$) and $\widehat{x}$ (temporary observer’s interdiction plan in $[Sub\left(\widehat{x}\right)]$) are fixed and known in their respective solutions. The basic Benders decomposition algorithm for InfoGRCT can be found in [63], and the Benders decomposition based problem-solving algorithm for InfoGRCT is proposed in Algorithm 1.

Algorithm 1 The Benders decomposition based problem-solving algorithm for InfoGRCT

Input:  An instance of InfoGRCT. Output:  An optimal observer’s interdiction plan for goal recognition 1: $\widehat{x}\leftarrow \mathbf{1}$, solve $[Sub\left(\widehat{x}\right)]$ to obtain the $\overline{\theta }$; 2: while$\tilde{\theta }\le \overline{\theta }$do 3:     $\widehat{X}\widehat{Y}\leftarrow \varnothing ,\widehat{x}\leftarrow 0$ 4:     $\mathbf{repeat}$: solve $[Sub\left(\widehat{x}\right)]$ to obtain $\widehat{y}$ and $\theta$; 5:          $\widehat{X}\widehat{Y}\leftarrow \widehat{X}\widehat{Y}\cup (\widehat{x},\widehat{y})$; 6:          solve $[Master\left(\widehat{y}\right)]$ for $\widehat{x}$ and $r_{\widehat{y}}$; 7:     $\mathbf{until}$ $\theta \ge \tilde{\theta }$ 8:     $x^{*}\leftarrow \widehat{x},r^{*}=r_{\widehat{y}}$ 9: end while 10: Return$x^{*},r^{*}$

4. Experiments

Experiments were conducted on synthetic path datasets upon two small artificially generated network and one real-world road network. Here, we assume the actor to be rational, which means the path datasets will contain some sub-optimal paths but without some loopy or zigzagging paths. We first evaluate the effectiveness and then compare the performance under different interdiction.

4.1. Experimental Setup

The experimental programs are coded with python, the experiments are run on one MacbookPro that runs macOS Sierra 10.12.6 with 4 CPU and 8 GB RAM. The InfoGRC/InfoGRCT have been reformulated as bi-level mixed-integer programming (BLMIP) problems and solved using the MIP solvers (Gurobi and MiniZinc). We simply set $\alpha =\beta =1$, more details will be introduced below.

As for goal recognition, early prediction, precision and recall, are properties required. We use F-$\mathit{measure}$ as the accuracy metric [4]. F-$\mathit{measure}$ is an integration of precision and recall, where precision is used to scale the reliability of the recognized results and recall is used to scale the efficiency of the algorithm applied. They are computed as follows:

$$\mathrm{F}-\mathit{measure}=\frac{2·\mathit{precision}·\mathit{recall}}{\mathit{precision}+\mathit{recall}}$$

(48)

$$\mathit{precision}=\frac{1}{N_G}\sum _{i=1}^{N_G}\frac{T{P}_i}{T{I}_i}$$

(49)

$$\mathit{recall}=\frac{1}{N_G}\sum _{i=1}^{N_G}\frac{T{P}_i}{T{T}_i}$$

(50)

where $N_G$ is the number of possible goals, $T{P}_i$, $T{I}_i$ and $T{T}_i$ are the true positives, total of true labels, and the total of inferred labels for class i respectively. The value of F-$\mathit{measure}$ will be between 0 and 1, and a higher value means better performance.

As for early prediction, if the goal recognition model converged (the final prediction was correct), the convergence point metric [4] represents the point where the following predictions are correct, which can be defined as follow:

$$N_{CP}\in \mathcal{N}$$

(51)

$$s.t.{\mathcal{P}}_{po}\left(g_r\right|{\mathcal{O}}_{N_{CP}})\ge \gamma$$

(52)

where $N_{CP}$ denoted the convergence point at which the posterior of the actor’s real goal will not be less than $\gamma$, here we set $\gamma =0.8$.

We may want to compare the relative early prediction ability between two goal recognition models given the path that contains the real goal:

$$R_{EP}=\frac{|N_{CP}^1-N_{CP}^2|}{PS=|\langle s_0,\dots N_i\dots g_r\rangle |}$$

(53)

where $R_{EP}$ represents the relative early prediction ability, $PS$ is the path steps from the start node to the real goal.

As for network interdiction, we employ the path interdiction efficiency for evaluation [35], which is defined as follows:

$$e=\delta L/{\mathbf{d}}^T\mathbf{x},$$

(54)

where $\delta L$ is the increased path cost for the actor after interdiction and ${\mathbf{d}}^T\mathbf{x}$ is the total path cost increment in the network.

4.2. Experimental Scenarios

Different network topologies may indicate different application domains and greatly affect the efficiency of the InfoGRC and InfoGRCT. We adopt two small artificially generated networks to verify the feasibility, as shown in Figure 10 and Figure 11, and then adopt one real-world road network to further verify the scalability, see Figure 12 for detail.

Hexagon grid network: We employ one $7\times 7$ hexagonal discrete grid with 7 rows and 7 columns. Since the hexagonal discrete grid owns great symmetrical properties and is widely used in simulation systems to represent the environment. The hexagonal grid on Offset coordinate is shown in Figure 10, the start node is $(0,3)$, and the goal nodes are $(6,1)$ and $(6,5)$. The actor has one fixed starting node S and two possible goals ($G_1$ and $G_2$). The path cost between nodes $c\left(a\right)$, the interdiction increment $d\left(a\right)$, and resource consumption $r\left(a\right)$ are generated to be uniform distribution on $[1,10]$, $[1,10]$, $[1,10]$, respectively.

Random Graph Network: We employ the Erdős–Rényi model [64] to generate one random graph network, which is composed of $\left|\mathcal{N}\right|=30$ nodes and $\left|\mathcal{E}\right|=60$ edges, and the edges are added uniformly randomly. As shown in Figure 11, the actor has one fixed starting node S and two possible goals ($G_1$ and $G_2$). The path cost between nodes $c\left(a\right)$ is generated to be uniform distribution on $[1,10]$, the interdiction increment $d\left(a\right)$, and resource consumption $r\left(a\right)$ is linearly proportional to the node degree.

Real-world road network: As shown in Figure 12, it is the real-world Chicago Sketch road network [65], which contains 933 nodes and 2950 edges. Here, the network is assumed to be undirected, the node indexes of the start and possible goals are $\left\{368\right\}$ and $\{377,597,575\}$, respectively. The cost of each edge $c\left(a\right)$ is an approximate integer of the real distance between two nodes, the interdiction increment $d\left(a\right)$ and resource consumption $r\left(a\right)$ are linearly proportional to the node degrees. A dataset consists of 50 labeled paths for each goal is generated with about 20 steps without goal switch during the midway. Each path is separated into 10 stages so as to evaluate paths with different steps.

4.3. Goal Recognition Control under Network Interdiction

As for goal recognition, experimental evaluations are performed on four models, the “normal” without metric, “delay” and “accelerate” with metric, and the “control” model (InfoGRC). The actor has one start state and two or three predefined possible goals, which are selected with equal probability at the beginning. If the actor reaches its goal, then the goal is achieved, otherwise, the probabilistic goal recognition module will generate goal distribution over goals. In the following test, we will statistically evaluate different goal recognition models with the metric F-$\mathit{measure}$, and $R_{EP}$, which are widely used to measure the performance of different goal recognition models. As shown in Figure 13, the statistical performance of different models for the three scenarios is measured by the F-$\mathit{measure}$ value.

The actor’s actions involve privacy information, which are tightly associated with the goal uncertainty and indeed seriously hinder the goal recognition of the observer. After incorporating the action privacy information metric, the F-$\mathit{measure}$ values of the “Accelerate” model were greater than the “normal” and “delay” model, while the “delay” model performs poor compared to the “normal” model. The big gap of the F-$\mathit{measure}$ values between the “accelerate” model and the “delay” model showed that the actor’s actions are tightly associated with the goal uncertainty, the action privacy information metric ${\mathcal{I}}_A\left(a\right)$ could be employed by the observer during the goal recognition process. As for the “control” model, the values of F-$\mathit{measure}$ under network interdiction were usually higher compared with the “normal”, “accelerate”, and “delay” model, which proves that the control model with ${\mathcal{I}}_A\left(a\right)$ metric assisted could be employed to control the goal recognition process.

Here, using the total 150 paths for the Chicago Sketch road network scenario, we compute the “relative early prediction” ability of the “normal” model and “dontrol” model on three different goals. As shown in Figure 14, there are still 54 paths whose $R_{E}P$ is 0, when the actor traverse over these paths, no privacy information about the goal will be leaked. So, even if the actor could manipulate the asymmetric information about their action-goal, but there are still paths that possess little goal uncertainty.

After evaluating the performance of our models in goal recognition, here, we compared the network interdiction efficiency of InfoGRC and InfoGRCT under different network interdiction. As shown in

Table 2. The expectation of network interdiction efficiency on the three scenarios for each goal.

$\mathit{E}\left(\mathit{e}\right)$$(\%)$	Scenario 1	Scenario 2	Scenario 3
InfoGRC	65.4/63.7	62.7/78.4	88.7/77.5/90.8
InfoGRCT	65.1/63.3	62.1/78.1	88.2/77.2/90.4

, the expectation of the e are almost more than $50\%$, the values of the Chicago Sketch road network scenario are almost $80\%$. This demonstrates the average impact of InfoGRC and InfoGRCT model in network interdiction.

5. Conclusions and Future Work

Goal recognition is vital in the defense and security domain, such as in CIP. Goals of the attacker are in need of timely recognized and the actions of the attacker should be restricted. In this paper, from the perspective of explainable agent behavior, we first adopt a privacy information metric to quantify the privacy information leakage of the actions taken by the actor, since these actions are tightly associated with the goal uncertainty. Then, we defined two different interdiction models (InfoGRC and InfoGRCT) to control the goal recognition process. Experimental results demonstrate the effectiveness of our models in the fully observable and deterministic environment with multiple goals. These models above provide one paradigm, from generative path planning, probabilistic goal recognition to proactively response interdiction resource allocation, which is simple but inspiring for decision-making (such as offline proactive planning, threat analysis) in the defense and security domain. Also, considering the dual use of these models, we could attempt to do inverse privacy-preserving path planning. Goal recognition control under network interdiction with bounded resource may be a suitable and soft method to facilitate goal recognition offline compared to the goal recognition design with the hard environment redesign.

However, it is noteworthy that our work is suggestive but still simple, the applicability of our models under network interdiction still face many challenges. As for the goal recognition, partial observable environment, noisy observation, adversarial goal recognition, and online recognition are very realistic need. As for the action model, durative action, midway goal change, deceptive action, active attacker, multiple attacker, higher dimensionality, and bounded rationality drive us to develop more robust opponent modeling methods. As for the interdiction model, nodal interdiction, threshold sensitivity, network resilience are still worthy of further study. As for the metric model, deceptive action metric and goal-related mutual information metric inspire us to design learning based goal recognition model. All of these are still open in our future work.

As a continuation of this work, allocating interdiction resource can be modeled as one dynamic process assisted with online goal recognition. In the future, we will attempt to use a stochastic game-theoretic framework to model the attacker-defender interaction in the partial observable environment, where the attacker would perform active deceptive actions or irrational actions to mislead the goal recognition process of the observer.