A Kernel Recursive Maximum Versoria-Like Criterion Algorithm for Nonlinear Channel Equalization
Abstract
:1. Introduction
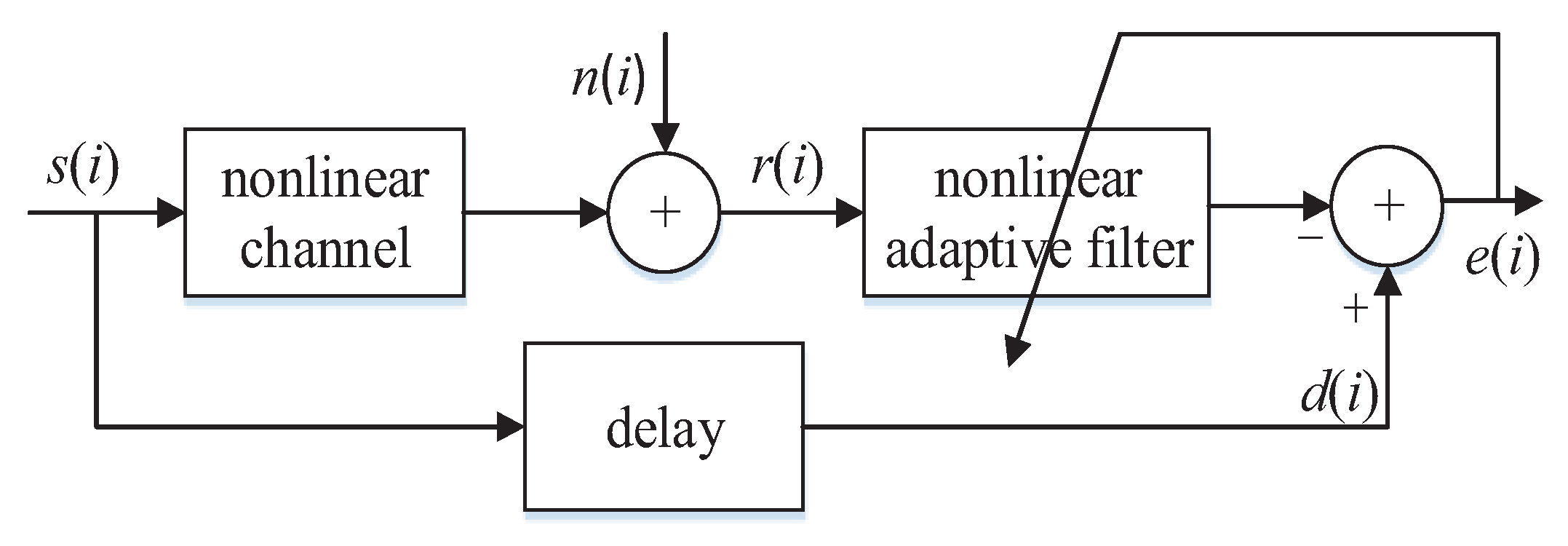
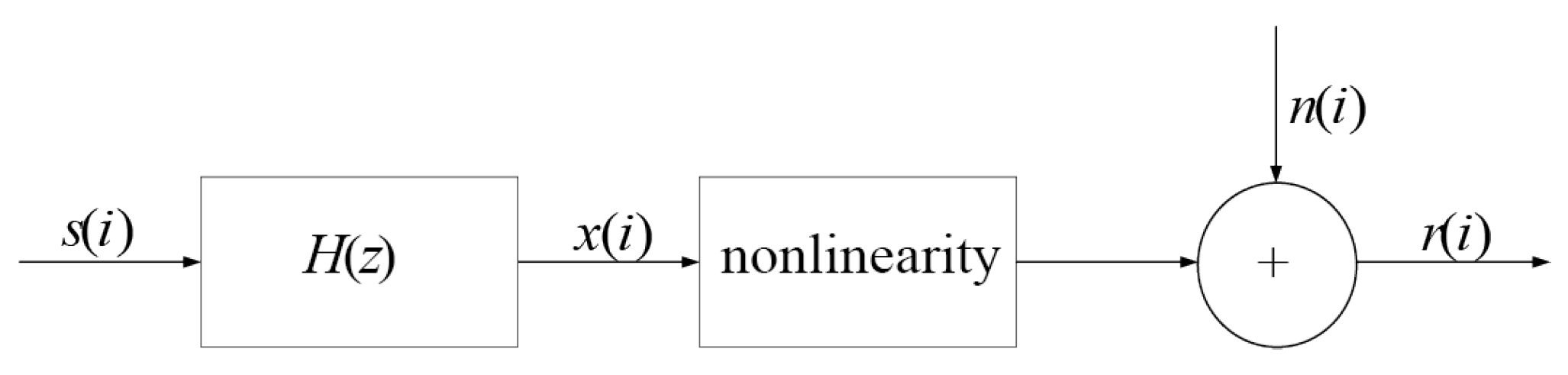
2. The KRMVLC Algorithm
| Algorithm 1 KRMVLC. |
|
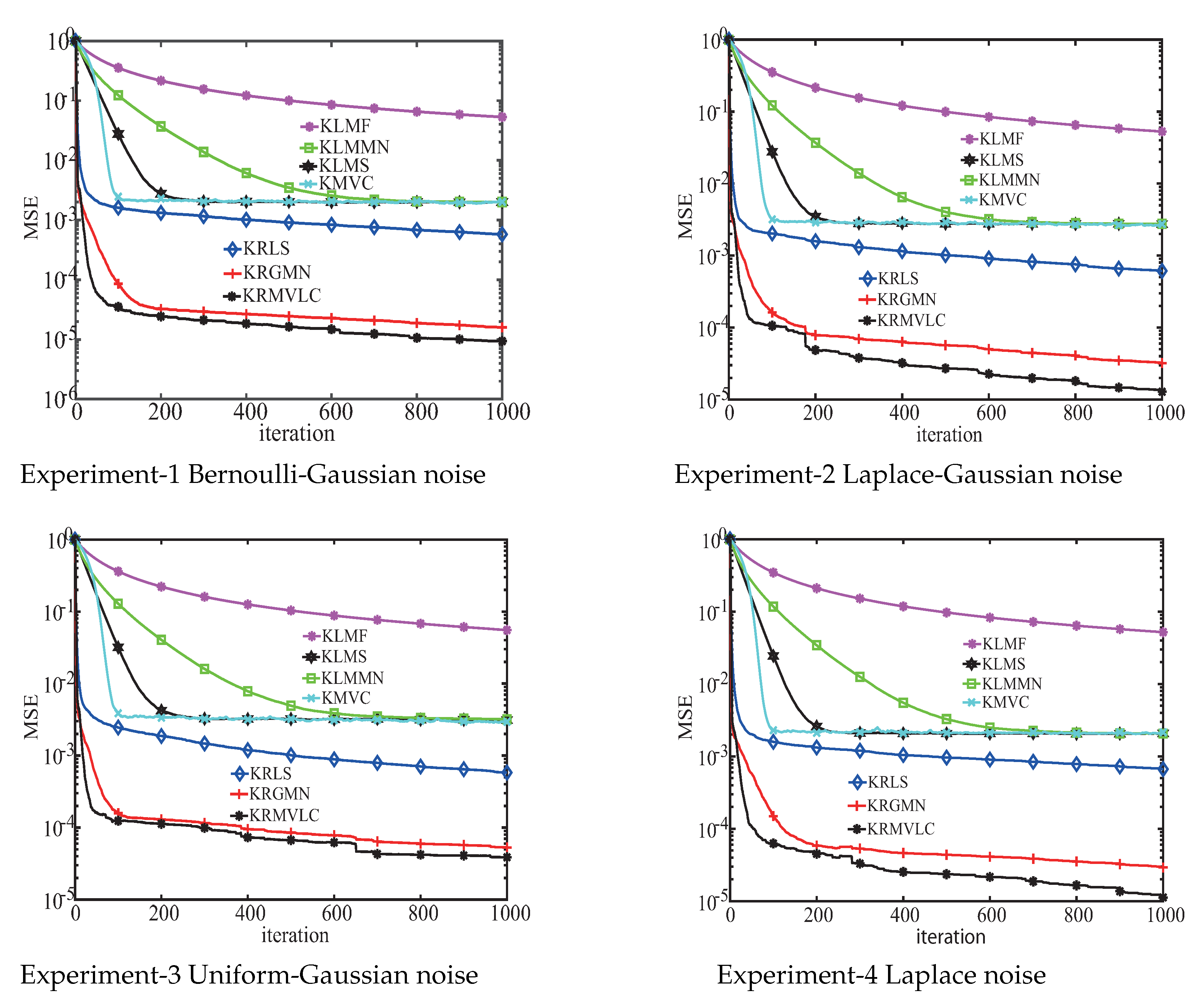
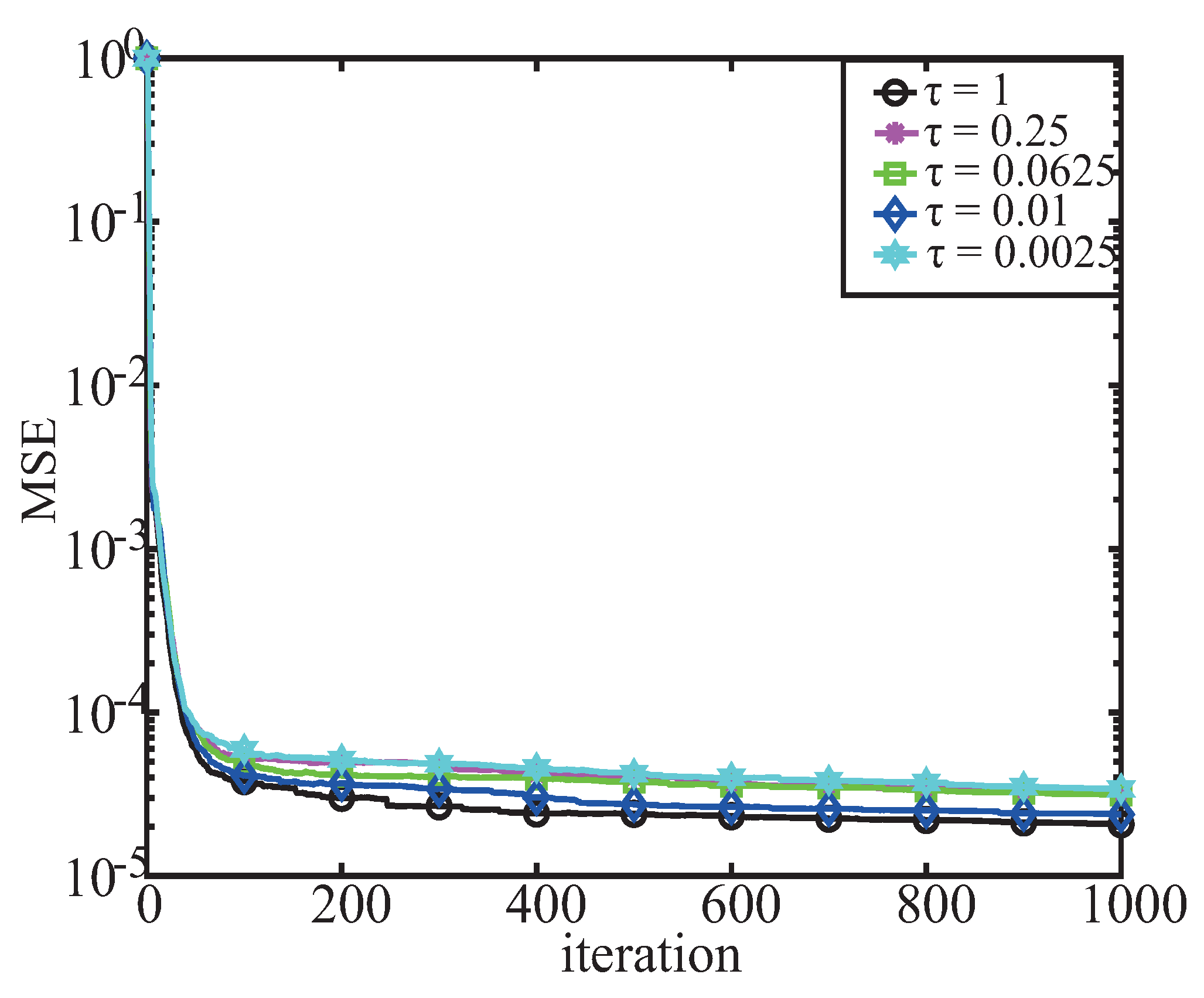
3. Simulation Result
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Liu, W.; Príncipe, J.C.; Haykin, S. Kernel Adaptive Filtering: A Comprehensive Introduction; John Wiley & Sons: Hoboken, NJ, USA, 2010. [Google Scholar]
- Liu, W.; Pokharel, P.P.; Príncipe, J.C. The kernel least mean square algorithm. IEEE Trans. Signal Process. 2018, 56, 543–554. [Google Scholar] [CrossRef]
- Li, Y.; Wang, Y.; Jiang, T. Sparse-aware set-membership NLMS algorithms and their application for sparse channel estimation and echo cancelation. AEU Int. J. Electron. Commun. 2016, 70, 895–902. [Google Scholar] [CrossRef]
- Shi, W.; Li, Y.; Zhao, L.; Liu, X. Controllable sparse antenna array for adaptive beamforming. IEEE Access 2019, 7, 6412–6423. [Google Scholar] [CrossRef]
- Lu, L.; Zhao, H.; Chen, B. Time series prediction using kernel adaptive filter with least mean absolute third loss function. Nonlinear Dyn. 2017, 90, 999–1013. [Google Scholar] [CrossRef]
- Engel, Y.; Mannor, S.; Meir, R. The kernel recursive least squares algorithm. IEEE Trans. Signal Process. 2004, 52, 2275–2285. [Google Scholar] [CrossRef]
- Chen, B.; Zhao, S.; Zhu, P.; Príncipe, J.C. Quantized kernel least mean square algorithm. IEEE Trans. Neural Netw. Learn. Syst. 2012, 23, 22–32. [Google Scholar] [CrossRef] [PubMed]
- Chen, B.; Zhao, S.; Zhu, P.; Príncipe, J.C. Quantized kernel recursive least squares algorithm. IEEE Trans. Neural Netw. Learn. Syst. 2013, 24, 1484–1491. [Google Scholar] [CrossRef] [PubMed]
- Liu, W.; Park, I.; Príncipe, J.C. An information theoretic approach of designing sparse kernel adaptive filters. IEEE Trans. Neural Netw. 2009, 20, 1950–1961. [Google Scholar] [CrossRef]
- Liu, W.; Park, I.; Wang, Y.; Príncipe, J.C. Extended kernel recusive least squares algorithm. IEEE Trans. Signal Process. 2009, 57, 3081–3814. [Google Scholar]
- Wang, S.; Zheng, Y.; Ling, C. Regularized kernel least mean square algorithm with multiple-delay feedback. IEEE Signal Process. Lett. 2016, 23, 98–101. [Google Scholar] [CrossRef]
- Zhao, J.; Liao, X.; Wang, S.; Tse, C.K. Kernel least mean square with single feedback. IEEE Signal Process. Lett. 2015, 22, 953–957. [Google Scholar] [CrossRef]
- Chen, B.; Liang, J.; Zheng, N.; Príncipe, J.C. Kernel least mean square with adaptive kernel size. Neurocomputing 2016, 191, 95–106. [Google Scholar] [CrossRef] [Green Version]
- Shi, L.; Lin, Y.; Xie, X. Combination of affine projection sign algorithms for robust adaptive filtering in non-gaussian impulsive interference. Electron. Lett. 2014, 50, 466–467. [Google Scholar] [CrossRef]
- Pelekanakis, K.; Chitre, M. Adaptive sparse channel estimation under symmetric α-stable noise. IEEE Trans. Wirel. Commun. 2014, 13, 3183–3195. [Google Scholar] [CrossRef]
- Pei, S.C.; Tseng, C.C. Least mean p-power error criterion for adaptive FIR filter. IEEE J. Sel. Areas Commun. 1994, 12, 1540–1547. [Google Scholar]
- Li, Y.; Wang, Y.; Jiang, T. Norm-adaption penalized least mean square/fourth algorithm for sparse channel estimation. Signal Process. 2016, 128, 243–251. [Google Scholar] [CrossRef]
- Tanrikulu, O.; Chambers, J.A. Convergence and steady-state properties of the least-mean mixed-norm (LMMN) adaptive algorithm. IEE Proc. Vis. Image Signal Process. 1994, 143, 137–142. [Google Scholar] [CrossRef]
- Chambers, J.A.; Tanrikulu, O.; Constantinides, A.G. Least mean mixed-norm adaptive filtering. Electron. Lett. 1994, 30, 1574–1575. [Google Scholar] [CrossRef]
- Miao, Q.Y.; Li, C.G. Kernel least-mean mixed-norm algorithm. In Proceedings of the International Conference on Automatic Control and Artificial Intelligence (ACAI), Xiamen, China, 3–5 March 2012; pp. 1285–1288. [Google Scholar]
- Luo, X.; Deng, J.; Liu, J.; Li, A.; Wang, W.; Zhao, W. A novel entropy optimized kernel least-mean mixed-norm algorithm. In Proceedings of the 2016 International Joint Conference on Neural Networks (IJCNN), Vancouver, BC, Canada, 24–29 July 2016; pp. 1716–1722. [Google Scholar]
- Ma, W.; Qiu, X.; Duan, J.; Li, Y.; Chen, B. Kernel recursive generalized mixed norm algorithm. J. Frankl. Inst. 2018, 355, 1596–1613. [Google Scholar] [CrossRef]
- Huang, F.; Zhang, J.; Zhang, S. Maximum versoria criterion-based robust adaptive filtering algorithm. IEEE Trans. Circuits Syst. II Exp. Briefs 2017, 355, 1596–1613. [Google Scholar] [CrossRef]
- Jain, S.; Mitra, R.; Bhatia, V. Kernel adaptive filtering based on maximum versoria criterion. In Proceedings of the 2018 IEEE International Conference on Advanced Networks and Telecommunications Systems (ANTS), Indore, India, 16–19 December 2018. [Google Scholar]
- Li, Y.; Jiang, Z.; Shi, W.; Han, X.; Chen, B. Blocked maximum correntropy criterion algorithm for cluster-sparse system identifi-cations. IEEE Trans. Circuits Syst. II Exp. Briefs 2019. [Google Scholar] [CrossRef]
- Shi, W.; Li, Y.; Wang, Y. Noise-free maximum correntropy criterion algorithm in non-Gaussian environment. IEEE Trans. Circuits Syst. II Exp. Briefs 2019. [Google Scholar] [CrossRef]
- Li, Y.; Jiang, Z.; Osman, O.; Han, X.; Yin, J. Mixed norm constrained sparse APA algorithm for satellite and network echo channel estimation. IEEE Access 2018, 6, 65901–65908. [Google Scholar] [CrossRef]
- Lerga, J.; Sucic, V.; Sersic, D. Performance analysis of the LPA-RICI denoising method. In Proceedings of the 2009 6th International Symposium on Image and Signal Processing and Analysis, Salzburg, Austria, 16–18 September 2009. [Google Scholar]
- Lerga, J.; Grbac, E.; Sucic, V. An ICI based algorithm for fast denoising of video signals. Automatika 2014, 55, 351–358. [Google Scholar] [CrossRef]
- Segon, G.; Lerga, J.; Sucic, V. Improved LPA-ICI-based estimators embedded in a signal denoising virtual instrument. Signal Image Video Process. 2017, 11, 211–218. [Google Scholar] [CrossRef]
- Filipovic, V.Z. Consistency of the robust recursive Hammerstein model identification algorithm. J. Frankl. Inst. 2015, 352, 1932–1945. [Google Scholar] [CrossRef]


| Algorithm | |||||
|---|---|---|---|---|---|
| KLMS | - | 0 | 0.02 | - | - |
| KLMF | - | 0 | 0.01 | - | - |
| KLMMN | - | 0.25 | 0.0225 | - | - |
| KMVC | - | 0 | 0.02 | - | - |
| KRLS | 1 | 0.25 | - | 0.45 | 1 |
| KRGMN | 1 | 0.25 | - | 0.45 | 1 |
| KRMVLC | 1 | 0.25 | - | 0.45 | 1 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, Q.; Li, Y.; Xue, W. A Kernel Recursive Maximum Versoria-Like Criterion Algorithm for Nonlinear Channel Equalization. Symmetry 2019, 11, 1067. https://doi.org/10.3390/sym11091067
Wu Q, Li Y, Xue W. A Kernel Recursive Maximum Versoria-Like Criterion Algorithm for Nonlinear Channel Equalization. Symmetry. 2019; 11(9):1067. https://doi.org/10.3390/sym11091067
Chicago/Turabian StyleWu, Qishuai, Yingsong Li, and Wei Xue. 2019. "A Kernel Recursive Maximum Versoria-Like Criterion Algorithm for Nonlinear Channel Equalization" Symmetry 11, no. 9: 1067. https://doi.org/10.3390/sym11091067
APA StyleWu, Q., Li, Y., & Xue, W. (2019). A Kernel Recursive Maximum Versoria-Like Criterion Algorithm for Nonlinear Channel Equalization. Symmetry, 11(9), 1067. https://doi.org/10.3390/sym11091067





