Geometric and Kinematic Analyses and Novel Characteristics of Origami-Inspired Structures

Abstract

In recent years, origami structures have been gradually applied in aerospace, flexible electronics, biomedicine, robotics, and other fields. Origami can be folded from two-dimensional configurations into certain three-dimensional structures without cutting and stretching. This study first introduces basic concepts and applications of origami, and outlines the common crease patterns, whereas the design of crease patterns is focused. Through kinematic analysis and verification on origami structures, origami can be adapted for practical engineering. The novel characteristics of origami structures promote the development of self-folding robots, biomedical devices, and energy absorption members. We briefly describe the development of origami kinematics and the applications of origami characteristics in various fields. Finally, based on the current research progress of crease pattern design, kinematic analysis, and origami characteristics, research directions of origami-inspired structures are discussed.

1. Introduction

Origami is an ancient art that originated in China. It spread to Japan in the Tang Dynasty, and then it was remarkably promoted by the Japanese. For example, Figure 1 shows a four-fold origami pattern, which is a classic flat-foldable tessellation with periodic and parallel creases. As shown in Figure 1, this origami retains a single degree-of-freedom during folding. Notably, flat-foldable origami can be neatly folded from two-dimensional configurations into certain three-dimensional configurations without cutting and stretching. In recent years, origami and origami-inspired structures have attracted great attention and obtained pioneer applications in different fields.

In the early days, origami was only regarded as an art form to meet certain aesthetic needs. Since the twentieth century, a series of symbolic codes consisting of dots, dashes, and arrows have been introduced to create an origami language for communication. On the basis of the mathematical principles like 2D and 3D geometry, calculus, spherical triangulation, graph products, and group theory [1], the relationship between origami art and origami science is gradually established.

With the development of computer science and computational geometry [2], origami design has been promoted. Then, the concept of origami has begun to be applied into deployable structures [3,4], flexible electronics [5], biomedical devices [6,7,8], metamaterials [9,10], robots [11,12], optical systems [13,14,15], and so on. Miura [16] first invented the “Miura folding” and applied it to fold solar panels, so that the panels could be loaded into narrow launch capsules in a smaller volume in a folded state and expand to a large area in space navigation. Also, Miura folding is widely applied to map folding [17], which allows visitors to fold a map into a smaller size. Since then, Miura folding has gradually been adopted for the mobility and kinematic of deployable structures [18]. Based on the rigid folding of origami, Song et al. [19] introduced the Miura pattern into a lithium-ion battery with high deformation. Thereafter, the deformability of the origami lithium-ion battery could be obtained from the rotation of the rigid panels around the creases. Nam et al. [20] proposed an all-solid-state origami-type foldable supercapacitor, which can accommodate highly stable stretching and consist of periodically assembled isolated electrodes and sectionalized ion transferring paper. Huang et al. [21] introduced origami into a nanoscale tetrahedral structure assembled by a DNA helix, which can be applied in biosensors and drug delivery. Randall et al. [22] reviewed the applications of self-folding, reconfigurable origami structures in biomedical fields, including multiscale polygonal biological containers, cell growth scaffolds, and new surgical instruments. Silverberg et al. [23] proposed a mechanical metamaterial folded by a tessellated pattern of repetitive units, which reversibly switched between soft and hard states.

Because of the rapid development and application of origami-inspired structures in recent years, it is very necessary to systematically describe these novel structures and review the latest research progress and challenges. Figure 2 shows a schematic of the process for developing origami-inspired structures and how it relates to the organization of this paper. The rest of this paper is organized as follows. Section 2 introduces the common crease patterns and the existing methods of crease pattern design. Section 3 presents recent research on the rigid folding, kinematics, and bifurcation behavior of the origami structures. Section 4 describes a few innovative characteristics of origami-inspired structures. Section 5 discusses the existing problems of origami design and kinematic theory as well as the future prospects.

2. Design Method of a Crease Pattern

To obtain a three-dimensional desired shape, origami designers usually lay out creases on a two-dimensional plane according to mathematical and computational origami. All the creases form a crease pattern. Thereafter, a complex three-dimensional structure with certain load-bearing capacity can be obtained by folding planar sheet along the designed crease pattern. Hence, how to reasonably arrange creases on a two-dimensional plane and then fold them into a three-dimensional structure with an expected shape is the primary problem to be solved.

The early origami design relied entirely on the experience of origami artists. Admittedly, it fails to establish effective theoretical analysis or computational models in time. Until the 1980s, origami art and mathematical theory were ingeniously combined to present its charm.

2.1. Mathematical Theory for Origami Design

At present, the basic mathematical theory of origami design mainly includes Huzita–Justin (or Huzita–Hatori) axioms, two-color theorem, Maekawa’s theorem, and Kawasaki’s theorem.

The Huzita–Hatori axioms are a set of rules in paper folding [2] that define a single fold by alignment of combinations of points and finite line segments. They are described as follows:

(a)

Given two points of P1 and P2, we can make a crease over P1 and P2;

(b)

Given two points of P1 and P2, we can fold P1 onto P2 along a crease to make the two points coincide;

(c)

Given two straight lines L1 and L2, we can fold line L1 onto L2 along a crease to make the two lines coincide;

(d)

Given a point P1 and a line L1, we can fold line L1 onto itself along a crease passing through point P1;

(e)

Given two points P1 and P2 and a line L1, we can fold point P1 onto line L1 along a crease passing through point P2;

(f)

Given two points P1 and P2 and two lines L1 and L2, we can fold P1 and P2 onto L1 and L2, respectively, along a crease; and

(g)

Given a point P and two lines L1 and L2, we can fold point P onto line L1 along a crease perpendicular to L2.

The local flat-foldability of each vertex ensures that the crease pattern emanating from the vertex can be completely folded into another planar state. Kawasaki’s theorem, Maekawa’s theorem, and two-color theorem give the conditions for crease distribution at a single vertex to satisfy the flat-foldability.

Kawasaki’s theorem [24] points out that, around the vertex, if the angles between the creases are numbered sequentially, the sum of odd-numbered angles is equal to the sum of even-numbered angles, and the sum must be 180° for flat-foldable origami. Maekawa’s theorem [25] points out that the difference between the number of valley creases and mountain creases is constant to two among the creases emanating from any vertex in a crease pattern. Since there are only two kinds of creases in the crease pattern, the number of creases in the crease pattern is always even, which also ensures that the number of angles between creases at any vertex is even. Two-color theorem [26] indicates that, for a complete origami design with multiple vertices, the crease pattern must be two-colored, which means that each face in the crease pattern can be colored with only one of the two colors without having the same color at any boundary. This is a precondition for multivertex origami to retain flat-foldability, whereas each vertex should satisfy the above criteria.

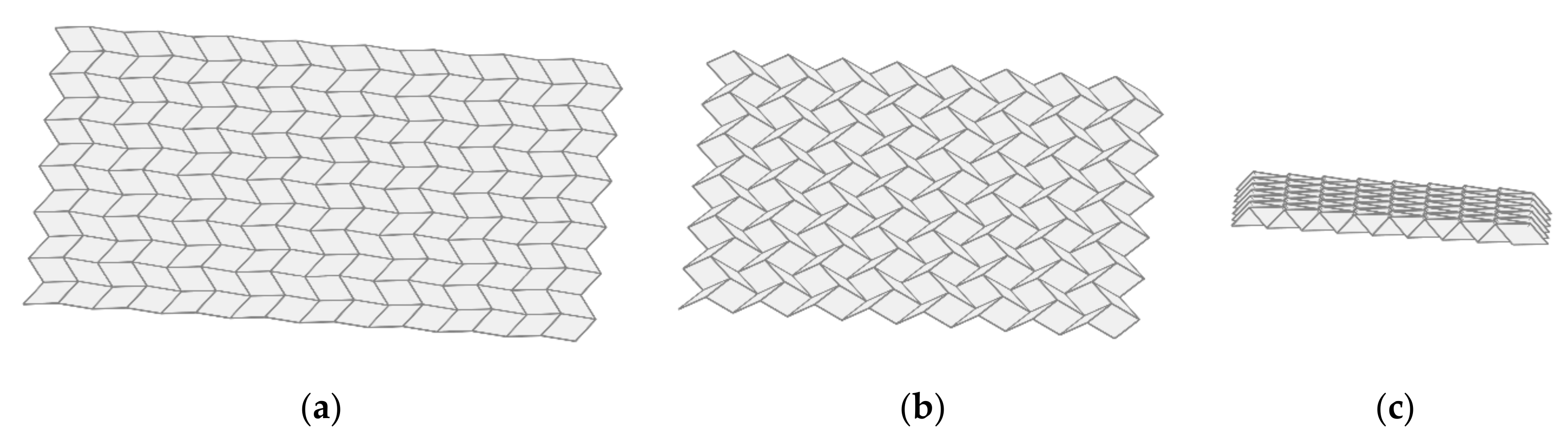
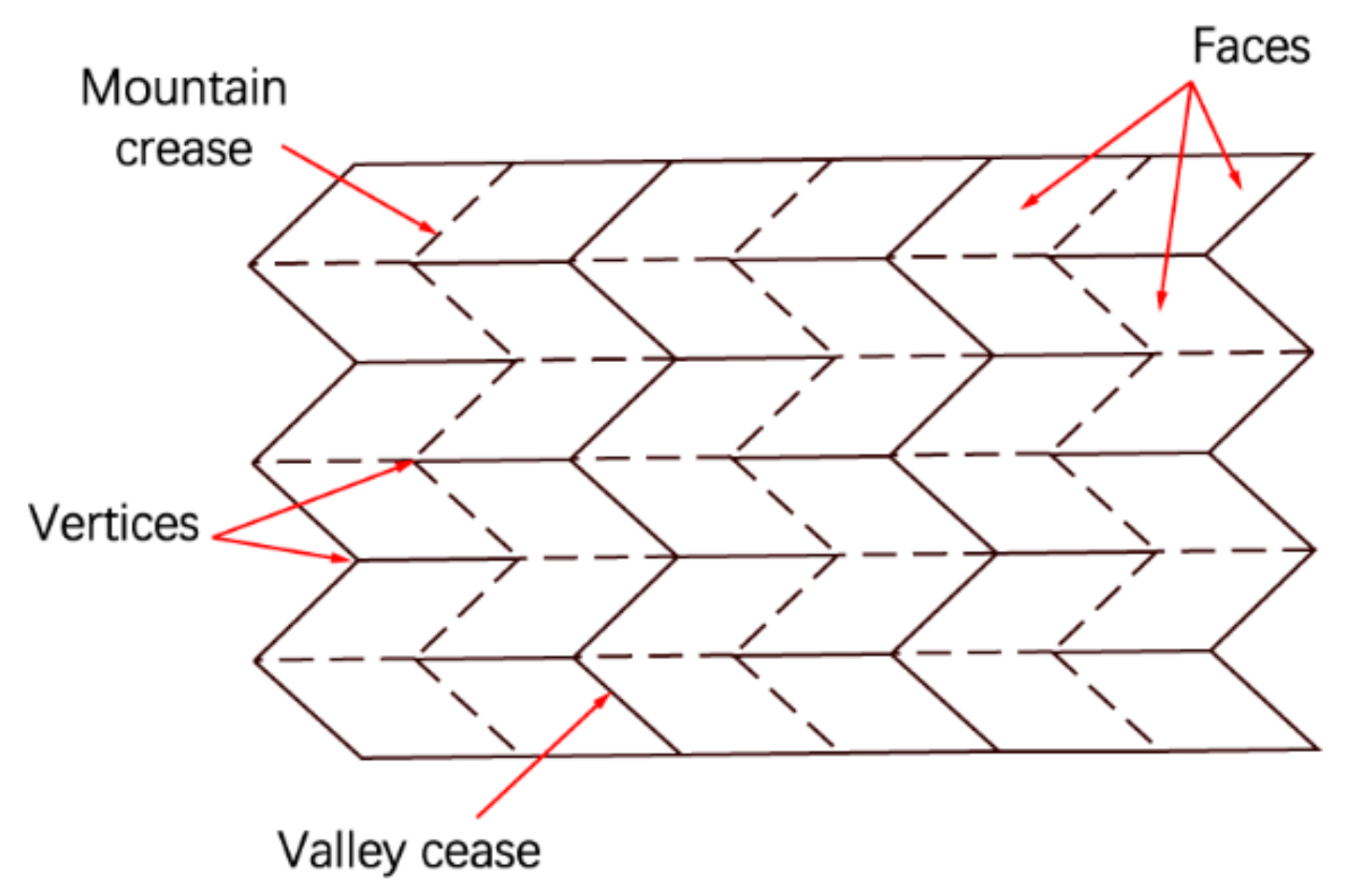
2.2. Common Crease Patterns

At present, common crease patterns include the Miura-ori pattern, the Waterbomb pattern, the Yoshimura pattern, and the diagonal pattern. These crease patterns belong to tessellation origami, which can be obtained from a series of transformations (e.g., translation, rotation, or reflection) on a basic unit.

The Miura-ori pattern is a well-known origami pattern with rigid foldability and one degree-of-freedom. It was first proposed by Miura and was initially utilized in solar panels [27]. By applying tension along the diagonal line of Miura-ori pattern, the origami can be fully expanded to a flat state from the folded state. Its crease pattern has been illustrated in Figure 3. In fact, a crease refers to the line segment produced on the paper after being folded. According to the direction in which the paper is folded, creases can be divided into mountain creases and valley creases, as shown in Figure 3. The intersection point of multiple creases is known as the vertex of the creases. The creases distributed in a specific way form a crease pattern. The area surrounded by these creases is a face of the origami, which will not be deformed during folding in an ideal case.

The Waterbomb pattern is actually a single-vertex bistable mechanism [28]. It has a simple geometry and multiple equilibrium configurations, and it can be used as a test platform for intelligent materials and driving modes. In addition, the Waterbomb pattern is easy to manufacture, and it has a convertible crease pattern that enables it to be extended for different designs. More importantly, this pattern is rigid-foldable, so it can be transformed from a long cylinder to a flat one. For instance, Figure 4 shows two stable configurations of a paper model with the Waterbomb pattern.

The Yoshimura pattern (proposed by Yoshimura [29]) is also known as the diamond pattern. It is usually applied in tube folding. All the valley creases in the Yoshimura pattern are perpendicular to the axis of the tube, where the radius of the curve at a folded state depends on the geometry of the basic unit in the crease pattern.

A diagonal pattern is often applied for energy absorption. Unlike the Yoshimura pattern, the cylinder with diagonal crease mode does not collapse in a translational way, but it rotates and folds with the torsional buckling of the cylinder [30]. As shown in Figure 5, the diagonal pattern is common in cylinder folding. Its crease pattern is composed of parallelograms, which fold along the direction of their diagonal lines and the opposite direction of their parallel lines.

2.3. Design of Crease Patterns

Nowadays, research on origami design has been widely carried out, which has mainly focused on the derivative design of common crease patterns such as the Miura-ori pattern. Lang et al. [31] obtained the generalized Miura-ori by changing the angles between the creases under the condition of maintaining the mirror symmetry of the vertices of the Miura-ori. This generalized Miura-ori pattern has many different vertices and forms a cylindrical surface with a certain curvature during transformation. Recently, Sareh and Guest [32,33] studied isomorphically generalized symmetric variations [33] and non-isomorphic variations [34] of the Miura-ori. By reducing the symmetry of Miura-ori pattern while preserving the flat-foldability of the vertices, they made appropriate variations on the original pattern, and they proposed a framework [35] for the systematic generation of symmetric derivations of the Miura-ori pattern. For example, Figure 6 shows the folding behavior of a generalized Miura-ori, which appears as a curve face during unfolding.

To obtain a general method for origami design, Lang et al. [36] studied the mathematical theory behind origami. Demaine et al. [37] proposed the computational origami theory. Belcastro and Hull [38] proposed a matrix method to describe the successive rotation of origami with respect to creases based on affine transformations and closed-loop equations. According to the formula for a single-vertex origami with four-fold lines and the geometric constraints of edge lines and intersection points, Tachi [39] established a set of equations with boundary constraints. He proposed a general design method for four-fold origami, which could preserve both rigid foldability and flat foldability. In fact, the flat-foldability condition can be generalized from a four-fold origami into a 2n-fold origami (the integer $n\ge 2$),

$${\displaystyle \sum _{i=1}^n{\alpha }_{2i-1}}={\displaystyle \sum _{i=1}^{n-1}{\alpha }_{2i}}=\pi .$$

(1)

Equation (1) is utilized to evaluate the flat-foldability at each vertex i of a 2n-fold origami. More importantly, the mobility m of a novel origami pattern should satisfy

$$m\ge 1, \mathrm{and} {\mathsf{\Gamma }}_m\supset {\mathsf{\Gamma }}^{(1)},$$

(2)

where ${\mathsf{\Gamma }}^{(1)}$ indicates full symmetry, and ${\mathsf{\Gamma }}_m$ describes the symmetry of the internal mechanism modes [18,33]. This equation provides a necessary condition for developing a rigid-foldable origami, which should possess at least a single mode of finite mechanism during folding.

Wu and You [40] utilized the quaternion and dual quaternion methods to study origami, and they explored the relationship of folding angles and the locations of different vertices. Zhou et al. [41] put forward a mathematical method to construct three-dimensional origami structures according to the given nodal coordinates and the applicability of engineering. Based on graph theory, Chen et al. [42] proposed an integrated geometric graph theoretic method to generate tessellated creased patterns using undirected and directed graphs products. For example, a four-fold origami pattern G can be generally obtained from the Cartesian product [42] of two simple subgraphs G₁ and G₂, which act as two independent edges of the origami pattern. That is,

G = G₁ □ G₂.

(3)

Furthermore, the adjacency matrix A(G) for the four-fold origami pattern can be easily computed by those of the subgraphs, $A\left(G_1\right)$ and $A\left(G_2\right)$. That is,

$$\mathbf{A}\left(G\right) = \mathbf{A}(G_1 \square G_2) = A\left(G_1\right)\otimes I_{n2}+I_{n1}\otimes A\left(G_1\right),$$

(4)

where ${\mathbf{I}}_{n1}$ denotes the $n_1\times n_1$ identity matrix, $n_1$ denotes the number of vertices of the subgraph G₁, ${\mathbf{I}}_{n2}$ denotes the $n_2\times n_2$ identity matrix, and $n_2$ denotes the number of vertices of the subgraph G₂. This graph-theoretic method can effectively construct the involved matrices and origami models and, thus, enhance the configuration processing for origami structures.

3. Kinematic Analysis of Origami-Inspired Structures

Kinematic analysis of folding is difficult and is the frontier for origami-inspired deployable structures, as whether an origami structure can be successfully folded and deployed is the key to the kinematic design. Currently, kinematic methods for the folding process mainly include force method, screw theory and group theory [43], generalized inverse theory [44], multibody dynamics, finite element method [45], and graph products [46].

3.1. Rigid Folding of Origami

Before the beginning of this section, it is necessary to introduce a special folding behavior, rigid folding. Rigid origami [47,48] is an ideal structure with rigid foldability, where the deformation occurs only at the creases. Thus, during kinematic analysis on a rigid origami, all the faces and creases can be respectively regarded as rigid panels and hinges [9,49]. As rigid folding permits only relative rotation of the panel around the creases, the whole configuration [39] can be determined by the angle between adjacent faces. Thus, the structure can be controlled by a small number of variables. The Miura-ori pattern, Waterbomb pattern, Yoshimura pattern, and the diagonal pattern belong to rigid origami. Rigid folding allows origami application to use materials other than paper. In addition, the developability and flat foldability of rigid origami are easier to popularize than those of nonrigid origami [31,39].

Rigid folding is a hot topic for origami structures [9]. Based on spherical triangulation, Huffman [50] derived the relationship between the dihedral angles of four-fold rigid origami during transformation. Mentrasti [51] described the rigid folding problem of origami structures by devising stereographic projection. Zhang et al. [52] used the force method and generalized inverse of a matrix to analyze the rigid folding process of origami structures. Zhao et al. [53] and Ding et al. [54] studied the transformations of over-constrained systems using screw theory, and they proposed a variety of new deployable structures, respectively. Cai et al. [55] established the constraint equations and studied the kinematic paths of origami structures. Chen et al. [56] studied the kinematic of symmetric deployable scissor-hinge structures according to group-theoretic method [57]. Considering the inherent full symmetry and potential interference of these structures, they proposed the concept of integral mechanism mode and tracked the motion path of a scissor-hinge structure. Wu et al. [40] proposed a rotating vector model for the single-vertex crease pattern, and they introduced quaternion and dual quaternion to describe finite motions of the origami structures. By tracking panel positions during folding, the proposed method can effectively track the entire rigid-folding procedure of an initially flat or a nonflat pattern, thereby providing judgment for its rigid foldability and flat foldability.

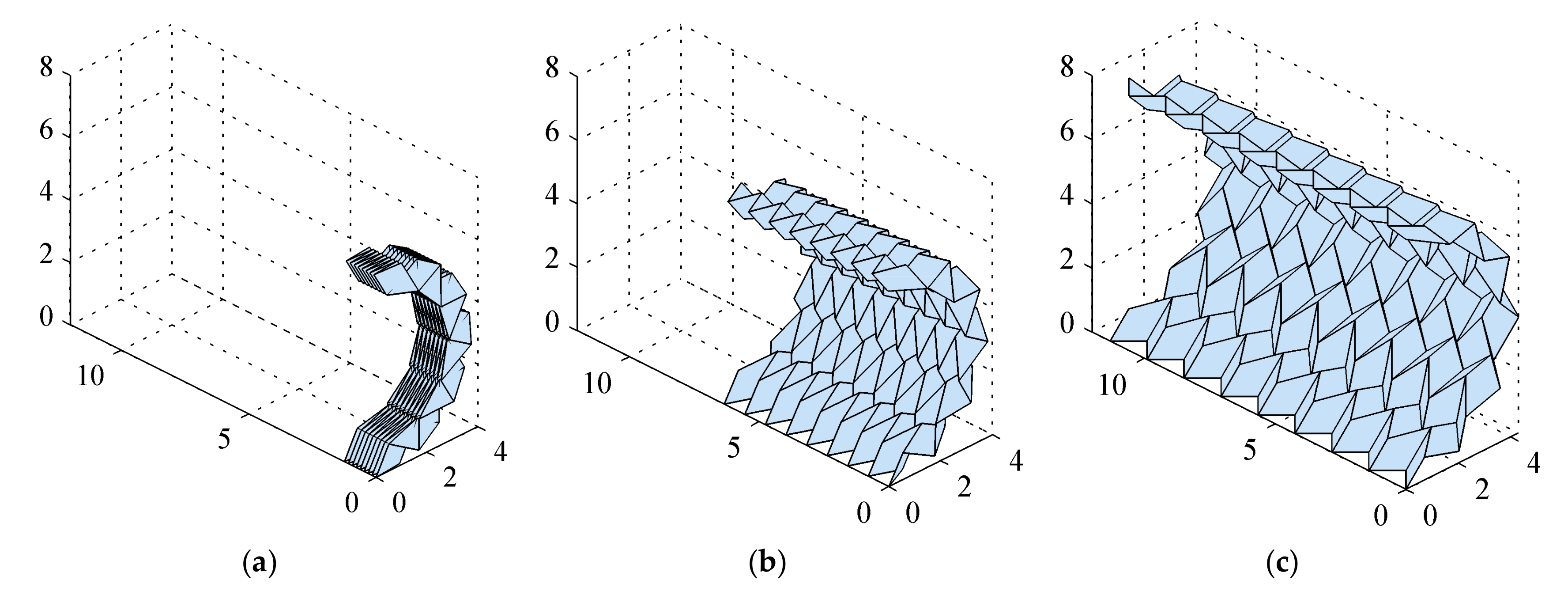
3.2. Large Deformations of Origami Structures

To analyze the large deformation of origami structures, geometric, finite element, and rod-hinge equivalent models are usually established. Based on the rigid-foldable assumption [39,40], a geometric model could determine the kinematic characteristics from the folding angles, especially for the transformation of origami with periodic geometry [58]. However, due to elastic and plastic deformation of real materials, origami structures often exhibit additional degrees-of-freedom [59]. Therefore, the rigid-foldable assumption cannot accurately reflect the mechanical or deformation characteristics of origami structures. In addition, some origami configurations do not satisfy the rigid-foldability condition. They rely on the deformation of materials to achieve finite folding. To obtain strain distributions and predict the folding behavior, Chen et al. [60] and Zhou et al. [61] established finite element models of origami structures.

Admittedly, finite element analysis is computationally expensive. Recently, some researchers have proposed simple and efficient pin-jointed models [60] or bar-hinge models [62,63] to analyze the deformation behavior of origami structures. Chen and Feng [60] simulated the Miura origami structures by pin-jointed structures and verified rigid folding behavior of such kind of structures from the very small strains of the members. Friedman et al. [64] established a bar model of Yoshimura origami and deduced the stress–displacement relationship of the model. Based on the equivalent bar-hinge models, Liu and Paulino [63] introduced the nonlinear mechanics into the large deformation analysis of origami structures. Each origami model could be simplified to a truss structure with hinges, which can predict the mechanical response of the whole structure and reflect the deformation modes of origami.

3.3. Kinematic Singularity and Potential Bifurcation of Origami Structures

During folding, on account of geometric imperfection, topological interference, or coplanarity of nonadjacent components, an origami-inspired structure may undergo some bifurcation behavior (such as the sudden change of structural configuration). Thus, this origami structure would leave the ideal motion path and fail to reach the designed configuration [65], making the motion path complex and unpredictable. In this case, kinematic singularity and potential bifurcation are of great significance to robust kinematic design and engineering applications of origami structures.

Using the energy theory, Lengyel and You [66] explained kinematic bifurcation of deployable structures. Based on a nonlinear prediction–correction algorithm and the singular value decomposition on the involved matrices, Kumar and Pellegrino [67] followed the motion path of a two-dimensional pin-jointed mechanism and discussed the bifurcation problem. They pointed out that the singular point can be detected by judging whether the minimum nonzero singular value gets close to zero. Based on group theory, Chen et al. [65] studied kinematic singularity and bifurcation behavior of symmetric pin-jointed structures, and they found low-order symmetry of the mechanism modes of those deployable structures in bifurcation paths. Figure 7a shows the motion paths of the C_2v symmetric four-bar linkage and the typical configurations along the motion path. $(x_3-x_1)/L_1$ represents the ratio of the difference between the coordinates along the x-axis of the nodes 1 and 3 to the length of link 1, while ${\theta }_{14}$ denotes the angle between the links 1 and 4.

The solid line represents the primary path of four-bar linkage, and the dashed line represents the bifurcation path. When ${\theta }_{14}=0$ or 2π, the structure reaches one critical point, denoted as the critical point I, and the four-bar linkage can either go on following the primary path or transform into the bifurcation path I. When ${\theta }_{14 }=\pi$, the structure reaches the critical point II, and the four-bar linkage can either go on following the primary path or transform into the bifurcation path II. Figure 7b shows the geometry and motion paths of a C_3v symmetric deployable pin-jointed structure. The solid line represents the primary path, and the dashed lines represent the bifurcation paths. Nodes 7–12 are free nodes. Kinematic bifurcations can be easily noticed from the variation of the distance from a typical free node 7 to the center of the structure. When the structure transforms along the primary path and reaches the critical point, three different motion paths appear, which reveal that the structure can go on following the original path and keep C_3v symmetry, or it can transform into one of the bifurcation paths and keep C_v symmetry. Gan et al. [68] studied kinematic singularity of closed-loop mechanisms. Based on bifurcation of single-vertex four-fold origami, Waitukatis et al. [69] proposed a multistable origami structure with reconfigurable stiffness, and they pointed out that more than five stable states could be obtained by adjusting energy parameters. Silverberg et al. [59] studied bifurcation characteristics of torsional origami structures, and they found that such structures can be switched from monostable to bistable by bending.

On solving motion singularity, Chen et al. [1,65] searched for singularities according to the adaptive step size method. The method performs a prediction-correction iteration by automatically adjusting the iteration step size β, avoiding crossing the singular point and improving the efficiency.

The iteration process of the adaptive step size method can be described as follows:

(a)

Set the initial iteration step size to $\left|{\beta }^0\right|=0.1L_{max}$, as the ideal structure moves along the unique motion path before singularity. $L_{max}$ is the maximum size of the members. Set the initial value ${\mathsf{\Sigma }}_{rr}^0$ of ${\mathsf{\Sigma }}_{rr}$ to ${\mathsf{\Sigma }}_{rr}^0=1$, and ${\mathsf{\Sigma }}_{rr}$ denotes the entry of the r-th row and r-th column in the singular matrix $\mathsf{\Sigma }$.

(b)

In each iteration, the generalized displacement compatibility matrix J of the structure can be obtained according to the geometric configuration of the iteration step $t=t+1$, and the corresponding minimum nonzero singular value ${\mathsf{\Sigma }}_{rr}^t$ can be obtained.

(c)

The size of iteration step ${\beta }^t$ is determined by ${\mathsf{\Sigma }}_{rr}^t$. When ${\mathsf{\Sigma }}_{rr}^t\le 0.1{ \mathrm{and} \mathsf{\Sigma }}_{rr}^t\le {\mathsf{\Sigma }}_{rr}^{t-1}$, the minimum nonzero singular value decreases and approaches zero; take ${\beta }^t={\mathsf{\Sigma }}_{rr}^t{\beta }^0, \left|{\beta }^t\right|\ge 0.1t_{max}^{-1}\left|{\beta }^0\right|$ to avoid crossing singularities. $t_{max}$ is the maximum number of iteration steps. When ${\mathsf{\Sigma }}_{rr}^t>0.1{ \mathrm{or} \mathsf{\Sigma }}_{rr}^t>{\mathsf{\Sigma }}_{rr}^{t-1}$, it moves away from singularities, take ${\beta }^t=5{\beta }^{t-1}, \left|{\beta }^t\right|\le \left|{\beta }^0\right|$ to accelerate the solution process.

(d)

After determining the size of ${\beta }^t$, the motion path can be tracked and the configuration can be updated according to the nonlinear prediction-correction method.

(e)

When t is greater than the maximum number of iteration steps $t_{max}$, the configuration is singular and the iteration ends.

4. Novel Characteristics of Origami Structures

Different from traditional structures, origami structures possess a few remarkable and novel characteristics, including reconfigurable configuration, tunable stiffness [70], negative Poisson’s ratio, high folding ratio [71], multistability [69], satisfactory strength [72], and energy absorption capacity [73].

Recongifurable Stiffness and Configuration

Origami structures have been adopted for medical devices because of their excellent folding behavior at a very small scale. For example, in drug delivery, it is necessary to accurately construct drug encapsulation packages to prevent premature degradation and side effects in the delivery process. Interestingly, the self-folding origami introduced in the design of drug containers can deal with this problem. It is easy to obtain 3D biocompatible all-polymeric containers that meet the requirements of size, shape, wall thickness, porosity, surface patterns, and chemical properties. Fernandes et al. [74] discussed the self-folding mechanism of polymeric containers driven by different stresses or surface tension, and they explored the applications of self-folding polymers in drug delivery. Azam et al. [6] confirmed that cells encapsulated in self-folding polymeric containers survived for more than a week. Using shape memory alloy as raw material, You et al. [8] introduced origami patterns to invent a self-folding stent that can be folded small enough to put into the blood vessel. Hou et al. [12] assembled graphene oxide andpolydopamine nanolayers by a gravity self-assembly method to prepare graphene paper with micron thickness. Temperature or light is used to control the adsorption and desorption of water molecules between the nanolayers, which enabled graphene paper to fold rapidly into a predetermined shape. According to computational origami and the reconfigurable shape of origami, Felton et al. [11] developed self-folding robots, which allow a plate assembly set to fold along the hinges of a predetermined crease pattern under the drive of embedded electronics. Such robots can be sent through collapsed buildings or tunnels and then assemble autonomously into their final functional forms.

In fact, the technology of self-folding origami, which produces spontaneous deformation through functional materials and specific excitation-induced structures, has attracted much attention [6,75]. It has shown good prospects in wearable electronic devices, soft robots, and mechanical metamaterials [23,76]. As material properties of mechanical metamaterials [45] arise from their geometry and structural layout, origami is a substantial source of inspiration for the innovative design of mechanical metamaterials. Because of the strong coupling of mechanical properties and crease patterns of metamaterials, their properties are flexible [23,70]. Inspired by the kinematics of a single degree-of-freedom zigzag strip, Maryam et al. [9] introduced a class of cellular folded mechanical metamaterials by combining origami with kirigami, which is a variation of origami including cutting of the paper without using glue instead of solely folding the paper as is the case with origami. These mechanical metamaterials are formed by connecting zigzag strips of parallelogram facets with identical kinematics, and can be applied to deployable structures at both small and large scales. Bertoldi et al. [70] proposed a 3D programmable mechanical metamaterial with tunable shape, volume, and stiffness. As shown in Figure 8, such a metamaterial is a mosaic structure composed of extruded cubes, which can be actively deformed into many specific shapes.

A significance of the metamaterials with Miura-ori pattern is that they exhibit a negative Poisson’s ratio [45,77]. The magnitude of the in-plane Poisson’s ratio is the same as that of the out-of-plane Poisson’s ratio, whereas the signs of the two ratios are opposite. Moreover, they are basically unaffected by the properties of materials.

In addition, origami-inspired structures offer satisfactory capacity for energy absorption [78]. You et al. [79] introduced origami patterns into the design of thin-walled square tubes to improve the energy absorption of components under axial compression. To promote the popularization and application of origami structures in automotive energy absorption boxes, Ma et al. [73] and You et al. [61] put forward a series of origami thin-walled tubes, and they carried out numerical simulations and dynamic impact tests on these structures. The results show that the energy absorption characteristics of these origami structures are better than those of traditional square tubes.

5. Discussion

Although there has been a lot of study on crease pattern designs based on Miura and other common patterns, the study of origami geometry focuses on flat foldability and rigid foldability. Considering the materials of actual engineering structures, it is not necessary for origami to strictly satisfy the above two characteristics. For origami structures to have better functionality and applicability, modularity, spatial periodicity, ductility, and folding mechanisms should be further considered. Additionally, in order to effectively obtain the accurate three-dimensional origami configurations required for engineering, it is necessary to explore the differences of geometric configurations and mechanical properties under different folding states of the same crease pattern and to analyze the relationship between crease patterns, folding modes, and mechanical properties. Despite that, various analytical models and methods have been developed to analyze the folding process of origami structures. The analysis methods mostly focus on rigid folding, and it is difficult to consider the elastic and plastic deformation of members. The folding deformation analysis theory for origami structures has not yet been established, and the study on the motion singularity of origami structures is relatively rare. Indeed, flexible electronics and artificial vascular stents have been developed based on the reconfiguration of origami. The characteristics of a negative Poisson’s ratio give rise to the field of mechanical metamaterials with adjustable stiffness, while the characteristics of energy absorption of origami structures have been widely used in automotive energy absorption boxes. Origami structures have good engineering application prospects in many industries. As a result, it is necessary to further improve the basic theory of origami to obtain new characteristics of origami structures and extend certain inherent characteristics of origami structures.

6. Conclusions

This paper introduces basic concepts of origami structures and their engineering applications. Recent advances on crease pattern design, kinematic analysis, and characteristics of origami structures are further reviewed. Notably, most methods for crease pattern design focus on rigid foldable origami patterns. To make origami structures widely applicable to engineering applications, the material characteristics of origami need to be considered in future research. In addition, it is necessary to improve the kinematic and dynamic models of origami structures so that they can effectively reflect the considerable deformation, rigid-flexible coupling, and other folding behaviors during transformation. As there are limited studies on potential bifurcation of origami structures, it is important to carry out future research on the singularity of origami structures and to achieve the desired multistability and tunable stiffness by utilizing bifurcation behaviors.