Research on an Optimization Method for a Partially Responsive Continuous Phase Modulated (CPM) Signal Based on an Optimal Generic Function
Abstract
:1. Introduction
2. Establishment of an Optimal Generic Function Model
3. Optimization and Solution of Partial Response CPM Symbol Signal
3.1. Optimization of CPM Signals of Different Lengths
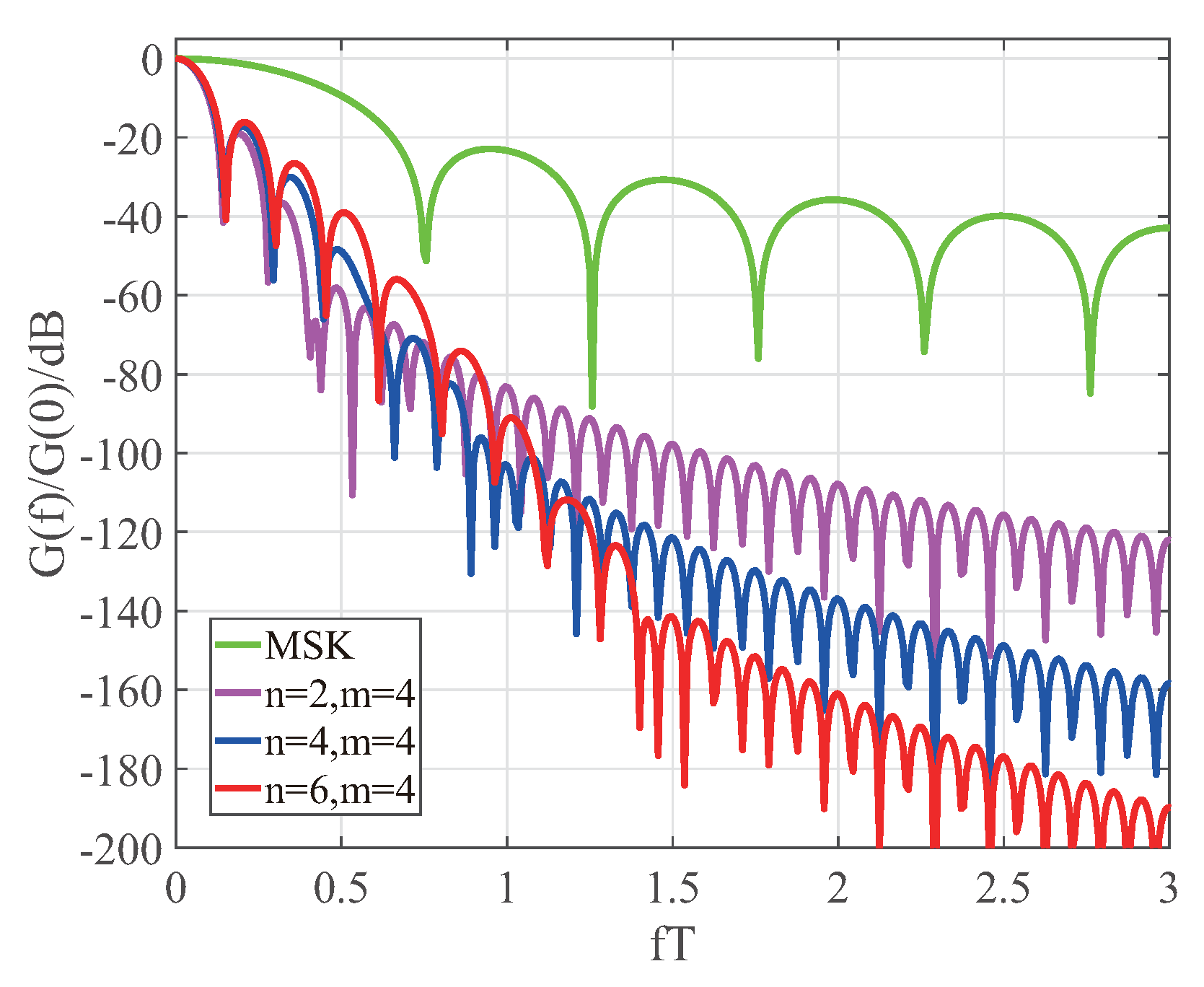
3.2. The Effect of the N-Value of the Optimal Generic Function Model on the CPM Function
3.3. Transient and Steady-State Modulation Method for Six-Way Parallel Transmission
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Zhang, Y.; Li, Q.; Huang, L.; Dai, K.; Song, J. Optimal Design of Cascade LDPC-CPM System Based on Bionic Swarm Optimization Algorithm. IEEE Trans. Broadcast. 2018, 64, 762–770. [Google Scholar] [CrossRef]
- Barbieri, A.; Fertonani, D.; Colavolpe, G. Spectrally-Efficient Continuous Phase Modulations. IEEE Trans. Wireless Commun. 2009, 8, 1564–1572. [Google Scholar] [CrossRef]
- Zhang, J.; Wang, F.; Zhong, Z.; Wang, S. Continuous Phase Modulation Classification via Baum-Welch Algorithm. IEEE Trans. Wireless Commun. 2018, 22, 1390–1393. [Google Scholar] [CrossRef]
- Zhou, J.; Pang, Q.; Xu, D.; Wu, W.; Yang, H. Minimum Frequency Shift Keying. In Principle of Communication; Higher Education Press: Beijing, China, 2015; pp. 185–192. [Google Scholar]
- Fan, C.; Cao, L. Minimum Frequency Shift Keying and Gaussian Minimum Frequency Shift Keying. In Principle of Communication; National Defense Industry Press: Beijing, China, 2015; pp. 231–242. [Google Scholar]
- Yang, Z.; Yu, S.; Chen, L.; Leng, H.; Lan, M.; Qiao, Y.; Gu, W. Constant Envelop Minimum-Shift Keying OFDM Coherent Optical Communication System. J. Lightw. Technol. 2012, 30, 3627–3632. [Google Scholar] [CrossRef]
- Liu, W.; Santhanam, B. Wideband partial response CPM demodulation via multirate frequency transformations and decision feedback equalization. EURASIP J. Wireless Commun. 2018, 2018. [Google Scholar] [CrossRef]
- Li, C.; Mathew, G. Analytical Solution for Optimum Partial-Response Target in Viterbi-Based Receivers. IEEE Trans. Commun. 2006, 54, 1715–1719. [Google Scholar]
- Ishkaev, I.R.; Shevelev, A.E.; Ovsyannikova, A.S.; Zavjalov, S.V.; Volvenko, S.V.; Makarov, S.B. Possibility of Peak-to-Avegare Power Ratio Reduction by Application of Optimal Signal for Transmitter Based on SDR HackRF One. In Proceedings of the 2018 IEEE International Conference on Electrical Engineering and Photonics (EExPolytech), St. Petersburg, Russia, 22–23 October 2018. [Google Scholar]
- Makarov, S.B.; Ovsyannikova, A.S.; Lavrenyuk, I.I.; Zavjalov, S.V.; Volvenko, S.V. Distributions of Probability of Power Values for Random Sequences of Optimal FTN Signals. In Proceedings of the 2018 International Symposium on Consumer Technologies (ISCT), St. Petersburg, Russia, 11–12 May 2018. [Google Scholar]
- Li, J.; Narayanan, K.R.; Georghiades, C.N. An Efficient Algorithm to Compute the Euclidean Distance Spectrum of a General Intersymbol Interference Channel and Its Applications. IEEE Trans. Commun. 2004, 52, 2041–2046. [Google Scholar] [CrossRef]
- Munawar, T.; Saleem, S.; Hassan, S.A.; Zaidi, S.M.H. Estimation of Modulation Index for Partial Response CPM Signal. IEEE Access 2018, 6, 7664–7674. [Google Scholar] [CrossRef]
- Alhussien, H.; Moon, J. The Error-Pattern-Correcting Turbo Equalizer: Spectrum Thinning at High SNRs. IEEE Trans. Inf. Theory 2011, 57, 953–971. [Google Scholar] [CrossRef] [Green Version]
- Perrins, E. A Timing False Lock Detector for M-ary Partial-Response CPM. IEEE Trans. Wireless Commun. 2013, 2, 671–674. [Google Scholar] [CrossRef]
- Naghsh, M.M.; Omidi, M.J. Reduction of out of band radiation usingcarrier-by-carrier partial response signallingin orthogonal frequency division multiplexing. IET Commun. 2010, 4, 1433–1442. [Google Scholar] [CrossRef]
- Huang, X.; Li, Y. Simple CPM receivers based on a switched linear modulation model. IEEE Trans. Commun. 2005, 53, 1100–1103. [Google Scholar] [CrossRef]
- Li, Y.; Jiang, Z.; Osman, O.; Han, X.; Yin, J. Mixed Norm Constrained Sparse APA Algorithm for Satellite and Network Echo Channel Estimation. IEEE Access 2018, 6, 65901–65908. [Google Scholar] [CrossRef]
- Shi, W.; Li, Y.; Wang, Y. Noise-free Maximum Correntropy Criterion Algorithm in Non-Gaussian Environment. IEEE Trans. Circuits Syst. Ii Express Briefs 2019, 2019. [Google Scholar] [CrossRef]
- Shi, W.; Li, Y.; Zhao, L.; Liu, X. Controllable Sparse Antenna Array for Adaptive Beamforming. IEEE Access 2019, 7, 6412–6423. [Google Scholar] [CrossRef]
- Xu, Y.; Xue, W.; Shang, W.A. Pan-Function Model for the Utilization of Bandwidth Improvement and PAPR Reduction. Math. Probl. Eng. 2014, 2014. [Google Scholar] [CrossRef]
- Wu, D.; Zhang, Y.; Wang, S.; Guo, B. The Basic Properties of the Fourier Transform. In Signal and Linear System Analysis; Higher Education Press: Beijing, China, 2005; pp. 46–48. [Google Scholar]
- Xue, W.; Guo, L.; Zhang, X.; Ma, W. Inter-code Interference and Symbol Cross-correlation Properties Affect the Signal. J. Harb. Engin. Univ. 2010, 31, 109–114. [Google Scholar]
- Song, S.; Kim, J.; Kim, J. A Passive Equalizer Optimization Method Based on Time-Domain Inter-Symbol Interference Cancellation Technique. IEEE Trans. Electromagn. Compat. 2018, 60, 807–810. [Google Scholar] [CrossRef]
- Chen, M.; Liu, G.; Zhou, H.; Chen, Q.; He, J. Inter-Symbol Differential Detection-Enabled Sampling Frequency Offset Compensation for DDO-OFDM. IEEE Photon. Technol. Lett. 2018, 30, 2095–2098. [Google Scholar] [CrossRef]
- Yang, Y.; Tao, R.; Wang, Y. A New GMSK Orthogonal Modulation Signal Generation Method. Electr. J. 2005, 6, 1095–1098. [Google Scholar]








| Length of Symbol | n | K | |||||
|---|---|---|---|---|---|---|---|
| 2 | 1.1743 | 0.5569 | −0.0241 | −0.0241 | −0.0015 | 1.3377 | |
| 2T | 4 | 1.0388 | 0.6630 | 0.1291 | −0.0122 | 0.0023 | 1.5121 |
| 6 | 0.9479 | 0.6961 | 0.2548 | 0.0284 | −0.00428 | 1.6571 | |
| 2 | 0.8302 | 0.3937 | −0.0170 | 0.0033 | −0.0010 | 0.9460 | |
| 4T | 4 | 0.7361 | 0.4698 | 0.0915 | −0.0087 | 0.0016 | 1.0670 |
| 6 | 0.6590 | 0.4933 | 0.1958 | 0.0317 | −0.0003 | 1.1917 | |
| 2 | 0.6778 | 0.3215 | −0.0139 | 0.0027 | −0.0009 | 0.7724 | |
| 6T | 4 | 0.6007 | 0.3834 | 0.0747 | −0.0071 | 0.0013 | 0.8745 |
| 6 | 0.5481 | 0.4025 | 0.1473 | 0.0164 | −0.0024 | 0.9552 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qi, J.; Makarov, S.B.; Liu, M.; Li, B.; Xue, W. Research on an Optimization Method for a Partially Responsive Continuous Phase Modulated (CPM) Signal Based on an Optimal Generic Function. Symmetry 2019, 11, 1114. https://doi.org/10.3390/sym11091114
Qi J, Makarov SB, Liu M, Li B, Xue W. Research on an Optimization Method for a Partially Responsive Continuous Phase Modulated (CPM) Signal Based on an Optimal Generic Function. Symmetry. 2019; 11(9):1114. https://doi.org/10.3390/sym11091114
Chicago/Turabian StyleQi, Junwei, Sergey B. Makarov, Mingxin Liu, Beiming Li, and Wei Xue. 2019. "Research on an Optimization Method for a Partially Responsive Continuous Phase Modulated (CPM) Signal Based on an Optimal Generic Function" Symmetry 11, no. 9: 1114. https://doi.org/10.3390/sym11091114
APA StyleQi, J., Makarov, S. B., Liu, M., Li, B., & Xue, W. (2019). Research on an Optimization Method for a Partially Responsive Continuous Phase Modulated (CPM) Signal Based on an Optimal Generic Function. Symmetry, 11(9), 1114. https://doi.org/10.3390/sym11091114





