Simulation of Passenger Evacuation Process in Cruise Ships Based on A Multi-Grid Model
Abstract
:1. Introduction
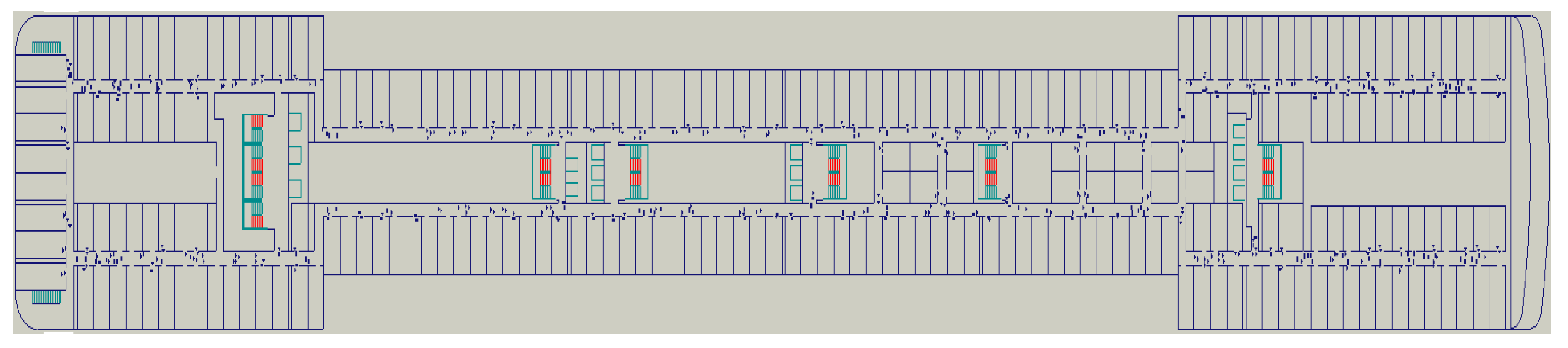
2. The Evacuation Scenario
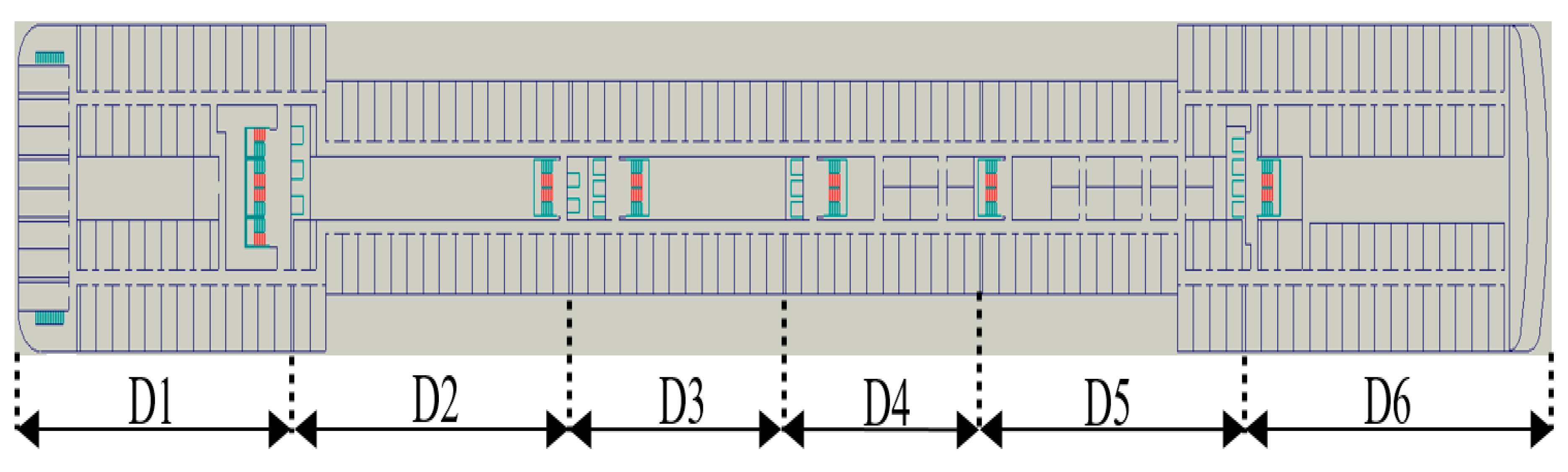
2.1. Geometrical Category
2.2. Population Category
2.3. Environmental Category
2.4. Procedural Category
3. Modeling of Multi-Grid in a Cruise Ship
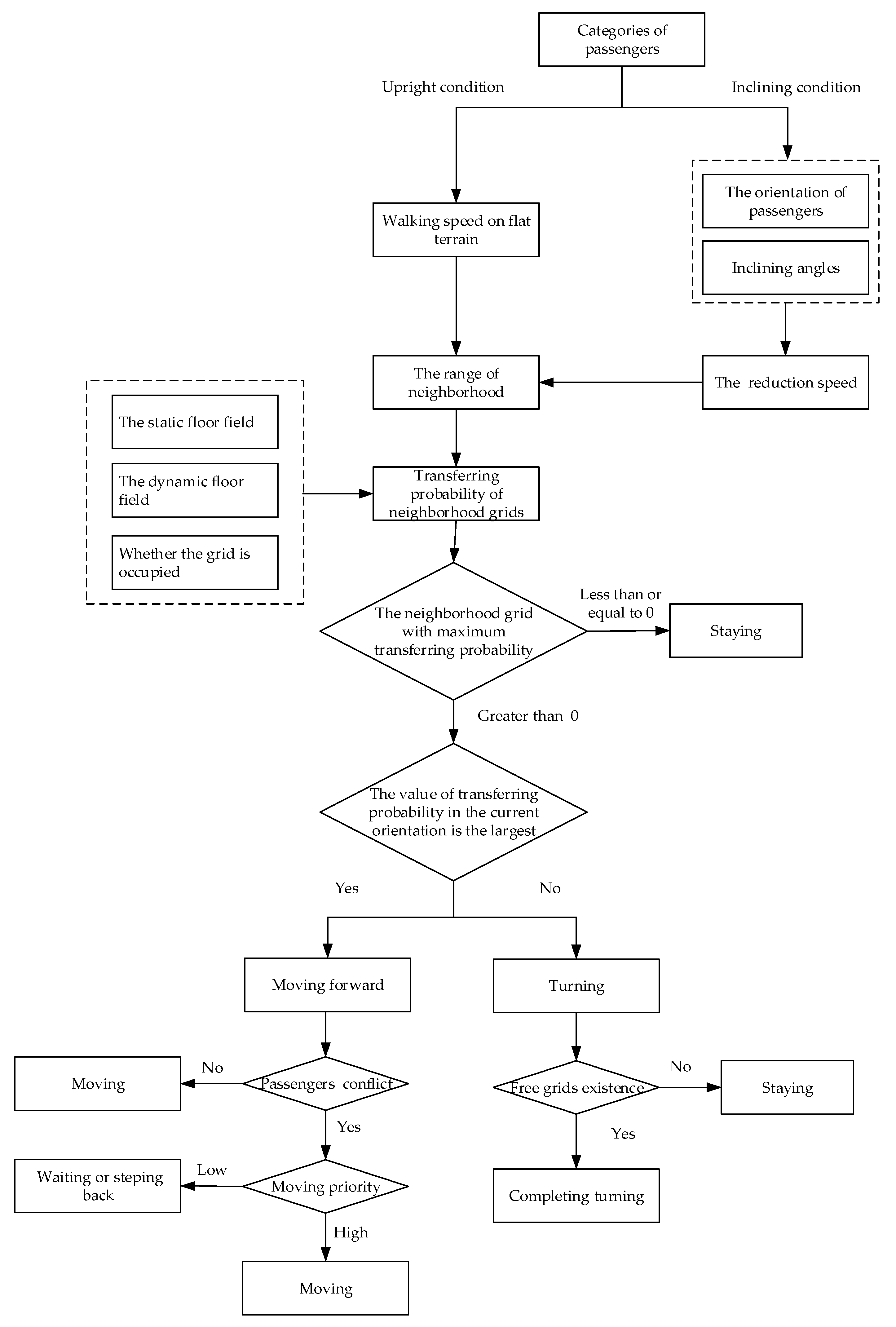
3.1. The Passenger Moving Rules of the Multi-Grid Model
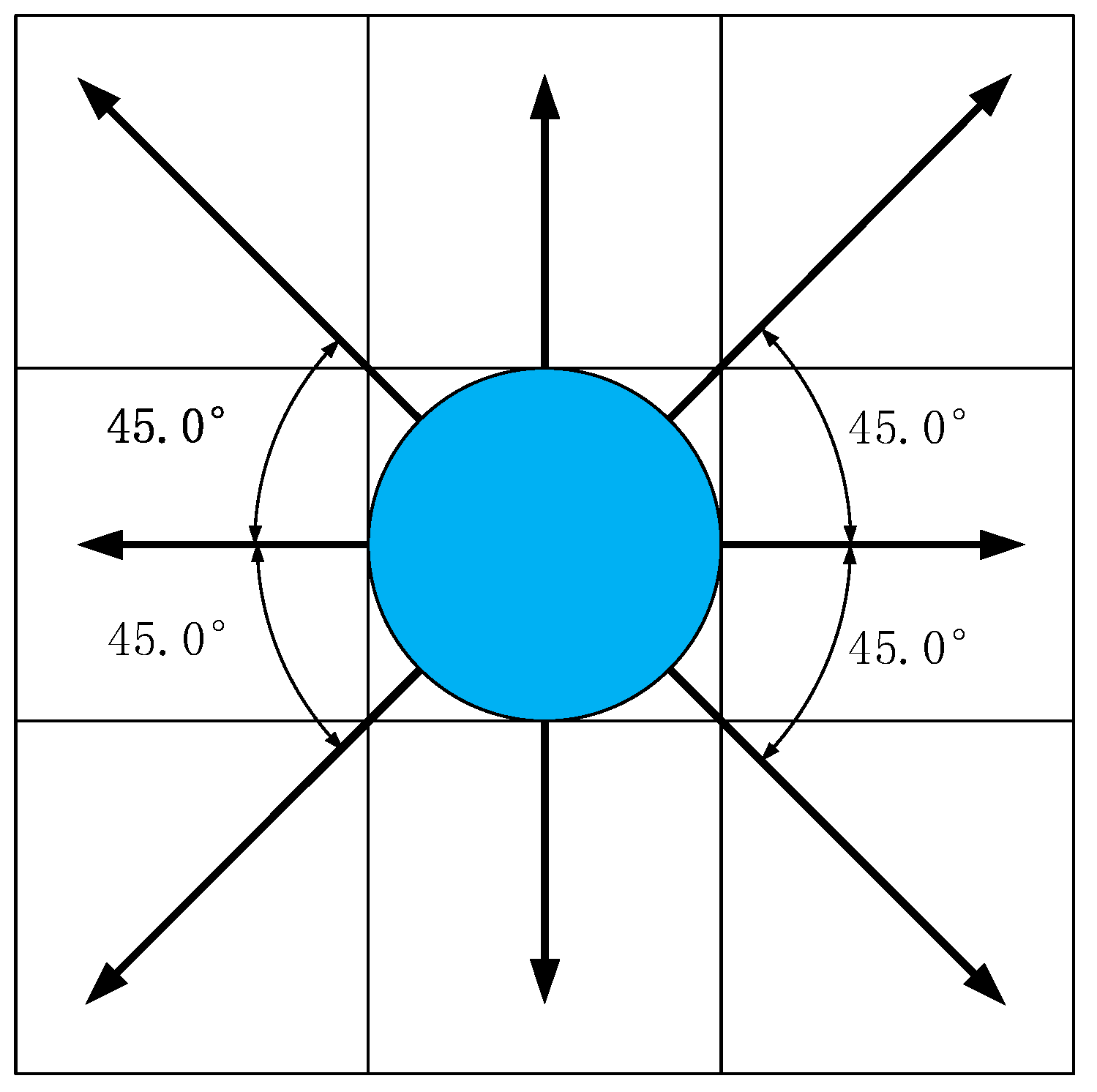
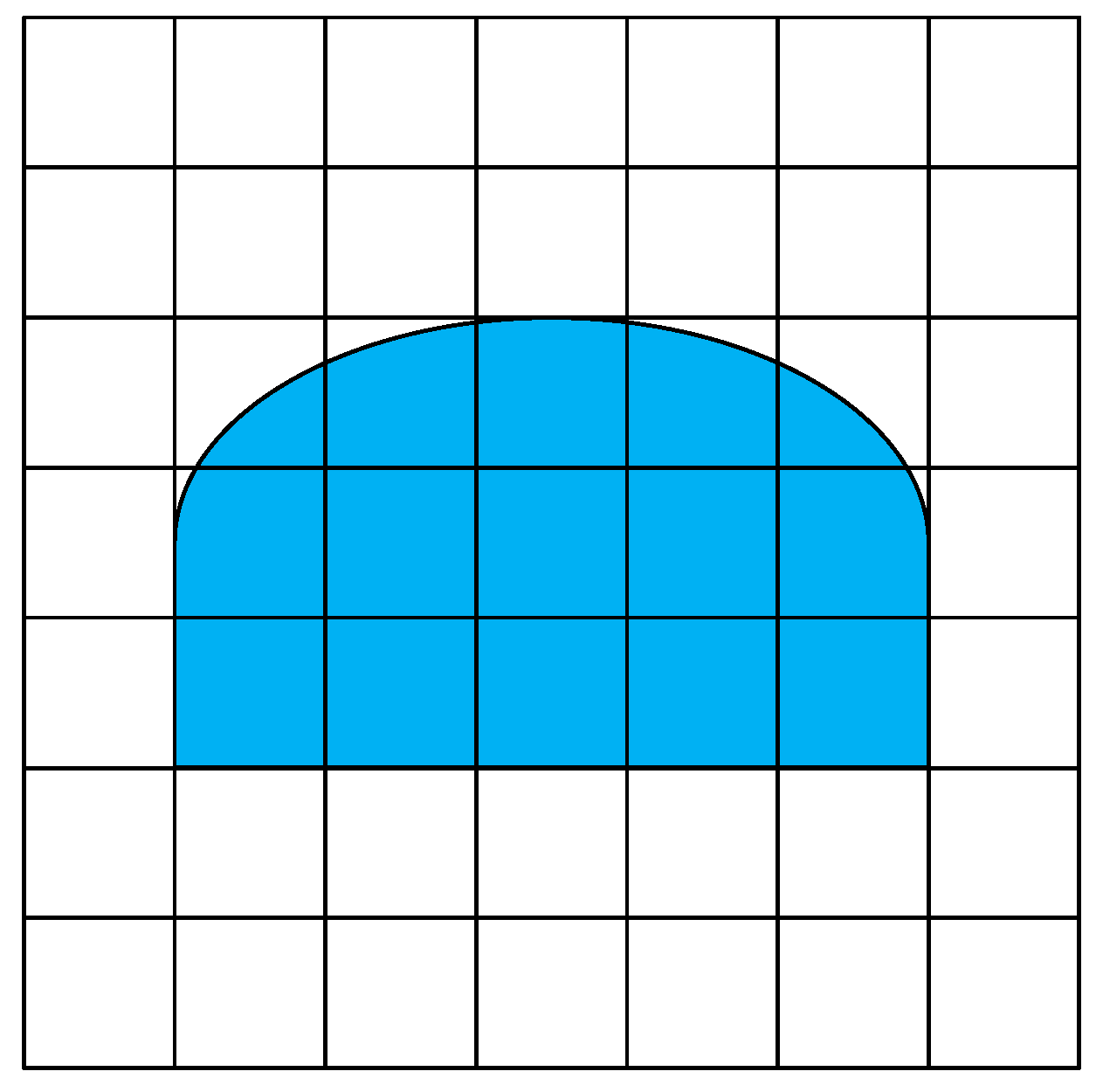
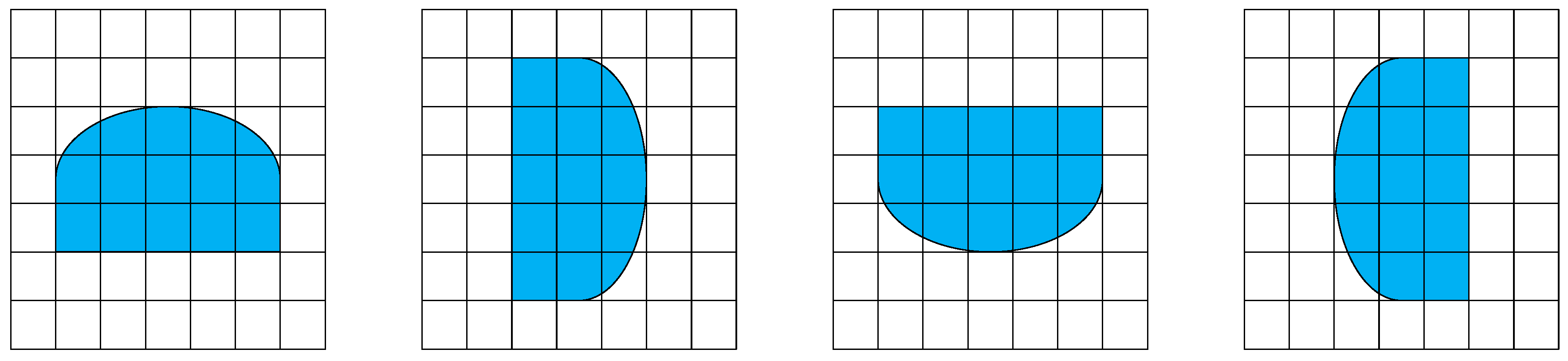
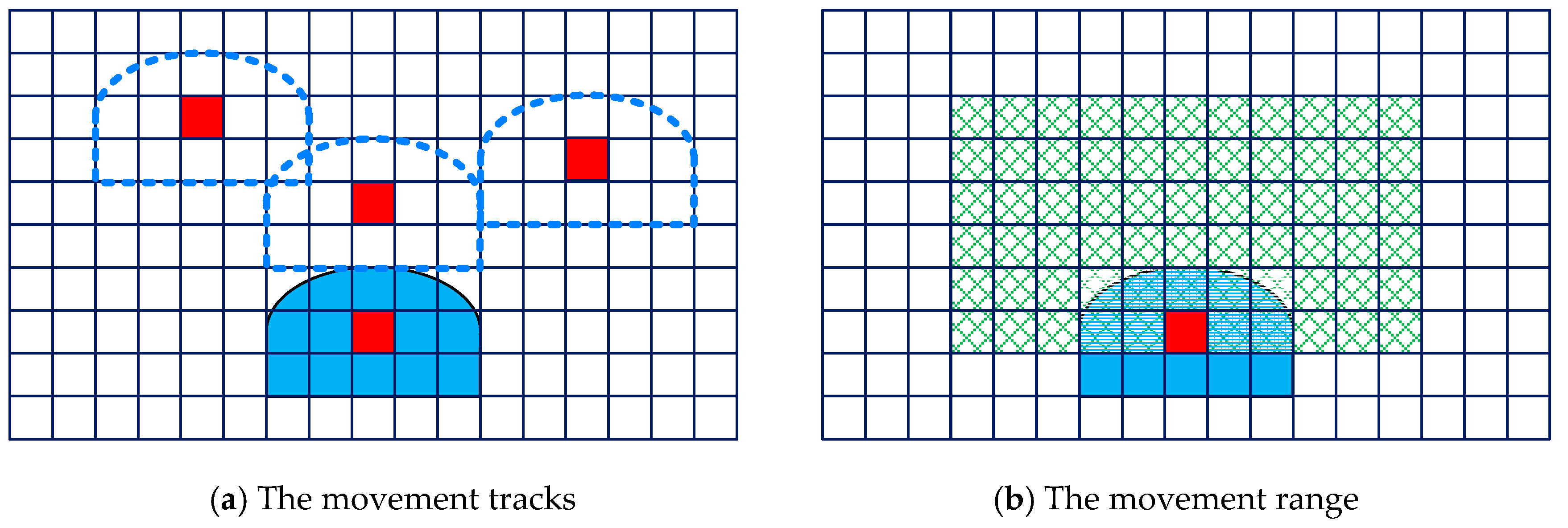
3.1.1. The Moving Range
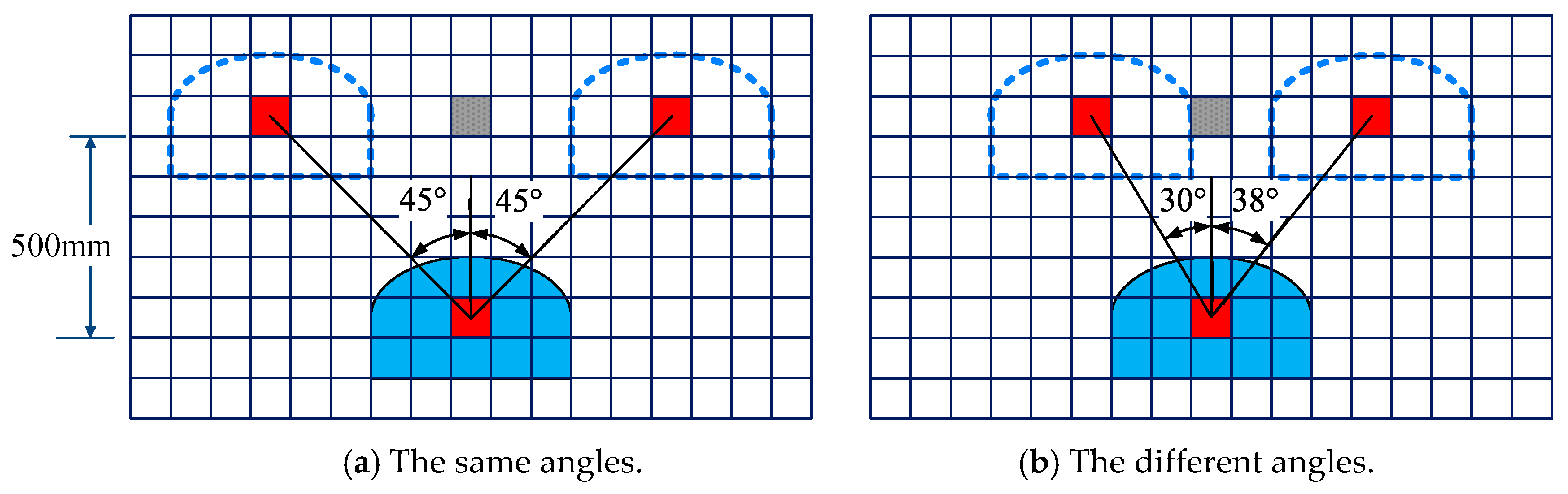
3.1.2. The Turning Rules
3.1.3. The Anti-Collision Rule
3.2. The Static Floor Field
3.3. The Dynamic Floor Field
3.3.1. Attraction of Mainstream Crowd
3.3.2. Exclusion Between Individuals
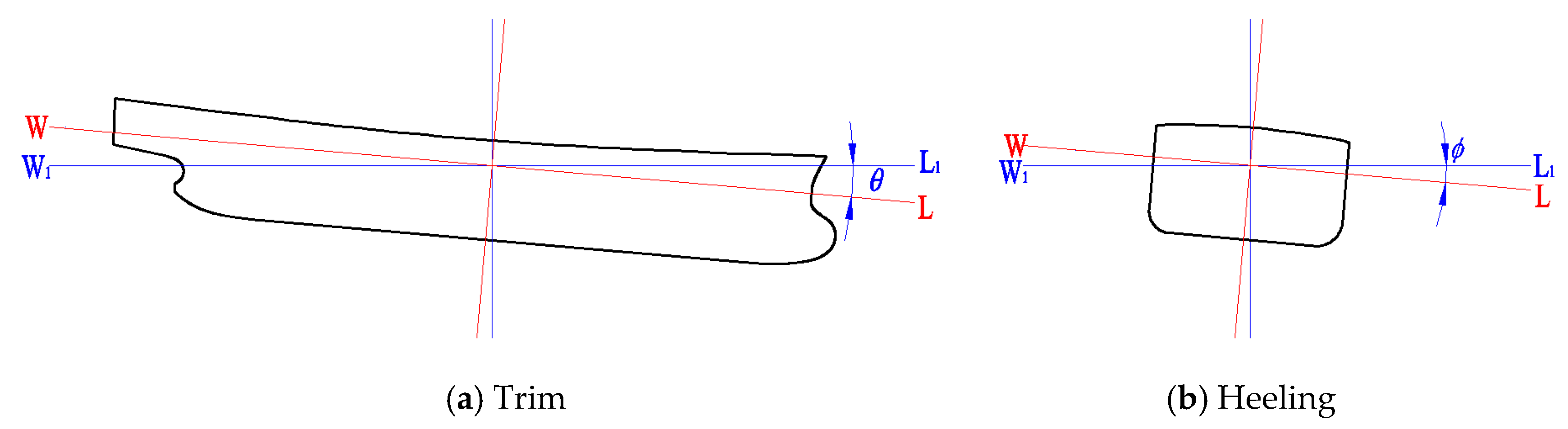
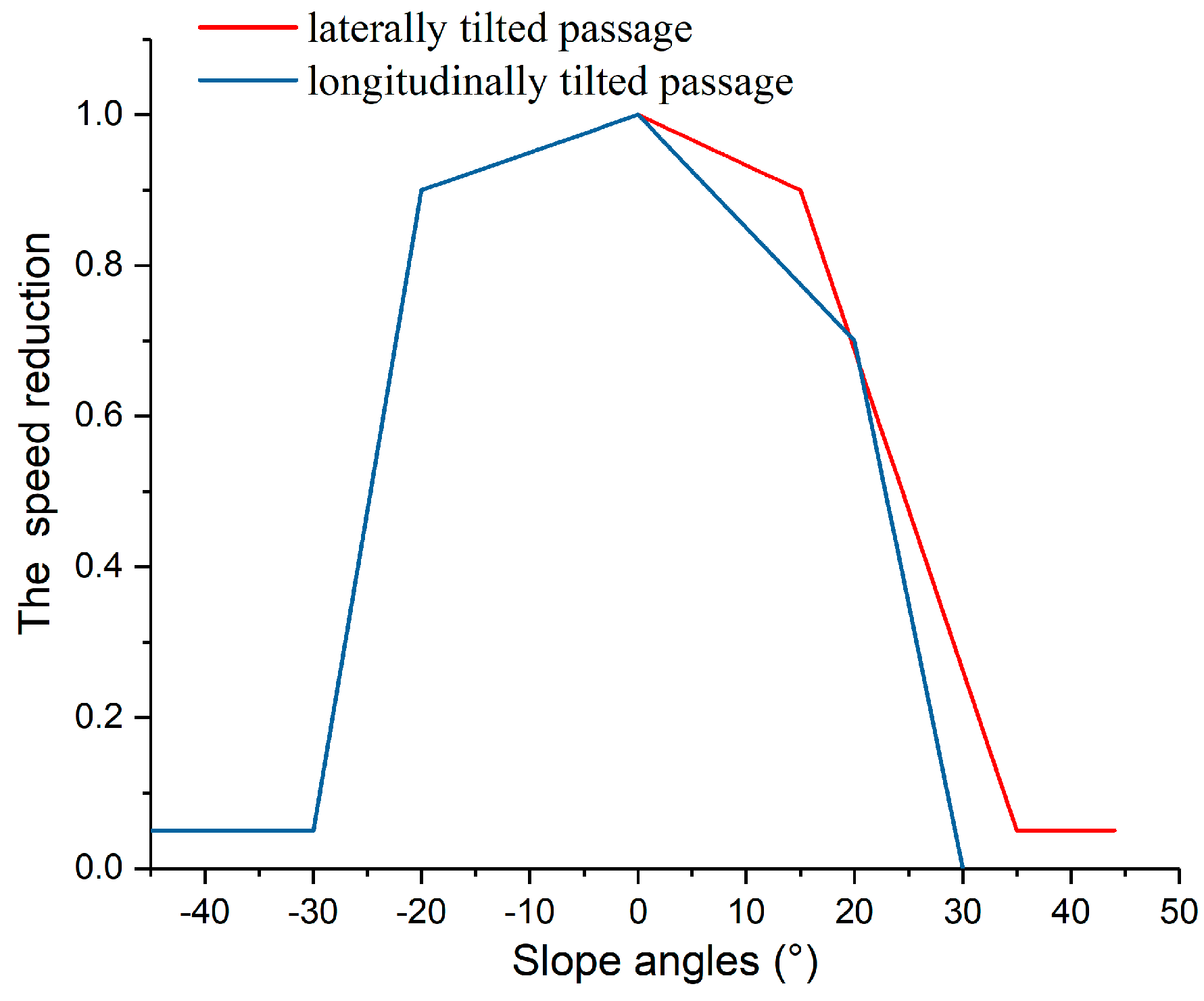
3.4. The Change of Walking Speeds Under the Inclining Condition
3.5. The Transferring Rule
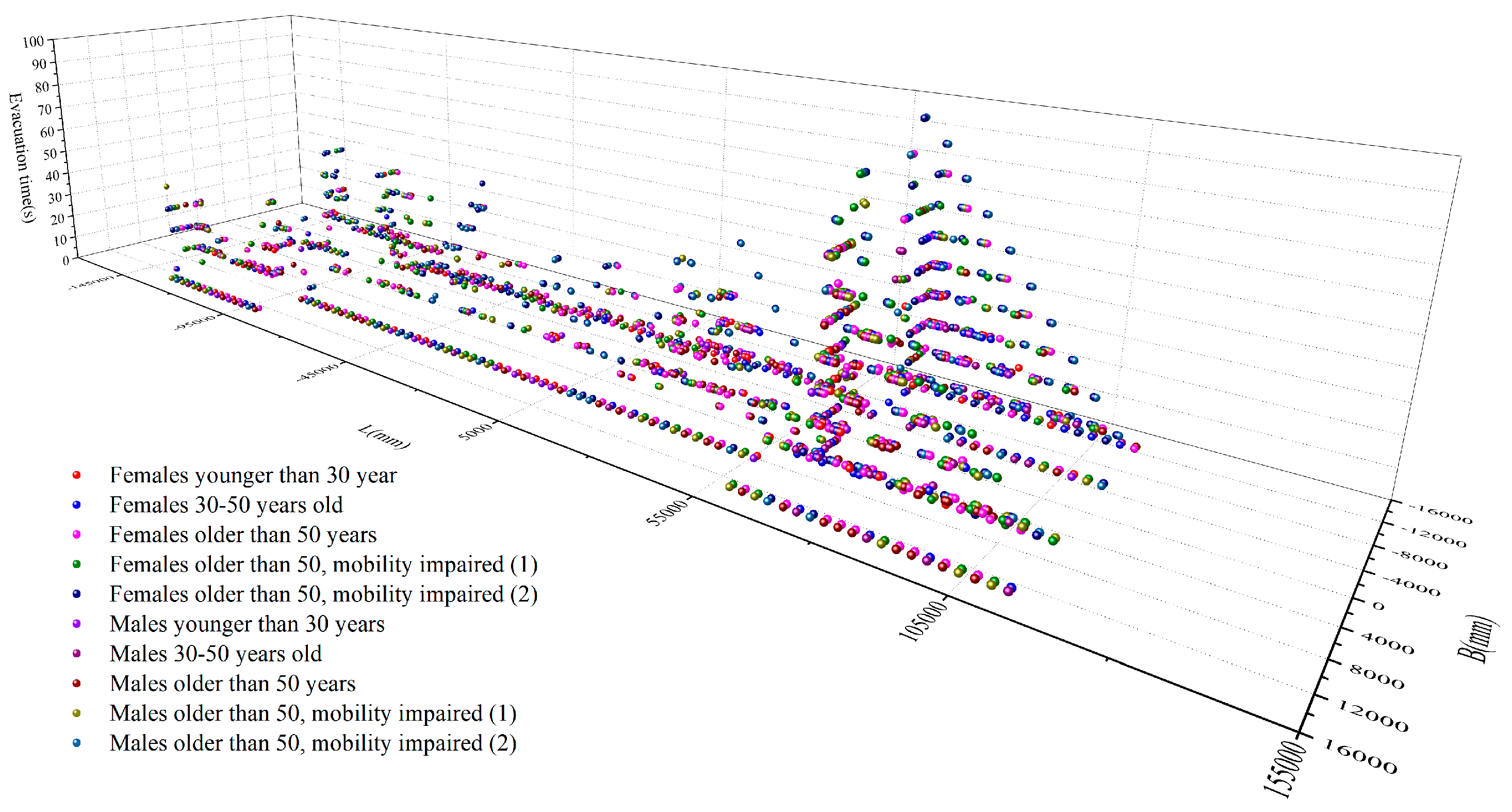
4. Simulation and Results
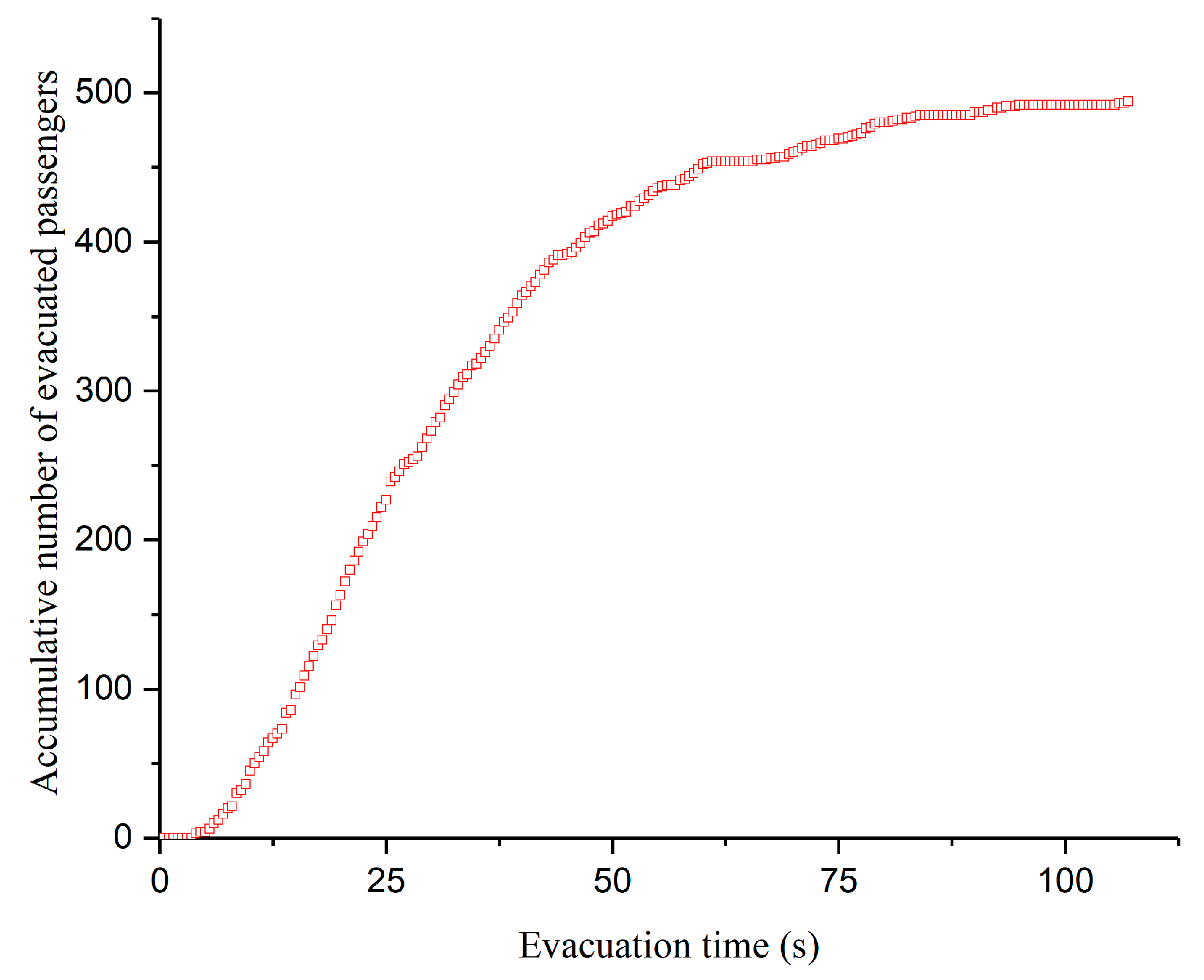
4.1. The Evacuation Simulation Under the Upright Condition
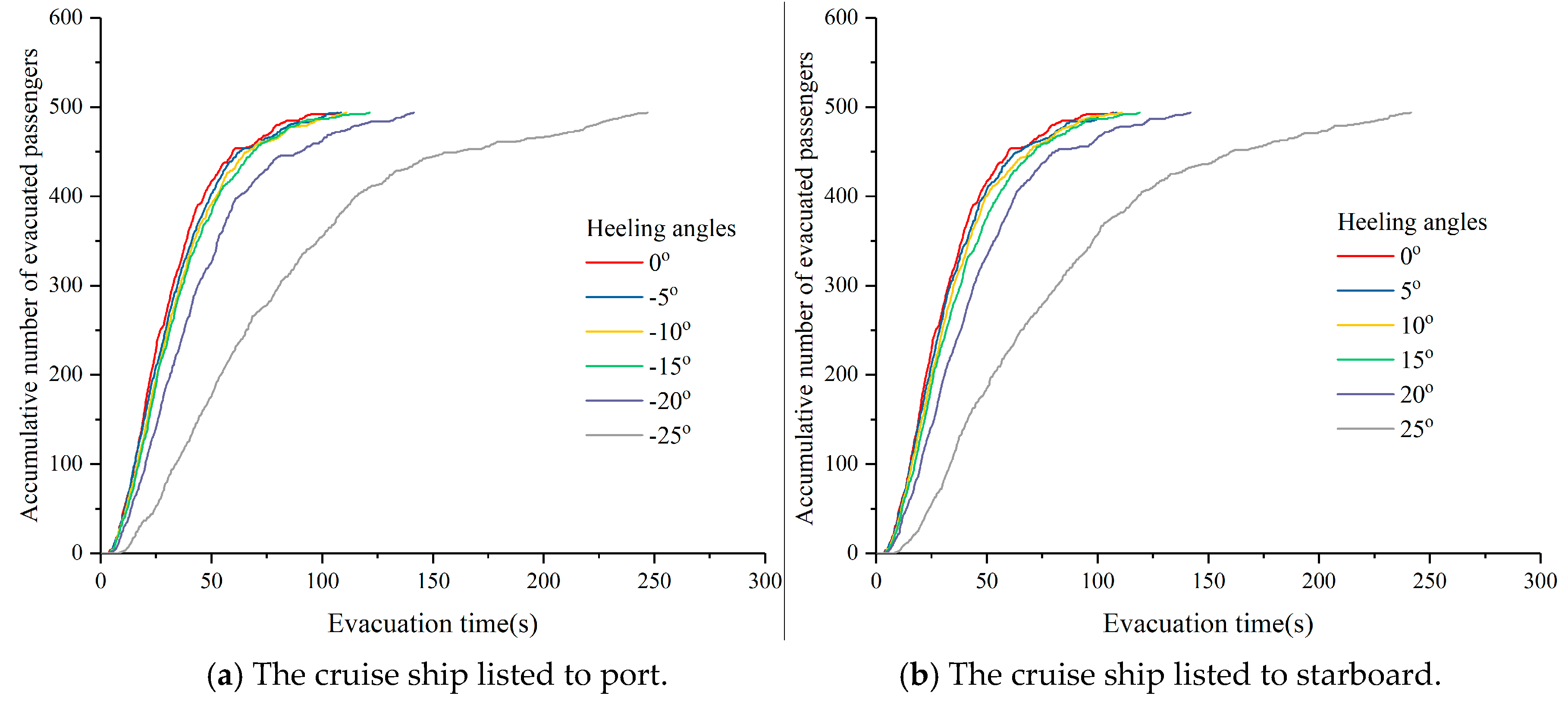
4.2. The Evacuation Simulation Under the Inclining Condition
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Wang, H. Annual Report on China’s Cruise Industry 2018; Social Sciences Academic Press: Beijing, China, 2018; pp. 3–4. [Google Scholar]
- International Maritime Organization. Guidelines for Evacuation Analysis for New and Existing Passenger Ships; International Maritime Organization: London, UK, 2016; p. 32. [Google Scholar]
- Vanem, E.; Skjong, R. Designing for safety in passenger ships utilizing advanced evacuation analyses—A risk based approach. Saf. Sci. 2006, 44, 111–135. [Google Scholar] [CrossRef]
- Vanem, E.; Skjong, R. Fire and evacuation risk assessment for passenger ships. In Proceedings of the 10th International Fire Science & Engineering Conference (Interflam), Edinburgh, Scotland, 5–7 July 2004. [Google Scholar]
- Vanem, E.; Skjong, R. Collision and Grounding of Passenger Ships—Risk Assessment and Emergency Evacuations. In Proceedings of the 3rd International Conference on Collision and Grounding of Ships(ICCGS), Izu, Japan, 25–27 October 2004; pp. 195–202. [Google Scholar]
- Pagiaziti, A.; Maliaga, E.; Eliopoulou, E.; Zaraphonitis, G.; Hamann, R. Statistics of collision, grounding and contact accidents of passenger and container ships. In Proceedings of the 5th International Symposium on ship Operations, Management and Economics (SOME), Athens, Greece, 28–29 May 2015; pp. 28–29. [Google Scholar]
- Galea, E.R.; Deere, S.; Filippidis, L.; Brown, R.; Nicholls, I.; Hifi, Y.; Besnard, N. The SAFEGUARD validation data-set and recommendations to IMO to update MSC Circ 1238. RINA, Royal Institution of Naval Architects. In Proceedings of the Safeguard: Passenger Evacuation Seminar 2012, London, UK, 30 November 2012; pp. 41–60. [Google Scholar]
- Galea, E.R.; Deere, S.; Brown, R.; Filippidis, L. An Experimental Validation of an Evacuation Model using Data Sets Generated from Two Large Passenger Ships. J. Ship Res. 2013, 57, 155–170. [Google Scholar] [CrossRef]
- Galea, E.R.; Deere, S.; Brown, R.; Filippidis, L. A Validation Data-Set and Suggested Validation Protocol for Ship Evacuation Models. Fire Saf. Sci. 2014, 11, 1115–1128. [Google Scholar] [CrossRef] [Green Version]
- EVI—Evacuation Analysis Software. Available online: http://www.brookesbell.com/service/software/evi-escape-evacuation-analysis (accessed on 27 August 2019).
- Fire Safety Engineering Group. Available online: http://fseg.gre.ac.uk/leaflets/exodusleaflets.html (accessed on 27 August 2019).
- Gwynne, S.M.V.; Galea, E.R.; Lyster, C.; Glen, I. Analysing the Evacuation Procedures Employed on a Thames Passenger Boat Using the maritimeEXODUS Evacuation Model. Fire Technol. 2003, 39, 225–246. [Google Scholar] [CrossRef]
- Elnabawybahriz, M.N.; Hassan, M.H.N. The impact of low efficient evacuation plan during costa concordia accident. Int. J. Mech Sci. 2016, 5, 43–54. [Google Scholar]
- Kim, H.; Roh, M.; Han, S. Passenger evacuation simulation considering the heeling angle change during sinking. Int. J. Nav Arch. Ocean. 2019, 11, 329–343. [Google Scholar] [CrossRef]
- Ha, S.; Ku, N.; Roh, M.; Lee, K. Cell-based evacuation simulation considering human behavior in a passenger ship. Ocean. Eng 2012, 53, 138–152. [Google Scholar] [CrossRef]
- Yuan, G.; Zhang, L.; Liu, L.; Wang, K. Passengers’ Evacuation in Ships Based on Neighborhood Particle Swarm Optimization. Math. Probl. Eng. 2014. [Google Scholar] [CrossRef]
- Nevalainen, J.; Ahola, M.K.; Kujala, P. Modeling passenger ship evacuation from passenger perspective. In Proceedings of the Marine Design 2015, London, UK, 2–3 September 2015. [Google Scholar]
- Zhu, C.; Han, D.; Chen, M.; Yao, J. Accessibility evaluation of ship evacuation based on DEA. J. Harbin Eng. Univ. 2015, 6, 741–745. [Google Scholar]
- Balakhontceva, M.; Karbovskii, V.; Rybokonenko, D.; Boukhanovsky, A.V. Multi-agent Simulation of Passenger Evacuation Considering Ship Motions. Procedia Comput. Sci. 2015, 66, 140–149. [Google Scholar] [CrossRef] [Green Version]
- Rybokonenko, D.; Balakhontceva, M.; Voloshin, D.V.; Karbovskii, V. Agent-based Modeling of Crowd Dynamics on a Moving Platform. Procedia Comput. Sci. 2015, 66, 317–327. [Google Scholar] [CrossRef] [Green Version]
- Balakhontceva, M.; Karbovskii, V.; Sutulo, S.; Boukhanovsky, A.V. Multi-agent Simulation of Passenger Evacuation from a Damaged Ship under Storm Conditions. In Proceedings of the International Conference on Conceptual Structures, Annecy, France, 5–7 July 2016; pp. 2455–2464. [Google Scholar]
- Li, J.; Zhu, H. A Risk-based Model of Evacuation Route Optimization under Fire. Procedia Eng. 2018, 211, 365–371. [Google Scholar] [CrossRef]
- Park, K.; Ham, S.; Ha, S. Validation of advanced evacuation analysis on passenger ships using experimental scenario and data of full-scale evacuation. Comput. Ind. 2015, 71, 103–115. [Google Scholar] [CrossRef]
- Roh, M.; Ha, S. Advanced ship evacuation analysis using a cell-based simulation model. Comput. Ind. 2013, 64, 80–89. [Google Scholar] [CrossRef]
- Ginnis, A.I.; Kostas, K.V.; Politis, C.G.; Kaklis, P.D. VELOS: A VR platform for ship-evacuation analysis. Comput. Aid. Des. 2010, 42, 1045–1058. [Google Scholar] [CrossRef] [Green Version]
- Kim, H.; Park, J.; Lee, D.; Yang, Y. Establishing the methodologies for human evacuation simulation in marine accidents. Comput. Ind. Eng. 2004, 46, 725–740. [Google Scholar] [CrossRef]
- Schmidt, B. Modelling of Human Behavior: The PECS Reference Model. In Proceedings of the 14th European Simulation Symposium and Exhibition, Dresden, Germany, 23–26 October 2002. [Google Scholar]
- Liu, B.Y.; Zhou, X.S.; Yan, S.Y. Influence of carrier corridor configuration on evacuation performance. Chin. J. Ship Res. 2018, 13, 1–6. [Google Scholar]
- Ni, B.; Zhen, L.; Pei, Z.; Xiang, L. An Evacuation Model for Passenger Ships That Includes the Influence of Obstacles in Cabins. Math. Probl. Eng. 2017. [Google Scholar] [CrossRef]
- Ni, B.; Li, Z.; Li, X. Agent-Based Evacuation in Passenger Ships Using a Goal-Driven Decision-Making Model. Pol. Marit. Res. 2017, 24, 56–67. [Google Scholar] [CrossRef] [Green Version]
- Ni, B.; Lin, Z.; Li, P. Agent-based evacuation model incorporating life jacket retrieval and counterflow avoidance behavior for passenger ships. J. Stat. Mech. Theory Exp. 2018, 12, 123405. [Google Scholar] [CrossRef]
- Sarvari, P.A.; Cevikcan, E. A Simulation-Based Methodology for Evaluating the Factors on Ship Emergency Evacuation. Trans. R. Inst. Nav. Archit. Part A 2017, 159, 415–434. [Google Scholar]
- Bles, W.; Nooy, S.; Boer, L.C. Influence of Ship Listing and Ship Motion on Walking Speed. In Proceedings of the First Conference on Pedestrian and Evacuation Dynamics, Duisburg, Germany, 4–6 April 2001; pp. 437–452. [Google Scholar]
- Lee, D.; Park, J.H.; Kim, H. A study on experiment of human behavior for evacuation simulation. Ocean. Eng. 2004, 31, 931–941. [Google Scholar] [CrossRef]
- Sun, J.; Lu, S.; Lo, S.; Jian, M.; Xie, Q. Moving characteristics of single file passengers considering the effect of ship trim and heeling. Physica A 2018, 490, 476–487. [Google Scholar] [CrossRef]
- Koss, L.L.; Moore, A.; Porteous, B. Human mobility data for movement on ships. In Proceedings of the International Conference on Fire at Sea, London, UK, 20–21 November 1997; pp. 11–21. [Google Scholar]
- International Maritime Organization. Passenger Ship Safety Time Dependent Survival Probability of a Damaged Passenger Ship; International Maritime Organization: London, UK, 2006; pp. 46–47. [Google Scholar]
- Kirchner, A.; Schadschneider, A. Simulation of evacuation processes using a bionics-inspired cellular automaton model for pedestrian dynamics. Physica A 2002, 312, 260–276. [Google Scholar] [CrossRef] [Green Version]
- Nishinari, K.; Kirchner, A.; Namazi, A.; Schadschneider, A. Extended Floor Field CA Model for Evacuation Dynamics. Trans. Inf. Syst. D 2004, 87, 726–732. [Google Scholar]
- Nagai, R.; Fukamachi, M.; Nagatani, T. Experiment and simulation for counterflow of people going on all fours. Physica A 2005, 358, 516–528. [Google Scholar] [CrossRef]
- Helbing, D.; Molnar, P. Social force model for pedestrian dynamics. Phys. Rev. E 1995, 51, 4282–4286. [Google Scholar] [CrossRef] [Green Version]
- Helbing, D.; Farkas, I.J.; Vicsek, T. Simulating dynamical features of escape panic. Nature 2000, 407, 487–490. [Google Scholar] [CrossRef] [Green Version]
- Henderson, L.F. On the fluid mechanics of human crowd motion. Trans. Res. 1974, 8, 509–515. [Google Scholar] [CrossRef]
- Helbing, D. A Fluid-Dynamic Model for the Movement of Pedestrians. Complex. Syst. 1992, 6, 391–415. [Google Scholar]
- Mei, Y.; Liang, Y.; Tu, Y. A Multi-Granularity 2-Tuple QFD Method and Application to Emergency Routes Evaluation. Symmetry 2018, 10, 484. [Google Scholar] [CrossRef]
- Okazaki, S.; Yamamoto, C. A Study of Pedestrian Movement in Architectural Space Part 4: Pedestrian Movement Represented in Perspective. Trans. AIJ 1981, 299, 105–113. [Google Scholar]
- Yu, W.J.; Chen, R.; Dong, L.Y.; Dai, S.Q. Centrifugal force model for pedestrian dynamics. Phys. Rev. E Stat. Nonlin. Soft Matter. Phys. 2005, 72, 26112. [Google Scholar] [CrossRef] [PubMed]
- Yang, W.; Hu, Y.; Hu, C.; Yang, M. An Agent-Based Simulation of Deep Foundation Pit Emergency Evacuation Modeling in the Presence of Collapse Disaster. Symmetry 2018, 10, 581. [Google Scholar] [CrossRef]
- Hai-Jun, H.; Ren-Yong, G. Static floor field and exit choice for pedestrian evacuation in rooms with internal obstacles and multiple exits. Phys. Rev. E Stat. Nonlin. Soft Matter. Phys. 2008, 78, 21131. [Google Scholar]
- Fu, Z.; Zhou, X.; Zhu, K.; Chen, Y.; Zhuang, Y.; Hu, Y.; Yang, L.; Chen, C.; Jian, L. A floor field cellular automaton for crowd evacuation considering different walking abilities. Physica A 2015, 420, 294–303. [Google Scholar] [CrossRef]
- Zheng, Y.; Li, X.; Jia, B.; Jiang, R. Simulation of pedestrians’ evacuation dynamics with underground flood spreading based on cellular automaton. Simul. Model. Pract. Theory 2019, 94, 149–161. [Google Scholar] [CrossRef]
- Song, W.; Xu, X.; Wang, B.H.; Ni, S. Simulation of evacuation processes using a multi-grid model for pedestrian dynamics. Physica A 2006, 363, 492–500. [Google Scholar] [CrossRef]
- China National Institute of Standardization. Human Dimension of Chinese Adults; Standards Press of China: Beijing, China, 1988; pp. 10–11. [Google Scholar]
- Gong, J. Human Size and Indoor Space; Tianjin Science and Technology Press: Tianjin, China, 1999; 208p. [Google Scholar]
- Cao, S.; Song, W.; Lv, W.; Fang, Z. A multi-grid model for pedestrian evacuation in a room without visibility. Phys. A 2015, 436, 45–61. [Google Scholar] [CrossRef]
- Fu, L.B. A Study on Pedestrian and Evacuation Dynamics Involving Human Behavior. Ph.D. Thesis, University of Science and Technology of China, Hefei, China, 2017. [Google Scholar]
- Gallup, A.C.; Hale, J.J.; Sumpter, D.J.T.; Simon, G.; Alex, K.; Krebs, J.R.; Couzin, I.D. Visual attention and the acquisition of information in human crowds. Proc. Natl. Acad. Sci. USA 2012, 109, 7245–7250. [Google Scholar] [CrossRef] [Green Version]





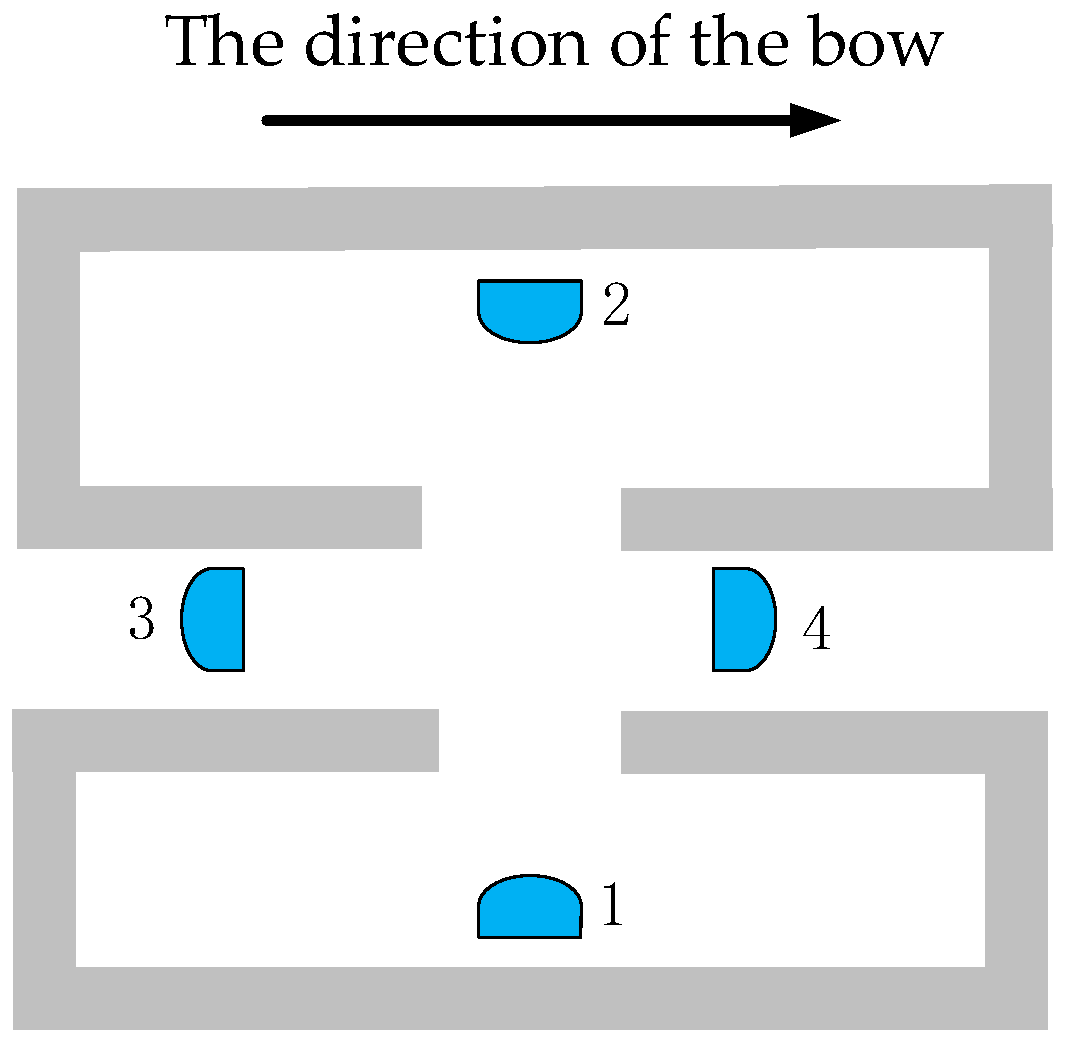

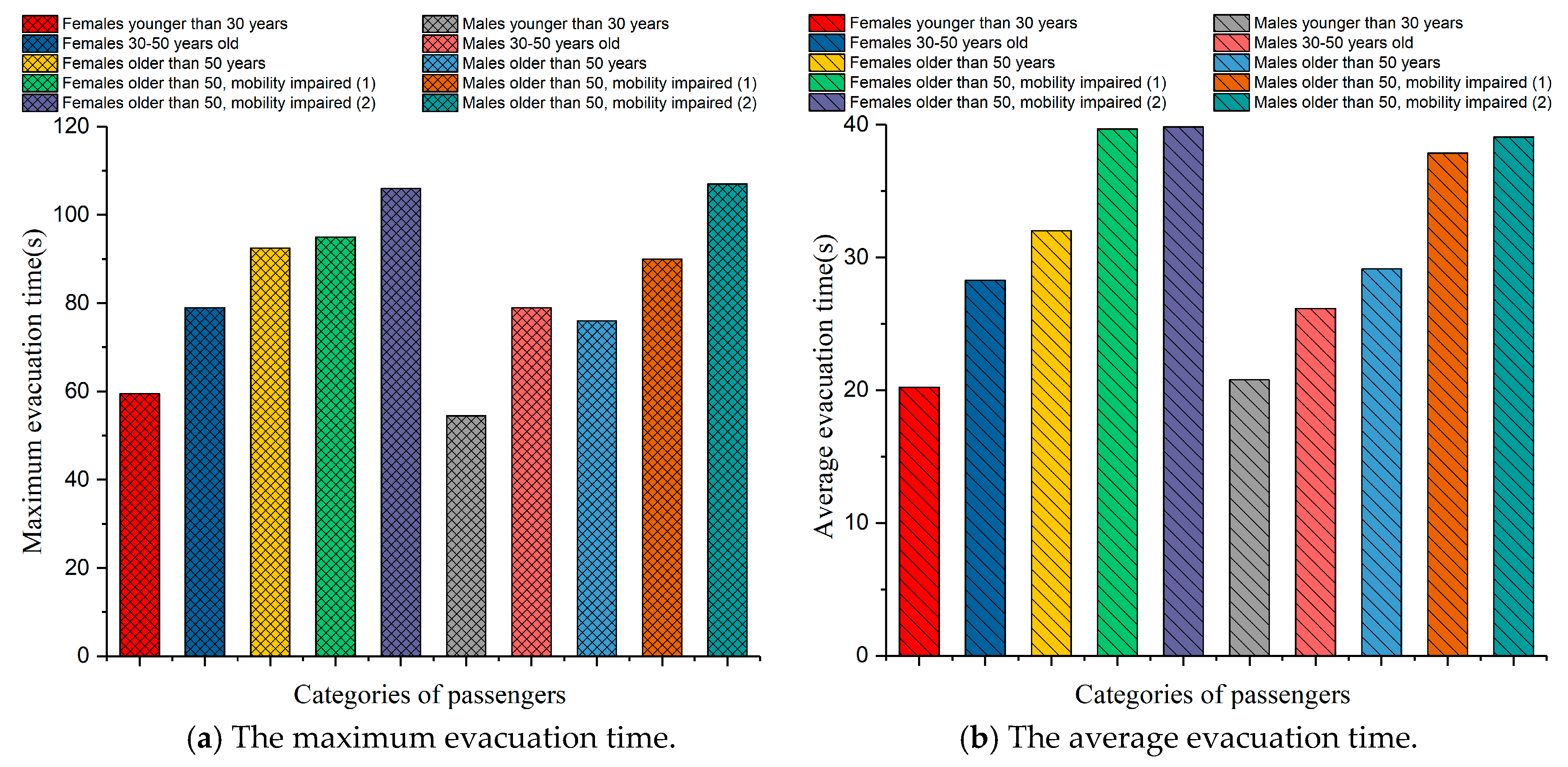


| Passengers | Percentage of Passengers (%) | Average Walking Speed on Flat Terrain (m/s) |
|---|---|---|
| Females younger than 30 years | 7 | 1.24 |
| Females 30–50 years old | 7 | 0.95 |
| Females older than 50 years | 16 | 0.75 |
| Females older than 50, mobility impaired (1) | 10 | 0.57 |
| Females older than 50, mobility impaired (2) | 10 | 0.49 |
| Males younger than 30 years | 7 | 1.48 |
| Males 30–50 years old | 7 | 1.30 |
| Males older than 50 years | 16 | 1.12 |
| Males older than 50, mobility impaired (1) | 10 | 0.85 |
| Males older than 50, mobility impaired (2) | 10 | 0.73 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hu, M.; Cai, W.; Zhao, H. Simulation of Passenger Evacuation Process in Cruise Ships Based on A Multi-Grid Model. Symmetry 2019, 11, 1166. https://doi.org/10.3390/sym11091166
Hu M, Cai W, Zhao H. Simulation of Passenger Evacuation Process in Cruise Ships Based on A Multi-Grid Model. Symmetry. 2019; 11(9):1166. https://doi.org/10.3390/sym11091166
Chicago/Turabian StyleHu, Min, Wei Cai, and Haiou Zhao. 2019. "Simulation of Passenger Evacuation Process in Cruise Ships Based on A Multi-Grid Model" Symmetry 11, no. 9: 1166. https://doi.org/10.3390/sym11091166
APA StyleHu, M., Cai, W., & Zhao, H. (2019). Simulation of Passenger Evacuation Process in Cruise Ships Based on A Multi-Grid Model. Symmetry, 11(9), 1166. https://doi.org/10.3390/sym11091166





