Single-Qubit Driving Fields and Mathieu Functions
Abstract
:1. Introduction
2. Analytically Solvable Driving Fields
3. Dynamics in a Precessing Field with Oscillating Amplitude
3.1. The Dynamics of Driving Fields and the Theory of Mathieu Functions
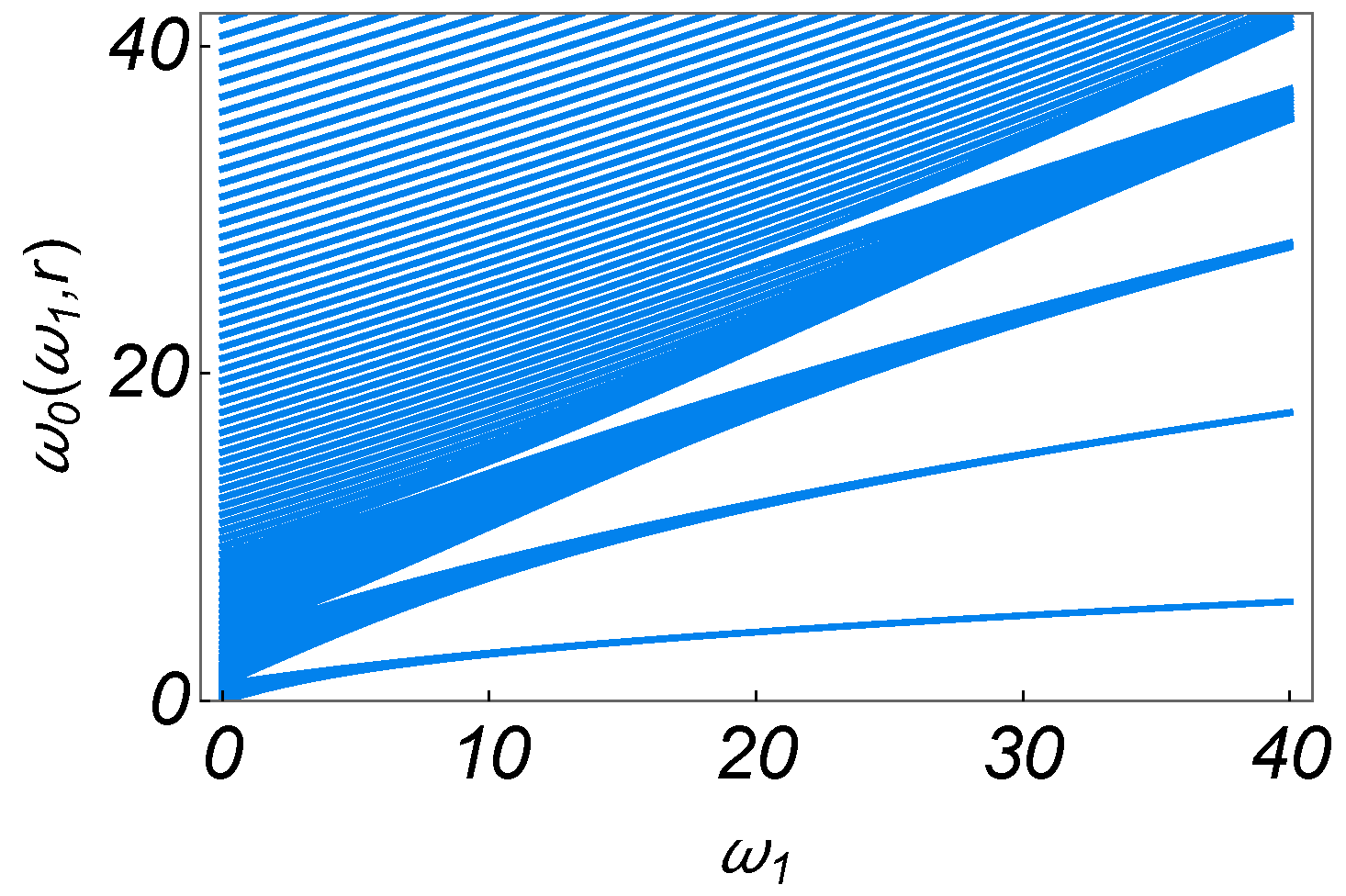
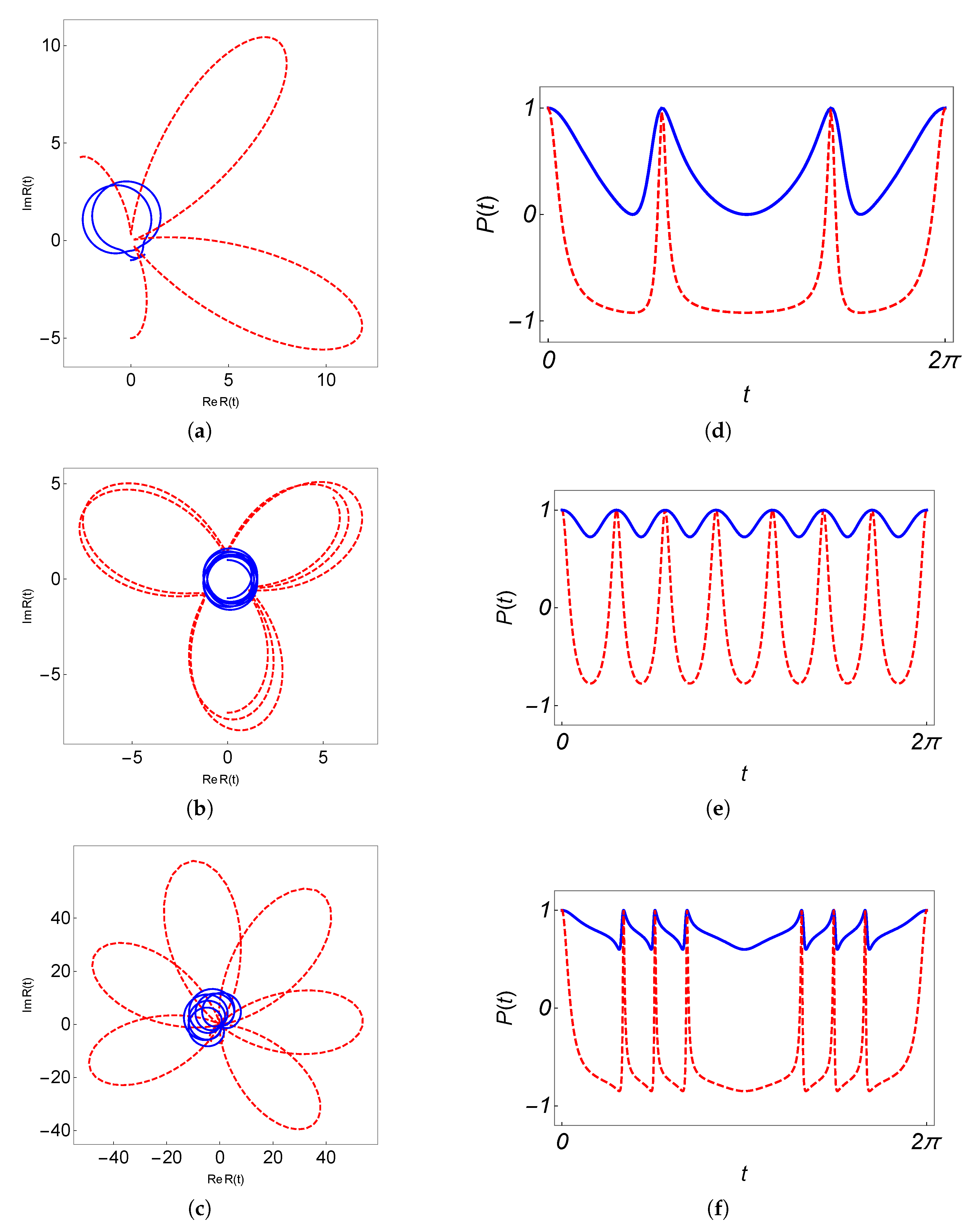
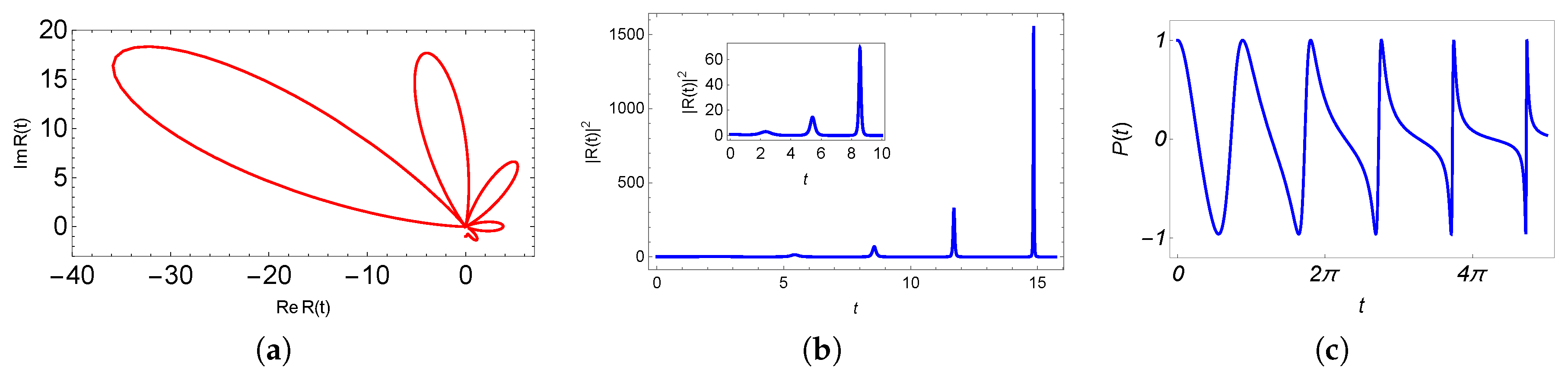
3.1.1. Driving Fields in the Region
3.1.2. Driving Fields in the Region
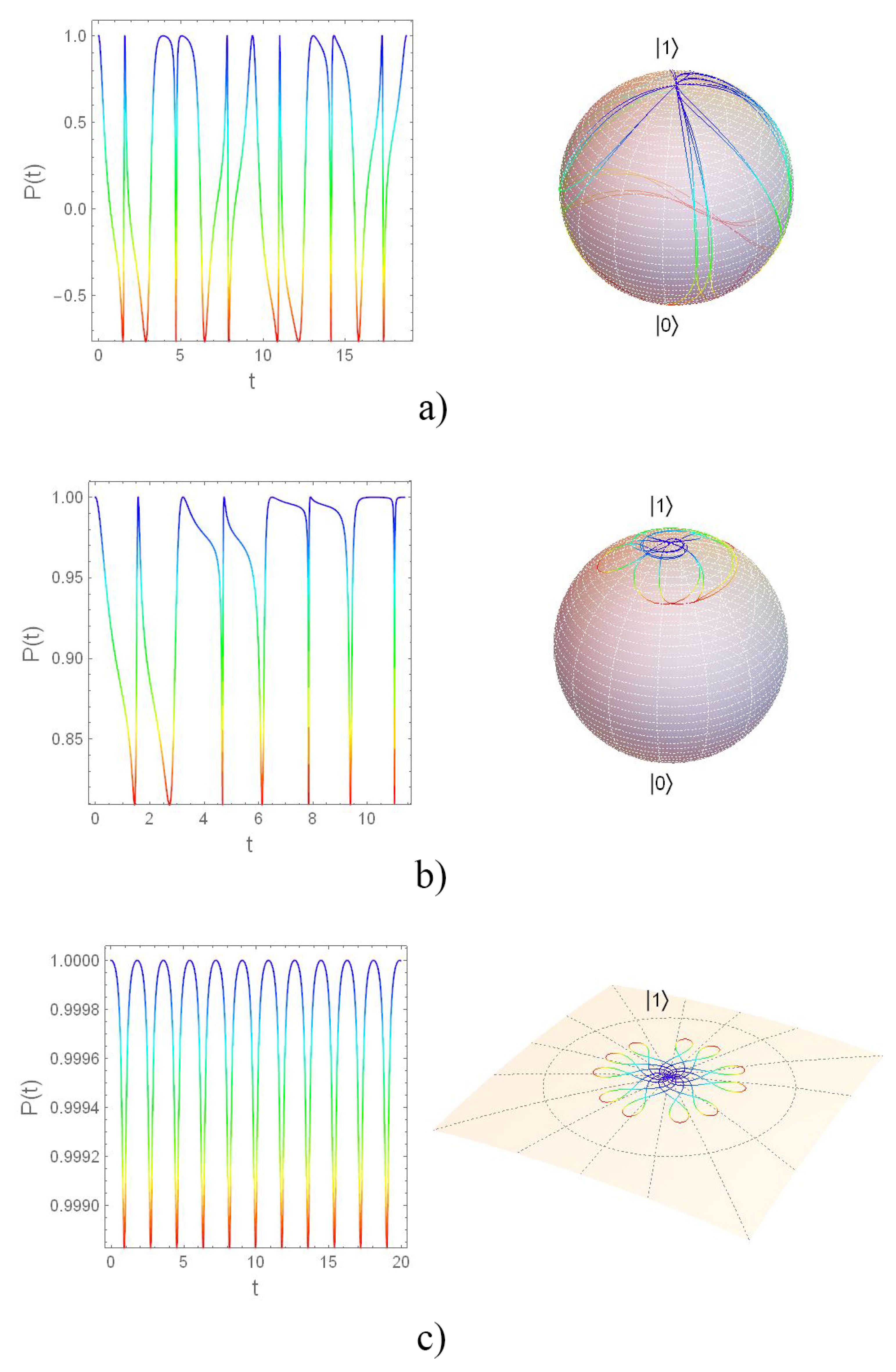
4. Evolution Loops, Cyclic Evolution and Phases
Dynamical and Geometric Phases
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Rabi, I. Space quantization in a gyrating magnetic field. Phys. Rev. 1937, 51, 652. [Google Scholar] [CrossRef]
- Zener, C. Non-adiabatic crossing of energy levels. Proc. R. Soc. A 1932, 137, 696–702. [Google Scholar] [CrossRef]
- Schwinger, J. On non-adiabatic processes in inhomogeneous fields. Phys. Rev. 1937, 51, 648. [Google Scholar] [CrossRef]
- Nielsen, M.A.; Chuang, I.L. Quantum Computation and Quantum Information; Cambridge University Press: Cambridge, UK, 2000. [Google Scholar]
- Zeng, J.; Barnes, E. Fastest pulses that implement dynamically corrected single-qubit phase gates. Phys. Rev. A 2018, 98, 012301. [Google Scholar] [CrossRef] [Green Version]
- Motzoi, F.; Wilhelm, F.K. Improving frequency selection of driven pulses using derivative-based transition suppression. Phys. Rev. A 2013, 88, 062318. [Google Scholar] [CrossRef]
- Stefanatos, D.; Paspalakis, E. Resonant shortcuts for adiabatic rapid passage with only z-field control. Phys. Rev. A 2019, 100, 012111. [Google Scholar] [CrossRef]
- Fernández, D.J.; Rosas-Ortiz, O. Inverse techniques and evolution of spin-1/2. Phys. Lett. A 1997, 236, 275. [Google Scholar] [CrossRef]
- Barnes, E.; Das Sarma, S. Analytically solvable driven time-dependent two-level quantum systems. Phys. Rev. Lett. 2012, 109, 060401. [Google Scholar] [CrossRef]
- Vitanov, N.V. Complete population inversion by a phase jump: An exactly soluble model. New J. Phys. 2007, 9, 58. [Google Scholar] [CrossRef]
- Messina, A.; Nakazato, H. Analytically solvable Hamiltonians for quantum two-level systems and their dynamics. J. Phys. A Math. Theor. 2014, 47, 445302. [Google Scholar] [CrossRef]
- Enríquez, M.; Cruz, S.C.y. Exactly Solvable One-Qubit Driving Fields Generated via Nonlinear Equations. Symmetry 2018, 10, 567. [Google Scholar] [CrossRef]
- Wei, J.; Norman, E. Lie algebraic solution of linear differential equations. J. Math. Phys. 1963, 4, 575–581. [Google Scholar] [CrossRef]
- Enríquez, M.; Cruz, S.C.y. Disentangling the time-evolution operator of a single qubit. J. Phys. Conf. Ser. 2017, 839, 012015. [Google Scholar] [CrossRef]
- Datolli, G.; Solimeno, S.; Torre, A. Algebraic time-ordering technics and harmonic oscillator with time-dependent frequency. Phys. Rev. A 1986, 34, 2646. [Google Scholar] [CrossRef] [PubMed]
- Datolli, G.; Torre, A. SU(2) and SU(1,1) time-ordering theorems and Bloch-type equations. J. Math. Phys. 1987, 28, 618. [Google Scholar] [CrossRef]
- Datolli, G.; Richetta, M.; Torre, A. Evolution of SU(2) and SU(1,1) states: A further mathematical analysis. J. Math. Phys. 1988, 29, 2586. [Google Scholar] [CrossRef]
- Mathieu, É. Le mouvement vibratoire d’une membrane de forme elliptique. J. Math. Pures Appl. 1868, 13, 137–203. [Google Scholar]
- McLachlan, N.W. Theory and Application of Mathieu Functions; Oxford University Press: London, UK, 1951. [Google Scholar]
- Li, S.; Wang, B.S. Field expressions and patterns in elliptical waveguides. IEEE Trans. Microw. Theory Tech. 2000, 48, 864–867. [Google Scholar]
- Gutiérrez-Vega, J.C.; Iturbe-Castillo, M.D.; Chávez-Cerda, S. Alternative formulation for invariant optical fields: Mathieu beams. Opt. Lett. 2000, 25, 1493–1495. [Google Scholar] [CrossRef]
- Carver, T.R. Mathieu’s functions and electrons in a periodic lattice. Am. J. Phys. 1971, 39, 1225–1231. [Google Scholar] [CrossRef]
- Sinha, A.; Roychoudhury, R. Spectral singularity in confined symmetric optical potential. J. Math. Phys. 2013, 54, 112106. [Google Scholar] [CrossRef]
- Bruno-Alfonso, A.; Latgé, A. Aharonov-Bohm oscillations in a quantum ring: Eccentricity and electric-field effects. Phys. Rev. B 2005, 71, 125312. [Google Scholar] [CrossRef] [Green Version]
- Mielnik, B. Evolution loops. J. Math. Phys. 1986, 27, 2290–2306. [Google Scholar] [CrossRef]
- Delgado, F.; Mielnik, B. Are there Floquet quanta? Phys. Lett. A 1998, 249, 369–375. [Google Scholar] [CrossRef] [Green Version]
- Pinney, E. The nonlinear differential equation y′′ + p(x)y + cy−3 = 0. Proc. Am. Math. Soc. 1950, 1, 581. [Google Scholar] [CrossRef]
- Ermakov, V.P. Second order differential equations. Conditions to complete integrability. Kiev Univ. Izvestia Ser. III 1880, 9, 125. (In Russian) [Google Scholar] [CrossRef]
- Klimov, A.B.; Chumakov, S.M. A Group-Theoretical Approach to Quantum Optics; Wiley-VCH: Weinheim, Germany, 2009. [Google Scholar]
- Gutiérrez-Vega, J.C.; Rodríguez-Dagnino, R.M.; Meneses-Nava, M.A.; Chávez-Cerda, S. Mathieu functions, a visual approach. Am. J. Phys. 2003, 71, 233–242. [Google Scholar] [CrossRef] [Green Version]
- Haroche, S.; Raimond, J.M. Exploring the Quantum: Atoms, Cavities, and Photons; Oxford University Press: Oxford, UK, 2006. [Google Scholar]
- Anandan, J. The geometric phase. Nature 1992, 360, 307–313. [Google Scholar] [CrossRef]
- Cohen, E.; Larocque, H.; Bouchard, F.; Nejadsattari, F.; Gefen, Y.; Karimi, E. Geometric phase from Aharonov-Bohm to Pancharatnam-Berry and beyond. Nat. Rev. Phys. 2019, 1, 437–449. [Google Scholar] [CrossRef]
- Zanardi, P.; Rasetti, M. Holonomic quantum computation. Phys. Lett. A 1999, 264, 94–99. [Google Scholar] [CrossRef] [Green Version]
- Jones, J.A.; Vedral, V.; Ekert, A.; Castagnoli, G. Geometric quantum computation using nuclear magnetic resonance. Nature 2000, 403, 869–871. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Aharonov, Y.; Anandan, J. Phase change during a cyclic quantum evolution. Phys. Rev. Lett. 1987, 58, 1593–1596. [Google Scholar] [CrossRef] [PubMed]
- Menda, I.; Buric, N.; Popovic, D.B.; Prvanovic, S.; Radonjic, M. Geometric Phase for Analytically Solvable Driven Time-Dependent Two-Level Quantum Systems. Acta Phys. Polonica 2014, 126, 670–672. [Google Scholar] [CrossRef]
- Chruściński, D.; Jamiołkowski, A. Geometric Phases in Classical and Quantum Mechanics; Birkhäuser: Boston, MA, USA, 2004. [Google Scholar]


© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Enríquez, M.; Jaimes-Nájera, A.; Delgado, F. Single-Qubit Driving Fields and Mathieu Functions. Symmetry 2019, 11, 1172. https://doi.org/10.3390/sym11091172
Enríquez M, Jaimes-Nájera A, Delgado F. Single-Qubit Driving Fields and Mathieu Functions. Symmetry. 2019; 11(9):1172. https://doi.org/10.3390/sym11091172
Chicago/Turabian StyleEnríquez, Marco, Alfonso Jaimes-Nájera, and Francisco Delgado. 2019. "Single-Qubit Driving Fields and Mathieu Functions" Symmetry 11, no. 9: 1172. https://doi.org/10.3390/sym11091172
APA StyleEnríquez, M., Jaimes-Nájera, A., & Delgado, F. (2019). Single-Qubit Driving Fields and Mathieu Functions. Symmetry, 11(9), 1172. https://doi.org/10.3390/sym11091172





