In-Situ Plasma Monitoring during the Pulsed Laser Deposition of Ni₆₀Ti₄₀ Thin Films

Abstract

The properties of pulsed laser deposited of Ni₆₀Ti₄₀ shape memory thin films generated in various deposition conditions were investigated. In-situ plasma monitoring was implemented by means of space- and time-resolved optical emission spectroscopy, and ICCD fast camera imaging. Structural and chemical analyses were performed on the thin films using SEM, AFM, EDS, and XRD equipment. The deposition parameters influence on the chemical composition of the thin films was investigated. The peeled layer presented on DSC a solid-state transformation in a different transformation domain compared to the target properties. A fractal model was used to describe the dynamics of laser produced plasma through various non-differentiable functionalities. Through hydrodynamic type regimes, space-time homographic transformations were correlated with the global dynamics of the ablation plasmas. Spatial simultaneity of homographic transformation through a special SL(2R) invariance implies the description of plasma dynamics through Riccati type equations, establishing correlations with the optical emission spectroscopy measurements.

1. Introduction

Due to the demand of applications in the field of engineering, the new materials are kept in a developing state in order to improve their performance, but also for creating new functions. Among these, there is a group of materials that are able to respond to a special stimulus through the alteration of the encircling physical and chemical features. These stimuli include the temperature (thermo-receptive materials), tension or pressure (mechanical-receptive materials), current or electrical tension (electro-receptive materials), magnetic field (magneto-receptive materials), change of the pH, of the solvent, or humidity (chemical-receptive materials) and light (photo-sensitive materials) [1,2,3].

Such a special class of materials are the shape memory alloys (SMA) that possess a range of desired properties, especially a high mechanical capacity in comparison with their weight, through which is developed the ability of recovery, a deformation produced by a massive transformation and a deformation due to heating and cooling, pseudo-elasticity (super elasticity), high capacity of damping, high chemical corrosion resistance, and bio-compatibility (in the case of alloys based on Ti and Fe) [4,5,6].

In the past few years shape memory alloy thin films were proven promising with high performance in the field of applications of micro-electric mechanical systems (M.E.M.S) because they can be implemented through standard techniques of lithography or depositing, fabricated at an industrial scale [7]. The thin layers of shape memory alloys need only a small amount of thermic capacity to heat or cool, which is why the answer time is substantially reduced and the working speed increases considerably. The effective power capacity on a volume corresponding to a layer obtained from an alloy with shape memory exceeds the one of the classic mechanisms proposed for micro-activation [8,9,10]. The transformation process of a bulk alloy with shape memory in thin film is accompanied by numerous important changes at the level of the mechanical, physical, chemical, electric, and optical properties such as the load resistance, elastic module, hardness, and attenuation capacity, regaining the initial form, electric resistivity, thermic conductivity, thermic expansion coefficient, surface rugosity, vapors permeability, and the dielectric constant, etc.

This transformation can be used in designing and fabricating micro-sensors and micro-actuators. However, due to the lack of a complete understanding of the AMF layers, combined with the difficulty of controlling the depositing parameters, these films have not benefitted of too much attention in the MEMS technology of production, in comparison to other technologies of obtaining the micro-actuators. Thin films based on Ni-Ti are the most SMA used materials under thin film form, and they are obtained through the atomization method. There are also depositing methods: laser ablation, depositing with ions fascicle, plating with jet of ion plasma, the plasma atomization and the blitz evaporation, but with certain inherent problems such as the lack of uniformity of the layer thickness and the composition’s lack of uniformity, low coating speed, or low handling and incompatibility with the process performed by MEMS, etc. The depositing processes through laser ablation surpass the majority of these problems [11,12,13,14]. The transformation temperatures, behavior of shape memory, and the super-elasticity of the pulverized layers of Ni-Ti are sensitive at the most metallurgical factors (the alloy composition, contamination, thermic-mechanical treatments of re-annealing and ageing), at the atomization conditions (co-atomization with multi-aims, the target, the gas pressure, the distance from the target to the sub-layer, the depositing temperature, obliquity sub-layer, etc.), as well as to the application conditions (loading conditions, temperature of the environment, heat dissipation, heating/cooling speed, mechanical loading speed) [15,16]. The shape memory effect involves the crystallographic transformation thermo-elastic with reversible stage or the martensitic transformation from the initial stage of high temperature to that final stage of low temperature [17,18,19,20,21,22]. Generally speaking, there are 2 types of martensitic transformation, one with a single stage A→M and the other with 2 stages A→R→M, where A is the austenitic phase of high temperature, R is the rhombohedral intermediary phase, and M is the martensitic phase of low temperature. The experimental results presented an in-depth presentation of the efficiency of the pulsed laser deposition process towards obtaining shame memory alloy thin films and the effect of the deposition conditions on the properties of the thin film.

In this paper we report the experimental results on the deposition of thin films with special properties using Nitinol targets (shape memory alloy). Also, there are followed aspects about with the target behavior, and the transmitted plasma during the depositing and created thin layers. A fractal model used to describe the dynamics of laser produced plasma through various functionalities of non-differentiable type was established. Hydrodynamic type regimes by means of space time homographic transformations were corelated with the global dynamics of the ablation plasmas. In such a context, spatial simultaneity of homographic transformation through a special SL(2R) invariance implies the description of plasma dynamics through Riccati type equations can be used to describe the dynamics of ablation plasma seen through the optical emission spectroscopy measurements.

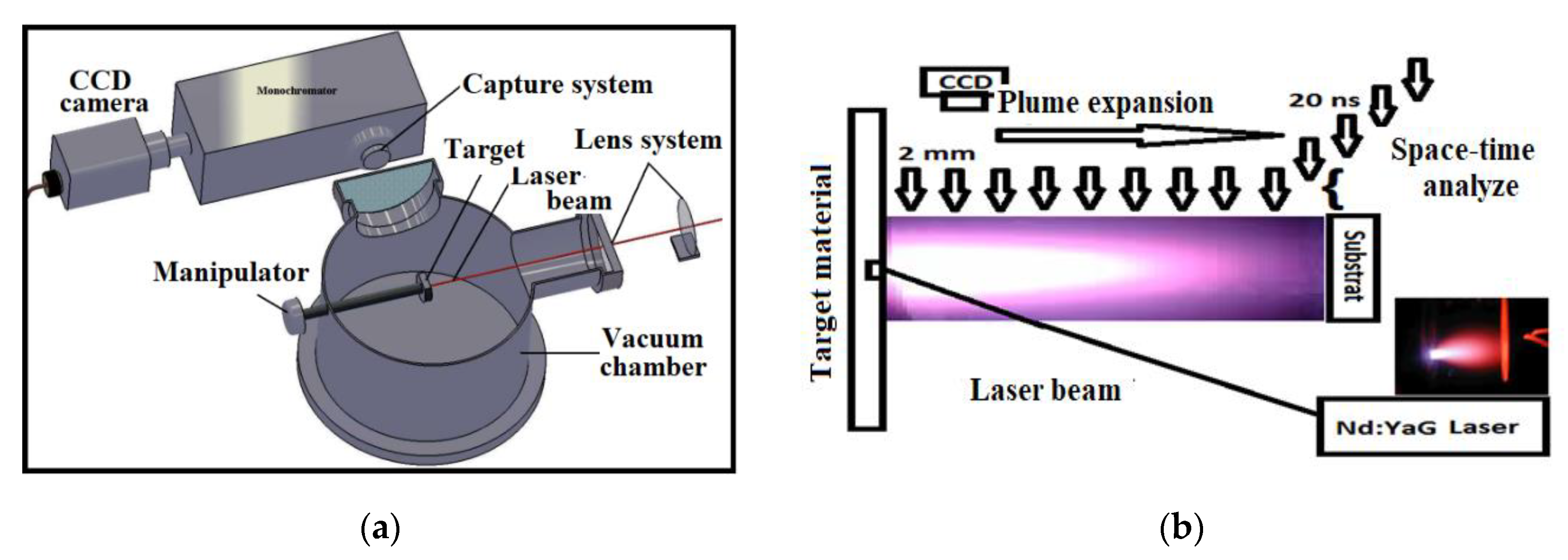
2. Experimental Set-Up

The properties of the thin films and the plasma investigation were performed using an Nd: YAG laser (λ = 266, 355 or 532 nm, pulse width 5 ns) working at a 10 Hz repetition rate. The laser beam was focused with lens with a focal distance f = 35 cm, on a target NiTi placed in a vacuum chamber (p = 10⁻² Torr). The NiTi alloy (nitinol60) was acquired from the firm Saes Getters [17], in softened state. The estimated diameter in the impact point was almost 400 µm. The energy laser fascicle was monitored continuously using a joule meter Ophir. The energy used usually was of 30 mJ/impulse, that leads to a typical intensity of the laser of 6 GW/cm².

The target of shape memory alloy is moved in the XY plan with a micrometer manipulator in order to expose a new area towards the laser fascicle (to obtain a uniform ablation, the target was rotated and translated simultaneously). The formation and dynamics of plume were studied with an intensified camera ICCD (PI MAX, 576_384, with minimum gate of 2 ns) placed perpendicularly on the direction of expansion of plasma, Figure 1a.

The spectral composition of plasma formed in the ablation process depends on the chemical composition of the sample, which was analyzed with a high resolution spectrometer. This technique reaches a high potential of using as analysis method in real time of the chemical elements.

In the case of analysis of the metallic ablated materials it was used an identification of the base spectral lines through the analogy with those identified in the NIST library [18]. The spatial–temporal dynamics of the transitory plasmas generated through laser ablation of high fluency with pulses at nanoseconds was analyzed using optical methods (optical emission spectroscopy and ICCD fast camera imaging), the analysis figure being presented in Figure 1b.

Throughout the experiment, the substrate was maintained in a fixed position at room temperature. The target was fitted on a support of 45° that would direct the plasma of metallic ablated material towards the substrate. There were deposited a series of thin films from targets of Nitinol at two different distances between target and substrate (2 and 4 cm) using energies of laser of 40, 80, 100 mJ and two different deposition times (45 and 90 min). Given the substantial set of different deposition conditions attempted, a total of 30 samples were generated. In-situ plasma investigation was also implemented by means of both global and space- and time-resolved optical emission spectroscopy analyses. The global investigations focused on recording the overall emission of the plasma to analyze the overall dynamics of the ablated particle cloud while local investigations were performed by means of optical emission spectroscopy where the kinetics and thermal energy of individual species was investigated.

Usually there are two routes to achieve a shape memory crystallin thin films: one using a heated substrate and a second with post annealing heat treatment. Because the films deposited at high substrate temperatures (400–600 °C) are crystalline, they do not require any post-annealing treatments. However, initial tests have revealed that the heated substrate route was not resulting in high quality films, as the thin films became unstable at high temperatures and the growth of the thin film was accompanied by the formation of precipitates due to interfacial chemical reactions; also, these layers were more susceptible to cracking. Due to these reasons, in this case we chose to do a post deposition heat treatment of annealing by heating the layers to 800 °C in Ar atmosphere and cool them in air in order to crystalize the thin film structure.

The behavior of the shape memory materials that present transformations in a solid state was investigated in initial form and also of thin layer form through differential calorimetry on equipment DSC Maya 200 with a heating speed of 10 K/min in the atmosphere of Argon. The chemical analysis of the thin layers was performed through EDS analysis (detector Bruker: energy resolution up to 100 kcps count rate, use a self-calibrating P/B-ZAF analysis, minimum 90 nm diameter spot for analyze) and XRD (X’Pert Pro MRD, Scan-Continous, Start Angle: 20, End Angle: 120, Step size: 0.0131303, Time per step: 61.20, Scan speed: 0.05471, Number of steps: 7616, 45 KV, 40 mA, Anode X-ray Tube: Cu, 20:20–90) and the surface was analyzed through electron microscopy (SEM VegaTescan LMH II, work in a high vacuum of approximately 1 × 10⁻² Pa, electron gun work 1–30 kV, 100,000×, 15.5 mm WD, SE detector and program VegaTC) and through atomic force microscopy (Nanosurf EasyScan 2 equipment, maximum Scan range: 110 µm, maximum Z-range: 22 µm, drive resolution Z: 0.34 nm, drive resolution XY 1.7 nm, XY-Linearity Mean Error: <0.6%, Z measurement noise level (RMS, Static Mode) 0.4 nm (max. 0.55 nm)).

3. Experimental Results

3.1. The Analysis of the Nitinol Target after the Ablation Process

The state of the surface of shape memory material that is used as a target in the process of depositing through laser ablation is presented in Figure 2 with the highlight of the traces left by the laser fascicle in Figure 2a and the thermic affected area in Figure 2b.

We can observe an area of approximately 200 µm around the traces left by the laser, thermally affected by the laser action constituted from welded compounds of circa 1–3 µm. The action of laser in the contact area is characterized by a release of material on a surface of 314 µm² for a diameter of 20 µm as we can observe in Figure 2a. The surface affected by the laser beam was chemically analyzed on an area of 0.4 mm² by 10 t and the average of the values of identified chemical elements was of Ni: 47% wt., Ti: 41.5% wt. și O:11.5. The apparition of a high percentage of oxygen can be observed, a fact that signals a pronounced oxidation of the surface after the laser exposure with a decrease of the content of Ni that transformed at the surface in oxides. Another important aspect worth noting here is the fact that the heat affected area is large and there is a lot of redeposited material on the edges of the ablation crater. The presence of huge droplets on the targets is also a signature of the dominant effect induced by thermal ablation mechanisms, as opposed to the electrostatic ones. This is especially the case of explosive boiling, during which the ejection of large parts of materials can occur. This could translate into a high density of clusters or nanoparticles on the deposited films.

3.2. In-Situ Plasma Monitoring during Pulsed Laser Deposition of NiTi by Means of OES and ICCD Fast Camera Imaging

The central idea behind in-situ plasma monitoring during pulsed laser deposition of thin films is to potentially asses the quality and properties of the desired films by understanding the fundamentals of the deposition process. In order to obtain this, we performed in-depth characterization of irradiated target, resulted transient plasma and the thin films. One of the general accepted technique for in-situ plasma monitoring is optical emissions spectroscopy due to its non-perturbative nature. This approach is usually completed by ICCD fast camera imaging. Therefore, in order to understand the structure and the dynamics of the laser produced plasma, we employed a global to local approach. Global investigations involved ICCD fast camera imaging and the local ones the space and time resolved optical spectroscopy with the focus being on individual excited states seen in the ablation plasma.

The general dynamics of plasma (plume) resulted after the interaction between the laser fascicle and the target from Nitinol was analyzed through ICCD imaging of the laser produced plasma, with a gate width of 30 ns, for different moments of time. In Figure 3 there are presented some snapshots from the expansion of plasma in the precinct at different periods of time (from 25 to 1000 ns) after the impact between the laser fascicle and the target.

Starting with the first image where the plume was recorded at 200 ns after the interaction moment between the laser beam and the NiTi target (seen as ∆t = 0), that the laser produced plasma has a quasi-spherical shape that increases in volume as it expands. At later moments, we noticed a split of the ablated cloud into three distinct structures (Figure 4). This separation is justified by the constituents of plume. The process was observed also in other studies [23,24] and can be attributed to a heterogeneity in the velocity of the ejected particles based on their nature and the ejection mechanisms involved.

The first structure, also known as the fast structure, is generated by electrostatic mechanisms (Coulomb explosion) and describes high energetic particles (mainly ions in various ionization states); the second structure is generated by thermal mechanism and usually describes a strongly atomized structure moving with a lower velocity, and the third structure, which is also of thermal nature and contains a heavier, more complex structure with a considerably lower expansion velocity [25]. In order to characterize the behavior of plume we estimated the velocities per each species by plotting the displacement of the maximum emission area in space and time. The values found were 1.6 km/s for the third structure, 2.8 km/s for the second one, and for the first one 5 km/s. The obtained value for the third structure is relatively high, meaning the ejected clusters have relatively high energy and there is a strong possibility of a high density of clusters on the deposited films. On the other hand the fast structure have a lower velocity in comparison to other reports from the literature, a sign that the forces driving the Coulomb explosion ejection mechanism are secondary to the thermal ones.

For the analysis of the contributions of the metallic species, which can be found in the plasma obtained from the NiTi target, a spectroscopic study was performed focusing on their evolution in space and time. The first global spectra of plasma for an area of 0.2 mm² from the plasma at a distance of 5 mm to the target surface was recorded in the 300–510 nm spectral range. In Figure 5 an example of spectra emitted for the NiTi sample is presented. Using appropriate databases [18] we identified all the emission lines observed empirically. We noticed both atomic and ionic Ti lines, and only atomic species of Ni. The abundance of Ti with respect to the Ni lines seen in the spectra can be explained by the lower evaporation heat and lower melting point of Ti coupled with an atomic radius almost three times higher than the Ni one. A higher atomic radius will translate into a higher collision cross-section of Ti, which in term could lead to the showcase of more excited states.

By performing space and time resolved optical emission spectroscopy and following the emission lines for the Ti and Ni atoms, we can determine according to the algorithm presented in [14] the expansion velocity of each species. We obtained for the Ni atom a velocity of 2.7 km/s, while for the Ti atoms a velocity of 5.7 km/s. We noticed that these velocities are close to the ones obtained by ICCD fast camera imaging. Thus, we can conclude that the splitting of the plume, in this case, is based on the nature of its components, as opposed to the mechanisms involved in the ablation process [14]. This is in good agreement with the high thermal effected area on the sample and with the mostly atomic emission lines observed, meaning that thermal mechanisms are dominant. With a dominant thermal ejection scenario, the composing particles of the ablated cloud will be separated on the basis of the individual thermal properties. This will result in a fast structure containing mainly Ti species, and a second structure mainly containing Ni species.

We further used the well-known Boltzmann plot method [14] to determine the individual excitation temperature of the two atomic species (Ni I and Ti I). For Ti I species we found an excitation temperature of 6500 K, while for Ni we found a relatively lower value of 7200 K, values determined at a distance of 0.5 mm from the target. This difference is in line with the differences in the thermal properties of the two components.

3.3. The Analysis of the Thin Layers Obtained through Laser Ablation from Targets with Shape Memory (NiTi)

The accurate control of the ratio Ni/Ti in the Ni-Ti films has an essential importance. The problems that may occur as seen through the plasma monitoring techniques is the differential evaporation of the two components from the target, coupled with the large scale non-uniformity of the PLD generated films, as well as structural changes to the target during the deposition process. In order to prevent these drawbacks, we implemented a combinatorial approach with the use of the NiTi target and simultaneously of a Ti sample to compensate the depleted Ti concentration from the films.

The resulted thin films were investigated by means of EDX technique. Selective spectra from the target and the thin films are presented in Figure 6. We observed a few peaks corresponding to the Ti and Ni species in the target and we have seen their corresponding peaks in the films with a reduced intensity. Due to this correspondence of the peaks, we can conclude that from a qualitative point of view, the stoichiometry of the ablated material is transferred to the substrate.

In order to determine the optimal conditions of depositing, but also to study the influence of the distance between the target and substrate on the properties of the films, we performed the study depicted in Figure 6. With this aim, areas of 0.4 mm² were analyzed from two samples obtained in different experimental conditions. The results obtained (in m/weight and atomic percentages) are presented in

Table 1. The chemical composition of the thin film according to the distribution in Figure 7.

	Chemical Element		Target	Zone 1	Zone 2	Zone 3	Zone 4	Zone 5	Zone 6	Zone 7	Zone 8	Zone 9
Sample B	Ni (accuracy 0.2%)	wt.%	60.0	63.3	62.6	63.9	63.4	63.1	61.5	62.9	65.01	64.9
		at%	55.01	58.4	57.7	59.2	58.6	58.2	56.6	57.9	60,25	60.2
	Ti accuracy 0.15%)	wt.%	40.0	36.7	37.4	36.01	36.6	36.9	38.5	37.1	34.9	35.1
		at%	44.99	41.6	42.3	40.8	41.4	41.8	43.3	42.1	39.7	39.8
Sample A	Ni (accuracy 0.2%)	wt.%	60.0	61.3	60.9	58.7	60.1	58.74	58.1	58.2	59.6	57.3
		at%	55.01	56.4	55.9	53.6	55.1	53.7	53.1	53.2	54.6	52.3
	Ti (accuracy 0.15%)	wt.%	40.0	38.7	39.1	41.4	39.9	41.3	41.9	41.8	40.4	42.7
		at%	44.99	43.6	44.1	46.4	44.9	46.3	46.9	46.8	45.4	47.7

. The analyses were realized on a surface of approximately 1 mm² (Figure 7), which can contain various concentrations of clusters on their surfaces.

In Figure 7 it is specified the propagation direction of the material plasma from the target placed parallel with the sub layer of Si. The chemical analysis 1, 4, and 7 were selected on larger surfaces to determine the influence of the particle distribution within the plasma plume on the formation and development of the thin film. In the table is placed the chemical composition of target (Ni40Ti) used in the pulsed laser deposition process as reference value. We observed an area where we could achieve quasi-complete stoichiometric transfer in areas 4–6, situated in the center of the thin film, meaning that in the center of the plume keep the stoichiometry of the target while in the wider regions of the plasma some depletion of the Ti can occur. This result is in good agreement with those presented in [14] where it was shown that lighter elements are distribution mainly on the outer range of the plasma, as opposed to the heavier ones which are centered around the main expansion axis.

The standard variation of the Ni and Ti elements, from the base material (target), were determined: Ni: ±0.2 and Ti: ±0.1. In the case of TiNi thin film (sample a) positioned at a distance of 40 mm to the NiTi target, it was observed good stoichiometric transfer is achieved for almost all areas, most of them in the same experimental conditions in which sample B (20 mm) was also produced. The average atomic variation was in this case much lower than in the majority of the performed experiments, indicating a stoichiometric transfer according to the requirements of obtaining thin films with shape memory and with a percentage value higher than the data reported in the field of growing thin films through other methods such as thermic atomization.

In order to investigate the NiTi films formed on the Si base we used the XRD technique. Using this method, we could preserve equivalence between the base material (target with shape memory) and the material obtained on a substrate of Si. In Figure 8 a part of the XRD analyses performed on the obtained thin films is presented. Figure 8a highlights the characteristic peaks of a shape memory alloy NiTi in martensitic state at the room temperature. According to the database of the analysis equipment (ICC Database) [26], we established the main characteristic peaks of this material and the compound phases with their properties. In Figure 8b the spectrum obtained on a thin film is presented, for the NiTi alloy transported through laser ablation in amorphous state where we can find the majority of the thin layers obtained through laser ablation. Furthermore, we analyzed thin film through X ray diffraction, but after we applied a treatment of re-annealing of re crystallization, the result being presented in detail in Figure 8c.

We observed numerous peaks specific to crystallized NiTi alloy. The size of the peaks was very low because the tests were performed in difficult conditions given by the reduced thickness of the layer (around 200 nm). The apparition of the peaks B2 and B19 characteristic to the austenitic and martensitic phase (in a very high percentage) were observed. After the annealing treatment, the material had a structure transformed to martensite. The formation of precipitates was not reported after the annealing treatment [27]. The appearance of untransformed phase: B₂, Figure 8c, was connected to the very fast formation of an Ni-rich layer near the oxide surface during the heat treatment.

In the case of shape memory films deposited under vacuum, the chemical composition of the new layers was influenced by the substrate temperature. Our results suggest that the chemical composition of a Nitinol layer can be precisely controlled without involving the substrate temperature using pulsed laser deposition but considering the distance between the target and substrate, and the orientation of the substrate contact surface with the plume.

3.3.1. Calorimetric Study

The removal of the samples from the Si layer was performed through debarking, and after the mass analyses the samples with the mass between 4 and 32 mg were investigated. Among these, only on the TiNi thin film crystallized through thermic treatment and with a net mass of 4 mg, an intern endotherm mass appeared around the temperature of 333 K (60 °C). The variation of the temperature flow in the case of this sample is presented in Figure 9.

All the other DSC analyses did not present transformations in the analysis area TC- 473 °C, but there is the possibility that will be taken into consideration in the future, for this domain to be too small and the transformation temperatures to be shifted even to negative temperatures in the case of NiTi alloys.

3.3.2. Surface Analyses

The condition of the surface of shape memory alloys is very important given that the relief state of the martensitic phase plays a major role in manifesting the shape memory effect [28]. We observed a pleated relief, characteristic for the martensitic variants, with an accurate arrangement of these and similar spatial dimensions with those resulted through SEM electronic microscopy. Also, a characteristic height of the profile with an average of 262 nm and a width of 2 µm of the martensitic plates is highlighted. The state of the thin film surface deposited through laser ablation from the target of Nitinol on the TiNi thin films (sample A) is presented in Figure 10 where we observe a typical relief to the variants of martensitic plates. The analyzed area does not contain large formations of material. The relief of the deposited thin layer is very low with an average value of 92.9 nm, Figure 10c a thermic treatment of partial recrystallization and annealing at 1073 K.

Using the specialized soft Vega TC of the scanning microscope, we followed morphologically the state of the surface of the material layer. In Figure 11 it is presented the state of the thin layer obtained through PLD from NiTi targets where we can notice the apparition of the characteristic drops of the depositing process through laser ablation. Depending on the depositing parameters and the ablated material, different morphologies of the thin layer surface presented. Only formations larger than 1 µm were analyzed, the rest being considered a part of the layer or too small to influence the characteristics of shape memory thin layer realized. All samples were investigated on the same material surface and in the same experimental conditions.

From the microstructural dimensional analysis (Figure 11) of the thin layers we observed that on the sample B were noticed 17 large particles (with an average of 2.62 µm) and the rest small particles under 1 µm (it is mentioned that the tests took place in all the cases on the surface of 115 × 115 µm). On the sample A there were observed 8 large particles with an average of 1.43 µm and the rest smaller than a micron. After the crystallization process normally, the grains grow isotopically until they press on each other or until they reach the layer surface or the substrate.

In the case of the layers obtained for a distance of 2 cm between target and substrate, the following values were obtained: at 40 mJ → 30 large particles with an average of 1.56 µm, at 80 mJ → approximately 50 large particles with an average of 2.39 µm and at the 100 mJ → appeared only 7 particles with an average of 2.02 µm.

The influence of material drops on the properties of the submicronic layer deposited is given generally by differences of chemical composition that appear among these. In the case of shape memory alloys transformed in thin layers, it is essential to establish the behavior of the two materials that assemble the final layer (the layer and the material drops), the influence of the drops on the general properties of the thin layer, the increase or decrease of the number of micrometric droplets. For this reason, in the future we will pursue the investigation of these characteristics in order to increase the quality of thin layers with special properties.

4. The Dynamics of Transient Plasmas Generated by Laser Ablation of Memory Shape Alloy in a Fractal Paradigm

The laser-produced plasmas are non-differentiable (fractal) media induced by the collisions between the composing structural units (atoms, clusters, nanoparticles, etc.). The behavior of such a medium can be explicitly described in the Fractal Theory of Movement through dynamics on continuous and nondifferentiable curves (fractal curves [29,30]). In the following we will specify several types of nondifferentiable dynamics (either through hydrodynamic type regime at various scale resolutions, or through Schrodinger type regime at various scale resolutions) which will later be calibrated to the experimental results presented in the previous section.

If we further assimilate the ablation plasma with a complex system, the dynamics of its structural units can be described through the scale covariant derivative [30]:

$$\frac{\hat{d}}{dt}={\partial }_t+{\hat{V}}^l{\partial }_l-i\lambda {\left(dt\right)}^{\left(\frac{2}{D_F}\right)-1}{\partial }_l{\partial }^l$$

(1)

where

$${\hat{V}}^l=V_{}^l-i{U}_{}^l,i=\sqrt{-1}$$

(2)

$${\partial }_t=\frac{\partial }{\partial t},{\partial }_l=\frac{\partial }{\partial X^l},{\partial }_l{\partial }^l=\frac{{\partial }^2}{\partial X^l}\left(\frac{\partial }{\partial X^l}\right)$$

(3)

In (1)–(3) X^l is the fractal spatial coordinate, t is the nonfractal temporal coordinate having the role of an affine parameter of the movement curves, ${\hat{V}}^l$ is the complex velocity, $V_{}^l$ is the real, differentiable, component of the velocity, independent of the scale resolution dt, U^l is the imaginary (nondifferentiable) component of velocity, dependent on the scale resolution, λ is the “diffusion coefficient” associated to the fractal-nonfractal transitions and D_F is the movement curve fractal dimension. For the previously defined fractal dimension we can choose any accepted definition: in a Kolmogorov sense, in a Haussdorff-Besikovici etc. [31]. However, once one definition is accepted it has to be constant throughout the study: D_F < 2 for correlative type processes, D_F < 2 for uncorrelated type processes etc.

The movement equation (geodesics equation) can be derived by implementing the scale covariance principle [29]. Then, through (1) and (2) it results:

$$\frac{\hat{d}{\hat{V}}^i}{dt}={\partial }_t{\hat{V}}^i+{\hat{V}}^l{\partial }_l{\hat{V}}^i-i\lambda {\left(dt\right)}^{\left(\frac{2}{D_F}\right)-1}{\partial }_l{\partial }^l{\hat{V}}^i=0$$

(4)

This means that in any point of the movement trajectory the fractal acceleration, ${\partial }_t{\hat{V}}^i$, the fractal convection, ${\hat{V}}^l{\partial }_l{\hat{V}}^i$, and the fractal dissipation, ${\partial }_l{\partial }^l{\hat{V}}^i$ are reaching an equilibrium.

For the particular case of the irrotational movement:

$${\hat{V}}^i=-2i\lambda {(dt)}^{\left(2/D_F\right)-1}{\partial }^{i}ln\Psi$$

(5)

where $\Psi$ is the fractal state function and $\ln \Psi$ is the complex scalar potential of the complex velocity field, the movement Equation (4) takes the from of Schrödinger equation of fractal type [30]:

$${\lambda }^2{(dt)}^{\left(4/D_F\right)-2}{\partial }^l{\partial }_l\Psi +i\lambda {(dt)}^{\left(2/D_F\right)-1}{\partial }_t\Psi =0$$

(6)

Moreover, by writing $\Psi$ in an explicit manner:

$$\Psi =\sqrt{\rho }exp\left(is\right)$$

(7)

where $\sqrt{\rho }$ is an amplitude and s is a phase, the movement Equation (6) with the following substitutions:

$$\begin{gathered} V^l=2\lambda {(dt)}^{\left(\frac{2}{D_F}\right)-1}{\partial }_{l}s \\ {U}^l=\lambda {(dt)}^{\left(\frac{2}{D_F}\right)-1}{\partial }_{l}ln\rho \end{gathered}$$

(8)

can be simplified by separating the dynamics of the ablation system on scale resolution. We obtain the equation system of fractal hydrodynamics:

$${\partial }_t{V}^l+V^l{\partial }_l{V}^l=-{\partial }_{l}Q$$

(9)

$${\partial }_t\rho +{\partial }_l\left(\rho V^l\right)=0$$

(10)

with Q the specific fractal potential:

$$Q=\frac{U_l{U}^l}{2}+\frac{\lambda {(dt)}^{\left(2/D_F\right)-1}}{2}{\partial }_l{U}^l=-2{\lambda }^2{(dt)}^{\left(4/D_F\right)-2}\frac{{\partial }_l{\partial }^l\sqrt{\rho }}{\sqrt{\rho }}$$

(11)

Equation (9) defined the specific momentum conservation law, while Equation (10) defines the state density conservation law. The specific fractal potential is a measure of the fractalization of the movement trajectory.

In the unidimensional case, the equation system of the fractal hydrodynamics:

$${\partial }_{t}V+V{\partial }_{x}V=2{\lambda }^2{(dt)}^{\left(4/D_F\right)-2}{\partial }_x\left(\frac{{\partial }_x{\partial }_x\sqrt{\rho }}{\sqrt{\rho }}\right)$$

(12)

$${\partial }_t\rho +{\partial }_x\left(\rho V\right)=0$$

(13)

with $V_x\equiv V$ and adequate initial and boundary conditions admits the analytical solution:

$$V=\frac{V_0{\alpha }^2+{\mathsf{\mu }}^{2}xt}{{\alpha }^2+{\mathsf{\mu }}^2{t}^2}+i\lambda \frac{\left(x-V_{0}t\right)}{{\alpha }^2+{\mathsf{\mu }}^2{t}^2}$$

(14)

$$\rho =\frac{{\left(\pi \right)}^{-1/2}}{{\left[{\alpha }^2+{\mathsf{\mu }}^2{t}^2\right]}^{1/2}}exp\left[-\frac{\left(x-V_{0}t\right)}{{\alpha }^2+{\mathsf{\mu }}^2{t}^2}\right]$$

(15)

$$\mathsf{\mu }=\frac{\lambda {\left(dt\right)}^{\left(\frac{2}{D_F}-1\right)}}{\alpha }$$

(16)

in (14)–(16) V₀ is the initial velocity of a Gaussian packet described by $\rho \left(x,0\right)={\rho }_0\exp [-{\left(x/\alpha \right)}^2]$.

In such a context, using the second relation (8), the nondifferentiable velocity $U_x\equiv U$, has the expression:

$$U=\alpha \mathsf{\mu }\frac{x-V_{0}t}{{\alpha }^2+{\mathsf{\mu }}^2{t}^2}$$

(17)

From (17) and (14) it results the space-time homographic transformation:

$$x=\frac{U{V}_0{\alpha }^2+\alpha \mathsf{\mu }V{V}_{0}t}{\mathsf{\mu }\alpha V+{\mathsf{\mu }}^{2}Ut}$$

(18)

Since at a differentiable resolution scale the following constriction is satisfied $\frac{V}{U}\gg \mu {\alpha }^{-1}t$, (18) takes the following form:

$$x\cong \frac{{\alpha }^2}{\lambda {\left(dt\right)}^{\left(\frac{2}{D_F}-1\right)}}\frac{U{V}_0}{V}+V_{0}t$$

(19)

which specifies a linear relationship of $x=x\left(t\right)$ type, having an unrestricted term of invers proportionality with the fractalization degree $\lambda {\left(dt\right)}^{\left(\frac{2}{D_F}-1\right)}$. In the following we will calibrate the theoretical model on the real dynamics of the laser produced plasma. Therefore, if we associate the fractalization degree with the nature of the atoms composing the target, through (19) the theoretical model can be corelated with the technique used to determine the expansion velocity from the ICCD fast camera imaging results.

Let us rewrite the homographic transformation under the following form:

$$x\left(t\right)=\frac{\alpha t+\beta }{\gamma t+\delta }$$

(20)

Since the optical emission spectroscopy measurement implies a “spatial simultaneity”, dx = 0, then this restriction can be expressed through differential form:

$$dt={\Omega }^1{t}^2+{\Omega }^{2}t+{\Omega }^3$$

(21)

where ${\Omega }^1,{\Omega }^2,{\Omega }^3$ are the differential 1-forms of the SL(2R) algebra:

$${\Omega }^1=\frac{\alpha d\gamma -\gamma d\alpha }{\alpha \delta -\beta \gamma },{\Omega }^2=\frac{\alpha d\delta -\delta d\alpha +\beta d\gamma -\gamma d\beta }{\alpha \delta -\beta \gamma },{\Omega }^3=\frac{\beta d\gamma -\beta d\alpha }{\alpha \delta -\beta \gamma }$$

(22)

If there is a continuum parameter θ towards which the 1-forms are total differentials:

$${\Omega }^1=a^{1}d\theta ,{\Omega }^2=2a^{2}d\theta ,{\Omega }^3=a^{3}d\theta$$

(23)

with $a^1,a^2,a^3$ constants (21) can pe reduced to a Riccati type equation:

$$\frac{dt}{d\theta }=a^1{t}^2+2a^{2}t+a^3$$

(24)

Let us know find the solution of (24) for a specific case:

$$A\frac{dt}{d\theta }=t^2-2B{t}^{}-AC$$

(25)

where we sued the following notations:

$$A=\frac{1}{a^1},B=-\frac{a^2}{a^1},AC=-\frac{a^3}{a^1}$$

(26)

with $a^1>0$. Admitting now that the roots of the following polynom:

$$P\left(t\right)=t^2-2B{t}^{}-AC$$

(27)

are given by the relation:

$$t_1=B+iAk,t_2=B-iAk,k=\frac{C}{A}-{\left(\frac{B}{A}\right)}^2$$

(28)

The homographic substitution:

$$z=\frac{t-t_1}{t-t_2}$$

(29)

transforms (25) in:

$$\frac{dz}{d\theta }=2ikz$$

(30)

The solution of this equation takes the following form:

$$z\left(t\right)=z\left(0\right)exp\left(2ik\theta \right)$$

(31)

or even more:

$$t=\frac{t_1+rexp\left(2ik\theta \right)t_2}{1+rexp\left(2ik\theta \right)}$$

(32)

where r is a real constant specific to this particular solution. Using the relation (28), solution (32) in real terms becomes:

$$z=B+Ak\left[\frac{2rsin\left(2k\theta \right)}{1+r^2+2rcos\left(2k\theta \right)}+i\frac{1-r^2}{1+r^2+2rcos\left(2k\theta \right)}\right]$$

(33)

which will specify a self-modulation of the k characteristic through a Stoller type transformation [32]. In Figure 12a,b we represent the 3D and contour plot representation of $Re(\left(z-B\right)/A$ as a function of r and 2kθ for a scale resolution given by the maximum value of k. If we manage to calibrate this fractal representation onto the dynamics of laser produced plasmas, we have to identify the $Re(\left(z-B\right)/A$ with the overall spectral emission of the plasma (in non-dimensional coordinates), with 2kθ being the non-dimensional time and r being a non-dimensional specific length of the plasma (considered to the distance across the main expansion axis). We can see in Figure 12 that the for the overall emission of the plasma, a self-structuring phenomenon occurred. Each of the self-generated patterns characterizes a plasma structure which is generated by means of different ablation mechanism. Therefore, each structure will be characterized by a different fractalization degree. The connection between generation of self-structuring patterns and each observed plasma structure underlined the connection between the ablation mechanism and the fractalization degree was previously reported by our group [33].

5. Conclusions

In order to obtain thin layers that can keep the properties of the bulk material, depositing technique through laser ablation was proposed. The NiTi targets oxidized in the impact area during the depositing process, impacting the particle removal mechanism during the ablation process. The plasma produced by laser ablation split during expansion in three structures. Each structure expands with different velocities correlated with the abundance of specific species presented in each structure. The kinetic properties of the structures were corelated with the individual kinetic and thermal properties of the Ti and Ni species. The chemical composition of the deposited layer depended of the distance of placing of the sub layer from the target and of the incidence angle between the material plasma and sub layer. The experimental results suggest that the chemical composition of a Nitinol layer can be precisely controlled without involving the substrate temperature using pulsed laser deposition considering the distance between the target and substrate, and the orientation of the substrate contact surface with the plume. The number of droplets on the deposited thin film decreased with the distance between the target and sub layer, and value of the laser fluence. Stoichiometric transfer was achieved for a series of samples.

A fractal model for describing the laser produced plasma dynamic, through various non-differential functionalities, was developed. Non-differentiable functionalities used for describing the laser produced plasmas dynamics through hydrodynamic type regime could be reduced to space-time homographic transformation. Transformations were correlated with the technique used to determine the global dynamics through ICCD fast camera imaging. Spatial simultaneity of the homographic type transformation implies through a special SL(2R) invariance dynamics defined through Riccati type equations. Such dynamics were correlated with optical emission spectroscopy measurements.