Multi-Criteria Group Decision-Making for Selection of Green Suppliers under Bipolar Fuzzy PROMETHEE Process
Abstract
1. Introduction
- The PROMETHEE method is extended to a bipolar fuzzy PROMETHEE method to deal with the double-sided information of human reasoning. More generally, trapezoidal bipolar fuzzy numbers are used to obtain more accurate results.
- The personal interest or influence of decision makers towards the criteria is minimized by using the Shannon entropy weighting technique to calculate the normalized weights of criteria.
- The partial and complete ranking of alternatives are determined by applying the PROMETHEE I and PROMETHEE II, respectively.
- A numerical example for the selection of green suppliers is presented that shows the validity and authenticity of the proposed method.
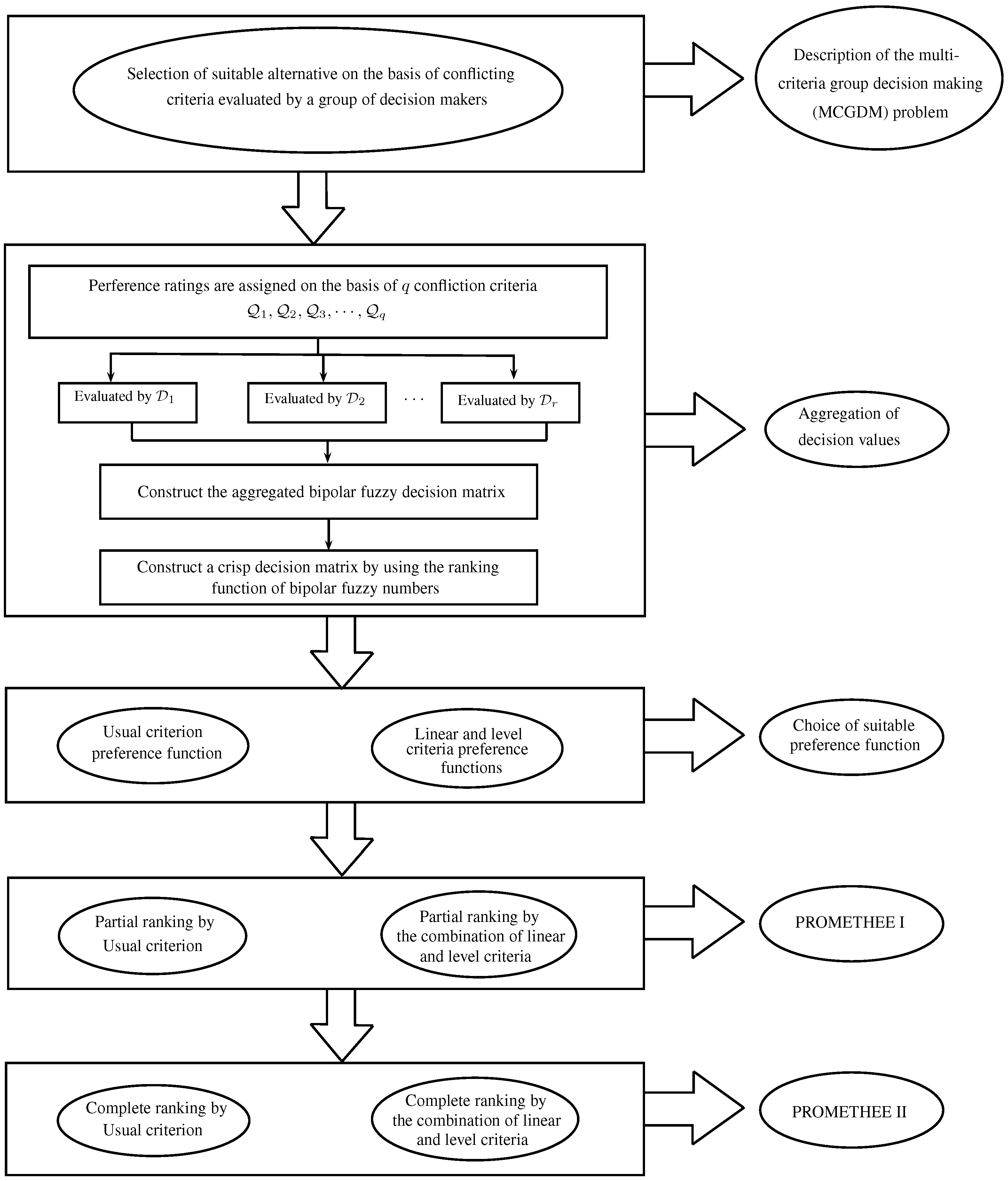
2. Methodology of the Bipolar Fuzzy PROMETHEE Method
2.1. Procedure of Bipolar Fuzzy PROMETHEE Method
- Step 1.
- Identify the linguistic variables.Linguistic variables are used by decision-makers to determine the ratings of an alternative with respect to different criteria. It is most important to identify the relevant and appropriate set of linguistic variables and define their respective values. In this method, a set of seven linguistic variables in the form of trapezoidal bipolar fuzzy numbers are considered and shown in Figure 1. The values of these trapezoidal bipolar fuzzy numbers are taken from the numerical domain [0,1].
- Step 2.
- Construct a decision matrix.Suppose that the alternatives are evaluated on the basis of conflicting criteria which are assessed by every decision maker . Then, r decision matrices are constructed containing the rating values of linguistic variables given by r decision-makers in the following manner:where each entry represents a trapezoidal bipolar fuzzy number. The aggregated bipolar fuzzy decision value of each alternative with respect to the criteria , denoted by is computed by using the averaging operator as follows:These aggregated values are used to construct an aggregated decision matrix as follows:
- Step 3.
- Rank the bipolar fuzzy numbers.The bipolar fuzzy numbers of aggregated values are then converted into the crisp values of real numbers by using the ranking function of bipolar fuzzy numbers as follows:and these crisp values are used to construct a simple decision matrix for further calculation.
- Step 4.
- Determine the deviation by pairwise comparison.The deviation of alternatives is computed by the pairwise comparison of alternatives on the basis of criteria by using the following expression:where represents the difference or deviation of any two alternatives and with respect to each criterion. The terms and denote the crisp ratings of alternatives and , respectively, with respect to some criterion .
- Step 5.
- Define the preference function.A preference function is defined to evaluate the preference of alternative regarding alternative on the basis of each criterion and has a value ranging from 0 to 1. If the value of the preference function is zero or negative then there is the indifference of the decision maker between the alternatives with respect to that criterion. On the other hand, a value closer to 1 shows a greater preference. This preference function represents the intensity of preference of an alternative over another alternative and is categorized as follows:
- -
- shows an indifference between and , or no preference of over ;
- -
- represents a weak preference of over ;
- -
- represents a strong preference of over ;
- -
- shows a strict preference of over .
- Step 6.
- Calculate the normalized weights.The weight value of each criterion shows the relative importance of that criterion towards the other criteria of that problem. These weight values may be completely or partially unknown for decision makers, and can be calculated by using various techniques or methods. If all the criteria have the same importance for a decision maker, then all weights can be assigned equal value. In this methodology, the entropy weight measuring information is used to enumerate the normalized weights of conflicting criteria. In order to calculate the weights by entropy measure, first we should normalize the decision values of each criterion and obtain the projection values of criteria as follows:These projection values are then used to calculate the entropy value for each criterion as follows:where is a constant. Afterward, the degree of divergence of the intrinsic information for each criterion is calculated by using the following expression:The divergence value denotes the inherent contrast intensity of criteria . The higher value of shows that the criterion is considered as more important for that problem. Then, the weights of criteria are calculated as:such that, and
- Step 7.
- Determine the multi-criteria preference index.When a preference function and weight is assigned to each criterion by a decision maker for the considered problem, then the multi-criteria preference index of alternatives is determined. The multi-criteria preference index ∏ is calculated as the weighted average of the preference functions :Since the normalized weights are used in this method, Equation (12) is reduced as follows:The multi-criteria preference index ∏ has a value between 0 and 1, such that
- -
- represents the weak preference of alternative over with respect to all criteria;
- -
- represents the strong preference of alternative over with respect to all criteria.
This preference index induces an outranking relation on the set of alternatives which is further represented by an outranking graph. The nodes of this outranking graph are the alternatives and, between any two nodes and , there are two arcs with values , and which have no particular relation. - Step 8.
- Find the preference order.The outranking relation is then used to obtain the ranking of alternatives, which may be partial or complete. The alternatives are ranked partially by using the PROMETHEE I, whereas complete ranking can be obtain by proceeding one more step of PROMETHEE II.
- (i)
- Ordering the alternatives by partial ranking or PROMETHEE I.For each alternative in the outranking graph, the leaving or outgoing flow is defined as:which is the sum of values of outward arcs of alternative and thus gives the outgoing flow of as shown in Figure 2. This positive outranking flow measures how an alternative dominates all other alternatives.Similarly, for each alternative in outranking graph, the entering or incoming flow is defined as:which is the sum of values of inward arcs of alternative and thus gives the incoming flow of as shown in Figure 3. This negative outranking flow determines how an alternative is dominated by all other alternatives.The alternative which has the greater value of and the lower value of is chosen as the most suitable alternative. The outgoing and incoming flows determine the preferences as given in Equations (12) and (13), respectively.The PROMETHEE I partial ordering is then obtained by taking the intersection of the two previously mentioned preferences as:Since all the alternatives are not comparable in PROMETHEE I, the computation of the net outranking flow of alternatives is as follows.
- (ii)
- Ordering the alternatives by complete ranking or PROMETHEE II.The net flow of each alternative is the difference of outgoing and incoming flows, which is computed as:The net flow provides the complete ordering of alternatives by avoiding any incomparability, the PROMETHEE II complete ranking is given in Equation (16).Thus, all the alternatives can be compared on the basis of net flows . The alternative with maximum net flow is observed as the most suitable alternative.The framework of the procedure of the bipolar fuzzy PROMETHEE method is provided in Figure 4. This framework consists of the goal of the selection procedure, the environmental and economical criteria, the alternatives for evaluation, the preference functions, and the net outranking flows of PROMETHEE I and PROMETHEE II in the form of partial and complete ranking, respectively.
This multi-criteria outranking approach is based on a series of computations, in which all steps remain the same other than the definition of the preference function and the computation of normalized weights. The normalized weights can be calculated by using an appropriate method according to the choice of decision values or the preference of the decision makers. The preference function defined in Step 5 is an irrational choice of preference function which depends on the nature of the criteria or the desire of the decision-makers. The choice of types of preference function is very important as it may change the net outranking flow or the ranking of alternatives.
2.2. Preference Function
3. Green Supplier Selection
- MVG Food Marketing Sdn Bhd;
- CF Org Noodle Sdn Bhd;
- Hexa Food Sdn Bhd;
- SCS Food Manufacturing Sdn Bhd.
- Cost of products (consists of transportation, purchasing, inventory, maintenance, holding, security etc.);
- Quality of products (indicated by the principles, techniques, and practices of companies);
- Service provided (low costs, high productivity, quick response, minimum wastage, no damage, etc.);
- Delivery (at the correct time, at the right place, and in good condition);
- Pollution control (an important criterion, as pollution is obtained as a byproduct of energy use in the production procedures);
- Environmental management system (the environmental dimension has been recently added in assessment procedures);
- Green packaging (a type of packaging which aims protect the environment by using environmentally friendly material).
- Step 1.
- Step 2.
- The preference ratings of alternatives with respect to conflicting criteria given by decisions makers in the form of linguistic terms are shown in Table 2.The rating values of these linguistic variables in the form of trapezoidal bipolar fuzzy numbers were used as defined in Table 1, and the results are given in Table 3. The aggregated decision values of these trapezoidal bipolar fuzzy numbers were computed by employing the Equation (1), and an aggregated decision matrix was constructed as shown in Table 4.For example, the aggregated decision value of supplier with respect to criterion was computed by arithmetic mean as,
- Step 3.
- In this step, a simple decision matrix consisting of real numbers as entries was constructed for further calculations by using the ranking function of bipolar fuzzy numbers. Equation (2) was applied to the entries of Table 1, and the bipolar fuzzy numbers were converted to crisp values, which are shown in matrix T.For instance, is the performance value of supplier on the basis of criterion , which was calculated as follows:
- Step 4.
- Step 5.
- A preference function is required for the implementation of the PROMETHEE method. The preference function was used to define the deviation of any pair of alternatives on the basis of each criterion. In this step, the usual criterion preference function was used as defined in Definition 5, and the results are summarized in Table 6.
- Step 6.
- The weights of criteria specify the importance of each criterion towards the alternatives of the problem. In this method, the entropy weight information technique is used to calculate the normalized weights of criteria. The first step of this technique is the computation of projection values of criteria in order to normalize the decision values of criteria. The projection values for all criteria were calculated using Equation (4), and the results shown in Table 7. For example, is the projection value of criterion regarding the supplier and was calculated as follows:The entropy value and the degree of divergence for each criterion were calculated by using the projection values given in Table 7, and deploying Equations (5) and (6), respectively, which were further utilized to determine the normalized weights of criteria. The results of entropy values, degrees of divergence, and weights of criteria are respectively shown in Table 8.
- Step 7.
- In this step, the multi-criteria preference index of each alternative is calculated, taking into account the weight criteria. The preference index of each alternative shows the value of preference of a supplier over other suppliers. The values of multi-criteria preference index were computed using Equation (9), and the results are summarized in Table 9.
- Step 8.
- This step concludes the whole procedure and the partial as well as net flows of alternatives are computed.
- (i)
- Positive and negative flows of alternatives (PROMETHEE I).The outgoing and incoming flows of alternatives are obtained which are positive and negative outranking flows, respectively. The positive outranking flow of an alternative determines how an alternative dominates all other alternatives and the negative flow shows how an alternative is dominated by all other alternatives. Equations (10) and (11) were used to calculate the outgoing and incoming flows of each alternative, and the results are given in Table 10. The partial ordering of suppliers was then obtained by taking the intersection of preorders and , which is given as follows:and the partial results of PROMETHEE I are illustrated in Figure 5.The results of positive outranking flow show that the supplier is most preferable with greatest outgoing flow rate and determine that the supplier is more dominant over all other suppliers. On the other hand, the negative outranking flow shows that the supplier is less dominated by all other suppliers with minimum incoming flow value. These results are not able to compare all the alternatives nor to determine the most suitable supplier. For this reason, we need to calculate the net outranking flow of suppliers to obtain the complete preference of suppliers in the next step.
- (ii)
- Net flow of alternatives (PROMETHEE II).The net flow of each alternative was calculated by using Equation (15), which is the combination of positive and negative flows. The net outranking flow provides the complete ranking of alternatives by avoiding the incomparability. The results of the net flow of alternatives are shown in Table 11. These results can be justified by sketching the PROMETHEE diamond, which is a chart used to elaborate the results of PROMETHEE I and PROMETHEE II simultaneously. The positions of suppliers or complete ranking (PROMETHEE II) as well as the outgoing and incoming flows are also displayed in Figure 6.
4. Comparative Study
- Step 5.
- In this step, the combination of level and linear preference functions were adopted for conflicting criteria. The list of all criteria and their corresponding preference functions is given in Table 12.The linear preference function has a preference threshold value and the level function evaluates the criteria on the basis of preference and indifference threshold values, which are given by decision makers. In this multi-criteria decision-making problem, the indifference and preference threshold values were considered as and , respectively, for both linear and level preference functions. The deviations between every pair of alternatives were obtained using Equations (6) and (7), and the results are shown in Table 13.
- Step 6.
- Step 7.
- Step 8.
- The partial and net flows are determined in this step.
- (i)
- The positive and negative outranking flows of the suppliers were computed by deploying the Equations (10) and (11), respectively. The respective results of outgoing and incoming flows for PROMETHEE I are shown in Table 15.The partial ordering of suppliers was then obtained by taking the intersection of preorders and , which is given as follows:and the partial results of PROMETHEE I are illustrated in Figure 7.
- (ii)
- The net outranking flow of each alternative was calculated by deploying Equation (15), and the results of PROMETHEE II are given in Table 16.It can be clearly seen that supplier is chosen as the most preferable alternative under the combination of linear and level preference functions and the suppliers can be ordered as
5. Discussion and Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Awasthi, A.; Chauhan, S.S.; Goyal, S.K. A fuzzy multicriteria approach for evaluating environmental performance of suppliers. Int. J. Prod. Econ. 2010, 126, 370–378. [Google Scholar] [CrossRef]
- Handfield, R.; Walton, S.V.; Sroufe, R.; Melnyk, S.A. Applying environmental criteria to supplier assessment: A study in the application of the Analytical Hierarchy Process. Eur. J. Oper. Res. 2002, 141, 70–87. [Google Scholar] [CrossRef]
- Mousakhani, S.; Nazari-Shirkouhi, S.; Bozorgi-Amiri, A. A novel interval type-2 fuzzy evaluation model based group decision analysis for green supplier selection problems: A case study of battery industry. J. Clean. Prod. 2017, 168, 205–218. [Google Scholar] [CrossRef]
- Yeh, W.C.; Chuang, M.C. Using multi-objective genetic algorithm for partner selection in green supply chain problems. Expert Syst. Appl. 2011, 38, 4244–4253. [Google Scholar] [CrossRef]
- Hou, B.; Yanrong, W. Supplier evaluation and selection based on improved TOPSIS method in green supply chain. J. Hunan Univ. Technol. 2014, 2, 17–25. [Google Scholar]
- Yazdani, M.; Zolfani, S.H.; Zavadskas, E.K. New integration of MCDM methods and QFD in the selection of green suppliers. J. Bus. Econ. Manag. 2016, 17, 1097–1113. [Google Scholar] [CrossRef]
- Saaty, T.L. Axiomatic foundation of the analytic hierarchy process. Manag. Sci. 1986, 32, 841–855. [Google Scholar] [CrossRef]
- Brans, J.P.; Vincle, P.V. A Preference Ranking Organization Method. Manag. Sci. 1985, 31, 647–656. [Google Scholar] [CrossRef]
- Benayoun, R.; Roy, B.; Sussman, B. ELECTRE: Une Methode pour Guider le Choix en Presence de Points de vue Multiples; Note de Travail, 49, SEMA-METRA International, Direction Scientifique; SEMA: Montrouge, France, 1966; 43p. [Google Scholar]
- Opricovic, S.; Tzeng, G.H. Compromise solution by MCDM methods: A comparative analysis of VIKOR and TOPSIS. Eur. J. Oper. Res. 2004, 156, 445–455. [Google Scholar] [CrossRef]
- Hwang, C.L.; Yoon, K. Multiple Attribute Decision Making Methods and Applications; Springer: Berlin, Germany, 1981. [Google Scholar]
- Bellman, R.E.; Zadeh, L.A. Decision-making in a fuzzy environment. Manag. Sci. 1970, 4, 141–164. [Google Scholar] [CrossRef]
- Chiou, C.Y.; Hsu, C.W.; Hwang, W.Y. Comparative investigation on green supplier selection of the American, Japanese and Taiwanese electronics industry in China. In Proceedings of the 2008 IEEE International Conference on Industrial Engineering and Engineering Management, Singapore, 8–11 December 2008; pp. 1909–1914. [Google Scholar]
- Sanayei, A.; Mousavi, S.F.; Yazdankhah, A. Group decision making process for supplier selection with VIKOR under fuzzy environment. Expert Syst. Appl. 2010, 37, 24–30. [Google Scholar] [CrossRef]
- Liu, B.; Huo, T.; Wang, X.; Shen, Q.; Chen, Y. The decision model of the intuitionistic fuzzy group bid evaluation for urban infrastructure projects considering social costs. Can. J. Civil Eng. 2013, 40, 263–273. [Google Scholar] [CrossRef]
- Kannan, D.; Jabbour, A.B.L.d.; Jabbour, C.J.C. Selecting green suppliers based on GSCM practices: Using fuzzy TOPSIS applied to a Brazilian electronics company. Eur. J. Oper. Res. 2014, 233, 432–447. [Google Scholar] [CrossRef]
- Awasthi, A.; Kannan, G. Green supplier development program selection using NGT and VIKOR under fuzzy environment. Comput. Ind. Eng. 2016, 91, 100–108. [Google Scholar] [CrossRef]
- Hamdan, S.; Cheaitou, A. Supplier selection and order allocation with green criteria: An MCDM and multi-objective optimization approach. Comput. Oper. Res. 2017, 81, 282–304. [Google Scholar] [CrossRef]
- Akram, M.; Al-Kenani, A.N. Multiple-Attribute Decision Making ELECTRE II Method under Bipolar Fuzzy Model. Algorithms 2019, 12, 226. [Google Scholar]
- Ziemba, P.; Piwowarski, M.; Jankowski, J.; Watrobski, J. Method of criteria selection and weights calculation in the process of web projects evaluation. In Proceedings of the International Conference on Computational Collective Intelligence, Seoul, Korea, 24–26 September 2014; pp. 684–693. [Google Scholar]
- Brans, J.P.; Vincle, P.; Mareschal, B. How to select and how to rank projects: The PROMETHEE method. Eur. J. Oper. Res. 1986, 24, 228–238. [Google Scholar] [CrossRef]
- Brans, J.P.; Mareschal, B. PROMETHEE methods. In Multiple Criteria Decision Analysis: State of the Art Surveys; Springer: Berlin, Germany, 2005; pp. 163–186. [Google Scholar]
- Abdullah, L.; Chan, W.; Afshari, A. Application of PROMETHEE method for green supplier selection: A comparative result based on preference functions. J. Ind. Eng. Int. 2019, 15, 271–285. [Google Scholar] [CrossRef]
- Behzadian, M.; Kazemzadeh, R.B.; Albadvi, A.; Aghdasi, M. PROMETHEE: A comprehensive literature review on methodologies and applications. Eur. J. Oper. Res. 2010, 200, 198–215. [Google Scholar] [CrossRef]
- Govindan, K.; Kadzinski, M.; Sivakumar, R. Application of a novel PROMETHEE-based method for construction of a group compromise ranking to prioritization of green suppliers in food supply chain. Omega 2017, 71, 129–145. [Google Scholar] [CrossRef]
- Goumas, M.; Lygerou, V. An extension of the PROMETHEE method for decision making in fuzzy environment: Ranking of alternative energy exploitation projects. Eur. J. Oper. Res. 2000, 123, 606–613. [Google Scholar] [CrossRef]
- Krishankumar, R.; Ravichandran, K.S.; Saeid, A.B. A new extension to PROMETHEE under intuitionistic fuzzy environment for solving supplier selection problem with linguistic preferences. Appl. Soft Comput. 2017, 60, 564–576. [Google Scholar]
- Ziemba, P. NEAT F-PROMETHEE-A new fuzzy multiple criteria decision making method based on the adjustment of mapping trapezoidal fuzzy numbers. Expert Syst. Appl. 2018, 110, 363–380. [Google Scholar] [CrossRef]
- Zhang, W.R. Bipolar fuzzy sets and relations: A computational framework for cognitive modeling and multiagent decision analysis. In Proceedings of the IEEE Conference Fuzzy Information Processing Society Biannual Conference, San Antonio, TX, USA, 18–21 December 1994; pp. 305–309. [Google Scholar]
- Zhang, W.R. (Yin)(Yang) bipolar fuzzy sets. In Proceedings of the 1998 IEEE International Conference on Fuzzy Systems Proceedings, IEEE World Congress on Computational Intelligence (Cat. No. 98CH36228), Anchorage, AK, USA, 4–9 May 1998; Volume 1, pp. 835–840. [Google Scholar]
- Zadeh, L.A. Fuzzy sets. Inf. Control 1965, 8, 338–353. [Google Scholar] [CrossRef]
- Akram, M.; Arshad, M. A novel trapezoidal bipolar fuzzy TOPSIS method for group decision-making. Group Decis. Negot. 2019, 28, 565–584. [Google Scholar] [CrossRef]
- Alghamdi, M.A.; Alshehri, N.O.; Akram, M. Multi-criteria decision-making methods in bipolar fuzzy environment. Int. J. Fuzzy Syst. 2018, 20, 2057–2064. [Google Scholar] [CrossRef]
- Akram, M.; Shumaiza; Arshad, M. Bipolar fuzzy TOPSIS and bipolar fuzzy ELECTRE-I methods to diagnosis. Comput. Appl. Math. 2020, 39, 1–23. [Google Scholar] [CrossRef]
- Akram, M.; Al-Kenani, A.N.; Alcantud, J.C.R. Group decision-making based on the VIKOR method with trapezoidal bipolar fuzzy information. Symmetry 2019, 11, 1313. [Google Scholar]
- Lihong, M.; Yanping, Z.; Zhiwei, Z. Improved VIKOR algorithm based on AHP and Shannon entropy in the selection of thermal power enterprise’s coal suppliers. In Proceedings of the International Conference on Information Management, Innovation Management and Industrial Engineering, Taipei, Taiwan, 19–21 December 2008; Volume 2, pp. 129–133. [Google Scholar]
- Shemshadi, A.; Shirazi, H.; Toreihi, M.; Tarokh, M.J. A fuzzy VIKOR method for supplier selection based on entropy measure for objective weighting. Expert Syst. Appl. 2011, 38, 12160–12167. [Google Scholar] [CrossRef]
- Alcantud, J.C.R.; Biondo, A.E.; Giarlotta, A. Fuzzy politics I: The genesis of parties. Fuzzy Sets Syst. 2018, 349, 71–98. [Google Scholar] [CrossRef]
- Gurel, O.; Acar, A.Z.; Onden, I.; Gumus, I. Determinants of the green supplier selection. Procedia-Soc. Behav. Sci. 2015, 181, 131–139. [Google Scholar] [CrossRef]







| Linguistic Variable | Abbreviation | Bipolar Fuzzy Number |
|---|---|---|
| −0.277 | −0.355 | −0.355 | |||||
| −0.177 | −0.177 | −0.077 | |||||
| −0.525 | −0.077 | −0.077 | |||||
| 0.277 | 0.355 | 0.355 | |||||
| 0.1 | 0.178 | 0.278 | |||||
| −0.248 | 0.278 | 0.278 | |||||
| 0.177 | 0.177 | 0.077 | |||||
| −0.1 | −0.178 | −0.278 | |||||
| −0.348 | 0.1 | 0.0 | |||||
| 0.525 | 0.077 | 0.077 | |||||
| 0.248 | −0.278 | −0.278 | |||||
| 0.348 | −0.1 | 0.0 |
| 1 | 1 | 1 | 0 | 0 | 0 | 0 | |
| 1 | 1 | 0 | 0 | 0 | 0 | 0 | |
| 0 | 1 | 1 | 0 | 0 | 0 | 0 | |
| 0 | 0 | 0 | 1 | 1 | 1 | 1 | |
| 1 | 0 | 0 | 0 | 1 | 1 | 1 | |
| 0 | 0 | 1 | 0 | 0 | 1 | 1 | |
| 0 | 0 | 1 | 1 | 1 | 1 | 1 | |
| 0 | 1 | 1 | 1 | 0 | 0 | 0 | |
| 0 | 0 | 1 | 1 | 0 | 1 | 0 | |
| 0 | 0 | 0 | 1 | 1 | 1 | 1 | |
| 1 | 1 | 0 | 1 | 1 | 0 | 0 | |
| 1 | 1 | 0 | 0 | 1 | 0 | 0 |
| Suppliers | ||||
|---|---|---|---|---|
| − | ||||
| − | ||||
| − | ||||
| − |
| Suppliers | ||
|---|---|---|
| Suppliers | |
|---|---|
| Criteria | Preference Function |
|---|---|
| Cost of products | Linear |
| Quality of products | Level |
| Services | Level |
| Delivery | Level |
| Pollution control | Level |
| Environmental management system | Level |
| Green packaging | Level |
| 1 | 1 | 0 | 0 | 0 | 0 | ||
| 1 | 0 | 0 | 0 | 0 | 0 | ||
| 0 | 0 | 1 | 0 | 0 | 0 | 0 | |
| 0 | 0 | 0 | 1 | 1 | 1 | 1 | |
| 1 | 0 | 0 | 0 | 1 | 1 | ||
| 0 | 0 | 0 | 0 | 1 | 1 | ||
| 0 | 0 | 1 | 1 | 1 | 1 | ||
| 0 | 1 | 0 | 0 | 0 | |||
| 0 | 0 | 1 | 0 | 0 | 0 | ||
| 0 | 0 | 0 | 1 | 1 | |||
| 1 | 1 | 0 | 1 | 0 | 0 | ||
| 1 | 0 | 0 | 1 | 0 | 0 |
| Suppliers | ||||
|---|---|---|---|---|
| − | ||||
| − | ||||
| − | ||||
| − |
| Suppliers | ||
|---|---|---|
| Suppliers | |
|---|---|
| Suppliers | Usual Criterion | Linear and Level Criteria |
|---|---|---|
| Preference Function | Preference Functions | |
| Supplier | 4 | 4 |
| Supplier | 1 | 1 |
| Supplier | 3 | 3 |
| Supplier | 2 | 2 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Akram, M.; Shumaiza; Al-Kenani, A.N. Multi-Criteria Group Decision-Making for Selection of Green Suppliers under Bipolar Fuzzy PROMETHEE Process. Symmetry 2020, 12, 77. https://doi.org/10.3390/sym12010077
Akram M, Shumaiza, Al-Kenani AN. Multi-Criteria Group Decision-Making for Selection of Green Suppliers under Bipolar Fuzzy PROMETHEE Process. Symmetry. 2020; 12(1):77. https://doi.org/10.3390/sym12010077
Chicago/Turabian StyleAkram, Muhammad, Shumaiza, and Ahmad N. Al-Kenani. 2020. "Multi-Criteria Group Decision-Making for Selection of Green Suppliers under Bipolar Fuzzy PROMETHEE Process" Symmetry 12, no. 1: 77. https://doi.org/10.3390/sym12010077
APA StyleAkram, M., Shumaiza, & Al-Kenani, A. N. (2020). Multi-Criteria Group Decision-Making for Selection of Green Suppliers under Bipolar Fuzzy PROMETHEE Process. Symmetry, 12(1), 77. https://doi.org/10.3390/sym12010077





