Exact Solutions and Conservation Laws of the (3 + 1)-Dimensional B-Type Kadomstev–Petviashvili (BKP)-Boussinesq Equation

Abstract

In this paper, Lie symmetry analysis is presented for the (3 + 1)-dimensional BKP-Boussinesq equation, which seriously affects the dispersion relation and the phase shift. To start with, we derive the Lie point symmetry and construct the optimal system of one-dimensional subalgebras. Moreover, according to the optimal system, similarity reductions are investigated and we obtain exact solutions of reduced equations by means of the Tanh method. In the end, we establish conservation laws using Ibragimov’s approach.

1. Introduction

In the past few years, nonlinear evolution equations have been used to explore physical phenomena, such as marine engineering, plasma physics, fluid dynamics, etc. In order to understand many complex physical phenomena better, we need to research explicit solutions of nonlinear evolution equations. Wazwaz [1] proposed the (3 + 1)-dimensional generalized BKP equation

$$-u_{xxxy}+u_{ty}+3u_{xz}-3{\left(u_x{u}_y\right)}_x=0,$$

(1)

which explains evolution of quasi-one dimensional shallow water waves when the effects of viscosity and surface tension are taken to be negligible [2]. Recently, a host of exact solutions of Equation (1), including grammian-type determinant solutions [3], periodic wave solutions [4], lump solutions [5] and multiple wave solutions [6], have been discussed. Moreover, adding an extra term $u_{tt}$, Wazwaz and El-Tantawy got an expansion of Equation (1), that is a new form of the (3 + 1)-dimensional BKP-Boussinesq Equation [7]

$$u_{ty}-u_{xxxy}-3{\left(u_x{u}_y\right)}_x+u_{tt}+3u_{xz}=0,$$

(2)

where $u(x,y,t,z)$ is an unknown function and subscripts denote the partial derivatives. This equation possesses the properties of both the Boussinesq and the BKP equations, which can be used to describe the propagation of long waves in shallow water [8]. By using analysis of the Painlevé property, the integrability properties of Equation (2) have been proved [2]. One and two soliton solutions were derived by utilizing the simplified Hirota’s method in [7]. It was reported that coefficients of spatial variables were left as free parameters. Based on the Bäcklund transformation, the rational solutions and exponential wave solutions of Equation (2) were obtained in [8].

Quite a few methods have been researched to find crucially exact solutions for nonlinear partial differential equations (PDEs). Some of the most remarkable methods are the Hirota bilinear method [9], the homogeneous balance method [10], the Sine–Gordon expansion method [11], the Darboux transformation [12], the $(G^{\prime }/G)$-expansion method [13,14], Lie symmetry analysis [15,16,17,18], the inverse scattering method [19], etc. Lie symmetry analysis, a very powerful method among those listed above, plays a significant role in obtaining exact solutions of PDEs. The basic idea of this method is to keep the solution set of the partial differential equations invariant under infinitesimal transformation. Using the symmetry method, we construct the optimal system of Equation (2), from which some interesting exact solutions are obtained by using the classical Tanh method [20,21]. Another important aspect is conservation laws of PDEs which have important influence on finding solutions of PDEs [22,23]. We will construct the conservation laws of Equation (2) by applying Ibragimov’s approach [24].

Eventually, the framework of this paper is as follows. In Section 2, we derive the Lie point symmetry of the (3 + 1)-dimensional BKP-Boussinesq equation. In Section 3, the optimal system of Equation (2) is constructed. We handle similarity reductions and obtain the reduced equations in Section 4. In Section 5, exact solutions of the reduced equations are presented by means of the Tanh method. Based on lbragimov’s method, we build the conservation laws in Section 6. The last section is made up of some brief statements.

2. Lie Point Symmetry

In this section, carrying out the Lie symmetry analysis method for Equation (2), we consider a one-parameter Lie group transformation

$$\begin{array}{c}x\to x+ϵ{\xi }^1(x,y,t,z,u),\hfill \\ y\to y+ϵ{\xi }^2(x,y,t,z,u),\hfill \\ t\to t+ϵ{\xi }^3(x,y,t,z,u),\hfill \\ z\to z+ϵ{\xi }^4(x,y,t,z,u),\hfill \\ u\to u+ϵ{\eta }^1(x,y,t,z,u),\hfill \end{array}$$

with a small parameter $ϵ\ll 1$. The infinitesimal generator linked with the above group transformation is given as

$$\begin{array}{c}X={\xi }^1(x,y,t,z,u)\frac{\partial }{\partial x}+{\xi }^2(x,y,t,z,u)\frac{\partial }{\partial y}+{\xi }^3(x,y,t,z,u)\frac{\partial }{\partial t}+{\xi }^4(x,y,t,z,u)\frac{\partial }{\partial z}\hfill \\ +{\eta }^1(x,y,t,z,u)\frac{\partial }{\partial u}.\hfill \end{array}$$

and its fourth-order prolongation is

$$\begin{array}{c}{\mathrm{pr}}^{\left(4\right)}X=X+{\eta }_x^1\frac{\partial }{\partial u_x}+{\eta }_y^1\frac{\partial }{\partial u_y}+{\eta }_{ty}^1\frac{\partial }{\partial u_{ty}}+{\eta }_{xx}^1\frac{\partial }{\partial u_{xx}}+{\eta }_{yx}^1\frac{\partial }{\partial u_{yx}}+{\eta }_{tt}^1\frac{\partial }{\partial u_{tt}}\hfill \\ +{\eta }_{xz}^1\frac{\partial }{\partial u_{xz}}+{\eta }_{xxxy}^1\frac{\partial }{\partial u_{xxxy}},\hfill \end{array}$$

where

$$\begin{array}{c}{\eta }_x^1=D_x\left({\eta }^1\right)-u_x{D}_x\left({\xi }^1\right)-u_y{D}_x\left({\xi }^2\right)-u_t{D}_x\left({\xi }^3\right)-u_z{D}_x\left({\xi }^4\right),\hfill \\ {\eta }_y^1=D_y\left({\eta }^1\right)-u_x{D}_y\left({\xi }^1\right)-u_y{D}_y\left({\xi }^2\right)-u_t{D}_y\left({\xi }^3\right)-u_z{D}_y\left({\xi }^4\right),\hfill \\ {\eta }_{ty}^1=D_t{D}_y({\eta }^1-{\xi }^1{u}_x-{\xi }^2{u}_y-{\xi }^3{u}_t-{\xi }^4{u}_z)+{\xi }^1{u}_{xty}+{\xi }^2{u}_{yty}+{\xi }^3{u}_{tty}+{\xi }^4{u}_{zty},\hfill \\ {\eta }_{xx}^1=D_x^2({\eta }^1-{\xi }^1{u}_x-{\xi }^2{u}_y-{\xi }^3{u}_t-{\xi }^4{u}_z)+{\xi }^1{u}_{xxx}+{\xi }^2{u}_{yxx}+{\xi }^3{u}_{txx}+{\xi }^4{u}_{zxx},\hfill \\ {\eta }_{yx}^1=D_y{D}_x({\eta }^1-{\xi }^1{u}_x-{\xi }^2{u}_y-{\xi }^3{u}_t-{\xi }^4{u}_z)+{\xi }^1{u}_{xyx}+{\xi }^2{u}_{yyx}+{\xi }^3{u}_{tyx}+{\xi }^4{u}_{zyx},\hfill \\ {\eta }_{tt}^1=D_t^2({\eta }^1-{\xi }^1{u}_x-{\xi }^2{u}_y-{\xi }^3{u}_t-{\xi }^4{u}_z)+{\xi }^1{u}_{xtt}+{\xi }^2{u}_{ytt}+{\xi }^3{u}_{ttt}+{\xi }^4{u}_{ztt},\hfill \\ {\eta }_{xz}^1=D_x{D}_z({\eta }^1-{\xi }^1{u}_x-{\xi }^2{u}_y-{\xi }^3{u}_t-{\xi }^4{u}_z)+{\xi }^1{u}_{xxz}+{\xi }^2{u}_{yxz}+{\xi }^3{u}_{txz}+{\xi }^4{u}_{zxz},\hfill \\ {\eta }_{xxxy}^1=D_x^3{D}_y({\eta }^1-{\xi }^1{u}_x-{\xi }^2{u}_y-{\xi }^3{u}_t-{\xi }^4{u}_z)+{\xi }^1{u}_{xxxxy}+{\xi }^2{u}_{yxxxy}+{\xi }^3{u}_{txxxy}+{\xi }^4{u}_{zxxxy},\hfill \end{array}$$

and $D_x,D_y,D_t,D_z$, respectively, represent the total derivatives concerning $x,y,t$ and z. Then, the determining equations generated by the invariance conditions can be written as

$$\begin{array}{c}{\mathrm{pr}}^{\left(4\right)}{X\left(\mathsf{\Delta }\right)|}_{\mathsf{\Delta }=0}=0,\hfill \end{array}$$

where $\mathsf{\Delta }=u_{ty}-u_{xxxy}-3{\left(u_x{u}_y\right)}_x+u_{tt}+3u_{xz}$. Furthermore, we obtain the following system of overdetermined equations

$$\begin{array}{c}{\xi }_t^1=-\frac{3}{2}{\xi }_z^3,{\xi }_u^1={\xi }_y^1=0,{\xi }_x^1=\frac{1}{5}{\xi }_z^4,\hfill \\ {\xi }_t^2={\xi }_u^2={\xi }_x^2=0,{\xi }_y^2=\frac{3}{5}{\xi }_z^4,\hfill \\ {\xi }_t^3=\frac{3}{5}{\xi }_z^4,{\xi }_u^3={\xi }_x^3={\xi }_y^3=0,\hfill \\ {\eta }_t^4={\xi }_u^4={\xi }_x^4={\xi }_y^4={\xi }_{zz}^4=0,\hfill \\ {\eta }_u^1=-\frac{1}{5}{\eta }_z^4,{\eta }_x^1=\frac{1}{2}{\xi }_z^3-{\xi }_z^2,{\eta }_y^1=-{\eta }_z^1,{\xi }_{tt}^1=-3{\xi }_{zz}^3+3{\xi }_{zz}^2.\hfill \end{array}$$

Solving this system, we can get

$$\begin{array}{c}{\xi }^1=\frac{1}{3}{c}_{1}x-\frac{3}{2}t{\left(F_1\right)}_z+F_3\left(z\right),{\xi }^2=c_{1}y+F_2\left(z\right),{\xi }^3=c_{1}t+F_1\left(z\right),{\xi }^4=\frac{5}{3}{c}_{1}z+c_2,\hfill \\ {\eta }^1=-\frac{3}{2}t(t-y){\left(F_1\right)}_{zz}-\frac{1}{3}{c}_{1}u+\frac{1}{2}x{\left(F_1\right)}_z-x{\left(F_2\right)}_z+F_4\left(z\right)t-y{\left(F_3\right)}_z+\frac{3}{2}{t}^2{\left(F_2\right)}_{zz}+F_5\left(z\right),\hfill \end{array}$$

where $c_1,c_2$ are arbitrary constants and $F_1\left(z\right),F_2\left(z\right),F_3\left(z\right),F_4\left(z\right)$ and $F_5\left(z\right)$ are arbitrary functions. To obtain physically crucial solutions, we take $F_1\left(z\right)=c_3,F_2\left(z\right)=c_4,F_3\left(z\right)=c_5,F_4\left(z\right)=c_6,F_5\left(z\right)=c_7$, then substituting the above and obtaining

$$\begin{array}{c}{\xi }^1=\frac{1}{3}{c}_{1}x+c_5,{\xi }^2=c_{1}y+c_4,{\xi }^3=c_{1}t+c_3,{\xi }^4=\frac{5}{3}{c}_{1}z+c_2,{\eta }^1=-\frac{1}{3}{c}_{1}u+c_{6}t+c_7,\hfill \end{array}$$

where $c_1,c_2,c_3,c_4,c_5,c_6$ and $c_7$ are arbitrary constants. Thus seven-dimensional Lie algebra made up of infinitesimal symmetries is spanned by the following generators

$$\begin{array}{c}{X}_1=\frac{1}{3}x\frac{\partial }{\partial x}+y\frac{\partial }{\partial y}+t\frac{\partial }{\partial t}+\frac{5}{3}z\frac{\partial }{\partial z}-\frac{1}{3}u\frac{\partial }{\partial u},\hfill \\ X_2=\frac{\partial }{\partial z},\hfill \\ X_3=\frac{\partial }{\partial t},\hfill \\ X_4=\frac{\partial }{\partial y},\hfill \\ X_5=\frac{\partial }{\partial x},\hfill \\ X_6=t\frac{\partial }{\partial u},\hfill \\ X_7=\frac{\partial }{\partial u}.\hfill \end{array}$$

(3)

After getting the infinitesimal generators, the following group transformations, which are formed by the $X_i$ for $i=1,2,3,4,5,6,7$ can be given as

$$\begin{array}{c}{G}_1:(x,y,t,z,u)\to (x{e}^{\frac{1}{3}ϵ},y{e}^{ϵ},t{e}^{ϵ},z{e}^{\frac{5}{3}ϵ},u{e}^{-\frac{1}{3}ϵ}),\hfill \\ G_2:(x,y,t,z,u)\to (x,y,t,z+ϵ,u),\hfill \\ G_3:(x,y,t,z,u)\to (x,y,t+ϵ,z,u),\hfill \\ G_4:(x,y,t,z,u)\to (x,y+ϵ,t,z,u),\hfill \\ G_5:(x,y,t,z,u)\to (x+ϵ,y,t,z,u),\hfill \\ G_6:(x,y,t,z,u)\to (x,y,t,z,tϵ+u),\hfill \\ G_7:(x,y,t,z,u)\to (x,y,t,z,u+ϵ),\hfill \end{array}$$

where $ϵ$ is any real number. We discover that $G_1$ is a scalar transformation, $G_2$ is a z -translation, $G_3$ is a t -translation, $G_4$ is a y -translation, $G_5$ is an x -translation, $G_6$ and $G_7$ are Galilean transformations.

Therefore, if $u(x,y,t,z)$ is a solution of Equation (2), the following solutions are equivalent to the solutions of Equation (2)

$$\begin{array}{c}{G}_1\left(ϵ\right)·u(x,y,t,z)=e^{\frac{1}{3}ϵ}u(e^{-\frac{1}{3}ϵ}x,e^{-ϵ}y,e^{-ϵ}t,e^{-\frac{5}{3}ϵ}z),\hfill \\ G_2\left(ϵ\right)·u(x,y,t,z)=u(x,y,t,z-ϵ),\hfill \\ G_3\left(ϵ\right)·u(x,y,t,z)=u(x,y,t-ϵ,z),\hfill \\ G_4\left(ϵ\right)·u(x,y,t,z)=u(x,y-ϵ,t,z),\hfill \\ G_5\left(ϵ\right)·u(x,y,t,z)=u(x-ϵ,y,t,z),\hfill \\ G_6\left(ϵ\right)·u(x,y,t,z)=u(x,y,t,z)-tϵ,\hfill \\ G_7\left(ϵ\right)·u(x,y,t,z)=u(x,y,t,z)-ϵ,\hfill \end{array}$$

where $ϵ$ is any real number.

3. The Optimal System of One-Dimensional Subalgebras

It is impractical for us to list all possible group-invariant solutions. Consequently, we need an effective and systematic way to classify these solutions; after doing this we form an optimal system of group-invariant solutions. Ibragimov et al. introduced a succinct method that relies only on the commutator table [25] to obtain the optimal system of one-dimensional subalgebras. The commutation relations about Lie algebra determined by $X_1,X_2,X_3,X_4,X_5,X_6,X_7$ are given in

Table 1. Table of Lie brackets.

$[{\mathit{X}}_{\mathit{i}},{\mathit{X}}_{\mathit{j}}]$	${\mathit{X}}_1$	${\mathit{X}}_2$	${\mathit{X}}_3$	${\mathit{X}}_4$	${\mathit{X}}_5$	${\mathit{X}}_6$	${\mathit{X}}_7$
$X_1$	0	$-\frac{5}{3}{X}_2$	$-X_3$	$-X_4$	$-\frac{1}{3}{X}_5$	$\frac{4}{3}{X}_6$	$\frac{1}{3}{X}_7$
$X_2$	$\frac{5}{3}{X}_2$	0	0	0	0	0	0
$X_3$	$X_3$	0	0	0	0	$X_7$	0
$X_4$	$X_4$	0	0	0	0	0	0
$X_5$	$\frac{1}{3}{X}_5$	0	0	0	0	0	0
$X_6$	$-\frac{4}{3}{X}_6$	0	$-X_7$	0	0	0	0
$X_7$	$-\frac{1}{3}{X}_7$	0	0	0	0	0	0

. Evidently, $\{X_1,X_2,X_3,X_4,X_5,X_6,X_7\}$ is closed under the Lie bracket.

An arbitrary operator $X\in L_7$ is expressed as

$$\begin{array}{c}X=l_1{X}_1+l_2{X}_2+l_3{X}_3+l_4{X}_4+l_5{X}_5+l_6{X}_6+l_7{X}_7.\hfill \end{array}$$

In order to find the linear transformations about the vector $l=(l_1,l_2,l_3,l_4,l_5,l_6,l_7)$, we have the following generator

$$\begin{array}{c}{E}_i=c_{ij}^k{l}_j\frac{\partial }{\partial l_k},i=1,2,3,4,5,6,7,\hfill \end{array}$$

(4)

where $c_{ij}^k$ is given as the formula $[X_i,X_j]=c_{ij}^k{X}_k$. Based on Equation (4) and Table 1, $E_1,E_2,E_3,E_4,$ $E_5,E_6,E_7$ are written as

$$\begin{array}{c}{E}_1=-\frac{5}{3}{l}_2\frac{\partial }{\partial l_2}-l_3\frac{\partial }{\partial l_3}-l_4\frac{\partial }{\partial l_4}-\frac{1}{3}{l}_5\frac{\partial }{\partial l_5}+\frac{4}{3}{l}_6\frac{\partial }{\partial l_6}+\frac{1}{3}{l}_7\frac{\partial }{\partial l_7},\hfill \\ E_2=\frac{5}{3}{l}_1\frac{\partial }{\partial l_2},\hfill \\ E_3=l_1\frac{\partial }{\partial l_3}+l_6\frac{\partial }{\partial l_7},\hfill \\ E_4=l_1\frac{\partial }{\partial l_4},\hfill \\ E_5=\frac{1}{3}{l}_1\frac{\partial }{\partial l_5},\hfill \\ E_6=-\frac{4}{3}{l}_1\frac{\partial }{\partial l_6}-l_3\frac{\partial }{\partial l_7},\hfill \\ E_7=-\frac{1}{3}{l}_1\frac{\partial }{\partial l_7}.\hfill \end{array}$$

With regard to the generators $E_1,E_2,E_3,E_4,E_5,E_6$ and $E_7$, the Lie equations that have parameters $a_1,a_2,a_3,a_4,a_5,a_6$ and $a_7$ with the initial condition $\tilde{l}{|}_{a_i=0}=l,i=1\dots 7$ can be given as

$$\begin{array}{c}\frac{d\widetilde{l_1}}{d{a}_1}=0,\frac{d\widetilde{l_2}}{d{a}_1}=-\frac{5}{3}\widetilde{l_2},\frac{d\widetilde{l_3}}{d{a}_1}=-\widetilde{l_3},\frac{d\widetilde{l_4}}{d{a}_1}=-\widetilde{l_4},\frac{d\widetilde{l_5}}{d{a}_1}=-\frac{1}{3}\widetilde{l_5},\frac{d\widetilde{l_6}}{d{a}_1}=\frac{4}{3}\widetilde{l_6},\frac{d\widetilde{l_7}}{d{a}_1}=\frac{1}{3}\widetilde{l_7},\hfill \\ \frac{d\widetilde{l_1}}{d{a}_2}=0,\frac{d\widetilde{l_2}}{d{a}_2}=\frac{5}{3}\widetilde{l_1},\frac{d\widetilde{l_3}}{d{a}_2}=0,\frac{d\widetilde{l_4}}{d{a}_2}=0,\frac{d\widetilde{l_5}}{d{a}_2}=0,\frac{d\widetilde{l_6}}{d{a}_2}=0,\frac{d\widetilde{l_7}}{d{a}_2}=0,\hfill \\ \frac{d\widetilde{l_1}}{d{a}_3}=0,\frac{d\widetilde{l_2}}{d{a}_3}=0,\frac{d\widetilde{l_3}}{d{a}_3}=\widetilde{l_1},\frac{d\widetilde{l_4}}{d{a}_3}=0,\frac{d\widetilde{l_5}}{d{a}_3}=0,\frac{d\widetilde{l_6}}{d{a}_3}=0,\frac{d\widetilde{l_7}}{d{a}_3}=\widetilde{l_6}\hfill \\ \frac{d\widetilde{l_1}}{d{a}_4}=0,\frac{d\widetilde{l_2}}{d{a}_4}=0,\frac{d\widetilde{l_3}}{d{a}_4}=0,\frac{d\widetilde{l_4}}{d{a}_4}=\widetilde{l_1},\frac{d\widetilde{l_5}}{d{a}_4}=0,\frac{d\widetilde{l_6}}{d{a}_4}=0,\frac{d\widetilde{l_7}}{d{a}_4}=0\hfill \\ \frac{d\widetilde{l_1}}{d{a}_5}=0,\frac{d\widetilde{l_2}}{d{a}_5}=0,\frac{d\widetilde{l_3}}{d{a}_5}=0,\frac{d\widetilde{l_4}}{d{a}_5}=0,\frac{d\widetilde{l_5}}{d{a}_5}=\frac{1}{3}\widetilde{l_1},\frac{d\widetilde{l_6}}{d{a}_5}=0,\frac{d\widetilde{l_7}}{d{a}_5}=0,\hfill \\ \frac{d\widetilde{l_1}}{d{a}_6}=0,\frac{d\widetilde{l_2}}{d{a}_6}=0,\frac{d\widetilde{l_3}}{d{a}_6}=0,\frac{d\widetilde{l_4}}{d{a}_6}=0,\frac{d\widetilde{l_5}}{d{a}_6}=0,\frac{d\widetilde{l_6}}{d{a}_6}=-\frac{4}{3}\widetilde{l_1},\frac{d\widetilde{l_7}}{d{a}_6}=-\widetilde{l_3},\hfill \\ \frac{d\widetilde{l_1}}{d{a}_7}=0,\frac{d\widetilde{l_2}}{d{a}_7}=0,\frac{d\widetilde{l_3}}{d{a}_7}=0,\frac{d\widetilde{l_4}}{d{a}_7}=0,\frac{d\widetilde{l_5}}{d{a}_7}=0,\frac{d\widetilde{l_6}}{d{a}_7}=0,\frac{d\widetilde{l_7}}{d{a}_5}=-\frac{1}{3}\widetilde{l_1}.\hfill \end{array}$$

Then, we present the following transformations of the solutions of these equations

$$\begin{array}{c}{T}_1:\widetilde{l_1}=l_1,\widetilde{l_2}=e^{-\frac{5}{3}{a}_1}{l}_2,\widetilde{l_3}=e^{-a_1}{l}_3,\widetilde{l_4}=e^{-a_1}{l}_4,\widetilde{l_5}=e^{-\frac{1}{3}{a}_1}{l}_5,\widetilde{l_6}=e^{\frac{4}{3}{a}_1}{l}_6,\widetilde{l_7}=e^{\frac{1}{3}{a}_1}{l}_7,\hfill \\ T_2:\widetilde{l_1}=l_1,\widetilde{l_2}=\frac{5}{3}{a}_2{l}_1+l_2,\widetilde{l_3}=l_3,\widetilde{l_4}=l_4,\widetilde{l_5}=l_5,\widetilde{l_6}=l_6,\widetilde{l_7}=l_7,\hfill \\ T_3:\widetilde{l_1}=l_1,\widetilde{l_2}=l_2,\widetilde{l_3}=a_3{l}_1+l_3,\widetilde{l_4}=l_4,\widetilde{l_5}=l_5,\widetilde{l_6}=l_6,\widetilde{l_7}=a_3{l}_6+l_7,\hfill \\ T_4:\widetilde{l_1}=l_1,\widetilde{l_2}=l_2,\widetilde{l_3}=l_3,\widetilde{l_4}=a_4{l}_1+l_4,\widetilde{l_5}=l_5,\widetilde{l_6}=l_6,\widetilde{l_7}=l_7,\hfill \\ T_5:\widetilde{l_1}=l_1,\widetilde{l_2}=l_2,\widetilde{l_3}=l_3,\widetilde{l_4}=l_4,\widetilde{l_5}=\frac{1}{3}{a}_5{l}_1+l_5,\widetilde{l_6}=l_6,\widetilde{l_7}=l_7,\hfill \\ T_6:\widetilde{l_1}=l_1,\widetilde{l_2}=l_2,\widetilde{l_3}=l_3,\widetilde{l_4}=l_4,\widetilde{l_5}=l_5,\widetilde{l_6}=-\frac{4}{3}{a}_6{l}_1+l_6,\widetilde{l_7}=-l_3{a}_6+l_7,\hfill \\ T_7:\widetilde{l_1}=l_1,\widetilde{l_2}=l_2,\widetilde{l_3}=l_3,\widetilde{l_4}=l_4,\widetilde{l_5}=l_5,\widetilde{l_6}=l_6,\widetilde{l_7}=-\frac{1}{3}{l}_1{a}_7+l_7.\hfill \end{array}$$

The structure of the optimal system demands simplification of the vector

$$\begin{array}{c}l=(l_1,l_2,l_3,l_4,l_5,l_6,l_7),\hfill \end{array}$$

(5)

via the transformations $T_1-T_7$. We are absorbed in seeking the simplest representative of each class of the similar vectors of Equation (5). The structure is classified into two cases.

Case 3.1$l_1\ne 0$

We take $a_2=-\frac{3l_2}{5l_1}$ in the transformation $T_2$, causing $\widetilde{l_2}=0$. As a result, Vector (5) is simplified as follows

$$\begin{array}{c}l=(l_1,0,l_3,l_4,l_5,l_6,l_7).\hfill \end{array}$$

(6)

Moreover, taking $a_3=-\frac{l_3}{l_1}$ in the transformation $T_3$, $a_4=-\frac{l_4}{l_1}$ in the transformation $T_4$, $a_5=-\frac{3l_5}{l_1}$ in the transformation $T_5$, $a_6=\frac{3l_6}{4l_1}$ in the transformation $T_6$, and $a_7=\frac{3l_7}{l_1}$ in the transformation $T_7$, we reduce Vector (6) to the form

$$\begin{array}{c}l=(l_1,0,0,0,0,0,0).\hfill \end{array}$$

In consequence, considering all the possible combinations, we derive the following representative

$$\begin{array}{c}{X}_1.\hfill \end{array}$$

(7)

Case 3.2$l_1=0$

We consider Vector (5) of the form

$$\begin{array}{c}l=(0,l_2,l_3,l_4,l_5,l_6,l_7).\hfill \end{array}$$

(8)

3.2.1$l_6\ne 0$

We take $a_3=-\frac{l_7}{l_6}$ in the transformation $T_3$, causing $\widetilde{l_7}=0$. Therefore, Vector (8) is simplified as follows

$$\begin{array}{c}l=(0,l_2,l_3,l_4,l_5,l_6,0).\hfill \end{array}$$

Taking all the possible combinations, we derive the following representatives

$$\begin{array}{c}{X}_6,X_6\pm X_2,X_6\pm X_3,X_6\pm X_4,X_6\pm X_5,X_6\pm X_2\pm X_3,X_6\pm X_2\pm X_4,X_6\pm X_2\pm X_5,\hfill \\ X_6\pm X_3\pm X_4,X_6\pm X_3\pm X_5,X_6\pm X_4\pm X_5,X_6\pm X_2\pm X_3\pm X_4,X_6\pm X_2\pm X_3\pm X_5,\hfill \\ X_6\pm X_2\pm X_4\pm X_5,X_6\pm X_3\pm X_4\pm X_5,X_6\pm X_2\pm X_3\pm X_4\pm X_5.\hfill \end{array}$$

(9)

3.2.2$l_6=0$

We consider Vector (8) of the form

$$\begin{array}{c}l=(0,l_2,l_3,l_4,l_5,0,l_7).\hfill \end{array}$$

Taking all the possible combinations, we derive the following representatives

$$\begin{array}{c}{X}_2,X_3,X_4,X_5,X_7,X_2\pm X_3,X_2\pm X_4,X_2\pm X_5,X_2\pm X_7,X_3\pm X_4,X_3\pm X_5,\hfill \\ X_3\pm X_7,X_4\pm X_5,X_4\pm X_7,X_5\pm X_7,X_2\pm X_3\pm X_4,X_2\pm X_3\pm X_5,X_2\pm X_3\pm X_7,\hfill \\ X_2\pm X_4\pm X_5,X_2\pm X_4\pm X_7,X_2\pm X_5\pm X_7,X_3\pm X_4\pm X_5,X_3\pm X_4\pm X_7,\hfill \\ X_3\pm X_5\pm X_7,X_4\pm X_5\pm X_7,X_2\pm X_3\pm X_4\pm X_5,X_2\pm X_3\pm X_4\pm X_7,\hfill \\ X_2\pm X_3\pm X_5\pm X_7,X_2\pm X_4\pm X_5\pm X_7,X_3\pm X_4\pm X_5\pm X_7,\hfill \\ X_2\pm X_3\pm X_4\pm X_5\pm X_7.\hfill \end{array}$$

(10)

Ultimately, by collecting Operators (7), (9) and (10), we reach the following theorem:

Theorem 1.

An optimal system of subalgebras of seven-dimensional Lie algebras of Equation (2) is offered in the following operators:

$$\begin{array}{c}{X}_1,X_2,X_3,X_4,X_5,X_6,X_7,X_6\pm X_2,X_6\pm X_3,X_6\pm X_4,X_6\pm X_5,X_6\pm X_2\pm X_3,\hfill \\ X_6\pm X_2\pm X_4,X_6\pm X_2\pm X_5,X_6\pm X_3\pm X_4,X_6\pm X_3\pm X_5,X_6\pm X_4\pm X_5,X_6\pm X_2\hfill \\ \pm X_3\pm X_4,X_6\pm X_2\pm X_3\pm X_5,X_6\pm X_2\pm X_4\pm X_5,X_6\pm X_3\pm X_4\pm X_5,X_6\pm X_2\pm X_3\hfill \\ \pm X_4\pm X_5,X_2\pm X_3,X_2\pm X_4,X_2\pm X_5,X_2\pm X_7,X_3\pm X_4,X_3\pm X_5,X_3\pm X_7,\hfill \\ X_4\pm X_5,X_4\pm X_7,X_5\pm X_7,X_2\pm X_3\pm X_4,X_2\pm X_3\pm X_5,X_2\pm X_3\pm X_7,X_2\pm X_4\hfill \\ \pm X_5,X_2\pm X_4\pm X_7,X_2\pm X_5\pm X_7,X_3\pm X_4\pm X_5,X_3\pm X_4\pm X_7,X_3\pm X_5\pm X_7,\hfill \\ X_4\pm X_5\pm X_7,X_2\pm X_3\pm X_4\pm X_5,X_2\pm X_3\pm X_4\pm X_7,X_2\pm X_3\pm X_5\pm X_7,X_2\pm X_4\hfill \\ \pm X_5\pm X_7,X_3\pm X_4\pm X_5\pm X_7,X_2\pm X_3\pm X_4\pm X_5\pm X_7.\hfill \end{array}$$

4. Similarity Reductions of the BKP-Boussinesq Equation

In the preceding sections, we studied Lie symmetry analysis and constructed the optimal system of Equation (2). Next, we cope with the similarity reductions and obtain the reduced equations.

Case 4.1

For the generator $X_2$, we have similarity variables

$$\begin{array}{c}\tilde{x}=x,\tilde{y}=y,\tilde{t}=t,\hfill \end{array}$$

and the group invariant solution is written as

$$\begin{array}{c}u=f(\tilde{x},\tilde{y},\tilde{t}).\hfill \end{array}$$

(11)

Substituting Equation (11) into Equation (2), we obtain the following reduced equation

$$f_{\tilde{t}\tilde{y}}-f_{\tilde{x}\tilde{x}\tilde{x}\tilde{y}}-3f_{\tilde{x}\tilde{x}}{f}_{\tilde{y}}-3f_{\tilde{x}}{f}_{\tilde{y}\tilde{x}}+f_{\tilde{t}\tilde{t}}=0.$$

(12)

Case 4.2

For generator $X_4+X_5+X_7$, we have similarity variables $u=f(\tilde{y},\tilde{t},\tilde{z})+x$ where $\tilde{y}=-x+y,\tilde{z}=z,\tilde{t}=t$. Substituting them into Equation (2) enables f to satisfy the following reduced equation

$$f_{\tilde{t}\tilde{y}}+f_{\tilde{y}\tilde{y}\tilde{y}\tilde{y}}-3f_{\tilde{y}\tilde{y}}{f}_{\tilde{y}}-3f_{\tilde{y}}{f}_{\tilde{y}\tilde{y}}+3f_{\tilde{y}\tilde{y}}+f_{\tilde{t}\tilde{t}}-3f_{\tilde{y}\tilde{z}}=0.$$

(13)

Case 4.3

For generator $X_3+X_5+X_7$, we have $\tilde{x}=-x+t,\tilde{y}=y,\tilde{z}=z,u=f(\tilde{x},\tilde{y},\tilde{z})+x$. The reduced equation is given as follows

$$4f_{\tilde{x}\tilde{y}}+f_{\tilde{x}\tilde{x}\tilde{x}\tilde{y}}-3f_{\tilde{x}\tilde{x}}{f}_{\tilde{y}}-3f_{\tilde{x}}{f}_{\tilde{x}\tilde{y}}+f_{\tilde{x}\tilde{x}}-3f_{\tilde{x}\tilde{z}}=0.$$

(14)

Case 4.4

For generator $X_3+X_4+X_7$, we have $\tilde{x}=x,\tilde{t}=-y+t,\tilde{z}=z,u=f(\tilde{x},\tilde{z},\tilde{t})+y$. Substituting them into Equation (2) enables f to satisfy the following reduced equation

$$f_{\tilde{x}\tilde{x}\tilde{x}\tilde{t}}+3f_{\tilde{x}\tilde{x}}{f}_{\tilde{t}}+3f_{\tilde{x}}{f}_{\tilde{t}\tilde{x}}-3f_{\tilde{x}\tilde{x}}+3f_{\tilde{x}\tilde{z}}=0.$$

(15)

Case 4.5

For generator $X_2+X_3$, we have $u=f(\tilde{x},\tilde{y},\tilde{z})$ in which $\tilde{x}=x,\tilde{y}=y,\tilde{z}=-t+z$. Substituting them into Equation (2) causes f to satisfy the following reduced equation

$$-f_{\tilde{z}\tilde{y}}-f_{\tilde{x}\tilde{x}\tilde{x}\tilde{y}}-3f_{\tilde{x}\tilde{x}}{f}_{\tilde{y}}-3f_{\tilde{x}}{f}_{\tilde{x}\tilde{y}}+f_{\tilde{z}\tilde{z}}+3f_{\tilde{x}\tilde{z}}=0.$$

(16)

Case 4.6

For generator $X_2+X_7$, we have $\tilde{x}=x,\tilde{y}=y,\tilde{t}=t,u=f(\tilde{x},\tilde{y},\tilde{t})+z$. By substituting them into Equation (2), we have the following reduced equation

$$f_{\tilde{t}\tilde{y}}-f_{\tilde{x}\tilde{x}\tilde{x}\tilde{y}}-3f_{\tilde{x}\tilde{x}}{f}_{\tilde{y}}-3f_{\tilde{x}}{f}_{\tilde{y}\tilde{x}}+f_{\tilde{t}\tilde{t}}=0.$$

(17)

Case 4.7

For generator $X_2+X_3+X_4$, we have $u=f(\tilde{x},\tilde{y},\tilde{z})$ where $\tilde{x}=x,\tilde{y}=-y+t,\tilde{z}=-y+z$. By substituting them into Equation (2), the following reduced equation is expressed as follows

$$-f_{\tilde{z}\tilde{y}}+f_{\tilde{x}\tilde{x}\tilde{x}\tilde{y}}+f_{\tilde{x}\tilde{x}\tilde{x}\tilde{z}}+3f_{\tilde{x}\tilde{x}}{f}_{\tilde{y}}+3f_{\tilde{x}\tilde{x}}{f}_{\tilde{z}}+3f_{\tilde{x}}{f}_{\tilde{x}\tilde{y}}+3f_{\tilde{x}}{f}_{\tilde{x}\tilde{z}}+3f_{\tilde{x}\tilde{z}}=0.$$

(18)

Case 4.8

For generator $X_3+X_5$, we have $\tilde{x}=-x+t,\tilde{y}=y,\tilde{z}=z,u=f(\tilde{x},\tilde{y},\tilde{z})$. By substituting them into Equation (2), we obtain the following reduced equation

$$f_{\tilde{x}\tilde{y}}+f_{\tilde{x}\tilde{x}\tilde{x}\tilde{y}}-3f_{\tilde{x}\tilde{x}}{f}_{\tilde{y}}-3f_{\tilde{x}}{f}_{\tilde{x}\tilde{y}}+f_{\tilde{x}\tilde{x}}-3f_{\tilde{x}\tilde{z}}=0.$$

(19)

Case 4.9

For generator $X_3+X_4$, we have $\tilde{x}=x,\tilde{y}=-y+t,\tilde{z}=z,u=f(\tilde{x},\tilde{y},\tilde{z})$. The form of the reduced equation is

$$f_{\tilde{x}\tilde{x}\tilde{x}\tilde{y}}+3f_{\tilde{x}\tilde{x}}{f}_{\tilde{y}}+3f_{\tilde{x}}{f}_{\tilde{x}\tilde{y}}+3f_{\tilde{x}\tilde{z}}=0.$$

(20)

Case 4.10

For generator $X_2+X_6$, we obtain $\tilde{x}=x,\tilde{y}=y,\tilde{t}=t,u=f(\tilde{x},\tilde{y},\tilde{t})+tz$. The corresponding reduced equation is

$$f_{\tilde{t}\tilde{y}}-f_{\tilde{x}\tilde{x}\tilde{x}\tilde{y}}-3f_{\tilde{x}\tilde{x}}{f}_{\tilde{y}}-3f_{\tilde{x}}{f}_{\tilde{x}\tilde{y}}+f_{\tilde{t}\tilde{t}}=0.$$

(21)

5. The Explicit Solutions of Reduced Equations

In the previous section, we have dealt with the similarity reductions and derived the corresponding reduced equations. In this section, we perform the Tanh method on reduced equations and obtain exact solutions of Equation (2). With the help of exact solutions, we can clearly understand the properties and applications of the (3 + 1)-dimensional BKP-Boussinesq equation. Here, we consider Equations (12)–(16); the others can be obtained in the same way.

5.1. Description of the Tanh Method

The main steps of the Tanh method [20,21] are expressed as follows:

• Consider a general form of nonlinear partial differential equation

  $$F(u,u_x,u_{xx},\dots ,u_y,\dots ,u_z,\dots ,u_t)=0,$$

  (22)

  where F is a polynomial of the u and its derivatives.
• By using wave transformation

  $$u(x,y,z,t)=\mathsf{\Phi }\left(\xi \right),\xi =lx+my+nz+ct,$$

  (23)

  where $l,m,n$ and c are unknown constants. Substituting Equation (23) into Equation (22), we obtain the following nonlinear ordinary differential equation

  $$F(\mathsf{\Phi },l{\mathsf{\Phi }}^{\prime },l^2{\mathsf{\Phi }}^{″},\dots ,m{\mathsf{\Phi }}^{\prime },\dots ,n{\mathsf{\Phi }}^{\prime },\dots ,c{\mathsf{\Phi }}^{\prime })=0.$$

  (24)
• Next, we introduce an independent variable

  $$Y=\mathrm{Tanh}\left(\xi \right),$$

  (25)

  which has the following changes

  $$\begin{array}{c}\frac{d\mathsf{\Phi }}{d\xi }=(1-Y^2)\frac{d\mathsf{\Phi }}{dY},\hfill \\ \frac{d^2\mathsf{\Phi }}{d{\xi }^2}=(1-Y^2)[-2Y\frac{d\mathsf{\Phi }}{dY}+(1-Y^2)\frac{d^2\mathsf{\Phi }}{d{Y}^2}],\hfill \\ \frac{d^3\mathsf{\Phi }}{d{\xi }^3}=(1-Y^2)[(6Y^2-2)\frac{d\mathsf{\Phi }}{dY}-6Y(1-Y^2)\frac{d^2\mathsf{\Phi }}{d{Y}^2}+{(1-Y^2)}^2\frac{d^3\mathsf{\Phi }}{d{Y}^3}],\hfill \\ \frac{d^4\mathsf{\Phi }}{d{\xi }^4}=(1-Y^2)[(16Y-24Y^3)\frac{d\mathsf{\Phi }}{dY}+(36Y^2-8)(1-Y^2)\frac{d^2\mathsf{\Phi }}{d{Y}^2}+{(1-Y^2)}^2(-12Y)\frac{d^3\mathsf{\Phi }}{d{Y}^3}\hfill \\ +{(1-Y^2)}^3\frac{d^4\mathsf{\Phi }}{d{Y}^4}].\hfill \end{array}$$

  (26)
• We assume that the solution of Equation (24) is written in the following form

  $$\mathsf{\Phi }\left(Y\right)=\sum _{i=0}^k{a}_i{Y}^i,$$

  (27)

  where k is an integer, which is determined by balancing the highest order derivative terms with the nonlinear terms in the resulting equation. After determining k, putting Equations (26) and (27) into Equation (24), we get a polynomial concerning $Y^i(i=0,1,2,\cdots )$. Then we collect all terms of $Y^i(i=0,1,2,\cdots )$ and make each of them equal to zero, which obtaina the algebraic equations containing unknown numbers $a_i(i=0,1,\cdots ),l,m,n,$ and c. Solving these equations, we get the values of unknowns. Finally, plugging these values into equations, we derive exact solutions of equations.

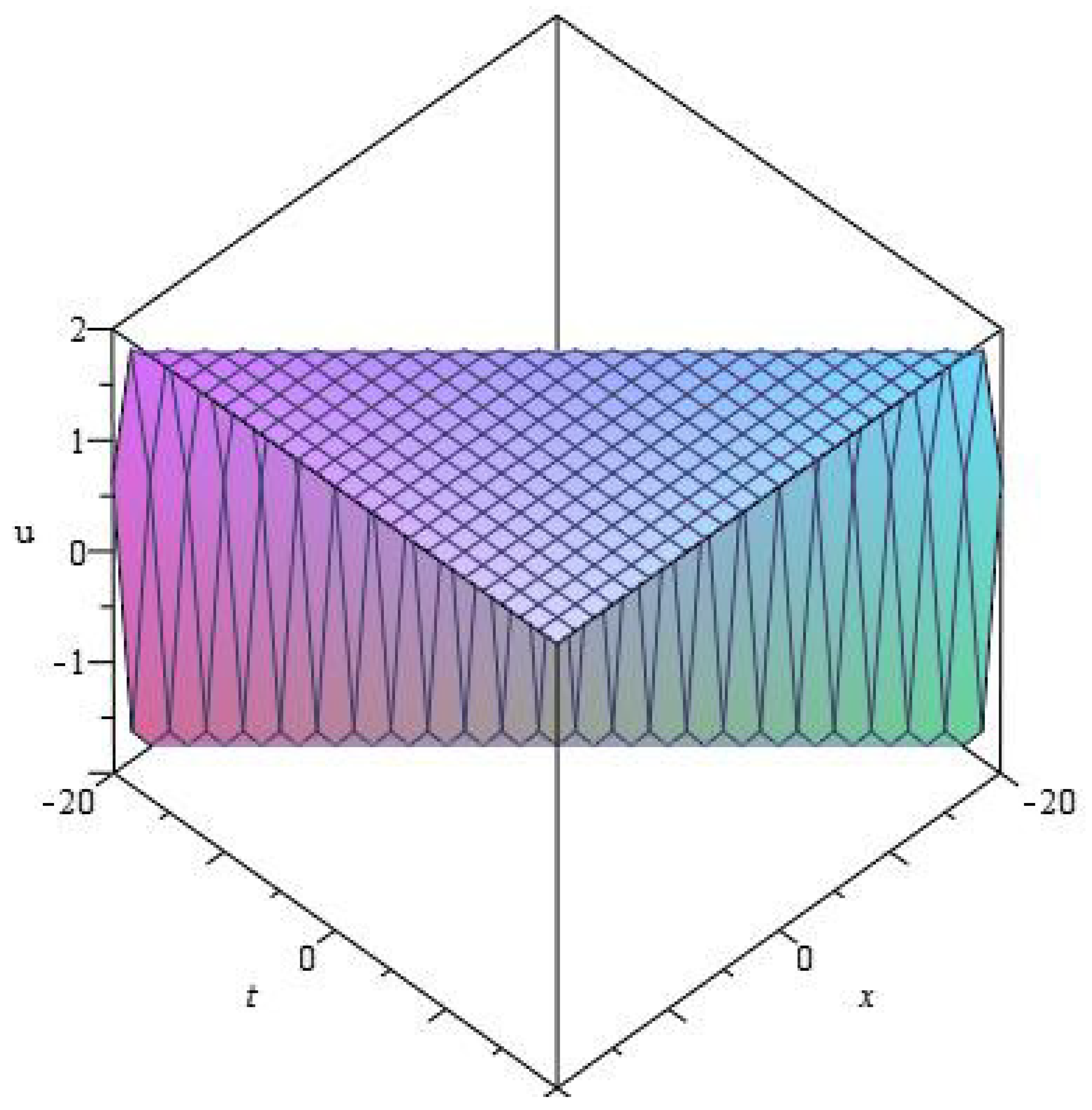
5.2. Exact Solution of Equation (12)

For Equation (12), substituting Equation (23) into Equation (12), we obtain the following ordinary differential equation

$$(mc+c^2){\mathsf{\Phi }}^{″}-l^{3}m{\mathsf{\Phi }}^{\left(4\right)}-6l^{2}m{\mathsf{\Phi }}^{\prime }{\mathsf{\Phi }}^{″}=0.$$

(28)

Concerning Equation (28), balancing ${\mathsf{\Phi }}^{\left(4\right)}$ with ${\mathsf{\Phi }}^{\prime }{\mathsf{\Phi }}^{″}$, we have

$$\begin{array}{c}2\times 4+k-4=2\times 1+k-1+2\times 2+k-2⟹k=1.\hfill \end{array}$$

Hence, according to the Equation (27), the solution of Equation (12) is assumed as

$$\mathsf{\Phi }\left(Y\right)=a_0+a_{1}Y.$$

(29)

Then, substituting Equations (26) and (29) into Equation (28), we collect all terms of $Y^i$ and obtain the algebraic equations including unknown numbers $a_i(i=0,1),l,m$ and c. By solving these equations, we have the following solutions

$$l=l,c=c,m=-\frac{c^2}{c-4l^3},a_0=a_0,a_1=2l.$$

(30)

Putting Equation (30) into Equation (12), we obtain the exact solution of Equation (12) as follows

$$\begin{array}{c}f(\tilde{x},\tilde{y},\tilde{t})=a_0+2l\mathrm{Tanh}(l\tilde{x}-\frac{c^2}{c-4l^3}\tilde{y}+c\tilde{t}),\hfill \end{array}$$

where $c\ne 4l^3$, $a_0$ and l are arbitrary constants. By using similarity variables $\tilde{x}=x,\tilde{y}=y,$$\tilde{t}=t,$ and the group invariant solution $u=f(\tilde{x},\tilde{y},\tilde{t}),$ we obtain the exact solution of Equation (2) as follows

$$\begin{array}{c}u(x,y,z,t)=a_0+2l\mathrm{Tanh}(lx-\frac{c^2}{c-4l^3}y+ct),\hfill \end{array}$$

(31)

where $c\ne 4l^3$, $a_0$ and l are arbitrary constants.

Figure 1 depicts the kink solution of Equation (2), which is obtained by taking $a_0=0,l=1,c=1$ at $y=1$.

5.3. Exact Solution of Equation (13)

Similarly, substituting Equation (23) into Equation (13), we have the following ordinary differential equation

$$(mc+3m^2+c^2-3mn){\mathsf{\Phi }}^{″}+m^4{\mathsf{\Phi }}^{\left(4\right)}-6m^3{\mathsf{\Phi }}^{\prime }{\mathsf{\Phi }}^{″}=0.$$

(32)

Then, balancing ${\mathsf{\Phi }}^{\left(4\right)}$ with ${\mathsf{\Phi }}^{\prime }{\mathsf{\Phi }}^{″}$ for (32), we have $k=1$.

Therefore, on the basis of Equation (27), the solution of Equation (13) can be assumed as

$$\mathsf{\Phi }\left(Y\right)=a_0+a_{1}Y.$$

(33)

Next, substituting Equation (26) and Equation (33) into Equation (32), we make all coefficients of $Y^i$ vanish and obtain the algebraic equations including unknown numbers $a_i(i=0,1),m,n,$ and c. Solving these equations, we have the following solutions

$$\begin{array}{c}c=c,m=m,n=\frac{mc+c^2+3m^2+4m^4}{3m},a_0=a_0,a_1=-2m.\hfill \end{array}$$

So, the exact solution of Equation (2) is

$$\begin{array}{c}u(x,y,z,t)=a_0-2m\mathrm{Tanh}[m(y-x)+\frac{mc+c^2+3m^2+4m^4}{3m}z+ct]+x,\hfill \end{array}$$

where $m\ne 0$, $a_0$ and c are arbitrary constants.

When we take $a_0=0,m=1,c=1$ at $y=1,x=1$, the value of u is as illustrated in Figure 2 below.

5.4. Exact Solution of Equation (14)

Equally, substituting Equation (23) into Equation (14), we get the following ordinary differential equation

$$(4lm+l^2-3ln){\mathsf{\Phi }}^{″}+l^{3}m{\mathsf{\Phi }}^{\left(4\right)}-6l^{2}m{\mathsf{\Phi }}^{\prime }{\mathsf{\Phi }}^{″}=0.$$

(34)

Furthermore, balancing ${\mathsf{\Phi }}^{\left(4\right)}$ with ${\mathsf{\Phi }}^{\prime }{\mathsf{\Phi }}^{″}$ for (34), we have $k=1$.

Therefore, based on Equation (27), the solution of Equation (14) can be assumed as

$$\mathsf{\Phi }\left(Y\right)=a_0+a_{1}Y.$$

(35)

Next, substituting Equation (26) and Equation (35) into Equation (34), we make all coefficients of $Y^i$ vanish and obtain the algebraic equations including unknown numbers $a_i(i=0,1),l,m,$ and n. Solving these equations, we have the following solutions

$$\begin{array}{c}l=-\frac{1}{2}{a}_1,m=m,n=\frac{4}{3}m+\frac{1}{3}{a}_1^{2}m-\frac{1}{6}{a}_1,a_0=a_0,a_1=a_1.\hfill \end{array}$$

So, the exact solution of Equation (2) is

$$\begin{array}{c}u(x,y,z,t)=a_0+a_1\mathrm{Tanh}[-\frac{1}{2}{a}_1(t-x)+my+(\frac{4}{3}m+\frac{1}{3}{a}_1^{2}m-\frac{1}{6}{a}_1)z]+x,\hfill \end{array}$$

where $a_0$, $a_1$ and m are arbitrary constants.

Figure 3 portrays the solution of Equation (2), which is obtained by taking $a_0=0,a_1=2,m=1$ at $y=1,z=1$.

5.5. Exact Solution of Equation (15)

In the same way, substituting Equation (23) into Equation (15), we have the following ordinary differential equation

$$(3ln-3l^2){\mathsf{\Phi }}^{″}+l^{3}c{\mathsf{\Phi }}^{\left(4\right)}+6c{l}^2{\mathsf{\Phi }}^{\prime }{\mathsf{\Phi }}^{″}=0.$$

(36)

Then, balancing ${\mathsf{\Phi }}^{\left(4\right)}$ with ${\mathsf{\Phi }}^{\prime }{\mathsf{\Phi }}^{″}$ for (36), we have $k=1$.

Therefore, based on the Equation (27), the solution of Equation (15) can be assumed to be

$$\mathsf{\Phi }\left(Y\right)=a_0+a_{1}Y.$$

(37)

Next, substituting Equations (26) and (37) into Equation (36), we make all coefficients of $Y^i$ vanish and obtain the algebraic equations including unknown numbers $a_i(i=0,1),l,n,$ and c. Solving these equations, we have the following solutions

$$\begin{array}{c}c=\frac{3(-n+1)}{4l^2},l=l,n=n,a_0=a_0,a_1=2l.\hfill \end{array}$$

So, the exact solution of Equation (2) is

$$\begin{array}{c}u(x,y,z,t)=a_0+2l\mathrm{Tanh}[lx+nz+\frac{3(-n+1)}{4l^2}(t-y)]+y,\hfill \end{array}$$

where $l\ne 0$, $a_0$ and n are arbitrary constants.

When we take $a_0=0,l=-1,n=2$ at $y=1,z=2$, the value of u is illustrated in Figure 4 below.

5.6. Exact Solution of Equation (16)

Likewise, substituting Equation (23) into Equation (16), we get the following ordinary differential equation

$$(-mn+n^2+3ln){\mathsf{\Phi }}^{″}-l^{3}m{\mathsf{\Phi }}^{\left(4\right)}-6l^{2}m{\mathsf{\Phi }}^{\prime }{\mathsf{\Phi }}^{″}=0.$$

(38)

Then, balancing ${\mathsf{\Phi }}^{\left(4\right)}$ with ${\mathsf{\Phi }}^{\prime }{\mathsf{\Phi }}^{″}$ for Equation (38), we have $k=1$.

Therefore, based on Equation (27), the solution of Equation (16) can be assumed to be

$$\mathsf{\Phi }\left(Y\right)=a_0+a_{1}Y.$$

(39)

Next, substituting Equations (26) and (39) into Equation (38), we make all coefficients of $Y^i$ vanish and obtain the algebraic equations including unknown numbers $a_i(i=0,1),l,m,$ and n. Solving these equations, we have the following solutions

$$\begin{array}{c}l=l,m=\frac{n(n+3l)}{n+4l^3},n=n,a_0=a_0,a_1=2l.\hfill \end{array}$$

So, exact solution of Equation (2) is

$$\begin{array}{c}u(x,y,z,t)=a_0+2l\mathrm{Tanh}[lx+\frac{n(n+3l)}{n+4l^3}y+n(z-t)],\hfill \end{array}$$

where $n\ne -4l^3$, $a_0$ and l are arbitrary constants.

Figure 5 depicts the kink solution of Equation (2), which is obtained by taking $a_0=0,l=1,n=2$ at $y=1,z=2$.

6. Construction of Conservation Laws

In this section, we chiefly construct conservation laws of Equation (2) using Ibragimov’s method [24,26]. First, we prove that Equation (2) is nonlinear self-adjoint.

6.1. Nonlinear Self-Adjointness of Equation (2)

With regard to Equation (2), the conservation law multiplier [27] has the following form

$$\begin{array}{c}\mathsf{\Lambda }=\mathsf{\Lambda }(x,y,t,z,u).\hfill \end{array}$$

Moreover,

$$\begin{array}{c}{E}_u\left[\mathsf{\Lambda }(u_{ty}-u_{xxxy}-3{\left(u_x{u}_y\right)}_x+u_{tt}+3u_{xz})\right]=0,\hfill \end{array}$$

(40)

where the Euler operator $E_u$ is expressed as

$$\begin{array}{c}{E}_u=\frac{\partial }{\partial u}-D_t\frac{\partial }{\partial u_t}-D_x\frac{\partial }{\partial u_x}+D_x^2\frac{\partial }{\partial u_{xx}}\cdots .\hfill \end{array}$$

(41)

Substituting Equation (41) into Equation (40), equating the coefficients of the various monomials in the first, second, and the other order partial derivatives and various powers of u, we obtain a system which only has an unknown variable $\mathsf{\Lambda }$,

$$\begin{array}{c}{\mathsf{\Lambda }}_u=0,{\mathsf{\Lambda }}_x=0,{\mathsf{\Lambda }}_{yt}+{\mathsf{\Lambda }}_{tt}+3{\mathsf{\Lambda }}_{zx}-{\mathsf{\Lambda }}_{yxx}=0.\hfill \end{array}$$

Solving this system, we have $\mathsf{\Lambda }=F_1(z,y)+F_2(z,t-y)$, where $F_1(z,y)$ and $F_2(z,t-y)$ are arbitrary functions.

Consider a PDE system of order m

$$\begin{array}{c}{\mathcal{R}}^{\oslash }(x,u,\cdots ,u_{\left(k\right)})=0,\alpha =1,\cdots ,m,\hfill \end{array}$$

(42)

where $x=(x^1,x^2,\cdots ,x^n)$, $u=(u^1,u^2,\cdots ,u^m)$ and $u_{\left(1\right)},u_{\left(2\right)},\cdots u_{\left(k\right)}$ represent the set of all first, second, …, kth-order derivatives of u in regards to x.

The adjoint equations of Equation (42) are written as

$$\begin{array}{c}{\left({\mathcal{R}}^{\oslash }\right)}^{*}(x,u,v,\cdots ,u_{\left(k\right)},v_{\left(k\right)})=0,\alpha =1,\cdots ,m,v=v\left(x\right).\hfill \end{array}$$

Besides,

$$\begin{array}{c}{\left({\mathcal{R}}^{\oslash }\right)}^{*}(x,u,v,\cdots ,u_{\left(k\right)},v_{\left(k\right)})=\frac{\delta \mathcal{L}}{\delta u^{\alpha }},\hfill \end{array}$$

where $\mathcal{L}$ is a formal Lagrangian of the following form

$$\begin{array}{c}\mathcal{L}=v^{\beta }{\mathcal{R}}^{\odot }(x,u,\cdots ,u_{\left(k\right)}),\beta =1,2,\dots ,m,\hfill \end{array}$$

and the Euler–Lagrange operator is expressed as

$$\begin{array}{c}\frac{\delta }{\delta u^{\alpha }}=\frac{\partial }{\partial u^{\alpha }}+\sum _{j=1}^{\infty }{(-1)}^j{D}_{i_1}\cdots D_{i_j}\frac{\partial }{\partial u_{i_1\cdots i_j}^{\alpha }},\alpha =1,2,\cdots ,m.\hfill \end{array}$$

Definition 1

([28]). System (42) is said to be nonlinearly self-adjoint if the adjoint system is satisfied for all the solutions u of System (42) upon a substitution $v=\phi (x,u)$ such that $\phi (x,u)\ne 0$. In particular, the system

$$\begin{array}{c}{\left({\mathcal{R}}^{\oslash }\right)}^{*}(x,u,\phi ,\cdots ,u_{\left(k\right)},{\phi }_{\left(k\right)})=0,\alpha =1,\cdots ,m,\hfill \end{array}$$

is identical to the system

$$\begin{array}{c}{\lambda }_{\alpha }^{\beta }{\mathcal{R}}^{\odot }(x,u,u,\cdots ,u_{\left(k\right)},u_{\left(k\right)})=0,\beta =1,\cdots ,m,\hfill \end{array}$$

that is

$$\begin{array}{c}{\left({\mathcal{R}}^{\oslash }\right)}^{*}{|}_{v=\phi (x,u)}={\lambda }_{\alpha }^{\beta }{\mathcal{R}}^{\odot },\beta =1,\cdots ,m,\hfill \end{array}$$

where ${\lambda }_{\alpha }^{\beta }$ is a certain function.

Theorem 2

([29]). The determining system of the multiplier $\mathsf{\Lambda }(x,u)$ of System (42) is identical to the system of nonlinearly self-adjoint substitution.

If the formal Lagrangian of Equation (2) is given as

$$\begin{array}{c}\mathcal{L}=\phi (x,y,t,z,u)(u_{ty}-u_{xxxy}-3{\left(u_x{u}_y\right)}_x+u_{tt}+3u_{xz}),\hfill \end{array}$$

based on Theorem 2, we can get

$$\begin{array}{c}\phi (x,y,t,z,u)=\mathsf{\Lambda }(x,y,t,z,u)=F_1(z,y)+F_2(z,t-y).\hfill \end{array}$$

(43)

Therefore, Equation (2) is nonlinearly self-adjoint with Equation (43).

6.2. Construction of Conservation Laws

Theorem 3

([28]). The system of differential Equation (42) is nonlinearly self-adjoint, so every Lie point, Lie-Bäcklund, nonlocal symmetry

$$\begin{array}{c}X={\xi }^i(x,u,u_{\left(1\right)},\cdots )\frac{\partial }{\partial x^i}+{\eta }^{\alpha }(x,u,u_{\left(1\right)},\cdots )\frac{\partial }{\partial u^{\alpha }},\hfill \end{array}$$

admitted by the system of Equation (42) gives rise to a conservation law, where the components ${\mathcal{C}}^i$ of the conserved vector $\mathcal{C}=({\mathcal{C}}^1,\cdots ,{\mathcal{C}}^n)$ are determined by

$$\begin{array}{c}{\mathcal{C}}^i=W^{\alpha }[\frac{\partial \mathcal{L}}{\partial u_i^{\alpha }}-D_j(\frac{\partial \mathcal{L}}{\partial u_{ij}^{\alpha }})\hfill \\ +D_j{D}_k(\frac{\partial \mathcal{L}}{\partial u_{ijk}^{\alpha }})-\cdots ]+D_j(W^{\alpha })[\frac{\partial \mathcal{L}}{\partial u_{ij}^{\alpha }}-D_k(\frac{\partial \mathcal{L}}{\partial u_{ijk}^{\alpha }})+\cdots ]+D_j{D}_k(W^{\alpha })[\frac{\partial \mathcal{L}}{\partial u_{ijk}^{\alpha }}-\cdots ],\hfill \end{array}$$

and $W^{\alpha }={\eta }^{\alpha }-{\xi }^j{u}_j^{\alpha }$. The formal Lagrangian $\mathcal{L}$ should be written in the symmetric form concerning all mixed derivatives $u_{ij}^{\alpha },u_{ijk}^{\alpha },\cdots .$

The Lagrangian $\mathcal{L}$ is given as follows

$$\begin{array}{c}\mathcal{L}=\mathsf{\Lambda }(u_{ty}-u_{xxxy}-3{\left(u_x{u}_y\right)}_x+u_{tt}+3u_{xz}).\hfill \end{array}$$

For the generator $X={\xi }^1\frac{\partial }{\partial x}+{\xi }^2\frac{\partial }{\partial y}+{\xi }^3\frac{\partial }{\partial t}+{\xi }^4\frac{\partial }{\partial z}+{\eta }^1\frac{\partial }{\partial u},$ in line with the Theorem 3, we obtain $W={\eta }^1-{\xi }^1{u}_x-{\xi }^2{u}_y-{\xi }^3{u}_t-{\xi }^4{u}_z$, so the components of the conservation vector have the following form

$$\begin{array}{c}{\mathcal{C}}^x=W[\frac{\partial \mathcal{L}}{\partial u_x}-D_y\frac{\partial \mathcal{L}}{\partial u_{xy}}-D_x\frac{\partial \mathcal{L}}{\partial u_{xx}}-D_z\frac{\partial \mathcal{L}}{\partial u_{xz}}-D_x{D}_x{D}_y\frac{\partial \mathcal{L}}{\partial u_{xxxy}}]+D_y\left(W\right)\frac{\partial \mathcal{L}}{\partial u_{xy}}\hfill \\ \hfill \\ +D_z\left(W\right)\frac{\partial \mathcal{L}}{\partial u_{xz}}+D_x\left(W\right)[\frac{\partial \mathcal{L}}{\partial u_{xx}}-D_x\frac{\partial \mathcal{L}}{\partial u_{xxx}}+D_x{D}_y\frac{\partial \mathcal{L}}{\partial u_{xxxy}}]+D_x{D}_x\left(W\right)[\frac{\partial \mathcal{L}}{\partial u_{xxx}}\hfill \\ -D_y\frac{\partial \mathcal{L}}{\partial u_{xxxy}}]+D_x{D}_x{D}_y\left(W\right)\frac{\partial \mathcal{L}}{\partial u_{xxxy}},\hfill \\ {\mathcal{C}}^y=W(\frac{\partial \mathcal{L}}{\partial u_y}),\hfill \\ {\mathcal{C}}^t=W(\frac{\partial \mathcal{L}}{\partial u_t}-D_t\frac{\partial \mathcal{L}}{\partial u_{tt}}-D_y\frac{\partial \mathcal{L}}{\partial u_{ty}})+D_t\left(W\right)\frac{\partial \mathcal{L}}{\partial u_{tt}}+D_y\left(W\right)\frac{\partial \mathcal{L}}{\partial u_{ty}},\hfill \\ {\mathcal{C}}^z=0.\hfill \end{array}$$

By substituting the Lagrangian $\mathcal{L}$ into above components of the conservation vector, ${\mathcal{C}}^x,{\mathcal{C}}^y,{\mathcal{C}}^t,{\mathcal{C}}^z$ are simplified as

$$\begin{array}{c}{\mathcal{C}}^x=W[-3u_{xy}\mathsf{\Lambda }-D_y(-3u_x\mathsf{\Lambda })-D_x(-3u_y\mathsf{\Lambda })-D_z\left(3\mathsf{\Lambda }\right)-D_x{D}_x{D}_y(-\mathsf{\Lambda })]+D_y\left(W\right)(-3u_x\mathsf{\Lambda })\hfill \end{array}$$

$$\begin{array}{c}+D_z\left(W\right)\left(3\mathsf{\Lambda }\right)+D_x\left(W\right)[-3u_y\mathsf{\Lambda }+D_x{D}_y(-\mathsf{\Lambda })]+D_x{D}_x\left(W\right)D_y\left(\mathsf{\Lambda }\right)-D_x{D}_x{D}_y\left(W\right)\mathsf{\Lambda },\hfill \end{array}$$

(44)

$$\begin{array}{c}{\mathcal{C}}^y=W(-3u_{xx}\mathsf{\Lambda }),\hfill \end{array}$$

(45)

$$\begin{array}{c}{\mathcal{C}}^t=W[-D_t\left(\mathsf{\Lambda }\right)-D_y\left(\mathsf{\Lambda }\right)]+D_t\left(W\right)\mathsf{\Lambda }+D_y\left(W\right)\mathsf{\Lambda },\hfill \end{array}$$

(46)

$$\begin{array}{c}{\mathcal{C}}^z=0.\hfill \end{array}$$

(47)

For generator $X_1=\frac{1}{3}x\frac{\partial }{\partial x}+y\frac{\partial }{\partial y}+t\frac{\partial }{\partial t}+\frac{5}{3}z\frac{\partial }{\partial z}-\frac{1}{3}u\frac{\partial }{\partial u}$, we have $W=-\frac{1}{3}u-\frac{1}{3}x{u}_x-y{u}_y-t{u}_t-\frac{5}{3}z{u}_z$. According to Equations (44)–(47), the components of the conserved vector of generator $X_1$ have the following form

$$\begin{array}{c}{\mathcal{C}}_1^x=(-\frac{1}{3}u-\frac{1}{3}x{u}_x-y{u}_y-t{u}_t-\frac{5}{3}z{u}_z)[(-3u_{yx})(F_1(z,y)+F_2(z,t-y))+3u_x({\left(F_1\right)}_y-{\left(F_2\right)}_y)\hfill \\ -3({\left(F_1\right)}_z+{\left(F_2\right)}_z)]+(-\frac{4}{3}{u}_y-\frac{1}{3}x{u}_{xy}-y{u}_{yy}-t{u}_{ty}-\frac{5}{3}z{u}_{zy})(-3u_x)(F_1(z,y)+F_2(z,t-y))\hfill \\ +(-2u_z-\frac{1}{3}x{u}_{xz}-y{u}_{yz}-t{u}_{tz}-\frac{5}{3}z{u}_{zz})(3F_1(z,y)+3F_2(z,t-y))+(-\frac{2}{3}{u}_x-\frac{1}{3}x{u}_{xx}\hfill \\ -y{u}_{yx}-t{u}_{tx}-\frac{5}{3}z{u}_{zx})(-3u_y)(F_1(z,y)+F_2(z,t-y))+(-\frac{2}{3}{u}_{xx}-\frac{1}{3}x{u}_{xxx}-y{u}_{yxx}\hfill \\ -t{u}_{txx}-\frac{5}{3}z{u}_{zxx})({\left(F_1\right)}_y-{\left(F_2\right)}_y)-(-\frac{5}{3}{u}_{yxx}-\frac{1}{3}x{u}_{xxxy}-y{u}_{yxxy}-t{u}_{txxy}-\frac{5}{3}z{u}_{zxxy})\hfill \\ (F_1(z,y)+F_2(z,t-y)),\hfill \\ {\mathcal{C}}_1^y=(-\frac{1}{3}u-\frac{1}{3}x{u}_x-y{u}_y-t{u}_t-\frac{5}{3}z{u}_z)[-3u_{xx}(F_1(z,y)+F_2(z,t-y))],\hfill \\ {\mathcal{C}}_1^t=(-\frac{1}{3}u-\frac{1}{3}x{u}_x-y{u}_y-t{u}_t-\frac{5}{3}z{u}_z)[-{\left(F_2\right)}_t-({\left(F_1\right)}_y-{\left(F_2\right)}_y)]+(-\frac{4}{3}{u}_t-\frac{1}{3}x{u}_{xt}-y{u}_{yt}\hfill \\ -t{u}_{tt}-\frac{5}{3}z{u}_{zt})(F_1(z,y)+F_2(z,t-y))+(-\frac{4}{3}{u}_y-\frac{1}{3}x{u}_{xy}-y{u}_{yy}-t{u}_{ty}-\frac{5}{3}z{u}_{zy})\hfill \\ (F_1(z,y)+F_2(z,t-y)),\hfill \\ {\mathcal{C}}_1^z=0.\hfill \end{array}$$

For generator $X_2=\frac{\partial }{\partial z}$, we have $W=-u_z$. According to Equations (44)–(47), the components of the conserved vector of generator $X_2$ can be expressed as follows

$$\begin{array}{c}{\mathcal{C}}_2^x=(-u_z)[(-3u_{yx})(F_1(z,y)+F_2(z,t-y))+3u_x({\left(F_1\right)}_y-{\left(F_2\right)}_y)-3({\left(F_1\right)}_z+{\left(F_2\right)}_z)]\hfill \\ +3u_x{u}_{zy}(F_1(z,y)+F_2(z,t-y))-3u_{zz}(F_1(z,y)+F_2(z,t-y))+3u_y{u}_{zx}(F_1(z,y)\hfill \\ +F_2(z,t-y))-u_{zxx}({\left(F_1\right)}_y-{\left(F_2\right)}_y)+u_{zyxx}(F_1(z,y)+F_2(z,t-y)),\hfill \\ {\mathcal{C}}_2^y=3u_z{u}_{xx}(F_1(z,y)+F_2(z,t-y)),\hfill \\ {\mathcal{C}}_2^t=(-u_z)[-{\left(F_2\right)}_t-{\left(F_1\right)}_y+{\left(F_2\right)}_y]-u_{zt}(F_1(z,y)+F_2(z,t-y))-u_{zy}(F_1(z,y)+F_2(z,t-y)),\hfill \\ {\mathcal{C}}_2^z=0.\hfill \end{array}$$

For generator $X_3=\frac{\partial }{\partial t}$, we have $W=-u_t$. According to Equations (44)–(47), the components of the conserved vector of generator $X_3$ can be written in the following form

$$\begin{array}{c}{\mathcal{C}}_3^x=(-u_t)[(-3u_{yx})(F_1(z,y)+F_2(z,t-y))+3u_x({\left(F_1\right)}_y-{\left(F_2\right)}_y)-3({\left(F_1\right)}_z+{\left(F_2\right)}_z)]\hfill \\ +3u_x{u}_{ty}(F_1(z,y)+F_2(z,t-y))-3u_{tz}(F_1(z,y)+F_2(z,t-y))+3u_y{u}_{tx}(F_1(z,y)\hfill \\ +F_2(z,t-y))-u_{txx}({\left(F_1\right)}_y-{\left(F_2\right)}_y)-u_{tyxx}(F_1(z,y)+F_2(z,t-y)),\hfill \\ {\mathcal{C}}_3^y=3u_t{u}_{xx}(F_1(z,y)+F_2(z,t-y)),\hfill \\ {\mathcal{C}}_3^t=-u_t[-{\left(F_2\right)}_t-({\left(F_1\right)}_y-{\left(F_2\right)}_y)]-u_{tt}(F_1(z,y)+F_2(z,t-y))-u_{ty}(F_1(z,y)+F_2(z,t-y)),\hfill \\ {\mathcal{C}}_3^z=0.\hfill \end{array}$$

For generator $X_4=\frac{\partial }{\partial y}$, we have $W=-u_y$. According to Equations (44)–(47), the components of the conserved vector of generator $X_4$ are given as

$$\begin{array}{c}{\mathcal{C}}_4^x=(-u_y)[(-3u_{yx})(F_1(z,y)+F_2(z,t-y))+3u_x({\left(F_1\right)}_y-{\left(F_2\right)}_y)-3({\left(F_1\right)}_z+{\left(F_2\right)}_z)]\hfill \\ +3u_x{u}_{yy}(F_1(z,y)+F_2(z,t-y))-3u_{yz}(F_1(z,y)+F_2(z,t-y))+3u_y{u}_{yx}(F_1(z,y)\hfill \\ +F_2(z,t-y))-u_{yxx}({\left(F_1\right)}_y-{\left(F_2\right)}_y)-u_{yyxx}(F_1(z,y)+F_2(z,t-y)),\hfill \\ {\mathcal{C}}_4^t=-u_y[-{\left(F_2\right)}_t-({\left(F_1\right)}_y-{\left(F_2\right)}_y)]-u_{yt}(F_1(z,y)+F_2(z,t-y))-u_{yy}(F_1(z,y)+F_2(z,t-y)),\hfill \\ {\mathcal{C}}_4^z=0.\hfill \end{array}$$

For generator $X_5=\frac{\partial }{\partial x}$, we have $W=-u_x$. According to Equations (44)–(47), the components of the conserved vector of the generator $X_5$ can be expressed as

$$\begin{array}{c}{\mathcal{C}}_5^x=(-u_x)[(-3u_{yx})(F_1(z,y)+F_2(z,t-y))+3u_x({\left(F_1\right)}_y-{\left(F_2\right)}_y)-3({\left(F_1\right)}_z+{\left(F_2\right)}_z)]\hfill \\ +3u_x{u}_{xy}(F_1(z,y)+F_2(z,t-y))-3u_{xz}(F_1(z,y)+F_2(z,t-y))+3u_y{u}_{xx}(F_1(z,y)\hfill \\ +F_2(z,t-y))-u_{xxx}({\left(F_1\right)}_y-{\left(F_2\right)}_y)-u_{xyxx}(F_1(z,y)+F_2(z,t-y)),\hfill \\ {\mathcal{C}}_5^y=3u_x{u}_{xx}(F_1(z,y)+F_2(z,t-y)),\hfill \\ {\mathcal{C}}_5^t=-u_x[-{\left(F_2\right)}_t-({\left(F_1\right)}_y-{\left(F_2\right)}_y)]-u_{xt}(F_1(z,y)+F_2(z,t-y))-u_{xy}(F_1(z,y)+F_2(z,t-y)),\hfill \\ {\mathcal{C}}_5^z=0.\hfill \end{array}$$

For generator $X_6=t\frac{\partial }{\partial u}$, we have $W=t$. According to Equations (44)–(47), the components of the conserved vector about the generator $X_6$ can be written as

$$\begin{array}{c}{\mathcal{C}}_6^x=t[(-3u_{yx})(F_1(z,y)+F_2(z,t-y))+3u_x({\left(F_1\right)}_y-{\left(F_2\right)}_y)-3({\left(F_1\right)}_z+{\left(F_2\right)}_z)],\hfill \\ {\mathcal{C}}_6^y=t[-3u_{xx}(F_1(z,y)+F_2(z,t-y))],\hfill \\ {\mathcal{C}}_6^t=t[-{\left(F_2\right)}_t-({\left(F_1\right)}_y-{\left(F_2\right)}_y)]+(F_1(z,y)+F_2(z,t-y)),\hfill \\ {\mathcal{C}}_6^z=0.\hfill \end{array}$$

For generator $X_7=\frac{\partial }{\partial u}$, we have $W=1$. According to the formulas (44)–(47), the components of the conserved vector concerning the generator $X_7$ are written as

$$\begin{array}{c}{\mathcal{C}}_7^x=(-3u_{yx})(F_1(z,y)+F_2(z,t-y))+3u_x({\left(F_1\right)}_y-{\left(F_2\right)}_y)-3({\left(F_1\right)}_z+{\left(F_2\right)}_z),\hfill \\ {\mathcal{C}}_7^y=-3u_{xx}(F_1(z,y)+F_2(z,t-y)),\hfill \\ {\mathcal{C}}_7^t=-{\left(F_2\right)}_t-({\left(F_1\right)}_y-{\left(F_2\right)}_y),\hfill \\ {\mathcal{C}}_7^z=0.\hfill \end{array}$$

7. Conclusions

In this paper, the Lie symmetry analysis method is applied to the (3 + 1)-dimensional BKP-Boussinesq equation. Based on this method, we construct the optimal system of one-dimensional subalgebras. Furthermore, some similarity reductions are handled and exact solutions of the reduced equations are obtained by means of the Tanh method. Finally, it is shown that Equation (2) is nonlinearly self-adjoint. Meanwhile, using Ibragimov’s method, we derive the conservation laws widely used in the field of mathematical physics. After obtaining the exact solutions of Equation (2), we can depict the propagation of long waves in shallow water better and know more applications in the physical field, such as the percolation of water in porous subsurfaces of a horizontal layer of material.