Axle Temperature Monitoring and Neural Network Prediction Analysis for High-Speed Train under Operation
Abstract
:1. Introduction
2. Temperature Monitoring of Axle Bearing under Operation
2.1. Detection Method
2.2. Test Results
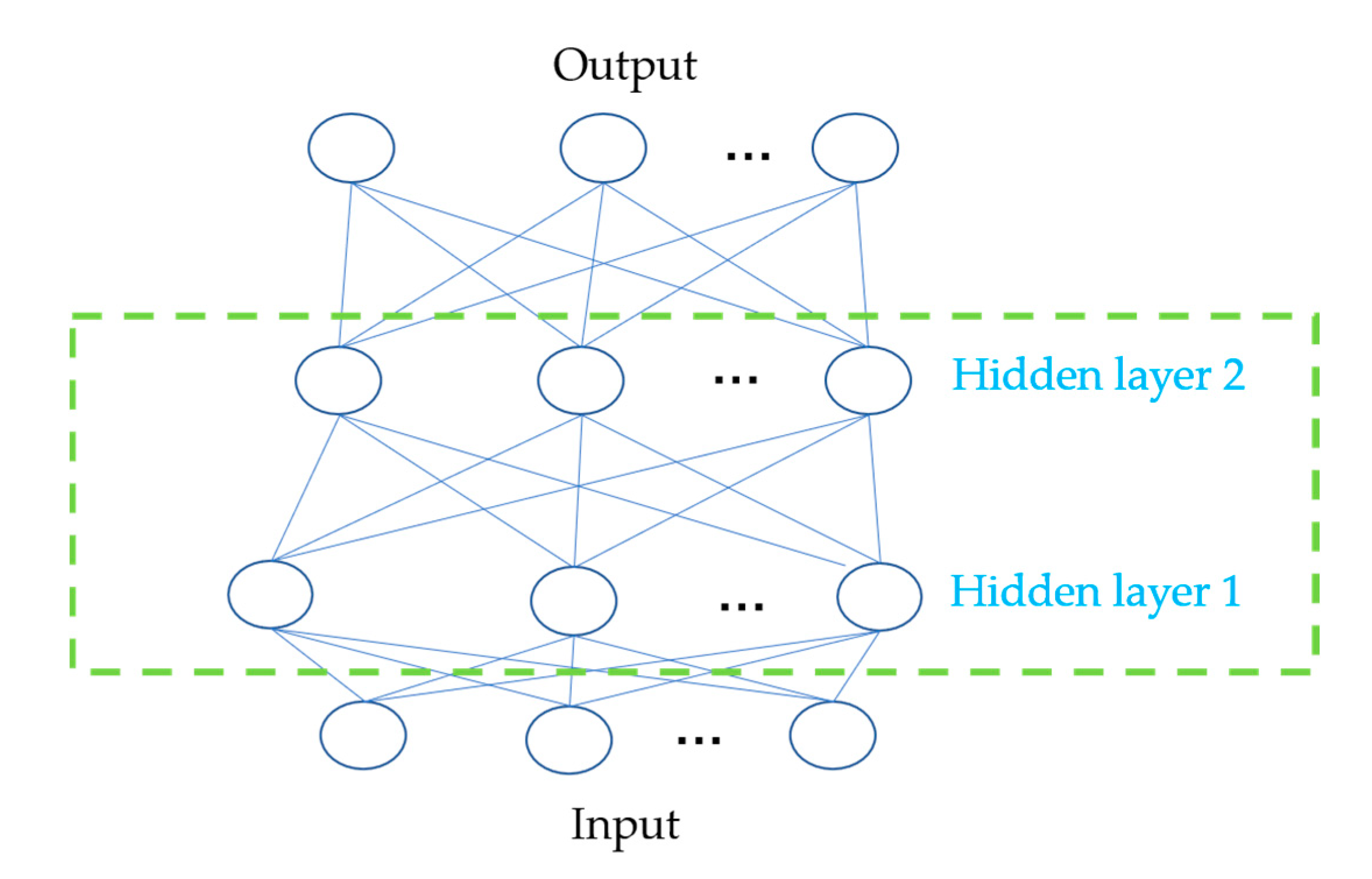
3. Neural Network Prediction
3.1. Method
3.2. Data Input
4. Model Training and Result Analysis
4.1. Model Training
4.2. Prediction versus Reality
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Wang, Y.; Wu, Z.R. A Train Hot Bearing Detection System Based on Infrared Array Sensor. Appl. Mech. Mater. 2013, 672–676. [Google Scholar] [CrossRef] [Green Version]
- Ha, D.; Wang, Q.; Jiang, T.; Zhang, Y.W. Application of New Axle Temperature Monitoring System on High-Speed EMUs. J. Dalian Jiaotong Univ. 2013, 34, 89–94. (In Chinese) [Google Scholar]
- Hao, W.; Liu, F. Imbalanced Data Fault Diagnosis Based on an Evolutionary Online Sequential Extreme Learning Machine. Symmetry 2020, 12, 1204. [Google Scholar] [CrossRef]
- Xin-Zhi, C.; Kun, W. High Speed Train Axle Temperature Monitoring System Based on nRF905. Nucl. Electron.Detect. Technol. 2010, 30, 1387–1390. (In Chinese) [Google Scholar]
- Zhao, Y.; Huang, R. Metro Vehicle Axle Temperature Monitoring Device Based on Piezoelectric Vibration. Int. J. Transp. Eng. Technol. 2019, 5, 88. [Google Scholar] [CrossRef]
- Xiao-bo, A. Axle Temperature Analysis of 120 km/h Freight Trains and Prediction of Hotbox. Roll. Stock 2008, 46, 33–37. [Google Scholar]
- Xie, G.; Wang, Z.X.; Hei, X.H.; Takahashi, S.; Mochizuki, H. Axle temperature threshold prediction model of high-speed train for hot axle fault. J. Traffic Transp. Eng. 2018, 3, 129–137. [Google Scholar]
- Yu-gan, C.H.I. Analysis of Predicting the Regular Patterns of Hot Box and Axle Temperatures of Vehicles in Operation. Roll. Stock 2007, 7, 11. [Google Scholar]
- Lei, Z. Research on the Axle Temperature Changing Pattern of 120 km/h Freight Trains. Roll. Stock 2009, 47, 28–31. [Google Scholar]
- Shengjun, H. Discussion about Improvement of Prediction Quality in Hot Axle Detection. Roll. Stock 2000, 38, 37–39. [Google Scholar]
- Yin-Dong, C. Passenger Car Axle Temperature Prediction Algorithm Based on Metabolic GM (1,1) Model. Railw. Locomot. Car 2011, 31, 49–52. [Google Scholar]
- Xie, G.; Wang, Z.; Hei, X.; Takahashi, S.; Nakamura, H. Data-Based Axle Temperature Prediction of High Speed Train by Multiple Regression Analysis. In Proceedings of the 2016 12th International Conference on Computational Intelligence and Security (CIS), Wuxi, China, 16–19 December 2016; pp. 349–353. [Google Scholar]
- Ma, W.; Tan, S.; Hei, X.; Zhao, J.; Xie, G. A Prediction Method Based on Stepwise Regression Analysis for Train Axle Temperature. In Proceedings of the 2016 12th International Conference on Computational Intelligence and Security (CIS), Wuxi, China, 16–19 December 2016; pp. 386–390. [Google Scholar]
- Luo, C.; Yang, D.; Huang, J.; Deng, Y.-D. LSTM-Based Temperature Prediction for Hot-Axles of Locomotives. ITM Web Conf. 2017, 12, 1013. [Google Scholar] [CrossRef] [Green Version]
- Huang, M.T.; Gao, X.M. Motor Front Axle Temperature Forecasting Based on Phase Space Reconstruction and BP Neural Network. Adv. Mater. Res. 2013, 823, 406–410. [Google Scholar] [CrossRef]
- Franzoni, V.; Milani, A. Heuristic semantic walk for concept chaining in collaborative networks. Int. J. Web Inf. Syst. 2014, 10, 85–103. [Google Scholar] [CrossRef]
- Floreano, D.; Dürr, P.; Mattiussi, C. Neuroevolution: From architectures to learning. Evol. Intell. 2008, 1, 47–62. [Google Scholar] [CrossRef]
- Baioletti, M.; Di Bari, G.; Poggioni, V. Differential Evolution for Neural Networks Optimization. Mathematics 2020, 8, 69. [Google Scholar] [CrossRef] [Green Version]
- Glowacz, A. Fault diagnostics of acoustic signals of loaded synchronous motor using SMOFS-25-EXPANDED and selected classifiers. Teh. Vjesn. Tech. Gaz. 2016, 23, 1365–1372. [Google Scholar] [CrossRef] [Green Version]
- Glowacz, A. Recognition of Acoustic Signals of Synchronous Motors with the Use of MoFS and Selected Classifiers. Meas. Sci. Rev. 2015, 15, 167–175. [Google Scholar] [CrossRef] [Green Version]












| Sensor Number | Sensor Location | Sensor Number | Sensor Location |
|---|---|---|---|
| 1~8 | Bearing of two end of axle-1/2/3/4 | 21~24 | axle-1/axle-2/axle-3/axle-4 motor stator |
| 9~12 | axle-1/axle-2/axle-3/axle-4 Pinion gearbox motor side bearing (PMB) | 25~28 | axle-1/axle-2/axle-3/axle-4 motor non-drive end bearing (NMDB) |
| 13~16 | axle-1/axle-2/axle-3/axle-4 Pinion gearbox wheel side bearing (PWB) | 29~32 | axle-1/axle-2/axle-3/axle-4 -large gearbox motor side bearing (GMB) |
| 17~20 | axle-1/axle-2/axle-3/axle-4 motor drive end bearing (MDB) | 33~36 | axle-1/axle-2/axle-3/axle-4 large gearbox wheel side bearing (GWB) |
| Predicted Location | RMSE | MAPE | Predicted Location | RMSE | MAPE |
|---|---|---|---|---|---|
| Axle-1 EB1 | 0.7858 | 1.5609% | GMB | 0.8198 | 1.8473% |
| PWB | 0.8519 | 1.4176% | MDB | 0.9455 | 2.2800% |
| PMB | 0.7708 | 2.6951% | Motor stator | 0.9162 | 2.6949% |
| GWB | 0.8203 | 2.3608% | NMDB | 0.4569 | 1.6366% |
| Advance Time | RMSE | MAPE |
|---|---|---|
| 1 min | 0.6080 | 1.2593% |
| 2 min | 0.7965 | 2.2658% |
| 3 min | 0.9455 | 2.2800% |
| 5 min | 1.0302 | 3.3790% |
| Method of Prediction | RMSE | MAPE |
|---|---|---|
| BP neural network | 0.9446 | 2.4416% |
| GM (1,1) | 9.9448 | 24.2271% |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hao, W.; Liu, F. Axle Temperature Monitoring and Neural Network Prediction Analysis for High-Speed Train under Operation. Symmetry 2020, 12, 1662. https://doi.org/10.3390/sym12101662
Hao W, Liu F. Axle Temperature Monitoring and Neural Network Prediction Analysis for High-Speed Train under Operation. Symmetry. 2020; 12(10):1662. https://doi.org/10.3390/sym12101662
Chicago/Turabian StyleHao, Wei, and Feng Liu. 2020. "Axle Temperature Monitoring and Neural Network Prediction Analysis for High-Speed Train under Operation" Symmetry 12, no. 10: 1662. https://doi.org/10.3390/sym12101662
APA StyleHao, W., & Liu, F. (2020). Axle Temperature Monitoring and Neural Network Prediction Analysis for High-Speed Train under Operation. Symmetry, 12(10), 1662. https://doi.org/10.3390/sym12101662




