On the Outer-Independent Roman Domination in Graphs

Abstract

Let G be a graph with no isolated vertex and $f:V\left(G\right)\to \{0,1,2\}$ a function. Let $V_i=\{v\in V\left(G\right):f\left(v\right)=i\}$ for every $i\in \{0,1,2\}$. The function f is an outer-independent Roman dominating function on G if $V_0$ is an independent set and every vertex in $V_0$ is adjacent to at least one vertex in $V_2$. The minimum weight $\omega \left(f\right)={\sum }_{v\in V\left(G\right)}f\left(v\right)$ among all outer-independent Roman dominating functions f on G is the outer-independent Roman domination number of G. This paper is devoted to the study of the outer-independent Roman domination number of a graph, and it is a contribution to the special issue “Theoretical Computer Science and Discrete Mathematics” of Symmetry. In particular, we obtain new tight bounds for this parameter, and some of them improve some well-known results. We also provide closed formulas for the outer-independent Roman domination number of rooted product graphs.

1. Introduction

Throughout this paper, we consider $G=\left(V\right(G),E(G\left)\right)$ as a simple graph with no isolated vertex. Given a vertex v of G, $N\left(v\right)$ and $N\left[v\right]$ represent the open neighbourhood and the closed neighbourhood of v, respectively. We also denote by $deg\left(v\right)=\left|N\right(v\left)\right|$ the degree of vertex v. For a set $D\subseteq V\left(G\right)$, its open neighbourhood and closed neighbourhood are $N\left(D\right)={\cup }_{v\in D}N\left(v\right)$ and $N\left[D\right]=N\left(D\right)\cup D$, respectively. Moreover, the subgraph of G induced by $D\subseteq V\left(G\right)$ will be denoted by $G\left[D\right]$.

Domination theory is an interesting topic in the theory of graphs, as well as one of the most active topic of research in this area. A set $D\subseteq V\left(G\right)$ is a dominating set of G if $N\left[D\right]=V\left(G\right)$. The domination number of G, denoted by $\gamma \left(G\right)$, is the minimum cardinality amongst all dominating sets of G. Numerous results on this issue obtained in the previous century are shown in [1,2]. We define a $\gamma \left(G\right)$-set as a dominating set of cardinality $\gamma \left(G\right)$. The same terminology will be assumed for optimal parameters associated with other sets or functions defined in the paper.

Moreover, in the last two decades, the interest in the domination theory in graphs has increased. In that sense, a very high number of variants of domination parameters have been studied, many of which are combinations of two or more parameters. Next, we expose some of them.

• A set $S\subseteq V\left(G\right)$ is an independent set of G if the subgraph induced by S is edgeless. The maximum cardinality among all independent sets of G is the independence number of G, and is denoted by $\beta \left(G\right)$. In some kind of “opposed” side of an independent set, we find a vertex cover, which is a set $D\subseteq V\left(G\right)$ such that $V\left(G\right)\backslash D$ is an independent set of G. The vertex cover number of G, denoted by $\alpha \left(G\right)$, is the minimum cardinality among all vertex covers of G. It is well-known that for any graph G of order n, $\alpha \left(G\right)+\beta \left(G\right)=n$ (see [3]).
• A set $S\subseteq V\left(G\right)$ is an independent dominating set of G if S is an independent and dominating set at the same time. The independent domination number of G is the minimum cardinality among all independent dominating sets of G and is denoted by $i\left(G\right)$. Independent domination in graphs was formally introduced in [4,5]. However, a fairly complete survey on this topic was recently published in [6].
• A function $f:V\left(G\right)\to \{0,1,2\}$ is called a Roman dominating function on G, if every $v\in V\left(G\right)$ for which $f\left(v\right)=0$ is adjacent to at least one vertex $u\in V\left(G\right)$ for which $f\left(u\right)=2$. The Roman domination number of G, denoted by ${\gamma }_R\left(G\right)$, is the minimum weight $\omega \left(f\right)={\sum }_{v\in V\left(G\right)}f\left(v\right)$ among all Roman dominating functions f on G. This parameter was introduced in [7]. Let $V_i=\{v\in V\left(G\right):f\left(v\right)=i\}$ for $i\in \{0,1,2\}$. We will identify a Roman dominating function f with the subsets $V_0$, $V_1$, $V_2$ of $V\left(G\right)$ associated with it, and so we will use the unified notation $f(V_0,V_1,V_2)$ for the function and these associated subsets.
• A Roman dominating function $f(V_0,V_1,V_2)$ is called an outer-independent Roman dominating function, abbreviated OIRDF, if $V_0$ is an independent set of G. Notice that then $V_1\cup V_2$ is a vertex cover of G. The outer-independent Roman domination number of G is the minimum weight among all outer-independent Roman dominating functions on G, and is denoted by ${\gamma }_{oiR}\left(G\right)$. This parameter was introduced in [8] and also studied in [9,10,11].

All the previous parameters are, in one way or another, related to each other. Next, we show the most natural relationships that exist between them, which are easily deductible by definition.

Remark 1.

For any graph G of order n with no isolated vertex,

(i) 

$\gamma \left(G\right)\le i\left(G\right)\le \beta \left(G\right)=n-\alpha \left(G\right)$.

(ii) 

$\gamma \left(G\right)\le {\gamma }_R\left(G\right)\le {\gamma }_{oiR}\left(G\right)$.

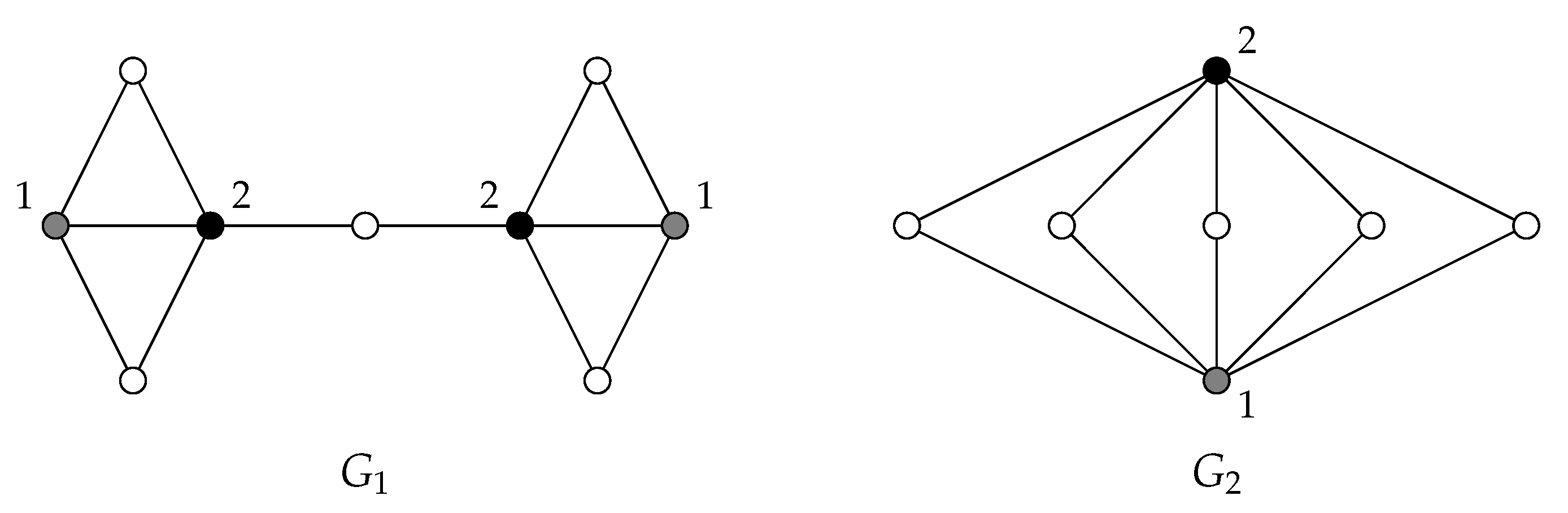
For the graphs shown in Figure 1 we have the following.

• $\gamma \left(G_1\right)=2<i\left(G_1\right)<4=\alpha \left(G_1\right)={\gamma }_R\left(G_1\right)<\beta \left(G_1\right)<{\gamma }_{oiR}\left(G_1\right)=6$.
• $\gamma \left(G_2\right)=i\left(G_2\right)=\alpha \left(G_2\right)=2<{\gamma }_R\left(G_2\right)={\gamma }_{oiR}\left(G_2\right)=3<\beta \left(G_2\right)=5$.

In this paper, we continue the study of the outer-independent Roman domination number of graphs. For instance, in Section 2 we give some new relationships between this parameter and the others mentioned above. Several of these results improve other bounds previously given. Finally, in Section 3 we provide closed formulas for this parameter in rooted product graphs. In particular, we show that there are four possible expressions for the outer-independent Roman domination number of a rooted product graph, and we characterize the graphs reaching these expressions.

2. Bounds and Relationships with Other Parameters

Abdollahzadeh Ahangar et al. [8] in 2017, established the following result.

Theorem 1

([8]). For any graph G with no isolated vertex,

$$\alpha \left(G\right)+1\le {\gamma }_{oiR}\left(G\right)\le 2\alpha \left(G\right).$$

Observe that any graph G with no isolated vertex, order n and maximum degree $\Delta$, satisfies that $1\le ⌈\frac{n-\alpha \left(G\right)}{\Delta }⌉$. It is also well-know that $\gamma \left(G\right)\le \alpha \left(G\right)$, which implies $\alpha \left(G\right)+\gamma \left(G\right)\le 2\alpha \left(G\right)$. With the above inequalities in mind, we state the following theorem, which improves the bounds given in Theorem 1.

Theorem 2.

For any graph G with no isolated vertex, order n and maximum degree Δ,

$$\alpha \left(G\right)+⌈\frac{n-\alpha \left(G\right)}{\Delta }⌉\le {\gamma }_{oiR}\left(G\right)\le \alpha \left(G\right)+\gamma \left(G\right).$$

Proof. 

We first prove the upper bound. Let D be a $\gamma \left(G\right)$-set and S an $\alpha \left(G\right)$-set. Let $g(W_0,W_1,W_2)$ be a function defined by $W_0=V\left(G\right)\backslash (D\cup S)$, $W_1=(D\cup S)\backslash (D\cap S)$ and $W_2=D\cap S$. We claim that g is an OIRDF on G. Without loss of generality, we may assume that $W_0\ne \varnothing$. Notice that $W_0=V\left(G\right)\backslash (D\cup S)$ is an independent set of G as S is a vertex cover. Now, we prove that every vertex in $W_0$ has a neighbour in $W_2$. Let $x\in W_0=V\left(G\right)\backslash (D\cup S)$. Since S is a vertex cover and D is a dominating set, we deduce that $N\left(x\right)\subseteq S$ and $N\left(x\right)\cap D\ne \varnothing$, respectively. Hence $N\left(x\right)\cap D\cap S\ne \varnothing$, or equivalently, $N\left(x\right)\cap W_2\ne \varnothing$. Thus, g is an OIRDF on G, as required. Therefore, ${\gamma }_{oiR}\left(G\right)\le \omega \left(g\right)=|(D\cup S)\backslash (D\cap S)|+2|D\cap S|=\alpha \left(G\right)+\gamma \left(G\right)$.

We now proceed to prove the lower bound. Let $f(V_0,V_1,V_2)$ be a ${\gamma }_{oiR}\left(G\right)$-function. By definition, we have that $V_0$ is an independent set, and so, $V_1\cup V_2$ is a vertex cover. Moreover, we note that every vertex in $V_2$ has at most $\Delta$ neighbours in $V_0$. Hence, $|V_0|\le \Delta |V_2|$. By inequality above, and the fact that $n-\alpha \left(G\right)=\beta \left(G\right)\ge |V_0|$, we have

$$\begin{array}{ccc}\hfill \Delta {\gamma }_{oiR}\left(G\right)& =& \Delta \left(\right|V_1|+2|V_2\left|\right)\hfill \\ & =& \Delta \left(\right|V_1|+|V_2\left|\right)+\Delta |V_2|\hfill \\ & \ge & \Delta (n-|V_0\left|\right)+|V_0|\hfill \\ & =& n\Delta -(\Delta -1)|V_0|\hfill \\ & \ge & n\Delta -(\Delta -1)(n-\alpha (G\left)\right)\hfill \\ & =& \Delta \alpha \left(G\right)+(n-\alpha (G\left)\right).\hfill \end{array}$$

Therefore, ${\gamma }_{oiR}\left(G\right)\ge \alpha \left(G\right)+⌈\frac{n-\alpha \left(G\right)}{\Delta }⌉$, which completes the proof. □

The bounds above are tight. To see this, let us consider the vertex cover Roman graphs G. These graphs were defined in [8] and satisfy the equality ${\gamma }_{oiR}\left(G\right)=2\alpha \left(G\right)$. Since $\gamma \left(G\right)\le \alpha \left(G\right)$, we deduce that for every vertex cover Roman graph G it follows that ${\gamma }_{oiR}\left(G\right)=\alpha \left(G\right)+\gamma \left(G\right)$. Note also that both bounds are achieved for the graph $G_1$ given in Figure 1, i.e., $\alpha \left(G_1\right)+⌈\frac{|V\left(G_1\right)|-\alpha \left(G_1\right)}{\Delta \left(G_1\right)}⌉={\gamma }_{oiR}\left(G_1\right)=\alpha \left(G_1\right)+\gamma \left(G_1\right).$

The following result is an immediate consequence of Theorem 2.

Corollary 1.

If G is a graph such that $\gamma \left(G\right)=1$, then

$${\gamma }_{oiR}\left(G\right)=\alpha \left(G\right)+1.$$

However, the graphs G with $\gamma \left(G\right)=1$ are not the only ones that satisfy the equality ${\gamma }_{oiR}\left(G\right)=\alpha \left(G\right)+1$. For instance, the path $P_4$ satisfies that $\gamma \left(P_4\right)=2$ and ${\gamma }_{oiR}\left(P_4\right)=3=\alpha \left(P_4\right)+1$. In such a sense, we next give a theoretical characterization of the graphs that satisfy this equality above.

Theorem 3.

If G is a graph with no isolated vertex, then the following statements are equivalent.

(i) 

${\gamma }_{oiR}\left(G\right)=\alpha \left(G\right)+1$.

(ii) 

There exist an $\alpha \left(G\right)$-set S and a vertex $v\in S$ such that $V\left(G\right)\backslash S\subseteq N\left(v\right)$.

Proof. 

We first suppose that (i) holds, i.e., ${\gamma }_{oiR}\left(G\right)=\alpha \left(G\right)+1$. Let $f(V_0,V_1,V_2)$ be a ${\gamma }_{oiR}\left(G\right)$-function such that $|V_2|$ is maximum. Hence, $V_2\ne \varnothing$. Let $v\in V_2$. Since $V_1\cup V_2$ is a vertex cover of G, it follows that $\alpha \left(G\right)+1\le \left(\right|V_1|+|V_2\left|\right)+|V_2|={\gamma }_{oiR}\left(G\right)=\alpha \left(G\right)+1$. Hence, we have equalities in the previous inequality chain, which implies that $S=V_1\cup V_2$ is an $\alpha \left(G\right)$-set and $V_2=\left\{v\right\}$. So, $V\left(G\right)\backslash S=V_0\subseteq N\left(V_2\right)=N\left(v\right)$. Therefore, (ii) follows.

On the other hand, suppose that (ii) holds, i.e., suppose there exist an $\alpha \left(G\right)$-set S and $v\in S$ such that $V\left(G\right)\backslash S\subseteq N\left(v\right)$. Observe that the function $g(W_0,W_1,W_2)$, defined by $W_2=\left\{v\right\}$, $W_1=S\backslash \left\{v\right\}$ and $W_0=V\left(G\right)\backslash S$, is an OIRDF on G. Therefore, and using the lower bound given in the Theorem 1, we obtain that $\alpha \left(G\right)+1\le {\gamma }_{oiR}\left(G\right)\le \omega \left(g\right)=\left|S\right|+1=\alpha \left(G\right)+1$. Hence, ${\gamma }_{oiR}\left(G\right)=\alpha \left(G\right)+1$, which completes the proof. □

A tree T is an acyclic connected graph. A leaf vertex of T is a vertex of degree one. The set of leaves is denoted by $L\left(T\right)$. We say that a vertex $v\in V\left(T\right)$ is a support vertex (strong support vertex) if $\left|N\right(v)\cap L(T\left)\right|\ge 1$ ($\left|N\right(v)\cap L(T\left)\right|\ge 2$). The set of support vertices and strong support vertices are denoted by $S\left(T\right)$ and $S_s\left(T\right)$, respectively.

With this notation in mind, we next characterize the trees T with ${\gamma }_{oiR}\left(T\right)=\alpha \left(T\right)+1$. Before we do this, we shall need to state the following useful lemma, in which $diam\left(T\right)$ represents the diameter of T.

Lemma 1.

If T is a tree such that ${\gamma }_{oiR}\left(T\right)=\alpha \left(T\right)+1$, then the following statements hold.

(i) 

$diam\left(T\right)\le 4$.

(ii) 

$V\left(T\right)=L\left(T\right)\cup S\left(T\right)$.

Proof. 

We first proceed to prove (i). By Theorem 3 there exist an $\alpha \left(T\right)$-set S and $v\in S$ such that $V\left(T\right)\backslash S\subseteq N\left(v\right)$. Now, we suppose that $k=diam\left(T\right)\ge 5$. Let $P=v_0{v}_1\cdots v_{k-1}{v}_k$ be a diametrical path of T. Hence, $\varnothing \ne \{v_0,v_1,v_{k-1},v_k\}\cap (V\left(T\right)\backslash S)\neg \subseteq N\left(v\right)$, which is a contradiction. Therefore, $diam\left(T\right)\le 4$, as desired.

Finally, we proceed to prove (ii). By (i) we have that $diam\left(T\right)\le 4$. If $V\left(T\right)\backslash \left(L\right(T)\cup S(T\left)\right)\ne \varnothing$, then for every $\alpha \left(T\right)$-set S and $v\in S$ it follows that $V\left(T\right)\backslash S\neg \subseteq N\left(v\right)$, which is a contradiction with Theorem 3. Hence, $V\left(T\right)=L\left(T\right)\cup S\left(T\right)$, which completes the proof. □

Let $\mathcal{T}$ be the family of trees $T_{r,s}$ of order $r+s+1$ with $r\ge 1$ and $r-1\ge s\ge 0$, obtained from a star $K_{1,r}$ by subdividing s edges exactly once. In Figure 2 we show the tree $T_{5,3}$.

Theorem 4.

Let T be a nontrivial tree. Then ${\gamma }_{oiR}\left(T\right)=\alpha \left(T\right)+1$ if and only if $T\in \mathcal{T}$.

Proof. 

If $T\in \mathcal{T}$, then it is easy to check that ${\gamma }_{oiR}\left(T\right)=\alpha \left(T\right)+1$. Now, we prove the converse. Let T be a nontrivial tree such that ${\gamma }_{oiR}\left(T\right)=\alpha \left(T\right)+1$. By Lemma 1-(i) we have that $diam\left(T\right)\le 4$. If $diam\left(T\right)\le 2$, then $T\cong T_{r,0}\in \mathcal{T}$. If $diam\left(T\right)=3$, then $T\cong T_{r,1}\in \mathcal{T}$. We now suppose that $diam\left(T\right)=4$. By Lemma 1-(ii) we have that $V\left(T\right)=L\left(T\right)\cup S\left(T\right)$. We claim that for any diametrical path $P=v_0{v}_1{v}_2{v}_3{v}_4$ of T, it follows that $v_1,v_3\in S\left(T\right)\backslash S_s\left(T\right)$. First, we observe that $v_1,v_3\in S\left(T\right)$. Without loss of generality, suppose that $v_1\in S_s\left(T\right)$. Hence, $v_1$ belongs to every $\alpha \left(T\right)$-set. By Theorem 3 there exist an $\alpha \left(T\right)$-set S and $v\in S$ such that $V\left(T\right)\backslash S\subseteq N\left(v\right)$. Since $v_0\in V\left(T\right)\backslash S$, then $v=v_1$. Notice also that $\varnothing \ne \{v_3,v_4\}\cap (V\left(T\right)\backslash S)\neg \subseteq N\left(v_1\right)$, which is a contradiction. Therefore, $v_1,v_3\in S\left(T\right)\backslash S_s\left(T\right)$, as desired. From above, we deduce that $T\cong T_{r,s}\in \mathcal{T}$, where $r\ge 3$ and $r-1\ge s\ge 2$. Therefore, the proof is complete. □

The following result is another consequence of Theorem 2.

Theorem 5.

Let G be a graph with no isolated vertex. For any ${\gamma }_R\left(G\right)$-function $f(V_0,V_1,V_2)$,

$${\gamma }_{oiR}\left(G\right)\le {\gamma }_R\left(G\right)+\alpha \left(G\right)-\left|V_2\right|.$$

Proof. 

Let $f(V_0,V_1,V_2)$ be a ${\gamma }_R\left(G\right)$-function. Since $V_1\cup V_2$ is a dominating set of G, it follows that $\gamma \left(G\right)\le |V_1|+|V_2|={\gamma }_R\left(G\right)-\left|V_2\right|$. Therefore, Theorem 2 leads to ${\gamma }_{oiR}\left(G\right)\le \alpha \left(G\right)+\gamma \left(G\right)\le {\gamma }_R\left(G\right)+\alpha \left(G\right)-\left|V_2\right|$, which completes the proof. □

The bound above is tight. For instance, in the corona graph $G\odot N_r$ with $r\ge 3$, the unique ${\gamma }_R(G\odot N_r)$-function $f(V_0,V_1,V_2)$, defined by $V_2=V\left(G\right)$ and $V_1=\varnothing$, is also a ${\gamma }_{oiR}(G\odot N_r)$-function, and so, ${\gamma }_R(G\odot N_r)={\gamma }_{oiR}(G\odot N_r)={\gamma }_R(G\odot N_r)+\alpha (G\odot N_r)-|V_2|=2|V\left(G\right)|.$ The following result, which is a consequence of Remark 1 and Theorem 5, generalizes the previous example.

Proposition 1.

If there exists a ${\gamma }_R\left(G\right)$-function $f(V_0,V_1,V_2)$ such that $|V_2|=\alpha \left(G\right)$, then

$${\gamma }_{oiR}\left(G\right)={\gamma }_R\left(G\right).$$

We now relate the outer-independent Roman domination number with other domination parameters of graphs. Before, we shall state the following proposition.

Proposition 2.

For any graph G with no isolated vertex, there exists a ${\gamma }_{oiR}\left(G\right)$-function $f(V_0,V_1,V_2)$ such that $V_0$ is an independent dominating set of G.

Proof. 

Let $f(V_0,V_1,V_2)$ be a ${\gamma }_{oiR}\left(G\right)$-function such that $|V_2|$ is maximum. By definition we have that $V_0$ is an independent set. We next prove that $V_0$ is a dominating set of G. It is clear that $V_2\subseteq N\left(V_0\right)$. Let $v\in V_1$. If $N\left(v\right)\subseteq V_1\cup V_2$, then the function $f^{\prime }(V_0^{\prime },V_1^{\prime },V_2^{\prime })$, defined by $f^{\prime }\left(v\right)=0$, $f^{\prime }\left(u\right)=f\left(u\right)+1$ for some vertex $u\in N\left(v\right)\cap V_1$ and $f^{\prime }\left(x\right)=f\left(x\right)$ whenever $x\in V\left(G\right)\backslash \{v,u\}$, is a ${\gamma }_{oiR}\left(G\right)$-function and $|V_2^{\prime }|>|V_2|$, which is a contradiction. Hence, $N\left(v\right)\cap V_0\ne \varnothing$, which implies that $V_0$ is an independent dominating set of G, as desired. □

Theorem 6.

For any graph G with no isolated vertex, order n, minimum degree δ and maximum degree Δ,

$$⌈\frac{i\left(G\right)\delta }{\Delta }⌉+1\le {\gamma }_{oiR}\left(G\right)\le n-i\left(G\right)+\gamma \left(G\right).$$

Proof. 

The upper bound follows by Theorem 2 and the fact that $\alpha \left(G\right)=n-\beta \left(G\right)\le n-i\left(G\right)$. Now, we proceed to prove the lower bound. Let $f(V_0,V_1,V_2)$ be a ${\gamma }_{oiR}\left(G\right)$-function which satisfies Proposition 2. Since every vertex in $V_1\cup V_2$ has at most $\Delta$ neighbours in $V_0$ and $V_0$ is an independent dominating set, it follows that $\delta |V_0|\le \Delta (|V_1|+|V_2\left|\right)$ and $|V_0|\ge i\left(G\right)$. Hence,

$$\begin{array}{ccc}\hfill {\gamma }_{oiR}\left(G\right)& =& \left(\right|V_1|+|V_2\left|\right)+|V_2|\hfill \\ & \ge & \frac{|V_0|\delta }{\Delta }+\left|V_2\right|\hfill \\ & \ge & \frac{i\left(G\right)\delta }{\Delta }+1.\hfill \end{array}$$

Therefore, the proof is complete. □

The bounds above are tight. For example, the lower bound is achieved for the complete bipartite graphs $K_{r,r}$, where ${\gamma }_{oiR}\left(K_{r,r}\right)=r+1=⌈\frac{r^2}{r}⌉+1=⌈\frac{i\left(K_{r,r}\right)\delta \left(K_{r,r}\right)}{\Delta \left(K_{r,r}\right)}⌉+1$. In addition, the upper bound is achieved for the case of complete graphs, and in connection with this fact, we pose the following question.

Open question: Is it the case that ${\gamma }_{oiR}\left(G\right)=n-i\left(G\right)+\gamma \left(G\right)$ if and only if G is a complete graph?

Next, we give new bounds for the outer-independent Roman domination number of triangle-free graphs. Recall that in these graphs, no pair of adjacent vertices can have a common neighbor. For this purpose, we shall need to introduce the following definitions.

A set $S\subseteq V\left(G\right)$ is a 3-packing if the distance between u and v is greater than three for every pair of different vertices $u,v\in S$. The 3-packing number of G, denoted by ${\rho }_3\left(G\right)$, is the maximum cardinality among all 3-packings of G. We also define

$${\mathcal{P}}_3\left(G\right)=\{S\subseteq V\left(G\right):S\mathrm{is}\mathrm{a}3\text{-}\mathrm{packing}\mathrm{of}G\}.$$

Theorem 7.

For any triangle-free graph G of order n,

$${\displaystyle {\gamma }_{oiR}\left(G\right)\le n-\underset{S\in {\mathcal{P}}_3\left(G\right)}{max}\left\{\sum _{v\in S}(deg\left(v\right)-1)\right\}.}$$

Proof. 

Let $S\in {\mathcal{P}}_3\left(G\right)$. As G is triangle-free, it follows that $N\left(v\right)$ is an independent set of G for every $v\in V\left(G\right)$. Hence, $N\left(S\right)$ is an independent set of G, which implies that the function $f(V_0,V_1,V_2)$, defined by $V_2=S$, $V_0=N\left(S\right)$ and $V_1=V\left(G\right)\backslash N\left[S\right]$, is an OIRDF on G. Thus, ${\gamma }_{oiR}\left(G\right)\le 2|V_2|+|V_1|=2|S|+(n-\left|N\left[S\right]\right|)=n-{\sum }_{v\in S}(deg\left(v\right)-1)$. Since the inequality holds for every $S\in {\mathcal{P}}_3\left(G\right)$, the result follows. □

Corollary 2.

For any triangle-free graph G of order n and minimum degree δ,

$${\gamma }_{oiR}\left(G\right)\le n-{\rho }_3\left(G\right)(\delta -1).$$

In [8], the bound ${\gamma }_{oiR}\left(G\right)\le n-\Delta \left(G\right)+1$ was given for the case of triangle-free graph. Next, we state a result which improve the bound above for the triangle-free graphs G that satisfy the condition $diam\left(G\right)\left(\delta \right(G)-1)\ge 4(\Delta (G)-1)$.

Proposition 3.

Let G be a connected triangle-free graph of order n, minimum degree δ and maximum degree Δ. If $diam\left(G\right)\ge 4$, then

$${\gamma }_{oiR}\left(G\right)\le n-⌈\frac{diam\left(G\right)}{4}⌉(\delta -1).$$

Proof. 

Assume that $diam\left(G\right)\ge 4$. Let $P=v_0{v}_1\cdots v_k$ be a diametrical path of G (notice that $k=diam\left(G\right)$), and $S=\{v_0,v_4,\dots ,v_{4\lfloor k/4\rfloor }\}$. It is easy to see that $S\in {\mathcal{P}}_3\left(G\right)$, and so, by Theorem 7 we deduce that ${\gamma }_{oiR}\left(G\right)\le n-{\sum }_{v\in S}(deg\left(v\right)-1)\le n-⌈\frac{diam\left(G\right)}{4}⌉(\delta -1)$ which completes the proof. □

The bounds given in Corollary 2 and Proposition 3 are tight. For instance, they are achieved for the cycle $C_{10}$.

3. Rooted Product Graphs

Let G be a graph of order n with vertex set $\{u_1,\dots ,u_n\}$ and H a graph with root $v\in V\left(H\right)$. The rooted product graph $G{\circ }_{v}H$ is defined as the graph obtained from G and n copies of H, by identifying the vertex $u_i$ of G with the root v in the $i^{th}$-copy of H, where $i\in \{1,\cdots ,n\}$ [12]. If H or G is a trivial graph, then $G{\circ }_{v}H$ is equal to G or H, respectively. In this sense, to obtain the rooted product $G{\circ }_{v}H$, hereafter we will only consider graphs G and H of orders at least two. Figure 3 shows an example of a rooted product graph.

For every $x\in V\left(G\right)$, $H_x$ will denote the copy of H in $G{\circ }_{v}H$ containing x. The restriction of any ${\gamma }_{oiR}\left(G{\circ }_{v}H\right)$-function f to $V\left(H_x\right)$ will be denoted by $f_x$ and the restriction to $V\left(H_x\right)\backslash \left\{x\right\}$ will be denoted by $f_x^{-}$.

If v is a vertex of a graph H, then the subgraph $H-v$ is the subgraph of H induced by $V\left(H\right)\backslash \left\{v\right\}$. The following three results will be the main tools to deduce our results.

Lemma 2.

Let H be a graph without isolated vertices. For any $v\in V\left(H\right)$,

$${\gamma }_{oiR}(H-v)\ge {\gamma }_{oiR}\left(H\right)-1.$$

Proof. 

Let $g^{\prime }$ be a ${\gamma }_{oiR}(H-v)$-function. Notice that the function g, defined by $g\left(v\right)=1$ and $g\left(u\right)=g^{\prime }\left(u\right)$ whenever $u\in V\left(H\right)\backslash \left\{v\right\}$, is an OIRDF on H. Hence, ${\gamma }_{oiR}\left(H\right)-1\le \omega \left(g\right)-1=\omega \left(g^{\prime }\right)={\gamma }_{oiR}(H-v)$, which completes the proof. □

Lemma 3.

Let G and H be two graphs without isolated vertices. If G has order n and $v\in V\left(H\right)$, then the following statements hold.

(i) 

If $g\left(v\right)=0$ for some ${\gamma }_{oiR}\left(H\right)$-function g, then ${\gamma }_{oiR}\left(G{\circ }_{v}H\right)\le \alpha \left(G\right)+n{\gamma }_{oiR}\left(H\right).$

(ii) 

If $g\left(v\right)>0$ for some ${\gamma }_{oiR}\left(H\right)$-function g, then ${\gamma }_{oiR}\left(G{\circ }_{v}H\right)\le n{\gamma }_{oiR}\left(H\right).$

(iii) 

If there exists a ${\gamma }_{oiR}(H-v)$-function g such that $g\left(x\right)>0$ for every $x\in N\left(v\right)$, then ${\gamma }_{oiR}\left(G{\circ }_{v}H\right)\le {\gamma }_{oiR}\left(G\right)+n{\gamma }_{oiR}(H-v).$

Proof. 

From any ${\gamma }_{oiR}\left(H\right)$-function g such that $g\left(v\right)=0$ and any $\alpha \left(G\right)$-set, we can construct an OIRDF on $G{\circ }_{v}H$ of weight $\alpha \left(G\right)+n{\gamma }_{oiR}\left(H\right)$. Thus, ${\gamma }_{oiR}\left(G{\circ }_{v}H\right)\le \alpha \left(G\right)+n{\gamma }_{oiR}\left(H\right)$ and (i) follows.

Now, if there exists a ${\gamma }_{oiR}\left(H\right)$-function g such that $g\left(v\right)>0$, then from g we can construct an OIRDF on $G{\circ }_{v}H$ of weight $n\omega \left(g\right)$. Thus, ${\gamma }_{oiR}\left(G{\circ }_{v}H\right)\le n\omega \left(g\right)=n{\gamma }_{oiR}\left(H\right)$, and (ii) follows.

Finally, if there exists a ${\gamma }_{oiR}(H-v)$-function g such that $g\left(x\right)>0$ for every $x\in N\left(v\right)$, then from g and any ${\gamma }_{oiR}\left(G\right)$-function we can construct an OIRDF on $G{\circ }_{v}H$ of weight ${\gamma }_{oiR}\left(G\right)+n{\gamma }_{oiR}(H-v)$, which completes the proof. □

Lemma 4.

Let $f(V_0,V_1,V_2)$ be a ${\gamma }_{oiR}\left(G{\circ }_{v}H\right)$-function. The following statements hold for any vertex $x\in V\left(G\right)$.

(i) 

$\omega \left(f_x\right)\ge {\gamma }_{oiR}\left(H\right)-1$.

(ii) 

If $\omega \left(f_x\right)={\gamma }_{oiR}\left(H\right)-1$, then $x\in V_0$ and $N\left(x\right)\cap V\left(H_x\right)\subseteq V_1$.

Proof. 

Let $x\in V\left(G\right)$. Observe that $V_0\cap V\left(H_x\right)$ is an independent set of $H_x$ and also, every vertex in $V_0\cap (V\left(H_x\right)\backslash \left\{x\right\})$ has a neighbour in $V_2\cap V\left(H_x\right)$. So, it is easy to see that the function g, defined by $g\left(x\right)=max\{1,f(x\left)\right\}$ and $g\left(u\right)=f\left(u\right)$ whenever $u\in V\left(H_x\right)\backslash \left\{x\right\}$, is an OIRDF on $H_x$. Hence, ${\gamma }_{oiR}\left(H\right)-1={\gamma }_{oiR}\left(H_x\right)-1\le \omega \left(g\right)-1\le \omega \left(f_x\right)$, which completes the proof of (i).

Now, we suppose that $\omega \left(f_x\right)={\gamma }_{oiR}\left(H\right)-1$. If $x\in V_1\cup V_2$ or $x\in V_0$ and $N\left(x\right)\cap V\left(H_x\right)\cap V_2\ne \varnothing$, then $f_x$ is an OIRDF on $H_x$, which is a contradiction. Hence, $x\in V_0$ and as $V_0\cap V\left(H_x\right)$ is an independent set, we deduce that $N\left(x\right)\cap V\left(H_x\right)\subseteq V_1$, which completes the proof. □

From Lemma 4 (i) we deduce that any ${\gamma }_{oiR}\left(G{\circ }_{v}H\right)$-function f induces three subsets ${\mathcal{A}}_f$, ${\mathcal{B}}_f$ and ${\mathcal{C}}_f$ of $V\left(G\right)$ as follows.

$$\begin{array}{cc}\hfill {\mathcal{A}}_f& =\{x\in V\left(G\right):\omega \left(f_x\right)>{\gamma }_{oiR}\left(H\right)\},\hfill \\ \hfill {\mathcal{B}}_f& =\{x\in V\left(G\right):\omega \left(f_x\right)={\gamma }_{oiR}\left(H\right)\},\hfill \\ \hfill {\mathcal{C}}_f& =\{x\in V\left(G\right):\omega \left(f_x\right)={\gamma }_{oiR}\left(H\right)-1\}.\hfill \end{array}$$

Next, we state the four possible values of ${\gamma }_{oiR}\left(G{\circ }_{v}H\right)$.

Theorem 8.

Let G and H be two graphs with no isolated vertex and $\left|V\right(G\left)\right|=n$. If $v\in V\left(H\right)$, then

$${\gamma }_{oiR}\left(G{\circ }_{v}H\right)\in \{\alpha \left(G\right)+n{\gamma }_{oiR}\left(H\right),n{\gamma }_{oiR}\left(H\right),{\gamma }_{oiR}\left(G\right)+n({\gamma }_{oiR}\left(H\right)-1),\alpha \left(G\right)+n({\gamma }_{oiR}\left(H\right)-1)\}.$$

Proof. 

Let $f(V_0,V_1,V_2)$ be a ${\gamma }_{oiR}\left(G{\circ }_{v}H\right)$-function. By Lemma 3 (i) and (ii) we deduce the upper bound ${\gamma }_{oiR}\left(G{\circ }_{v}H\right)\le \alpha \left(G\right)+n{\gamma }_{oiR}\left(H\right)$. Now, we consider the subsets ${\mathcal{A}}_f,{\mathcal{B}}_f,{\mathcal{C}}_f\subseteq V\left(G\right)$ associated to f and distinguish the following cases.

Case 1. ${\mathcal{C}}_f=\varnothing$. In this case, for any $x\in V\left(G\right)$ we have that $\omega \left(f_x\right)\ge {\gamma }_{oiR}\left(H\right)$ and, as a consequence, ${\gamma }_{oiR}\left(G{\circ }_{v}H\right)=\omega \left(f\right)\ge n{\gamma }_{oiR}\left(H\right)$. If ${\mathcal{A}}_f=\varnothing$, then ${\gamma }_{oiR}\left(G{\circ }_{v}H\right)=n{\gamma }_{oiR}\left(H\right)$. Hence, assume that ${\mathcal{A}}_f\ne \varnothing$. This implies that $\omega \left(f\right)>n{\gamma }_{oiR}\left(H\right)$. Moreover, we note that ${\mathcal{B}}_f\ne \varnothing$ because $\alpha \left(G\right)<n$ and $\omega \left(f\right)\le \alpha \left(G\right)+n{\gamma }_{oiR}\left(H\right)$. Thus, by Lemma 3 (ii) we obtain that ${\mathcal{B}}_f\subseteq V_0$, and as $V_0$ is an independent set, we have that ${\mathcal{A}}_f$ is a vertex cover of G. Therefore,

$$\begin{array}{cc}\hfill {\gamma }_{oiR}\left(G{\circ }_{v}H\right)& =\sum _{x\in {\mathcal{A}}_f}\omega \left(f_x\right)+\sum _{x\in {\mathcal{B}}_f}\omega \left(f_x\right)\hfill \\ \hfill & \ge \sum _{x\in {\mathcal{A}}_f}({\gamma }_{oiR}\left(H\right)+1)+\sum _{x\in {\mathcal{B}}_f}{\gamma }_{oiR}\left(H\right)\hfill \\ \hfill & =|{\mathcal{A}}_f|+\sum _{x\in V\left(G\right)}{\gamma }_{oiR}\left(H\right)\hfill \\ \hfill & \ge \alpha \left(G\right)+n{\gamma }_{oiR}\left(H\right).\hfill \end{array}$$

Hence, ${\gamma }_{oiR}\left(G{\circ }_{v}H\right)=\alpha \left(G\right)+n{\gamma }_{oiR}\left(H\right)$.

Case 2. ${\mathcal{C}}_f\ne \varnothing$. Let $z\in {\mathcal{C}}_f$. By Lemma 4 (ii) we obtain that $z\in V_0$ and $N\left(z\right)\cap V\left(H_z\right)\subseteq V_1$. Hence, $f_z^{-}$ is an OIRDF on $H_z-z$, and so ${\gamma }_{oiR}(H-v)={\gamma }_{oiR}(H_z-z)\le \omega \left(f_z^{-}\right)={\gamma }_{oiR}\left(H\right)-1$. Thus, Lemma 2 leads to ${\gamma }_{oiR}(H_z-z)={\gamma }_{oiR}\left(H\right)-1$. This implies that $f_z^{-}$ is a ${\gamma }_{oiR}(H_z-z)$-function which satisfies Lemma 3 (iii). Therefore, ${\gamma }_{oiR}\left(G{\circ }_{v}H\right)\le {\gamma }_{oiR}\left(G\right)+n({\gamma }_{oiR}\left(H\right)-1)$.

Now, observe the following inequality chain.

$${\gamma }_{oiR}\left(G{\circ }_{v}H\right)=\sum _{x\in {\mathcal{A}}_f\cup {\mathcal{B}}_f}\omega \left(f_x\right)+\sum _{x\in {\mathcal{C}}_f}\omega \left(f_x\right)\ge \left(2\right|{\mathcal{A}}_f|+|{\mathcal{B}}_f\left|\right)+n({\gamma }_{oiR}\left(H\right)-1).$$

(1)

By Lemma 4 (ii) we have that ${\mathcal{C}}_f\subseteq V_0$, which implies that ${\mathcal{A}}_f\cup {\mathcal{B}}_f$ is a vertex cover of G. Thus, Inequality chain (1) leads to ${\gamma }_{oiR}\left(G{\circ }_{v}H\right)=\omega \left(f\right)\ge \alpha \left(G\right)+n({\gamma }_{oiR}\left(H\right)-1)$. Next, we consider the following two subcases.

Subcase 1. There exists a ${\gamma }_{oiR}\left(H\right)$-function g such that $g\left(v\right)=2$. Let D be an $\alpha \left(G\right)$-set. From D, g and $f_z$, we define a function h on $G{\circ }_{v}H$ as follows. For every $x\in D$, the restriction of h to $V\left(H_x\right)$ is induced from g. Moreover, if $x\in V\left(G\right)\backslash D$, then the restriction of h to $V\left(H_x\right)$ is induced from $f_z$. By the construction of g and $f_z$, it is straightforward to see that h is an OIRDF on $G{\circ }_{v}H$. Thus,

$$\begin{array}{cc}\hfill {\gamma }_{oiR}\left(G{\circ }_{v}H\right)& \le \sum _{x\in D}\omega \left(h_x\right)+\sum _{x\in V\left(G\right)\backslash D}\omega \left(h_x\right)\hfill \\ \hfill & =\sum _{x\in D}\omega \left(g\right)+\sum _{x\in V\left(G\right)\backslash D}\omega \left(f_z\right)\hfill \\ \hfill & =\sum _{x\in D}{\gamma }_{oiR}\left(H\right)+\sum _{x\in V\left(G\right)\backslash D}({\gamma }_{oiR}\left(H\right)-1)\hfill \\ \hfill & =\left|D\right|+\sum _{x\in V\left(G\right)}({\gamma }_{oiR}\left(H\right)-1)\hfill \\ \hfill & =\alpha \left(G\right)+n({\gamma }_{oiR}\left(H\right)-1).\hfill \end{array}$$

Therefore, ${\gamma }_{oiR}\left(G{\circ }_{v}H\right)=\alpha \left(G\right)+n({\gamma }_{oiR}\left(H\right)-1)$.

Subcase 2. $g\left(v\right)\le 1$ for every ${\gamma }_{oiR}\left(H\right)$-function g. This condition implies that $V_2\cap {\mathcal{B}}_f=\varnothing$. Since every vertex $x\in {\mathcal{C}}_f$ has a neighbour in $V_2$, and as Lemma 4 (ii) leads to $N\left(x\right)\cap V\left(H_x\right)\subseteq V_1$, then we deduce that $N\left(x\right)\cap V_2\cap {\mathcal{A}}_f\ne \varnothing$. Hence, and as ${\mathcal{C}}_f\subseteq V_0$, the function $f^{\prime }(V_0^{\prime },V_1^{\prime },V_2^{\prime })$, defined by $V_2^{\prime }={\mathcal{A}}_f$, $V_1^{\prime }={\mathcal{B}}_f$ and $V_0^{\prime }={\mathcal{C}}_f$, is an OIRDF on G. So ${\gamma }_{oiR}\left(G\right)\le \omega \left(f^{\prime }\right)=2|{\mathcal{A}}_f|+|{\mathcal{B}}_f|$. Therefore, Inequality chain (1) leads to ${\gamma }_{oiR}\left(G{\circ }_{v}H\right)\ge {\gamma }_{oiR}\left(G\right)+n({\gamma }_{oiR}\left(H\right)-1)$, which implies that ${\gamma }_{oiR}\left(G{\circ }_{v}H\right)={\gamma }_{oiR}\left(G\right)+n({\gamma }_{oiR}\left(H\right)-1)$.

Therefore, the proof is complete. □

In order to see that the four possible values of ${\gamma }_{oiR}\left(G{\circ }_{v}H\right)$ described in Theorem 8 are realizable, we consider the following example.

Example 1.

Let G be a graph with no isolated vertex. If H is the graph shown in Figure 4, then the resulting values of ${\gamma }_{oiR}\left(G{\circ }_{x}H\right)$ for some specific roots $x\in V\left(H\right)$ are described below.

• ${\gamma }_{oiR}\left(G{\circ }_{v}H\right)=\alpha \left(G\right)+n{\gamma }_{oiR}\left(H\right).$
• ${\gamma }_{oiR}\left(G{\circ }_{w}H\right)=n{\gamma }_{oiR}\left(H\right).$
• ${\gamma }_{oiR}\left(G{\circ }_{v^{\prime }}H\right)={\gamma }_{oiR}\left(G\right)+n({\gamma }_{oiR}\left(H\right)-1).$
• ${\gamma }_{oiR}\left(G{\circ }_{w^{\prime }}H\right)=\alpha \left(G\right)+n({\gamma }_{oiR}\left(H\right)-1).$

Now, we characterize the graphs with ${\gamma }_{oiR}\left(G{\circ }_{v}H\right)=\alpha \left(G\right)+n{\gamma }_{oiR}\left(H\right)$.

Theorem 9.

Let G and H be two graphs with no isolated vertex, let $\left|V\right(G\left)\right|=n$ and $v\in V\left(H\right)$. The following statements are equivalent.

(i) 

${\gamma }_{oiR}\left(G{\circ }_{v}H\right)=\alpha \left(G\right)+n{\gamma }_{oiR}\left(H\right)$.

(ii) 

$g\left(v\right)=0$ for every ${\gamma }_{oiR}\left(H\right)$-function g.

Proof. 

We first assume that (i) holds, i.e., ${\gamma }_{oiR}\left(G{\circ }_{v}H\right)=\alpha \left(G\right)+n{\gamma }_{oiR}\left(H\right)$. If there exists a ${\gamma }_{oiR}\left(H\right)$-function g such that $g\left(v\right)>0$, then by Lemma 3 (ii) it follows that ${\gamma }_{oiR}\left(G{\circ }_{v}H\right)\le n{\gamma }_{oiR}\left(H\right)$, which is a contradiction. Therefore, (ii) holds.

On the other hand, we assume that (ii) holds, i.e., $g\left(v\right)=0$ for every ${\gamma }_{oiR}\left(H\right)$-function g. Let $f(V_0,V_1,V_2)$ be a ${\gamma }_{oiR}\left(G{\circ }_{v}H\right)$-function. If ${\mathcal{C}}_f\ne \varnothing$, then by Lemma 4 (ii) we can obtain a ${\gamma }_{oiR}\left(H\right)$-function g such that $g\left(v\right)=1$, which is a contradiction. Hence, ${\mathcal{C}}_f=\varnothing$, and so, by Theorem 8 we deduce that ${\gamma }_{oiR}\left(G{\circ }_{v}H\right)\in \{\alpha \left(G\right)+n{\gamma }_{oiR}\left(H\right),n{\gamma }_{oiR}\left(H\right)\}$. Now, suppose that ${\gamma }_{oiR}\left(G{\circ }_{v}H\right)=n{\gamma }_{oiR}\left(H\right)$. Since ${\mathcal{C}}_f=\varnothing$, it follows that ${\mathcal{B}}_f=V\left(G\right)$ and as $V_0$ is an independent set, there exists $x\in {\mathcal{B}}_f\backslash V_0$. This implies that $f_x$ is a ${\gamma }_{oiR}\left(H_x\right)$-function such that $f_x\left(x\right)>0$, which is a contradiction. Therefore, ${\gamma }_{oiR}\left(G{\circ }_{v}H\right)=\alpha \left(G\right)+n{\gamma }_{oiR}\left(H\right)$, which completes the proof. □

Next, we characterize the graphs with ${\gamma }_{oiR}\left(G{\circ }_{v}H\right)=\alpha \left(G\right)+n({\gamma }_{oiR}\left(H\right)-1)$.

Theorem 10.

Let G and H be two graphs with no isolated vertex, let $\left|V\right(G\left)\right|=n$ and $v\in V\left(H\right)$. The following statements are equivalent.

(i) 

${\gamma }_{oiR}\left(G{\circ }_{v}H\right)=\alpha \left(G\right)+n({\gamma }_{oiR}\left(H\right)-1)$.

(ii) 

There exist two ${\gamma }_{oiR}\left(H\right)$-functions $g_1$ and $g_2$ such that $g_1\left(x\right)=1$ for every $x\in N\left[v\right]$ and $g_2\left(v\right)=2$.

Proof. 

We first assume that (i) holds, i.e., ${\gamma }_{oiR}\left(G{\circ }_{v}H\right)=\alpha \left(G\right)+n({\gamma }_{oiR}\left(H\right)-1)$. Let $f(V_0,V_1,V_2)$ be a ${\gamma }_{oiR}\left(G{\circ }_{v}H\right)$-function. As $\alpha \left(G\right)<n$, it follows that ${\mathcal{C}}_f\ne \varnothing$, and so, by Lemma 4 (ii) we can obtain a ${\gamma }_{oiR}\left(H\right)$-function $g_1$ such that $g_1\left(x\right)=1$ for every $x\in N\left[v\right]$. Moreover, if $g\left(v\right)\le 1$ for every ${\gamma }_{oiR}\left(H\right)$-function g, then, by proceeding analogously to Subcase 2 in the proof of Theorem 8 we deduce that ${\gamma }_{oiR}\left(G{\circ }_{v}H\right)\ge {\gamma }_{oiR}\left(G\right)+n({\gamma }_{oiR}\left(H\right)-1)$, which is a contradiction as ${\gamma }_{oiR}\left(G\right)>\alpha \left(G\right)$. Therefore, there exists a ${\gamma }_{oiR}\left(H\right)$-function $g_2$ such that $g_2\left(v\right)=2$, and (ii) follows.

On the other hand, we assume that there exist two ${\gamma }_{oiR}\left(H\right)$-functions $g_1$ and $g_2$ such that $g_1\left(x\right)=1$ for every $x\in N\left[v\right]$ and $g_2\left(v\right)=2$. Let D be an $\alpha \left(G\right)$-set and let $g_1^{\prime }$ be a function on H such that $g_1^{\prime }\left(v\right)=0$ and $g_1^{\prime }\left(x\right)=g_1\left(x\right)$ whenever $x\in V\left(H\right)\backslash \left\{v\right\}$. From D, $g_1^{\prime }$ and $g_2$, we define a function h on $G{\circ }_{v}H$ as follows. For every $x\in D$, the restriction of h to $V\left(H_x\right)$ is induced from $g_2$. Moreover, if $x\in V\left(G\right)\backslash D$, then the restriction of h to $V\left(H_x\right)$ is induced from $g_1^{\prime }$. Notice that h is an OIRDF on $G{\circ }_{v}H$, and so ${\gamma }_{oiR}\left(G{\circ }_{v}H\right)\le \omega \left(h\right)=\left|D\right|{\gamma }_{oiR}\left(H\right)+|V\left(G\right)\backslash D|({\gamma }_{oiR}\left(H\right)-1)=\alpha \left(G\right)+n({\gamma }_{oiR}\left(H\right)-1)$. Therefore, Theorem 8 leads to ${\gamma }_{oiR}\left(G{\circ }_{v}H\right)=\alpha \left(G\right)+n({\gamma }_{oiR}\left(H\right)-1)$, which completes the proof. □

Next we proceed to characterize the graphs with ${\gamma }_{oiR}\left(G{\circ }_{v}H\right)={\gamma }_{oiR}\left(G\right)+n({\gamma }_{oiR}\left(H\right)-1)$. Notice that it is excluded the case ${\gamma }_{oiR}\left(G\right)=n$, since then ${\gamma }_{oiR}\left(G{\circ }_{v}H\right)=n{\gamma }_{oiR}\left(H\right)$.

Theorem 11.

Let G be a graph of order n with no isolated vertex such that ${\gamma }_{oiR}\left(G\right)<n$ and let H be a graph with no isolated vertex and $v\in V\left(H\right)$. The following statements are equivalent.

(i) 

${\gamma }_{oiR}\left(G{\circ }_{v}H\right)={\gamma }_{oiR}\left(G\right)+n({\gamma }_{oiR}\left(H\right)-1)$.

(ii) 

$g\left(v\right)\le 1$ for every ${\gamma }_{oiR}\left(H\right)$-function g and also, there exists a ${\gamma }_{oiR}\left(H\right)$-function $g_1$ such that $g_1\left(x\right)=1$ for every $x\in N\left[v\right]$.

Proof. 

We first assume that (i) holds, i.e., ${\gamma }_{oiR}\left(G{\circ }_{v}H\right)={\gamma }_{oiR}\left(G\right)+n({\gamma }_{oiR}\left(H\right)-1)$. Let $f(V_0,V_1,V_2)$ be a ${\gamma }_{oiR}\left(G{\circ }_{v}H\right)$-function. Since ${\gamma }_{oiR}\left(G\right)<n$, it follows that ${\mathcal{C}}_f\ne \varnothing$, and so, by Lemma 4 (ii) we can obtain a ${\gamma }_{oiR}\left(H\right)$-function $g_1$ such that $g_1\left(x\right)=1$ for every $x\in N\left[v\right]$. Moreover, if there exists a ${\gamma }_{oiR}\left(H\right)$-function $g_2$ such that $g_2\left(v\right)=2$, then by Theorem 10 we deduce that ${\gamma }_{oiR}\left(G{\circ }_{v}H\right)=\alpha \left(G\right)+n({\gamma }_{oiR}\left(H\right)-1)$, which is a contradiction as ${\gamma }_{oiR}\left(G\right)>\alpha \left(G\right)$. Therefore, $g\left(v\right)\le 1$ for every ${\gamma }_{oiR}\left(H\right)$-function g, which implies that (ii) follows.

On the other side, we assume that $g\left(v\right)\le 1$ for every ${\gamma }_{oiR}\left(H\right)$-function g and also, that there exists a ${\gamma }_{oiR}\left(H\right)$-function $g_1$ such that $g_1\left(x\right)=1$ for every $x\in N\left[v\right]$. Under these assumptions, observe that the function $g_1$ restricted to $V\left(H\right)\backslash \left\{v\right\}$, namely $g_1^{\prime }$, is an OIRDF on $H-v$. Hence, ${\gamma }_{oiR}(H-v)\le \omega \left(g_1^{\prime }\right)=\omega \left(g_1\right)-1={\gamma }_{oiR}\left(H\right)-1$ and by Lemma 2 we deduce that ${\gamma }_{oiR}(H-v)={\gamma }_{oiR}\left(H\right)-1$. Hence, $g_1^{\prime }$ is a ${\gamma }_{oiR}(H-v)$-function which satisfies Lemma 3 (iii). Therefore, Lemma 3 and Theorem 8 lead to ${\gamma }_{oiR}\left(G{\circ }_{v}H\right)\in \{{\gamma }_{oiR}\left(G\right)+n({\gamma }_{oiR}\left(H\right)-1),\alpha \left(G\right)+n({\gamma }_{oiR}\left(H\right)-1)\}$. Finally, as $g\left(v\right)\le 1$ for every ${\gamma }_{oiR}\left(H\right)$-function g, by Theorem 10 we deduce that ${\gamma }_{oiR}\left(G{\circ }_{v}H\right)={\gamma }_{oiR}\left(G\right)+n({\gamma }_{oiR}\left(H\right)-1)$, which completes the proof. □

From Theorem 8 we have that there are four possible expressions for ${\gamma }_{oiR}\left(G{\circ }_{v}H\right)$. Theorems 9–11 characterize three of these expressions. In the case of the expression ${\gamma }_{oiR}\left(G{\circ }_{v}H\right)=n{\gamma }_{oiR}\left(H\right)$, the corresponding characterization can be derived by elimination from the previous results.