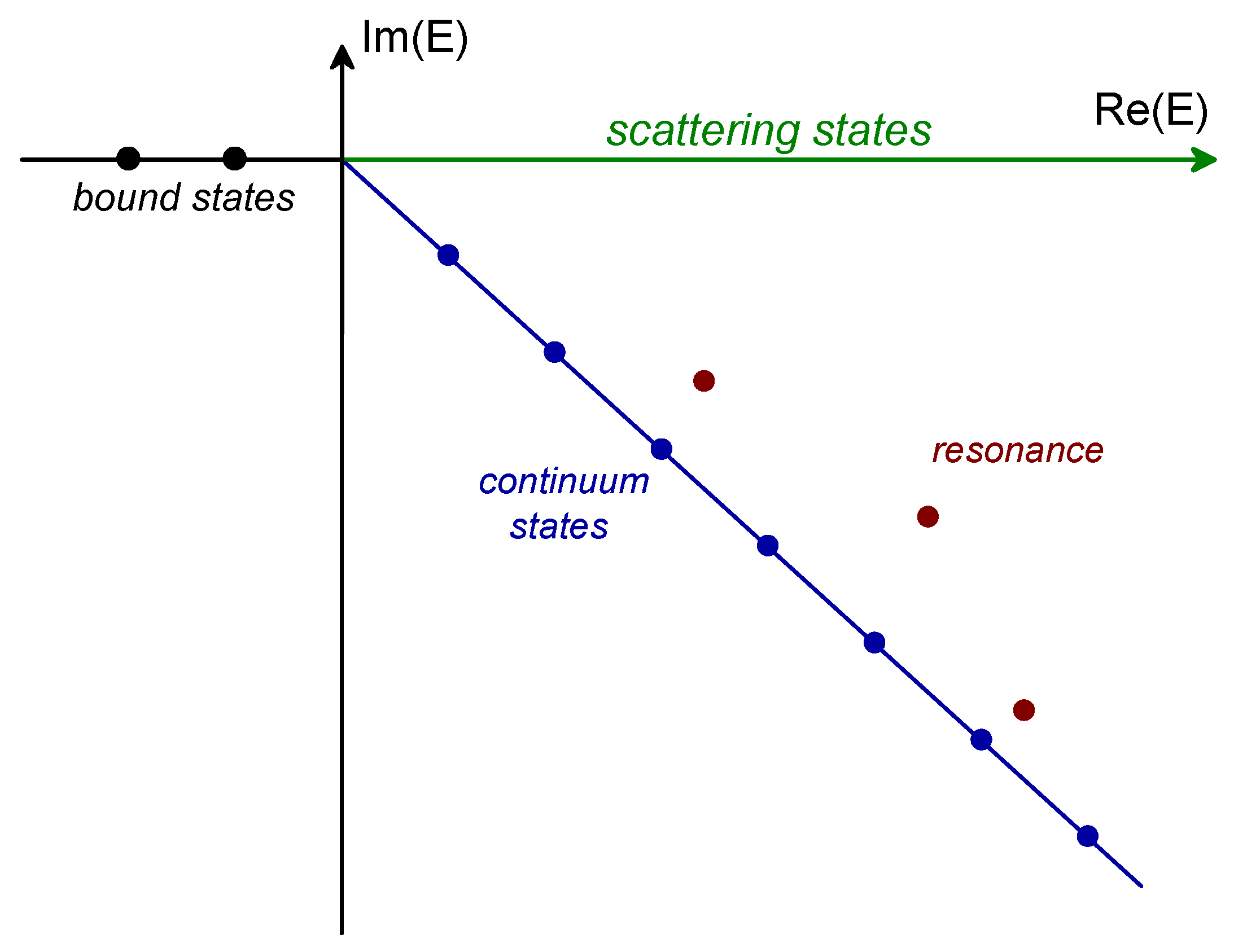
Figure 1.
Schematic complex energy distribution in the single-channel two-body system.
Figure 1.
Schematic complex energy distribution in the single-channel two-body system.
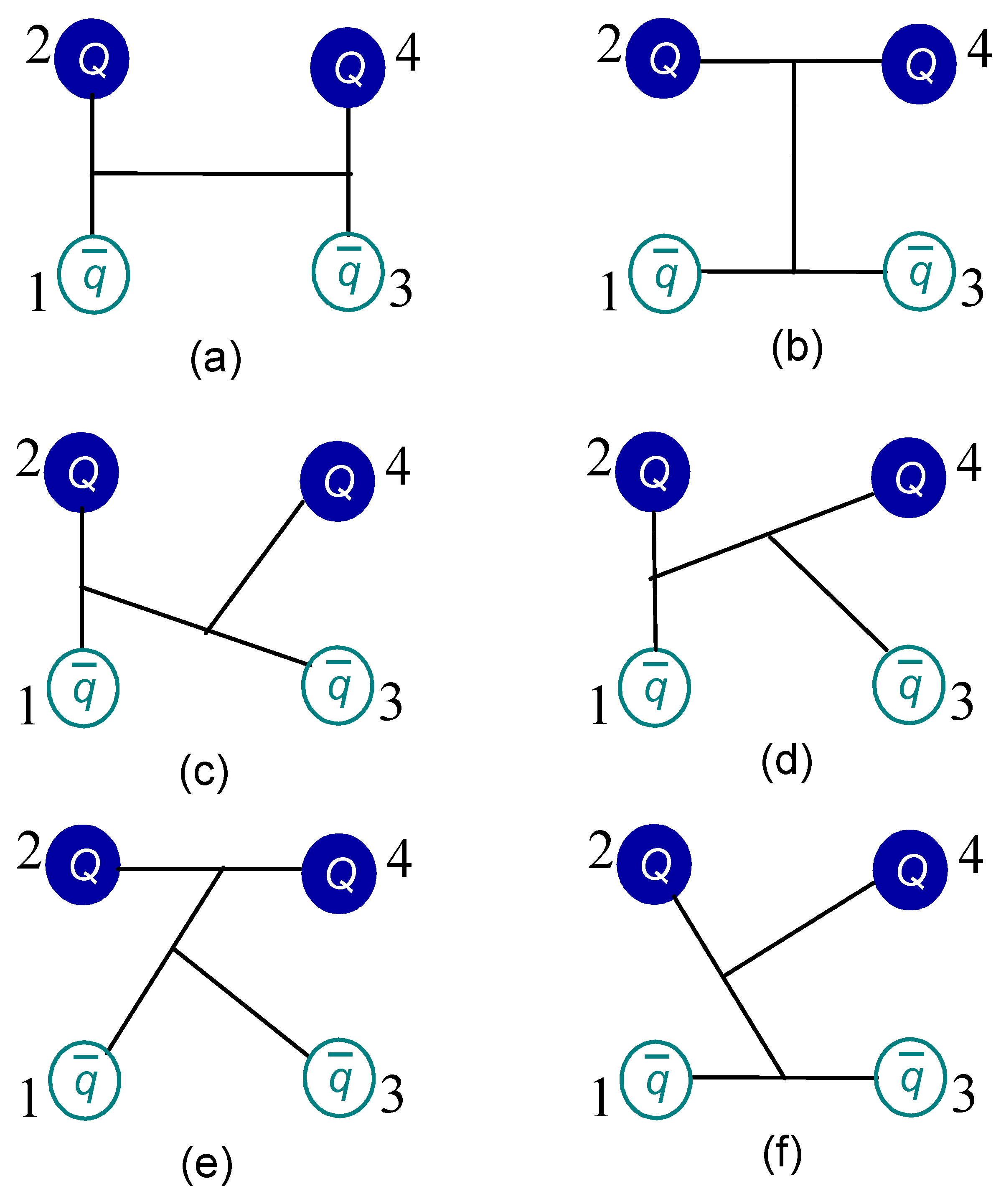
Figure 2.
Six types of configurations in tetraquarks. Panel (a) is meson-meson structure, panel (b) is diquark-antidiquark one and the other K-type structures are from panel (c–f). .
Figure 2.
Six types of configurations in tetraquarks. Panel (a) is meson-meson structure, panel (b) is diquark-antidiquark one and the other K-type structures are from panel (c–f). .
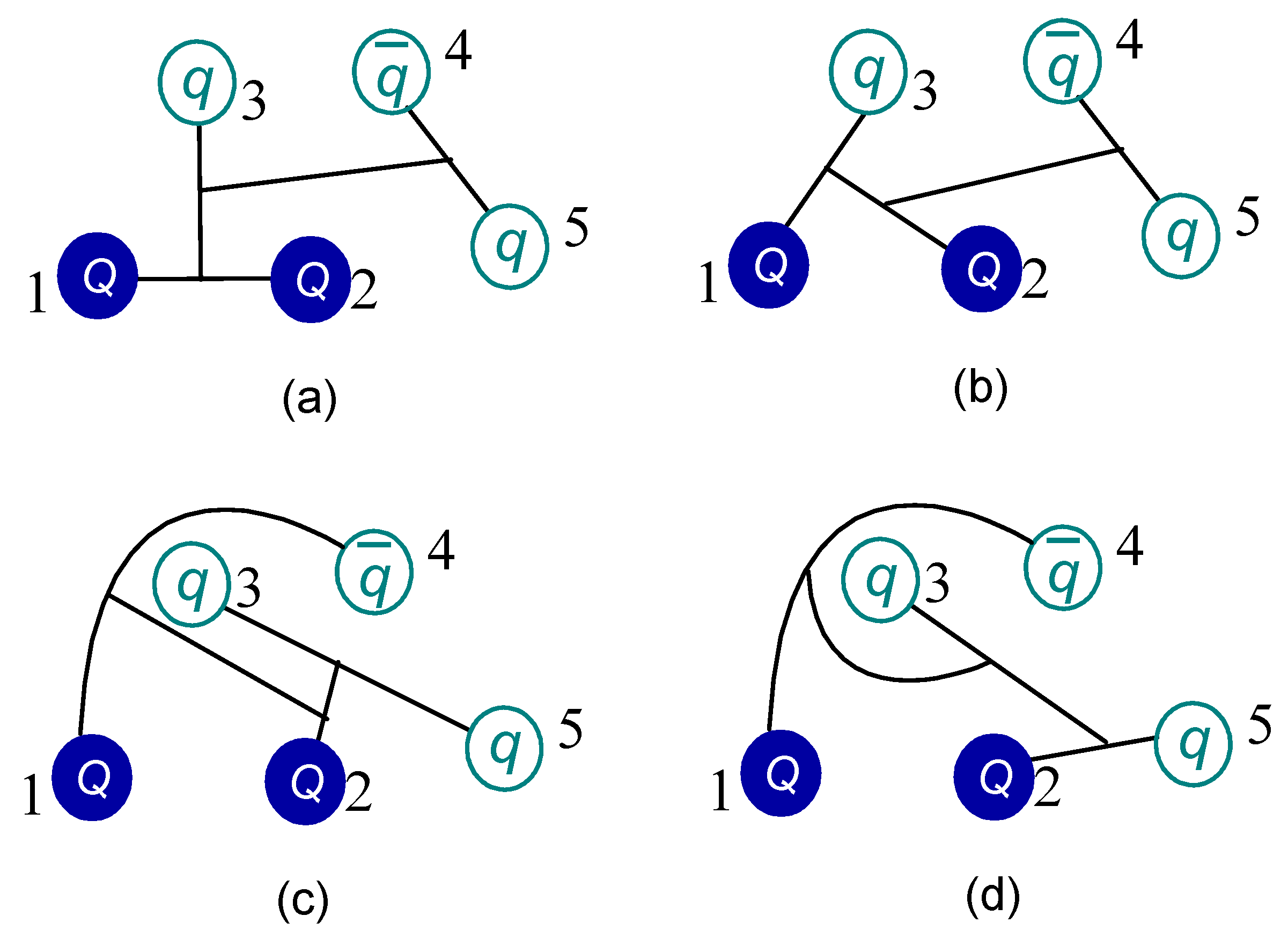
Figure 3.
Two types of configurations in hidden-flavor pentaquarks. . The distribution of heavy quark is considered in 3-quark (b) and quark-antiquark (a) cluster, respectively.
Figure 3.
Two types of configurations in hidden-flavor pentaquarks. . The distribution of heavy quark is considered in 3-quark (b) and quark-antiquark (a) cluster, respectively.
Figure 4.
Four types of configurations in doubly-flavor pentaquarks. . (a,b) are two heavy quarks coupled in one 3-quark cluster, and the other two panels, (c) and (d), stand for these two heavy quarks distributing in each two sub-clusters.
Figure 4.
Four types of configurations in doubly-flavor pentaquarks. . (a,b) are two heavy quarks coupled in one 3-quark cluster, and the other two panels, (c) and (d), stand for these two heavy quarks distributing in each two sub-clusters.
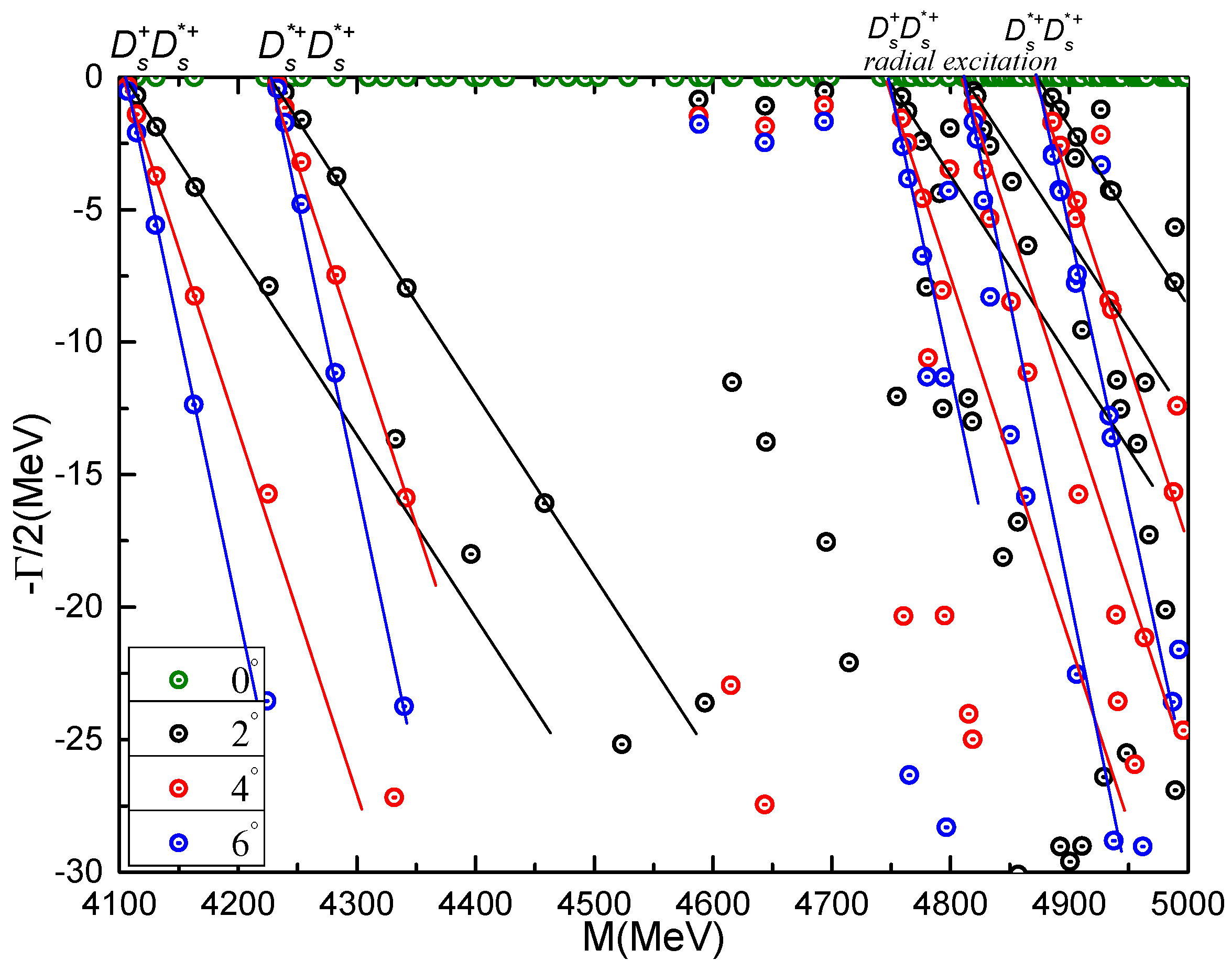
Figure 5.
Complex energies of double-charm tetraquarks with in the coupled channels calculation, varying from 0° to 6°.
Figure 5.
Complex energies of double-charm tetraquarks with in the coupled channels calculation, varying from 0° to 6°.
Figure 6.
Complex energies of double-bottom tetraquarks with in the coupled channels calculation, varying from 0° to 6°.
Figure 6.
Complex energies of double-bottom tetraquarks with in the coupled channels calculation, varying from 0° to 6°.
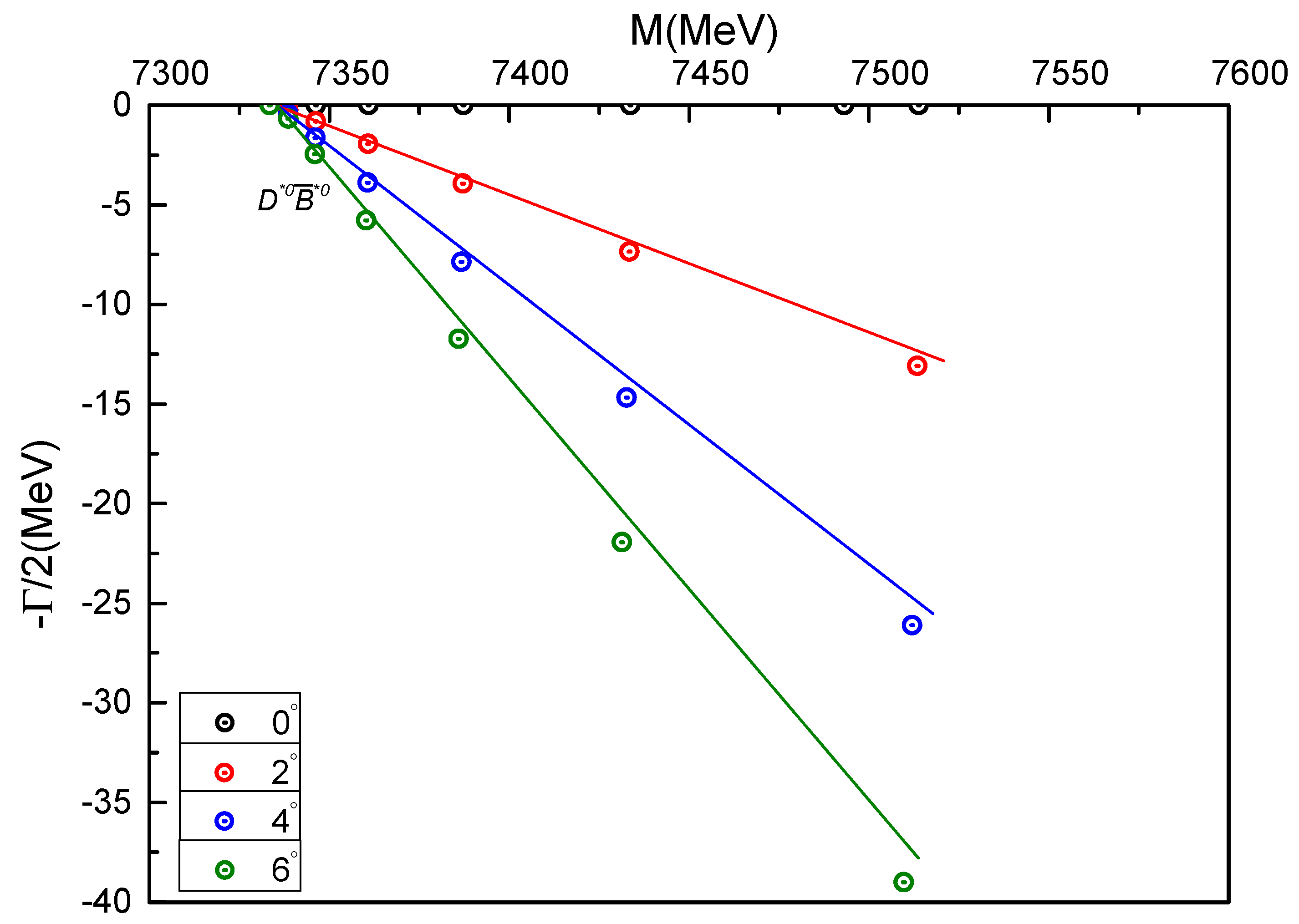
Figure 7.
Complex energies of charm-bottom tetraquarks with in the coupled channels calculation, varying from 0° to 6°.
Figure 7.
Complex energies of charm-bottom tetraquarks with in the coupled channels calculation, varying from 0° to 6°.
Figure 8.
Complex energies of charm-bottom tetraquarks with in the coupled channels calculation, varying from 0° to 6°.
Figure 8.
Complex energies of charm-bottom tetraquarks with in the coupled channels calculation, varying from 0° to 6°.
Figure 9.
Complex energies of charm-bottom tetraquarks with in the coupled channels calculation, varying from 0° to 6°.
Figure 9.
Complex energies of charm-bottom tetraquarks with in the coupled channels calculation, varying from 0° to 6°.
Figure 10.
Complex energies of tetraquarks with in the complete coupled channels calculation, varying from 0° to 6°.
Figure 10.
Complex energies of tetraquarks with in the complete coupled channels calculation, varying from 0° to 6°.
Figure 11.
Complex energies of tetraquarks with in the coupled channels calculation, varying from 0° to 6°.
Figure 11.
Complex energies of tetraquarks with in the coupled channels calculation, varying from 0° to 6°.
Figure 12.
Complex energies of tetraquarks with in the coupled channels calculation, varying from 0° to 6°.
Figure 12.
Complex energies of tetraquarks with in the coupled channels calculation, varying from 0° to 6°.
Figure 13.
Complex energies of tetraquarks with in the coupled channels calculation, varying from 0° to 6°.
Figure 13.
Complex energies of tetraquarks with in the coupled channels calculation, varying from 0° to 6°.
Figure 14.
Complex energies of tetraquarks with in the coupled channels calculation, varying from 0° to 6°.
Figure 14.
Complex energies of tetraquarks with in the coupled channels calculation, varying from 0° to 6°.
Figure 15.
Complex energies of tetraquarks with in the coupled channels calculation, varying from 0° to 6°.
Figure 15.
Complex energies of tetraquarks with in the coupled channels calculation, varying from 0° to 6°.
Figure 16.
Complex energies of tetraquarks with in the coupled channels calculation, varying from 0° to 6°.
Figure 16.
Complex energies of tetraquarks with in the coupled channels calculation, varying from 0° to 6°.
Figure 17.
Complex energies of tetraquarks with in the coupled channels calculation, varying from 0° to 6°.
Figure 17.
Complex energies of tetraquarks with in the coupled channels calculation, varying from 0° to 6°.
Figure 18.
Complex energies of tetraquarks with in the coupled channels calculation, varying from 0° to 6°.
Figure 18.
Complex energies of tetraquarks with in the coupled channels calculation, varying from 0° to 6°.
Figure 19.
Complex energies of fully-charm tetraquarks with in the coupled channels calculation, varying from 0° to 6°.
Figure 19.
Complex energies of fully-charm tetraquarks with in the coupled channels calculation, varying from 0° to 6°.
Figure 20.
Complex energies of fully-charm tetraquarks with in the coupled channels calculation, varying from 0° to 6°.
Figure 20.
Complex energies of fully-charm tetraquarks with in the coupled channels calculation, varying from 0° to 6°.
Figure 21.
Complex energies of fully-charm tetraquarks with in the coupled channels calculation, varying from 0° to 6°.
Figure 21.
Complex energies of fully-charm tetraquarks with in the coupled channels calculation, varying from 0° to 6°.
Figure 22.
Complex energies of fully-bottom tetraquarks with in the coupled channels calculation, varying from 0° to 6°.
Figure 22.
Complex energies of fully-bottom tetraquarks with in the coupled channels calculation, varying from 0° to 6°.
Figure 23.
Complex energies of fully-bottom tetraquarks with in the coupled channels calculation, varying from 0° to 6°.
Figure 23.
Complex energies of fully-bottom tetraquarks with in the coupled channels calculation, varying from 0° to 6°.
Figure 24.
Complex energies of fully-bottom tetraquarks with in the coupled channels calculation, varying from 0° to 6°.
Figure 24.
Complex energies of fully-bottom tetraquarks with in the coupled channels calculation, varying from 0° to 6°.
Figure 25.
(Top panel): Pentaquark’s complex energies of coupled-channels calculation with quantum numbers and for (green), 2 (black), 4 (red) and 6 (blue). (Bottom panel): Enlarged top panel, with real values of energy ranging from to .
Figure 25.
(Top panel): Pentaquark’s complex energies of coupled-channels calculation with quantum numbers and for (green), 2 (black), 4 (red) and 6 (blue). (Bottom panel): Enlarged top panel, with real values of energy ranging from to .
Figure 26.
(Top panel): Pentaquark’s complex energies of coupled-channels calculation with quantum numbers and for (green), 2 (black), 4 (red) and 6 (blue). (Bottom panel): Enlarged top panel, with real values of energy ranging from to .
Figure 26.
(Top panel): Pentaquark’s complex energies of coupled-channels calculation with quantum numbers and for (green), 2 (black), 4 (red) and 6 (blue). (Bottom panel): Enlarged top panel, with real values of energy ranging from to .
Figure 27.
Pentaquark’s complex energies of coupled-channels calculation with quantum numbers and for (green), 2 (black), 4 (red) and 6 (blue).
Figure 27.
Pentaquark’s complex energies of coupled-channels calculation with quantum numbers and for (green), 2 (black), 4 (red) and 6 (blue).
Figure 28.
(Top panel): Pentaquark’s complex energies of coupled-channels calculation with quantum numbers and for (green), 2 (black), 4 (red) and 6 (blue). (Middle panel): Enlarged top panel, with real values of energy ranging from to . (Bottom panel): Enlarged top panel, with real values of energy ranging from to .
Figure 28.
(Top panel): Pentaquark’s complex energies of coupled-channels calculation with quantum numbers and for (green), 2 (black), 4 (red) and 6 (blue). (Middle panel): Enlarged top panel, with real values of energy ranging from to . (Bottom panel): Enlarged top panel, with real values of energy ranging from to .
Figure 29.
(Top panel): Pentaquark’s complex energies of coupled-channels calculation with quantum numbers and for (green), 2 (black), 4 (red) and 6 (blue). (Bottom panel): Enlarged top panel, with real values of energy ranging from to .
Figure 29.
(Top panel): Pentaquark’s complex energies of coupled-channels calculation with quantum numbers and for (green), 2 (black), 4 (red) and 6 (blue). (Bottom panel): Enlarged top panel, with real values of energy ranging from to .
Figure 30.
Pentaquark’s complex energies of coupled-channels calculation with quantum numbers and for (green), 2 (black), 4 (red) and 6 (blue).
Figure 30.
Pentaquark’s complex energies of coupled-channels calculation with quantum numbers and for (green), 2 (black), 4 (red) and 6 (blue).
Table 1.
Chiral quark model parameters.
Table 1.
Chiral quark model parameters.
| Quark masses | (MeV) | 313 |
| (MeV) | 555 |
| (MeV) | 1752 |
| (MeV) | 5100 |
| Goldstone-bosons | (fm) | 4.20 |
| (fm) | 5.20 |
| 0.54 |
| −15 |
| Confinement | (MeV) | 430 |
| (fm | 0.70 |
| (MeV) | 181.10 |
| OGE | | 2.118 |
| (fm) | 0.113 |
| (MeV) | 36.976 |
| (MeV fm) | 28.170 |
Table 2.
Theoretical and experimental (in parentheses) masses of the ground states of selected mesons and baryons, in units of MeV.
Table 2.
Theoretical and experimental (in parentheses) masses of the ground states of selected mesons and baryons, in units of MeV.
| | | | D | | | |
| 149 (135) | 689 (548) | 772 (770) | 696 (783) | 1897 (1870) | 2017 (2007) | 1989 (1968) | 2115 (2112) |
| B | | | | | | | |
| 5278 (5280) | 5319 (5325) | 5355 (5366) | 5400 (5415) | 6276 (6276) | 6331 (-) | 2989 (2984) | 9454 (9398) |
| | | | | | | |
| 3097 (3097) | 9505 (9460) | | | | | | |
| N | | | | | | | |
| 744 (939) | 2099 (2286) | 2505 (2454) | 2549 (2518) | 3663 (3519) | 3717 (-) | 5626 (5619) | 5817 (5811) |
| | | | | | | |
| 5834 (5832) | | | | | | | |
Table 3.
Potential model parameters.
Table 3.
Potential model parameters.
| Quark masses | | 1290 |
| 4700 |
| Coulomb | | 0.4105 |
| Confinement | () | 0.2 |
| Spin-Spin | | 1.982 |
| 2.06 |
| 0.318 |
Table 4.
Theoretical and experimental masses of the S-wave mesons, unit in MeV.
Table 4.
Theoretical and experimental masses of the S-wave mesons, unit in MeV.
| State | | |
|---|
| 2968 | 2981 |
| 3655 | 3639 |
| 3102 | 3097 |
| 3720 | 3686 |
| 9401 | 9398 |
| 9961 | 9999 |
| 9463 | 9460 |
| 9981 | 10,023 |
Table 5.
Index of spin-wave functions from Equations (
51)–(61), their numbers are listed in the column according to each configuration, respectively.
Table 5.
Index of spin-wave functions from Equations (
51)–(61), their numbers are listed in the column according to each configuration, respectively.
| | Dimeson | Diquark-Antidiquark | | | | |
|---|
| 1 | 3 | | | | |
| 2 | 4 | | | | |
| | | 5 | 7 | 9 | 11 |
| | | 6 | 8 | 10 | 12 |
| 1 | 4 | | | | |
| 2 | 5 | | | | |
| 3 | 6 | | | | |
| | | 7 | 10 | 13 | 16 |
| | | 8 | 11 | 14 | 17 |
| | | 9 | 12 | 15 | 18 |
Table 6.
All possible channels for tetraquark systems.
Table 6.
All possible channels for tetraquark systems.
| Index | | |
|---|
| ; ; | Channel | ; ; | Channel |
|---|
| | | |
|---|
| 1 | | | | |
| | 2 | | | | |
| | 3 | | | | |
| | 4 | | | | |
| | 5 | | | | |
| | 6 | | | | |
| 1 | | | | |
| | 2 | | | | |
| | 3 | | | | |
| | 4 | | | | |
| | 5 | | | | |
| | 6 | | | | |
| 1 | | | | |
| | 2 | | | | |
| | 3 | | | | |
Table 7.
Lowest-lying states of double-charm tetraquarks with quantum numbers , unit in MeV.
Table 7.
Lowest-lying states of double-charm tetraquarks with quantum numbers , unit in MeV.
| Channel | Color | M | | |
|---|
| S | 3915 | 0 | 3877 |
| H | 4421 | | 4383 |
| | S+H | 3914 | | 3876 |
| | Percentage (S;H): 97.3%; 2.7% |
| S | 4034 | 0 | 4018 |
| H | 4390 | | 4374 |
| | S+H | 4033 | | 4017 |
| | Percentage (S;H): 95.5%; 4.5% |
| | 3778 | | |
| | 4220 | | |
| Mixed | | 3726 | | |
Table 8.
The distance, in fm, between any two quarks of the found tetraquark bound-states in coupled-channels calculation .
Table 8.
The distance, in fm, between any two quarks of the found tetraquark bound-states in coupled-channels calculation .
| | |
|---|
| 0.658 | 0.666 | 0.522 |
Table 9.
Component of each channel in coupled-channels calculation with , the numbers 1 and 8 of superscript are for singlet-color and hidden-color channel respectively.
Table 9.
Component of each channel in coupled-channels calculation with , the numbers 1 and 8 of superscript are for singlet-color and hidden-color channel respectively.
| | | |
| 25.8% | 15.4% | 10.7% | 11.2% |
| | | |
| 36.7% | 0.2% | | |
Table 10.
All possible channels for tetraquark systems.
Table 10.
All possible channels for tetraquark systems.
| Index | | |
|---|
| ; ; | Channel | ; ; | Channel |
|---|
| | | |
|---|
| 1 | | | | |
| | 2 | | | | |
| | 3 | | | | |
| | 4 | | | | |
| | 5 | | | | |
| | 6 | | | | |
| 1 | | | | |
| | 2 | | | | |
| | 3 | | | | |
| | 4 | | | | |
| | 5 | | | | |
| | 6 | | | | |
| 1 | | | | |
| | 2 | | | | |
| | 3 | | | | |
Table 11.
Lowest-lying states of double-bottom tetraquarks with quantum numbers , unit in MeV.
Table 11.
Lowest-lying states of double-bottom tetraquarks with quantum numbers , unit in MeV.
| Channel | Color | M | | |
|---|
| S | 10,585 | | 10,592 |
| H | 10,987 | | 10,994 |
| | S + H | 10,562 | | 10,569 |
| | Percentage (S;H): 83.0%; 17.0% |
| S | 10,627 | | 10,639 |
| H | 10,974 | | 10,986 |
| | S + H | 10,601 | | 10,613 |
| | Percentage (S;H): 79.6%; 20.4% |
| | 10,261 | | |
| | 10,787 | | |
| Mixed | | 10,238 1st | | |
| | | 10,524 2nd | | |
Table 12.
Component of each channel in coupled-channels calculation with , the numbers 1 and 8 of superscript are for singlet-color and hidden-color channel respectively.
Table 12.
Component of each channel in coupled-channels calculation with , the numbers 1 and 8 of superscript are for singlet-color and hidden-color channel respectively.
| | | | |
| 1st | 20.7% | 17.9% | 9.3% |
| 2nd | 25.6% | 14.8% | 9.5% |
| | | | |
| 1st | 9.4% | 42.6% | 0.1% |
| 2nd | 9.1% | 40.2% | 0.8% |
Table 13.
The distance, in fm, between any two quarks of the found tetraquark bound-states in coupled-channels calculation, .
Table 13.
The distance, in fm, between any two quarks of the found tetraquark bound-states in coupled-channels calculation, .
| | | | |
|---|
| 1st | 0.604 | 0.608 | 0.328 |
| 2nd | 0.830 | 0.734 | 0.711 |
Table 14.
All possible channels for tetraquark systems. For a brief purpose, only the structures are listed and the corresponding ones are absent in . However, all these configurations are still employed in constructing the wave functions of 4-quark systems.
Table 14.
All possible channels for tetraquark systems. For a brief purpose, only the structures are listed and the corresponding ones are absent in . However, all these configurations are still employed in constructing the wave functions of 4-quark systems.
| Index | | |
|---|
| ; ; | Channel | ; ; | Channel |
|---|
| | | |
|---|
| 1 | | | | |
| | 2 | | | | |
| | 3 | | | | |
| | 4 | | | | |
| | 5 | | | | |
| | 6 | | | | |
| 1 | | | | |
| | 2 | | | | |
| | 3 | | | | |
| | 4 | | | | |
| | 5 | | | | |
| | 6 | | | | |
| | 7 | | | | |
| | 8 | | | | |
| | 9 | | | | |
| 1 | | | | |
| | 2 | | | | |
| | 3 | | | | |
Table 15.
Lowest-lying states of charm-bottom tetraquarks with quantum numbers , unit in MeV.
Table 15.
Lowest-lying states of charm-bottom tetraquarks with quantum numbers , unit in MeV.
| Channel | Color | M | | |
|---|
| S | 7172 | | 7143 |
| H | 7685 | | 7656 |
| | S+H | 7171 | | 7142 |
| | Percentage (S;H): 96.4%; 3.6% |
| S | 7327 | | 7325 |
| H | 7586 | | 7584 |
| | S+H | 7297 | | 7295 |
| | Percentage (S;H): 87.8%; 12.2% |
| | 7028 | | |
| | 7482 | | |
| Mixed | | 6980 | | |
Table 16.
Lowest-lying states of charm-bottom tetraquarks with quantum numbers , unit in MeV.
Table 16.
Lowest-lying states of charm-bottom tetraquarks with quantum numbers , unit in MeV.
| Channel | Color | M | | |
|---|
| S | 7214 | | 7190 |
| H | 7694 | | 7670 |
| | S+H | 7213 | | 7189 |
| | Percentage (S;H): 96.8%; 3.2% |
| S | 7293 | | 7286 |
| H | 7707 | | 7700 |
| | S+H | 7292 | | 7285 |
| | Percentage (S;H): 96.8%; 3.2% |
| S | 7334 | | 7332 |
| H | 7691 | | 7688 |
| | S+H | 7326 | | 7324 |
| | Percentage (S;H): 89.3%; 10.7% |
| | 7039 | | |
| | 7531 | | |
| | 7507 | | |
| Mixed | | 6997 | | |
Table 17.
Lowest-lying states of charm-bottom tetraquarks with quantum numbers , unit in MeV.
Table 17.
Lowest-lying states of charm-bottom tetraquarks with quantum numbers , unit in MeV.
| Channel | Color | M | | |
|---|
| S | 7334 | | 7332 |
| H | 7720 | | 7718 |
| | S+H | 7334 | | 7332 |
| | Percentage (S;H): 99.8%; 0.2% |
| | 7552 | | |
| Mixed | | 7333 | | |
Table 18.
Component of each channel in coupled-channels calculation, the numbers 1 and 8 of superscript are for singlet-color and hidden-color channel respectively, .
Table 18.
Component of each channel in coupled-channels calculation, the numbers 1 and 8 of superscript are for singlet-color and hidden-color channel respectively, .
| | | | |
| 26.4% | 21.5% | 1.6% | 1.9% |
| | | | | |
| | 48.5% | 0.1% | | |
| | | | |
| | 20.2% | 11.6% | 16.8% | 1.4% |
| | | | | |
| | 1.3% | 1.8% | 46.4% | 0.1% |
| | | | | |
| | 0.4% | | | |
| | | | |
| | 98.6% | 0.3% | 1.1% | |
Table 19.
The distance, in fm, between any two quarks of the found tetraquark bound-states in coupled-channels calculation, .
Table 19.
The distance, in fm, between any two quarks of the found tetraquark bound-states in coupled-channels calculation, .
| | | | |
|---|
| 0.635 | 0.653 | 0.610 | 0.428 |
| 0.632 | 0.661 | 0.616 | 0.434 |
| 2.248 | 1.612 | 1.597 | 2.102 |
Table 20.
Theoretical and experimental masses of and mesons, their theoretical sizes are also calculated.
Table 20.
Theoretical and experimental masses of and mesons, their theoretical sizes are also calculated.
| Meson | nL | The. | Exp. |
|---|
| | 1989 MeV; fm | 1969 MeV |
| 2703 MeV; fm | - |
| | 2116 MeV; fm | 2112 MeV |
| 2767 MeV; fm | - |
| | 5355 MeV; fm | 5367 MeV |
| 6017 MeV; fm | - |
| | 5400 MeV; fm | 5415 MeV |
| 6042 MeV; fm | - |
Table 21.
The lowest-lying eigen-energies of tetraquarks with in the real range calculation. (unit: MeV).
Table 21.
The lowest-lying eigen-energies of tetraquarks with in the real range calculation. (unit: MeV).
| Channel | Index | ; ; | | Mixed |
|---|
|
|---|
| 1 (S) | | 3978 | |
| 2 (S) | | 4232 | 3978 |
| 3 (H) | | 4619 | |
| 4 (H) | | 4636 | 4377 |
| 5 | | 4433 | |
| 6 | | 4413 | 4379 |
| 7 | | 4802 | |
| 8 | | 4369 | |
| 9 | | 4698 | |
| 10 | | 4211 | 4201 |
| 11 | | 4343 | |
| 12 | | 4753 | |
| 13 | | 4166 | |
| 14 | | 4838 | 4158 |
| 15 | | 4414 | |
| 16 | | 4427 | 4373 |
| 17 | | 4413 | |
| 18 | | 4439 | 4379 |
| All of the above channels: | 3978 | |
Table 22.
The lowest-lying eigen-energies of tetraquarks with in the real range calculation. (unit: MeV).
Table 22.
The lowest-lying eigen-energies of tetraquarks with in the real range calculation. (unit: MeV).
| Channel | Index | ; ; | | Mixed |
|---|
|
|---|
| 1(S) | | 4105 | |
| 2(S) | | 4232 | 4105 |
| 3(H) | | 4401 | |
| 4(H) | | 4607 | 4400 |
| 5 | | 4424 | 4424 |
| 6 | | 4537 | |
| 7 | | 4536 | |
| 8 | | 4528 | |
| 9 | | 4440 | |
| 10 | | 4445 | |
| 11 | | 4371 | 4305 |
| 12 | | 4417 | |
| 13 | | 4419 | |
| 14 | | 4326 | |
| 15 | | 4699 | |
| 16 | | 4787 | |
| 17 | | 4802 | 4266 |
| 18 | | 4442 | |
| 19 | | 4443 | |
| 20 | | 5013 | 4424 |
| 21 | | 4427 | |
| 22 | | 4426 | |
| 23 | | 4953 | 4423 |
| All of the above channels: | 4105 | |
Table 23.
The lowest-lying eigen-energies of tetraquarks with in the real range calculation. (unit: MeV).
Table 23.
The lowest-lying eigen-energies of tetraquarks with in the real range calculation. (unit: MeV).
| Channel | Index | ; ; | | Mixed |
|---|
|
|---|
| 1 (S) | | 4232 | 4232 |
| 2 (H) | | 4432 | 4432 |
| 3 | | 4446 | 4446 |
| 4 | | 4522 | |
| 5 | | 4385 | 4381 |
| 6 | | 4355 | |
| 7 | | 4666 | 4354 |
| 8 | | 4448 | 4448 |
| 9 | | 4446 | 4446 |
| All of the above channels: | 4232 | |
Table 24.
The lowest-lying eigen-energies of tetraquarks with in the real range calculation. (unit: MeV).
Table 24.
The lowest-lying eigen-energies of tetraquarks with in the real range calculation. (unit: MeV).
| Channel | Index | ; ; | | Mixed |
|---|
|
|---|
| (10,734) | 1 (S) | | 10,710 | |
| (10,830) | 2(S) | | 10,800 | 10,710 |
| 3 (H) | | 11,184 | |
| 4 (H) | | 11,205 | 10,943 |
| 5 | | 10,967 | |
| 6 | | 10,901 | 10,896 |
| 7 | | 11,445 | |
| 8 | | 10,928 | |
| 9 | | 11,259 | |
| 10 | | 10,863 | 10,843 |
| 11 | | 10,877 | |
| 12 | | 11,445 | |
| 13 | | 10,815 | |
| 14 | | 11,441 | 10,802 |
| 15 | | 10,902 | |
| 16 | | 10,960 | 10,895 |
| 17 | | 10,901 | |
| 18 | | 10,980 | 10,897 |
| All of the above channels: | 10,710 | |
Table 25.
The lowest-lying eigen-energies of tetraquarks with in the real range calculation. (unit: MeV).
Table 25.
The lowest-lying eigen-energies of tetraquarks with in the real range calculation. (unit: MeV).
| Channel | Index | ; ; | | Mixed |
|---|
|
|---|
| (10,782) | 1 (S) | | 10,755 | |
| (10,830) | 2 (S) | | 10,800 | 10,755 |
| 3 (H) | | 10,949 | |
| 4 (H) | | 11,185 | 10,949 |
| 5 | | 10,906 | 10,906 |
| 6 | | 11,041 | |
| 7 | | 11,048 | |
| 8 | | 11,038 | |
| 9 | | 10,936 | |
| 10 | | 10,949 | |
| 11 | | 10,917 | 10,870 |
| 12 | | 10,911 | |
| 13 | | 10,914 | |
| 14 | | 10,879 | |
| 15 | | 11,216 | |
| 16 | | 11,483 | |
| 17 | | 11,373 | 10,840 |
| 18 | | 10,928 | |
| 19 | | 10,929 | |
| 20 | | 11,557 | 10,907 |
| 21 | | 10,911 | |
| 22 | | 10,908 | |
| 23 | | 11,458 | 10,906 |
| All of the above channels: | 10,755 | |
Table 26.
The lowest-lying eigen-energies of tetraquarks with in the real range calculation. (unit: MeV).
Table 26.
The lowest-lying eigen-energies of tetraquarks with in the real range calculation. (unit: MeV).
| Channel | Index | ; ; | | Mixed |
|---|
|
|---|
| 1(S) | | | |
| 2(H) | | | |
| 3 | | | |
| 4 | | | |
| 5 | | | |
| 6 | | | |
| 7 | | | |
| 8 | | | |
| 9 | | | |
| All of the above channels: | | |
Table 27.
The lowest-lying eigen-energies of tetraquarks with in the real range calculation. (unit: MeV).
Table 27.
The lowest-lying eigen-energies of tetraquarks with in the real range calculation. (unit: MeV).
| Channel | Index | ; ; | | Mixed |
|---|
|
|---|
| 1(S) | | 7344 | |
| 2(S) | | 7516 | 7344 |
| 3(H) | | 7910 | |
| 4(H) | | 7927 | 7678 |
| 5 | | 7726 | |
| 6 | | 7675 | 7662 |
| 7 | | 8171 | |
| 8 | | 8274 | |
| 9 | | 8369 | |
| 10 | | 8145 | 7613 |
| 11 | | 7896 | |
| 12 | | 8266 | |
| 13 | | 7758 | |
| 14 | | 8282 | 7629 |
| 15 | | 8647 | |
| 16 | | 8181 | |
| 17 | | 8321 | |
| 18 | | 8675 | 8010 |
| 19 | | 8199 | |
| 20 | | 8359 | 8063 |
| All of the above channels: | 7344 | |
Table 28.
The lowest-lying eigen-energies of tetraquarks with in the real range calculation. (unit: MeV).
Table 28.
The lowest-lying eigen-energies of tetraquarks with in the real range calculation. (unit: MeV).
| Channel | Index | ; ; | | Mixed |
|---|
|
|---|
| 1(S) | | 7389 | |
| 2(S) | | 7471 | |
| 3(S) | | 7516 | 7389 |
| 4(H) | | 7900 | |
| 5(H) | | 7891 | |
| 6(H) | | 7920 | 7684 |
| 7 | | 7683 | |
| 8 | | 7680 | |
| 9 | | 7725 | 7671 |
| 10 | | 7796 | |
| 11 | | 8172 | |
| 12 | | 8009 | |
| 13 | | 7695 | |
| 14 | | 7760 | |
| 15 | | 7634 | 7620 |
| 16 | | 7607 | |
| 17 | | 7621 | |
| 18 | | 7510 | |
| 19 | | 8137 | |
| 20 | | 8211 | |
| 21 | | 8209 | 7505 |
| 22 | | 7705 | |
| 23 | | 7706 | |
| 24 | | 7682 | |
| 25 | | 7734 | |
| 26 | | 7733 | |
| 27 | | 8298 | 7666 |
| 28 | | 7687 | |
| 29 | | 7677 | |
| 30 | | 7771 | 7670 |
| All of the above channels: | 7389 | |
Table 29.
The lowest-lying eigen-energies of tetraquarks with in the real range calculation. (unit: MeV).
Table 29.
The lowest-lying eigen-energies of tetraquarks with in the real range calculation. (unit: MeV).
| Channel | Index | ; ; | | Mixed |
|---|
|
|---|
| 1(S) | | 7516 | 7516 |
| 2(H) | | 7712 | 7712 |
| 3 | | 7698 | 7698 |
| 4 | | 7804 | |
| 5 | | 7705 | 7704 |
| 6 | | 7624 | |
| 7 | | 8205 | 7622 |
| 8 | | 8311 | |
| 9 | | 7701 | 7696 |
| 10 | | 7697 | 7697 |
| All of the above channels: | 7516 | |
Table 30.
Comparison of theoretical masses on the iso-scalar double-heavy tetraquark in bound states by different predictions. (unit: MeV).
Table 30.
Comparison of theoretical masses on the iso-scalar double-heavy tetraquark in bound states by different predictions. (unit: MeV).
| | | | | | | | | | |
|---|
| | | | |
| This work | - | 3726 | - | 6980 | 6997 | 7333 | - | 10,238, 10,524 | - |
| Ref. [33] | - | 3935 | - | 7239 | 7246 | - | - | 10,502 | - |
| Ref. [41] | - | 3931 | - | 7206 | 7244 | - | - | 10,525 | - |
| Ref. [44] | - | 3876 | - | - | - | - | - | 10,504 | - |
| Ref. [43] | - | - | - | - | - | - | - | 10,558 | - |
| Ref. [51] | - | 3764 | - | - | - | - | - | 10,261 | - |
| Ref. [29] | - | 3927 | - | - | - | - | - | 10,426 | - |
| Ref. [45] | - | 3905 | - | - | - | - | - | - | - |
Table 31.
Possible resonance states of fully-charm tetraquarks with quantum numbers , unit in MeV.
Table 31.
Possible resonance states of fully-charm tetraquarks with quantum numbers , unit in MeV.
| Channel | Index | ; ; | |
|---|
|
|---|
| 1 | | 6536 |
| 2 | | 6536 |
| 3 | | 6657 |
| 4 | | 6657 |
| 5 | | 6683 |
| 6 | | 6469 |
| Mixed | | | 64231st |
| | | | 66502nd |
Table 32.
Component of each channel in the coupled-channels calculation of fully-charm resonance states with .
Table 32.
Component of each channel in the coupled-channels calculation of fully-charm resonance states with .
| | | | | |
| 31.1% | 17.8% | 23.7% | 21.0% |
| 14.0% | 17.0% | 21.7% | 26.1% |
| | | | | |
| 3.0% | 3.4% | | |
| 21.1% | 0.1% | | |
Table 33.
The distances, between any two quarks of the found fully-charm resonance states with in coupled-channels calculation, unit in fm.
Table 33.
The distances, between any two quarks of the found fully-charm resonance states with in coupled-channels calculation, unit in fm.
| | | | |
|---|
| 1st | 0.325 | 0.342 | 0.342 |
| 2nd | 0.344 | 0.353 | 0.353 |
Table 34.
Possible resonance states of fully-charm tetraquarks with quantum numbers , unit in MeV.
Table 34.
Possible resonance states of fully-charm tetraquarks with quantum numbers , unit in MeV.
| Channel | Index | ; ; | |
|---|
| 1 | | 6671 |
| 2 | | 6671 |
| 3 | | 6674 |
| Mixed | | | 6627 |
| Component (1; 2; 3): 55.5%; 34.7%; 9.8% |
Table 35.
The distances, between any two quarks of the found fully-charm resonance states with in coupled-channels calculation, unit in fm.
Table 35.
The distances, between any two quarks of the found fully-charm resonance states with in coupled-channels calculation, unit in fm.
| | |
|---|
| 0.342 | 0.357 | 0.357 |
Table 36.
Possible resonance states of fully-charm tetraquarks with quantum numbers , unit in MeV.
Table 36.
Possible resonance states of fully-charm tetraquarks with quantum numbers , unit in MeV.
| Channel | Index | ; ; | |
|---|
| 1 | | 7030 |
| 2 | | 7030 |
| 3 | | 7026 |
| Mixed | | | 7014 |
| Component (1; 2: 3): 52.8%; 33.0%; 14.2% |
Table 37.
The distances, between any two quarks of the found fully-charm resonance states with in coupled-channels calculation, unit in fm.
Table 37.
The distances, between any two quarks of the found fully-charm resonance states with in coupled-channels calculation, unit in fm.
| | |
|---|
| 0.375 | 0.389 | 0.389 |
Table 38.
Possible bound and resonance states of fully-bottom tetraquarks with quantum numbers , unit in MeV.
Table 38.
Possible bound and resonance states of fully-bottom tetraquarks with quantum numbers , unit in MeV.
| Channel | Index | ; ; | | |
|---|
| 1 | | | |
| | | | | |
| 2 | | | |
| | | | | |
| 3 | | | |
| | | | | |
| 4 | | | |
| | | | | |
| 5 | | | |
| | | | | |
| 6 | | | |
| | | | | |
| Mixed | | | | |
| | | | | |
| | | | | |
Table 39.
Component of each channel in the coupled-channels calculation of fully-bottom bound and resonance states with .
Table 39.
Component of each channel in the coupled-channels calculation of fully-bottom bound and resonance states with .
| | | | | |
| 1st | 27.3% | 19.4% | 21.6% | 20.5% |
| 2nd | 13.5% | 32.8% | 14.0% | 29.8% |
| 3rd | 20.6% | 15.8% | 30.0% | 30.1% |
| | | | | |
| 1st | 0.9% | 10.3% | | |
| 2nd | 9.7% | 0.2% | | |
| 3rd | 3.5% | 0.0% | | |
Table 40.
The distances, between any two quarks of the found fully-bottom bound and resonance states with in coupled-channels calculation, unit in fm.
Table 40.
The distances, between any two quarks of the found fully-bottom bound and resonance states with in coupled-channels calculation, unit in fm.
| | | | |
|---|
| 1st | 0.160 | 0.166 | 0.166 |
| 2nd | 0.163 | 0.168 | 0.168 |
| 3rd | 0.246 | 0.292 | 0.292 |
Table 41.
Possible bound and resonance states of fully-bottom tetraquarks with quantum numbers , unit in MeV.
Table 41.
Possible bound and resonance states of fully-bottom tetraquarks with quantum numbers , unit in MeV.
| Channel | Index | ; ; | | |
|---|
| 1 | | | |
| | | | | |
| 2 | | | |
| | | | | |
| 3 | | | |
| | | | | |
| Mixed | | | | |
| | | | | |
| | | | | |
| Component : 50.9%; 31.9%; 17.2% |
| Component : 48.6%; 51.4%; 0.0% |
| Component : 28.1%; 17.5%; 54.4% |
Table 42.
The distances, between any two quarks of the found fully-bottom bound and resonance states with in coupled-channels calculation, unit in fm.
Table 42.
The distances, between any two quarks of the found fully-bottom bound and resonance states with in coupled-channels calculation, unit in fm.
| | | | |
|---|
| 1st | 0.163 | 0.169 | 0.169 |
| 2nd | 0.248 | 0.295 | 0.295 |
| 3rd | 0.279 | 0.265 | 0.265 |
Table 43.
Possible bound and resonance states of fully-bottom tetraquarks with quantum numbers , unit in MeV.
Table 43.
Possible bound and resonance states of fully-bottom tetraquarks with quantum numbers , unit in MeV.
| Channel | Index | ; ; | | |
|---|
| 1 | | | |
| | | | | |
| 2 | | | |
| | | | | |
| 3 | | | |
| | | | | |
| Mixed | | | | |
| | | | | |
| | | | | |
| Component : 53.2%; 33.2%; 13.6% |
| Component : 48.8%; 51.2%; 0.0% |
| Component : 28.3%; 17.7%; 54.0% |
Table 44.
The distances, between any two quarks of the found fully-bottom bound and resonance states with in coupled-channels calculation, unit in fm.
Table 44.
The distances, between any two quarks of the found fully-bottom bound and resonance states with in coupled-channels calculation, unit in fm.
| | | | |
|---|
| 0.168 | 0.174 | 0.174 |
| 0.254 | 0.302 | 0.302 |
| 0.284 | 0.268 | 0.268 |
Table 45.
Comparison of theoretical masses for the fully-heavy tetraquark resonance states by different predictions. (unit: MeV).
Table 45.
Comparison of theoretical masses for the fully-heavy tetraquark resonance states by different predictions. (unit: MeV).
| | | | | | | |
|---|
| | | |
| This work | 6449, 6659 | 6657 | 7022 | 19,005, 19,049 | 19,067 | 19,189 |
| Ref. [76] | 5960, 6198 | 6009, 6246 | 6100, 6323 | 18,723, 18,754 | 18,738, 18,768 | 18,768, 18,797 |
| Ref. [66] | 5883 | 6120 | 6246 | 18,748 | 18,828 | 18,900 |
| Ref. [67] | 5966 | 6051 | 6223 | 18,754 | 18,808 | 18,916 |
| Ref. [91] | 7016 | 6899 | 6956 | 20,275 | 20,212 | 20,243 |
| Ref. [93] | 6487 | 6500 | 6524 | 19,322 | 19,329 | 19,341 |
| Ref. [94] | 6420, 6436 | 6425, 6450 | 6432, 6479 | 19,246, 19,297 | 19,247, 19,311 | 19,249, 19,325 |
Table 46.
The lowest eigen-energies of the system with (unit: MeV). The percentages of color-singlet (S) and hidden-color (H) channels are also given.
Table 46.
The lowest eigen-energies of the system with (unit: MeV). The percentages of color-singlet (S) and hidden-color (H) channels are also given.
| Channel | E | | | | E’ |
|---|
| 3745 | 3745 | 0 | 3919() | 3919 |
| 4714 | | | | |
| color-singlet+hidden color | 3745 | |
| 3841 | 3841 | 0 | 4036() | 4036 |
| 4964 | | | | |
| color-singlet+hidden color | 3841 | |
| 3996 | 3996 | 0 | 4151() | 4151 |
| 4663 | | | | |
| color-singlet+hidden color | 3996 | |
| 4115 | 4115 | 0 | 4293() | 4293 |
| 4599 | | | | |
| color-singlet+hidden color | 4115 | |
| 4398 | 4402 | | 4320() | 4316 |
| 4835 | | | | |
| color-singlet+hidden color | 4394 | 4402 | | 4320 | 4312 |
| | | percentage(S;H): 91.0%; 7.0% |
| 4518 | 4520 | | 4462() | 4460 |
| 4728 | | | | |
| color-singlet+hidden color | 4479 | 4520 | | 4462 | 4421 |
| | | percentage(S;H): 67.4%; 32.6% |
| 4563 | 4566 | | 4527() | 4524 |
| 4476 | | | | |
| color-singlet+hidden color | 4461 | 4566 | | 4527 | 4422 |
| | | percentage(S;H): 23.0%; 77.0% |
| mixed (only color singlet) | 3745 | | | | |
| mixed (color singlet+hidden color) | 3745 | | | | |
Table 47.
Distances between any two quarks (unit: fm).
Table 47.
Distances between any two quarks (unit: fm).
| Channel | | | | |
|---|
| () | 0.8 | 0.7 | 2.1 | 2.1 |
| | | 1.0 | 0.8 | 0.8 | 0.4 |
| | () | 0.8 | 0.7 | 2.2 | 2.1 |
| | | 0.9 | 0.8 | 0.8 | 0.4 |
| | () | 0.9 | 0.8 | 2.1 | 2.0 |
| | | 0.9 | 0.8 | 0.8 | 0.4 |
| () | 0.8 | 0.7 | 2.4 | 2.3 |
| | | 1.1 | 0.9 | 0.9 | 0.5 |
| | () | 0.9 | 0.8 | 2.2 | 2.2 |
| | | 1.0 | 0.9 | 0.9 | 0.5 |
| | () | 0.9 | 0.8 | 2.6 | 2.4 |
| | | 0.9 | 0.9 | 0.8 | 0.4 |
| () | 0.9 | 0.8 | 2.4 | 2.3 |
| | | 1.3 | 1.4 | 1.3 | 0.8 |
Table 48.
The lowest eigen-energies of the system with and (unit: MeV).
Table 48.
The lowest eigen-energies of the system with and (unit: MeV).
| Channel | E | | | | E’ |
|---|
|
| 3841 | 3841 | 0 | 4036() | 4036 |
| 4722 | | | | |
| color-singlet+hidden color | 3841 | |
| 4115 | 4115 | 0 | 4293() | 4293 |
| 4680 | | | | |
| color-singlet+hidden color | 4115 | |
| 4518 | 4520 | | 4462() | 4460 |
| 4961 | | | | |
| color-singlet+hidden color | 4517 | 4520 | | 4462 | 4459 |
| | | percentage(S;H): 96.3%; 3.7% |
| 4444 | 4447 | | 4385() | 4382 |
| 4754 | | | | |
| color-singlet+hidden color | 4432 | 4447 | | 4385 | 4370 |
| | | percentage(S;H): 82.6%; 17.4% |
| 4564 | 4566 | | 4527() | 4525 |
| 4623 | | | | |
| color-singlet+hidden color | 4549 | 4566 | | 4527 | 4510 |
| | | percentage(S;H): 61.1%; 38.9% |
| mixed (only color-singlet) | 3841 | | | | |
| mixed (color-singlet+hidden color) | 3841 | | | | |
|
| 4563 | 4566 | | 4527() | 4524 |
| 5002 | | | | |
| color-singlet+hidden color | 4477 | 4566 | | 4527 | 4438 |
| | | percentage(S;H): 66.2%; 33.8% |
Table 49.
Comparison of theoretical masses on the hidden-charm pentaquark systems by different predictions, the predicted masses and states are summarized in each column, respectively. (unit: MeV).
Table 49.
Comparison of theoretical masses on the hidden-charm pentaquark systems by different predictions, the predicted masses and states are summarized in each column, respectively. (unit: MeV).
| | | | |
|---|
| This work | | | |
| | | | |
| | | | |
| | | | |
| Ref. [125] | | | |
| | | | |
| | | | |
| Ref. [126] | | | - |
| | | | |
| | | | |
| Ref. [128] | - | | - |
| | | | |
| Ref. [136] | | | |
| | | | |
| | | | |
| Ref. [137] | | | - |
| | | | |
| Ref. [146] | | | - |
| | | | |
| Ref. [145] | | | |
| | | | |
| | | | |
Table 50.
All allowed channels for hidden-bottom pentaquark systems with negative parity.
Table 50.
All allowed channels for hidden-bottom pentaquark systems with negative parity.
| | | | |
|---|
| Index | ; ; | Channel | ; ; | Channel |
| | | | | | |
| 1 | | | | |
| | 2 | | | | |
| | 3 | | | | |
| | 4 | | | | |
| | 5 | | | | |
| | 6 | | | | |
| | 7 | | | | |
| | 8 | | | | |
| | 9 | | | | |
| | 10 | | | | |
| | 11 | | | | |
| | 12 | | | | |
| | 13 | | | | |
| | 14 | | | | |
| 1 | | | | |
| | 2 | | | | |
| | 3 | | | | |
| | 4 | | | | |
| | 5 | | | | |
| | 6 | | | | |
| | 7 | | | | |
| | 8 | | | | |
| | 9 | | | | |
| | 10 | | | | |
| 1 | | | | |
| | 2 | | | | |
| | 3 | | | | |
| | 4 | | | | |
Table 51.
Lowest-lying states of hidden-bottom pentaquarks with quantum numbers , unit in MeV. The baryon-meson channels that do not appear here have been also considered in the computation but no bound states were found.
Table 51.
Lowest-lying states of hidden-bottom pentaquarks with quantum numbers , unit in MeV. The baryon-meson channels that do not appear here have been also considered in the computation but no bound states were found.
| Channel | Color | M | | M’ |
|---|
| S | | | |
| H | | | |
| | S+H | | | |
| | Percentage (S;H): 98.5%; 1.5% |
| S | | | |
| H | | | |
| | S+H | | | |
| | Percentage (S;H): 57.9%; 42.1% |
| S | | | |
| H | | | |
| | S+H | | | |
| | Percentage (S;H): 15.8%; 84.2% |
Table 52.
Lowest-lying states of hidden-bottom pentaquarks with quantum numbers , unit in MeV. The baryon-meson channels that do not appear here have been also considered in the computation but no bound states were found.
Table 52.
Lowest-lying states of hidden-bottom pentaquarks with quantum numbers , unit in MeV. The baryon-meson channels that do not appear here have been also considered in the computation but no bound states were found.
| Channel | Color | M | | M’ |
|---|
| S | | | |
| H | | | |
| | S+H | | | |
| | Percentage (S;H): 99.6%; 0.4% |
| S | | | |
| H | | | |
| | S+H | | | |
| | Percentage (S;H): 55.5%; 44.5% |
| S | | | |
| H | | | |
| | S+H | | | |
| | Percentage (S;H): 22.2%; 77.8% |
Table 53.
Lowest-lying states of hidden-bottom pentaquarks with quantum numbers , unit in MeV. The baryon-meson channels that do not appear here have been also considered in the computation but no bound states were found.
Table 53.
Lowest-lying states of hidden-bottom pentaquarks with quantum numbers , unit in MeV. The baryon-meson channels that do not appear here have been also considered in the computation but no bound states were found.
| Channel | Color | M | | M’ |
|---|
| S | | | |
| H | | | |
| | S+H | | | |
| | Percentage (S;H): 99.6%; 0.4% |
Table 54.
Lowest-lying states of hidden-bottom pentaquarks with quantum numbers , unit in MeV. The baryon-meson channels that do not appear here have been also considered in the computation but no bound states were found.
Table 54.
Lowest-lying states of hidden-bottom pentaquarks with quantum numbers , unit in MeV. The baryon-meson channels that do not appear here have been also considered in the computation but no bound states were found.
| Channel | Color | M | | M’ |
|---|
| S | | 0 | |
| H | | | |
| | S+H | | | |
| | Percentage (S;H): 64.7%; 35.3% |
| S | | 0 | |
| H | | | |
| | S+H | | | |
| | Percentage (S;H): 18.4%; 81.6% |
| S | | 0 | |
| H | | | |
| | S+H | | | |
| | Percentage (S;H): 15.7%; 84.3% |
Table 55.
Lowest-lying states of hidden-bottom pentaquarks with quantum numbers , unit in MeV. The baryon-meson channels that do not appear here have been also considered in the computation but no bound states were found.
Table 55.
Lowest-lying states of hidden-bottom pentaquarks with quantum numbers , unit in MeV. The baryon-meson channels that do not appear here have been also considered in the computation but no bound states were found.
| Channel | Color | M | | M’ |
|---|
| S | | | |
| H | | | |
| | S+H | | | |
| | Percentage (S;H): 19.9%; 80.1% |
Table 56.
The distance, in fm, between any two quarks of the found pentaquark bound-states.
Table 56.
The distance, in fm, between any two quarks of the found pentaquark bound-states.
| Channel | Mixing | | | | |
|---|
| | S | 1.17 | 0.87 | 1.02 | 1.00 |
| | | S+H | 1.13 | 0.84 | 0.98 | 0.94 |
| | | S | 1.09 | 0.81 | 0.92 | 0.82 |
| | | S+H | 0.94 | 0.70 | 0.71 | 0.34 |
| | | S | 1.06 | 0.79 | 0.88 | 0.75 |
| | | S+H | 0.91 | 0.71 | 0.70 | 0.24 |
| | S | 1.23 | 0.90 | 1.09 | 1.09 |
| | | S+H | 1.21 | 0.90 | 1.07 | 1.07 |
| | | S | 1.18 | 0.88 | 1.04 | 1.01 |
| | | S+H | 0.98 | 0.74 | 0.74 | 0.34 |
| | | S | 1.17 | 0.87 | 1.02 | 0.97 |
| | | S+H | 0.95 | 0.72 | 0.72 | 0.25 |
| | S | 1.25 | 0.92 | 1.11 | 1.13 |
| | | S+H | 1.25 | 0.92 | 1.11 | 1.11 |
| | S+H | 1.02 | 0.78 | 0.77 | 0.27 |
| | | S+H | 1.02 | 0.84 | 0.82 | 0.26 |
| | | S+H | 1.05 | 0.83 | 0.81 | 0.26 |
| | S | 1.03 | 0.86 | 0.86 | 0.29 |
| | | S+H | 1.00 | 0.86 | 0.84 | 0.26 |
Table 57.
Comparison of theoretical masses on the hidden-bottom pentaquark systems by different predictions, the predicted masses and states are summarized in each column, respectively. (unit: MeV).
Table 57.
Comparison of theoretical masses on the hidden-bottom pentaquark systems by different predictions, the predicted masses and states are summarized in each column, respectively. (unit: MeV).
| | | | | | | |
|---|
| This work | | | | - | | |
| | | | | | | |
| | | | | | | |
| Ref. [125] | | | | - | - | - |
| | | | | | | |
| | | | | | | |
| Ref. [126] | | | - | - | - | - |
| | | | | | | |
| | | | | | | |
| Ref. [152] | | | - | - | - | - |
| | | | | | | |
| Ref. [138] | | | | - | - | - |
| | | | | | | |
| | | | | | | |
| Ref. [193] | | | | - | - | - |
| | | | | | | |
| | | | | | | |
Table 58.
All possible channels for open-charm pentaquark systems with .
Table 58.
All possible channels for open-charm pentaquark systems with .
| Index | | |
|---|
| ; ; ; | Channel | ; ; ; | Channel |
|---|
| | | |
|---|
| 1 | | | | |
| | 2 | | | | |
| | 3 | | | | |
| | 4 | | | | |
| | 5 | | | | |
| | 6 | | | | |
| | 7 | | | | |
| | 8 | | | | |
| | 9 | | | | |
| | 10 | | | | |
| | 11 | | | | |
| | 12 | | | | |
| | 13 | | | | |
| | 14 | | | | |
| | 15 | | | | |
| | 16 | | | | |
| | 17 | | | | |
| | 18 | | | | |
| | 19 | | | | |
| | 20 | | | | |
| | 21 | | | | |
| | 22 | | | | |
Table 59.
All possible channels for open-charm pentaquark systems with and .
Table 59.
All possible channels for open-charm pentaquark systems with and .
| Index | | |
|---|
| ; ; ; | Channel | ; ; ; | Channel |
|---|
| | | |
|---|
| 1 | | | | |
| | 2 | | | | |
| | 3 | | | | |
| | 4 | | | | |
| | 5 | | | | |
| | 6 | | | | |
| | 7 | | | | |
| | 8 | | | | |
| | 9 | | | | |
| | 10 | | | | |
| | 11 | | | | |
| | 12 | | | | |
| | 13 | | | | |
| | 14 | | | | |
| | 15 | | | | |
| | 16 | | | | |
| | 17 | | | | |
| | 18 | | | | |
| 1 | | | | |
| | 2 | | | | |
| | 3 | | | | |
| | 4 | | | | |
| | 5 | | | | |
| | 6 | | | | |
Table 60.
Possible bound and resonance states of doubly charm pentaquarks. The last column listed the binding energy or resonance width of each states.
Table 60.
Possible bound and resonance states of doubly charm pentaquarks. The last column listed the binding energy or resonance width of each states.
| | Quantum State | / (in MeV) |
|---|
| Bound state | | −2 |
| | | −1 |
| | | −4 |
| | | −3 |
| | | −3 |
| Resonance state | | 4.8 |
| | | 8.0 |
| | | 2.6 |
| | | 2.2 |
| | | 4.0 |
| | | 3.0 |
Table 61.
The lowest eigen-energies of doubly-charm pentaquarks with , and the rotated angle . (unit: MeV).
Table 61.
The lowest eigen-energies of doubly-charm pentaquarks with , and the rotated angle . (unit: MeV).
| Channel | Color | M | Channel | M |
|---|
| S | 4351 | | 4358 |
| H | 4787 | | 4608 |
| | S+H | 4351 | | 4358 |
| S | 3812 | | 4434 |
| H | 4620 | | 4613 |
| | S+H | 3812 | | 4434 |
| S | 4412 | | 4488 |
| H | 4568 | | 4576 |
| | S+H | 4412 | | 4488 |
| S | 3981 | | 4551 |
| H | 4299 | | 4779 |
| | S+H | 3981 | | 4551 |
| S | 4384 | | 4503 |
| H | 4701 | | 4691 |
| | S+H | 4384 | | 4503 |
Table 62.
The lowest eigen-energies of with , and the rotated angle . (unit: MeV).
Table 62.
The lowest eigen-energies of with , and the rotated angle . (unit: MeV).
| Channel | Color | M | | M’ |
|---|
| S | 4098 | | 4291 |
| H | 4312 | | 4505 |
| | S+H | 4098 | | 4291 |
Table 63.
The lowest eigen-energies of doubly-charm pentaquarks with , and the rotated angle . (unit: MeV).
Table 63.
The lowest eigen-energies of doubly-charm pentaquarks with , and the rotated angle . (unit: MeV).
| Channel | Color | M | Channel | M |
|---|
| S | 4358 | | 4434 |
| H | 4619 | | 4648 |
| | S+H | 4358 | | 4434 |
| S | 3866 | | 4412 |
| H | 4671 | | 4614 |
| | S+H | 3866 | | 4412 |
| S | 4488 | | 4100 |
| H | 4641 | | 4284 |
| | S+H | 4488 | | 4100 |
| S | 4503 | | 4432 |
| H | 4689 | | 4702 |
| | S+H | 4503 | | 4432 |
| S | 4551 | | |
| H | 4729 | | |
| | S+H | 4551 | | |
Table 64.
The lowest eigen-energies of with , and the rotated angle . (unit: MeV).
Table 64.
The lowest eigen-energies of with , and the rotated angle . (unit: MeV).
| Channel | Color | M | | M’ |
|---|
| S | 4503 | 0 | 4462 |
| H | 4689 | | 4648 |
| | S+H | 4502 | | 4461 |
Table 65.
The lowest eigen-energies of doubly-charm pentaquarks with , and the rotated angle . (unit: MeV).
Table 65.
The lowest eigen-energies of doubly-charm pentaquarks with , and the rotated angle . (unit: MeV).
| Channel | Color | M | Channel | M |
|---|
| S | 4412 | | 4488 |
| H | 4683 | | 4741 |
| | S+H | 4412 | | 4488 |
| S | 4551 | | |
| H | 4655 | | |
| | S+H | 4551 | | |
Table 66.
The lowest eigen-energies of doubly-charm pentaquarks with , and the rotated angle . (unit: MeV).
Table 66.
The lowest eigen-energies of doubly-charm pentaquarks with , and the rotated angle . (unit: MeV).
| Channel | Color | M | Channel | M |
|---|
| S | 3812 | | 4434 |
| H | 4682 | | 4685 |
| | S+H | 3812 | | 4434 |
| S | 4488 | | 4384 |
| H | 4647 | | 4714 |
| | S+H | 4488 | | 4384 |
| S | 4503 | | |
| H | 4627 | | |
| | S+H | 4503 | | |
Table 67.
The lowest eigen-energies of with , and the rotated angle . (unit: MeV).
Table 67.
The lowest eigen-energies of with , and the rotated angle . (unit: MeV).
| Channel | Color | M | | M’ |
|---|
| S | 4548 | | 4524 |
| H | 4693 | | 4669 |
| | S+H | 4547 | | 4523 |
Table 68.
The lowest eigen-energies of doubly-charm pentaquarks with , and the rotated angle . (unit: MeV).
Table 68.
The lowest eigen-energies of doubly-charm pentaquarks with , and the rotated angle . (unit: MeV).
| Channel | Color | M | Channel | M |
|---|
| S | 4434 | | 3866 |
| H | 4708 | | 4692 |
| | S+H | 4434 | | 3866 |
| S | 4488 | | 4503 |
| H | 4678 | | 4719 |
| | S+H | 4488 | | 4503 |
| S | 4432 | | |
| H | 4695 | | |
| | S+H | 4432 | | |
Table 69.
The lowest eigen-energies of with , and the rotated angle . (unit: MeV).
Table 69.
The lowest eigen-energies of with , and the rotated angle . (unit: MeV).
| Channel | Color | M | | M’ |
|---|
| S | 4551 | 0 | 4527 |
| H | 4667 | | 4643 |
| | S+H | 4548 | | 4524 |
Table 70.
The lowest eigen-energies of doubly-charm pentaquarks with , and the rotated angle . (unit: MeV).
Table 70.
The lowest eigen-energies of doubly-charm pentaquarks with , and the rotated angle . (unit: MeV).
| Channel | Color | M | Channel | M |
|---|
| S | 4488 | | 4551 |
| H | 4727 | | 4706 |
| | S+H | 4488 | | 4551 |
Table 71.
Comparison of theoretical masses on the double-charm pentaquark systems by different predictions, the predicted masses and states ( stands for petraquark) are summarized in each column, respectively. (unit: MeV).
Table 71.
Comparison of theoretical masses on the double-charm pentaquark systems by different predictions, the predicted masses and states ( stands for petraquark) are summarized in each column, respectively. (unit: MeV).
| | | | | | | |
|---|
| This work | | | - | | | |
| | | | | | | |
| | | | | | | |
| Ref. [155] | | | | | | |
| | | | | | | |
| | | | | | | |
| | | | | | | |
| | | | | | | |
| | | | | | | |
| | | | | | | |
| Ref. [156] | | | | - | - | - |
| | | | | | | |
| | | | | | | |
| | | | | | | |
| | | | | | | |
Table 72.
Bound and resonance states obtained in tetraquark and pentaquark systems. Mass M, resonance width and binding energy are listed in the third, fourth and fifth column, respectively, unit in MeV.
Table 72.
Bound and resonance states obtained in tetraquark and pentaquark systems. Mass M, resonance width and binding energy are listed in the third, fourth and fifth column, respectively, unit in MeV.
| Channel | M | | | Channel | M | | |
|---|
| | 6980 | − | −196 | | 7726 | 12.00 | 550 |
| | | 17,955 | − | −847 | | 4902 | 3.54 | 924 |
| | | 18,030 | − | −772 | | 7919 | 1.02 | 575 |
| | | | | | | 7993 | 3.22 | 649 |
| | | | | | | 11,306 | 1.86 | 596 |
| | | | | | | 11,333 | 1.84 | 623 |
| | | | | | | 11,412 | 1.54 | 702 |
| | | | | | | 6449 | − | 513 |
| | | | | | | 6659 | − | 723 |
| | | | | | | 19,005 | − | 203 |
| | | | | | | 19,049 | − | 247 |
| | 3726 | − | -189 | | 4312 | 16.00 | 397 |
| | | 6997 | − | −220 | | 7327 | 2.40 | 110 |
| | | 10,238 | − | −359 | | 10,814 | 2.00 | 217 |
| | | 10,524 | − | −73 | | 7920 | 1.20 | 531 |
| | | 18,046 | − | −818 | | 7995 | 4.96 | 606 |
| | | | | | | 6657 | − | 587 |
| | | | | | | 19,067 | − | 203 |
| | 7333 | − | −3 | | 4821 | 5.58 | 589 |
| | | 18,223 | − | −703 | | 4846 | 10.68 | 614 |
| | | | | | | 4775 | 23.26 | 543 |
| | | | | | | 8046 | 1.42 | 530 |
| | | | | | | 8096 | 2.90 | 580 |
| | | | | | | 11,329 | 1.48 | 529 |
| | | | | | | 11,356 | 4.18 | 556 |
| | | | | | | 11,410 | 2.52 | 610 |
| | | | | | | 7022 | − | 818 |
| | | | | | | 19,189 | − | 263 |
| | 4312 | − | −8 | | 4356 | 4.8 | 699 |
| | | 4421 | − | −41 | | 4291 | − | −2 |
| | | 4422 | − | −105 | | 11,072 | − | −17 |
| | | 11,041 | − | -93 | | 10,862 | − | −292 |
| | 4459 | − | -3 | | 4449 | 8.0 | 689 |
| | | 4370 | − | −15 | | 4461 | − | −1 |
| | | 4510 | − | −17 | | 3757 | − | −3 |
| | | 11,120 | − | −14 | | 11,042 | − | −67 |
| | | 10,959 | − | −195 | | | | |
| | 4438 | − | −89 | | 11,141 | − | −13 |
| | 4523 | − | −4 | | 4431 | 2.6 | 774 |
| | | | | | | 4446 | 2.2 | 789 |
| | 11,019 | − | −115 | | 4514 | 4.0 | 754 |
| | | 10,996 | − | −113 | | 4524 | − | −3 |
| | | 11,049 | − | −105 | | | | |
| | 10,932 | − | −222 | | 4461 | 3.0 | 65 |