Fault Diagnosis of an Analog Circuit Based on Hierarchical DVS
Abstract
:1. Introduction
2. IDVS–CNN Algorithm Principle
2.1. IDVS Algorithm
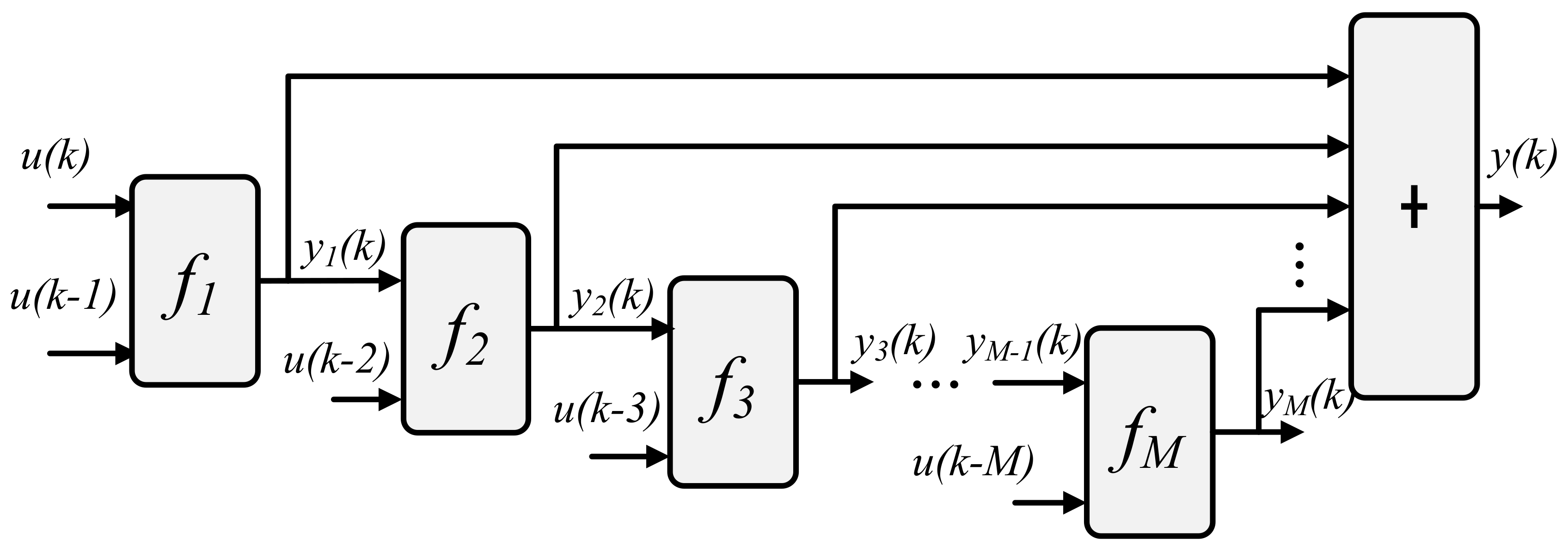
2.1.1. Hierarchical DVS Model
2.1.2. Complexity of the Hierarchical DVS
2.1.3. LM Optimization of the Hierarchical DVS
- (i)
- Initialize the adjustment factor λ, coefficient θ1(0), input matrices μ1 and μ2, and Jacobian matrix J.
- (ii)
- Calculate the trial iteration step size step_try using Equation (19).
- (iii)
- Calculate the trial coefficient θ_try = θ-step_try.
- (iv)
- Put θ_try substituting Equations (2) and (3) to obtain y_hat, and calculate the chi-square error χ2_try.
- (v)
- Calculate the judgment factor ρ using Equation (21).
- (vi)
- If ρ is greater than 0.01, update the adjustment factor using Equation (22) and accept θ_try, χ2_try and update the iteration matrix J; otherwise, update the adjustment factor using Equation (23).
- (vii)
- Repeat steps ii–vi until the mean squared error (MSE) meets the set value or the iteration number reaches the upper limit; finally, the optimal parameters θopt are obtained.
2.1.4. Feature Extraction
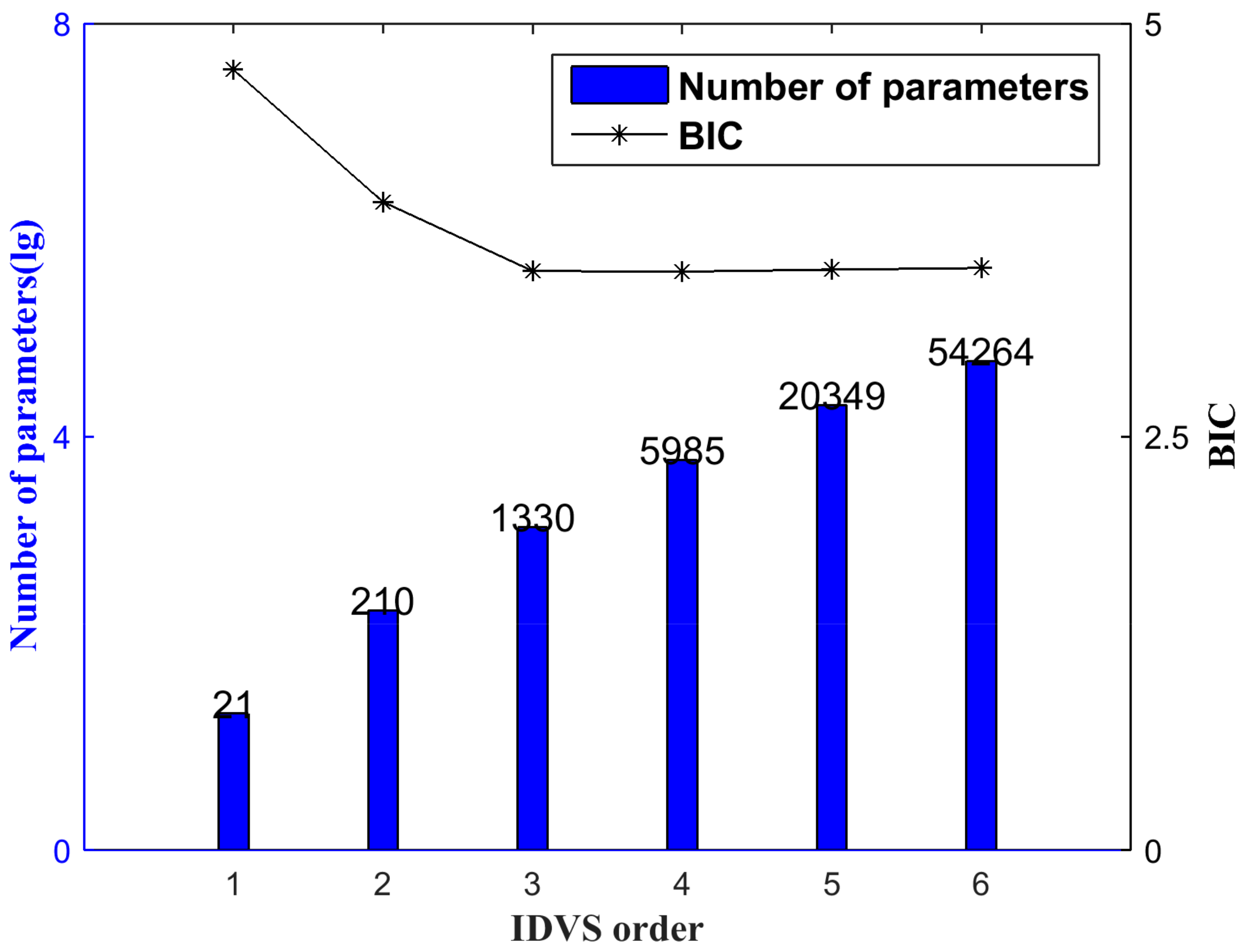
2.1.5. Order Selection of the Hierarchical DVS
2.2. CNN Algorithm
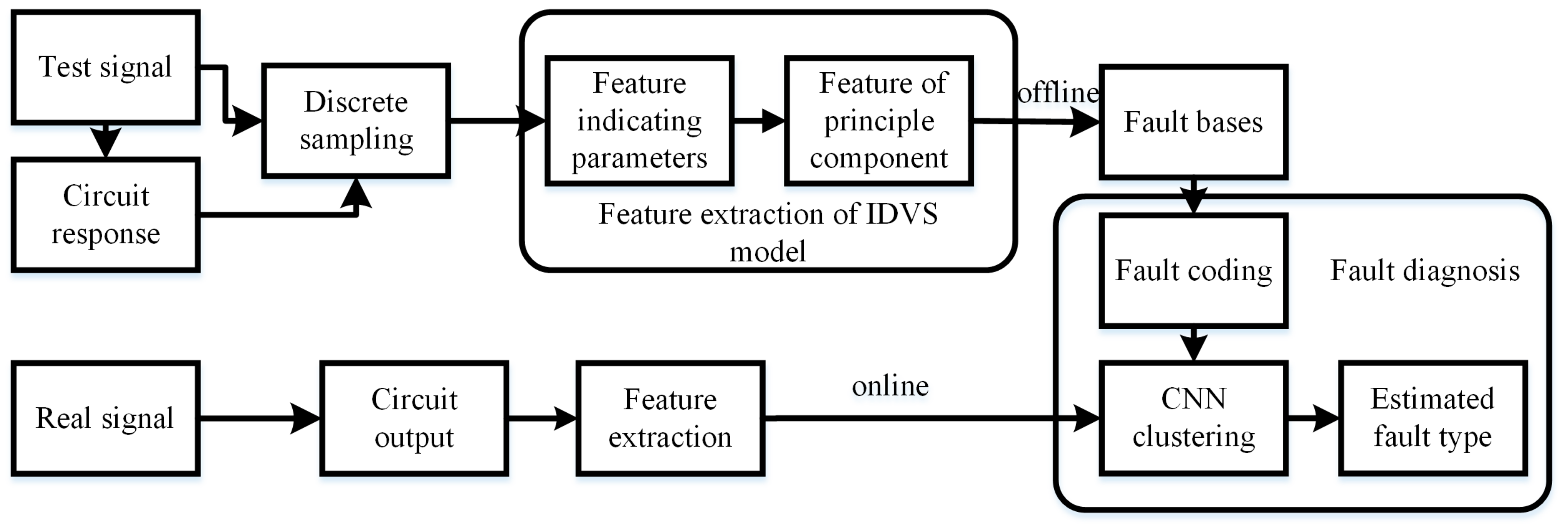
3. IDVS–CNN Diagnostic Procedures
- (i)
- Excitation u (n) is applied to the circuit and u (n) is saved, and the sample set of the circuit response in the normal state and the fault state [normal, fault_1, … fault_N] are collected.
- (ii)
- The IDVS algorithm is used to calculate the characteristic parameter set [h(NF), h(F1), …, h(Fi), …, h(FN)] of the circuit in each state; h (Fi) is the eigenvector of the circuit state I. r and M are set appropriately and the dimension of the parameters through PCA is reduced.
- (iii)
- The feature parameter set is used as the input to the CNN to build a diagnosis model, where the fault code is set as [normal, fault_1, …, fault_N] = [0, 1, 2 …, N], and k is set to the appropriate value.
- (iv)
- After calculating the IDVS characteristic parameter h(Fx) of the circuit response data under test, PCA is applied to reduce the dimension.
- (v)
- The characteristic parameters are input to the CNN model established in step (iii), and the corresponding fault mode code of the circuit under test is obtained.
4. Simulation Verification of the Improved Algorithm
4.1. Simulated Hardware Equipment
- CPU: Core i5-2450m 2.5 GHz.
- RAM memory: 4 G DDR3 1600.
- Hard disk: 1 TB.
- Software platform: MATLAB 2014B, PSpice 16.6.
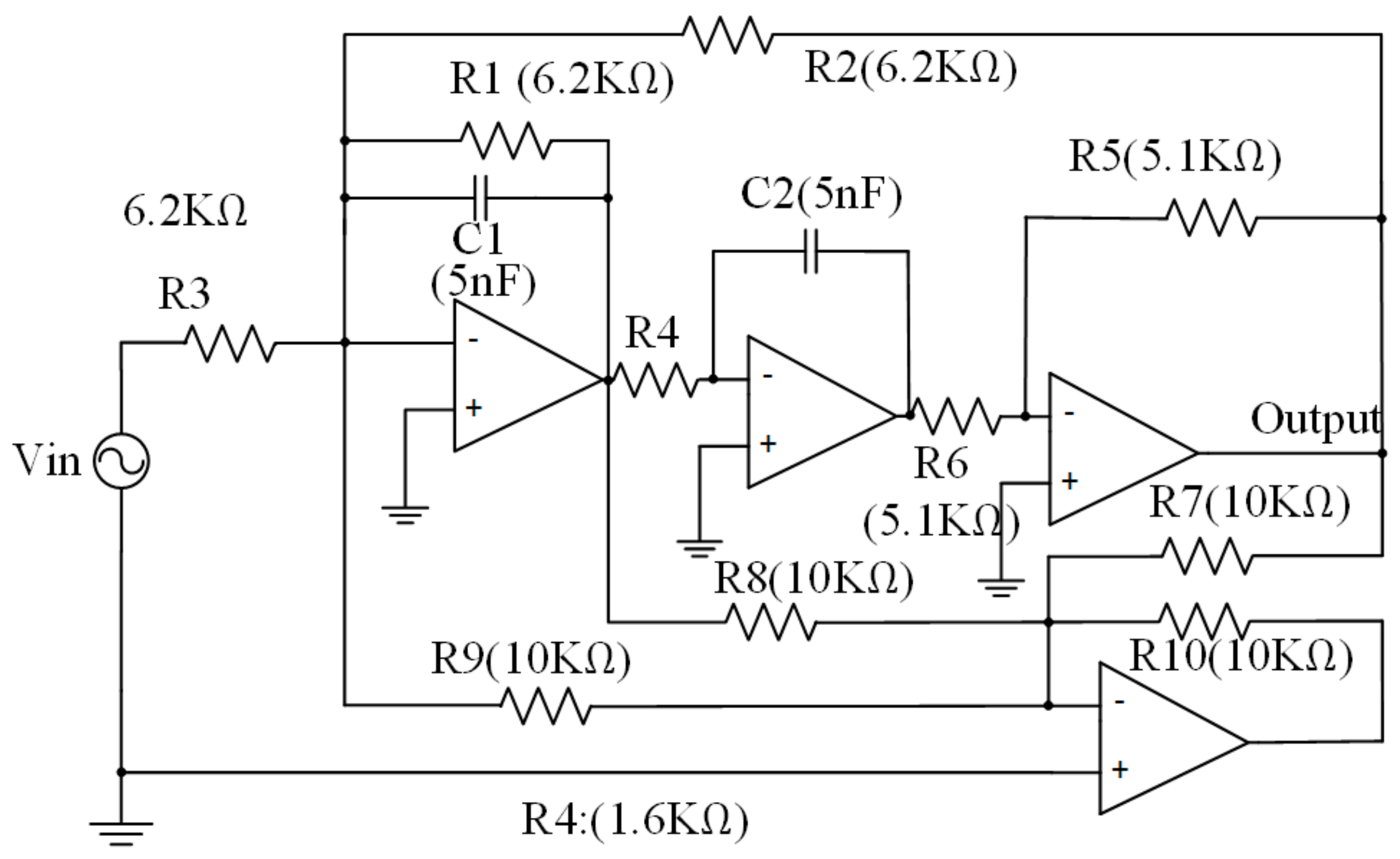
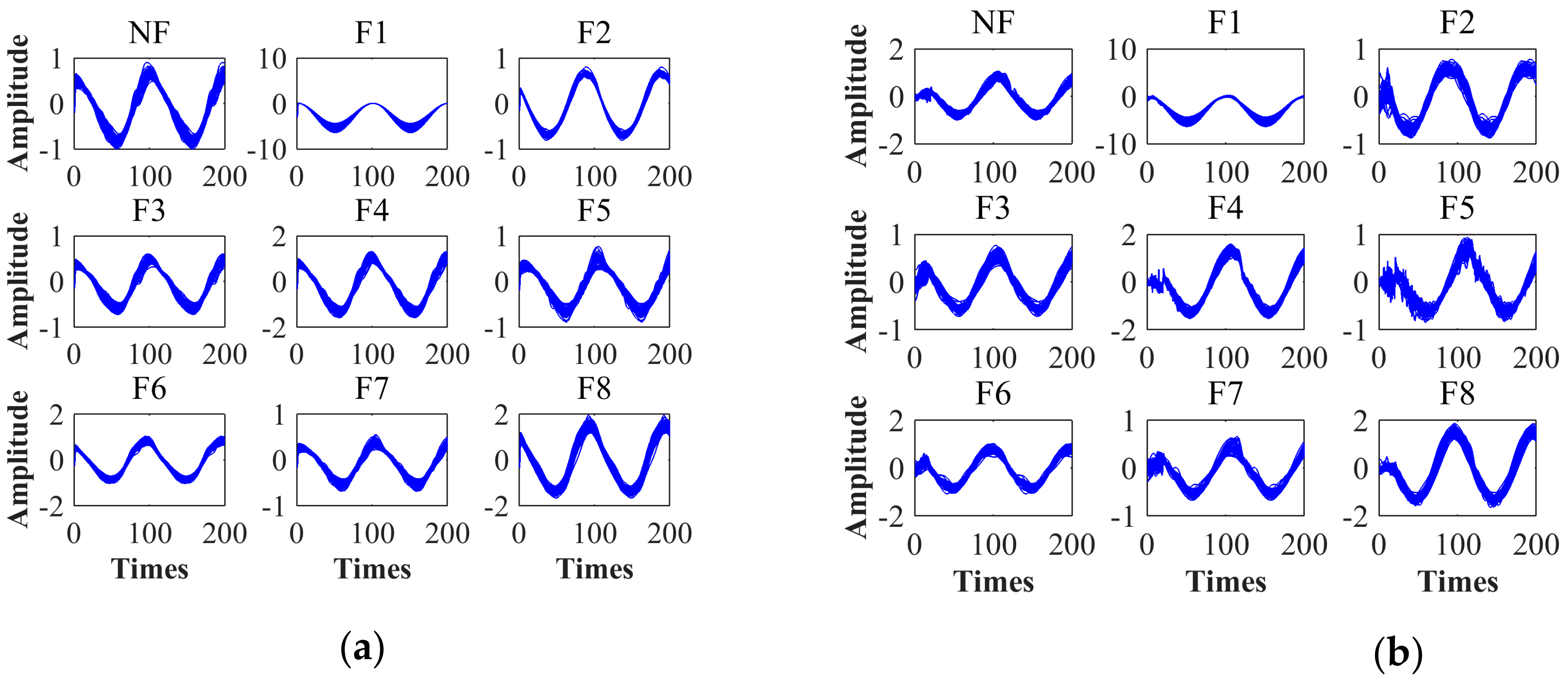
4.2. Fault Mode
4.3. Diagnostic Test Process
4.4. IDVS Order Selection
4.5. LM Optimization of Coefficients
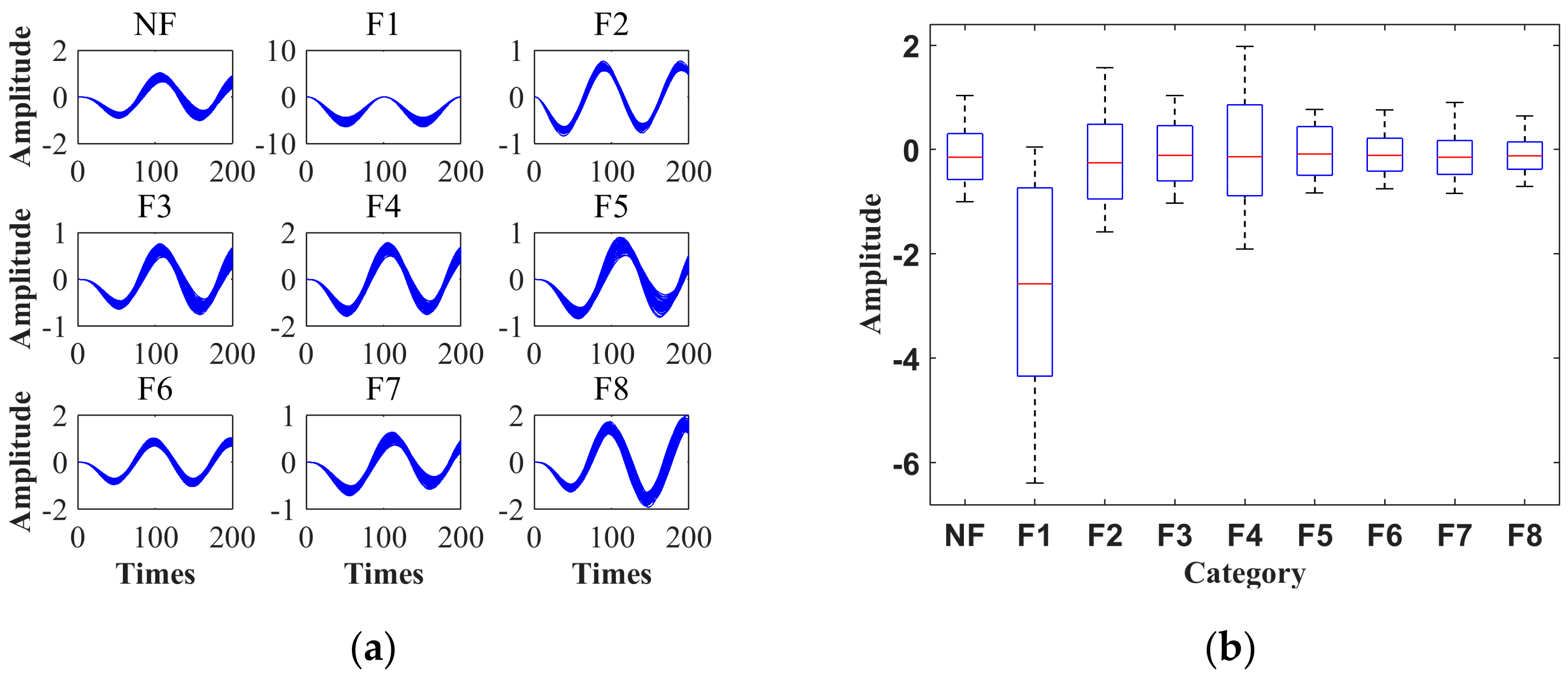
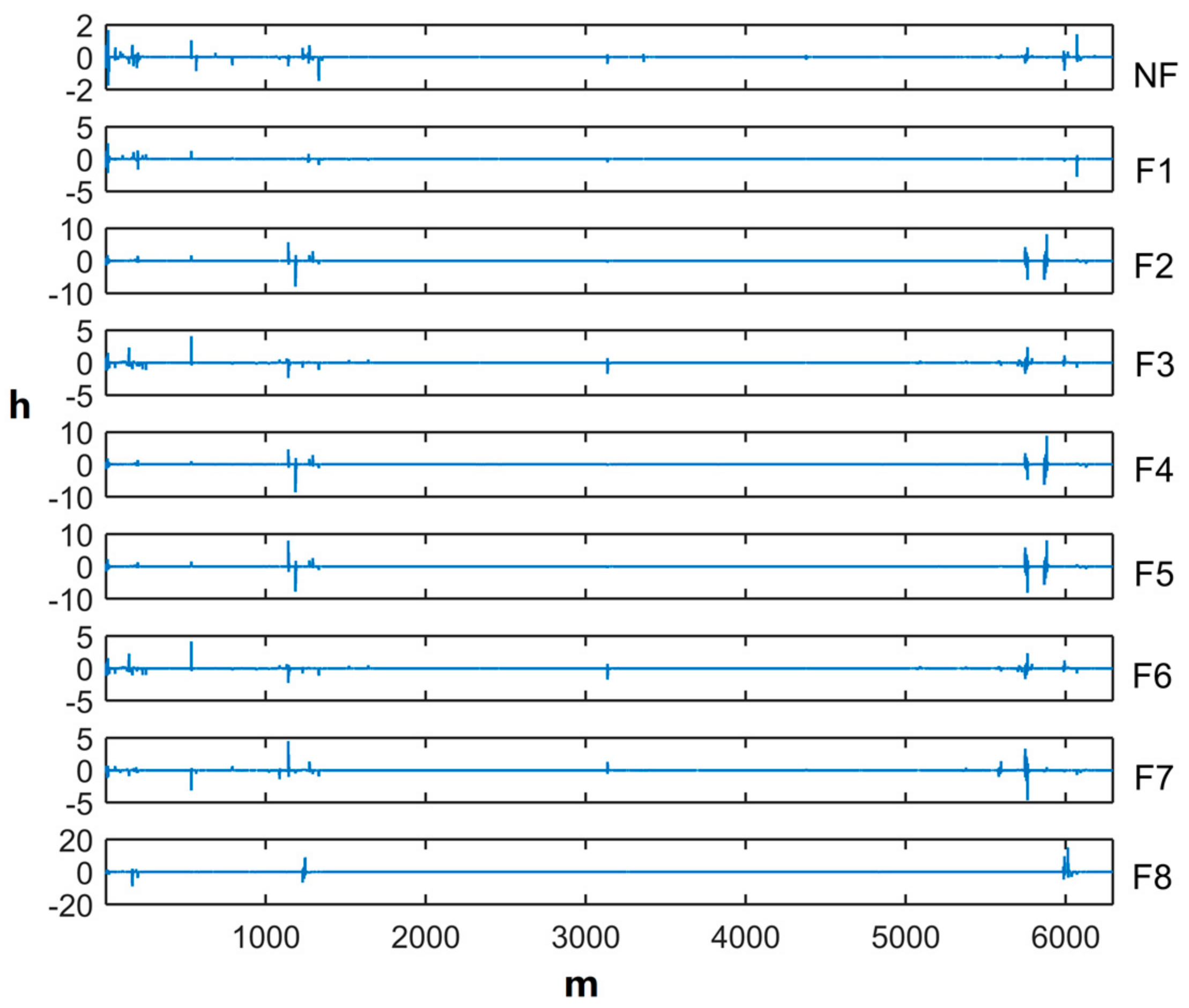
4.6. Calculation of the Characteristic Parameters
4.7. Distance Calculation
4.8. Comparison of the Diagnostic Effects
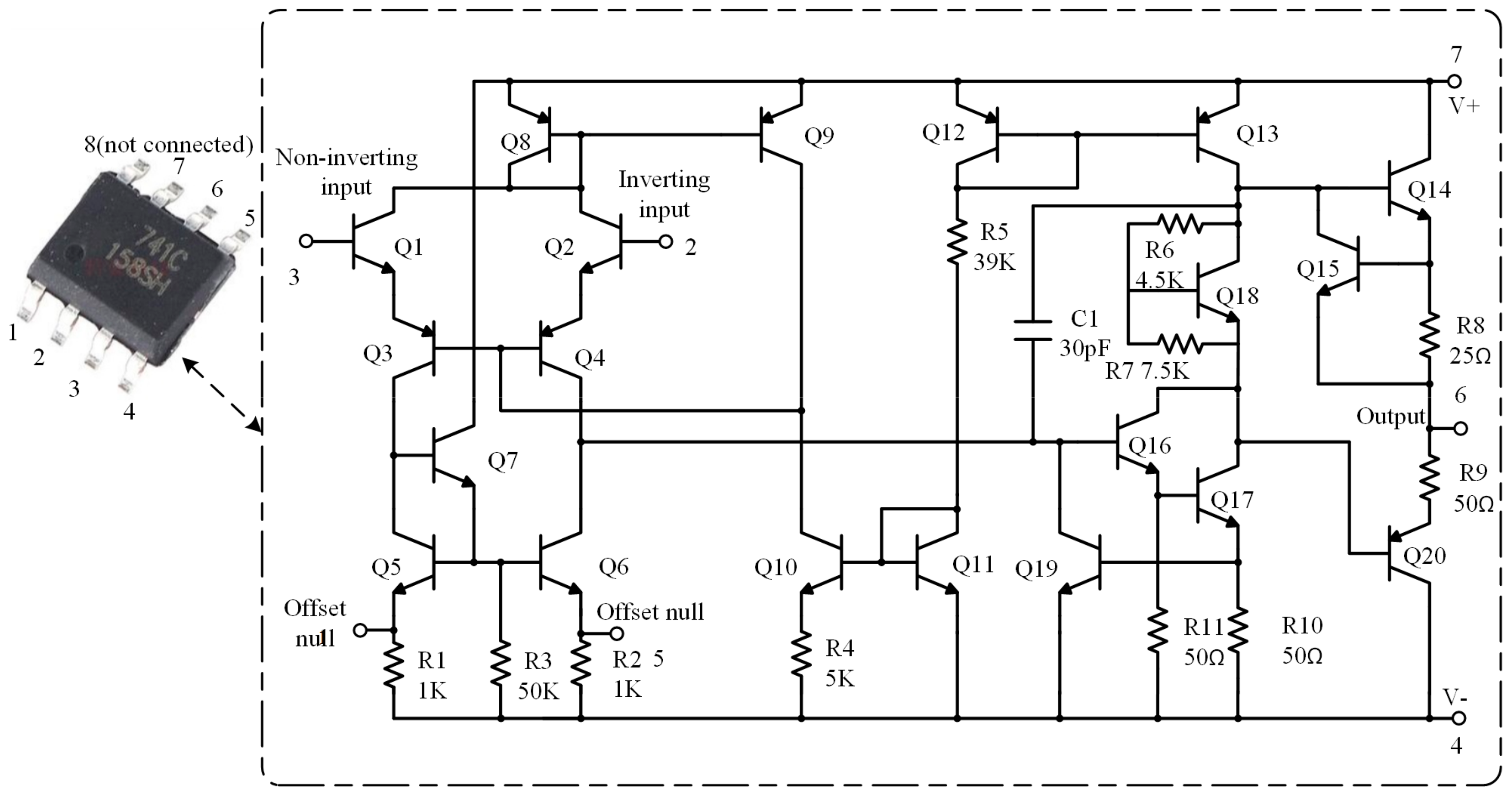
4.9. Real Circuits Experiment
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
References
- Bandler, J.; Salama, A. Fault diagnosis of analog circuits. Proc. IEEE 1985, 73, 1279–1325. [Google Scholar] [CrossRef]
- Li, F.; Woo, P. Fault detection for linear analog IC—The method of short-circuits admittance parameters. IEEE Trans. Circuits Syst. I Regul. Pap. 2002, 49, 105–108. [Google Scholar]
- Yang, S.; Hu, M.; Wang, H. Study on Soft Fault Diagnosis of Analog Circuits. Microelectron. Comput. 2008, 25, 1–8. [Google Scholar]
- Binu, D.; Kariyappa, B. A survey on fault diagnosis of analog circuits: Taxonomy and state of the art. Int. J. Electron. Commun. 2017, 73, 68–83. [Google Scholar] [CrossRef]
- Tang, H.; Liao, Y.; Cao, J.; Xie, H. Fault diagnosis approach based on Volterra models. Mech. Syst. Signal Process. 2010, 24, 1099–1113. [Google Scholar] [CrossRef]
- Cheng, C.; Peng, Z.; Zhang, W.; Meng, G. Volterra-series-based nonlinear system modeling and its engineering applications: A state-of-the-art review. Mech. Syst. Signal Process. 2017, 87, 340–364. [Google Scholar] [CrossRef]
- Peng, Z.; Cheng, C. Volterra series theory: A state-of-the-art review. Chin. Sci. Bull. 2015, 60, 1874–1888. [Google Scholar]
- Jiang, B.; Yang, J.; Zhang, E. QRD-RLS Algorithm for Sparse Adaptive Volterra filtering. Signal Process. 2008, 24, 595–599. [Google Scholar]
- Laura, D.; Jurair, D.; Luis, T. Efficient Volterra systems identification using hierarchical genetic algorithms. Appl. Soft. Comput. J. 2019, 85, 105745. [Google Scholar]
- Chang, W. Volterra filter modeling of nonlinear discrete time system using improved particle swarm optimization Digital. Signal Process. 2012, 22, 1056–1062. [Google Scholar]
- Li, M.; Billings, S. Piecewise Volterra modeling of the Duffing oscillator in the frequency-domain. Mech. Syst. Signal Process. 2012, 26, 118–127. [Google Scholar] [CrossRef]
- Cao, J.; Chen, L.; Zhang, J. Fault diagnosis of complex system based on nonlinear frequency spectrum fusion. Measurement 2013, 46, 125–131. [Google Scholar] [CrossRef]
- Cheng, C.; Peng, Z.; Dong, X.; Zhang, W.; Meng, G. Locating non-linear components in two dimensional periodic structures based on NOFRFs. Int. J. Non-Linear Mech. 2014, 67, 198–208. [Google Scholar] [CrossRef]
- Liu, Y.; Li, J. A novel fault diagnosis method for rotor rub-impact based on nonlinear output frequency response functions and stochastic resonance. J. Sound Vib. 2020, 481, 11541. [Google Scholar] [CrossRef]
- Garna, T.; Bouzrara, K.; Ragot, J.; Messaoud, H. Nonlinear system modeling based on bilinear Laguerre orthonormal bases. ISA Trans. 2013, 52, 301–317. [Google Scholar] [CrossRef]
- Luis, G.; Samuel, D.; Americo, C. Damage detection in uncertain nonlinear systems based on stochastic Volterra series. Mech. Syst. Signal Process. 2019, 125, 288–310. [Google Scholar]
- Koen, T.; Johan, S. Wiener system identification with generalized orthonormal basis functions. Automatica 2014, 50, 3147–3154. [Google Scholar]
- Mohsen, A.; Nadia, N. Practical realization of discrete-time Volterra series for high-order nonlinearities. Nonlinear Dyn. 2019, 98, 2309–2325. [Google Scholar]
- Ameer, A.; Atherton, W.; Rafid, M.; Khalid, R. Performance analysis of an evolutionary LM algorithm to model the load-settlement response of steel piles embedded in sandy soil. Measurement 2019, 140, 622–635. [Google Scholar]
- Zhao, J.; Jin, L.; Shi, L. Mixture model selection via hierarchical BIC. Comput. Stat. Data Anal. 2015, 88, 139–153. [Google Scholar] [CrossRef]
- Cao, J.; Wang, D.; Qu, Z.; Sun, H.; Li, B.; Chen, C.-L. An Improved Network Traffic Classification Model Based on a Support Vector Machine. Symmetry 2020, 12, 301. [Google Scholar] [CrossRef] [Green Version]
- Zhao, G.; Liu, X.; Zhang, B.; Liu, Y.; Niu, G.; Hu, C. A novel approach for analog circuit fault diagnosis based on Deep Belief Network. Measurement 2018, 121, 170–178. [Google Scholar] [CrossRef]
- Liu, W.; Deng, K.; Zhang, X.; Cheng, Y.; Zheng, Z.; Jiang, F.; Peng, J. A Semi-Supervised Tri-CatBoost Method for Driving Style Recognition. Symmetry 2020, 12, 336. [Google Scholar] [CrossRef] [Green Version]
- Liang, T.; Xu, X.; Xiao, M. A new image classification method based on modified condensed nearest neighbor and convolutional neural networks. Pattern Recognit. Lett. 2017, 94, 105–111. [Google Scholar] [CrossRef]
- Sara, S.; Seyyed, H.; Mahdi, E. Optimum test point selection method for analog fault dictionary techniques. Analog. Integr. Circuits Signal Process. 2019, 100, 167–179. [Google Scholar]
- Liu, Z.; Liu, T.; Han, J.; Bu, S.; Tang, X.; Michael, P. Signal Model-Based Fault Coding for Diagnostics and Prognostics of Analog Electronic Circuits. IEEE Trans. Ind. Electron. 2017, 64, 605–614. [Google Scholar] [CrossRef]
- Liu, L.; Wang, W. An efficient instance selection algorithm to reconstruct training set for support vector machine. Knowl. Based Syst. 2017, 166, 58–73. [Google Scholar] [CrossRef] [Green Version]
- Yuan, Z.; He, Y.; Yuan, L.; Cheng, Z. A Diagnostics Method for Analog Circuits Based on Improved Kernel Entropy Component Analysis. J. Electron Test. 2017, 33, 697–707. [Google Scholar] [CrossRef]
- He, W.; He, Y.; Li, B. Generative Adversarial Networks with Comprehensive Wavelet Feature for Fault Diagnosis of Analog Circuits. IEEE Trans. Instrum. Meas. 2020, 69, 6640–76650. [Google Scholar] [CrossRef]
- Zhao, D.; He, Y. A novel binary bat algorithm with chaos and Doppler effect in echoes for analog fault diagnosis. Analog. Integr. Circuits Signal Process. 2016, 87, 437–450. [Google Scholar] [CrossRef]









| CNN | DVS–CNN | IDVS–CNN | |
|---|---|---|---|
| S1 | 67% | 72% | 94% |
| S2 | 62% | 69% | 97% |
| S3 | 23% | 15% | 2.4% |
| MacroF1 | 0.544 | 0.607 | 0.903 |
| MicroF1 | 0.541 | 0.624 | 0.894 |
| Time cost | 11.2 s | 15.2 s | 13.5 s |
| Method | Mean Accuracy (%) | Mean Time Cost (s) | ||
|---|---|---|---|---|
| SNR = 30 dB | SNR = 20 dB | SNR = 10 dB | ||
| Reference [28] | 88 | 77 | 60 | 13 |
| Reference [29] | 87 | 78 | 62 | 12 |
| Reference [30] | 91 | 82 | 65 | 15 |
| IDVS–CNN | 92 | 85 | 76 | 12 |
| NF | R1↑ | R1↓ | R3↑ | R3↓ | C2↑ | C2↓ | |
|---|---|---|---|---|---|---|---|
| NF | 46 | 1 | - | - | 1 | 1 | 1 |
| R1↑ | - | 49 | - | - | - | 1 | - |
| R1↓ | 1 | - | 45 | - | - | 2 | 2 |
| R3↑ | - | - | - | 45 | - | 3 | 2 |
| R3↓ | - | - | - | - | 47 | 2 | 1 |
| C2↑ | 1 | - | - | - | 1 | 44 | 4 |
| C2↓ | 1 | - | - | - | - | 5 | 44 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Deng, Y.; Zhou, Y. Fault Diagnosis of an Analog Circuit Based on Hierarchical DVS. Symmetry 2020, 12, 1901. https://doi.org/10.3390/sym12111901
Deng Y, Zhou Y. Fault Diagnosis of an Analog Circuit Based on Hierarchical DVS. Symmetry. 2020; 12(11):1901. https://doi.org/10.3390/sym12111901
Chicago/Turabian StyleDeng, Yong, and Yuhao Zhou. 2020. "Fault Diagnosis of an Analog Circuit Based on Hierarchical DVS" Symmetry 12, no. 11: 1901. https://doi.org/10.3390/sym12111901





