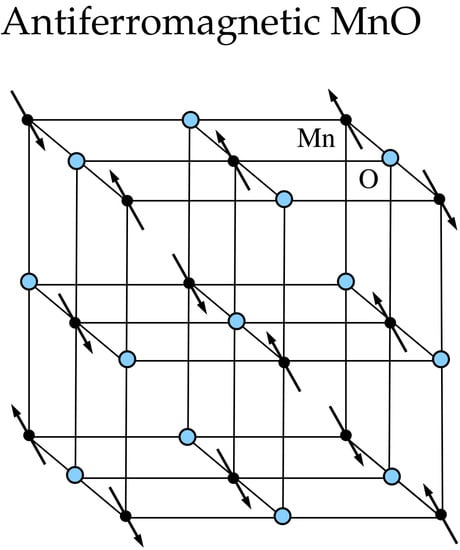
Nonadiabatic Atomic-Like State Stabilizing Antiferromagnetism and Mott Insulation in MnO

Abstract

This paper reports evidence that the antiferromagnetic and insulating ground state of MnO is caused by a nonadiabatic atomic-like motion, as is evidently the case in NiO. In addition, it is shown that experimental findings on the displacements of the Mn and O atoms in the antiferromagnetic phase of MnO corroborate the presented suggestion that the rhombohedral-like distortion in antiferromagnetic MnO, as well as in antiferromagnetic NiO is an inner distortion of the monoclinic base-centered Bravais lattice of the antiferromagnetic phases.

1. Introduction

The isomorphic transition-metal monoxides MnO and NiO are antiferromagnetic with the Néel temperatures $T_N=122$ K and $T_N=523$ K, respectively. Above $T_N$, both monoxides possess the fcc structure $Fm3m={\Gamma }_c^f{O}_h^5$ (225) (in parentheses, the international number), and below $T_N$, the antiferromagnetic structure in both materials is invariant under the monoclinic base-centered magnetic group $C_{c}2/c$ given in Equation (1) [1,2,3,4]. In both MnO and NiO, the antiferromagnetic state is accompanied by a small rhombohedral-like [5] contraction of the crystal. In addition, both compounds are Mott insulators in the antiferromagnetic, as well as in the paramagnetic phase [6].

1.1. Problem Statement

Since the discovery of antiferromagnetism and Mott insulation in the transition-metal monoxides MnO, NiO, CoO, and FeO, the striking electronic properties of these and similar materials have been considered as a manifestation of strongly correlated electrons [6,7,8,9,10,11,12]. However, the strongly correlated nonadiabatic atomic-like motion defined within the nonadiabatic Heisenberg model (NHM) [13] was not yet taken into consideration.

In two forgoing papers [5,14], I can provide evidence that, first, the nonadiabatic atomic-like motion in a special partly-filled energy band of NiO is responsible for both the antiferromagnetic and the insulating state and that, secondly, the (small) rhombohedral-like distortion of the crystal is necessary to stabilize an antiferromagnetic eigenstate in a system invariant under time inversion.

The present paper reports evidence that the electronic features and the distortion of MnO have the same physical origin as in NiO.

1.2. Organization of the Paper

The physical origin of the rhombohedral-like contraction in MnO is the same as in NiO because the concerned magnetic groups are identical. Therefore, in Section 2 and Section 3, only a brief summary of Sections 3 and 4 of [5] is given to make the paper self-contained. These sections provide the magnetic group of the antiferromagnetic state and repeat the definition of the term “rhombohedral-like contraction” used in the following sections.

In Section 4, the experimental findings of Goodwin et al. [15] on MnO will be interpreted. They corroborate the concept of the rhombohedral-like contraction being an inner deformation of the monoclinic base-centered Bravais lattice of antiferromagnetic MnO (and NiO).

In Section 5, the characteristics of the “conventional band structures” used within the NHM will be explained. On the basis of the symmetry of the Bloch functions in the conventional band structure of MnO, in Section 6, the NHM is applied to paramagnetic and antiferromagnetic MnO. First, in Section 6.1, it is shown that there exist optimally localized symmetry-adapted Wannier functions at the Fermi level of paramagnetic MnO, qualifying this material to be a Mott insulator. In the following Section 6.2, I provide evidence that the nonadiabatic atomic-like motion of the electrons in antiferromagnetic MnO is responsible for both the antiferromagnetism and the Mott insulation.

2. Magnetic Group of the Antiferromagnetic State

This section is a brief summary of Section 3 of [5] providing the terms needed in Section 4 and Section 6. The symmetry operations of the type IV Shubnikov magnetic group [4]:

$$C_{c}2/c=C2/c+K\left\{E\right|\mathit{\tau }\}C2/c,$$

(1)

leave invariant the antiferromagnetic structure of both NiO [4] and MnO. K denotes the anti-unitary operator of time inversion; E stands for the identity operation; and

$$\mathit{\tau }=\frac{1}{2}{\mathit{T}}_1$$

(2)

is the non-primitive translation in the group $C2/c$, as indicated in Figure 1.

The unitary subgroup $C2/c$ (15) of $C_{c}2/c$ is based on the monoclinic base-centered Bravais lattice ${\Gamma }_m^b$ and contains (besides the pure translations) the four elements given in Equation (2) of [5]. As in [5], I refer to the magnetic group $C_{c}2/c$ as:

$$M_{15}=C_{c}2/c,$$

(3)

emphasizing in this way the international number 15 of unitary subgroup $C2/c$. An electron system with the symmetry of the group $M_{15}$ cannot have antiferromagnetic eigenstates if it is invariant under time inversion. Instead, it is the subgroup:

$$M_9=Cc+K\left\{C_{2b}\right|\mathbf{0}\}Cc$$

(4)

of $M_{15}$ allowing the system to have eigenstates with the experimentally observed antiferromagnetic structure [5]. The symmetry operation $C_{2b}$ is the rotation through $\pi$ as indicated in Figure 1. Just as $M_{15}$, $M_9$ is based on the monoclinic base-centered Bravais lattice ${\Gamma }_m^b$. The unitary subgroup $Cc$ (9) of $M_9$ contains (besides the pure translations) two elements,

$$Cc=\left\{\left\{E\right|\mathbf{0}\},\left\{{\sigma }_{db}\right|\mathit{\tau }\}\right\},$$

(5)

where ${\sigma }_{db}$ stands for the reflection ${\sigma }_{db}=I{C}_{2b}$ and I denotes the inversion.

Consequently, the crystal is distorted in such a way that the Hamiltonian of the nonadiabatic electron system still commutes with the elements of $M_9$, but does not commute with the symmetry operations of $M_{15}-M_9$. This distortion is produced by a dislocation of the Mn atoms [5]: they are shifted in $\pm ({\mathit{T}}_2-{\mathit{T}}_3)$ direction from their positions at the lattice points ${\mathit{t}}_{Mn}$ in Equation (6); see Figure 1.

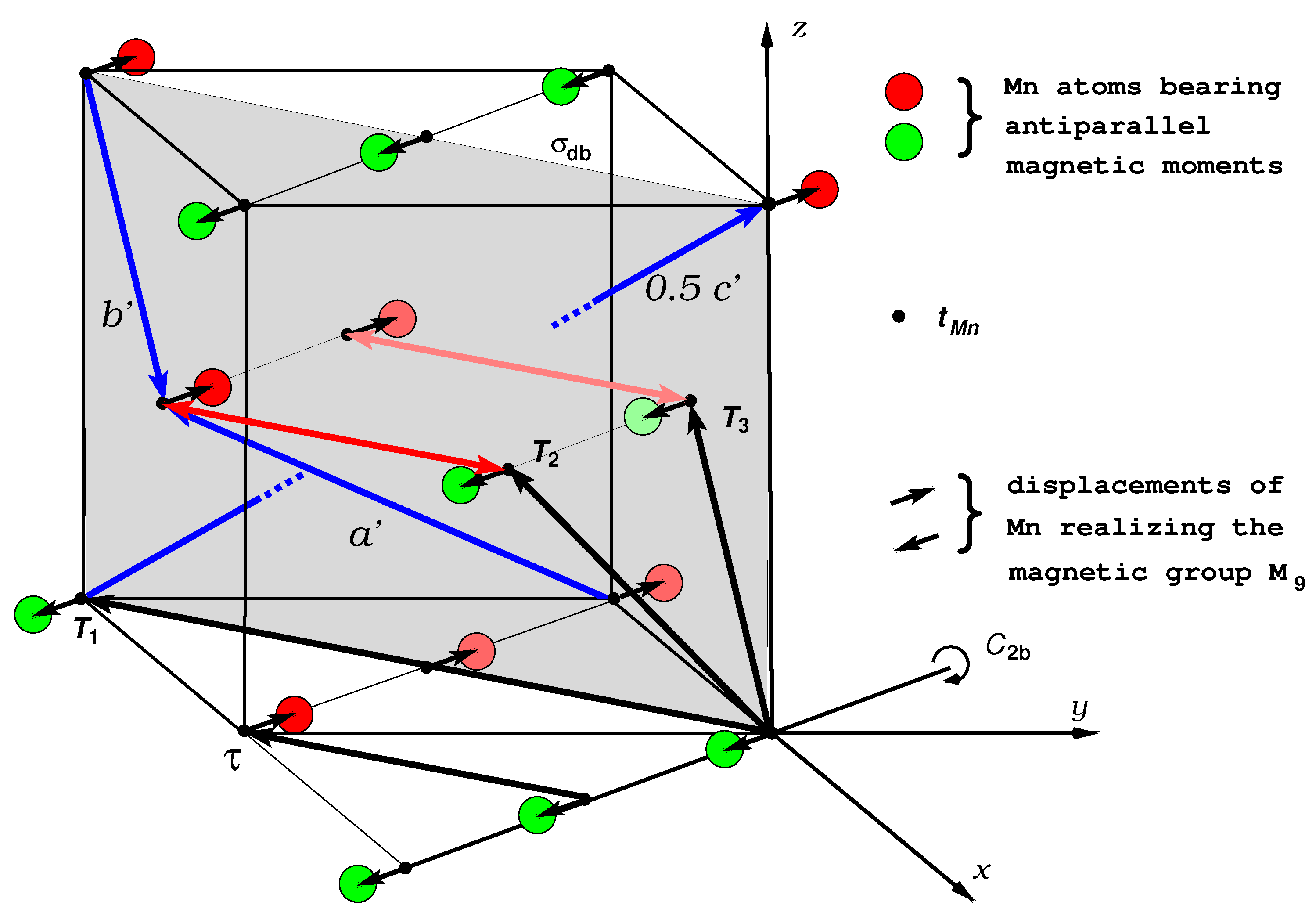
3. Rhombohedral-Like Distortion

As well as antiferromagnetic NiO, antiferromagnetic MnO is slightly deformed by a rhombohedral-like distortion, which may be interpreted as an inner distortion of the base-centered monoclinic Bravais lattice ${\Gamma }_m^b$ [5]. With “inner distortion”, I want to emphasize that the rhombohedral-like distortion does not break the symmetry of the magnetic group $M_9$. Figure 1 shows the dislocations of the Mn atoms stabilizing, on the one hand, the antiferromagnetic structure and producing, on the other hand, the rhombohedral-like distortion, as was substantiated in [5]. The crystal is distorted as a whole whereby the vectors ${\mathit{T}}_1$, ${\mathit{T}}_2$, and ${\mathit{T}}_3$ remain the basic vectors of ${\Gamma }_m^b$. The lattice points ${\mathit{t}}_{Mn}$ plotted in Figure 1 are not the positions of Mn in the fcc lattice, but are defined by the equations:

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill {\mathit{t}}_{Mn}& =n_1{\mathit{T}}_1+n_2{\mathit{T}}_2+n_3{\mathit{T}}_3\mathrm{or}\hfill \\ \hfill {\mathit{t}}_{Mn}& =\frac{1}{2}{\mathit{T}}_1+n_1{\mathit{T}}_1+n_2{\mathit{T}}_2+n_3{\mathit{T}}_3,\hfill \end{array}\end{array}$$

(6)

where ${\mathit{T}}_1$, ${\mathit{T}}_2$, and ${\mathit{T}}_3$ are the basic vectors of ${\Gamma }_m^b$ and $n_1$, $n_2$, and $n_3$ are integers.

4. Interpretation of the Experimental Findings of Goodwin et al.

Goodwin et al. [15] determined the displacements of the Mn and O atoms in the true monoclinic structure from their positions in an assumed rhombohedral structure and gave the result in Table I of their paper. They used the coordinates ${\mathbf{a}}^{\prime },{\mathbf{b}}^{\prime }$, and ${\mathbf{c}}^{\prime }$ depicted in Figure 1 by the blue vectors, depending on the translations of the base-centered monoclinic Bravais lattice according to:

$$\begin{array}{ccc}\hfill a^{\prime }& =& 2{\mathit{T}}_2-{\mathit{T}}_3\hfill \\ \hfill b^{\prime }& =& -{\mathit{T}}_3\hfill \\ \hfill c^{\prime }& =& -3{\mathit{T}}_1+2{\mathit{T}}_2+2{\mathit{T}}_3;\hfill \end{array}$$

(7)

see Figure 1. From Table I of [15], we get for the displacement $\Delta$ of a Mn1 atom:

$$\Delta =\alpha a^{\prime }+\beta b^{\prime }+\gamma c^{\prime }$$

(8)

which may be written as:

$$\Delta =-3\gamma {\mathit{T}}_1+\frac{3\alpha +\beta }{2}({\mathit{T}}_2-{\mathit{T}}_3)+\frac{\alpha -\beta +4\gamma }{2}({\mathit{T}}_2+{\mathit{T}}_3),$$

(9)

leading with $\alpha =-2.072·{10}^{-3}$, $\beta =10.11·{10}^{-3}$, and $\gamma =2.708·{10}^{-3}$ (Table I of [15]) to:

$$\Delta =-8.124{\mathit{T}}_1+1.947({\mathit{T}}_2-{\mathit{T}}_3)-0.675({\mathit{T}}_2+{\mathit{T}}_3),$$

(10)

omitting the common factor ${10}^{-3}$.

The vectors ${\mathit{T}}_1$ and $({\mathit{T}}_2+{\mathit{T}}_3)$ lie in the plane related to the reflection ${\sigma }_{db}$, referred to as “the plane ${\sigma }_{db}$”, as depicted in Figure 1. Hence, the first and the third summand in (10) describe a displacement of the Mn atoms parallel to the plane ${\sigma }_{db}$ resulting from a modification of the translations ${\mathit{T}}_1$, ${\mathit{T}}_2$, and ${\mathit{T}}_3$ occurring in such a way that the ${\mathit{T}}_i$ stay basis vectors of the base-centered monoclinic Bravais lattice [5]. Consequently, these summands are caused by a deformation of the crystal as a whole being still invariant under the translations of the monoclinic lattice.

The second summand, on the other hand, describes a shift of the Mn atoms perpendicular to the plane ${\sigma }_{db}$. It cannot be the result of a modification of the lattice vectors ${\mathit{T}}_i$ because such a modification would destroy the base-centered monoclinic Bravais lattice. These shifts of the Mn atoms in the $\pm ({\mathit{T}}_2-{\mathit{T}}_3)$ directions clearly identify the base-centered monoclinic magnetic group $M_9$ as the magnetic group of antiferromagnetic MnO because $M_9$ is the only magnetic group invariant under both the antiferromagnetic structure and a shift of the Mn atoms perpendicular to the plane ${\sigma }_{db}$ [5]. Thus, we may interpret this result of Goodwin et al. as follows:

(i)

The significant shifts of the Mn atoms in the $\pm ({\mathit{T}}_2-{\mathit{T}}_3)$ direction realize the magnetic group $M_9$ and stabilize in this way the antiferromagnetic structure; see Section 2.

(ii)

The observed displacements of the Mn atoms in Equation (10) are greatest in the ${\mathit{T}}_1$ direction; they are even 12 times greater than in the $({\mathit{T}}_2+{\mathit{T}}_3)$ direction. This corroborates my supposition [5] that the mutual attraction between Mn atoms with opposite shifts in the $\pm ({\mathit{T}}_2-{\mathit{T}}_3)$ direction is mainly responsible for the rhombohedral-like deformation of the crystal. The displacements are maximal in the ${\mathit{T}}_1$ direction since in this direction, they are parallel to the plane ${\sigma }_{db}$ and, thus, do not destroy the magnetic group $M_9$, as illustrated by the red line in Figure 1.

Furthermore, Goodwin et al. found that the symmetry of the threefold rotational axis implicit in a rhombohedral lattice is (slightly) broken in MnO. This demonstrates again that we only have a rhombohedral-like deformation rather than an (exact) rhombohedral symmetry in antiferromagnetic MnO (just as in antiferromagnetic NiO [5]). On the other hand, a break of the monoclinic base-centered symmetry with the magnetic group $M_9$ must not happen because this would destabilize the magnetic structure of MnO.

The small dislocations of the O atoms in the $c^{\prime }$ direction (i.e., parallel to ${\sigma }_{db}$) observed by Goodwin et al. are simply the result of the modification of the translations ${\mathit{T}}_1$, ${\mathit{T}}_2$, and ${\mathit{T}}_3$ produced by the Mn atoms. The O atoms do not actively deform the crystal.

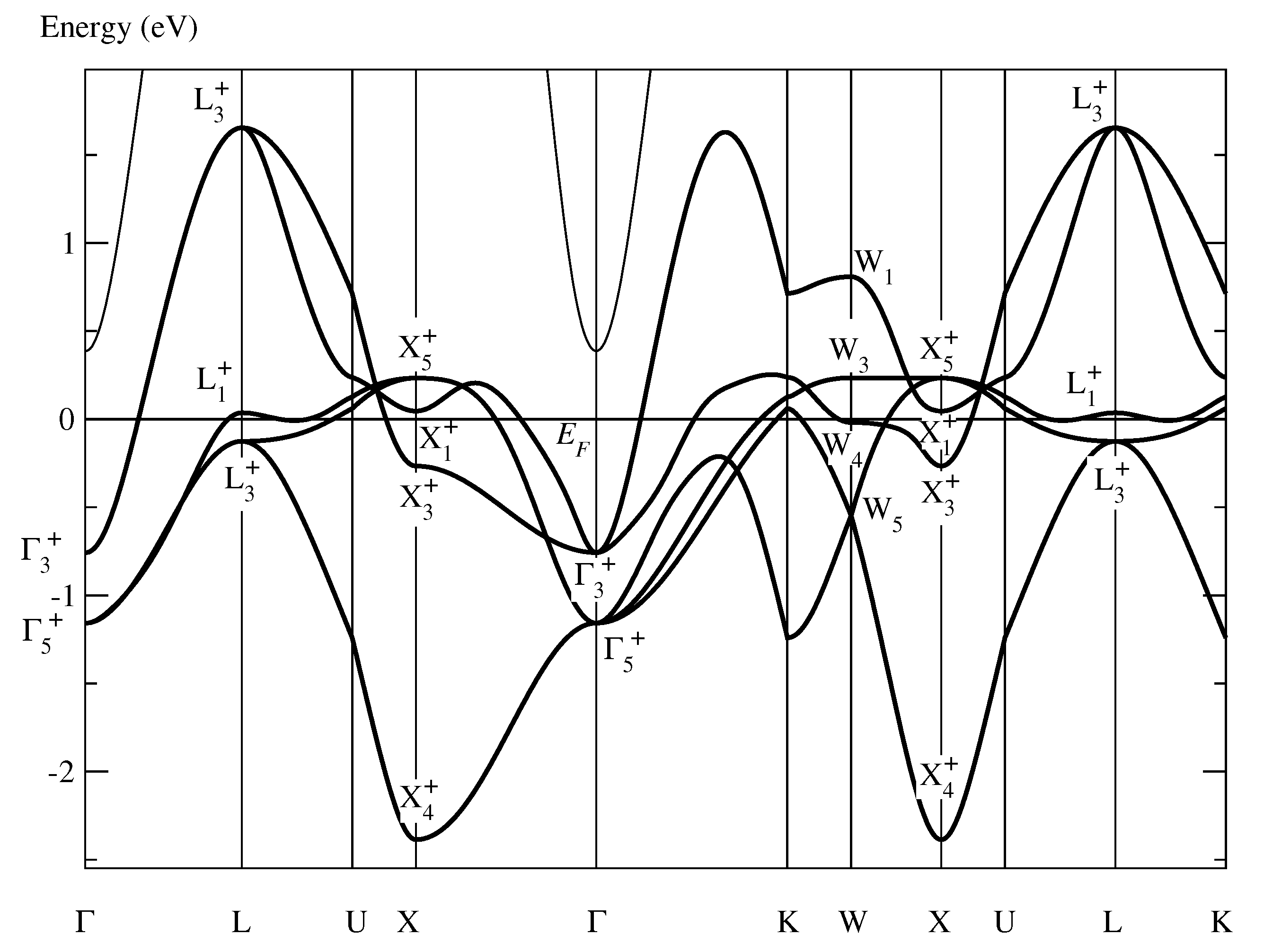
5. Conventional Band Structure

The band structure of paramagnetic MnO in Figure 2 is calculated by the FHI-aims (“Fritz Haber Institute ab initio molecular simulations”) [16,17] computer program. It may be called a “conventional” band structure, because it is a one electron band structure not taking into account correlation effects. The correlation effects responsible for the stable antiferromagnetic state and the nonmetallic behavior of MnO enter by the postulates [13] of the group-theoretical NHM defining a strongly correlated nonadiabatic atomic-like motion at the Fermi level.

The NHM uses only a more qualitative run of the energy $E_{\mathit{k}}$ in the Brillouin zone. It is the symmetry of the Bloch states in the points of symmetry of the Brillouin zone that characterizes an energy band. The FHI-aims program uses spherical harmonics as basis functions and may output the special linear combinations of these functions used at a point $\mathit{k}$. Therefore, I am able (by means of a C++ program) to determine the symmetry of the Bloch functions at the points of symmetry in the Brillouin zone using the symmetry of the spherical harmonics as given in [18].

6. Symmetry-Adapted and Optimally Localized Wannier Functions in MnO

The group-theoretical NHM defines in narrow, partly filled electronic energy bands an atomic-like motion that cannot be described within the adiabatic approximation because it is stabilized by that part of the motion of the atomic cores following non-adiabatically the electronic motion [13]. The related localized states are represented by symmetry-adapted and optimally localized Wannier functions [19]. When the band is roughly half filled and one of narrowest bands in the band structure, the special symmetry and the spin-dependence of these Wannier functions qualify a material to be superconducting [19,20], magnetic [19,21,22,23], or a Mott insulator [5,23]. In the following Section 6.1, it is shown that paramagnetic MnO possesses optimally localized Wannier functions including all the electrons at the Fermi level and adapted to the fcc symmetry of the paramagnetic phase. These functions define a nonadiabatic atomic-like motion evidently responsible for the Mott insulation. In the second Section 6.2, it is shown that the electrons near the Fermi level of antiferromagnetic MnO can be represented by Wannier functions comprising all the electrons at the Fermi level and adapted to the magnetic group $M_9$ of the antiferromagnetic phase.

6.1. Optimally Localized Wannier Functions Symmetry-Adapted to the Paramagnetic fcc Structure

Figure 2 and

Table 1. Symmetry labels of two energy bands in the Brillouin zone for paramagnetic MnO with Bloch functions that can be unitarily transformed into optimally localized Wannier functions symmetry-adapted to the space group $Fm3m$ (225) and centered at the Mn atoms.

	Mn (000)	$\mathbf{\Gamma }$	X	L	W
Band 5	${\Gamma }_3^{+}$	${\Gamma }_3^{+}$	$X_1^{+}$ + $X_3^{+}$	$L_3^{+}$	$W_1$ + $W_4$
Band 8	${\Gamma }_5^{+}$	${\Gamma }_5^{+}$	$X_4^{+}$ + $X_5^{+}$	$L_1^{+}$ + $L_3^{+}$	$W_3$ + $W_5$

provide the information we need to apply the NHM to paramagnetic MnO. In Figure 2, the band structure of paramagnetic MnO is depicted, and Table 1 is an excerpt of Table 1 of [14]. While Table 1 of [14] lists all the optimally localized symmetry-adapted Wannier functions in MnO centered at the Mn or O atoms and adapted to the paramagnetic space group $Fm3m$ (225), Table 1 lists only the two bands with Wannier functions of ${\Gamma }_3^{+}$ and ${\Gamma }_5^{+}$ symmetry centered at the Mn atoms. The bands have two and three branches, respectively, yielding together five Wannier functions at each Mn atom.

Notes to Table 1:

(i)

The notations of the points of symmetry in the Brillouin zone for ${\Gamma }_c^f$ follow Figure 3.14 of [18], and the symmetry notations of the Bloch functions were defined in Table A1 of [5].

(ii)

The bands are determined by means of Theorem 5 of [19]; cf. Section 2 of [14].

(iii)

The point group $G_{0Mn}$ of the positions [19] of the Mn atoms is equal to the full cubic point group $O_h$. The Wannier functions belong to the representation of $G_{0Mn}$ included below the atom.

The band highlighted in Figure 2 by the bold lines is characterized by the symmetry:

$${\Gamma }_3^{+}+{\Gamma }_5^{+},L_3^{+}+L_1^{+}+L_3^{+},X_5^{+}+X_1^{+}+X_3^{+}+X_4^{+},W_1+W_3+W_4+W_5$$

(11)

of the two bands listed Table 1. The related five Wannier functions are centered at the Mn atoms and have d symmetry; see Table 2.7 of [18]. On the other hand, in Table 1b of [14], we find no band crossing the Fermi level in the band structure of paramagnetic MnO. Hence, the energy band (11) originates entirely from a d orbital of Mn. This d band is an insulating band qualifying paramagnetic MnO to be a Mott insulator because it consists of all the branches crossing the Fermi level [14].

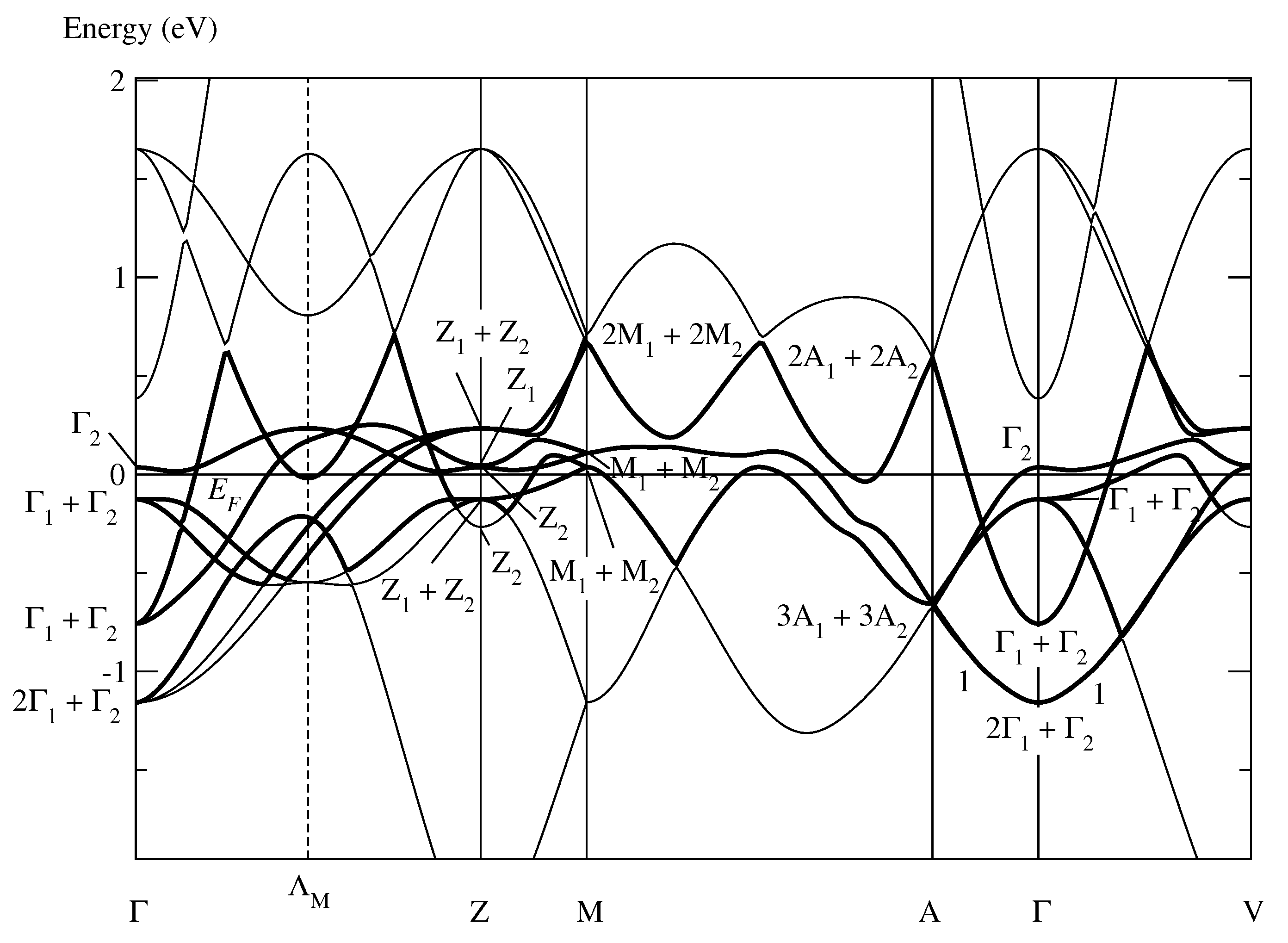
6.2. Optimally Localized Wannier Functions Symmetry-Adapted to the Antiferromagnetic Structure

Figure 3 and

Table 2. Symmetry labels of all energy bands in the Brillouin zone for antiferromagnetic MnO with Bloch functions that can be unitarily transformed into optimally localized Wannier functions symmetry-adapted to the magnetic group $M_9=Cc+K\left\{C_{2b}\right|\mathbf{0}\}Cc$ and centered at the Mn (Table (a)) or O (Table (b)) atoms, respectively.

(a) Mn	Mn${}_1$ (000)	Mn${}_2$ $\left(\overline{\frac{1}{2}}00\right)$	$\mathit{K}\left\{{\mathit{C}}_{2\mathit{b}}\right|0\}$	$\mathbf{\Gamma }$	A	Z	M	L	V
Band 1	${\mathit{d}}_1$	${\mathit{d}}_1$	OK	${\Gamma }_1$ + ${\Gamma }_2$	$A_1$ + $A_2$	$Z_1$ + $Z_2$	$M_1$ + $M_2$	2$L_1$	2$V_1$
(b) O	O${}_1$ $\left(\overline{\frac{1}{4}}\frac{1}{2}\overline{\frac{1}{2}}\right)$	O${}_2$ $\left(\overline{\frac{3}{4}}\frac{1}{2}\overline{\frac{1}{2}}\right)$	$K\left\{C_{2b}\right|\mathbf{0}\}$	$\Gamma$	A	Z	M	L	V
Band 1	${\mathit{d}}_1$	${\mathit{d}}_1$	OK	${\Gamma }_1$ + ${\Gamma }_2$	$A_1$ + $A_2$	$Z_1$ + $Z_2$	$M_1$ + $M_2$	2$L_1$	2$V_1$

provide the information we need to apply the NHM to antiferromagnetic MnO. Table 2 is a shortened copy of Table A2 of [5] omitting the detailed notes to this table in [5] (of course, these notes are also valid for Table 2 in this paper when “Ni” is replaced by “Mn”). Table 2 lists all the bands with optimally localized Wannier functions centered at the Mn or O atoms and symmetry-adapted to the magnetic group $M_9$. In both cases, there exists only one band with coinciding symmetries.

Figure 3 shows the band structure of paramagnetic MnO folded into the Brillouin zone of the monoclinic base-centered magnetic structure. The narrow band highlighted by the bold lines comprises six branches with the symmetry:

$$3{\Gamma }_1+3{\Gamma }_2,3Z_1+3Z_2,3M_1+3M_2,3A_1+3A_2.$$

(12)

Thus, Band 1 (with two branches) listed in Table 2a, as well as Band 1 in Table 2b exist three times in the band structure of antiferromagnetic MnO. Hence, in the highlighted band, we may transform the Bloch functions into optimally localized Wannier functions symmetry adapted to the magnetic group $M_9$. In doing so, we first have four possibilities: we may generate either six Wannier functions centered at the two manganese atoms (with three Wannier functions at Mn${}_1$ and three Wannier functions at Mn${}_2$), four Wannier functions centered at the manganese atoms and two Wannier functions centered at the oxygen atoms, two Wannier functions centered at the manganese atoms and four Wannier functions centered at the oxygen atoms, or six Wannier functions centered at the oxygen atoms in the unit cell. The first possibility certainly does not lead to a stable atomic-like state as a consequence of the Coulomb repulsion between localized states at the same position, and the last possibility has no physical significance because it does not provide localized states at the Mn atoms that bear the magnetic moments. In the remaining two cases, the highlighted band is a magnetic band. The localized Wannier states belonging to this band define a nonadiabatic atomic-like motion stabilizing a magnetic state with the magnetic group $M_9$ [5,21]. Moreover, it is a magnetic super band since it contains all the branches crossing the Fermi level. Thus, it qualifies MnO to be a Mott insulator also in the antiferromagnetic phase [5].

Notes to Table 2:

(i)

The symmetry labels were defined in Table A4 of [5], and the notations of the points of symmetry were defined in Figure 3.4 of [18].

(ii)

The bands are determined by means of Theorem 5 of [19].

(iii)

The point groups $G_{0Mn}$ and $G_{0O}$ of the positions [19] of the Mn respective O atoms contain, in each case, only the identity operation:

$$G_{0Mn}=G_{0O}=\left\{\left\{E\right|\mathbf{0}\}\right\}.$$

(13)

Thus, the Wannier functions at the Mn or O atoms belong to the simple representation:

	$\left\{E\right|\mathbf{0}\}$
${\mathit{d}}_1$	1

of $G_{0Mn}$ and $G_{0O}$.

(iv)

The symmetry of Band 1 in Table 2(a) coincides fully with the symmetry of Band 1 in Table 2(b).

(v)

The entry “OK” indicates that the Wannier functions follow not only Theorem 5, but also Theorem 7 of [19]. Consequently, they may not only be chosen symmetry-adapted to the space group $Cc$, but also to the complete magnetic group $M_9$.

cf. the more detailed notes to Table A2 in [5] (and replace everywhere “Ni” by “Mn”).

7. Results

The paper is concerned with three striking features of MnO:

(i)

The insulating ground state of both paramagnetic and antiferromagnetic MnO,

(ii)

the stability of the antiferromagnetic state,

(iii)

the rhombohedral-like deformation in the antiferromagnetic phase,

characterizing likewise the isomorphic transition-metal monoxide NiO. The aim of this paper is to show that these striking electronic properties of MnO have the same physical origin as in NiO:

Just as in NiO [5],

• The antiferromagnetic state in MnO is evidently stabilized by strongly correlated atomic-like electrons in a magnetic band. The magnetic band in MnO is even a magnetic super band because it comprises all the electrons at the Fermi level. Thus, the special atomic-like motion in this band qualifies antiferromagnetic MnO to be a Mott insulator.
• The Bloch functions of a (roughly) half filled energy band in the paramagnetic band structure of MnO can be unitarily transformed into optimally localized Wannier functions symmetry-adapted to the fcc symmetry of the paramagnetic phase. These Wannier functions are situated at the Mn atoms, have d symmetry, and comprise all the electrons at the Fermi level. Thus, the atomic-like motion represented by these Wannier functions qualifies also paramagnetic MnO to be a Mott insulator.
• The magnetic structure is stabilized by a shift of the Mn atoms in the $\pm ({\mathit{T}}_2-{\mathit{T}}_3)$ direction. These shifts evidently produce the rhombohedral-like deformation of the crystal because the attraction between the Mn atoms increases slightly when the Mn atoms are shifted in opposite directions. This concept presented in [5] was corroborated by the experimental observations of Goodwin et al. [15].
• The rhombohedral-like distortion does not possess a rhombohedral (trigonal) space group, but is an inner distortion of the base-centered monoclinic magnetic group $M_9$ in Equation (4). The group $M_9$, on the other hand, must not be broken because it stabilizes the antiferromagnetic structure.

8. Conclusions

The results of this paper demonstrate once more the physical reality of the nonadiabatic atomic-like motion defined within the NHM. Therefore, they confirm my former findings suggesting that superconductivity [19,20], magnetism [19,21,22,23], and Mott insulation [5,14,23] are produced by the nonadiabatic atomic-like motion defined within the NHM.

In addition, the paper corroborates my former suggestion [5,21] that we can determine by group theory whether or not a magnetic state with the magnetic group M may be an eigenstate in a system invariant under time inversion.

The theory presented in this paper should also be applied to the other transition-metal monoxides CoO and FeO.