Exact Inference for an Exponential Parameter under Generalized Adaptive Progressive Hybrid Censored Competing Risks Data
Abstract
:1. Introduction
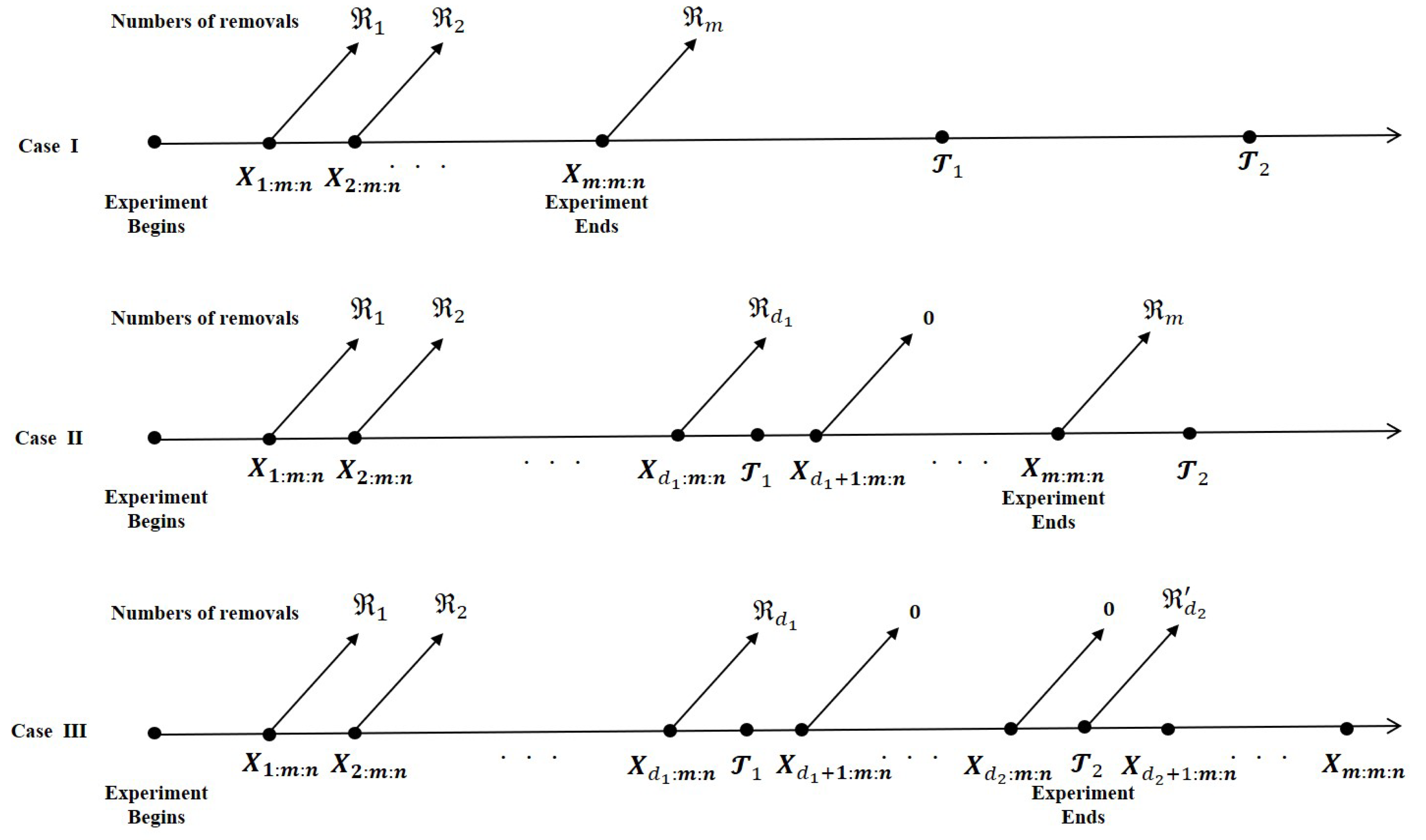
- Case I:
- , if .
- Case II:
- , if .
- Case III:
- , if .
2. Model and Conditional MLEs
2.1. Model
2.2. Exact Conditional Inference for MLE
3. Simulation Results and Data Analysis
3.1. Simulation Results
3.2. Data Analysis
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| RisF | risk factor |
| CoRiM | competing risk model |
| ConMGF | conditional moment generating function |
| ExpD | exponential distribution |
| GeAdPHCS | generalized adaptive progressive hybrid censoring scheme |
| CoR | competing risks |
| CI | confidence interval |
| Ad1PHCS | adaptive Type I progressive hybrid censoring |
| Pr2CS | progressive Type II censoring scheme |
| CL | confidence lengths |
| CP | coverage percentages |
| probability density function | |
| CDF | cumulative distribution function |
Appendix A. Proof of Theorem 1
Appendix B. Proof of Theorem 3
References
- Cox, D.R. The analysis of exponentially distributed lifetimes with two types of failure. J. R. Stat. Soc. Ser. B Methodol. 1959, 21, 411–421. [Google Scholar]
- Mao, S.; Shi, Y.M.; Sun, Y.D. Exact inference for competing risks model with generalized Type I hybrid censored exponential data. J. Stat. Comput. Simul. 2014, 84, 2506–2521. [Google Scholar] [CrossRef]
- Lone, S.A.; Rahman, A.; Arif-ul-Islam. Step stress partially accelerated life testing plan for competing risk using adaptive Type I progressive hybrid censoring. Pak. J. Stat. 2017, 33, 237–248. [Google Scholar]
- Chacko, M.; Mohan, R. Bayesian analysis of Weibull distribution based on progressive Type II censored competing risks data with binomial removals. Comput. Stat. 2019, 34, 233–252. [Google Scholar] [CrossRef]
- Nie, J.; Gui, W. Parameter estimation of Lindley distribution based on progressive Type II censored competing risks data with binomial removals. Mathematics 2019, 7, 646. [Google Scholar] [CrossRef] [Green Version]
- Ahmed, E.; Alhussain, Z.A.; Salah, M.M.; Ahmed, H.H.; Eliwa, M.S. Inference of progressively Type II censored competing risks data from Chen distribution with an application. J. Appl. Stat. 2020, 47, 2492–2524. [Google Scholar] [CrossRef]
- Ashour, S.K.; Nassar, M. Inference for Weibull distribution under adaptive Type I progressive hybrid censored competing risks data. Commun. Stat. Theory Methods 2017, 46, 4756–4773. [Google Scholar] [CrossRef]
- Nassar, M.; Abo-Kasem, O.E. Estimation of the inverse Weibull parameters under adaptive Type II progressive hybrid censoring scheme. J. Comput. Appl. Math. 2017, 315, 228–239. [Google Scholar] [CrossRef]
- Sobhi, M.M.A.; Soliman, A.A. Estimation for the exponentiated Weibull model with adaptive Type II progressive censored schemes. Appl. Math. Model. 2016, 40, 1180–1192. [Google Scholar] [CrossRef]
- Xu, B.; Gui, W. Entropy estimation of inverse Weibull distribution under adaptive Type II progressive hybrid censoring schemes. Symmetry 2019, 11, 1463. [Google Scholar]
- Yan, Z.; Wang, N. Statistical analysis based on adaptive progressive hybrid censored sample from alpha power generalized exponential distribution. IEEE Access 2020, 8, 54691–54697. [Google Scholar] [CrossRef]
- Lee, H.; Lee, K. Exact likelihood inference for an exponential parameter under generalized adaptive progressive hybrid censoring. J. Appl. Stat. 2020, 12, 1149. [Google Scholar] [CrossRef]
- Balakrishnan, N.; Childs, A.; Chandrasekar, B. An efficient computational method for moments of order statistics under progressive censoring. Stat. Probab. Lett. 2002, 60, 359–365. [Google Scholar] [CrossRef]
- Lawless, J. Statistical Models and Methods for Lifetime Data; Wiley: Hoboken, NJ, USA, 2011. [Google Scholar]
- Cho, Y.; Lee, K. Exact inference for competing risks model with generalized progressive hybrid censored exponential data. J. Korean Data Anal. Soc. 2017, 19, 565–575. [Google Scholar] [CrossRef]
| RMSE (Bias) | |||||||
|---|---|---|---|---|---|---|---|
| ℜ | |||||||
| 20 | 18 | 0.2 | (0*17, 2) | 0.1458 (0.0219) | 0.3657 (0.0715) | 0.1393 (0.0176) | 0.2966 (0.0541) |
| (1*2†, 0*16‡) | 0.1499 (0.0243) | 0.4263 (0.0897) | 0.1428 (0.0203) | 0.3251 (0.0617) | |||
| (1, 0*16, 1) | 0.1482 (0.0230) | 0.3963 (0.0830) | 0.1441 (0.0202) | 0.3076 (0.0564) | |||
| 16 | (0*15, 4) | 0.1540 (0.0231) | 0.3888 (0.0738) | 0.1502 (0.0212) | 0.3473 (0.0659) | ||
| (1*4, 0*12) | 0.1822 (0.0370) | 0.4841 (0.1075) | 0.1609 (0.0255) | 0.4072 (0.0813) | |||
| (1*2, 0*13, 2) | 0.1633 (0.0287) | 0.4048 (0.0843) | 0.1520 (0.0219) | 0.3523 (0.0672) | |||
| 14 | (0*13, 6) | 0.1768 (0.0292) | 0.3977 (0.0974) | 0.1722 (0.0282) | 0.3975 (0.0969) | ||
| (1*6, 0*8) | 0.2068 (0.0430) | 0.4947 (0.1349) | 0.1926 (0.0365) | 0.4130 (0.1084) | |||
| (1*3, 0*10, 3) | 0.1928 (0.0337) | 0.4047 (0.1028) | 0.1723 (0.0283) | 0.3970 (0.0967) | |||
| 12 | (0*11, 8) | 0.2058 (0.0353) | 0.5057 (0.1154) | 0.2054 (0.0352) | 0.5058 (0.1154) | ||
| (1*8, 0*4) | 0.2635 (0.0657) | 0.5636 (0.1638) | 0.2573 (0.0705) | 0.5752 (0.1644) | |||
| (1*4, 0*7, 4) | 0.2165 (0.0385) | 0.5095 (0.1167) | 0.2054 (0.0352) | 0.5058 (0.1154) | |||
| 30 | 28 | 0.2 | (0*27, 2) | 0.1162 (0.0192) | 0.3160 (0.0582) | 0.1097 (0.0138) | 0.2325 (0.0459) |
| (1*2, 0*26) | 0.1208 (0.0193) | 0.3124 (0.0605) | 0.1123 (0.0160) | 0.3123 (0.0517) | |||
| (1, 0*26, 1) | 0.1169 (0.0184) | 0.3172 (0.0610) | 0.1114 (0.0148) | 0.2461 (0.0474) | |||
| 26 | (0*25, 4) | 0.1146 (0.0159) | 0.2197 (0.0343) | 0.1109 (0.0129) | 0.2138 (0.0300) | ||
| (1*4, 0*22) | 0.1252 (0.0205) | 0.2472 (0.0453) | 0.1127 (0.0150) | 0.2259 (0.0358) | |||
| (1*2, 0*23, 2) | 0.1180 (0.0186) | 0.2363 (0.0404) | 0.1096 (0.0131) | 0.2152 (0.0311) | |||
| 24 | (0*23, 6) | 0.1149 (0.0123) | 0.2550 (0.0469) | 0.1141 (0.0117) | 0.2457 (0.0434) | ||
| (1*6, 0*18) | 0.1315 (0.0182) | 0.3223 (0.0677) | 0.1185 (0.0139) | 0.2674 (0.0512) | |||
| (1*3, 0*20, 3) | 0.1219 (0.0158) | 0.2721 (0.0554) | 0.1143 (0.0118) | 0.2468 (0.0437) | |||
| 22 | (0*21, 8) | 0.1246 (0.0124) | 0.2547 (0.0380) | 0.1240 (0.0122) | 0.2550 (0.0380) | ||
| (1*8, 0*14) | 0.1429 (0.0228) | 0.2884 (0.0525) | 0.1278 (0.0147) | 0.2604 (0.0430) | |||
| (1*4, 0*17, 4) | 0.1293 (0.0151) | 0.2587 (0.0416) | 0.1240 (0.0122) | 0.2549 (0.0380) | |||
| 20 | (0*19, 10) | 0.1321 (0.0185) | 0.2730 (0.0551) | 0.1316 (0.0184) | 0.2729 (0.0550) | ||
| (1*10, 0*10) | 0.1592 (0.0305) | 0.3456 (0.0759) | 0.1497 (0.0257) | 0.2853 (0.0631) | |||
| (1*5, 0*14, 5) | 0.1349 (0.0200) | 0.2733 (0.0565) | 0.1316 (0.0184) | 0.2729 (0.0550) | |||
| 18 | (0*17, 12) | 0.1378 (0.0169) | 0.2942 (0.0534) | 0.1378 (0.0169) | 0.2942 (0.0534) | ||
| (1*12, 0*6) | 0.1646 (0.0365) | 0.4243 (0.1003) | 0.1639 (0.0433) | 0.3895 (0.1008) | |||
| (1*6, 0*11, 6) | 0.1384 (0.0173) | 0.2963 (0.0541) | 0.1378 (0.0169) | 0.2942 (0.0534) | |||
| 40 | 38 | 0.2 | (0*37, 2) | 0.0963 (0.0109) | 0.1836 (0.0197) | 0.0889 (0.0067) | 0.1715 (0.0138) |
| (1*2, 0*36) | 0.1001 (0.0120) | 0.1909 (0.0213) | 0.0919 (0.0081) | 0.1782 (0.0161) | |||
| (1, 0*36, 1) | 0.0981 (0.0118) | 0.1853 (0.0190) | 0.0899 (0.0074) | 0.1751 (0.0150) | |||
| 36 | (0*35, 4) | 0.0944 (0.0097) | 0.2006 (0.0283) | 0.0916 (0.0088) | 0.1834 (0.0195) | ||
| (1*4, 0*32) | 0.0975 (0.0098) | 0.2149 (0.0335) | 0.0943 (0.0093) | 0.1970 (0.0252) | |||
| (1*2, 0*33, 2) | 0.0962 (0.0104) | 0.2111 (0.0323) | 0.0931 (0.0096) | 0.1881 (0.0215) | |||
| 34 | (0*33, 6) | 0.0953 (0.0087) | 0.2008 (0.0289) | 0.0923 (0.0069) | 0.1915 (0.0260) | ||
| (1*6, 0*28) | 0.1000 (0.0101) | 0.2294 (0.0383) | 0.0954 (0.0083) | 0.2028 (0.0295) | |||
| (1*3, 0*30, 3) | 0.0973 (0.0094) | 0.2179 (0.0350) | 0.0930 (0.0073) | 0.1940 (0.0264) | |||
| 32 | (0*31, 8) | 0.1017 (0.0100) | 0.1900 (0.0205) | 0.1001 (0.0092) | 0.1890 (0.0195) | ||
| (1*8, 0*24) | 0.1133 (0.0148) | 0.2161 (0.0274) | 0.1045 (0.0105) | 0.1956 (0.0210) | |||
| (1*4, 0*27, 4) | 0.1074 (0.0129) | 0.2037 (0.0239) | 0.1002 (0.0093) | 0.1889 (0.0195) | |||
| 30 | (0*29, 10) | 0.1042 (0.0108) | 0.1987 (0.0268) | 0.1040 (0.0108) | 0.1981 (0.0264) | ||
| (1*10, 0*20) | 0.1156 (0.0155) | 0.2361 (0.0413) | 0.1079 (0.0121) | 0.2186 (0.0321) | |||
| (1*5, 0*24, 5) | 0.1075 (0.0123) | 0.2194 (0.0321) | 0.1040 (0.0108) | 0.1982 (0.0265) | |||
| 28 | (0*16, 1*12) | 0.1080 (0.0131) | 0.2273 (0.0446) | 0.1080 (0.0131) | 0.2273 (0.0446) | ||
| (1*12, 0*16) | 0.1171 (0.0182) | 0.3150 (0.0605) | 0.1128 (0.0160) | 0.3133 (0.0520) | |||
| (1*6, 0*16, 1*6) | 0.1110 (0.0144) | 0.2317 (0.0462) | 0.1080 (0.0131) | 0.2273 (0.0446) | |||
| Confidence Length (Coverage Probability) | |||||||
|---|---|---|---|---|---|---|---|
| ℜ | |||||||
| 20 | 18 | 0.2 | (0*17, 2) | 0.5807 (94.7) | 1.3001 (95.3) | 0.5540 (94.6) | 1.1730 (95.3) |
| (1*2, 0*16) | 0.6163 (95.2) | 1.4882 (94.9) | 0.5723 (94.8) | 1.2355 (95.1) | |||
| (1, 0*16, 1) | 0.5962 (95.0) | 1.3901 (95.0) | 0.5631 (94.6) | 1.1896 (95.3) | |||
| 16 | (0*15, 4) | 0.6104 (94.8) | 1.4075 (95.5) | 0.6027 (94.8) | 1.3495 (95.7) | ||
| (1*4, 0*12) | 0.6973 (95.0) | 1.7466 (95.3) | 0.6266 (94.5) | 1.4713 (95.3) | |||
| (1*2, 0*13, 2) | 0.6372 (94.7) | 1.4858 (95.7) | 0.6048 (94.7) | 1.3567 (95.7) | |||
| 14 | (0*13, 6) | 0.6704 (95.2) | 1.5825 (94.9) | 0.6667 (95.1) | 1.5794 (94.9) | ||
| (1*6, 0*8) | 0.7688 (94.2) | 1.9668 (95.3) | 0.7029 (94.2) | 1.6595 (95.0) | |||
| (1*3, 0*10, 3) | 0.6935 (95.0) | 1.6221 (95.1) | 0.6669 (95.2) | 1.5790 (94.9) | |||
| 12 | (0*11, 8) | 0.7755 (94.7) | 2.0278 (94.5) | 0.7751 (94.7) | 2.0279 (94.5) | ||
| (1*8, 0*4) | 0.9108 (93.8) | 2.3713 (94.4) | 0.8669 (93.1) | 2.2177 (93.5) | |||
| (1*4, 0*7, 4) | 0.7900 (94.7) | 2.0405 (94.6) | 0.7752 (94.7) | 2.0280 (94.5) | |||
| 30 | 28 | 0.2 | (0*27, 2) | 0.4496 (94.7) | 0.9645 (95.4) | 0.4240 (94.4) | 0.8656 (95.4) |
| (1*2, 0*26) | 0.4667 (95.0) | 1.0045 (95.7) | 0.4355 (94.2) | 0.9287 (95.2) | |||
| (1, 0*26, 1) | 0.4561 (94.6) | 0.9884 (95.7) | 0.4281 (94.8) | 0.8784 (95.4) | |||
| 26 | (0*25, 4) | 0.4517 (95.3) | 0.8881 (95.7) | 0.4409 (95.4) | 0.8676 (95.8) | ||
| (1*4, 0*22) | 0.4892 (95.7) | 0.9813 (95.8) | 0.4533 (95.5) | 0.9006 (95.6) | |||
| (1*2, 0*23, 2) | 0.4673 (95.6) | 0.9300 (95.8) | 0.4421 (95.2) | 0.8715 (95.7) | |||
| 24 | (0*23, 6) | 0.4595 (94.8) | 0.9557 (94.9) | 0.4571 (94.8) | 0.9431 (94.8) | ||
| (1*6, 0*18) | 0.5067 (94.4) | 1.1165 (94.9) | 0.4709 (94.8) | 0.9891 (94.8) | |||
| (1*3, 0*20, 3) | 0.4752 (94.3) | 1.0009 (94.5) | 0.4575 (94.7) | 0.9444 (94.9) | |||
| 22 | (0*21, 8) | 0.4862 (93.8) | 0.9956 (94.3) | 0.4857 (93.9) | 0.9956 (94.3) | ||
| (1*8, 0*14) | 0.5444 (94.8) | 1.1201 (94.3) | 0.4995 (93.9) | 1.0275 (94.5) | |||
| (1*4, 0*17, 4) | 0.4955 (93.7) | 1.0129 (94.5) | 0.4858 (93.9) | 0.9956 (94.3) | |||
| 20 | (0*19, 10) | 0.5198 (94.1) | 1.0913 (95.6) | 0.5195 (94.1) | 1.0911 (95.6) | ||
| (1*10, 0*10) | 0.5832 (93.8) | 1.2706 (95.7) | 0.5425 (93.2) | 1.1311 (95.1) | |||
| (1*5, 0*14, 5) | 0.5245 (94.1) | 1.0975 (95.6) | 0.5195 (94.1) | 1.0911 (95.6) | |||
| 18 | (0*17, 12) | 0.5518 (94.6) | 1.1689 (95.3) | 0.5518 (94.6) | 1.1689 (95.3) | ||
| (1*12, 0*6) | 0.6181 (93.8) | 1.4257 (94.5) | 0.5991 (94.4) | 1.3025 (94.6) | |||
| (1*6, 0*11, 6) | 0.5530 (94.5) | 1.1722 (95.3) | 0.5518 (94.6) | 1.1689 (95.3) | |||
| 40 | 38 | 0.2 | (0*37, 2) | 0.3736 (94.5) | 0.7129 (94.1) | 0.3527 (94.8) | 0.6721 (94.3) |
| (1*2, 0*36) | 0.3857 (94.7) | 0.7372 (93.5) | 0.3603 (94.9) | 0.6882 (94.2) | |||
| (1, 0*36, 1) | 0.3799 (94.5) | 0.7217 (93.8) | 0.3556 (94.9) | 0.6787 (93.8) | |||
| 36 | (0*35, 4) | 0.3732 (94.9) | 0.7335 (93.8) | 0.3634 (94.8) | 0.6987 (93.8) | ||
| (1*4, 0*32) | 0.3930 (95.6) | 0.7858 (93.6) | 0.3718 (94.5) | 0.7262 (93.6) | |||
| (1*2, 0*33, 2) | 0.3829 (95.2) | 0.7606 (93.9) | 0.3657 (94.7) | 0.7051 (93.7) | |||
| 34 | (0*33, 6) | 0.3777 (94.8) | 0.7478 (94.8) | 0.3727 (94.9) | 0.7359 (95.0) | ||
| (1*6, 0*28) | 0.4055 (94.9) | 0.8252 (94.6) | 0.3823 (95.3) | 0.7596 (95.1) | |||
| (1*3, 0*30, 3) | 0.3878 (94.7) | 0.7807 (95.1) | 0.3735 (94.8) | 0.7377 (95.1) | |||
| 32 | (0*31, 8) | 0.3900 (94.2) | 0.7506 (94.8) | 0.3882 (94.1) | 0.7481 (94.7) | ||
| (1*8, 0*24) | 0.4266 (94.0) | 0.8271 (94.1) | 0.3983 (94.2) | 0.7674 (94.3) | |||
| (1*4, 0*27, 4) | 0.4014 (93.8) | 0.7731 (94.6) | 0.3884 (94.1) | 0.7481 (94.7) | |||
| 30 | (0*29, 10) | 0.4040 (96.0) | 0.7894 (94.8) | 0.4039 (95.9) | 0.7885 (94.9) | ||
| (1*10, 0*20) | 0.4416 (95.6) | 0.8875 (95.4) | 0.4141 (95.6) | 0.8197 (95.0) | |||
| (1*5, 0*24, 5) | 0.4104 (95.6) | 0.8116 (94.6) | 0.4039 (95.9) | 0.7887 (94.9) | |||
| 28 | (0*16, 1*12) | 0.4218 (94.5) | 0.8598 (95.3) | 0.4218 (94.5) | 0.8598 (95.3) | ||
| (1*12, 0*16) | 0.4602 (94.9) | 0.9968 (95.8) | 0.4342 (94.5) | 0.9271 (95.1) | |||
| (1*6, 0*16, 1*6) | 0.4257 (94.5) | 0.8676 (95.3) | 0.4218 (94.5) | 0.8598 (95.3) | |||
| 11.0 | 35.0 | 49.0 | 170.0 | 329.0 | 381.0 | 708.0 | 958.0 | 1062.0 | 1167.0 | |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 1594.0 | 1925.0 | 1990.0 | 2223.0 | 2327.0 | 2400.0 | 2451.0 | 2471.0 | 2551.0 | 2565.0 | |
| 0 | 1 | 1 | 1 | 0 | 1 | 0 | 1 | 1 | 0 | |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 2568.0 | 2702.0 | 2831.0 | 3059.0 | 3214.0 | 3504.0 | 4329.0 | 6976.0 | |||
| 1 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | |||
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| SE () | 95% CI | SE () | 95% CI | ||||||
|---|---|---|---|---|---|---|---|---|---|
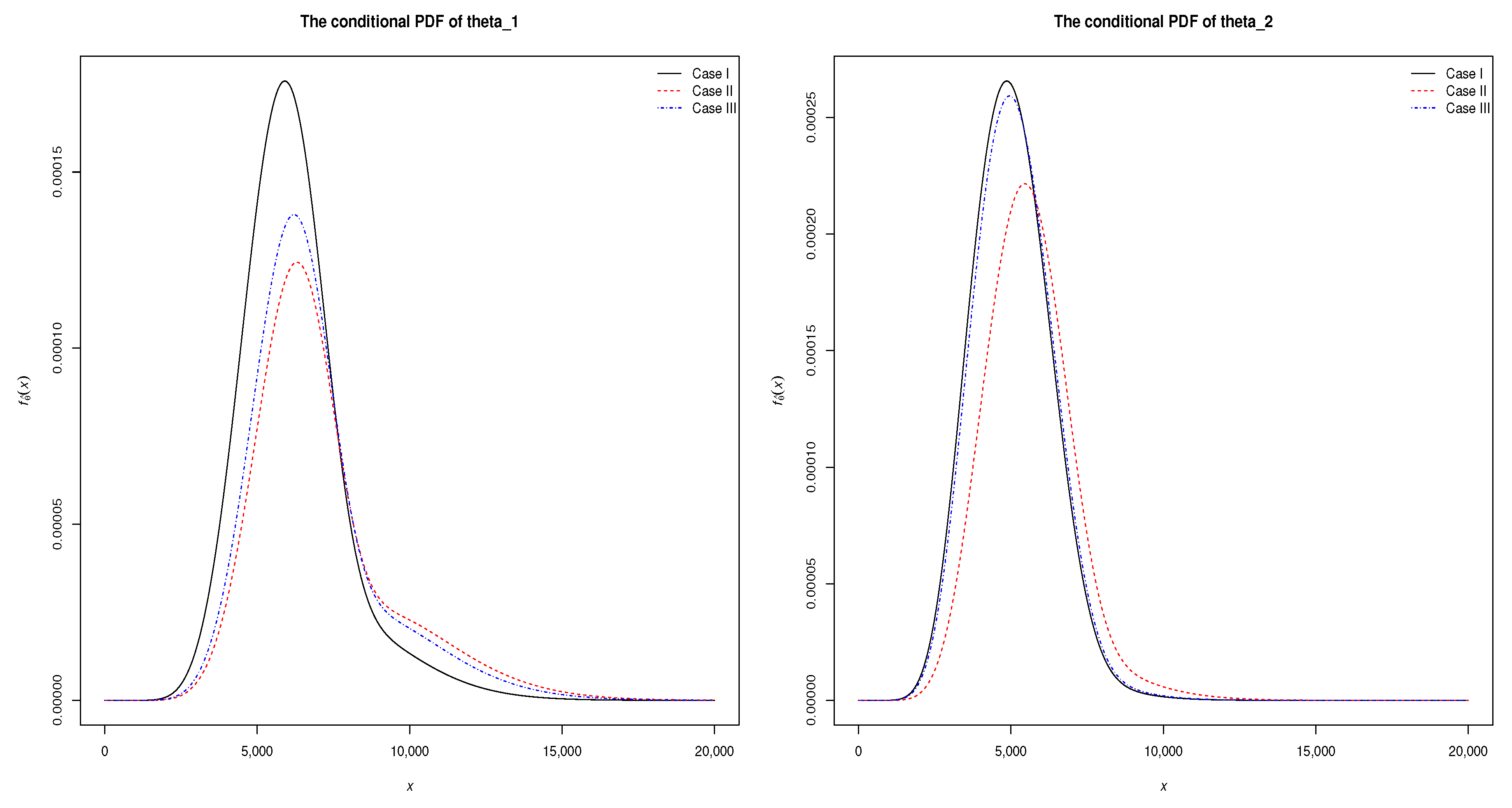
| 7000 | 8000 | 12 | 16 | 7144.417 | 2062.415 | (4057.341, 12,580.330) | 5358.312 | 1339.578 | (3282.644, 8746.460) |
| 3000 | 7000 | 12 | 16 | 8294.250 | 2394.344 | (4710.336, 14,605.030) | 6220.688 | 1555.172 | (3810.957, 10,154.130) |
| 3000 | 5000 | 11 | 16 | 7970.455 | 2403.182 | (4057.341, 14,392.450) | 5479.688 | 1369.922 | (3357.001, 8944.583) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cho, Y.; Lee, K. Exact Inference for an Exponential Parameter under Generalized Adaptive Progressive Hybrid Censored Competing Risks Data. Symmetry 2020, 12, 2005. https://doi.org/10.3390/sym12122005
Cho Y, Lee K. Exact Inference for an Exponential Parameter under Generalized Adaptive Progressive Hybrid Censored Competing Risks Data. Symmetry. 2020; 12(12):2005. https://doi.org/10.3390/sym12122005
Chicago/Turabian StyleCho, Youngseuk, and Kyeongjun Lee. 2020. "Exact Inference for an Exponential Parameter under Generalized Adaptive Progressive Hybrid Censored Competing Risks Data" Symmetry 12, no. 12: 2005. https://doi.org/10.3390/sym12122005
APA StyleCho, Y., & Lee, K. (2020). Exact Inference for an Exponential Parameter under Generalized Adaptive Progressive Hybrid Censored Competing Risks Data. Symmetry, 12(12), 2005. https://doi.org/10.3390/sym12122005





