1. Introduction
A management system is the collection of many factors in the form of values and goals, regulations, and structures, as well as method and decision-making practices. This system functions in a specific manner as a continuous and organized set of information and decision-making activities that serve to achieve the organization’s goals. The decision-making process takes place in several stages. It begins with recognizing and defining the essence of the decision situation. In the next steps, the alternative options are identified and the best one is selected. The last phase consists of putting the process into practice. Due to the complex and dynamic nature of reality, changes that occur in the process require quick reactions. This situation means that decision-making models are created that are used by a large percentage of information management systems. Models based on the multicriteria decision making (MCDM) approach play a dominant role in this area. As part of this approach, many discrete methods and their modifications were developed to take into account aspects of uncertainty (fuzzy MCDM) or group decision making (multicriteria group decision making, MCGDM). The methods provide algorithms that allow ordering and grouping of decision alternatives and indication of the preferred option. These methods have become very popular in recent years and are widely used in solving real decision-making problems [
1,
2,
3,
4,
5].
A popular and widely used method of MCDM is the technique for order preference by similarity to the ideal solution (TOPSIS) method [
6], which was proposed by Hwang and Yoon [
7]. The basic version of this method is based on the assessments provided by the decision maker in the form of precise numerical values. In the case of many complex, real decision problems solved with the participation of a group of decision makers (experts), it is important to capture the uncertainty of opinions and preferences expressed [
8]. In such situations, many of the available modifications of the TOPSIS method can be used [
6,
9] with various forms of data representation, for example fuzzy numbers (FN) [
10,
11,
12,
13], intuitionistic fuzzy sets (IFS) [
14,
15], hesitant fuzzy sets (HFS) [
16,
17], hesitant fuzzy N-soft sets [
18], dual extended hesitant fuzzy sets (DEHFS) [
19], probabilistic soft sets (PSS) [
20], ordered fuzzy numbers (OFNs) [
21,
22], and interval data [
23,
24].
The focus is on the TOPSIS method based on FN. The literature analysis showed that in fuzzy TOPSIS, two methods of aggregation of fuzzy expert opinions dominate, the first based on the technique of average value and the second one extended by the minimum and maximum functions for determining the support of the aggregated fuzzy number. An important disadvantage of both techniques is the fact that the agreement degree of expert opinions is not taken into account. The methodological contribution and the purpose of the article is to include the procedure for aggregating individual expert opinions into the fuzzy TOPSIS method, taking into account the degree of agreement of their opinions (called the similarity aggregation method, SAM) and the ranking of experts [
25,
26].
Section 2 presents a review of the literature, indicating the popularity of the fuzzy TOPSIS method in supporting real decision-making problems involving expert groups.
Section 3 describes the modified procedure for aggregating fuzzy expert assessments based on SAM and a discussion of the formal form of the fuzzy TOPSIS method algorithm. In
Section 4, the reference decision problem in the management area was solved using the fuzzy TOPSIS method using modified SAM and aggregation procedures based on the average value and min-max (minimum and maximum) support.
Section 4 also compares the results obtained using individual methods for aggregating expert opinions. The article ends with conclusions and an indication of further research directions.
2. Literature Review
In MCGDM, conflict and agreement situations occur in general. Experts express their opinions or estimates for individual alternatives under each criterion. In order to obtain a joint opinion, it is necessary to find the function of a group consensus aggregating expert estimates. Fuzzy set theory (FST) helps in quantitative problem solving based on human judgments, which are characterized by subjectivity, inaccuracy, and ambiguity in estimates. FST captures the uncertainty of opinions expressed (or imprecise estimates of physical variables) in the form of fuzzy numbers. It constitutes the foundation for the creation of fuzzy number aggregation methods and techniques, for example combining individual opinions in a group decision process. One study [
27] proposed five techniques for combining these numbers into one fuzzy number estimation, namely crisp weighting, fuzzy weighting, minimal fuzzy extension, convex fuzzy extension, and mixed linear extension. These were compared, guidelines for their selection were given, and their use was illustrated on a practical example of estimation of nitrate concentration in ground water. Hsu and Chen [
28] presented an interesting procedure for aggregating expert opinions using the consensus index and the importance (rank) of each expert. They proposed the determination of the consensus index of each expert relative to other experts using the similarity measure function. They illustrated the procedure using a simple numerical example. Wei and Chen [
29] presented a new similarity measure between generalized fuzzy numbers developed for the fuzzy risk analysis method. In order to calculate the degree of similarity, they took into account the following concepts: geometrical distance, circumference, and height. They performed an experiment using 15 sets of generalized fuzzy numbers and compared the results of the proposed method with existing measures of similarity.
The literature describes many practical examples of fuzzy number aggregation, taking into account the imprecision of estimation of physical variables or the uncertainty of opinions expressed by experts. In the work by Beskese et al. [
30], a multicriteria intuitive human resource management model was proposed. It was recognized that building an appropriate performance management system is a problem concerning many criteria and requiring the participation of experts from various fields; performance management requires verbal assessment. In the determination of the criteria weights of the model, both the aggregated and compromised assessments of the experts are used in order to observe the effects of these two methods on the results. In turn, the article by Qu et al. [
31] presents the application of the group decision-making to a practical problem of environmental management in an interesting way, concerning the assessment and selection of technology for removal of low-concentration cadmium ions from water. The study focused on effectively preventing loss of decision information and rationally gathering expert opinions. Triangular fuzzy numbers (TrFNs) with interval values were used to express expert opinions. To include fuzzy information provided by individual experts into group consensus opinion, group G1 and a Hamming-based weighted polymerization operator was used. Srinivas and Singh [
32] proposed a new approach to capture the uncertainty associated with making group decisions by using fuzzy sets with valuable ranges in the Delphi method. As part of the study on the impact of wastewater on the Ganges river basin in India, industry ratings from experts were analyzed and aggregated using a fuzzy approach. Lanzotti et al. [
33] explored the assessment of different design candidates by means of product experts acting as assessors or customers enrolled as testers. They discussed the candidate identification using virtual and physical prototypes and a practical fuzzy approach toward the evaluation of the optimal design. Experts expressed their opinion by choosing finer or coarser linguistic scales as well as the related shapes of fuzzy sets to adequately represent the level of fuzziness of their judgments. Santos-Buitrago et al. [
34] used soft set theory for decision making in computational biology. In particular, they adopted the mathematical methods to capture imprecision, vagueness, and uncertainty in the available data. In turn, Alcantud et al. [
35] designed a procedure to predict patient survival in lung cancer resections from soft set and fuzzy set theory perspectives. Other interesting examples of the use of MCGDM and methods that use expert opinions and fuzzy sets can be found in the literature [
36,
37,
38].
In accordance with the subject of the fuzzy TOPSIS method, it is interesting to review the modifications (extensions) and applications of this method in terms of aggregation of fuzzy expert assessments. The literature analysis showed that in fuzzy TOPSIS, two methods of aggregation of fuzzy expert opinions dominate, the first based on the technique of average value and the second one extended by the minimum and maximum functions to determine the beginning and the end of the aggregate fuzzy number, respectively.
In 1997, Chen [
10] proposed an extension of the TOPSIS method towards group decision-making, taking into account fuzzy numbers. The assessment of each
i-th alternative (
i = 1, 2, …,
m) and weight of each
j-th criterion (
j = 1, 2, …,
n) by the
k-th expert (
k = 1, 2, …,
K) were described using seven linguistic values, which were expressed using TrFNs, assessment
, and weight
. For the group of experts consisting of
K persons, the aggregate of criteria validity and the aggregate of alternative assessments for each criterion were the average values of fuzzy numbers, and were calculated according to Equations (1) and (2):
where
,
and
.
where
,
and
.
Aggregation of expert assessments on criteria in accordance with Equation (1) was also used in [
39,
40,
41], where as part of creating hybrid approaches, the fuzzy TOPSIS method was combined with the Fuzzy AHP method. Examples of other fuzzy TOPSIS implementations using the technique of average value Shown in Equations (1) and (2) with TrFNs or trapezoidal fuzzy numbers (TFNs) were published in [
42,
43,
44].
Another way to aggregate expert assessments and criteria weights expressed using TFNs, evaluation
, and weight
was presented by Chen et al. [
11]. Aggregated fuzzy assessment (
) alternatives for each criterion were calculated according to Equation (3):
where
,
,
, and
.
Aggregated fuzzy weights (
) of each criterion were calculated in the same way according to Equation (4):
where
,
,
, and
.
Aggregation of expert assessments and weights for the criteria in accordance with Equations (3) and (4) was also used in extending the fuzzy TOPSIS method with fuzzy similarities [
45].
The technique of average value provides narrow fuzzy numbers (narrow fuzzy support) in relations to the second technique (min-max support), in which the width of the fuzzy number support depends on the minimum and maximum value determining the position of the extreme vertices. These vertices are, respectively, the beginnings and ends of the bases of trapeziums or triangles representing aggregated fuzzy numbers. Fuzzy numbers with a broader support are more imprecise. In addition, in the case of the min-max support technique, if two experts have similar views and the third one clearly stands out, then the third expert’s judgement significantly affects the aggregation results of fuzzy assessments. The opinion that does not conform will make the obtained aggregate more imprecise (
Figure 1b). For both techniques, the nucleus of the aggregate fuzzy number (upper edge of the trapezoid;
Figure 1a,b) will always be the same. The approaches cited do not take into account the importance of expert judgements. An important disadvantage of both techniques is the fact that the agreement degree of expert opinions is not taken into account (expert consensus).
3. Modified Aggregation of Expert Assessments in the Fuzzy TOPSIS Method
3.1. Aggregation of Fuzzy Assessments Taking into Account the Area of Similarities and Weights of Experts
Hsu and Chen [
28] proposed the similarity aggregation method (SAM), which combines TFNs
expressing views of individual experts
(
k = 1, 2, …,
K) in the form of one fuzzy number representing the joint opinion of these experts (
Figure 2).
The measure of consensus of opinion between each pair of experts
is the agreement degree in Equation (5), in [
25,
26] referred to as the similarity measure function. The SAM authors assume that if the opinions of experts do not have a common area, then it is necessary to use the Delphi method [
46,
47]. The purpose of this method is to reach a consensus through a repeated survey process. It follows that each pair of trapezoidal expert assessments must have a common intersection at a certain cutting level,
(
Figure 3).
In the case of combining SAM with the fuzzy TOPSIS method, the authors of the article departed from this assumption. The possibility of noncompliance of assessments between some pairs or all pairs of decision makers was allowed. The full form of the SAM procedure, including the modifications made, consisted of 8 steps.
Step 1: Each expert
(
k = 1, 2, …,
K) constructs a positive TFN
, according to the most likely range
and the largest range
, where
(
Figure 2), in order to represent a subjective estimate of the assessment value for a given criterion and alternative.
Step 2: We calculate the degree of compliance
for the opinions between each pair of experts, where
for
(
k = 1, 2, …,
K and
l = 1, 2, …,
K). This can be determined as the ratio of the surface area of the compatible area
for the entire area
according to the following rule:
where
Step 3: We build the agreement matrix
:
where
, and if
then
.
Step 4: We calculate the average degree of agreement
for the expert
(
k = 1, 2, …,
K):
Step 5: We determine the degrees of importance
for the expert
(
k = 1, 2, …,
K) and convert the obtained vector
to the vector of the
scale, where
Step 6: We calculate the relative agreement degree (RAD) for the expert
according to the rule:
Step 7: We calculate the consensus degree coefficients
for the expert
(
k = 1, 2, …,
K) and convert the resulting vector into a scale vector
Step 8: We aggregate fuzzy assessments using the consensus degree coefficient
for the expert
(
k = 1, 2, …,
K)
In order to ensure the feasibility of SAM calculations, rules were introduced in Equations (5) and (11) that eliminated the division by zero operations. As a result of the modification in Equation (5) for the expert , who did not reach a consensus with the other expert , the average agreement degree will amount to zero, . This value affects the calculation in Equation (9) of the average agreement degree , which in turn determines Equation (11), the relative agreement degree for the expert . The consensus degree coefficient of the expert (12) is the sum of its rank and relative compatibility with other experts, . The proportion of both measures is determined by the factor ; when , the degree of expert consensus equals its relative agreement (, otherwise for , it depends only on its rank (.
If there is a disagreement between all pairs of decision makers, when all trapezoidal expert assessments do not have common areas, the sum of the average degrees of compliance for all experts will be zero ). Equation (11) provides for such a situation, assigning the relative agreement degree of an expert with the value of his rank ). As a result, Equation (12) is reduced to the form (the coefficient does not matter), and the aggregate fuzzy rating in Equation (13) including all (noncompliant) experts depends only on their importance ranking (Equation (10)), which is adopted in decision-making proceedings.
3.2. Fuzzy TOPSIS Method
The fuzzy TOPSIS method [
11] considers a decision-making problem involving a set of
m decision alternatives and
n criteria. Initially, weights of criteria and evaluation of alternatives were obtained. Because fuzzy TOPSIS belongs to the MCGDM methods, these values are acquired from
K experts. The weights of criteria and assessment of alternatives are expressed in the form of trapezoidal fuzzy numbers (TFNs), where
represents the assessment of the
i-th alternative for the
j-th criterion expressed by the
k-th expert, and
means the weight of the
j-th criterion expressed by the
k-th expert. Assessments and weights are defined using 7-degree fuzzy linguistic scales. The scales used here are shown in
Figure 4.
Both weights and expert assessments are aggregated into TFNs as
and
, respectively. In the presented modification of fuzzy TOPSIS, the procedure discussed in
Section 3.1 was used for aggregation.
Based on aggregated assessments of alternatives, a fuzzy decision matrix (FDM) (14) and a weight vector (15) are constructed:
Because the criteria are divided into benefit criteria and cost criteria, they must be standardized according to Equation (16) for benefit criteria and Equation (17) for cost criteria:
In the next step, a normalized fuzzy decision matrix (NFDM) is built (18):
After taking into account the weight of the criteria, the weighted normalized fuzzy decision matrix (WNFDM) is obtained, the elements of which are calculated according to Equation (19):
Based on WNFDM, the following are determined: the fuzzy positive-ideal solution (FPIS) (Equation (20) and fuzzy negative-ideal solution (FNIS) (Equation (21).
The distances of the
i-th alternative from FPIS (
) and FNIS (
) are determined according to Equations (22) and (23), respectively:
where
is a crisp measure of the distance between two TFNs, determined using Equation (24):
The overall assessment of the
i-th alternative is expressed by the closeness coefficient, which represents the distances to the FPIS and FNIS in accordance with Equation (25):
5. Conclusions
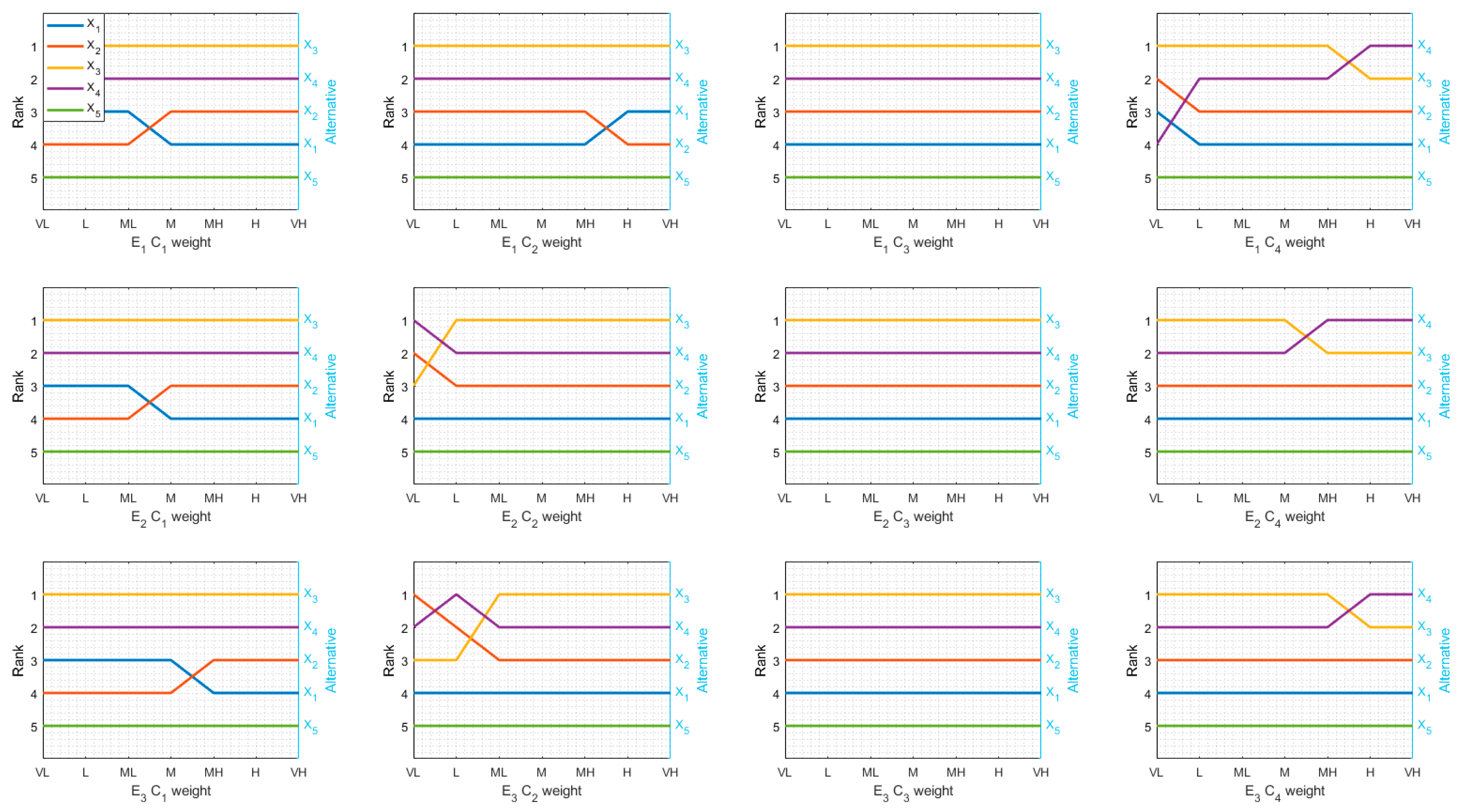
The results presented in the article indicate that the extension of the fuzzy TOPSIS method by a modified SAM procedure may give better results than the fuzzy TOPSIS method implementing aggregation using average value or min-max functions. Fuzzy TOPSIS with SAM aggregation allows a ranking to be obtained that is less susceptible to significant changes in the order of alternatives than the other considered variants of fuzzy TOPSIS. Meanwhile, too much susceptibility to significant changes in the order of alternatives may cause a lack of confidence of decision makers in the method and the resulting ranking. On the other hand, the ranking based on SAM is less stable than the ranking based on average value aggregation. However, it should be noted that lower ranking stability is also related to higher sensitivity of the decision model to changing preferences. Too little sensitivity to changes in the weight of criteria, especially if the criteria are not very differentiated, means that in practice the decision maker’s preferences do not affect the obtained order of alternatives. A single experiment does not provide the answer regarding the sensitivity of the ranking to changes in criteria weights and susceptibility to significant changes in the order of alternatives. These features can only be determined by a sensitivity analysis.
An important element of the developed modification of the SAM expert opinion aggregation procedure is the factor , determining the strength of the impact of the expert opinion consensus on aggregation results. It should be noted that if and the ranks of experts are equal, then the aggregation results using SAM are the same as using average value aggregation. As a result, rankings of alternatives are also identical. In turn, when SAM mitigates the impact of outlier opinions on the aggregation result and the ranking of alternatives. In general, the smaller the value , the smaller the fuzzy average value impact, and thus of the outlier opinions, on the result of aggregation and obtained rankings. The value adopted in this study is a compromise between the impacts of outliers and unanimous opinions. On the other hand, if all opinions are relatively consistent (no strong outliers), aggregation results using SAM and average value method are very similar.
Summing up the conducted research, it should be noted that the methodological and practical contributions of the article include:
Developing a modification of the SAM, allowing aggregation of expert opinions without the need for a consensus between them;
Incorporating the developed SAM modification into the MCGDM fuzzy TOPSIS method and a broad comparison of SAM aggregation with other aggregation procedures usually used in the fuzzy TOPSIS method;
Conducting a sensitivity analysis of the obtained solutions.
As a result, a modified fuzzy TOPSIS method was developed, which is applicable to all decision-making problems in which it is important to be able to determine the impact of an expert group consensus on the results. Further research should focus on the implementation of modified SAM aggregation in other MCGDM methods. It would also be interesting to incorporate the NEAT F-PROMETHEE (New Easy Approach To Fuzzy Preference Ranking Organization METHod for Enrichment Evaluation) method [
4,
8] into the MCGDM form based on the modified SAM procedure.